Genome and Environment Based Prediction Models and Methods of Complex Traits Incorporating Genotype × Environment Interaction

Abstract

Genomic-enabled prediction models are of paramount importance for the successful implementation of genomic selection (GS) based on breeding values. As opposed to animal breeding, plant breeding includes extensive multienvironment and multiyear field trial data. Hence, genomic-enabled prediction models should include genotype × environment (G × E) interaction, which most of the time increases the prediction performance when the response of lines are different from environment to environment. In this chapter, we describe a historical timeline since 2012 related to advances of the GS models that take into account G × E interaction. We describe theoretical and practical aspects of those GS models, including the gains in prediction performance when including G × E structures for both complex continuous and categorical scale traits. Then, we detailed and explained the main G × E genomic prediction models for complex traits measured in continuous and noncontinuous (categorical) scale. Related to G × E interaction models this review also examine the analyses of the information generated with high-throughput phenotype data (phenomic) and the joint analyses of multitrait and multienvironment field trial data that is also employed in the general assessment of multitrait G × E interaction. The inclusion of nongenomic data in increasing the accuracy and biological reliability of the G × E approach is also outlined. We show the recent advances in large-scale envirotyping (enviromics), and how the use of mechanistic computational modeling can derive the crop growth and development aspects useful for predicting phenotypes and explaining G × E.

Key words

1 Introduction

Selection in plant breeding is usually based on estimates of breeding values, which can be obtained with pedigree-based mixed models [1, 2]. In their multivariate formulation, these models can also accommodate G × E interaction [3, 4]. In the past, pedigree-based models have been successful for predicting breeding values of complex traits in plant and animal breeding by modeling the genetic covariance between any pair of related individuals (j and j′), due to their additive genetic effects, as being equal to two times the coefficient of parentage (2f_jj′ =A) times the additive genetic variance, ${\sigma}_a^2$($\boldsymbol{A}{\sigma}_a^2$). In self-pollinated species, $\boldsymbol{A}{\sigma}_a^2$ is the variance–covariance matrix of the breeding values (additive genetic effects). Closely related individuals contribute more to the prediction of breeding values of their relatives than less closely related genotypes. Moreover, when data from one individual or one selection candidate are missing (either partially or totally), its breeding value can still be predicted from its relatives, albeit less efficiently than if the data were complete.

Pedigree-based models cannot account for Mendelian segregation—a term that, under an infinitesimal additive model [5, 6] and in the absence of inbreeding, explains one half of the genetic variation [7, 8]. However, molecular markers allow tracing Mendelian segregation at several positions of the genome, which gives them enormous potential in terms of increasing the accuracy of estimates of breeding and genetic values and the genetic progress attainable when these predictions are used for selection purposes [9].

GS [10] and genomic prediction of complex traits predict breeding values that comprise the parental average (half the sum of the breeding values of both parents) plus a deviation due to Mendelian sampling. In annual crops GS has been applied mainly in two different contexts; one approach focuses on predicting additive effects in early generations of a breeding program such that a rapid selection cycle with a short interval cycle (i.e., GS at the F₂ level of a biparental cross) is achieved. Another approach consists of predicting the genotypic values of individuals where both additive and nonadditive effects determine the final commercial (genetic) value of the lines; here predicting lines established in multienvironment field evaluation is required.

Various models for analyzing variation arising from quantitative trait loci (QTL) and marker-assisted selection, as well as for identifying molecular markers closely linked to QTL have been widely used in plant breeding to improve a few traits controlled by major genes. However, adoption of these models has been limited because the biparental populations used for mapping QTL are not easily used in breeding applications and because only limited marker information (a few markers) is used. On the other hand, GS is an approach for improving quantitative complex traits that uses all available molecular markers across the genome to estimate breeding values for specific environments and across environments by adopting conventional single-environment or G × E interaction analyses [11,12,13].

Early plant and animal breeding data have shown that GS [10, 14, 15] significantly increases the prediction accuracy of pedigree based selection for complex traits [13, 16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Reviews on optimizing genomic-enabled prediction and application to annual and perennial plants were early published elsewhere [22, 32,33,34,35]. Since then, crop breeding programs worldwide have been studying and applying GS and, simultaneously, extensive research have been conducted on new statistical models for incorporating pedigree, genomic, and environmental covariates such as soil characteristics or weather data, among others.

Genomic models for incorporating G × E interaction have been proposed in an attempt to improve accuracy when predicting the breeding values of complex traits (e.g., grain yield) of individuals in different environments (site–year combinations) [11, 23, 36]. However, different statistical models are required for assessing the genomic-enabled prediction accuracy of noncontinuous categorical response variables (ordinal diseases as rates, counting data, etc.) using conventional genomic best linear unbiased predictors (GBLUP ). Furthermore, deep learning artificial neural networks (DL) are also being developed for assessing multitrait, multienvironment genomic-enabled prediction [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53].

Since the beginning of GS , several genetic and statistical factors had been pointed out as complications for the application of GS and genomic prediction. Genetic difficulty arises when deciding the size of the training population and the heritability of the traits to be predicted. Statistical challenges are related to the number of markers (p) being much larger than the number of observations (n) (p ≫ n), the multicollinearity among markers and the curse of dimensionality. One important genetic-statistical complexity of GS models arises when predicting unphenotyped individuals in specific environments (e.g., planting date–site–management combinations) by incorporating G × E interaction into the genomic-based statistical models. Moreover, the genomic complexity related to G × E interactions for multitraits is important because these interactions require statistical-genetic models that exploit the complex multivariate relations due to multitrait and multienvironment variance–covariance, and the genetic correlations between environments, between traits and between traits and environments. The abovementioned problem of p ≫ n results in a matrix of predictors that are rank-deficient and without having a likelihood identified, thus being prone to overfitting. Penalized regression, variable selection, and dimensionality reduction offer solutions to some of these problems.

Genomic-enabled prediction models are based on quantitative genetics theory, which considers two main structures of variation, one for the sum of genetic values (e.g., linear additive models), and a second for nongenetic residual noise [19]. Hence, most of the research on genomic prediction has been developing efficient parametric and nonparametric statistical and computational models to deal with those two main structures of variation, and many research articles show good prediction accuracy for complex traits such as grain yield. The use of relationship matrices based on genomics has also been expanded by developing and using linear and nonlinear kernels. Nonlinear genomic kernels have the ability to account for cryptic small effect interactions between markers (e.g., epistasis). Furthermore, these kernels are more efficient than GBLUP in incorporating large-scale environmental data (enviromics) and G × E realized by enviromics-aided relatedness among field trials [45,46,47,48,49,50,51,52,53,54].

In this chapter, we explain and review the complexity of genomic-enabled prediction and describe models for assessing different forms of G × E interaction and marker × environment interaction. We also describe GS models for categorical and counting traits that are not continuous and do not have a normal distribution. As intimately related with studding G × E interaction we briefly summarize the latest results of the use of methods that include Bayesian multitrait multienvironments as well as deep learning (DL) of artificial neural networks, and ecophysiology-enriched approaches such as the use of crop growth models and enviromics. Furthermore, we extend the study of G × E interaction when high throughput phenotype data are available.

2 Historical Timeline of G × E Modeling in Genomic Prediction

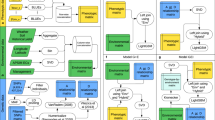
Since the study of Meuwissen et al. [10] researchers have been devoted to the use of whole-genome markers to adjust statistical and computation tools to predict particular phenotypes. Figure 1 presents a short timeline of the type of statistical and computational regressions and kernel methods used in GS research in the context of G × E. This timeline starts with two genomic G × E interaction models, the first is related to environment-specific genomic prediction effects [11] and the second to specific marker effects across environments [12]. At this point, the model of Burgueño et al. [11] takes into account pedigree and molecular marker information, and in the following eight years it was updated along with that of Schulz-Streeck et al. [12] with different statistical and computational processing methods. All models based on this source of data were highlighted as blue in Fig. 1. Green color in Fig. 1, highlighted aspects introduced by Heslot et al. [23] involving the use of environmental covariates (EC) over the marker effects. Models in green introduced the use of crop growth models (CGM). Briefly, the CGM is a mechanistic approach aimed to reproduce the main plant-environment relations through “crop-specific” parameters and environmental inputs. After running CGM, it is possible to derive EC that represent the plant-environment interactions, instead of the direct use of climatic information. It also includes research involving the direct use of CGM with genomic prediction models , which was a concept introduced by Cooper et al. [55] as CGM-whole genomic prediction. This approach uses the marker effects to predict intermediate phenotypes over the mechanistic structure of a certain CGM. Then, the tuned CGM is used for phenotype prediction.

Fig. 1

History of the main research involving genomic prediction and G × E interaction since the first published paper in 2012 until the articles published in 2020. A blue box denotes works using only DNA markers or genomic information. A green box refers to models in which DNA marker is complemented by crop growth modeling (CGM) outputs, such as stress index. A purple box refers to models in which DNA markers are complemented by the use of environmental covariates (EC), such as weather and soil information for the experimental trials

Lastly, purple-colored model in Fig. 1, involve the use of environmental data to fit reaction-norm structures (e.g., linear relation between phenotype and environmental variations). Since Jarquín et al. [36] there is a second interpretation of the so-called reaction-norm approach, which involves the use of environmental relatedness realized from EC together with genomic kinships under whole-genome regressions or kernel methods. Recently, Resende et al. [56] and Costa-Neto et al. [54] introduced the concept of ‘enviromics’ to describe the core of possible environmental factors acting over a target population of environments (TPE). It is expected that this type of approach will popularize the use of environment data in training prediction models for selection, which is especially useful for screening genotypes at novel growing conditions. Differently from the models in green color, here the philosophy ranges from using a large-scale environmental information [36, 45, 54, 56,57,58] to a very small number of ECs [26, 43, 44, 59, 60]. In the first case, the purpose is to shape a robust environmental relatedness, whereas the second relies in a two-stage analysis (e.g., factorial regression), where are found a few key ECs that explains a large amount of the trait G × E for that germplasm and experimental network. Each model structure and concept is described in the next sections.

Below, we discuss the basic genomic model used to reproduce particular gene–phenotype variations using phenotypic data from single trials. Thus, it is expected that these kind of models could capture specific environmental–phenotype covariances, related to the particular growing conditions faced by each genotype in the same field. Because of that, this type of model is named single-environment model. Then, we describe how single-environment models are fitted in terms of resemblance among relatives, captured by genomic or pedigree realized relationship kernels. Thus, in this section we will present novel options to model G × E interactions among several field trials (multienvironment trials). Furthermore, we will show Bayesian models for ordinal or count data, and finally describe models using climatic environmental data.

3 Genomic-Enabled Prediction Models Accounting for G × E

3.1 Basic Single-Environment Genomic Model

To explain how the multienvironment GS approach were developed, it is indispensable to first understand how the baseline single-environment genomic model was conceived. The basic genetic model describes the response of the jth phenotype (y_j) as the sum of an intercept (μ), a genetic value (g_j) plus a residual ε_j: y_j = μ + g_j + ε_j (j = 1, …, n individuals). Thus, this model takes into account a certain genetic-informed structure within the g_j effect, and considers that all nongenetic sources are split in a fixed main intercept plus the error variation. As the genes affecting a trait in a certain environment where the phenotyping was conducted are unknown, a complex function must be approximated by a regression of phenotype on marker genotypes with large numbers of markers {x_j1, …, x_jk, …, x_jp} (k = 1, …, p markers) to predict the genetic value of the jth individual. This function can be expressed as f(x) = f(x_j1, …, x_jp; β) such that y_j = μ + f(x_j1, …, x_jp; β) + ε_j.

Usually f(x; β) is a parametric linear regression of the form$f\left({x}_{j1},\dots, {x}_{jp};\boldsymbol{\beta} \right)=\sum \limits_{k=1}^p{x}_{jk}{\beta}_k$, where β_k is the substitution effect of the allele coded as ‘one’ at the kth marker. Then, the linear regression function on markers becomes${y}_j=\mu +\sum \limits_{k=1}^p{x}_{jk}{\beta}_k+{\varepsilon}_j$, or, in matrix notation,

$$ \boldsymbol{y}={\mathbf{1}}_n\mu +\boldsymbol{X}\boldsymbol{\beta } +\boldsymbol{\varepsilon}, $$

(1)

where 1_n is a vector of order n × 1, X is the n × p matrix of centered and standardized markers, β is the vector of unknown marker effects, and ε is an n × 1 vector of random errors, with $\boldsymbol{\varepsilon} \sim N\left(\mathbf{0},{\boldsymbol{I}}_n{\sigma}_{\varepsilon}^2\right),$ where ${\sigma}_{\varepsilon}^2$ is the random error variance component. When the vector of marker effects is assumed $\boldsymbol{\beta} \sim N\left(\mathbf{0},{\boldsymbol{I}}_p{\sigma}_{\beta}^2\right)$, where ${\sigma}_{\beta}^2$is the variance of marker effects, this is called the ridge regression best linear unbiased predictor (rrBLUP).

3.1.1 Kernel Methods to Reproduce Genomic Relatedness Among Individuals

From the last subsection, we can go deeper into the modeling of g effects using relatedness kernels. By letting g = Xβ with a variance–covariance matrix proportional to the genomic relationship matrix $\boldsymbol{G}=\boldsymbol{X}{\boldsymbol{X}}^{\prime }/\sum \limits_{k=1}^p2{q}_k\left(1-{q}_k\right)$(where q_k is the frequency of allele “1”) with $\boldsymbol{g}\sim N\left(\mathbf{0},\boldsymbol{G}{\sigma}_g^2\right)$, one can define the GBLUP prediction model as: [61, 62].

$$ \boldsymbol{y}={\mathbf{1}}_n\mu +\boldsymbol{g}+\boldsymbol{\varepsilon} . $$

(2)

GBLUP and rrBLUP are equivalent if the genomic relationship matrix is computed accordingly. Model 2 is computationally much simpler than the rrBLUP, which makes the kernel methods interesting for dealing with complex models involving G × E interactions.

It should be noted that different kinds of kernel can be used for G, potentially taking any structure capable of reproducing a certain degree of relatedness among individuals, such as nonlinear effects into account. One of the most used nonlinear kernels is the so-called Gaussian Kernel (GK). Results have consistently shown for single-environment models as well as for multienvironment models with G × E interaction, that GK performs better than GBLUP in terms of genomic-enabled prediction accuracy [39,40,41, 45, 63].

A second nonlinear approach that has been used is deep kernel (DK), which is implemented by the arc-cosine kernel (AK) function recently introduced by Cuevas et al. [41] in genomic prediction. This nonlinear DK is defined by a covariance matrix that emulates a deep learning model, but based on one hidden layer and a large number of neurons. To implement it, a recursive formula is used for altering the covariance matrix in a stepwise process, in which at each step, more hidden layers are added to the emulated deep neural network. In this function, the tuning parameter “number of layers” required for DK can be determined by a maximum marginal likelihood procedure [41].

Research involving near-infrared data [41], multiple G × E scenarios for several data sets [64] and modeling additive and nonadditive genomic-by-enviromic sources [54] have shown that DK genomic-enabled prediction accuracy is similar to that of the GK, but DK has the advantage over GK because (a) it is computationally more straightforward, since no bandwidth parameter is required, while performing similarly or slightly better than GK; (b) it is a data-driven kernel capable of linking genomic or enviromic kernels with empirical phenotypic covariance structures [41, 54, 64]. To implement DK in an R computational environment, Cuevas et al. [41] and Costa-Neto et al. [54] have provided codes and examples that are freely available. After the creation of DK for each genomic or enviromic source, this kernel can be incorporated in diverse packages to implement genomic prediction, such as BGLR [65] and BGGE [66].

3.2 Basic Marker × Environment Interaction Models

Multienvironment trials for assessing G × E interactions play an important role for selecting high performing and stable breeding lines across environments, or breeding lines adapted to local environmental constraints. A first way of modeling G × E is to allow environment-specific marker effect [12], or to model environment-specific genetic effects as proposed by Burgueño et al. [11]

A kernel model can be derived to allow environment-specific genetic effects as in model 2

$$ \boldsymbol{y}=\boldsymbol{\mu} +\boldsymbol{g}+\boldsymbol{\varepsilon}, $$

(3)

where $\boldsymbol{y}=\left[\begin{array}{c}\begin{array}{c}{\boldsymbol{y}}_1\\ {}\vdots \\ {}{\boldsymbol{y}}_i\end{array}\\ {}\vdots \\ {}{\boldsymbol{y}}_m\end{array}\right]$; $\boldsymbol{\mu} =\left[\begin{array}{c}\begin{array}{c}{\mathbf{1}}_{n_1}{\mu}_1\\ {}\mathbf{\vdots}\\ {}{\mathbf{1}}_{n_i}{\mu}_i\end{array}\\ {}\mathbf{\vdots}\\ {}{\mathbf{1}}_{n_m}{\mu}_m\end{array}\right];$ $\boldsymbol{g}=\left[\begin{array}{c}\begin{array}{c}{\boldsymbol{g}}_1\\ {}\mathbf{\vdots}\\ {}{\boldsymbol{g}}_i\end{array}\\ {}\mathbf{\vdots}\\ {}{\boldsymbol{g}}_m\end{array}\right];$ $\boldsymbol{\varepsilon} =\left[\begin{array}{c}\begin{array}{c}{\boldsymbol{\varepsilon}}_1\\ {}\mathbf{\vdots}\\ {}{\boldsymbol{\varepsilon}}_i\end{array}\\ {}\mathbf{\vdots}\\ {}{\boldsymbol{\varepsilon}}_m\end{array}\right]$, are vectors with elements corresponding to each of the environments, which are equivalent to Z_E μ_m, where Z_E is an incidence matrix for the environments and μ_m is a vector of order m, that represents one mean for each environment. When there are many environments, it is recommended to consider vector μ as random effect, such that $\boldsymbol{\mu} \sim \boldsymbol{N}\left(\mathbf{0},{\boldsymbol{Z}}_{\boldsymbol{E}}{\boldsymbol{Z}}_{\boldsymbol{E}}^{\prime }{\sigma}_e^2\right)$. Other fixed effects can also be included in the model. The random effects are the genetic effects g ~N(0, K₀) and the residuals ε~N(0, R). When the number of observations is the same in all the environments, then K₀ = U_E ⊗ K, and R = Σ ⊗ I, where ⊗ denotes the Kronecker product and K is a kernel matrix of relationships between the genotypes. Matrix K₀ is the product of one matrix with information between environments (U_E) and one kernel with information between individuals based on markers or pedigrees (K). The unstructured variance–covariance can be used for U_E,of order m × m such that:

$$ {\boldsymbol{U}}_E=\left[\ \begin{array}{ccc}{\sigma}_{g_1}^2& \dots & {\sigma}_{g_1{g}_i}\kern0.5em \dots \kern0.5em {\sigma}_{g_1{g}_m}\ \\ {}\vdots & \ddots & \vdots \kern0.5em \ddots \kern2.00em \vdots \\ {}\begin{array}{c}{\sigma}_{g_i{g}_1}\\ {}\vdots \\ {}{\sigma}_{g_m{g}_1}\end{array}& \begin{array}{c}\dots \\ {}\ddots \\ {}\dots \end{array}& \begin{array}{ccc}\begin{array}{c}{\sigma}_{g_i}^2\\ {}\vdots \\ {}{\sigma}_{g_m{g}_i}\end{array}& \begin{array}{c}\dots \\ {}\ddots \\ {}\dots \end{array}& \begin{array}{c}\ {\sigma}_{g_i{g}_m}\ \\ {}\vdots \\ {}{\sigma}_{g_m}^2\end{array}\end{array}\end{array}\right], $$

where the ith diagonal element is the genetic variance ${\sigma}_{g_i}^2$ within the ith environment, and the off-diagonal element is the genetic covariance ${\sigma}_{g_i{g}_{i\prime }}$ between the ith and i′th environments. Model 3 can be used with a linear kernel GBLUP , [11] Gaussian kernel [40] or deep kernel [67], which allows capturing small cryptic effects, such as epistasis.

To account for variations between individuals that was not captured by g., a random component f, representing the genetic variability among individuals across environments, can added to model 3 as:

$$ \boldsymbol{y}=\boldsymbol{\mu} +\boldsymbol{g}+\boldsymbol{f}+\boldsymbol{\varepsilon}, $$

(4)

where $\boldsymbol{f}=\left[\begin{array}{c}\begin{array}{c}{\boldsymbol{f}}_1\\ {}\boldsymbol{\vdots}\\ {}{\boldsymbol{f}}_i\end{array}\\ {}\boldsymbol{\vdots}\\ {}{\boldsymbol{f}}_m\end{array}\right]$ with the random vectors f independent of g and normally distributed f ~ N(0, Q). In general, when the number of individuals is not the same in all environments,

$$ \boldsymbol{Q}=\left[\ \begin{array}{ccc}{\sigma}_{f_1}^2{\boldsymbol{I}}_{n_1}& \dots & {\sigma}_{f_1{f}_i}{\boldsymbol{I}}_{n_1}\kern0.5em \dots \kern0.5em {\sigma}_{f_1{f}_m}{\boldsymbol{I}}_{n_1}\ \\ {}\vdots & \ddots & \begin{array}{ccc}\vdots & \ddots & \kern1.5em \vdots \end{array}\\ {}\begin{array}{c}{\sigma}_{f_i{f}_1}{\boldsymbol{I}}_{n_i}\\ {}\vdots \\ {}{\sigma}_{f_m{f}_1}{\boldsymbol{I}}_{n_m}\end{array}& \begin{array}{c}\dots \\ {}\ddots \\ {}\dots \end{array}& \begin{array}{ccc}\begin{array}{c}{\sigma}_{f_i}^2{\boldsymbol{I}}_{n_i}\\ {}\vdots \\ {}{\sigma}_{f_m{f}_i}{\boldsymbol{I}}_{n_m}\end{array}& \begin{array}{c}\dots \\ {}\ddots \\ {}\dots \end{array}& \begin{array}{c}\ {\sigma}_{f_i{f}_m}{\boldsymbol{I}}_{n_i}\ \\ {}\vdots \\ {}{\sigma}_{f_m}^2{\boldsymbol{I}}_{n_m}\end{array}\end{array}\end{array}\right] $$

where ${\sigma}_{f_i}^2$ is the genetic effects in the ith environment not explained by the random genetic effect g, and ${\sigma}_{f_i{f}_{i^{\prime }}}$ is the covariance of the genetic effects between two environments not explained by g. When the number of individuals is the same in all the environments, Q = F_E ⊗ I. The matrix F_E captures genetic variance–covariance effects between the individuals across environments that were not captured by the U_E matrix.

3.3 Basic Genomic × Environment Interaction Models

Before introducing the reaction-norm model, we will first consider the model 5, in which the response of the jth line in the ith environment (y_ij) is modeled by main random effects that account for the environment, (E_i), the genotypes (L_j), the genetic values (g_i) of the lines, a component assumed to be stable across environments, plus the random effects of the interaction (Eg_ij) between the ith environment (E_i) and the jth line (g_j), representing deviations from the main effects:

$$ {y}_{ij}=\mu +{E}_i+{L}_j+{g}_j+{Eg}_{ij}+{\varepsilon}_{ij}, $$

(5)

where μ is an intercept, ${E}_i\overset{iid}{\sim }N\left(0,{\sigma}_E^2\right)$ is the random effect of the ith environment, ${L}_j\overset{iid}{\sim }N\left(0,{\sigma}_L^2\right)$ is the random effect of the jth genotype, and ${\varepsilon}_{ij}\overset{iid}{\sim }N\left(0,{\sigma}_{\varepsilon}^2\right)$ is a model residual. Here N(∙, ∙) stands for a normally distributed random variable and iid stands for independent and identically distributed.

The vector of random effects g = (g₁, …, g_J)^′, $\boldsymbol{g}\sim N\left(\mathbf{0},\left({\boldsymbol{Z}}_g\boldsymbol{K}{\boldsymbol{Z}}_g^{\prime}\right){\sigma}_g^2\right)$, with Z_g being the incidence matrix for the effects of the genetic values of the genotypes and ${\sigma}_g^2$ is the variance component of g; K is a kernel or matrix of genetic relationships between the genotypes as in GBLUP (G) [36]. The vector $\boldsymbol{Eg}\sim N\left(\mathbf{0},\left({\boldsymbol{Z}}_g\boldsymbol{K}{\boldsymbol{Z}}_g^{\prime}\right)\#\left({\boldsymbol{Z}}_E{\boldsymbol{Z}}_E^{\prime}\right){\sigma}_{Eg}^2\right)$ denotes the interaction between the genotypes and the environments, where Z_E is the incidence matrix for environments and ${\sigma}_{Eg}^2$ is the variance component of Eg with # denoting the Hadamard cell-by-cell product. Note that $\boldsymbol{g}\sim N\left(\mathbf{0},\boldsymbol{K}{\sigma}_g^2\right)$ are correlated, such that model 5 allows borrowing information between the genotypes. Hence, prediction of genotype performance in environments where the genotypes were not observed is possible.

3.4 Illustrative Examples When Fitting Models 2–5 with Linear and Nonlinear Kernels

Examples of models 2–5 using a wheat data set comprising 599 wheat lines evaluated in four environments (E1–E4) were employed by Crossa et al. [19] and Cuevas et al. [29]. They are available in the BGLR R package [65]. A total of 50 random samples each with a training set composed of 70% of the wheat lines in each environment and a testing set composed of the remaining 30% of lines observed in only some environments but not in others. The predictive ability was calculated as the average Pearson’s correlation between observed and predicted lines. Table 1 lists the averages of these correlations for each of the four models in each environment and their standard deviations when using GBLUP or Gaussian kernel (GK). Models 2 and 5 were fitted with the BGLR package [65], whereas models 3 and 4 were fitted using the multitrait model (MTM) package of de los Campos and Grüneber [68].

Table 1 Mean prediction accuracies for the different environments of wheat breeding data for GBLUP and GK methods, and four models including a single environment (model 2) and three multienvironment models (models 3, 4, and 5). Values in parenthesis represent the standard deviations. Bold values represent the best predictions among the 4 models.

For these data and the sampling used to fit the four models, the Gaussian kernel (GK) showed higher prediction accuracy than the GBLUP in all four models. However, model 4 gave the best results. The differences in prediction accuracy between models 3 and 4 are greater with GBLUP ; that is, component f captured effects that are retained for the genetic component g. Models 3 and 4 allow capturing covariances close to 0 or negative between environments, but require a more intense computational effort than model 5. Model 5 allows estimating the main genetic effects and interactions and is very flexible for including other variables as environmental covariables. In addition, when the covariances between environments are positive, the prediction ability of model 5 is similar to those of model 4. For large data sets, fitting model 5 could present problems or require intense computer programming. A good option for large data sets including large numbers of environments is to use the approximate kernel [69].

The G × E prediction models presented in this section can predict new individuals in existing multienvironment trial using molecular or pedigree information, but they cannot predict new environments. In the next section, we discuss the use of EC and the so-called enviromics in creating reaction-norm models for dealing with this concern.

4 Genomic-Enabled Reaction-Norm Approaches for G × E Prediction

4.1 Basic Inclusion of Genome-Enabled Reaction Norms

Diverse researchers have modeled genotype-specific variations due to key environmental factors, [70,71,72,73,74,75,76,77] which afterward was named reaction norm; that is, the core of expressed phenotypes for a given genotype across a certain environmental gradient. From this concept, it is reasonable to expect that the core of reaction norm for a certain breeding population or germplasm, evaluated for a certain range of environments, will be the main driver of the statistical phenomena interpreted as G × E interaction. The models presented in the previous section considers only the G effects realized from molecular marker data. Thus, it is also reasonable to assume that in the same manner to the use of molecular data as a descriptor of the genotype resemblance, the use of environmental data can also contribute to explain a large amount of the nongenomic differences observed in phenotypic records from field trials.

In the GS context, modeling the interaction between markers and environmental covariates can be a complex task due to the high dimensionality of the matrix of markers, the environmental covariates, or both. Jarquín et al. [36] proposed modeling this interaction, using Gaussian processes where the associated variance–covariance matrix induces a reaction norm model. The authors showed that assuming normality for the terms involving the interaction and also assuming that the interaction obtained using a first-order multiplicative model is distributed normally, then the covariance function is the Hadamard product of two covariance structures, one describing the genetic information and the other describing the environmental effects. This approach was expanded by Morais-Júnior et al. [57] to account for an H matrix, based on genomic and pedigree-based data in field trials from different cycles of rice breeding in Brazil. Thereafter, Gillberg et al. [78] introduced the use of Kernelized Bayesian Matrix Factorization (KBMF) to account for the uncertainty of environmental covariates in environmental relatedness kernels. Finally, the use of the GK or DK to model both genomic and environmental relatedness was suggested by Costa-Neto et al. [45] and will be described with details in further sections.

4.2 Modeling Reaction-Norm Effects Using Environmental Covariables (EC)

Jarquín et al. [36] considered model 5 but modeled the interaction Eg_ij,

$$ {y}_{ij}=\mu +{E}_i+{L}_j+{g}_j+{\left({Eg}_{ij}\right)}^{\ast }+{\varepsilon}_{ij}, $$

(6)

where all the components are defined in model 5 except the interaction vector (Eg_ij)^∗ that is defined as ${\left(\boldsymbol{Eg}\right)}^{\ast}\sim N\left(\mathbf{0},\left({\boldsymbol{Z}}_{\boldsymbol{g}}\boldsymbol{K}{\boldsymbol{Z}}_{\boldsymbol{g}}^{\prime}\right)\#\left({\boldsymbol{Z}}_{\boldsymbol{E}}\boldsymbol{\Omega} {\boldsymbol{Z}}_{\boldsymbol{E}}^{\prime}\right){\sigma}_{Eg}^2\right)$. The originality of this model is that the relationship matrix between environments Ω is estimated using environmental covariables and proportional to WW′, with W being a matrix with centered and standardized values of the environmental covariables. The construction of matrix Ω can also be guided by the phenotypic data of the calibration set together with the environmental covariables [44]. Heslot et al. [23] proposed an alternative method based on factorial regressions at the marker level, which increased prediction accuracy in 11.1% on average in a large winter wheat dataset. Ly et al. [43] proposed a similar model based on a single environmental covariate, which allows predicting the response of new varieties to the change of a given factor (e.g., temperature variations, drought-stress).

Heslot et al. [23] novel approach consisted in using crop models to predict the main developmental stages for a better characterization of the environmental conditions faced by the plants. Since then, several publications have shown that environmental covariates directly simulated by the crop model (nitrogen stress in Ly et al. [42] dry matter stress index in Rincent et al. [44]) captured more G × E than simple climatic covariates. Millet et al. [59] applied a factorial regression genomic model based on three environmental covariates, which resulted in promising prediction accuracy of maize yield at the European scale. It is important to note that the use of environmental covariates results in sharing information between environments. This means that these models can predict new environments as long as they are characterized by environmental covariates.

4.3 Inclusion of Dominance Effects in G × E and Reaction-Norm Modeling

The main product of most allogamous breeding programs is the development of highly adapted and productive hybrids (single-cross F₁s). In maize, an important allogamous species, recent research suggests that the G × E variation is the end-result of two main genomic-based sources: the additive × environment (A × E) plus dominance × environment (D × E) interactions [80,81,82]. Thus, for predicting single-crosses across diverse contrasting environments, it is necessary to incorporate both genomic-related sources of variation in a computational efficient and biological accurate way.

Costa-Neto et al. [45] tested five prediction models including D × E and enviromics (W) for predicting grain yield over two maize germplasm. All models were run with three different kernel methods (GBLUP , GK and DK), but a coincidence trend of increment for D and A + D + W models were observed for all kernels. In average, for both data sets evaluated, for predicting novel genotypes at know growing conditions (the so-called random cross-validation CV1 scheme) using GBLUP , these authors found accuracy gains ranging from to 22% to 169%, compared with the baseline additive GBLUP . These authors concluded that the inclusion of dominance effects is an important source for predicting novel environments in cross-pollinated crops.

Rogers et al. [83] conducted an extensive multienvironment framework analysis involving 1918 hybrids across 65 environments, in which the use of factor analytic (FA) structures were used for both defining clusters of environments and finding patterns of genomic and enviromic relatedness. The use of FA is a common practice since the classic phenotypic-based G × E analysis. This means that the variance–covariance matrices are dissected in orthogonal factors and these loadings are used as variance–covariance structures, priors of any Bayesian approach [68] or for clustering genotypes or environments for targeting better and adapted cultivars for certain environments [84]. FA was important to identify the environmental factors related to the main A and D effects and how it can boost accuracy for predicting these phenotypes [83].

Gathering results from Costa-Neto et al. [45] and Rogers et al. [83] it is possible to infer that the dominance-related factors are responsible for a sizeable proportion of the phenotypic variation for grain yield in hybrid maize. The inclusion of environmental covariates is important, but some key aspects should be taken into account: (a) the statistical structure to model the A, D, and W effects, in which linear kernel GBLUP models might be limited and the use of FA or other nonlinear kernels may overcome this limitation; (b) how the environmental data were processed and integrated in the genomic prediction model for modeling A × W and D × W; (c) the nature of G × E for each trait under prediction. Below we discuss some results related to the use of nonlinear kernels for those purposes.

4.4 Nonlinear Kernels and Enviromic Structures for Genomic Prediction

Three kernel methods were adopted for the genomic and enviromic sources: nonlinear GK, nonlinear arc-cosine, named as deep kernel and the linear GBLUP used as the benchmark approach. It is important to highlight the differences in creating the environmental relatedness kernel, which in this study was designed the percentile distributions of each environmental factor (e.g., soil, weather, management) across five key crop development stages, and because of that, it takes into account a large amount of environmental typologies as markers of relatedness (W). This bridges the gap between raw environmental data, and what has really happened in the field.

In order to differ from the reaction norm using quantitative covariables (e.g., factorial regression on ECs), Costa-Neto et al. [45, 54] named this model as “envirotyping-informed” GS , because it takes into account the environments of the experimental network. A generalization of the enviromic-enriched genomic prediction model can be described in matrix form as follows.

$$ \boldsymbol{y}=\mathbf{1}\boldsymbol{\mu } +{\boldsymbol{X}}_{\boldsymbol{f}}\boldsymbol{\beta} +\sum \limits_{\boldsymbol{s}=\mathbf{1}}^{\boldsymbol{k}}{\boldsymbol{g}}_{\boldsymbol{s}}+\sum \limits_{\boldsymbol{r}=\mathbf{1}}^{\boldsymbol{l}}{\boldsymbol{w}}_{\boldsymbol{r}}+\boldsymbol{\varepsilon} $$

(7)

where y is the vector combining the means of each genotype across each one of the q environments in the experimental network, in which y = [y₁, y₂, …y_q]^T. The scalar 1μ is the common intercept or the overall mean. The matrix X_f represents the design matrix associated with the vector of fixed effects β. In some cases, this vector is associated with environmental effects (target as fixed-effect). Random vectors for genomic effects (g_s) and enviromic-based effects (w_r) are assumed to be independent of other random effects, such as residual variation (ε).

Equation 7 is a generalization for a reaction-norm model because, in some scenarios, the genomic effects may be divided as additive, dominance, and other sources (epistasis) and the G × E multiplicative effect. In addition, the envirotyping-informed data can be divided into several environmental kernels and a subsequent genomic by enviromic (GW) reaction-norm kernels. The baseline genomic models assumes ${\sum}_{\boldsymbol{s}=\mathbf{1}}^{\boldsymbol{p}}{\boldsymbol{g}}_{\boldsymbol{s}}\ne 0$ and ${\sum}_{\boldsymbol{r}=\mathbf{1}}^{\boldsymbol{q}}{\boldsymbol{w}}_{\boldsymbol{r}}=0$, without any enviromic data. However, the enviromic enriched models might assume ${\sum}_{\boldsymbol{s}=\mathbf{1}}^{\boldsymbol{p}}{\boldsymbol{g}}_{\boldsymbol{s}}\ne 0$ and ${\sum}_{\boldsymbol{r}=\mathbf{1}}^{\boldsymbol{q}}{\boldsymbol{w}}_{\boldsymbol{r}}\ne 0$, in which ${\sum}_{\boldsymbol{r}=\mathbf{1}}^{\boldsymbol{q}}{\boldsymbol{w}}_{\boldsymbol{r}}$ can describe a main enviromic effect (given by W), analogous to a random environment effect, but with a structured matrix from ECs (Ω), and a reaction-norm GW effect as multiplicative effect such as described by Jarquin et al. [36]. Thus, some enviromic-enriched models can be more accurate with less parameters, depending on the way that the genomic and enviromic kernels are built. It has been observed that nonlinear kernels are more efficient than the reaction-norm GBLUP [36].

4.5 Genomic Prediction Accounting for G × E Under Uncertain Weather Conditions at Target Locations

In most crops, genetic and environmental factors interact in complex ways, giving rise to substantial and complex G × E. The combination of G × E and the uncertainty about future weather conditions make agricultural research and plant breeding extremely challenging. In this context, de los Campos et al. [58] proposed that computer simulations leveraging field trial data, DNA sequences, and historical weather records can be used to predict the future performance of genotypes under largely uncertain weather conditions. The authors used field trial data linked to DNA sequences and environmental covariates in order to learn how genotypes react to specific environmental conditions. These patterns are then used, together with DNA sequences and historical weather records, to simulate the expected performance of genotypes at target locations.

The approach of de los Campos et al. [58] uses Monte Carlo methods that integrate uncertainty about future weather conditions as well as model parameters. Using extensive maize data from 16 years and 242 locations in France, the authors demonstrate that it is possible to predict the performance distributions of genotypes at locations where the genotypes have had limited testing data or lacking them. They also showed that predictions that incorporate historical weather records are more robust with respect to year-to-year variation in environmental conditions than the ones that can be derived using field trials only.

As the use of EC information can really improve the accuracy of genomic prediction across multienvironment conditions, most research has focused on quantitative traits (e.g., grain yield) or traits with a simpler genomic architecture, such as days to heading [60] and flowering time [85] which also are measured using a continuous scale. Below we present Bayesian models for dealing with ordinal data, which is a complex problem, particularly for quality traits.

5 G × E Genome-Based Prediction Under Ordinal Variables and Big Data

5.1 Genomic-Enabled Prediction Models for Ordinal Data Including G × E Interaction

In this section, we present Bayesian genomic-enabled prediction models for ordinal data including G × E interaction. Several genomic-enabled prediction models have been developed for predicting complex traits in genomic-assisted animal and plant breeding. These models include linear, nonlinear, and nonparametric models, mostly for continuous responses and less frequently for categorical responses. Linear and nonlinear models used in GS can fit different types of responses (e.g., continuous, ordinal, binary). Several linear and nonlinear models are special cases of a more general family of statistical models known as artificial neural networks.

Recently Pérez-Rodriguez et al. [86] introduced a neural network that generalizes existing models for the prediction of ordinal responses. The authors proposed a Bayesian Regularized Neural Network (BRNNO) for modeling ordinal data. The proposed model was fitted in a Bayesian framework using data augmentation algorithm to facilitate computations and was compared with the Bayesian Ordered Probit Model (BOPM). Results indicated that the BRNNO model performed better in terms of genomic-based prediction than the BOPM model. Results are consistent with the findings of previous research [47]. It should be pointed out that the BRNNO approach for modeling ordinal data could be applied not only in the GS context but also in the context of conventional phenotypic breeding for host plant resistance to pathogens and pests, and many other ordinal traits.

In general, models for nonnormal data are scarce in the context of genome-enabled prediction since most of the models developed so far are linear mixed models (mixed models for Gaussian data). Statistical research has shown that using linear Gaussian models for ordinal and count data frequently produces poor parameter estimates, lower prediction accuracy and lower power, while increasing the complexity of parameter interpretation when transformations are used [47, 49, 87, 88]. Few models for genome-enabled prediction of ordinal and count variables are available [46,47,48,49, 88, 89].

The ordinal probit model assumes that conditioned to x_i (covariates of dimension p), Y_i is a random variable that takes values 1, ..., C, with the following probabilities:

$$ {\displaystyle \begin{array}{l}P\left({Y}_i=c\right)=P\left({\gamma}_{c-1}\le {l}_i\le {\gamma}_c\right)\\ {}=\Phi \left({\gamma}_c+{E}_i+{g}_j+{Eg}_{ij}\right)-\Phi \left({\gamma}_{c-1}+{E}_i+{g}_j+{Eg}_{ij}\right),\kern1.5em c=1,\dots, C\end{array}} $$

(8)

where − ∞  = γ₀ < γ₁ < … < γ_C = ∞ are threshold parameters. A Bayesian formulation of this model assumes the following independent priors for the parameters: a flat prior distribution for γ = (γ₁, …, γ_C − 1) (f(γ) ∝ 1), a normal distribution for beta coefficients, g = (g₁, …, g_J)^′, $\boldsymbol{g}\sim N\left(\mathbf{0},\left({\boldsymbol{Z}}_{\boldsymbol{g}}\boldsymbol{K}{\boldsymbol{Z}}_{\boldsymbol{g}}^{\prime}\right){\sigma}_g^2\right)$ and a scaled inverse chi-squared distribution for ${\sigma}_g^2,$${\sigma}_g^2\sim {\chi}_{v_g,{S}_g}^{-2},$$\boldsymbol{Eg}\sim N\left(\mathbf{0},\left({\boldsymbol{Z}}_{\boldsymbol{g}}\boldsymbol{K}{\boldsymbol{Z}}_{\boldsymbol{g}}^{\prime}\right)\#\left({\boldsymbol{Z}}_{\boldsymbol{E}}{\boldsymbol{Z}}_{\boldsymbol{E}}^{\prime}\right){\sigma}_{Eg}^2\right)$ denotes the G × E interaction, where Z_E is the incidence matrix for environments and ${\sigma}_{Eg}^2$ is the variance component of Eg, also with a scaled inverse chi-squared distribution for ${\sigma}_{Eg}^2$, ${\sigma}_{Eg}^2\sim {\chi}_{v_{Eg},{S}_{Eg}}^{-2}$.

This threshold model assumes that the process that gives rise to the observed categories is an underlying or latent continuous normal random variable l_i =  − E_i − g_j − Eg_ij + ϵ_i where ϵ_i is a normal random variable with mean 0 and variance 1, and the values of l_i are called “liabilities.” The ordinal categorical phenotypes in model 1 are generated from the underlying phenotypic values, l_i, as follows: y_i = 1 if − ∞  < l_i < γ₁, y_i = 2 if γ₁ < l_i < γ₂,… ., and y_i = C if γ_C − 1 < l_i < ∞.

5.2 Illustrative Application Bayesian Genomic-Enabled Prediction Models Including G × E Interactions, to Ordinal Variables

Gray leaf spot (GLS), caused by Cercospora zeae-maydis, is a foliar disease of global importance in maize production. The disease was evaluated using an ordinal scale [1 (no disease), 2 (low infection), 3 (moderate infection), 4 (high infection), and 5 (complete infection)] at three environments (in Colombia, Mexico, and Zimbabwe), in 240 maize lines. The 240 lines were genotyped using the 55k single-nucleotide polymorphism (SNP) Illumina platform. The final genotypic data contained 46,347 SNPs [46].

Table 2 gives the prediction performance for each environment of the GLS data set. The prediction performance is reported as an average Brier Score [90], which was computed as: $\mathrm{BS}={n}^{-1}\sum \limits_{i=1}^n\sum \limits_{c=1}^C{\left({\hat{\pi}}_{ic}-{d}_{ic}\right)}^2$, where d_ic takes the value of 1 if the ordinal categorical response observed for individual i falls in category c; otherwise, d_ic = 0. The closer to zero, the better the prediction performance. The average Brier Score was computed with the testing set of the 20 random partitions implemented. The best predictions were obtained with model E + G + GE that takes into account the G × E interaction. Relative to models based on main effects only, the models that included G × E gave gains in prediction accuracy between 9% and 14% [46].

Table 2 Brier scores (mean, minimum and maximum; smaller indicates better prediction) evaluated for the validation samples. Model E + L contains in the predictor only the information of environment + lines without markers, model E + G contains in the predictor information of environment + genomic data and model E + G + GE has the same information as E + G plus the genotype-by-environment (GE) interaction [46]

5.3 Approximate Genomic-Enabled Kernel Models for Big Data

When the number of observations (n) is large (thousands or millions), there are computational difficulties for inverting and decomposing large genomic kernel relationship matrices. This problem increases when G × E and multitrait kernels are included in the model. Cuevas et al. [69] proposed selecting a small number of lines m (m < n) for constructing an approximate kernel of lower rank than the original and thus exponentially decreasing the required computing time.

The method of approximate kernels proposes a simple input that originally had a kernel matrix K_{n, n} of order n × n from where a smaller submatrix is selected, K_{m, m} of order m × m with the restriction that m < n, with the aim of finding an approximate matrix Q of rank m, smaller than the rank of K_{n, n} such that:

$$ \boldsymbol{K}\approx \boldsymbol{Q}={\boldsymbol{K}}_{n,m}{\boldsymbol{K}}_{m,m}^{-1}{\boldsymbol{K}}_{n,m}^{\prime } $$

where K_{m, m} is a submatrix constructed with m selected individuals with p markers, K_{n, m} is a submatrix of K with the relation between the total n lines and the m selected ones. Thus, Q is of smaller rank than K, and computational time is significantly saved when performing the required spectral decomposition or/and inversion. Based on this approximation, Misztal et al. [91] and Misztal [92] employed recursive methods from the joint distribution of the random genetic effects when testing a large number of animal production.

Cuevas et al. [69] described the full genomic method for single environment (FGSE) with a covariance matrix (kernel) including all n lines. Then m lines (observations) approximate the original kernel for the single environment model (APSE model). Similarly, but including main effects and G × E (FGGE model), and including m lines, the kernel method was approximated by main effects and G × E (APGE model). The authors compared the prediction performance and computing time for FGGE vs APGE models and showed a competitive prediction performance of the approximated method with a significant reduction in computing time (Table 3). To predict the 2017–2018 cycle using the previous four cycles with the full genomic GE model (FGGE), it was necessary to manipulate large covariance matrices, one for the main effects of the genomic model and another for the interaction, of order 45,099 × 45,099. It was not possible to manage this matrix size with available laptops; therefore, the genomic-enabled prediction accuracy recently reported by Pérez-Rodríguez et al. [87] was used as a reference. The authors reported a genomic prediction accuracy of 0.426 for the 2017–2018 cycle using all the other cycles as a training set.

Table 3 The models FGGE and APGE considering the size of m, as 25% of the original training set. Average correlation between predictive and observed values (CORR), residual variance $\left({\hat{\sigma}}_{\varepsilon}^2\right)$ and average computing time required. Training set sizes contains 8000 to 10,000 wheat lines each cycle

Using the APGE model and only 25% of the total training set, matrices K_{m, m}, and K_{n, m}, are now of manageable sizes of order 9021 × 9021 and 45,099 × 9021, respectively, which gave a genomic prediction accuracy of 0.427; that is, there is no loss of prediction accuracy with respect to the full model FGGE. The computing time required, including the time for preparing the matrices for the approximation method, and the time for the eigenvalue decomposition and the 20,000 iterations, was 30,670 s or 8.5 h.

6 Open Source Software for Fitting Genomic Prediction Models Accounting for G × E

In this section, we present practical examples of use of three software for genomic prediction accounting for multitrait and multienvironment data in plant breeding. We emphasize open-source packages developed under the R computational-statistical environment, due to widespread use in plant breeding and quantitative genetics. Historically, the first open-source R software for genome-based prediction was developed by de los Campos et al. [16] Thereafter, Pérez et al. [93] formally described the Bayesian linear regression (BLR) that allows fitting high-dimensional linear regression models including dense molecular markers, pedigree information, and several other covariates. Then, Endelman [94] presented the frequentist ridge-regression approach (RR), that also allowed the estimation of marker effects and other kernel models that helped to popularize GS in plants. This package were named rrBLUP because it runs a RR-BLUP approach, that is, a whole-genome regression of the molecular markers over a certain phenotype.

The package rrBLUP is mostly used for single-environment studies or genome-wide association studies (GWAS ). On the other hand, BLR from Pérez et al. [93] allows not only including markers but also pedigree data jointly. In the seminal work of BLR, Pérez et al. [93] explained the challenges that arise when evaluating the genomic-enabled prediction accuracy through random cross-validation and how to select the best choice of hyperparameters of the Bayesian models. Thus, to facilitate the use of such Bayesian models in genomic prediction, the Bayesian generalized linear regression package (BGLR) [65, 95] was defined in 2014, as a generalization of the BLR package that implements several parametric and semiparametric regression models, which includes Bayesian Lasso and Bayesian ridge regression (BRR), BayesB, BayesCπ, and reproducing kernel Hilbert spaces (RKHS) for continuous and ordinal responses (either censored or not). This approach opened up the way for dealing with more complex structures of phenotypic records, specially concerning to the multienvironment data and the “black box” of the G × E interaction.

After the works of Jarquín et al. [36], López-Cruz et al. [37], and Souza et al. [63] the use of kernel models including several structures for main genotypic effect (MM model), MM plus single G × E deviation (MDs), MDs with environment-specific variation (MDe), inclusion of random intercepts [41] and environmental relatedness kernels [36] became an issue for a large number of genotypes and environments (thus large size of each kernel). Granato et al. [66] presented the Bayesian genotype plus genotype-by-environment (BGGE) software, which takes advantage of a singular-value decomposition (SVD) of those kernels to speed up Gibbs sampling and mixed model solving. This software runs the same kernel models of BGLR (using multienvironment RKHS) but it is about 5 times faster without accuracy loss.

Another software with great importance is the ASReml-R (version 3.0) [96], a non–open source software that is widely used. Briefly, the main advantage of this software is the possibility of easily running a wide number of structures genomic relationship (G), environmental relatedness (E), and G × E, thus allowing explicit modeling of variance–covariance matrices of G, E and G × E in different ways, such as unstructured (UN) and factor analytic structure (FA). Several publications show the benefits of using FA for modeling genomic and G × E sources [80, 82, 83] because this approach deals with the main patterns of variation in a more parsimonious and accurate manner.

Another way to model multivariate structures is through the open source software MTM [68]. It allows fitting a Bayesian multivariate Gaussian model with arbitrary number of random effects using a Gibbs sampler with several specifications for (co)variance parameters (unstructured, diagonal, factor analytic, etc.). In this package, the use of multienvironment structures can be interpreted as multitrait, where the phenotypic records for same genotype at different environments is visualized as a different trait. This concept traces back to the idea of the phenotypic correlation across environments [97] and its putative structure for modeling G × E effects, and measure its importance in phenotypic variation. The MTM package is able to fit model 3 and to estimate matrices U_E, and Σ. Matrix U_E can indeed be modeled with different levels of complexity as illustrated by Malosetti et al. [79].

Another option for creating unstructured environmental relatedness matrices is the use of explicit environmental data [36, 57]. The use of environmental data for this purpose must follow a certain biological reality, because the covariates must represent in silico the growing conditions expected for a certain environment, in which “environment” means a certain time interval for a certain location using a certain crop management.

The package EnvRtype [54] was developed to support quantitative geneticists to import environment data and use it in genomic prediction. This model runs the BGGE routine developed by Granato et al. [66] and Cuevas et al. [41]. Despite the mention as a software for genomic prediction, the main contribution of this package is related to the facility in importing, processing and incorporating environmental information as reliable source of variation. This package provides tools to implement reaction-norm model and other enviromic-enriched structures (see Eq. 7). The Bayesian prediction is implemented using the structure of both BGGE and BGLR packages.

Other open source packages commonly used are the Solving Mixed Model Equations in R (sommer), [98] Bayesian multitrait multienvironment (BMTME) [99], and linear mixed models for millions of observations (MegaLMM) [100]. Here, we focus on practical examples for two software: BGLR and MTM.

7 Practical Examples for Fitting Single Environment and Multi-Environment Modeling G × E Interactions

7.1 Single Environment Models with BGLR

This section gives the R codes to illustrate how to fit RR and GBLUP models described before. We have adapted the codes from previous publications. Here, we analyze the wheat dataset described in Crossa et al. [19]. The dataset includes phenotypic and genotypic information for 599 wheat lines. The response variable is grain yield, which was evaluated in four environments. Lines were genotyped using DArT markers, which were coded as 0 and 1. An additive relationship matrix (A) derived from the pedigree is also available.

R code in Box 1 shows how to load the BGLR package and load the data from an RData file. In this example the RData file can be downloaded from the following link: http://genomics.cimmyt.org/BookChapter_Rincent/. Note that the grain yield data contained in this dataset differs from the one included in the package because this response variable is not standardized in each environment. After loading the data, three objects are available in the R environment: (1) X, a matrix with markers whose dimensions are 599 rows (individuals) and 1279 columns (markers), (2) A, additive relationship matrix derived from pedigree, (3) Pheno, a data frame with 3 columns, Yield (t/ha), Var (Genotype) and Env (Environment). The R code also shows how to generate a boxplot for grain yield in each environment (Fig. 2).

Fig. 2

Distribution of grain yield in each environment

Box 1 Loading Bayesian Generalized Linear Regression (BGLR) and Wheat Data

1	library(BGLR)
2	load("wheat599.RData")
3	ls() #list objects
	#Boxplot for grain yield
	boxplot(Yield~Env,data=Pheno,xlab="Environment",
	ylab="Grain yield (t/ha)")

Box 2 includes R code to fit RR (model 1). We predict grain yield in environment 4 using the BGLR function. The number of burn-in, iterations and thin are parameters for the Gibbs sampler, in order to compute the posterior means of the parameters of interest. After the model is fitted, the estimated marker effects $\left(\hat{\boldsymbol{\beta}}\right)$ can be obtained for further processing (see Fig. 3). The structure of the output object returned by the BGLR function is described by Pérez and de los Campos [65] and in the corresponding package documentation.

Fig. 3

Estimated marker effects using Bayesian ridge regression

Box 2 Fitting Bayesian Ridge Regression (BRR)

1	#You need to run code in Box 1
2	#Specify linear predictor
3	EtaR<-list(markers=list(X=X,model="BRR"))
4
5	#Grain yield in environment 4
6	y<-as.vector(subset(Pheno,Env==4)$Yield)
7
8	#Set random seed
9	set.seed(456)
10	#Fit the model
11	fmR<-
12	BGLR(y=y,ETA=EtaR,nIter=10000,burnIn=5000,thin=10,verbose=FALSE)
13	#Estimated marker effects
14	betaHat<-fmR$ETA$markers$b
15
16	#Plot estimated marker effects
17	plot(betaHat,xlab="Marker",ylab="Estimated marker effect")abline(h=0,col="red",lwd=2)

Box 3 shows R code to fit G-BLUP model (Eq. 2). We predict grain yield for environment 4. The first lines of the script computes a genomic relationship matrix based on centered markers [37]. After that we define the linear predictor and fit the model using the BGLR function. Predicted random effects $\hat{\boldsymbol{u}}$ (BLUPs) are obtained from the output of the resulting object. The estimated variance parameters ${\hat{\sigma}}_{\varepsilon}^2$ and ${\hat{\sigma}}_g^2$ can be obtained using the code in lines 22–24.

Box 3 Fitting Genomic Best Linear Unbiased Predictor (GBLUP )

1	#You need to run code in Box 1
2	#A genomic relationship matrix
3	Z<-scale(X,center=TRUE,scale=TRUE)
4	G<-tcrossprod(Z)/ncol(Z)
5
6	#Specify linear predictor
7	EtaG<-list(markers=list(K=G,model="RKHS"))
8
9	#Grain yield in environment 4
10	y<-as.vector(subset(Pheno,Env==4)$Yield)
11
12	#Set random seed
13	set.seed(789)
14
15	#Fit the model
16	fmG<-BGLR(y=y,ETA=EtaG,nIter=10000,burnIn=5000,thin=10,
17	verbose=FALSE)
18
19	#BLUPs
20	uHat<-fmG$ETA$markers$u
21
22	#Variance parameters
23	fmG$varE #Residual
24	fmG$ETA$markers$varU #Genotypes

R codes to perform cross-validation analysis using the BGLR package are included in Pérez and de los Campos [65].

7.2 Multienvironment MDs Model with BGLR

In this example, we use the same wheat dataset described previously. Box 4 shows R code to fit model 5. Lines 6 and 7 obtains the incidence matrices for environments (Z_E) and genotypes (Z_g), lines 12 and 13 compute a genomic relationship matrix [37]. Lines 15 and 18 defines the kernels for the variance covariance matrices for random effects. Lines 20–22 define the linear predictor and finally the model is fitted in lines 24 and 25. Once the model is fitted, the resulting object contains information that can be used for further processing (prediction of response variable, variance parameters, prediction of random effects, etc.). Lines 37–41 show how to retrieve estimated variance parameters. We obtain ${\hat{\sigma}}_E^2=0.4942,$ ${\hat{\sigma}}_{\varepsilon}^2=0.2409$, ${\hat{\sigma}}_g^2=0.1067$ and ${\hat{\sigma}}_{Eg}^2=0.1499$, thus being 0.9920 the phenotypic variance. Hence, about 50% of variance was explained by the difference between environments, 15% was due to the interaction between genotypes and environment, and 11% due to the genotypes and the rest goes into the residuals (Fig. 4). CV1 and CV2 [11] can be implemented easily in BGLR, the software includes routines to predict missing values, so we assign missing values to the response vector to the entries to be predicted. Full codes are included in Jarquín et al. [36].

Fig. 4

Observed versus predicted grain yield, predictions were obtained using the fitted multienvironment with a block diagonal for genotype-by-environment (G × E) variation

Box 4 Fitting Multienvironment Model with a Block Diagonal for Genotype-by-Environment (GxE) Variation

1	library(BGLR)
2	load("wheat599.RData")
3
4	#incidence matrix for main eff. of environments.
5	Pheno$Env<-as.factor(Pheno$Env)
6	ZE<-model.matrix(~Pheno$Env-1)
7
8	#incidence matrix for main eff. of lines.
9	Pheno$Var<-as.factor(Pheno$Var)
10	ZVar<-model.matrix(~Pheno$Var-1)
11
12	Z<-scale(X,center=TRUE,scale=TRUE)
13	G<-tcrossprod(Z)/ncol(Z)
14
15	K1<-ZVar%*%G%*%t(ZVar)
16
17	ZEZE<-tcrossprod(ZE)
18	K2<-K1*ZEZE
19
20	EtaRN<-list(ENV=list(X=ZE,model="BRR"),
21	Grm=list(K=K1,model="RKHS"),
22	EGrm=list(K=K2,model="RKHS"))
23
24	fmRN<-BGLR(y=Pheno$Yield,ETA=EtaRN, nIter=10000,
25	burnIn=5000,thin=10,verbose=FALSE)
26
27	#Observed vs predicted values
28	plot(fmRN$y,fmRN$yHat,
29	pch=as.integer(Pheno$Env),
30	col=Pheno$Env,
31	xlab="Grain yield observed (t/ha)",
32	ylab="Grain yield predicted (t/ha)")
33
34	legend("topleft",legend=c(1,2,3,4),title="Environment",
35	bty="n",col=1:4,pch=1:4)
36
37	#Variance parameters
38	fmRN$varE #Residual
39	fmRN$ETA$ENV$varB #Environment
40	fmRN$ETA$Grm$varU #Genotypes
41	fmRN$ETA$EGrm$varU #Interaction

7.3 Multienvironment Factor Analytic Model Using MTM

Code in Box 5 shows how to fit model 3 using MTM package [68]. We use the wheat dataset described previously. The covariance matrix for the random effect and that for model residuals are unstructured. The relationship between individuals is computed using markers. Lines 28 and 29 fit the model. Lines 31–42 show how to retrieve the estimates for genetic and residual covariance matrices. Cross-validation analysis can be implemented easily in the package, we assign missing values to the entries of the phenotypes to be predicted, and the software includes routines to perform the predictions automatically.

Box 5 Multi Trait Model (MTM)

1	#install MTM package
2	install.packages("remotes") #install MTM
3	remotes::install_github("QuantGen/MTM") #install MTM
4	library(MTM)
5	load("wheat599.RData")
6
7	#Phenotypes
8	y1<-subset(Pheno,Env==1)$Yield
9	y2<-subset(Pheno,Env==2)$Yield
10	y3<-subset(Pheno,Env==3)$Yield
11	y4<-subset(Pheno,Env==4)$Yield
12	Y<-cbind(y1,y2,y3,y4)
13	#Genotypes
14	Z<-scale(X,center=TRUE,scale=TRUE)
15	G<-tcrossprod(Z)/ncol(Z)
16	#Linear predictor
17	EtaM<-list(
18	list(K = G, COV = list(type = "UN",df0 = 4,S0 =
19	diag(4)))
20	)
21	#Residual
22	residual<-list(type = "UN",S0 = diag(4),df0 = 4)
23	fmM <- MTM(Y = Y, K=EtaM,resCov=residual,
24	nIter=10000,burnIn=5000,thin=10)
25	#Predictions of phenotypical values
26	fmM$YHat
27	#Predictions of random effects
28	fmM$K[[1]]$U
29	#Residual covariance matrix
30	fmM$resCov$R
31	#Genetic covariance matrix
	fmM$K[[1]]$G

7.4 Multitrait or Multienvironment Factor Analytic Model Using MTM

As mentioned, the first study of genomic prediction using pedigree and genomic information with the factor analytic (FA) model for combining estimation of the main effects of cultivar plus G × E interaction was presented by Burgueño et al. [11] Code in Box 6 shows how to fit model 3 using FA structure. We used the same wheat dataset and molecular markers described previously. By using FA, a certain variance–covariance matrix (G_k) is decomposed into common and specific factors according to: G_k = B_KB_k^′ + ψ_K, where B_K is a matrix of loadings and ψ_K is a diagonal matrix whose nonnull entries give the variances of factors that are trait-specific (or environment-specific when assuming observations for same genotype at different environments as a different trait). Any factor analysis is equal to a regression on implicit covariates (now factors), in which every factor is orthogonal and captures a different pattern of variation from the linear combination of traits. In MTM, the loadings are assigned flat priors (normal priors with null mean and large variance) and the variances of the specific factors are assigned scaled-inverse chi-squared with degrees of freedom (df) and scale given by parameters df0 and S0 [68]. In Box 6, we exemplify the use of FA over the same model described in Box 5. The differences are given in Lines 17–19, where the FA is indicated.

Box 6 Multi Trait Model (MTM) with Factor Analytic (FA) Model

1	library(MTM)
2	load("wheat599.RData")
3
4	#Phenotypes
5	y1<-subset(Pheno,Env==1)$Yield
6	y2<-subset(Pheno,Env==2)$Yield
7	y3<-subset(Pheno,Env==3)$Yield
8	y4<-subset(Pheno,Env==4)$Yield
9
10	Y<-cbind(y1,y2,y3,y4)
11
12	#Genotypes
13	Z<-scale(X,center=TRUE,scale=TRUE)
14	G<-tcrossprod(Z)/ncol(Z)
15
16	#Linear predictor using factor analytic for G strucure
17	EtaFA<-list(
18	list(K = G, COV = list(type = 'FA', nF=1,M=matrix
19	(nrow = 4,ncol = 1, TRUE),df0 = rep(1,4),S0 = rep(1,4),var=100)))
20	#Residual
21	residual<-list(type = "UN",S0 = diag(4),df0 = 4)
22	fmFA <- MTM(Y = Y, K=EtaFA,resCov=residual,
23	nIter=10000,burnIn=5000,thin=10)
24
25	#Predictions of phenotypical values
26	fmFA$YHat
27
28	#Predictions of random effects
29	fmFA$K[[1]]$U
30
31	#Residual covariance matrix
32	fmFA$resCov$R
33
34	#Genetic covariance matrix
35	fmFA$K[[1]]$G

8 What to Expect for the Future of G × E in Genomic Prediction?

The G × E interactions at molecular level can be seen as a source of variability we can benefit from to develop materials adapted to specific pedoclimatic conditions. Because the phenotyping of variety or environment combinations is considerably constrained for practical reasons (e.g., costs, MET size), prediction models are of paramount importance for exploring G × E. Such models will be essential to develop cultivars adapted to upcoming environmental conditions in the context of climate change. Below, we put together some of the concepts described in this chapter and envisage key elements that will contribute to more accurate G × E predictions in the near future.

8.1 High-Throughput Phenotyping Opens an Avenue for Modeling Functional Traits Under G × E Scenarios

Large numbers of breeding lines, hybrids or cultivars, among other germplasm, can be screened at a very low unitary cost by using high-throughput phenotyping platforms (HTP). With HTP, it is possible to collect many phenotypes on large numbers of breeding individuals at different stages of plant growth, under different environmental conditions. Collecting data on primary and secondary traits in many testing genotypes at an early stage of plant growth could be of great value for reducing evaluation time and cost, while increasing selection intensity and prediction accuracy and, consequently, the response to selection. The main idea of HTP is to use predictor traits related to grain yield, disease resistance or end-use quality that may be useful in early-generation testing of lines. Models incorporating genomic × environmental covariables or pedigree × environmental interaction covariables already exist, and prediction during early-generation testing is fundamental for increasing genetic gains. The main objective of GS is to reduce phenotyping costs and accelerate genetic gains. This can increase both the accuracy and intensity of selection and therefore the selection response, while decreasing phenotyping costs. One example of G × E prediction involving HTP is given by Montesinos-Lopez et al. [49] who investigated models with genomic and near-infrared spectra (NIRS or light absorbance at different wavelengths) and observed that the models with wavelength × environment interaction terms were the most accurate models. NIRS can also be used to estimate environment specific similarity matrices [101, 102] that we hope to be useful for modeling G × E.

HTP instruments can also be used to calibrate crop-growth model (CGM) at the variety level, for instance for predicting the phenological stages [59] of each genotype in each environment. CGM are promising tools to predict G × E, as they were developed to model the response of the plants to various environmental conditions and were, for instance, adapted to directly produce stress covariates [42, 44] Stress indices simulated by the CGM was shown to better capture G × E than basic pedoclimatic covariates, although the improvement in prediction accuracy was only moderate. Complete integration of CGM and GS models was also proposed for phenological [103,104,105] or productivity traits [106, 107] thereby allowing predictions of contrasted variety/environment combinations.

8.2 Accurate Environmental Data and Optimized Experimental Designs Are Essential for Accurately Predicting G × E

One of the major gaps in GS research for G × E modeling using environmental data lies in the steps of collecting, processing and integrating those data in an ecophysiology-smart and parsimonious manner. The lack of hardware sensors for monitoring field growing conditions is also a problem, mostly for breeding programs located in developing regions with a limited budget to invest in those technologies. Luckily, the availability of public data bases derived from geographic information systems (GIS) allows: (1) the remote collection of past weather, elevation and soil data in any part of the world; and (2) the projection of future trends for specific growing regions. If this large amount of environmental data is available, it is possible to study in depth the typology of each environment (interval between sowing date and harvest for a specific location, using a specific crop management, and with a range of probable climatic conditions).

An environmental typology (envirotype) is defined by: (a) discretizing the gradient of some key environmental factor for G × E and crop adaptation (e.g., air temperature in maize) in types of stressful/optimum growing conditions; (b) discovering the frequency of occurrence of each class in order to identify the predominant envirotype for each environment, for a multienvironment trial (MET) or for an entire target population of environments (TPE). Considering an environment as a random sample of the possible growing conditions that the germplasm can face in the TPE, it is possible to check the representativeness of each environment in relation to the TPE, but also the similarity among environments in a specific MET. As the TPEs gather multispatial and temporal environments (e.g., worldwide locations from the past, present, and future trends), the core of possible frequent types of environmental and management factors represents the envirome of the TPE. Thus, breeders can take advantage of this approach to develop an “enviromic assembly” of each one of the environments, which can be useful to design better MET networks with reduced phenotyping costs, either for GS or crop modeling. It also can provide a more realistic environmental similarity matrix to be incorporated in predictive tools for G × E. As presented in the Subheading 5, this enviromic potentiality can be implemented in a cost-effective manner using open-source software, such as EnvRtype [54].

Apart from the representativeness and accurate descriptions of the MET, the selection of individuals composing the calibration set can have a major effect on GS accuracy [108], that has rarely been considered in the context of G × E [109]. One potential way for defining calibration set optimized for predicting G × E is to use multitrait criteria such as CDmulti [110], by considering each trial as a trait. The MET phenotypes are thus considered as a set of traits with correlation levels depending on the similarity between environments. The experimental costs of each trial can be taken into account with such criteria to optimize the phenotyping strategy [110].

8.3 Deep Learning Is a Promising Way of Combining Genomics, HTP and Enviromics

Deep learning (DL) is another technology that has great potential to be applied in any area of predictive data science and especially in GS-assisted breeding for multi-trait , multienvironment big data. It is fundamental to use high quality DL and sufficiently large training data. DL will be more and more valuable with the upcoming size increase of the datasets due to high-throughput phenotyping. Despite the fact that recent articles show that the use of DL for GS did not produce strong evidence for its superiority in terms of prediction accuracy compared to conventional genomic prediction models with actual datasets, there is evidence that DL algorithms are efficient for capturing nonlinear patterns more efficiently than conventional genomic prediction models and for integrating data from different sources without the need for feature engineering [50,51,52,53]. Likewise, DL algorithms have the potential to improve prediction accuracy by developing specific topologies for the type of data in plant breeding programs . Combined with enviromic sources, it is possible that DL algorithms can reveal implicit patterns of phenotype–envirotype–genotype relations, thereby resulting in a cost-effective data-driven approach to describe the phenotypic plasticity of plants in contrasting environments. This can be an alternative to a complex approach combining genetic modeling and CGM [111,112,113] that demands some degree of expertise in each CGM software. However, it is important to remember that CGM is still a state-of-the-art modeling approach that combines all ecophysiology knowledge in nonlinear equation models. In this sense, the CGM is also a supervised algorithm that has the ability to describe the response of intermediate phenotypes due to environmental variations. DL is a tool that may incorporate different sources of information related to high throughput phenotype, enviromics and genomics, in order to find pathways to better describe G × E, but in a context that may not be able to explain the true nature of those pathways.

9 Conclusion

Considerable progress has been made in the last decade for adapting GS models to the prediction of G × E. We have here introduced different kinds of modeling to address this issue, and many studies illustrated that such models result in more accurate predictions than standard GS models. Open-source packages were developed for an easy use of these models by the genetic and breeding communities. G × E prediction is an active field of research that will benefit from upcoming improvements of experimental designs, phenotyping throughput, as well as genetic, physiological, and statistical modeling. A trend can be noticed toward a multidisciplinary approach potentially involving genetics, ecophysiology, phenomics, and statistics. The main task for such an approach could be the advance in predicting novel genotypes at novel environments, which will be very important in a near future for several reasons, including anticipating climate change scenarios, designing crop ideotypes and for a better allocation of resources in large-scale breeding programs worldwide.