Analysis of fractional multi-dimensional Navier–Stokes equation

Abstract

In this paper, a hybrid method called variational iteration transform method has been implemented to solve fractional-order Navier–Stokes equation. Caputo operator describes fractional-order derivatives. The solutions of three examples are presented to show the validity of the current method without using Adomian and He’s polynomials. The results of the proposed method are shown and analyzed with the help of figures. It is shown that the proposed method is found to be efficient, reliable, and easy to implement for various related problems of science and engineering.

1 Introduction

Navier–Stokes equations (NSEs) depicting the physical interests of engineering and scientific research are viewed as beneficial. These equations are predominantly used to manage climate estimating, sea flows, water stream in a line, and wind current around a wing. Also, the basic plan of airplanes and vehicles, the investigation of the bloodstream, the goal of intensity stations, and the examination of contamination are firmly identified with NSEs. Moreover, the study of magnetohydrodynamics depends on the coupling of Maxwell’s and NSEs. Since their presentation, distinctive physical models have been exploited in the literature to manage arranged material circumstances. In this work, we consider a fractional-order NS equation for an incompressible fluid flow of kinematic viscosity $\upsilon =\frac{\phi }{\rho }$ and density ρ. It is indicated as

$$ \textstyle\begin{cases} D^{\beta }_{\eta }V+(V.\nabla )V=\rho \nabla ^{2}V-\frac{1}{\rho }\nabla g, \\ \nabla .V=0, \\ V=0,\quad \text{on } \Omega \times (0,T). \end{cases} $$

Here, $V=(\mathcal{U},\mathcal{V},\mathcal{W})$, q, and η represent fluid vector, pressure, and time, respectively. $({\chi },{\varphi },{\mathcal{Z}})$ represents the spatial components in Ω. ϕ is the dynamic viscosity. ρ is the density and the ratio of ϕ.

The above equations can also be defined as

$$\begin{aligned}& D_{\eta }^{{\Upsilon }}{(\Phi )}+{{{\Phi }}} \frac{\partial {{{\Phi }}}}{\partial {{\chi }}}+{{{\Psi }}} \frac{\partial {{{\Phi }}}}{\partial {\varphi }}+{{{\Theta }}} \frac{\partial {{{\Phi }}}}{\partial {{\mathcal{Z}}}}={ \rho } \biggl[{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{\chi }^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{\varphi }^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr]- \frac{1}{\rho }\frac{\partial g}{\partial {\chi }}, \\& D_{\eta }^{{{\Upsilon }}}{({\Psi })}+{{{\Phi }}} \frac{\partial {{{\Psi }}}}{\partial {{\chi }}}+{{{ \Psi }}} \frac{\partial {{{\Psi }}}}{\partial {{\varphi }}}+{{{\Theta }}} \frac{\partial {{{\Psi }}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{\chi }^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{\varphi }^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr]- \frac{1}{\rho }\frac{\partial g}{\partial {\varphi }}, \\& D_{\eta }^{{{\Upsilon }}}{(\Theta )}+{{{\Phi }}} \frac{\partial {{{\Theta }}}}{\partial {{\chi }}}+{{{ \Psi }}} \frac{\partial {{{\Theta }}}}{\partial {{\varphi }}}+{{{\Theta }}} \frac{\partial {{{\Theta }}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Theta }}}}{\partial {{\chi }^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }}}}{\partial {{\varphi }^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr]- \frac{1}{\rho }\frac{\partial g}{\partial {\mathcal{Z}}}. \end{aligned}$$

Mathematically, these equations are a problematic arrangement of nonlinear equations within sight of viscous flows [1].

Physical marvels of the incidental fields can be demonstrated properly using fractional partial differential equations (FPDEs). The hypothesis of partial analytic is outfitted with fabulous instruments to depict the dynamical conduct and memory-related qualities of logical frameworks and cycles from the last three decades. Different researchers have utilized FDEs in the displaying and investigation of logical phenomena in various fields of knowledge [2–11]. The hypothesis of fractional calculus has been generally used in different fields. It is becoming extremely quick in creating models because of its connection with memory and fractals plentiful in genuine physical frameworks. Fractional calculus demonstrating limits the mistake that emerges from the numbness of noteworthy genuine boundaries. It allows a more extraordinary level of opportunity in the model contrasted with an integral-order framework [12, 13]. FDEs are furnished with magnificent strategies to portray innate and memory attributes that are essentially disregarded by the whole number order framework. Likewise, they are also appropriate in demonstrating genuine frameworks and important in the examination of dynamical frameworks. FDEs are likewise suitable if there should be an occurrence of displaying frameworks with longer-go intuitiveness both in space and time. The soundness area increments in the event of a fractional-order framework when contrasted with its whole number order system. Fractional analytic likewise gives nonlocal operators and mathematical outcomes with high precision [14, 15]. Likewise, fractional-order frameworks, at last, meet the whole number order frameworks.

The nonlocal characteristic of the fractional operator is the most profitable element in this situation. The hypothesis of fractional analytic creates numerous speculations concerning non-neighborhood qualities, improved level of opportunity, most excessive use of data, and these attributes happen on account of fractional-order frameworks. The mathematical plans given by fractional analytic begin the more profound comprehension of complex frameworks and diminish the computational work concerning the solutions strategy [16–24]. Precise expository solutions are not found virtually on account of FDEs. Hence, over the most recent twenty years, numerous iterative plans, for example, homotopy perturbation method, Adomian decomposition method, variational iteration method, homotopy perturbation transform strategy, residual power series strategy, and so forth, have been created to obtain the solutions of a few classes of FDEs [25–36].

A Chinese mathematician has created the variational iteration method (VIM) He [37]. VIM is modified with the Laplace transform; the modified method is known as the variational iteration transform method (VITM). After the original work of He, a different adjustment of VIM has been utilized to take care of different nonlinear issues, for example, dissemination and wave equations [38–45]. Recently, several mathematicians have applied various strategies for the solutions of fractional NSEs. Interested readers can see [46–51] and the references therein.

In this paper, the variational iteration transform technique is implemented to analyze the solution of fractional-order multi-dimensional Navier–Stokes equations. Caputo operator describes the fractional-order derivatives. The solution of certain illustrative problems is provided to prove the feasibility of the proposed methodology. The results of the proposed method are shown and analyzed with the help of figures and tables. The current approach has lower computing costs and higher convergence rates. The proposed method is therefore constructive to solve other fractional-order PDEs.

The outline of this article is as follows. In Sect. 2, the basic definitions of Laplace transform and fractional calculus are discussed. In Sect. 3, the variational iteration transform method is discussed. In Sect. 4, three test examples of fractional-order Navier–Stokes equation are given to elucidate the suggested schemes. In Sect. 5, conclusions of the work are drawn.

2 Basic definitions

Definition 2.1

The fractional-order derivative of $g({\chi })$ in the Caputo sense is given as

$$ \begin{aligned} &D^{{{\Upsilon }}}g({\chi })= \frac{1}{\Gamma (k-{{\Upsilon }})} \int _{0}^{{\chi }}({\chi }-\tau )^{k-{{ \Upsilon }}-1}g^{(k)}( \tau )\,d\tau , \\ &\quad \text{for } k-1 < {{\Upsilon }} < k, k \in N, {\chi } >0, g \in C^{k}_{-1}. \end{aligned} $$

Definition 2.2

The Laplace transformation of $g({\chi })$, $\tau > 0$ is expressed as

$$ F(s)= L \bigl[g(\tau ) \bigr]= \int ^{\infty }_{0}e^{-s\tau }g(\tau )\,d\tau . $$

Definition 2.3

The Laplace transformation $L[g(\tau )]$ of the Caputo derivative is given as

$$ L \bigl[D^{{{\Upsilon }}}g(\tau ) \bigr]=s^{{\Upsilon }}{F(s)}-\sum _{m=0}^{k-1}s^{{{ \Upsilon }}-1-k}g^{m}(0), \quad k-1 < {{\Upsilon }} < k. $$

Definition 2.4

The Mittag-Leffler function $E_{{\Upsilon }}(z)$ with ${{\Upsilon }} > 0$ is given by

$$ E_{{\Upsilon }}(z)=\sum_{k=0}^{\infty } \frac{z^{k}}{\Gamma ({{\Upsilon }}{k}+1)}, \quad {{\Upsilon }} > 0, z \in C. $$

3 The procedure of VITM

This section describes the VITM solution of fractional PDEs [52, 53].

$$ \begin{aligned} &D_{\eta }^{{\Upsilon }}{{\Phi }({{\chi }},{\eta })}+ \mathcal{H}_{1}({\Phi },{\Psi })+\mathcal{M}_{1}({ \Phi },{\Psi })-q_{1}({{ \chi }},{\eta })=0, \\ &D_{\eta }^{{\Upsilon }}{{\Psi }({{\chi }},{\eta })}+ \mathcal{H}_{2}({ \Phi },{\Psi })+\mathcal{M}_{2}({\Phi },{ \Psi })-q_{2}({{\chi }},{\eta })=0, \quad m-1< {{\Upsilon }} \leq m, \end{aligned} $$

(1)

with the initial conditions

$$ {\Phi }({{\chi }},0)=g_{1}({{\chi }}),\quad\quad {\Psi }({{\chi }},0)=g_{2}({{ \chi }}), $$

(2)

where is $D_{\eta }^{{\Upsilon }}= \frac{\partial ^{{\Upsilon }}}{\partial {\eta }^{{\Upsilon }}}$ the Caputo fractional derivative of order ϒ, $\mathcal{H}_{1}$, $\mathcal{H}_{2}$ and $\mathcal{M}_{1}$, $\mathcal{M}_{2}$ are linear and nonlinear functions, respectively, and $q_{1}$, $q_{2}$ are source operators.

The Laplace transformation is applied to Eq. (1),

$$ \begin{aligned} &{L} \bigl[D_{\eta }^{{\Upsilon }}{{\Phi }({{ \chi }},{\eta })} \bigr]+{L} \bigl[ \mathcal{H}_{1}({\Phi },{\Psi })+ \mathcal{M}_{1}({\Phi },{\Psi })-q_{1}({{ \chi }},{\eta }) \bigr]=0, \\ &{L} \bigl[D_{\eta }^{{\Upsilon }}{{\Psi }({{\chi }},{\eta })} \bigr]+{L} \bigl[\mathcal{H}_{2}({ \Phi },{\Psi })+\mathcal{M}_{2}({\Phi },{\Psi })-q_{2}({{\chi }},{\eta }) \bigr]=0. \end{aligned} $$

(3)

Applying the differentiation property, we have

$$ \begin{aligned} &{L} \bigl[{{\Phi }({{\chi }},{\eta })} \bigr]-\sum _{k=0}^{m-1}s^{{{ \Upsilon }}-k-1} \frac{\partial ^{k}{\Phi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0}=-{L} \bigl[\mathcal{H}_{1}({\Phi },{\Psi })+\mathcal{M}_{1}({ \Phi },{\Psi })-q_{1}({{\chi }},{\eta }) \bigr], \\ &{L} \bigl[{{\Psi }({{\chi }},{\eta })} \bigr]-\sum _{k=0}^{m-1}s^{{{\Upsilon }}-k-1} \frac{\partial ^{k}{\Psi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0}=-{L} \bigl[\mathcal{H}_{2}({\Phi },{\Psi })+ \mathcal{M}_{2}({ \Phi },{\Psi })-q_{2}({{\chi }},{\eta }) \bigr]. \end{aligned} $$

(4)

Using the iterative technique, we get

$$ \begin{gathered} \begin{aligned} {L} \bigl[{{\Phi }_{m+1}({{ \chi }},{\eta })} \bigr]={}&{L} \bigl[{{\Phi }_{m}({{ \chi }},{\eta })} \bigr] \\ &{}+\lambda (s) \Biggl[{s^{{{\Upsilon }}}} {{\Phi }_{m}({{ \chi }},{ \eta })}-\sum_{k=0}^{m-1}s^{{{\Upsilon }}-k-1} \frac{\partial ^{k}{\Phi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0}-{L} \bigl[q_{1}({{\chi }},{\eta }) \bigr] \\ &{}-{L} \bigl\{ \mathcal{H}_{1}({\Phi },{\Psi })+\mathcal{M}_{1}({ \Phi },{ \Psi }) \bigr\} \Biggr], \end{aligned} \\ \begin{aligned} {L} \bigl[{{\Psi }_{m+1}({{\chi }},{\eta })} \bigr]={}&{L} \bigl[{{\Psi }_{m}({{\chi }},{\eta })} \bigr] \\ &{}+ \lambda (s) \Biggl[{s^{{{\Upsilon }}}} {{\Psi }_{m}({{\chi }},{\eta })}- \sum _{k=0}^{m-1}s^{{{\Upsilon }}-k-1} \frac{\partial ^{k}{\Psi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0}-{L} \bigl[q_{2}({{\chi }},{\eta }) \bigr] \\ &{}-{L} \bigl\{ \mathcal{H}_{2}({\Phi },{\Psi })+\mathcal{M}_{2}({ \Phi },{ \Psi }) \bigr\} \Biggr]. \end{aligned} \end{gathered} $$

(5)

A Lagrange multiplier as

$$ \lambda (s)=-\frac{1}{s^{{\Upsilon }}}, $$

(6)

the inverse Laplace transformation ${L^{-1}}$, the iteration method Eq. (5) can be given as follows:

$$\begin{aligned}& \begin{aligned}[b] {{\Phi }_{m+1}({{\chi }},{\eta })}={}&{{\Phi }_{m}({{\chi }},{ \eta })}-{L^{-1}} \Biggl[ \frac{1}{s^{{\Upsilon }}} \Biggl[\sum _{k=0}^{m-1}s^{{{ \Upsilon }}-k-1} \frac{\partial ^{k}{\Phi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0} \\ &{}-{L} \bigl[q_{1}({{\chi }},{\eta }) \bigr]-{L} \bigl\{ \mathcal{H}_{1}({ \Phi },{\Psi })+\mathcal{M}_{1}({\Phi },{ \Psi }) \bigr\} \Biggr] \Biggr], \end{aligned} \\& \begin{aligned} {{\Psi }_{m+1}({{\chi }},{\eta })}={}&{{\Psi }_{m}({{\chi }},{ \eta })}-{L^{-1}} \Biggl[ \frac{1}{s^{{\Upsilon }}} \Biggl[\sum_{k=0}^{m-1}s^{{{\Upsilon }}-k-1} \frac{\partial ^{k}{\Psi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0} \\ &{}-{L} \bigl[q_{2}({{\chi }},{\eta }) \bigr]-{L} \bigl\{ \mathcal{H}_{2}({ \Phi },{\Psi })+\mathcal{M}_{2}({\Phi },{ \Psi }) \bigr\} \Biggr] \Biggr]. \end{aligned} \end{aligned}$$

(7)

The initial iteration can be found as follows:

$$ \begin{aligned} &{{\Phi }_{0}({{\chi }},{\eta })}={L^{-1}} \Biggl[ \frac{1}{s^{{\Upsilon }}} \Biggl\{ \sum _{k=0}^{m-1}s^{{{\Upsilon }}-k-1} \frac{\partial ^{k}{\Phi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0} \Biggr\} \Biggr], \\ &{{\Psi }_{0}({{\chi }},{\eta })}={L^{-1}} \Biggl[ \frac{1}{s^{{\Upsilon }}} \Biggl\{ \sum_{k=0}^{m-1}s^{{{\Upsilon }}-k-1} \frac{\partial ^{k}{\Psi }({{\chi }},{\eta })}{\partial ^{k}{\eta }}\bigg| _{{ \eta }=0} \Biggr\} \Biggr]. \end{aligned} $$

(8)

The conveniences of this technique were shown in [52, 53].

4 Numerical examples

Example 1

Consider the time fractional-order $(1+1)$ dimensional Navier–Stokes equation

$$ \begin{aligned} &D_{\eta }^{{{\Upsilon }}}{({\Phi })}+{{{\Phi }}} \frac{\partial {{{\Phi }}}}{\partial {{{\chi }}}}+{{{\Psi }}} \frac{\partial {{{\Phi }}}}{\partial {{{\varphi }}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{{\varphi }}^{2}}}} \biggr]+{q}, \\ &D_{\eta }^{{{\Upsilon }}}{({\Psi })}+{{{\Phi }}} \frac{\partial {{{\Psi }}}}{\partial {{{\chi }}}}+{{{ \Psi }}} \frac{\partial {{{\Psi }}}}{\partial {{{\varphi }}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{{\varphi }}^{2}}}} \biggr]-{q}, \end{aligned} $$

(9)

with the initial conditions

$$ \textstyle\begin{cases} {{\Phi }({{\chi }},{{\varphi }},0)}=-\sin ({{{\chi }}+{{\varphi }}}), \\ {{\Psi }({{\chi }},{{\varphi }},0)}=\sin ({{{\chi }}+{{\varphi }}}). \end{cases} $$

(10)

Using the iterative method according to equation (7) in equation (9), we get

$$ \begin{gathered} \begin{aligned} {\Phi }_{m+1}({{\chi }},{{ \varphi }},{\eta })={}&{\Phi }_{m}({{ \chi }},{{\varphi }},{\eta })-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Phi }_{m}}{\partial {\eta }} \\ &{}+{{{\Phi }_{m}}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{{\chi }}}}+{{{\Psi }_{m}}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\ \begin{aligned} {\Psi }_{m+1}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{m}({{ \chi }},{{ \varphi }},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{m}}{\partial {\eta }} \\ &{}+{{{\Phi }_{m}}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{{\chi }}}}+{{{\Psi }_{m}}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \end{gathered} $$

(11)

where

$$ {\Phi }_{0}({{\chi }},{{\varphi }},{\eta })=-\sin ({{{\chi }}+{{ \varphi }}}),\quad\quad {\Psi }_{0}({{\chi }},{{ \varphi }},{ \eta })=\sin ({{{\chi }}+{{ \varphi }}}). $$

(12)

For $m=0,1,2,\ldots$ ,

$$\begin{aligned}& \begin{aligned} {\Phi }_{1}({{\chi }},{{\varphi }},{\eta })={}&{\Phi }_{0}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Phi }_{0}}{\partial {\eta }}+{{{ \Phi }_{0}}}\frac{\partial {{{\Phi }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Phi }_{0}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Psi }_{1}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{0}({{ \chi }},{{ \varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{0}}{\partial {\eta }}+{{{\Phi }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \\& {\Phi }_{1}({{\chi }},{{\varphi }},{\eta })=-\sin ({{{\chi }}+{{ \varphi }}})+ \sin ({{{\chi }}+{{\varphi }}}) \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\& {\Psi }_{1}({{\chi }},{{\varphi }},{\eta })=\sin ({{{\chi }}+{{ \varphi }}})- \sin ({{{\chi }}+{{\varphi }}}) \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\& \begin{aligned} {\Phi }_{2}({{\chi }},{{\varphi }},{\eta })={}&{\Phi }_{1}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Phi }_{1}}{\partial {\eta }}+{{{ \Phi }_{1}}} \frac{\partial {{{\Phi }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Phi }_{1}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Psi }_{2}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{1}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Psi }_{1}}{\partial {\eta }}+{{{ \Phi }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \\& {\Phi }_{2}({{\chi }},{{\varphi }},{\eta })=-\sin ({{{\chi }}+{{ \varphi }}})+\sin ({{{\chi }}+{{\varphi }}}) \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}-\sin ({{{\chi }}+{{ \varphi }}}) \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}, \\& {\Psi }_{2}({{\chi }},{{\varphi }},{\eta })=\sin ({{{\chi }}+{{\varphi }}})- \sin ({{{\chi }}+{{\varphi }}}) \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+\sin ({{{\chi }}+{{ \varphi }}}) \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}, \\& \begin{aligned} {\Phi }_{3}({{\chi }},{{\varphi }},{\eta })={}&{\Phi }_{2}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Phi }_{2}}{\partial {\eta }}+{{{ \Phi }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Psi }_{3}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{2}({{ \chi }},{{ \varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{2}}{\partial {\eta }}+{{{\Phi }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Phi }_{3}({{\chi }},{{\varphi }},{\eta })&=-\sin ({{{\chi }}+{{ \varphi }}})+\sin ({{{\chi }}+{{\varphi }}}) \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)} \\ &\quad{} -\sin ({{{\chi }}+{{\varphi }}}) \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}+ \sin ({{{\chi }}+{{\varphi }}}) \frac{(2\rho )^{3}{\eta }^{3{{\Upsilon }}}}{\Gamma (3{{\Upsilon }}+1)}, \end{aligned} \\& \begin{aligned} {\Psi }_{3}({{\chi }},{{\varphi }},{\eta })={}&\sin ({{{\chi }}+{{\varphi }}})- \sin ({{{\chi }}+{{\varphi }}}) \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)} \\ &{}+\sin ({{{\chi }}+{{\varphi }}}) \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}- \sin ({{{\chi }}+{{ \varphi }}}) \frac{(2\rho )^{3}{\eta }^{3{{\Upsilon }}}}{\Gamma (3{{\Upsilon }}+1)}, \end{aligned} \\& \begin{gathered} {\Phi }({{\chi }},{{\varphi }},{\eta })=\sum _{m=0}^{\infty }{ \Phi }_{m}({{\chi }},{{\varphi }})=-\sin ({{{\chi }}+{{\varphi }}})\sum _{m=0}^{ \infty } \frac{(-2\rho )^{m}{\eta }^{m{{\Upsilon }}}}{\Gamma (m{{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\ {\Psi }({{\chi }},{{\varphi }},{\eta })=\sum_{m=0}^{\infty }{ \Phi }_{m}({{ \chi }},{{\varphi }})=\sin ({{{\chi }}+{{\varphi }}}) \sum_{m=0}^{\infty } \frac{(-2\rho )^{m}{\eta }^{m{{\Upsilon }}}}{\Gamma (m{{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}. \end{gathered} \end{aligned}$$

(13)

The exact solution of equation (9) at ${{\Upsilon }}=1$ and $q=0$,

$$ \begin{aligned} &{\Phi }({{\chi }},{{\varphi }},{\eta })=-e^{-2\rho {\eta }} \sin ({{{\chi }}+{{\varphi }}}), \\ &{\Psi }({{\chi }},{{\varphi }},{\eta })=e^{-2\rho {\eta }}\sin ({{{\chi }}+{{ \varphi }}}). \end{aligned} $$

(14)

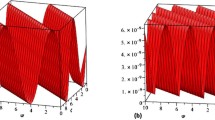
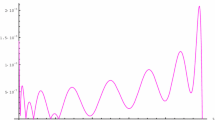
Figures 1 and 4 show the behavior of solutions of the exact and analytical results using the initial conditions given in equation (10). In Fig. 1 the exact and analytical solutions of Φ at ${\Upsilon }=1$ show close contact with each other. In Figs. 2 and 3 for different values of ${\Upsilon }=0.8,0.6$, and 0.4 for Φ. In Fig. 4, we show the exact and analytical solution of Ψ at ${\Upsilon }=1$. In Figs. 5 and 6 for different values of ${\Upsilon }=0.8,0.6$, and 0.4 for Ψ. The fractional results are investigated to be convergent to an integer-order result of each problem.

Figure 1

The graph of exact (a) and approximate (b) solution of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=1$ of Example 1

Figure 2

The graph of different approximate solution of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ at ϒ = (c) 0.8 and (d) 0.6 of Example 1

Figure 3

The graph of approximate solution (e) of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=0.4$ of Example 1

Figure 4

The graph of exact (a) and approximate (b) solution of ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=1$ of Example 1

Figure 5

The graph of different approximate solution of ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ϒ = (c) 0.8 and (d) 0.6 of Example 1

Figure 6

The graph of approximate solution (e) of ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=0.4$ of Example 1

Example 2

Consider the time fractional-order $(1+1)$ dimensional Navier–Stokes equation

$$ \begin{aligned} &D_{\eta }^{{{\Upsilon }}}{({\Phi })}+{{{\Phi }}} \frac{\partial {{{\Phi }}}}{\partial {{{\chi }}}}+{{{\Psi }}} \frac{\partial {{{\Phi }}}}{\partial {{{\varphi }}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{{\varphi }}^{2}}}} \biggr]+{q}, \\ &D_{\eta }^{{{\Upsilon }}}{({\Psi })}+{{{\Phi }}} \frac{\partial {{{\Psi }}}}{\partial {{{\chi }}}}+{{{ \Psi }}} \frac{\partial {{{\Psi }}}}{\partial {{{\varphi }}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{{\varphi }}^{2}}}} \biggr]-{q}, \end{aligned} $$

(15)

with the initial conditions

$$ \textstyle\begin{cases} {{\Phi }({{\chi }},{{\varphi }},0)}=-e^{{{\chi }}+{{\varphi }}}, \\ {{\Psi }({{\chi }},{{\varphi }},0)}=e^{{{\chi }}+{{\varphi }}}. \end{cases} $$

(16)

Using the iterative method according to equation (7) in equation (15), we get

$$ \begin{gathered} \begin{aligned} {\Phi }_{m+1}({{\chi }},{{ \varphi }},{\eta })={}&{\Phi }_{m}({{ \chi }},{{\varphi }},{\eta })-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Phi }_{m}}{\partial {\eta }} \\ &{}+{{{\Phi }_{m}}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{{\chi }}}}+{{{\Psi }_{m}}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\ \begin{aligned} {\Psi }_{m+1}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{m}({{\chi }},{{ \varphi }},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{m}}{\partial {\eta }} \\ &{}+{{{\Phi }_{m}}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{{\chi }}}}+{{{\Psi }_{m}}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \end{gathered} $$

(17)

where

$$ {\Phi }_{0}({{\chi }},{{\varphi }},{\eta })=-e^{{{\chi }}+{{ \varphi }}},\quad\quad {\Psi }_{0}({{\chi }},{{\varphi }},{ \eta })=e^{{{\chi }}+{{ \varphi }}}. $$

(18)

For $m=0,1,2,\ldots$ ,

$$\begin{aligned}& \begin{aligned} {\Phi }_{1}({{\chi }},{{\varphi }},{\eta })={}&{\Phi }_{0}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Phi }_{0}}{\partial {\eta }}+{{{ \Phi }_{0}}}\frac{\partial {{{\Phi }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Phi }_{0}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Psi }_{1}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{0}({{ \chi }},{{ \varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{0}}{\partial {\eta }}+{{{\Phi }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \\& {\Phi }_{1}({{\chi }},{{\varphi }},{\eta })=-e^{{{\chi }}+{{\varphi }}}+e^{{{ \chi }}+{{\varphi }}} \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\& {\Psi }_{1}({{\chi }},{{\varphi }},{\eta })=e^{{{\chi }}+{{\varphi }}}-e^{{{ \chi }}+{{\varphi }}} \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\& \begin{aligned} {\Phi }_{2}({{\chi }},{{\varphi }},{\eta })={}&{\Phi }_{1}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Phi }_{1}}{\partial {\eta }}+{{{ \Phi }_{1}}}\frac{\partial {{{\Phi }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Phi }_{1}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Psi }_{2}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{1}({{ \chi }},{{ \varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{1}}{\partial {\eta }}+{{{\Phi }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \\& {\Phi }_{2}({{\chi }},{{\varphi }},{\eta })=-e^{{{\chi }}+{{ \varphi }}}+e^{{{\chi }}+{{\varphi }}} \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}-e^{{{\chi }}+{{ \varphi }}} \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}, \\& {\Psi }_{2}({{\chi }},{{\varphi }},{\eta })=e^{{{\chi }}+{{\varphi }}}-e^{{{ \chi }}+{{\varphi }}} \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+e^{{{\chi }}+{{ \varphi }}} \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}, \\& \begin{aligned} {\Phi }_{3}({{\chi }},{{\varphi }},{\eta })={}&{\Phi }_{2}({{ \chi }},{{\varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}}\frac{\partial {\Phi }_{2}}{\partial {\eta }}+{{{ \Phi }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{{\varphi }}^{2}}}} \biggr)-{q} \biggr\} \biggr], \end{aligned} \\& \begin{aligned} {\Psi }_{3}({{\chi }},{{\varphi }},{\eta })={}&{\Psi }_{2}({{ \chi }},{{ \varphi }},{\eta }) \\ &{}-{L^{-1}} \biggl[\frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{ \Upsilon }}}}\frac{\partial {\Psi }_{2}}{\partial {\eta }}+{{{\Phi }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{{\varphi }}}}-{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{{\varphi }}^{2}}}} \biggr)+{q} \biggr\} \biggr], \end{aligned} \\& {\Phi }_{3}({{\chi }},{{\varphi }},{\eta })=-e^{{{\chi }}+{{ \varphi }}}+e^{{{\chi }}+{{\varphi }}} \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}-e^{{{\chi }}+{{ \varphi }}} \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}+e^{{{ \chi }}+{{\varphi }}} \frac{(2\rho )^{3}{\eta }^{3{{\Upsilon }}}}{\Gamma (3{{\Upsilon }}+1)}, \\& {\Psi }_{3}({{\chi }},{{\varphi }},{\eta })=e^{{{\chi }}+{{\varphi }}}-e^{{{ \chi }}+{{\varphi }}} \frac{2\rho {\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+e^{{{\chi }}+{{ \varphi }}} \frac{(2\rho )^{2}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}-e^{{{ \chi }}+{{\varphi }}} \frac{(2\rho )^{3}{\eta }^{3{{\Upsilon }}}}{\Gamma (3{{\Upsilon }}+1)}, \\& \begin{gathered} {\Phi }({{\chi }},{{\varphi }},{\eta })=\sum _{m=0}^{\infty }{ \Phi }_{m}({{\chi }},{{\varphi }})=-e^{{{\chi }}+{{\varphi }}}\sum_{m=0}^{ \infty } \frac{(-2\rho )^{m}{\eta }^{m{{\Upsilon }}}}{\Gamma (m{{\Upsilon }}+1)}+ \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\ {\Psi }({{\chi }},{{\varphi }},{\eta })=\sum_{m=0}^{\infty }{ \Phi }_{m}({{ \chi }},{{\varphi }})=e^{{{\chi }}+{{\varphi }}}\sum _{m=0}^{\infty } \frac{(-2\rho )^{m}{\eta }^{m{{\Upsilon }}}}{\Gamma (m{{\Upsilon }}+1)}- \frac{q{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}. \end{gathered} \end{aligned}$$

(19)

The exact result of equation (15) at ${{\Upsilon }}=1$ and $q=0$,

$$ \begin{aligned} &{\Phi }({{\chi }},{{\varphi }},{\eta })=-e^{{{\chi }}+{{ \varphi }}+2\rho {\eta }}, \\ &{\Psi }({{\chi }},{{\varphi }},{\eta })=e^{{{\chi }}+{{\varphi }}+2\rho { \eta }}. \end{aligned} $$

(20)

Figures 7 and 10 show the behavior of solutions of the exact and analytical results using the initial conditions given in equation (16). In Fig. 7, the exact and analytical solutions of Φ at ${\Upsilon }=1$ show close contact with each other. In Figs. 7 and 9 for different values of ${\Upsilon }=0.8,0.6$, and 0.4 for Φ. In Fig. 10, we show the exact and analytical solution of Ψ at ${\Upsilon }=1$. In Figs. 11 and 12 for different values of ${\Upsilon }=0.8,0.6$, and 0.4 for Ψ. The fractional results are investigated to be convergent to an integer-order result of each problem.

Figure 7

The graph of exact (a) and approximate (b) solution of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=1$ of Example 2

Figure 8

The graph of different approximate solution of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ at ϒ = (c) 0.8 and (d) 0.6 of Example 2

Figure 9

The graph of approximate (e) solution of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=0.4$ of Example 2

Figure 10

The graph of exact (a) and approximate (b) solution of ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=1$ of Example 2

Figure 11

The graph of different approximate solution of ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ϒ = (c) 0.8 and (d) 0.6 of Example 2

Figure 12

The graph of approximate (e) solution of ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=0.4$ of Example 2

Example 3

Consider the time fractional-order $(2+1)$ dimensional Navier–Stokes equation

$$\begin{aligned}& D_{\eta }^{{{\Upsilon }}}{({\Phi })}+{{{\Phi }}} \frac{\partial {{{\Phi }}}}{\partial {{{\chi }}}}+{{{\Psi }}} \frac{\partial {{{\Phi }}}}{\partial {{{\varphi }}}}+{{{\Theta }}} \frac{\partial {{{\Phi }}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr]+q_{1}, \\& D_{\eta }^{{{\Upsilon }}}{({\Psi })}+{{{\Phi }}} \frac{\partial {{{\Psi }}}}{\partial {{{\chi }}}}+{{{\Psi }}} \frac{\partial {{{\Psi }}}}{\partial {{{\varphi }}}}+{{{\Theta }}} \frac{\partial {{{\Psi }}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr]+{q_{2}}, \\& D_{\eta }^{{{\Upsilon }}}{({\Theta })}+{{{\Phi }}} \frac{\partial {{{\Theta }}}}{\partial {{{\chi }}}}+{{{ \Psi }}} \frac{\partial {{{\Theta }}}}{\partial {{{\varphi }}}}+{{{\Theta }}} \frac{\partial {{{\Theta }}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl[{ \frac{\partial ^{2}{{{\Theta }}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr]+{q_{3}}, \end{aligned}$$

(21)

with the initial conditions

$$ \textstyle\begin{cases} {{\Phi }({{\chi }},{{\varphi }},{\mathcal{Z}},0)}=-0.5{{\chi }}+{{ \varphi }}+{\mathcal{Z}}, \\ {{\Psi }({{\chi }},{{\varphi }},{\mathcal{Z}},0)}={{\chi }}-0.5{{\varphi }}+{ \mathcal{Z}}, \\ {{\Theta }({{\chi }},{{\varphi }},{\mathcal{Z}},0)}={{\chi }}+{{\varphi }}-0.5{ \mathcal{Z}}. \end{cases} $$

(22)

Further, if ρ is known, then $q_{1}=-\frac{1}{\rho }\frac{\partial g}{\partial {{\chi }}}$, $q_{2}=-\frac{1}{\rho }\frac{\partial g}{\partial {{\varphi }}}$, and $q_{1}=-\frac{1}{\rho }\frac{\partial g}{\partial {\mathcal{Z}}}$ can be determined.

According to equation (7), the iteration formulas for equation (21) are as follows:

$$ \begin{gathered} \begin{aligned} &{\Phi }_{m+1}({{\chi }},{{ \varphi }},{ \mathcal{Z}},{\eta }) \\ &\quad ={ \Phi }_{m}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Phi }_{m}}{\partial {\eta }} \\ &\quad\quad {}+{{{\Phi }_{m}}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{{\chi }}}}+{{{\Psi }}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{{\varphi }}}}+{{{\Theta }}} \frac{\partial {{{\Phi }_{m}}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{m}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr)+q_{1} \biggr\} \biggr], \end{aligned} \\ \begin{aligned} &{\Psi }_{m+1}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta }) \\ &\quad ={\Psi }_{m}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{m}}{\partial {\eta }} \\ &\quad\quad {}+{{{\Phi }_{m}}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{{\chi }}}}+{{{\Psi }_{m}}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{{\varphi }}}}+{{{\Theta }}} \frac{\partial {{{\Psi }_{m}}}}{\partial {{\mathcal{Z}}}}={\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{m}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr)+{q_{2}} \biggr\} \biggr], \end{aligned} \\ \begin{aligned} &{\Theta }_{m+1}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta }) \\ &\quad ={\Theta }_{m}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{m}}{\partial {\eta }} \\ &\quad\quad {}+{{{ \Phi }_{m}}}\frac{\partial {{{\Theta }_{m}}}}{\partial {{{\chi }}}}+{{{ \Psi }_{m}}} \frac{\partial {{{\Theta }_{m}}}}{\partial {{{\varphi }}}}+{{{ \Theta }_{m}}}\frac{\partial {{{\Theta }_{m}}}}{\partial {{\mathcal{Z}}}}={ \rho } \biggl({ \frac{\partial ^{2}{{{\Theta }_{m}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{m}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{m}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr)+{q_{3}} \biggr\} \biggr], \end{aligned} \end{gathered} $$

(23)

with the initial conditions

$$ \textstyle\begin{cases} {{\Phi }({{\chi }},{{\varphi }},{\mathcal{Z}},0)}=-0.5{{\chi }}+{{ \varphi }}+{\mathcal{Z}}, \\ {{\Psi }({{\chi }},{{\varphi }},{\mathcal{Z}},0)}={{\chi }}-0.5{{\varphi }}+{ \mathcal{Z}}, \\ {{\Theta }({{\chi }},{{\varphi }},{\mathcal{Z}},0)}={{\chi }}+{{\varphi }}-0.5{ \mathcal{Z}}. \end{cases} $$

(24)

Then $q_{1}$, $q_{2}$, and $q_{3}$ are equal to zero. For $m=0,1,2,\ldots$ ,

$$\begin{aligned}& \begin{aligned} {\Phi }_{1}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })={}&{ \Phi }_{0}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Phi }_{0}}{\partial {\eta }}+{{{\Phi }_{0}}} \frac{\partial {{{\Phi }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Phi }_{0}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{0}}} \frac{\partial {{{\Phi }_{0}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{0}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Psi }_{1}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{\Psi }_{0}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{0}}{\partial {\eta }}+{{{ \Phi }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{0}}} \frac{\partial {{{\Psi }_{0}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{0}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Theta }_{1}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{\Theta }_{0}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{0}}{\partial {\eta }}+{{{ \Phi }_{0}}} \frac{\partial {{{\Theta }_{0}}}}{\partial {{{\chi }}}}+{{{\Psi }_{0}}} \frac{\partial {{{\Theta }_{0}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{0}}} \frac{\partial {{{\Theta }_{0}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Theta }_{0}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{0}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{0}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & {\Phi }_{1}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })=-0.5{{ \chi }}+{{\varphi }}+{\mathcal{Z}}- \frac{2.25 {{\chi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\ & {\Psi }_{1}({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={{\chi }}-0.5{{ \varphi }}+{\mathcal{Z}}- \frac{2.25 {{\varphi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\ & {\Theta }_{1}({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={{\chi }}+{{ \varphi }}-0.5{\mathcal{Z}}- \frac{2.25 {\mathcal{Z}}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}, \\ & \begin{aligned} {\Phi }_{2}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })={}&{ \Phi }_{1}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Phi }_{1}}{\partial {\eta }}+{{{\Phi }_{1}}} \frac{\partial {{{\Phi }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Phi }_{1}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{1}}} \frac{\partial {{{\Phi }_{1}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{1}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Psi }_{2}({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={}&{\Psi }_{1}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{1}}{\partial {\eta }}+{{{ \Phi }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{1}}} \frac{\partial {{{\Psi }_{1}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{1}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Theta }_{2}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{\Theta }_{1}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{1}}{\partial {\eta }}+{{{ \Phi }_{1}}} \frac{\partial {{{\Theta }_{1}}}}{\partial {{{\chi }}}}+{{{\Psi }_{1}}} \frac{\partial {{{\Theta }_{1}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{1}}} \frac{\partial {{{\Theta }_{1}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Theta }_{1}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{1}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{1}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & {\Phi }_{2}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })=-0.5{{ \chi }}+{{\varphi }}+{\mathcal{Z}}- \frac{2.25 {{\chi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {{\chi }}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}(-0.5{{ \chi }}+{{\varphi }}+{ \mathcal{Z}},) \\ & {\Psi }_{2}({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={{\chi }}-0.5{{ \varphi }}+{\mathcal{Z}}- \frac{2.25 {{\varphi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {{\varphi }}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}({{ \chi }}-0.5{{\varphi }}+{\mathcal{Z}}), \\ & {\Theta }_{2}({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={{\chi }}+{{ \varphi }}-0.5{\mathcal{Z}}- \frac{2.25 {\mathcal{Z}}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {\mathcal{Z}}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)}({{ \chi }}+{{\varphi }}-0.5{\mathcal{Z}}), \\ & \begin{aligned} {\Phi }_{3}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })={}&{ \Phi }_{2}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Phi }_{2}}{\partial {\eta }}+{{{\Phi }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{2}}} \frac{\partial {{{\Phi }_{2}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Phi }_{2}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Psi }_{3}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{\Psi }_{2}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{2}}{\partial {\eta }}+{{{ \Phi }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{2}}} \frac{\partial {{{\Psi }_{2}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Psi }_{2}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Theta }_{3}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{\Theta }_{2}({{ \chi }},{{\varphi }},{\mathcal{Z}},{\eta })-{L^{-1}} \biggl[ \frac{1}{s^{{\Upsilon }}}{L} \biggl\{ {s^{{{\Upsilon }}}} \frac{\partial {\Psi }_{2}}{\partial {\eta }}+{{{ \Phi }_{2}}} \frac{\partial {{{\Theta }_{2}}}}{\partial {{{\chi }}}}+{{{\Psi }_{2}}} \frac{\partial {{{\Theta }_{2}}}}{\partial {{{\varphi }}}}+{{{\Theta }_{2}}} \frac{\partial {{{\Theta }_{2}}}}{\partial {{\mathcal{Z}}}} \\ &{}+{\rho } \biggl({ \frac{\partial ^{2}{{{\Theta }_{2}}}}{\partial {{{\chi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{2}}}}{\partial {{{\varphi }}^{2}}}}+{ \frac{\partial ^{2}{{{\Theta }_{2}}}}{\partial {{\mathcal{Z}}^{2}}}} \biggr) \biggr\} \biggr], \end{aligned} \\ & \begin{aligned} {\Phi }_{3}({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })={}&{-}0.5{{ \chi }}+{{\varphi }}+{\mathcal{Z}}- \frac{2.25 {{\chi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {{\chi }}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)} \\ &{}\times (-0.5{{\chi }}+{{\varphi }}+{\mathcal{Z}})- \frac{(2.25)^{2} {{\chi }}(4(\Gamma ({{\Upsilon }}+1))^{2}+\Gamma (2{{\Upsilon }}+1)){\eta }^{3{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1) (\Gamma ({{\Upsilon }}+1))^{2}}, \end{aligned} \\ & \begin{aligned} {\Psi }_{3}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{{\chi }}-0.5{{ \varphi }}+{\mathcal{Z}}- \frac{2.25 {{\varphi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {{\varphi }}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)} \\ &{}\times ({{\chi }}-0.5{{\varphi }}+{\mathcal{Z}})- \frac{(2.25)^{2} {{\varphi }}(4(\Gamma ({{\Upsilon }}+1))^{2}+\Gamma (2{{\Upsilon }}+1)){\eta }^{3{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)(\Gamma ({{\Upsilon }}+ 1))^{2}}, \end{aligned} \\ & \begin{aligned} {\Theta }_{3}({{\chi }},{{\varphi }},{\mathcal{Z}},{ \eta })={}&{{\chi }}+{{ \varphi }}-0.5{\mathcal{Z}}- \frac{2.25 {\mathcal{Z}}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {\mathcal{Z}}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)} \\ &{}\times ({{\chi }}+{{\varphi }}-0.5{\mathcal{Z}})- \frac{(2.25)^{2} {\mathcal{Z}}(4(\Gamma ({{\Upsilon }}+1))^{2}+\Gamma (2{{\Upsilon }}+1)){\eta }^{3{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)(\Gamma ({{\Upsilon }}+ 1))^{2}}. \end{aligned} \end{aligned}$$

In the same procedure, the remaining ${\Phi }_{m}$, ${\Psi }_{m}$, and ${\Theta }_{m}$ ($m>3$) components of the VITM solution can be obtained smoothly.

$$ \begin{gathered} \begin{aligned} {\Phi }({{\chi }},{{\varphi }},{ \mathcal{Z}},{\eta })={}&{-}0.5{{ \chi }}+{{\varphi }}+{\mathcal{Z}}- \frac{2.25 {{\chi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {{\chi }}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)} \\ &{}\times (-0.5{{\chi }}+{{\varphi }}+{\mathcal{Z}})- \frac{(2.25)^{2} {{\chi }}(4({\mathcal{Z}}({{\Upsilon }}+1))^{2}+\Gamma (2{{\Upsilon }}+1)){\eta }^{3{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)(\Gamma ({{\Upsilon }}+1))^{2}}+ \cdots , \end{aligned} \\ \begin{aligned} {\Psi }({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={}&{{\chi }}-0.5{{ \varphi }}+{\mathcal{Z}}- \frac{2.25 {{\varphi }}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {{\varphi }}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)} \\ &{}\times ({{\chi }}-0.5{{\varphi }}+{\mathcal{Z}})- \frac{(2.25)^{2} {{\varphi }}(4(\Gamma ({{\Upsilon }}+1))^{2}+\Gamma (2{{\Upsilon }}+1)){\eta }^{3{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)(\Gamma ({{\Upsilon }}+1))^{2}}+ \cdots , \end{aligned} \\ \begin{aligned} {\Theta }({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })={}&{{ \chi }}+{{ \varphi }}-0.5{\mathcal{Z}}- \frac{2.25 {\mathcal{Z}}{\eta }^{{\Upsilon }}}{\Gamma ({{\Upsilon }}+1)}+ \frac{2(2.25) {\mathcal{Z}}{\eta }^{2{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)} \\ &{}\times ({{\chi }}+{{\varphi }}-0.5{\mathcal{Z}})- \frac{(2.25)^{2} {\mathcal{Z}}(4(\Gamma ({{\Upsilon }}+1))^{2}+\Gamma (2{{\Upsilon }}+1)){\eta }^{3{{\Upsilon }}}}{\Gamma (2{{\Upsilon }}+1)(\Gamma ({{\Upsilon }}+1))^{2}}+ \cdots . \end{aligned} \end{gathered} $$

The exact result of equation (21) at ${{\Upsilon }}=1$ and $q_{1}=q_{2}=q_{3}=0$ is as follows:

$$ \begin{aligned} &{\Phi }({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })= \frac{-0.5{{\chi }}+{{\varphi }}+{\mathcal{Z}}-2.25{{\chi }}{\eta }}{1-2.25{\eta }^{2}}, \\ &{\Psi }({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })= \frac{{{\chi }}-0.5{{\varphi }}+{\mathcal{Z}}-2.25{{\varphi }}{\eta }}{1-2.25{\eta }^{2}}, \\ &{\Theta }({{\chi }},{{\varphi }},{\mathcal{Z}},{\eta })= \frac{{{\chi }}+{{\varphi }}-0.5{\mathcal{Z}}-2.25{\mathcal{Z}}{\eta }}{1-2.25{\eta }^{2}}. \end{aligned} $$

(25)

Figures 13 and 14 show the behavior of solutions of the exact and analytical results using the initial conditions given in equation (22). In Fig. 13 (a) of Φ, subfigure (b) of Ψ, and Fig. 14 of Θ the exact and analytical solutions at ${\Upsilon }=1$ show close contact with each other.

Figure 13

The (a) graph of exact and approximate solution of ${\Phi }({{\chi }},{{\varphi }},{\eta })$ (b) ${\Psi }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=1$ of Example 3

Figure 14

The graph of exact and approximate solution of ${\Theta }({{\chi }},{{\varphi }},{\eta })$ at ${{\Upsilon }}=1$ of Example 3

5 Conclusion

In this article, we evaluated the fractional-order multi-dimensional Navier–Stokes equations using a variational iteration transform technique. The solutions for specific examples are explained using the current method. The VITM result is in close contact with the exact result of the given problems. The graphical analysis of the fractional-order solutions obtained has verified the convergence towards the solutions of integer order. One may see that the obtained results are in excellent agreement with FRDTM [54] and HPETM [48]. Moreover, the present technique is straightforward, simple, and carrying less computational cost; the suggested method can be modified to solve other fractional-order partial differential equations.