1 Introduction

In recent years, due to the wide applications of fractional differential equations (FDEs) in nonlinear science [1], many phenomena can be described successfully by using FDEs such as chaotic oscillations [2], electrochemistry [3], engineering [4] and so on [5]. Searching for exact solutions of these FDEs plays an important and significant role in the study on the dynamics of those phenomena. Many powerful methods have been proposed to handle this subject, such as the Darboux transformation method [6], the split-step Fourier transform method [7], the fractional characteristic method [8, 9]. But because of the complexity of the nonlinear terms, most FDEs do not have exact analytic solutions, so approximate and numerical methods must be used. Many efforts have been proposed for these problems, including the homotopy analysis method (HAM) [10], the homotopy perturbation method (HPM) [11], the adomian decomposition method (ADM) [12].

The variational iteration method (VIM) and the fractional variational iteration method (FVIM) were established in [13] and [14, 15] by He, respectively, and they were thoroughly used by many researchers [16, 17]. Some new developments about the fractional derivative and its application are available in Refs. [18,19,20]. After giving some modification, Hong and Lu proposed the MFVIM for some complex nonlinear partial differential equations with fractional derivative [21]. The motivation of this paper is to construct some exact and approximate solutions for the VFNLS by using the MGMDM and MFVIM.

We give some definitions and properties of the fractional calculus theory which are used further in this paper [22,23,24].

Definition 1

The fractional derivative is defined as the following limit form:

$$ f^{\alpha } = \lim_{h \to 0}\frac{\Delta ^{\alpha } [f(x) - f(0)]}{h ^{\alpha }}. $$

Definition 2

The Riemann–Liouville fractional integral operator of order \(\alpha > 0\) for a function \(f(x)\) is defined as

$$ J_{x}^{\alpha } f(x) = \frac{1}{\varGamma (\alpha )} \int _{0}^{x} (x - \xi )^{\alpha - 1}f(\xi )\,d\xi ,\quad \alpha > 0,x > 0,J_{x}^{0}f(x) = f(x). $$

Also we have the following properties:

$$ J^{\alpha } J^{\beta } f(x) = J^{\alpha + \beta } f(x),\qquad J^{\alpha } J ^{\beta } f(x) = J^{\beta } J^{\alpha } f(x),\qquad J^{\alpha } x^{\gamma } = \frac{\varGamma (\gamma + 1)}{\varGamma (\alpha + \gamma + 1)}x^{\alpha + \gamma }. $$

Definition 3

For \(\alpha > 0\), \(x > 0\), \(f(x) \in C_{ - 1}^{n}\), the Caputo fractional derivative operator of order α on the whole space is defined as

$$ D^{\alpha } f(x) = J^{n - \alpha } D^{n}f(x) = \textstyle\begin{cases} \frac{1}{\varGamma (n - \alpha )}\int _{0}^{x} (x - \xi )^{n - \alpha - 1}f ^{(n)}(\xi )\,d\xi ,\quad n - 1 < \alpha < n,n \in N. \\ \frac{d^{(n)}f(x)}{dx^{n}},\quad \alpha = n. \end{cases} $$

We have the following properties:

$$\begin{aligned}& D^{\alpha } C = 0\quad (C \text{ is a constant}),\qquad D ^{\alpha } x^{\gamma } = \textstyle\begin{cases} \frac{\varGamma (\gamma + 1)}{\varGamma (\gamma - \alpha + 1)}x^{\gamma - \alpha },\quad \gamma > \alpha - 1, \\ 0,\quad \gamma \le \alpha - 1. \end{cases}\displaystyle \\& J^{\alpha } D^{\alpha } f(x) = f(x) - \sum _{k = 0}^{n - 1} f^{(k)} \bigl(0^{ +} \bigr)\frac{x^{k}}{k!},\quad n - 1 < \alpha < n, \qquad D^{\alpha } J^{\alpha } f(x) = f(x). \end{aligned}$$

Definition 4

The fractional derivative of compounded functions is defined as

$$ d^{\alpha } f = \varGamma (1 + \alpha )f. $$

Definition 5

The integral with respect to \(d(x)^{\alpha } \) is defined as the solution of the fractional differential equation

$$ dy = f(x)d(x)^{\alpha },\quad x \ge 0,y(0) = 0. $$

2 Exact solution and their structure of the GFNLS

Consider the following generalized time and space fractional nonlinear Schrödinger equation with variable coefficients:

$$ i\frac{\partial ^{\alpha } u}{\partial z^{\alpha }} + \frac{1}{2}a(z)\frac{ \partial ^{2\beta } u}{\partial t^{2\beta }} + b(z)u \vert u \vert ^{2} - ic(z)u = 0, \quad z > 0,0 < \alpha ,\beta \le 1, $$
(1)

where \(u = u(z,t)\), \(\frac{\partial u^{\alpha }}{\partial z} = D_{z}^{ \alpha } u\), \(\frac{\partial ^{2\beta } u}{\partial t^{2\beta }} = D_{t} ^{\beta } (D_{t}^{\beta } u)\), when \(\alpha = \beta = 1\), this equation turns to the famous nonlinear Schrödinger equations in an optical fiber [25,26,27]. Here \(u(z,t)\) is the complex envelope of the electrical field, z is the normalized propagation distance along the fiber, t is the retarded time and the subscripts denote partial derivatives, the real analytic functions \(a(z)\) and \(b(z)\) are the slowly increasing dispersion coefficient and nonlinear coefficient, respectively, which represent the group velocity dispersion (GVD) and the self-phase modulation (SPM), \(c(z)\) represents the heat-insulating amplification or loss. The transmission of a soliton in the real communication system of an optical soliton is described by Eq. (1) [9].

If we let \(t \to x\), \(z \to t\), Eq. (1) turns to the following form:

$$ i\frac{\partial ^{\alpha } u}{\partial t^{\alpha }} + \frac{1}{2}a(t)\frac{ \partial ^{2\beta } u}{\partial x^{2\beta }} + b(t)u \vert u \vert ^{2} - ic(t)u = 0, \quad t > 0,0 < \alpha ,\beta \le 1. $$
(2)

We can give the complex variable transformation as follows:

$$\begin{aligned}& u = A(t)\varphi (\xi )e^{i\eta }, \end{aligned}$$
(3)
$$\begin{aligned}& \begin{aligned}&\xi = \frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{\varGamma ( \alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} c_{1}(\tau )\,d\tau , \\ & \eta = \frac{k_{2}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{\varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} c_{2}(\tau )\,d\tau , \end{aligned} \end{aligned}$$
(4)

with the following consistency conditions:

$$ A(t) = ke^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0}^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau },\qquad c_{1}(t) = - k_{1}k_{2}a(t), $$
(5)

where k, \(k_{1}\), \(k_{2}\) are arbitrary nonzero constants.

Substituting (3), (4), (5) into (2), we obtain

$$ k_{1}^{2}a(t)\varphi _{\xi \xi } (\xi ) - \bigl[2c_{2}(t) + k_{2}^{2}a(t)\bigr] \varphi (\xi ) + 2b(t)A^{2}(t)\varphi ^{3}(\xi ) = 0, $$
(6)

where \(\varphi _{\xi \xi } (\xi ) = \frac{d^{2}\varphi (\xi )}{d\xi ^{2}}\), with the idea of the homogeneous balance principle, by balancing the highest-order linear term \(\varphi _{\xi \xi } (\xi )\) and the nonlinear \(\varphi ^{3}(\xi )\) in (6), we assume that Eq. (6) has the following solutions:

$$\begin{aligned}& \varphi = \varphi (\xi ) = A_{0} + A_{1}F(\xi ) = A_{0} + A_{1}F, \end{aligned}$$
(7)
$$\begin{aligned}& F^{\prime \,2} = \sum_{i = 0}^{4} a_{i}F^{i}, \end{aligned}$$
(8)

where \(a_{i}\) (\(i = 0,1,2,3,4\)) are constants to be determined. We write \(F = F(\xi )\) and \(F' = \frac{dF(\xi )}{d\xi } \).

Substituting (7) and (8) into (6), and setting the coefficients of \(F^{i}(\xi )\), \(i = 0,1,2, \ldots \) , to zero yield an ODE with respect to the unknowns \(A_{0}\), \(A_{1}\), \(a_{0}\), \(a_{1}\), \(a_{2}\), \(a_{3}\), \(a_{4}\), \(k_{1}\), \(k_{2}\), \(a(t)\), \(b(t)\) and \(c_{2}(t)\). After solving the ODE by Mathematica software we could determine the following solutions:

Case 1

$$\begin{aligned}& A_{0} = a_{1} = a_{3} = 0,\qquad A_{1} = \mathrm{const},\qquad c_{2}(t) = \frac{1}{2}\bigl(a_{2}k _{1}^{2} - k_{2}^{2}\bigr)a(t), \\& b(t) = - a_{4}k_{1}^{2}A_{1}^{ - 2}a(t)A ^{ - 2}(t). \end{aligned}$$

By using the general mapping deformation method [28], we can obtain the following solutions of the corresponding Eq. (2):

$$\begin{aligned}& u_{1_{j}} = kA_{1}e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0}^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k_{2}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{2\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{ \alpha - 1} (a_{2}k_{1}^{2} - k_{2}^{2})a(\tau )\,d\tau ]}F_{1_{j}}( \xi _{1_{j}}), \\& \xi _{1_{j}} = \frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} - \frac{k _{1}k_{2}}{\varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} a( \tau )\,d\tau ,\quad j = 1,2,3, \ldots . \end{aligned}$$

We have the consistency conditions

$$ b(t) = - a_{4}k_{1}^{2}A_{1}^{ - 2}a(t)A^{ - 2}(t). $$

Here \(F_{1_{j}}\) is an arbitrary solution of the equation \(F_{1_{j}}^{\prime \,2} = a_{0_{j}} + a_{2_{j}}F_{1_{j}}^{2} + a_{4_{j}}F_{1_{j}} ^{4}\),we can obtain the 52 classes of exact solutions \(F_{1_{j}}\) from Ref. [29]; for example, if we let \(a_{0_{1}} = 1 - m^{2}\), \(a_{2_{1}} = 2m ^{2} - 1\), \(a_{4_{1}} = - m^{2}\), \(F_{1_{1}} = cn\xi \), we have

$$ u_{1_{1}} = kA_{1}e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0}^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k_{2}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{2\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{ \alpha - 1} ((2m^{2} - 1)k_{1}^{2} - k_{2}^{2})a(\tau )\,d\tau ]}cn( \xi _{1_{j}}), $$

with the consistency conditions \(b(t) = m^{2}k_{1}^{2}A_{1}^{ - 2}a(t)A ^{ - 2}(t)\), \(A(t) = ke^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0} ^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau } \), if we let \(a_{0_{2}} = 1\), \(a_{2_{2}} = - 1 - m^{2}\), \(a_{4_{2}} = m^{2}\), \(F _{1_{2}} = sn\xi \), we have

$$ u_{1_{2}} = kA_{1}e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0}^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k_{2}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{2\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{ \alpha - 1} (( - m^{2} - 1)k_{1}^{2} - k_{2}^{2})a(\tau )\,d\tau ]}sn( \xi _{1_{j}}), $$

with the consistency conditions \(b(t) = - m^{2}k_{1}^{2}A_{1}^{ - 2}a(t)A ^{ - 2}(t)\), if we let \(a_{0_{3}} = m^{2} - 1\), \(a_{2_{3}} = 2 - m^{2}\), \(a_{4_{3}} = - 1\), \(F_{1_{3}} = dn\xi \), we derive

$$ u_{1_{3}} = kA_{1}e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0}^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k_{2}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{2\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{ \alpha - 1} ((2 - m^{2})k_{1}^{2} - k_{2}^{2})a(\tau )\,d\tau ]}dn( \xi _{1_{j}}), $$

with the consistency conditions \(b(t) = k_{1}^{2}A_{1}^{ - 2}a(t)A ^{ - 2}(t)\). And so on.

Remark 1

Let us take

$$\begin{aligned}& \alpha = \beta = 1,\qquad kA_{1} = c_{3}\sqrt{ \frac{ - k_{2}m^{2}}{k_{4}(2m ^{2} - 1)}}, \\& k_{2} = c_{2},\qquad k_{1} = c_{1}\sqrt{\frac{k_{2}}{(2m^{2} - 1)}},\qquad a(t) \to \beta (t),\qquad b(t) \to \delta (t), \\& c(t) \to \alpha (t),\qquad t \to z,\qquad x \to t. \end{aligned}$$

We find that \(u_{1_{1}}\) turns to the solutions \(u_{31}\) in Ref. [25],

$$\begin{aligned} u_{1_{1.1}} =& c_{3}\sqrt{\frac{ - k_{2}m^{2}}{k_{4}(2m^{2} - 1)}} e ^{\int _{0}^{z} \alpha (\tau )\,d\tau + i[c_{2}t + \frac{1}{2}\int _{0} ^{z} (c_{1}^{2}k_{2} - c_{2}^{2})\beta (\tau )\,d\tau ]} \\ &{}\times cn\biggl[c_{1}\sqrt{\frac{k _{2}}{2m^{2} - 1}} (t - c_{2}) \int _{0}^{z} \beta (\tau )\,d\tau \biggr]. \end{aligned}$$

Let us take

$$\begin{aligned}& \alpha = \beta = 1,\qquad m = 1,\qquad kA_{1} = cR,\qquad k_{2} = C_{1}, \\& k_{1} = \sqrt{R} C_{2},\qquad a(t) \to \beta (t), \qquad b(t) \to \delta (t),\qquad c(t) \to \alpha (t), \\& t \to z,\qquad t \to x. \end{aligned}$$

We find that \(u_{1_{1}}\) has degenerated to the famous bright-soliton solutions \(u_{31}\) in Ref. [26].

$$ u_{1_{1.2}} = cRe^{\int _{0}^{z} \alpha (\tau )\,d\tau + i[C_{1}t + \frac{1}{2}\int _{0}^{z} (C_{2}^{2}R - C_{1}^{2})\beta (\tau )\,d\tau ]} \sec h\biggl\{ \sqrt{R} \biggl[C_{2}t - C_{1}C_{2} \int _{0}^{z} \beta (\tau )\,d\tau \biggr]\biggr\} . $$

Let us take

$$\begin{aligned}& \alpha = \beta = 1,\qquad m = 1,\qquad k = \sqrt{ - \frac{c_{2}}{2c_{4}}},\qquad k_{2} = A_{3},\qquad k_{1} = \sqrt{\frac{2c_{2}}{ - m^{2} - 1}} A_{2}, \\& a(t) \to \beta (t),\qquad b(t) \to \alpha (t), \\& c(t) \to \gamma (t),\qquad t \to z,\qquad t \to x. \end{aligned}$$

We find that \(u_{1_{2}}\) has degenerated to the famous dark-soliton solutions

$$\begin{aligned} u_{1_{2.1}} =& A_{1}\sqrt{ - \frac{c_{2}}{2c_{4}}} e^{\int _{0}^{z} \gamma (\tau )\,d\tau + i[A_{3}t + \frac{2A_{2}^{2}c_{2} - A_{3}^{2}}{2}\int _{0}^{z} \beta (\tau )\,d\tau ]} \\ &{}\times \tanh \biggl[A_{2}\sqrt{ - c_{2}} \biggl(t - A_{3} \int _{0}^{z} \beta ( \tau )\,d\tau \biggr) \biggr],\quad c_{2} < 0,c_{4} > 0. \end{aligned}$$

Case 2

$$\begin{aligned}& A_{0} = \mathrm{const},\qquad A_{1} = \frac{4a_{4}A_{0}}{a_{3}},\qquad 8a_{1}a_{4}^{2} = 4a _{2}a_{3}a_{4} - a_{3}^{3}, \qquad a_{3}a_{4} \ne 0, \\& c_{2}(t) = \biggl(\frac{a_{1}a_{4}k_{1}^{2}}{a_{3}} - \frac{a_{3}^{2}k_{1} ^{2}}{16a_{4}} - \frac{k_{2}^{2}}{2}\biggr)a(t),\qquad b(t) = - \frac{a_{3}^{2}k _{1}^{2}}{16a_{4}A_{0}^{2}}a(t)A^{ - 2}(t). \end{aligned}$$

We acquire the following exact solutions of Eq. (2) by using Appendix B in Ref. [28]:

$$\begin{aligned}& u_{2_{j}} = kA_{0}\biggl(1 + \frac{4a_{4}}{a_{3}}\biggr)e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0}^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k _{2}x^{\beta }}{\varGamma (1 + \beta )} + \frac{1}{\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{\alpha - 1} (\frac{a_{1}a_{4}k_{1}^{2}}{a_{3}} - \frac{a_{3}^{2}k_{1}^{2}}{16a_{4}} - \frac{k_{2}^{2}}{2})a(\tau )\,d\tau ]} \\& \hphantom{u_{2_{j}} =}{}\times F_{2_{j}}\biggl[\frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} - \frac{k_{1}k _{2}}{\varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} a(\tau )\,d\tau \biggr], \\& j = 1,2,3, \ldots ,9. \end{aligned}$$

If we let \(a_{0_{4}} = 1\), \(a_{1_{4}} = - 4\), \(a_{2_{4}} = 8 - 4m^{2}\), \(a_{3_{4}} = 4 - 4m^{2}\), \(a_{4_{4}} = 8m^{2} - 8\), \(F_{4} = \frac{cn \xi }{cn\xi \pm sn\xi dn\xi } \), we get the general Jacobi elliptic functions solution.

$$\begin{aligned}& u_{2_{4}} = - 7kA_{0}e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0} ^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k_{2}x^{\beta }}{ \varGamma (1 + \beta )} + \frac{1}{\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{\alpha - 1} (8k_{1}^{2} - \!\frac{(m^{2} - 1)k_{1}^{2}}{8} - \frac{k _{2}^{2}}{2})a(\tau )\,d\tau ]} \frac{cn\xi }{cn\xi \pm sn\xi dn\xi }, \\& \xi = \frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} - \frac{k_{1}k_{2}}{ \varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} a(\tau )\,d\tau . \end{aligned}$$

We have the consistency conditions \(b(t) = - \frac{(m^{2} - 1)k_{1} ^{2}}{8A_{0}^{2}}a(t)A^{ - 2}(t)\).

If we let \(a_{0_{7}} = \frac{1}{4}\), \(a_{1_{7}} = 1\), \(a_{2_{7}} = 2 - m ^{2}\), \(a_{3_{7}} = 2 - 2m^{2}\), \(a_{4_{7}} = 1 - m^{2}\), \(F_{7} = \frac{sn \xi }{1 - sn\xi + cn\xi } \), we have

$$\begin{aligned} u_{2_{7}} =& 3kA_{0}e^{\frac{\alpha }{\varGamma (1 + \alpha )}\int _{0} ^{t} \tau ^{\alpha - 1} c(\tau )\,d\tau + i[\frac{k_{2}x^{\beta }}{ \varGamma (1 + \beta )} + \frac{1}{\varGamma (\alpha )}\int _{0}^{t} (t - \tau )^{\alpha - 1} (\frac{k_{1}^{2}}{2} - \frac{(1 - m^{2})k_{1}^{2}}{4} - \frac{k_{2}^{2}}{2})a(\tau )\,d\tau ]} \\ &{}\times \biggl(sn\biggl[\frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} - \frac{k_{1}k _{2}}{\varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} a(\tau )\,d\tau \biggr]\biggr) \\ &{}\Big/\biggl(1 - sn\biggl[\frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} - \frac{k _{1}k_{2}}{\varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} a( \tau )\,d\tau \biggr] \\ &{}+ cn\biggl[\frac{k_{1}x^{\beta }}{\varGamma (1 + \beta )} - \frac{k _{1}k_{2}}{\varGamma (\alpha )} \int _{0}^{t} (t - \tau )^{\alpha - 1} a( \tau )\,d\tau \biggr]\biggr) , \end{aligned}$$

with the consistency conditions \(b(t) = - \frac{(1 - m^{2})k_{1}^{2}}{4A _{0}^{2}}a(t)A^{ - 2}(t)\). And so on.

Remark 2

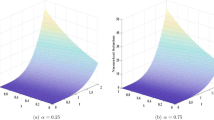
The solutions \(u_{1_{j}}\) and \(u_{2_{j}}\) are new exact solutions for Eq. (2) to the best of our knowledge. When the modulus of these Jacobi elliptic functions solutions has degenerated to 1 or 0, we can obtain the corresponding solitary-like solutions and triangular-like functions solutions. Some structure of these solutions of Eq. (1) are simulated in Fig. 1–Fig. 4

Figure 1
figure 1

(a) The evolution plot of the exact doubly periodic solutions \(u_{1_{2}}\) with the parameters \(k = k_{1} = k_{2} = A_{1} = 1\), \(a(t) = 1\), \(c(t) = 0\), \(m = 0.2\), \(\alpha = \beta = 1\). (b) \(\alpha = 0.5\), \(\beta = 0.5\)

Full size image
Figure 2
figure 2

(a) The evolution plot of the bell-shaped solitary wave solutions \(u_{1_{1}}\) with the parameters when \(k = k_{1} = k_{2} = A_{1} = 1\), \(a(t) = 1\), \(c(t) = 0\), \(m = 1\), \(\alpha = \beta = 1\). (b) \(\alpha = 0.5\), \(\beta = 0.5\)

Full size image
Figure 3
figure 3

(a) The evolution plot of the triangular functions solutions of \(u_{2_{4}}\) with the parameters \(k = k_{1} = k_{2} = A_{1} = 1\), \(a(t) = 1\), \(c(t) = 1\), \(m = 0\), \(\alpha = \beta = 1\). (b) \(\alpha = 0.7\), \(\beta = 0.92\)

Full size image
Figure 4
figure 4

(a) The evolution plot of the Jacobi elliptic functions solutions \(u_{2_{7}}\) with the parameters \(k = k_{1} = k_{2} = A_{1} = 1\), \(a(t) = 1\), \(c(t) = 1\), \(m = 0.1\), \(\alpha = \beta = 1\). (b) \(\alpha = 0.1\), \(\beta = 0.1\)

Full size image

3 The MFVIM and approximate solutions for the VFNLS

According to the idea of FVIM [17, 20] and MFVIM [21], we can build a correction functional for Eq. (2) as follows:

$$ u_{n + 1} = u_{n} + J_{t}^{\alpha } \biggl\{ \lambda (t,x)\biggl[i\frac{ \partial ^{\alpha } u_{n}}{\partial t^{\alpha }} + \frac{1}{2}a(t) \frac{ \partial ^{2\beta } \tilde{u}_{n}}{\partial x^{2\beta }} + b(t) \tilde{u}_{n} \vert \tilde{u}_{n} \vert ^{2} - ic(t)\tilde{u}_{n} \biggr] \biggr\} . $$
(9)

Here \(u_{0} = u(x,0) = f(x)\), \(\lambda (t,x)\) is a general Lagrange multiplier, which can be identified optimally with the variational theory. The function \(\tilde{u}_{n}\) is a restricted variation, which means \(\delta \tilde{u}_{n} = 0\). Therefore, we first determine the Lagrange multiplier \(\lambda (t,x)\) that will be identified optimally via integration by parts. The successive approximations \(u_{n + 1}\), \(n \ge 0\), of the solution \(u(x,t)\) will be readily obtained upon using the obtained \(\lambda (t,x)\) and any selective function \(u_{0}\). The initial values are usually used for choosing the zeroth approximation \(u_{0}\). Consequently, the exact solution may be procured by using \(u = \lim_{n \to \infty } u_{n}\).

In the following, we will apply the MFVIM to a model about Eq. (2) to illustrate the strength of the method.

Example

We now consider the following time-space fractional NLS equation [30,31,32]:

$$ i\frac{\partial ^{\alpha } u}{\partial t^{\alpha }} + a\frac{ \partial ^{2\beta } u}{\partial x^{2\beta }} + bu \vert u \vert ^{2} - icu = 0,\quad t > 0,0 < \alpha ,\beta \le 1,\qquad u(x,0) = Ae^{ix}. $$
(10)

Here a, b, c are constants. This equation occurs in various kinds of theoretical physics, such as nonlinear optics, superconductivity and plasma physics, which also can represent some dynamical system in quantum mechanics, fluid dynamics and nonlinear dynamics [31].

The correction functional for (10) reads

$$ u_{n + 1} = u_{n} + J_{t}^{\alpha } \biggl\{ \lambda (t,x)\biggl[i\frac{ \partial ^{\alpha } u_{n}}{\partial t^{\alpha }} + a\frac{\partial ^{2} \tilde{u}_{n}}{\partial x^{2}} + b \tilde{u}_{n} \vert \tilde{u}_{n} \vert ^{2} - ic\tilde{u}_{n}\biggr]\biggr\} . $$
(11)

Making the above correction functional stationary,

$$ \delta u_{n + 1} = \delta u_{n} + \lambda (t,x)i\delta u_{n} - J_{t} ^{\alpha } \bigl\{ \bigl[i\lambda ^{\alpha } (t,x)\delta u_{n}\bigr]\bigr\} . $$
(12)

After getting the coefficients of \(\delta u_{n}\) to zero we can determine the Lagrange multiplier

$$ \lambda = i. $$
(13)

We produces the iteration formulation as follows:

$$ u_{n + 1} = u_{n} + iJ_{t}^{\alpha } \biggl[i\frac{\partial ^{\alpha } u_{n}}{ \partial t^{\alpha }} + a\frac{\partial ^{2}u_{n}}{\partial x^{2}} + bu _{n} \vert u \vert ^{2} - icu_{n}\biggr],\qquad \vert u \vert ^{2} = \vert u_{0} \vert ^{2}. $$
(14)

As stated before, we can select \(u_{0} = u(x,0) = Ae^{ix}\), using the iteration (14) and the Mathematica software, we obtain the following successive approximations:

$$\begin{aligned}& u_{0} = Ae^{ix}, \\& u_{1} = Ae^{ix} + aAe^{i(x + \pi \beta )} \frac{it^{\alpha }}{\varGamma (1 + \alpha )} + bA^{3}e^{ix}\frac{it^{\alpha }}{\varGamma (1 + \alpha )} - icAe^{ix}\frac{it^{\alpha }}{\varGamma (1 + \alpha )} \\& \hphantom{u_{1}}= Ae^{ix}\biggl(1 + \frac{c_{1}it^{\alpha }}{\varGamma (1 + \alpha )} \biggr),\qquad c_{1} = ae^{i\pi \beta } + bA^{2} - ic , \\& u_{2} = u_{1} - Ae^{ix} \frac{c_{1}it^{\alpha }}{\varGamma (1 + \alpha )} + aAe^{i(x + \pi \beta )}\biggl[\frac{it^{\alpha }}{\varGamma (1 + \alpha )} + \frac{c_{1}i^{2}t^{2\alpha }}{\varGamma (1 + 2\alpha )}\biggr] \\& \hphantom{u_{2} =}{}+ bA^{3}e^{ix}\biggl[ \frac{it ^{\alpha }}{\varGamma (1 + \alpha )} + \frac{c_{1}i^{2}t^{2\alpha }}{ \varGamma (1 + 2\alpha )}\biggr] \\& \hphantom{u_{2} =}{} - icAe^{ix}\biggl[ \frac{it^{\alpha }}{\varGamma (1 + \alpha )} + \frac{c_{1}i ^{2}t^{2\alpha }}{\varGamma (1 + 2\alpha )}\biggr] \\& \hphantom{u_{2}}= Ae^{ix}\biggl[1 + \frac{c_{1}it^{\alpha }}{\varGamma (1 + \alpha )} + \frac{c _{1}^{2}i^{2}t^{2\alpha }}{\varGamma (1 + 2\alpha )}\biggr], \\& u_{3} = Ae^{ix}\biggl[1 + \frac{c_{1}it^{\alpha }}{\varGamma (1 + \alpha )} + \frac{c _{1}^{2}i^{2}t^{2\alpha }}{\varGamma (1 + 2\alpha )} + \frac{c_{1}^{3}i ^{3}t^{3\alpha }}{\varGamma (1 + 3\alpha )}\biggr], \\& \cdots , \\& u_{n} = Ae^{ix}\sum_{k = 0}^{n} \frac{1}{\varGamma (1 + k\alpha )}\bigl[c_{1}it ^{\alpha } \bigr]^{k}. \end{aligned}$$

The exact solution of Eq. (10) is

$$ u_{\mathrm{exact}} = Ae^{ix}\lim_{n \to \infty } \sum _{k = 0}^{n} \frac{1}{ \varGamma (1 + k\alpha )} \bigl[c_{1}it^{\alpha } \bigr]^{k} = Ae^{ix}E_{\alpha } \bigl[\bigl(ae ^{i\pi \beta } + bA^{2} - ic\bigr)it^{\alpha } \bigr]. $$
(15)

Here \(E_{\alpha } [(ae^{i\pi \beta } + bA^{2} - ic)it^{\alpha } \) is the Mittag-Leffler function.

Remark 3

If we select \(A = 1\), \(a = k\), \(b = 2k\), \(c = 0\), \(\alpha = 1\), the solution (15) contains the result (49) in Ref. [30], the result (3.18) and (3.21) in Ref. [31], the result (27) in Ref. [32], but we can find that this iteration is much more simple, standard and powerful than the HAM, the ADM and the VIM mentioned in Refs. [30,31,32]. The solution (15) is a new exact solution for Eq. (10) to the best of our knowledge.

4 Conclusion

In this paper, the modified general mapping deformation method and the MFVIM are used for finding exact and approximate solutions of the GFNLS equation with the Caputo derivative. The obtained results indicate that the MFVIM is an effective, and a convenient and powerful method for solving nonlinear fractional complex differential equations when compared with some other traditional asymptotic decomposition method such as HAM, VIM and ADM. We believe that these two methods should play an important role for finding exact and approximate solutions in mathematical physics.