Bifurcation and exact solutions for the ($2+1$)-dimensional conformable time-fractional Zoomeron equation

Abstract

In this paper, the bifurcation and new exact solutions for the ($2+1$)-dimensional conformable time-fractional Zoomeron equation are investigated by utilizing two reliable methods, which are generalized $(G'/G)$-expansion method and the integral bifurcation method. The exact solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation are obtained by utilizing the generalized $(G'/G)$-expansion method, these solutions are classified as hyperbolic function solutions, trigonometric function solutions, and rational function solutions. Giving different parameter conditions, many integral bifurcations, phase portraits, and traveling wave solutions for the equation are obtained via the integral bifurcation method. Graphical representations of different kinds of the exact solutions reveal that the two methods are of significance for constructing the exact solutions of fractional partial differential equation.

1 Introduction

It is well known that the fractional partial differential equations (FPDEs) [1–11] have received considerable attention [12–19] due to their wide use to describe various complex physical phenomena in the domain of science and engineering. Among the research of the FPDEs, analyzing the bifurcations and the exact traveling wave solutions of FPDEs have been widely investigated as an important subject. Recently, many effective methods have been established and developed to analyze the dynamical behavior of the FPDEs. These methods include the $(G'/G)$-expansion method, the integral bifurcations, the Lie symmetry analysis method, the exp-function method, the Kudryashov method, and so on.

It is worth noting that the $(G'/G)$-expansion method, which was first introduced in [20], has made significant achievements in searching for the exact traveling wave solutions of partial differential equations (PDEs). But the exact solutions of FPDEs have been developed very slowly compared to the exact traveling solutions of PDEs. Most of the methods directly transform an FPDE into an ordinary differential equation by a fractional complex transformation. But the Jumarie’s fractional chain rule does not hold. Therefore, the fractional complex transformation cannot be used to obtain the exact traveling solutions of FPDEs when the Riemann–Liouville derivative is used. Recently, Khalil and coworkers [21] introduced the conformable fractional derivative. After that, some scholars [22–25] have begun to discuss the exact solutions of FPDEs in the sense of the conformable fractional derivative. In this paper, we will introduce the procedure of the generalized $(G'/G)$-expansion method for FPDEs, and will discuss the exact traveling wave solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation by the generalized $(G'/G)$-expansion method together with conformable fractional derivative.

The bifurcation method first proposed by Liu and Li [26] is one of the most powerful tools to study the dynamic behavior of PDEs, especially in the analysis of the bifurcation and exact traveling wave solutions [27–30]. As far as we know, the bifurcation method has not been used to investigate the exact traveling wave solutions of FPDEs in the sense of the conformable fractional derivative. In the paper, we will introduce the procedure of bifurcation approach for constructing the exact traveling wave solutions of FPDEs. By using this method, we will analyze the bifurcation and exact solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation.

The Zoomeron equation is a very convenient model which displays the novel phenomena related with boomerons and trappons, this equation is usually used to describe the evolution of a single scalar field. Recently, Odabasi [31] studied the following ($2+1$)-dimensional conformable time-fractional Zoomeron equation:

$$ \frac{\partial ^{2\alpha }u}{\partial t^{2\alpha }} \biggl[\frac{u_{xy}}{u} \biggr]- \frac{\partial ^{2}u}{\partial x^{2}} \biggl[\frac{u_{xy}}{u} \biggr]+2 \frac{\partial ^{\alpha }u}{\partial t^{\alpha }} \bigl[u^{2} \bigr]_{x}=0, \quad 0< \alpha \leq 1, $$

(1.1)

where $\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}$ is the conformable fractional derivative of u depending on the variable t. Odabasi applied the modified trial equation method to obtain the exact solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation. Kumar and Kaplan [32] applied the extended $\exp (-\Phi (\xi ))$-expansion technique and the exponential rational functional technique to find the explicit and exact solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation. Hosseini et al. [33] adopted the $\exp (-\Phi (\xi ))$-expansion approach and modified Kudryashov method to search for the exact solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation.

The main objective of the paper is to employ the generalized $(G'/G)$-expansion method and bifurcation method to construct exact traveling wave solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation. The remainder of the article is structured as follows: In Sect. 2, we review the definition of the conformable fractional derivative, and introduce two effective methods for constructing the exact traveling wave solutions of FPDEs. Then in Sect. 3, we discuss the exact solutions of the ($2+1$)-dimensional conformable time-fractional Zoomeron equation by using the generalized $(G'/G)$-expansion method and bifurcation method, respectively. Moreover, we obtain the bifurcation and phase portraits of this equation. Finally, we give a brief conclusion in Sect. 4.

2 Mathematical preliminaries

2.1 The conformable fractional derivative

The definition of the conformable fractional derivative is defined as in [34].

Definition 2.1

Let $f:[0,\infty )\rightarrow \mathbf{R}$. Then, the conformable fractional derivative of f of order α is defined as

$$ D_{t}^{\alpha }f(t)=\lim_{\varepsilon \rightarrow 0} \frac{f(t+\varepsilon t^{1-\alpha })-f(t)}{\varepsilon },\quad \forall t \in (0,+\infty ), \alpha \in (0,1], $$

(2.1)

the function f is α-conformably differentiable at a point t if the limit in equation (2.1) exists.

Remark 2.1

The conformable fractional derivative possesses the following properties:

• (i) $D_{t}^{\alpha }(t^{\mu })=\mu t^{\mu -\alpha }$, $\forall \mu \in \mathbf{R}$.

• (ii) $D_{t}^{\alpha }(af(t)+bg(t))=aD_{t}^{\alpha }f(t)+bD_{t}^{\alpha }g(t)$, $\forall a,b\in \mathbf{R}$.

• (iii) $D_{t}^{\alpha }(f\circ g)(t)=t^{1-\alpha }g(t)^{\alpha -1}g'(t)D_{t}^{ \alpha }(f(t))|_{t=g(t)}$.

The conformable fractional derivative has many important properties. The detailed proof is given in the Appendix.

2.2 Description of the methods

Consider the following conformable FPDE:

$$ \mathrm{F} \biggl(u,\frac{\partial ^{\alpha }u}{\partial t^{\alpha }}, \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial ^{2\alpha }u}{\partial t^{2\alpha }}, \frac{\partial ^{2} u}{\partial x^{2}}, \frac{\partial ^{2}u}{\partial y^{2}},\dots \biggr)=0,\quad 0< \alpha \leq 1, $$

(2.2)

where $t,x,y\in \mathrm{R}$, $u=u(t,x,y)\in \mathrm{R}$, F is a polynomial in u and its partial fractional-order derivatives.

Introduce a traveling wave transformation

$$ u(t,x)=u(\xi ), \quad\xi =kx+my-\frac{lt^{\alpha }}{\alpha }, $$

(2.3)

where k, m and l are arbitrary constants.

Equation (2.2) is reduced to the following integer-order ordinary differential equation:

$$ \mathrm{P} \bigl(u,u',u'', \dots \bigr)=0, $$

(2.4)

where P is a polynomial in u and its derivatives, notation (′) means the derivative with respect to ξ. If it is possible, we should integrate several times equation (2.4) and take the integral constants as zero.

2.2.1 The generalized $(G'/G)$-expansion method

Step 1. Assume that the solution of equation (2.4) can be expressed as

$$ u(\xi )=\sum_{i=0}^{N}a_{i} \biggl(d+\frac{G'}{G} \biggr)^{i}+\sum _{i=1}^{N}b_{i} \biggl(d+ \frac{G'}{G} \biggr)^{-i}, $$

(2.5)

where d is an arbitrary constant, while $a_{i}\ (i=0,1,2,\dots,N)$ and $b_{i}\ (i=1,2,\dots,N)$ are to be determined later. Then $G=G(\xi )$ satisfies the following nonlinear ordinary differential equation:

$$ AGG{''}=BGG'+C \bigl(G' \bigr)^{2}+DG^{2}, $$

(2.6)

where A, B, C, and D are real parameters.

Step 2. The positive integer N can be computed by balancing the highest order derivative and nonlinear term appearing in equation (2.4).

Step 3. Substituting equation (2.5) together with equation (2.6) into equation (2.4), we get polynomials in $(d+\frac{G'}{G})^{N}\ (N=0,\pm 1,\pm 2,\dots )$. Setting all the coefficients of the resulting polynomial to zero, we obtain algebraic equations.

Step 4. By solving the algebraic equations obtained in Step 3, we can obtain the values of the constants $a_{i}\ (i=0,1,2,\dots )$ and $b_{i}\ (i=1,2,\dots,N)$. Replacing their values in equation (2.5), we construct the exact solutions of equation (2.2).

2.2.2 The bifurcation method

Step 1. Let $\frac{du}{d\xi }=y$. Equation (2.4) can be transformed into the following two-dimensional system:

$$ \textstyle\begin{cases} \frac{du}{d\xi }=y, \\ \frac{dy}{d\xi }=\mathrm{R}(u,y), \end{cases} $$

(2.7)

where $\mathrm{R}(u,y)$ is an integral expression.

Step 2. Solve system (2.7) is an integral system, which has the first integral

$$ \mathrm{H}(u,y)=h, $$

(2.8)

where h is an integral constant.

Step 3. By employing the first integral $\mathrm{H}(u,y)$ and analyzing the orbit properties in the phase plane, we can obtain the exact solutions of equation (2.2).

3 Applications

By employing the transformation $u(t,x,y)=u(\xi )$, $\xi =kx+my+\frac{lt^{\alpha }}{\alpha }$, the ($2+1$)-dimensional conformable time-fractional Zoomeron equation can be reduced to an ordinary differential equation having form

$$ kml^{2} \biggl[\frac{u''}{u} \biggr]''-k^{3}m \biggl[\frac{u''}{u} \biggr]''-2kl \bigl[u^{2} \bigr]''=0. $$

(3.1)

Integrating equation (3.1) twice with respect to ξ, we obtain

$$ km \bigl(l^{2}-k^{2} \bigr)u''-2klu^{3}- \rho u=0, $$

(3.2)

where ρ is a constant of integration.

3.1 Exact solutions of equation (1.1) using the generalized $(G'/G)$-expansion method

Balancing $u''$ and $u^{3}$ in equation (3.2), we obtain $N=1$. Therefore, the solution form of equation (3.2) is

$$ u(\xi )=a_{1} \biggl(d+\frac{G'}{G} \biggr)+a_{0}+b_{1} \biggl(d+\frac{G'}{G} \biggr)^{-1}. $$

(3.3)

Substituting (3.3) into (3.2) yields a polynomial in $(d+\frac{G'}{G})^{N}$ ($N=0,1,2,3$) and $(d+\frac{G'}{G})^{-N}$ ($N=1,2,3$). Collecting the coefficients of the resulting polynomial, we obtain a system of nonlinear algebraic equations:

$$\begin{aligned} &\biggl(d+\frac{G'}{G}\biggr)^{3}: km\bigl(l^{2}-k^{2} \bigr)\cdot \frac{2a_{1}(C-A)^{2}}{A^{2}}-2kla_{1}^{3}=0; \\ &\biggl(d+\frac{G'}{G}\biggr)^{2}: km\bigl(l^{2}-k^{2} \bigr)\cdot \frac{3a_{1}(C-A)[B-2d(C-A)]}{A^{2}}-2kl\cdot 3a_{0}a_{1}^{2}=0; \\ &\biggl(d+\frac{G'}{G}\biggr)^{1}: km\bigl(l^{2}-k^{2} \bigr)\biggl\{ \frac{2a_{1}(C-A)[(C-A)d^{2}+D-Bd]}{A^{2}}+ \frac{a_{1}[B-2d(C-A)]^{2}}{A^{2}}\biggr\} \\ &\quad{}-2kl \bigl(3a_{1}^{2}b_{1}+3a_{0}^{2}a_{1} \bigr)- \rho a_{1}=0; \\ &\biggl(d+\frac{G'}{G}\biggr)^{0}: km\bigl(l^{2}-k^{2} \bigr)\biggl\{ \frac{a_{1}[B-2d(C-A)][(C-A)d^{2}+D-Bd]}{A^{2}}\\ &\quad{}+ \frac{b_{1}(C-A)[B-2d(C-A)]}{A^{2}} \biggr\} -2kl \bigl(a_{0}^{3}+6a_{0}a_{1}b_{1} \bigr)- \rho a_{0}=0; \\ &\biggl(d+\frac{G'}{G}\biggr)^{-1}: km\bigl(l^{2}-k^{2} \bigr)\biggl\{ \frac{b_{1}[B-2d(C-A)]^{2}}{A^{2}}+ \frac{2b_{1}(C-A)[d^{2}(C-A)+D-Bd]}{A^{2}}\biggr\} \\ &\quad{}-2kl \bigl(3a_{1}b_{1}^{2}+3a_{0}^{2}b_{1} \bigr)- \rho b_{1}=0; \\ &\biggl(d+\frac{G'}{G}\biggr)^{-2}: km\bigl(l^{2}-k^{2} \bigr)\frac{3b_{1}[B-2d(C-A)][(C-A)d^{2}+D-Bd]}{A^{2}}-3kl \cdot 3a_{0}b_{1}^{2}=0; \\ &\biggl(d+\frac{G'}{G}\biggr)^{-3}: km\bigl(l^{2}-k^{2} \bigr)\frac{2b_{1}[d^{2}(C-A)+D-Bd]^{2}}{A^{2}}-2klb_{1}^{3}=0. \end{aligned}$$

Solving this system of algebraic equations using the computer algebra software Maple, we get the following results:

Case 1. $b_{1}=0$, $a_{0}=\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l|A\psi |}\sqrt{ \frac{l}{m(l^{2}-k^{2})}}$, $a_{1}=\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{|\psi |}{|A|}$, $\rho =-\frac{km(l^{2}-k^{2})(B^{2}+4D\psi )}{2A^{2}}$.

Case 2. $b_{1}=\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}} \frac{|d^{2}\psi -D+Bd|}{|A|}$, $a_{0}=\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l|A(d^{2}\psi -D+Bd)|} \sqrt{\frac{l}{m(l^{2}-k^{2})}}$, $\rho = -\frac{km(l^{2}-k^{2})(B^{2}+4D\psi )}{2A^{2}}$.

Substituting these solutions into (3.3), we obtain the traveling wave solutions as follows:

$$\begin{aligned} &u(\xi )=\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l \vert A\psi \vert }\sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\phantom{u(\xi )=}\pm \sqrt{ \frac{m(l^{2}-k^{2})}{l}} \frac{ \vert \psi \vert }{ \vert A \vert } \biggl(d+\frac{G'(\xi )}{G(\xi )} \biggr), \end{aligned}$$

(3.4)

$$\begin{aligned} & u(\xi )=\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l \vert A(d^{2}\psi -D+Bd) \vert } \sqrt{\frac{l}{m(l^{2}-k^{2})}} \\ &\phantom{u(\xi )=}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert d^{2}\psi -D+Bd \vert }{ \vert A \vert } \biggl(d+ \frac{G'(\xi )}{G(\xi )} \biggr)^{-1}, \end{aligned}$$

(3.5)

where $\frac{G'(\xi )}{G(\xi )}$ is defined in Sect. 2, $\xi =kx+my+\frac{lt^{\alpha }}{\alpha }$.

Family 1. When $B\neq 0$, $\psi =A-C$, and $\mu =B^{2}+4D\psi >0$, we have the traveling wave solutions as follows:

$$\begin{aligned} & u_{1}(t,x,y) \\ &\quad =\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l \vert A\psi \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}} \frac{ \vert \psi \vert }{ \vert A \vert } \biggl[d+ \frac{B}{2\psi } \\ &\qquad{}+\frac{\sqrt{\mu }}{2\psi } \frac{C_{1}\sinh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))+C_{2}\cosh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cosh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))+C_{2}\sinh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr], \end{aligned}$$

(3.6)

$$\begin{aligned} &u_{2}(t,x,y) \\ &\quad =\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l \vert A(d^{2}\psi -D+Bd) \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\qquad{}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert d^{2}\psi -D+Bd \vert }{ \vert A \vert } \biggl[d+ \frac{B}{2\psi } \\ &\qquad{}+\frac{\sqrt{\mu }}{2\psi } \frac{C_{1}\sinh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))+C_{2}\cosh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{ C_{1}\cosh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))+C_{2}\sinh (\frac{\sqrt{\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr]^{-1}, \end{aligned}$$

(3.7)

where $C_{1}$ and $C_{2}$ are arbitrary constants.

In particular, if $C_{1}\neq 0$, $\psi >0$, $l^{2}>k^{2}$, $m>0$, $A>0$, $l>0$, and $C_{2}=0$ in equation (3.6), we obtain the kink wave solutions

$$ u_{1_{1}}(t,x,y)= \frac{\sqrt{m(l^{2}-k^{2})(B^{2}+4D\psi )}}{2A\sqrt{l}}\tanh \biggl( \frac{\sqrt{B^{2}+4D\psi }}{2A} \biggl(kx+my+\frac{lt^{\alpha }}{\alpha } \biggr) \biggr). $$

(3.8)

Figure 1

Kink wave solution of equation (1.1) for $u_{1_{1}}(t,x,y)$ when $\alpha =\frac{1}{2}$, $A=B=l=2$, $C=D=k=1$, $m=3$

Figure 2

Periodic wave solution of equation (1.1) for $u_{3_{1}}(t,x,y)$ when $\alpha =\frac{1}{2}$, $l=A=m=2$, $k=B=C=1$, $D=-1$

Family 2. When $B\neq 0$, $\psi =A-C$, and $\mu =B^{2}+4D\psi <0$, we obtain the following exact solutions:

$$\begin{aligned} & u_{3}(t,x,y) \\ &\quad =\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l \vert A\psi \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}} \frac{ \vert \psi \vert }{ \vert A \vert } \biggl[d+ \frac{B}{2\psi } \\ &\qquad{}+\frac{\sqrt{-\mu }}{2\psi } \frac{-C_{1}\sin (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\cos (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cos (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\sin (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr]. \end{aligned}$$

(3.9)

$$\begin{aligned} & u_{4}(t,x,y) \\ &\quad =\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l \vert A(d^{2}\psi -D+Bd) \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\qquad{}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert d^{2}\psi -D+Bd \vert }{ \vert A \vert } \biggl[d+ \frac{B}{2\psi } \\ &\qquad{}+\frac{\sqrt{-\mu }}{2\psi } \frac{-C_{1}\sin (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\cos (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cos (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\sin (\frac{\sqrt{-\mu }}{2A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr]^{-1}. \end{aligned}$$

(3.10)

In particular, if $C_{1}\neq 0$, $\psi >0$, $l^{2}>k^{2}$, $m>0$, $A>0$, $l>0$, and $C_{2}=0$ in equation (3.9), we obtain the periodic wave solutions

$$ u_{3_{1}}(t,x,y)=- \frac{\sqrt{-m(l^{2}-k^{2})(B^{2}+4D\psi )}}{2A\sqrt{l}}\tan \biggl( \frac{\sqrt{-(B^{2}+4D\psi )}}{2A} \biggl(kx+my+\frac{lt^{\alpha }}{\alpha } \biggr) \biggr). $$

(3.11)

Family 3. When $B\neq 0$, $\psi =A-C$, and $\mu =B^{2}+4\psi D=0$, we obtain

$$\begin{aligned} &u_{5}(t,x,y) \\ &\quad =\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l \vert A\psi \vert }\sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\qquad{}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert \psi \vert }{ \vert A \vert } \biggl[d+ \frac{B}{2\psi } + \frac{C_{2}}{C_{1}+C_{2}(kx+my+\frac{lt^{\alpha }}{\alpha })} \biggr], \end{aligned}$$

(3.12)

$$\begin{aligned} & u_{6}(t,x,y) \\ &\quad =\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l \vert A(d^{2}\psi -D+Bd) \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\qquad{}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert d^{2}\psi -D+Bd \vert }{ \vert A \vert } \biggl[d+ \frac{B}{2\psi }+ \frac{C_{2}}{C_{1}+C_{2}(kx+my+\frac{lt^{\alpha }}{\alpha })} \biggr]^{-1}. \end{aligned}$$

(3.13)

Family 4. When $B=0$, $\psi =A-C$, and $\Delta =\psi D>0$, we obtain following traveling wave solutions:

$$\begin{aligned} & u_{7}(t,x,y) \\ &\quad =\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l \vert A\psi \vert }\sqrt{ \frac{l}{m(l^{2}-k^{2})}}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}} \frac{ \vert \psi \vert }{ \vert A \vert } \biggl[d \\ &\qquad{}+ \frac{\sqrt{\Delta }}{\psi } \frac{C_{1}\sinh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\cosh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cosh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))+C_{2} \sinh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr], \end{aligned}$$

(3.14)

$$\begin{aligned} & u_{8}(t,x,y) \\ &\quad =\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l \vert A(d^{2}\psi -D+Bd) \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\qquad{}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert d^{2}\psi -D+Bd \vert }{ \vert A \vert } \biggl[d \\ &\qquad{}+\frac{\sqrt{\Delta }}{\psi } \frac{C_{1}\sinh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\cosh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cosh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))+C_{2}\sinh (\frac{\sqrt{\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr]^{-1}. \end{aligned}$$

(3.15)

Family 5. When $B=0$, $\psi =A-C$, and $\Delta =\psi D<0$, we have

$$\begin{aligned} &u_{9}(t,x,y) \\ &\quad =\mp \frac{m\psi (l^{2}-k^{2})(B+2d\psi )}{2l \vert A\psi \vert }\sqrt{ \frac{l}{m(l^{2}-k^{2})}}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}} \frac{ \vert \psi \vert }{ \vert A \vert } \biggl[d \\ &\qquad{}+\frac{\sqrt{-\Delta }}{\psi } \frac{-C_{1}\sin (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\cos (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cos (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\sin (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr], \end{aligned}$$

(3.16)

$$\begin{aligned} &u_{10}(t,x,y) \\ &\quad =\mp \frac{m(l^{2}-k^{2})(B+2d\psi )(d^{2}\psi -D+Bd)}{2l \vert A(d^{2}\psi -D+Bd) \vert } \sqrt{ \frac{l}{m(l^{2}-k^{2})}} \\ &\qquad{}\pm \sqrt{\frac{m(l^{2}-k^{2})}{l}}\frac{ \vert d^{2}\psi -D+Bd \vert }{ \vert A \vert } \biggl[d \\ &\qquad{}+\frac{\sqrt{-\Delta }}{\psi } \frac{-C_{1}\sin (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\cos (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))}{C_{1}\cos (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha })) +C_{2}\sin (\frac{\sqrt{-\Delta }}{A}(kx+my+\frac{lt^{\alpha }}{\alpha }))} \biggr]^{-1}. \end{aligned}$$

(3.17)

3.2 Bifurcation, phase portraits, and exact solutions for equation (1.1) using the bifurcation method

Let $\frac{du}{d\xi }=y$. Then, equation (3.2) is equivalent to the following 2-dimensional system:

$$ \textstyle\begin{cases} \frac{du}{d\xi }=y, \\ \frac{dy}{d\xi }=-\beta u^{3}-\gamma u, \end{cases} $$

(3.18)

which has the first integral

$$ H(u,y)=\frac{1}{2}y^{2}+\frac{\beta }{4} u^{4}+\frac{\gamma }{2} u^{2}=h, $$

(3.19)

where $\beta =\frac{2l}{m(k^{2}-l^{2})}$ and $\gamma =\frac{\rho }{km(k^{2}-l^{2})}$.

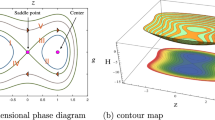
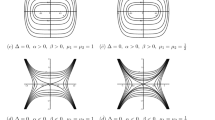
Let $f(u)=-\beta u^{3}-\gamma u$. If $\beta \gamma <0$, we obtain three zeros of $f(u)$: $u_{1}=-\sqrt{-\frac{\gamma }{\beta }}$, $u_{2}=0$, and $u_{3}=\sqrt{-\frac{\gamma }{\beta }}$. If $\beta \gamma >0$, we obtain one zero of $f(u)$, namely $u_{4}=0$. We assume that $P_{i}(u_{i},0)\ (i=1,2,3)$ is the equilibrium points of system (3.18). Clearly, the eigenvalue of system (3.18) at this point is $\lambda _{1,2}=\sqrt{f'(u)}$. By the bifurcation theory, we derive the phase portraits of system (3.18) shown in Fig. 3.

Figure 3

The phase portraits of system (3.18) for $\beta \gamma \neq 0$

I. The case $\beta <0$ , $\gamma >0$ .

In this case, there exist three equilibrium points of system (3.18), where $P_{1}(-\sqrt{-\frac{\gamma }{\beta }},0)$ and $P_{3}(\sqrt{-\frac{\gamma }{\beta }},0)$ are saddle points, while $P_{2}(0,0)$ is a center. Two heteroclinic orbits connect $P_{1}(-\sqrt{-\frac{\gamma }{\beta }},0)$ and $P_{3}(\sqrt{-\frac{\gamma }{\beta }},0)$; moreover, a family of periodic orbits enclose $P_{2}(0,0)$ in Fig. 3(a) defined by equation (3.19).

(i) Suppose that $h\in (0,-\frac{\gamma ^{2}}{4\beta })$. Then a family of periodic orbits of system (3.18) are defined by the algebraic equation

$$ y=\pm \sqrt{-\frac{\beta }{2}}\sqrt{u^{4}+ \frac{2\gamma }{\beta }u^{2}- \frac{4h}{\beta }}=\pm \sqrt{- \frac{\beta }{2}}\sqrt{ \bigl(\phi _{1h}^{2}-u^{2} \bigr) \bigl( \phi _{2h}^{2}-u^{2} \bigr)}, $$

(3.20)

where $\phi _{1h}=\sqrt{-\frac{\gamma }{\beta }-\frac{1}{\beta }\sqrt{\gamma ^{2}+4 \beta h}}$, $\phi _{2h}=\sqrt{-\frac{\gamma }{\beta }+\frac{1}{\beta }\sqrt{\gamma ^{2}+4 \beta h}}$.

By employing (3.20) and the first equation of (3.18), we integrate them along the periodic orbits and obtain

$$ \int _{0}^{u} \frac{d\varphi }{\sqrt{(\phi _{1h}^{2}-\varphi ^{2})(\phi _{2h}^{2}-\varphi ^{2})}}= \pm \sqrt{- \frac{\beta }{2}}(\xi -\xi _{0}). $$

(3.21)

Hence, we can obtain two families of periodic traveling wave solutions, namely

$$ u_{1}(t,x,y)=\pm \phi _{1h}\mathrm{sn} \biggl(\phi _{2h}\sqrt{- \frac{\beta }{2}} \biggl(kx+my+ \frac{lt^{\alpha }}{\alpha }-\xi _{0} \biggr), \frac{\phi _{1h}}{\phi _{2h}} \biggr). $$

(3.22)

Remark 3.1

In (3.22), $u_{1}(t,x,y)$ represents Jacobi elliptic function solutions. When $\frac{\phi _{1h}}{\phi _{2h}}\rightarrow 0$, $\mathrm{sn}(\phi _{2h}\sqrt{-\frac{\beta }{2}}(kx+my+ \frac{lt^{\alpha }}{\alpha }-\xi _{0}),\frac{\phi _{1h}}{\phi _{2h}})= \sin (\phi _{2h}\sqrt{-\frac{\beta }{2}}(kx+my+ \frac{lt^{\alpha }}{\alpha }-\xi _{0}))$. When $\frac{\phi _{1h}}{\phi _{2h}}\rightarrow 1$, $\mathrm{sn}(\phi _{2h}\sqrt{-\frac{\beta }{2}}(kx+my+ \frac{lt^{\alpha }}{\alpha }-\xi _{0}),\frac{\phi _{1h}}{\phi _{2h}})= \tanh (\phi _{2h}\sqrt{-\frac{\beta }{2}}(kx+my+ \frac{lt^{\alpha }}{\alpha }-\xi _{0}))$.

(ii) Suppose that $h=-\frac{\gamma ^{2}}{4\beta }$. Then we have $\phi _{1h}=\phi _{2h}=\sqrt{-\frac{\gamma }{\beta }}$ and obtain two families of kink solitary wave solutions,

$$ u_{2}(t,x,y)=\pm \sqrt{-\frac{\gamma }{\beta }}\tanh \biggl(\sqrt{ \frac{\gamma }{2}} \biggl(kx+my+\frac{lt^{\alpha }}{\alpha }-\xi _{0} \biggr) \biggr). $$

(3.23)

II. The case $\beta >0$ , $\gamma <0$ .

In this case, $P_{1}(-\sqrt{-\frac{\gamma }{\beta }},0)$ and $P_{3}(\sqrt{-\frac{\gamma }{\beta }},0)$ are center points, while $P_{2}(0,0)$ is a saddle point.

(i) Suppose that $h\in (-\frac{\gamma ^{2}}{4\beta },0)$. Two families of periodic orbits of system (3.18) are defined by the algebraic equation

$$\begin{aligned} y={}&\pm \sqrt{\frac{\beta }{2}}\sqrt{-u^{4}-\frac{2\gamma }{\beta }u^{2}+ \frac{4h}{\beta }} \\ ={}&\pm \sqrt{\frac{\beta }{4}}\sqrt{ \bigl(u^{2}-\chi ^{2}_{1h} \bigr) \bigl( \chi ^{2}_{2h}-u^{2} \bigr)}, \end{aligned}$$

(3.24)

where $\chi _{1h}=\sqrt{-\frac{\gamma }{\beta }-\frac{1}{\beta }\sqrt{\gamma ^{2}+4 \beta h}}$, $\chi _{2h}=\sqrt{-\frac{\gamma }{\beta }+\frac{1}{\beta }\sqrt{\gamma ^{2}+4 \beta h}}$.

Integrating them along the periodic orbits, we obtain two families of periodic traveling wave solutions, namely

$$ u_{3}(t,x,y)=\pm \chi _{2h}\mathrm{dn} \biggl(\chi _{2h}\sqrt{ \frac{\beta }{2}} \biggl(kx+my+\frac{lt^{\alpha }}{\alpha }-\xi _{0} \biggr), \frac{\sqrt{\chi _{2h}^{2}-\chi _{1h}^{2}}}{\chi _{2h}} \biggr). $$

(3.25)

(ii) Suppose that $h=0$. Then we obtain two bell solitary wave solutions

$$ u_{4}(t,x,y)=\pm \sqrt{-\frac{2\gamma }{\beta }}\mathrm{sech} \biggl( \sqrt{- \gamma } \biggl(kx+my+\frac{lt^{\alpha }}{\alpha }-\xi _{0} \biggr) \biggr). $$

(3.26)

(iii) Suppose that $h\in (0,+\infty )$. Then the function (3.19) can be rewritten as the following algebraic expression:

$$ y=\pm \sqrt{\frac{\beta }{2}}\sqrt{-u^{4}-\frac{2\gamma }{\beta }u^{2}+ \frac{4h}{\beta }}=\pm \sqrt{\frac{\beta }{2}}\sqrt{ \bigl(\chi ^{2}_{3h}+u^{2} \bigr) \bigl( \chi ^{2}_{4h}-u^{2} \bigr)}, $$

(3.27)

where $\chi _{3h}=\sqrt{\frac{\gamma }{\beta }+\frac{1}{\beta }\sqrt{\gamma ^{2}+4 \beta h}}$, $\chi _{4h}=\sqrt{-\frac{\gamma }{\beta }+\frac{1}{\beta }\sqrt{\gamma ^{2}+4 \beta h}}$.

Integrating them along the periodic orbits, we obtain two families of periodic traveling wave solutions, namely

$$ u_{5}(t,x,y)=\chi _{4h}\mathrm{cn} \biggl(\sqrt{ \frac{\beta (\chi _{3h}^{2}+\chi _{4h}^{2})}{2} \biggl(kx+my+ \frac{lt^{\alpha }}{\alpha }-\xi _{0} \biggr)}, \frac{\chi _{4h}}{\sqrt{\chi _{3h}^{2}+\chi _{4h}^{2}}} \biggr). $$

(3.28)

4 Conclusion

By using the generalized $(G'/G)$-expansion method and bifurcation theory method, we obtain exact traveling wave solutions, bifurcation, and phase portraits for the ($2+1$)-dimensional conformable time-fractional Zoomeron equation under the given parameter conditions. Many exact solutions have been obtained, which include hyperbolic function solutions, Jacobi elliptic function solutions, trigonometric function solutions, and rational function solutions. Compared with the previous work, the solution method obtained in the paper has not been reported. Furthermore, two methods we employ here can be used to analyze the exact solutions and bifurcation for other FPDE.

Appendix

In [35], Atangana et al. have proved some important properties of the conformable fractional derivative. Next, we give the proof details, which are taken from [35].

Proof

To prove Remark 2.1(i), let $\varepsilon =t^{\alpha -1}h$ in Definition 2.1. Then,

$$\begin{aligned} D_{t}^{\alpha }f(t)&=\lim_{\varepsilon \rightarrow 0} \frac{f(t+\varepsilon t^{1-\alpha })-f(t)}{\varepsilon }=\lim_{h \rightarrow 0}\frac{f(t+h)-f(t)}{ht^{\alpha -1}} \\ &=t^{1-\alpha }\lim_{h\rightarrow 0}\frac{f(t+h)-f(t)}{h}=t^{1-\alpha } \frac{df}{dt}(t); \end{aligned}$$

when $f(t)=t^{\mu }$, $\mu \in \mathbf{R}$, we obtain

$$ D_{t}^{\alpha }t^{\mu }=t^{1-\alpha } \frac{dt^{\mu }}{dt}=t^{1-\alpha } \mu t^{\mu -1}=\mu t^{\mu -\alpha }. $$

(A.1)

To prove Remark 2.1(iii), by Definition 2.1, we have the following:

$$ D_{t}^{\alpha }(f\circ g) (t)=\lim_{\varepsilon \rightarrow 0} \frac{(f\circ g)(t+\varepsilon t^{1-\alpha })-(f\circ g)(t)}{\varepsilon }. $$

Now putting $k=\varepsilon t^{1-\alpha }$, we obtain

$$ D_{t}^{\alpha }(f\circ g) (t)=t^{1-\alpha }\lim _{k\rightarrow 0} \frac{(f\circ g)(t+k)-(f\circ g)(t)}{k}, $$

(A.2)

with

$$ \lim_{k\rightarrow 0}\frac{(f\circ g)(t+k)-(f\circ g)(t)}{k}. $$

So we obtain

$$ \lim_{k\rightarrow 0}\frac{(f\circ g)(t+k)-(f\circ g)(t)}{k}=\lim _{k \rightarrow 0}\frac{f(g(t)+k)-f(g(t))}{k}, $$

(A.3)

If $k=\varepsilon (g(t))^{1-\alpha }$, then formula (A.3) can be transformed to

$$ \lim_{k\rightarrow 0}\frac{(f\circ g)(t+k)-(f\circ g)(t)}{k}= \bigl(g(t) \bigr)^{ \alpha -1}\lim_{\varepsilon \rightarrow 0} \frac{f(g(t)+\varepsilon (g(t))^{1-\alpha })-f(g(t))}{\varepsilon }. $$

(A.4)

Now replacing (A.4) in (A.2), we obtain the following:

$$ D_{t}^{\alpha }(f\circ g) (t)=t^{1-\alpha }g(t)^{\alpha -1} \lim_{ \varepsilon \rightarrow 0} \frac{f(g(t)+\varepsilon (g(t))^{1-\alpha })-f(g(t))}{\varepsilon }, $$

(A.5)

with, of course, yields

$$ D_{t}^{\alpha } \bigl(f(t) \bigr)|_{t=g(t)}=\lim _{\varepsilon \rightarrow 0} \frac{f(g(t)+\varepsilon (g(t))^{1-\alpha })-f(g(t))}{\varepsilon }. $$

 □