1 Introduction

The concept of fractional calculus (FC) is as old as the classical calculus. Even though its roots are planted in the period of Newton, recently it has magnetized the attention of a class of mathematicians and scientists. More precisely, the intriguing leaps of evolution and innovation in the associated fields of science and technology are found from the last thirty years within the frame of FC. There have been diverse definitions for the differential and integral with arbitrary order suggested by many pioneers in order to overcome the limitation of the previous definition, and this orientation lays the foundation [1–6]. Fractional calculus is comprehensively applied to investigate the nature and corresponding consequences of various phenomena, for instance, chaos theory [7], human diseases [8], optics [9], nanotechnology [10], and other areas [11–14].

The main purpose of studying the concept of FC is the heterogeneities phenomenon associated with complexities. Also it is proved that FC is the most efficient weapon to illustrate the mechanism related to the diffusion process since the integer order calculus is unable to capture the interesting behaviour of complex and nonlinear model related to time, history and their corresponding consequence. However, recently many researchers have proved and illustrated that the fractional calculus is able to describe these essential properties. Moreover, the authors [15–30] considered newly defined fractional operators in order to analyse and capture the simulating nature of various phenomena. For instance, the authors in [23] considered the fractional operator derived with the aid of Mittag-Leffler function in order to analyse the outbreak of dengue fever and presented some interesting results. The optimal control of tuberculosis and diabetes co-existence was investigated in [24], and the model of spring pendulum was analysed in [27] with the help of fractional calculus for different kernels. Many young researchers began to study generalised calculus due to rapid growth in the computer software with mathematical algorithms in order to examine the diverse class of complex phenomena and execute their viewpoints.

We investigate an EFK equation in the present study, and the EFK equation was suggested by Coullet, Elphick and Repauxin in 1987 [31], and later, in 1988, Dee and Saarloos [32, 33] proposed the generalization of the standard FK equation. Here, we consider the EFK equation [34, 35]

$$ u_{t} +\mu\Delta^{2} u- \Delta u+\phi ( u ) =0,\quad x\in \varOmega, t\in(0, T], $$
(1)

where \(\phi ( u ) = u^{3} -u\), \(T>0\), \(\varOmega\in ( 0, 1 )\) with boundary ∂Ω and μ signifies a positive constant. For \(\mu=0\), Eq. (1) reduces to the classical FK equation. Including fourth-order term to the classical FK equation, the authors in [31] illustrated and natured Eq. (1). This term plays an important role in phase transitions near critical points (Lipschitz points).

The considered model has diverse significance, it has been analysed and also illustrated by many researchers associated with science and technology. For instance, near to Lipschitz point the mesoscopic model of a phase transition was demonstrated by the authors in [36], the considered model describes the reaction-diffusion system by travelling waves [37]; in liquid crystals the authors in [38] illustrated the propagation of domain walls, pattern formation in bi-stable systems [32].

Many interesting and nonlinear models arising in associated fields of science and engineering have been effectively and systematically exemplified with the aid of generalised calculus in the present scenario. Many elder researchers suggested the distinct definition for both integral and differential operators having fractional order. Nevertheless, each basic notion has its own confines. The importance of the initial conditions is not described by Riemann–Liouville derivative, the singular kernel is not associated with the notion of fractional calculus described by Caputo. In order to overcome the above-mentioned limitations, Caputo and Fabrizio in 2015 defined the operator [39], and later many authors employed it to investigate and present some interesting behaviour for nonlinear complex problems. Recently, many researchers pointed out some issues related to essential properties describing the behaviour of nonlinear problems like the non-local and non-singular kernel. In order to overcome these limitations with the help of Mittag-Leffler functions, Atangana and Baleanu derived the new fractional derivative in 2016, namely Atangana–Baleanu (AB) derivative [40]. This derivative buried all the above-mentioned issues.

On the other hand, it is essential and very important to evaluate the solution for the integral and differential equations describing the above mechanisms. In connection with this, physicist and mathematicians established more accurate and very effective techniques. There are numerous methods available in the literature, for instance, decomposition method, perturbation methods, homotopy methods, iteration methods and many others. Among these schemes, the homotopy analysis method (HAM) [41, 42] has been extensively considered by many researchers due to its applicability, efficiency and accuracy. HAM has been employed to nonlinear problems for the purpose of examining the behaviour without linearization, transformation, discretization or perturbation. However, it necessitates huge computer memory and time, and hence the combination of HAM with well-established transform algorithm is imposed.

Here, we consider FEFK equation of the form

$$ {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} u ( x,t ) +\mu\Delta^{2} u- \Delta u+\phi ( u ) =0, \quad 0< \alpha\leq 1, $$
(2)

where α is fractional order. In this paper, we consider the improved method of HAM with the elegant amalgamation of Laplace transform in order to reduce huge computation and computer memory [43]. Due to efficacy and reliability, q-HATM has been applied to many nonlinear problems as well as models which describe the various phenomena by many researchers in order to present the nature, capture the behaviour and to illustrate the corresponding consequences [44–51]. The novelty of the considered algorithm is that it is fabricated with auxiliary and homotopy parameters, and these can help quick convergence in the obtained solution. Also, it provides a simple computational scheme to find the analytical solution. Further, it offers more freedom to consider the equation type nonlinear problems and a distinct class of initial conditions. The proposed solution procedure can preserve more exactness while reducing the huge computational work and time in comparison with other traditional schemes.

The projected model has fascinated the consideration of many authors since it plays a substantial role in describing various nonlinear models. Recently, many researchers have found and analysed the solution with the help of distinct methods. For instance, the authors in [52] found the heteroclinic solutions for Eq. (1) by variational algorithm; the authors in [53] employed the finite difference method and also presented existence and stability for the corresponding solution; the attractor bifurcation was illustrated by the authors in [54] for the proposed model; the authors in [55] presented the global dynamics of stationary solutions for Eq. (1); the periodic solution was obtained by the authors in [56]; the Fourier pseudo-spectral scheme was employed by the researchers in [35] to presented some simulating consequences of the results to understand the nature of the considered nonlinear problem.

In this paper, the equation describing the phase transitions near critical points, called EFK equation, is considered. In order to integrate the memory effect and essential properties like kernel and non-singularity, we generalise the considered nonlinear model by replacing time derivative with fractional derivative with the aid of AB operator. Moreover, with the assistance of fixed point hypothesis, the existence and uniqueness are presented for the solution of the considered problem. Moreover, we consider two different cases in order to demonstrate the applicability and the efficiency of the considered method. We present the numerical simulation in order to illustrate the accuracy of q-HATM. The remaining part of the paper is organised as follows: the essential fundamentals and basic notions are defined in Sect. 2; the solution procedure of the projected scheme is presented in Sect. 3, and in Sect. 4 we present the solution for the considered problem with the aid of q-HATM. The existence and uniqueness for the solution of FEFK equation are presented in Sect. 5 with the help of fixed point theorem. Further, the numerical results and discussion for two different cases and conclusion on the obtained results are respectively presented in Sect. 6 and Sect. 7.

2 Preliminaries

Here, we present the fundamental notions of fractional derivative and Laplace transform [57–61].

Definition 1

The Atangana–Baleanu–Caputo (ABC) derivative for the function \(f\in H^{1} ( a, b )\) (\(b>a\), \(\alpha\in [ 0, 1 ] \)) is presented as follows [40]:

$$ {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} \bigl( f ( t ) \bigr) = \frac{\mathcal{B} [ \alpha ]}{1-\alpha} \int_{a}^{t} f ' ( \vartheta ) E_{\alpha} \biggl[ -\alpha\frac{ ( t-\vartheta )^{\alpha}}{1-\alpha} \biggr] \,d\vartheta. $$
(3)

Definition 2

The fractional-order AB integral of a function \(f\in H^{1} ( a, b )\), \(b>a\), \(\alpha\in [ 0, 1 ]\), and then its fractional-order in Riemann–Liouville (RL) sense is defined as follows [40]:

$$ {}_{a}^{\mathit{ABR}} D_{t}^{\alpha} \bigl( f ( t ) \bigr) = \frac{\mathcal{B} [ \alpha ]}{1-\alpha} \frac{d}{dt} \int_{a}^{t} f ( \vartheta ) E_{\alpha} \biggl[ \alpha \frac{ ( t-\vartheta )^{\alpha}}{\alpha-1} \biggr]\, d\vartheta. $$
(4)

Definition 3

The AB integral of fractional order is presented as follows [40]:

$$ {}_{a}^{AB} I_{t}^{\alpha} \bigl( f ( t ) \bigr) = \frac{1-\alpha}{\mathcal{B} [ \alpha ]} f ( t ) + \frac{\alpha}{\mathcal{B} [ \alpha ] \varGamma ( \alpha )} \int_{a}^{t} f ( \vartheta ) ( t-\vartheta )^{\alpha-1}\, d\vartheta. $$
(5)

Definition 4

As reference to AB derivative of the function \(f ( t )\), the Laplace transform (LT) of \(f ( t )\) is presented as follows [40]:

$$ L \bigl[ {}_{0}^{\mathit{ABC}} D_{t}^{\alpha} \bigl( f ( t ) \bigr) \bigr] ( s ) = \frac{\mathcal{B} [ \alpha ]}{ 1-\alpha} \frac{s^{\alpha} L [ f ( t ) ] - s^{\alpha-1} f ( 0 )}{s^{\alpha} + ( \alpha/(1-\alpha) )}. $$
(6)

Theorem 1

The Lipschitz condition holds for the ABR and ABC derivatives [40]

$$ \bigl\Vert {}_{a}^{\mathit{ABR}} D_{t}^{\alpha} f_{1} ( t ) - {}_{a}^{\mathit{ABR}} D_{t}^{\alpha} f_{2} ( t ) \bigr\Vert < K_{2} \bigl\Vert f_{1} ( x ) - f_{2} ( x ) \bigr\Vert $$
(7)

and

$$ \bigl\Vert {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} f_{1} ( t ) - {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} f_{2} ( t ) \bigr\Vert < K_{1} \bigl\Vert f_{1} ( x ) - f_{2} ( x ) \bigr\Vert . $$
(8)

Theorem 2

The fractional differential equation\({}_{a}^{\mathit{ABC}} D_{t}^{\alpha} f_{1} ( t ) =s ( t )\)has a unique solution, which is presented as follows [40]:

$$ f ( t ) =\frac{(1-\alpha)}{\mathcal{B} [ \alpha ]} s ( t ) + \frac{\alpha}{\mathcal{B} [ \alpha ] \varGamma ( \alpha )} \int_{0}^{t} s ( \varsigma ) ( t-\varsigma )^{\alpha-1}\, d\varsigma. $$
(9)

3 Fundamental procedure of projected scheme

In this part, we take a fractional differential equation to present the solution procedure of the projected method [62–64]

$$ {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} v ( x,t ) +\mathcal{R} v ( x,t )+\mathcal{N} v ( x,t ) =f ( x,t ),\quad n-1< \alpha\leq n, $$
(10)

with the initial condition

$$ v ( x,0 )=\mathfrak{g} ( x ), $$
(11)

where \({}_{a}^{\mathit{ABC}} D_{t}^{\alpha} v ( x,t ) \) symbolises the AB derivative of \(v ( x,t ) \). By applying LT on Eq. (10), one can get

$$ \mathcal{L} \bigl[ v ( x,t ) \bigr] - \frac{\mathfrak{g} ( x )}{s} + \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1- \alpha+ \frac{\alpha}{s^{\alpha}} \biggr) \bigl\{ \mathcal{L} \bigl[ \mathcal{N} v ( x,t ) \bigr] +\mathcal{L} \bigl[ \mathcal {R} v ( x,t ) \bigr] -\mathcal{L} \bigl[ f ( x, t ) \bigr] \bigr\} =0. $$
(12)

Now, corresponding to foregoing equations, the nonlinear operator is presented as follows:

$$\begin{aligned}[b] &\mathcal{N} \bigl[ \varphi ( x,t;q ) \bigr]\\ &\quad= \mathcal{L} \bigl[ \varphi ( x,t;q ) \bigr] - \frac{\mathfrak{g} ( x )}{s}\\&\qquad + \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1- \alpha+ \frac{\alpha}{s^{\alpha}} \biggr) \bigl\{ \mathcal{L} \bigl[ \mathcal{R} \varphi ( x,t;q ) \bigr] +L \bigl[ \mathcal{N} \varphi ( x,t;q ) \bigr] -L \bigl[ f ( x,t ) \bigr] \bigr\} , \end{aligned} $$
(13)

where \(q\in [ 0, \frac{1}{\mathfrak{n}} ]\). Now, the homotopy is presented as follows with non-zero auxiliary parameter ℏ and embedding parameter \(q\in [ 0, \frac{1}{n} ] \) (\(n\geq1 \)):

$$ \hslash q \mathcal{N} \bigl[ \varphi ( x, t;q ) \bigr] = ( 1- \mathfrak{n} q ) \mathcal{L} \bigl[ \varphi ( x, t;q ) - v_{0} ( x,t ) \bigr], $$
(14)

where L signifies LT. For \(q=0\) and \(q= \frac{1}{n}\), the following are satisfied:

$$ \varphi ( x, t;0 ) = v_{0} ( x,t ), \qquad\varphi \biggl( x, t; \frac{1}{n} \biggr) = v ( x,t ). $$
(15)

By increasing q from 0 to \(\frac{1}{\mathfrak{n}}\), then \(\varphi( x, t;q)\) converges from \(v_{0} ( x,t )\) to \(v ( x,t )\). Then, with the help of Taylor’s theorem near to q, one can have

$$ \varphi ( x, t;q ) = v_{0} ( x,t ) + \sum _{m=1}^{\infty} v_{m} ( x,t ) q^{m}, $$
(16)

where

$$ v_{m} ( x,t ) = \frac{1}{m!} \frac{\partial^{m} \varphi( x, t;q)}{\partial q^{m}} \bigg\vert _{q=0}. $$
(17)

For the proper choice of \(v_{0} ( x,t )\), n and ℏ, the series (16) converges at \(q= \frac{1}{\mathfrak{n}}\). Then

$$ v ( x,t ) = v_{0} ( x,t ) + \sum_{m=1}^{\infty} v_{m} ( x,t ) \biggl( {\frac{1}{n}} \biggr)^{m}. $$
(18)

Multiplying by \(\frac{1}{m!}\) after differentiating Eq. (14) m-times with q and then putting \(q=0\), one gets

$$ \mathcal{L} \bigl[ v_{m} ( x,t ) - \mathsf{k}_{m} v_{m-1} ( x,t ) \bigr] = \hslash R_{m} ( \vec{v}_{m-1} ), $$
(19)

and later we define vectors as

$$ \vec{v}_{m} = \bigl\{ v_{0} ( x,t ), v_{1} ( x,t ),\dots, v_{m} ( x,t ) \bigr\} . $$
(20)

On applying inverse LT to Eq. (19), we obtain

$$ v_{m} ( x,t ) = \hslash\mathcal{L}^{-1} \bigl[ R_{m} ( \vec{v}_{m-1} ) \bigr] + \mathsf{k}_{m} v_{m-1} ( x,t ), $$
(21)

where

$$\begin{aligned}[b] R_{m} ( {\vec{v}_{m-1}} ) &=L \bigl[ v_{m-1} ( x,t ) \bigr] - \biggl( 1- \frac{\mathsf{k}_{m}}{n} \biggr) \biggl( \frac{\mathfrak{g} ( x )}{s} + \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1- \alpha+ \frac{\alpha}{s^{\alpha}} \biggr) L \bigl[ f ( x,t ) \bigr] \biggr)\\&\quad + \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1- \alpha+ \frac{\alpha}{s^{\alpha}} \biggr) L [ R v_{m-1} + \mathcal{H}_{m-1} ] \end{aligned} $$
(22)

and

$$ \mathsf{k}_{m} = \left \{ \textstyle\begin{array}{l@{\quad}l} 0, &m\leq1,\\ n, &m>1. \end{array}\displaystyle \right . $$
(23)

In Eq. (22), \(\mathcal{H}_{m}\) is a homotopy polynomial, which is defined as

$$ \mathcal{H}_{m} = \frac{1}{m!} \biggl[ \frac{\partial^{m} \varphi ( x, t;q )}{\partial q^{m}} \biggr]_{q=0}\quad \text{and}\quad \varphi ( x, t;q ) = \varphi_{0} +q \varphi_{1} + q^{2} \varphi_{2} +\cdots. $$
(24)

With the assistance of Eqs. (23) and (24), we have

$$\begin{aligned}[b] v_{m} ( x,t )& = ( \mathsf{k}_{m} + \hslash ) v_{m-1} ( x,t ) - \biggl( 1- \frac{\mathsf{k}_{m}}{n} \biggr) \mathcal{L}^{-1} \biggl( \frac{\mathfrak{g} ( x )}{s} + \frac{1}{ \mathcal{B} [ \alpha ]} \biggl( 1- \alpha+ \frac{\alpha}{ s^{\alpha}} \biggr) L \bigl[ f ( x,t ) \bigr] \biggr)\hspace{-12pt}\\&\quad + \hslash\mathcal{L}^{-1} \biggl\{ \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1- \alpha+ \frac{\alpha}{s^{\alpha}} \biggr) L [ R v_{m-1} + \mathcal{H}_{m-1} ] \biggr\} .\end{aligned} $$
(25)

Then we can find the terms of \(v_{m} ( x,t )\) with the aid of Eq. (25). The q-HATM solution is written as follows:

$$ v ( x,t ) = \sum_{m=0}^{\infty} v_{m} ( x,t ). $$
(26)

4 Solution for FEFK equation

Here, we examine the FEFK equation presented in Eq. (2) to find its solution with the assistance of the projected scheme

$$ {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} u ( x,y,t ) +\mu\Delta^{2} u- \Delta u+ u^{3} -u=0, \quad 0< \alpha\leq1, $$
(27)

with the initial conditions (ICs)

$$ u ( x,y,0 ) = u_{0} ( x,y,t ). $$
(28)

Taking LT on Eq. (27) and with the aid of Eq. (28), one can have

$$ L \bigl[ u ( x,y,t ) \bigr] = \frac{1}{s} \bigl( u_{0} ( x,y,t ) \bigr) + \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1-\alpha+ \frac{\alpha}{s^{\alpha}} \biggr) L \bigl\{ \mu\Delta^{2} u- \Delta u+ u^{3} -u \bigr\} . $$
(29)

Now, we present the nonlinear operator N as follows:

$$\begin{aligned}[b] N \bigl[ \varphi ( x,y,t;q ) \bigr] &=L \bigl[ \varphi ( x,y,t;q ) \bigr] - \frac{1}{s} \bigl( u_{0} ( x,y,t ) \bigr) \\&\quad+ \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1-\alpha+ \frac{\alpha}{s^{\alpha}} \biggr)\\&\quad\times L \bigl\{ \mu \Delta^{2} \varphi ( x,y,t;q ) - \Delta\varphi ( x,y,t;q ) + \varphi ( x,y,t;q )^{3} -\varphi ( x,y,t;q ) \bigr\} . \end{aligned} $$
(30)

At \(\mathcal{H} ( x,y, t)=1\), the mth order deformation equation by using q-HATM is expressed as

$$ L \bigl[ u_{m} ( x,y,t ) - \mathsf{k}_{m} u_{m-1} ( x,y,t ) \bigr] =\hslash R_{m} [ \vec{u}_{m-1} ], $$
(31)

where

$$\begin{aligned}[b] R_{m} [ \vec{u}_{m-1} ] &=L \bigl[ u_{m-1} ( x,y,t ) \bigr] - \biggl( 1- \frac{\mathsf{k}_{m}}{\mathfrak{n}} \biggr) \biggl\{ \frac{1}{s} \bigl( u_{0} ( x,y,t ) \bigr) \biggr\} \\&\quad+ \frac{1}{\mathcal{B} [ \alpha ]} \biggl( 1-\alpha+ \frac{\alpha}{s^{\alpha}} \biggr)\\&\quad\times L \Biggl\{ \mu\Delta^{2} u_{m-1} - \Delta^{2} u_{m-1} + \sum_{j=0}^{i} \sum_{i=0}^{m-1} u_{j} u_{i-j} u_{m-1-i} - u_{m-1} \Biggr\} .\end{aligned} $$
(32)

By utilizing the inversion of LT on Eq. (31), we get

$$ u_{m} ( x,y,t ) = \mathsf{k}_{m} u_{m-1} ( x,y, t ) +\hslash L^{-1} \bigl\{ R_{m} [ \vec{u}_{m-1} ] \bigr\} . $$
(33)

On solving the preceding equations by using \(u_{0} ( x,y,t )\), we can obtain the terms of

$$ u ( x,y,t ) = u_{0} ( x,y,t ) + \sum_{m=1}^{\infty} u_{m} ( x,y,t ) \biggl( \frac{1}{n} \biggr)^{m}. $$
(34)

5 Existence and uniqueness of solution

Here, with the aid of fixed point theory, we demonstrate the existence and uniqueness for the solution of the considered problem. Now, by the aid of Eq. (27), one can have

$$ {}_{0}^{\mathit{ABC}} D_{t}^{\alpha} \bigl[ u ( x,y,t ) \bigr] =\mathcal{G} ( x,y,t, u ). $$
(35)

With the help of Eq. (35) and Theorem 2, one can get

$$ u ( x,y,t ) -u ( x,y,0 ) = \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \mathcal{G} ( x,y,t,u ) + \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} \mathcal{G} ( x,y,\zeta,u ) ( t- \zeta )^{\alpha-1}\, d\zeta. $$
(36)

Theorem 3

The kernel\(\mathcal{G}\)satisfies the Lipschitz condition and also contraction if it satisfies\(0 \leq ( \mu \Delta^{2} - \Delta+ ( a^{2} + b^{2} +ab ) -1 ) <1\).

Proof

Let us choose two functions u and \(u_{1}\) to verify the required condition, therefore we get

$$\begin{aligned}[b] \bigl\Vert \mathcal{G} ( x,y,t, u ) -\mathcal{G} ( x,y,t, u_{1} ) \bigr\Vert &= \bigl\Vert \mu\Delta^{2} \bigl[ u ( x,y,t ) -u ( x,y, t_{1} ) \bigr] - \Delta \bigl[ u ( x,y,t ) -u ( x,y, t_{1} ) \bigr] \\ &\quad + \bigl[ u^{3} ( x,y,t ) - u^{3} ( x,y, t_{1} ) \bigr] - \bigl[ u ( x,y,t ) -u ( x,y, t_{1} ) \bigr] \bigr\Vert \\ &\leq \bigl\Vert \mu\Delta^{2} - \Delta+ \bigl( a^{2} + b^{2} +ab \bigr) -1 \bigr\Vert \bigl\Vert u ( x,y,t ) -u(x,y, t_{1} ) \bigr\Vert \\ &\leq \bigl( \mu\Delta^{2} - \Delta+ \bigl( a^{2} + b^{2} +ab \bigr) -1 \bigr) \bigl\Vert u ( x,y,t ) -u ( x,y, t_{1} ) \bigr\Vert .\end{aligned} $$
(37)

Since u and \(u_{1}\) are bounded and here \(a= \Vert u \Vert \) and \(b= \Vert u_{1} \Vert \). Inserting \(\eta=\mu\Delta^{2} - \Delta + ( a^{2} + b^{2} +ab ) -1\) in Eq. (37), we get

$$ \bigl\Vert \mathcal{G} ( x,y,t, u ) -\mathcal{G} ( x,y,t, u_{1} ) \bigr\Vert \leq\eta \bigl\Vert u ( x,y,t ) -u(x,y, t_{1} ) \bigr\Vert . $$
(38)

It is clear that the Lipschitz condition is achieved for \(\mathcal{G}_{1}\). Moreover, if \(0 \leq ( \mu\Delta^{2} - \Delta+ ( a^{2} + b^{2} +ab ) -1 ) <1\), then it leads to contraction. Now, the recursive form is present for the above relation and initial condition as follows:

$$ u_{n} ( x,y,t ) = \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \mathcal{G} ( x,y,t, u_{n-1} ) + \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} \mathcal{G} ( x,y,\zeta, u_{n-1} ) ( t-\zeta )^{\alpha-1} \,d\zeta $$
(39)

and

$$ u ( x,y,0 ) = u_{0} ( x,y,t ). $$
(40)

The difference between successive terms is defined as follows:

$$\begin{aligned}[b] \phi_{n} ( x,y,t ) &= u_{n} ( x,y,t ) - u_{n-1} ( x,y,t )\\& = \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \bigl( \mathcal{G}_{1} ( x,y,t, u_{n-1} ) -\mathcal{G} ( x,y,t, u_{n-2} ) \bigr)\\&\quad + \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} \mathcal{G} ( x,y,\zeta, u_{n-1} ) ( t-\zeta )^{\alpha-1}\, d\zeta. \end{aligned} $$
(41)

Notice that

$$ u_{n} ( x,y,t ) = \sum_{i=1}^{n} \phi_{i} ( x,y,t ). $$
(42)

By employing the norm on Eq. (41) and considering Eq. (38), we have

$$ \bigl\Vert \phi_{n} ( x,y,t ) \bigr\Vert \leq \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \eta \bigl\Vert \phi_{(n-1)} ( x,y,t ) \bigr\Vert + \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta \int_{0}^{t} \bigl\Vert \phi_{(n-1)} ( x,y,\zeta ) \bigr\Vert \,d\zeta. $$
(43)

 □

With the aid of foregoing results, we prove the following theorems.

Theorem 4

For the projected system (27), the solution will exist and be unique for a particular\(t_{0}\)such that

$$\frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \eta+ \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta< 1. $$

Proof

Let \(u (x,y, t )\) be a bounded function sustaining the Lipschitz condition. With the assistance of Eq. (43), we get

$$ \bigl\Vert \phi_{i} ( x,y,t ) \bigr\Vert \leq \bigl\Vert u_{n} ( x,y,0 ) \bigr\Vert \biggl[ \frac{ ( 1-\alpha )}{ \mathcal{B} ( \alpha )} \eta+ \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta \biggr]^{n}. $$
(44)

This proves the continuity and existence of the achieved solution. Further, to verify that the above equation is the solution for Eq. (27), we consider

$$ u ( x,y,t ) -u ( x,y,0 ) = u_{n} ( x,y,t ) - \mathcal{K}_{n} ( x,y,t ). $$
(45)

Then, we consider achieving the required result

$$\begin{aligned}[b] \bigl\Vert \mathcal{K}_{n} ( x,y,t ) \bigr\Vert &=\biggl\Vert \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \bigl( \mathcal{G} ( x,y,t,u ) -\mathcal{G}( x,y,t, u_{n-1} ) \bigr) \\ &\quad+ \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} ( t-\zeta )^{\mu-1} \bigl( \mathcal{G} ( x,y,\zeta,u ) -\mathcal{G} ( x,y,\zeta, u_{n-1} ) \bigr) \,d\zeta\biggr\Vert \\ &\leq\frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \bigl\Vert \mathcal{G} ( x,y,\zeta,u ) -\mathcal{G} ( x,y,\zeta, u_{n-1} ) \bigr\Vert \\ &\quad+ \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} \bigl\Vert \mathcal{G} ( x,y, \zeta,u ) -\mathcal{G} ( x,y,\zeta, u_{n-1} ) \bigr\Vert \,d\zeta \\ &\leq\frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \eta_{1} \Vert u- u_{n-1} \Vert + \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta_{1} \Vert u- u_{n-1} \Vert t.\end{aligned} $$
(46)

Similarly, at \(t_{0}\) we can obtain

$$ \bigl\Vert \mathcal{K}_{n} ( x,y,t ) \bigr\Vert \leq \biggl( \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} + \frac{\alpha t_{0}}{ \mathcal{B} ( \alpha ) \varGamma ( \alpha )} \biggr)^{n+1} \eta^{n+1} M. $$
(47)

We have from Eq. (47), for n tending to ∞, \(\Vert\mathcal{K}_{n} ( x,y,t ) \Vert\) approaches 0. Now, it is important to present the uniqueness for the obtained solution. Suppose that \(u^{*} ( t )\) is a different solution, then one can get

$$\begin{aligned}[b] u ( x,y,t ) - u^{*} ( x,y,t ) &= \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \bigl( \mathcal{G} ( x,y,t,u ) -\mathcal{G} \bigl( x,y,t, u^{*} \bigr) \bigr) \\&\quad+ \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} \bigl( \mathcal{G} ( x,y,\zeta,u ) -\mathcal{G} \bigl( x,y,\zeta, u^{*} \bigr) \bigr) \,d\zeta.\end{aligned} $$
(48)

With the help of properties of the norm, Eq. (48) reduces to

$$\begin{aligned}[b] \bigl\Vert u ( x,y,t ) - u^{*} ( x,y,t ) \bigr\Vert &= \biggl\Vert \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \bigl( \mathcal{G} ( x,y,t,u ) -\mathcal{G} \bigl( x,y,t, u^{*} \bigr) \bigr) \\&\quad+ \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \int_{0}^{t} \bigl( \mathcal{G} ( x,y,\zeta,u ) -\mathcal{G} \bigl( x,y,\zeta, u^{*} \bigr) \bigr) \,d\zeta \biggr\Vert \\&\leq\frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \eta \bigl\Vert u ( x,y,t ) - u^{*} ( x,y,t ) \bigr\Vert \\&\quad + \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta t \bigl\Vert u ( x,y,t ) - u^{*} ( x,y,t ) \bigr\Vert . \end{aligned} $$
(49)

On simplification

$$ \bigl\Vert u ( x,y,t ) - u^{*} ( x,y,t ) \bigr\Vert \biggl( 1- \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \eta- \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta t \biggr) \leq0. $$
(50)

From the above condition, it is clear that \(u ( t ) = u^{*} ( t )\), if

$$ \biggl( 1- \frac{ ( 1-\alpha )}{\mathcal{B} ( \alpha )} \eta- \frac{\alpha}{\mathcal{B} ( \alpha ) \varGamma ( \alpha )} \eta t \biggr) \geq0. $$
(51)

Hence, Eq. (51) shows our required result. □

Theorem 5

Let\(( B [ 0, T ], \Vert \cdot \Vert )\)be a Banach space. Suppose that\(u_{n} ( x,y,t )\)and\(u ( x,y,t )\)defineB, if\(0<\lambda<1\), then the series solution presented in Eq. (26) tends towards the solution of Eq. (10).

Proof

Let \(\{ \mathcal{S}_{n} \}\) be a partial sum of Eq. (26), then we need to show that \(\{ \mathcal{S}_{n} \}\) is a Cauchy sequence in \(( B [ 0, T ], \Vert \cdot \Vert )\). Then

$$\begin{aligned} \bigl\Vert \mathcal{S}_{n+1} ( x,y,t ) - \mathcal{S}_{n} ( x,y,t ) \bigr\Vert & = \bigl\Vert u_{n+1} ( x,y,t ) \bigr\Vert \\ &\leq\lambda \bigl\Vert u_{n} ( x,y,t ) \bigr\Vert \\ &\leq\lambda^{2} \bigl\Vert u_{n-1} ( x,y,t ) \bigr\Vert \leq\cdots\leq\lambda^{n+1} \bigl\Vert u_{0} ( x,y,t ) \bigr\Vert .\end{aligned} $$

For every \(n, m\in N\) (\(m\leq n\)), we have

$$\begin{aligned}[b] \Vert \mathcal{S}_{n} - \mathcal{S}_{m} \Vert & = \bigl\Vert ( \mathcal{S}_{m+1} - \mathcal{S}_{m} ) + \cdots+ ( \mathcal{S}_{n-1} - \mathcal{S}_{n-2} ) + ( \mathcal{S}_{n} - \mathcal{S}_{n-1} ) \bigr\Vert \\ &\leq \Vert \mathcal{S}_{m+1} - \mathcal{S}_{m} \Vert +\cdots+ \Vert \mathcal{S}_{n-1} - \mathcal{S}_{n-2} \Vert + \Vert \mathcal{S}_{n} - \mathcal{S}_{n-1} \Vert \\ &\leq \bigl( \lambda^{n} + \lambda^{n-1} +\cdots+ \lambda^{m+1} \bigr) \Vert u_{0} \Vert \\ &\leq\lambda^{m+1} \bigl( 1+\lambda+\cdots++ \lambda^{n-m-2} + \lambda^{n-m-1} \bigr) \Vert u_{0} \Vert \\ &\leq \biggl( \frac{1- \lambda^{n-m}}{1-\lambda} \biggr) \lambda^{m+1} \Vert u_{0} \Vert .\end{aligned} $$
(52)

But \(0<\lambda< 1\), therefore \(\lim_{n, m\rightarrow\infty} \Vert \mathcal{S}_{n} - \mathcal{S}_{m} \Vert =0\). Therefore, \(\{ \mathcal{S}_{n} \}\) is the Cauchy sequence. Hence, it shows the above-mentioned result. □

Theorem 6

The series solution for Eq. (10) is defined in (26), then the maximum absolute error is

$$\Biggl\Vert u ( x,y,t ) - \sum_{n=0}^{M} u_{n} (x,y,t ) \Biggr\Vert \leq\frac{\lambda_{1}^{M+1}}{1- \lambda_{1}} \bigl\Vert u_{0} ( x,y,t ) \bigr\Vert . $$

Proof

With the assistance of Eq. (52) we have

$$\bigl\Vert u ( x,y,t ) - \mathcal{S}_{n} \bigr\Vert = \lambda^{m+1} \biggl( \frac{1- \lambda^{n-m}}{1-\lambda} \biggr) \bigl\Vert u_{0} ( x,y,t ) \bigr\Vert . $$

But \(0<\lambda<0\Rightarrow1- \lambda^{n-m} <1\). Hence, we have

$$\Biggl\Vert u ( x,y,t ) - \sum_{n=0}^{M} u_{n} (x,t ) \Biggr\Vert \leq\frac{\lambda^{M+1}}{1-\lambda} \bigl\Vert u_{0} ( x,y,t ) \bigr\Vert . $$

This proves the required result. □

6 Numerical results and discussion

In this part, we consider two different cases of the FEFK equation to find the approximated analytical solution using q-HATM, in which the equation is associated with Mittag-Leffler kernel.

Case 1: Consider a homogeneous FEFK equation of the form

$$ {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} u ( x,y,t ) +\mu\Delta^{2} u- \Delta u+ u^{3} -u=0, \quad0< \alpha\leq1,$$
(53)

with the initial condition

$$ u ( x,y,0 ) = \sin ( x ) \sin ( y ). $$
(54)

Case 2: Consider a non-homogeneous FEFK equation of the form

$$ {}_{a}^{\mathit{ABC}} D_{t}^{\alpha} u ( x,y,t ) +\mu\Delta^{2} u- \Delta u+ u^{3} -u=g ( x,y,t ), \quad 0< \alpha\leq1, $$
(55)

with the initial condition defined in Eq. (54). Here the non-homogeneous term is given by \(g ( x,y,t ) =4\mu\sin ( x ) \sin ( y ) e^{-t} + ( \sin ( x ) \sin ( y ) e^{-t} )^{3}\). The corresponding exact solution for Eq. (55) is presented as follows:

$$ u ( x,y,t ) = \sin ( x ) \sin ( y ) e^{-t}. $$
(56)
Table 1 Numerical illustration for the q-HATM solution of FEFK equation defined in Case 2 for distinctα at \(n=1\), \(\hslash=1\) and \(y=0.1\)
Full size table

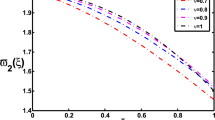
Here, we demonstrate the exactness of the future scheme with distinct fractional order. In Fig. 1, we capture the nature of achieved solution for the homogeneous case of FEFK equation defined in Case 1 with distinct fractional order (i.e. \(\alpha=0.5, 0.75 \) and 1) in terms of 2D and 3D plots. Similarly, for Case 2 the surfaces of q-HATM solution, analytical solution and absolute error are shown in Fig. 3. The variation of attained solution for various fractional order is presented in Fig. 4 for FEFK equation defined in the second case. As related to homotopy parameter (ℏ) and at different fractional order for both cases, we present the behaviour of the achieved solution respectively in Fig. 2 and Fig. 5. These curves aid to control and adjust the region of the convergence for q-HATM solution. Meanwhile, the horizontal line in the plots represents the convergence region. For a particular ℏ, the obtained solution swiftly inclines towards analytical solution. Further, the numerical simulation has been illustrated for the non-homogeneous case proposed problem in distinct fractional order. The presented numerical study elucidates that as the order tends to the classical case, the obtained solution gets near to the analytical solution, also it confirms the exactness of the applied computational scheme.

Figure 1
figure 1

Nature of q-HATM solution in terms of 3D and 2D for Case 1 with \(y=1\) at \(\hslash=-1\), \(n=1\) and \(t=1\) with (a) \(\alpha=0.50\), (b) \(\alpha=0.75\) and (c) \(\alpha=1\)

Full size image
Figure 2
figure 2

ℏ-curves for \(u ( x, t )\) defined in Case 1 with distinct α at \(x=1\), \(y=1\), \(n=1\) and \(t=0.01\) with (a) \(n=1\) and (b) \(n=2\)

Full size image
Figure 3
figure 3

Surfaces (a) q-HATM solution (b) analytical solution (c) absolute error defined in Case 2 at \(\hslash=-1\), \(n=1\), \(t=0.1\) and \(\alpha=1\)

Full size image
Figure 4
figure 4

Nature of the obtained solution defined in Case 2 with differentα for \(\hslash=-1\), \(n=1\), \(y=1 \) and \({x=1}\)

Full size image
Figure 5
figure 5

ℏ-curves for q-HATM solution considered in Case 2 with different α for \(x=1\), \(y=1\) and \(t=0.01\) with (a) \(n=1\) and (b) \(n=2\)

Full size image

7 Conclusion

In this study, we found the solution for FEKZ equation and presented the corresponding consequence by using the q-HATM. The present investigation confirms its competence while examining the real word problems; this is due to the considered fractional-order AB derivatives being defined with the help of Mittag-Leffler function. This function is non-singular and non-local kernel in nature. For the achieved solution, we considered fixed point hypothesis to illustrate the existence and uniqueness. Further, the novelty of the considered scheme is that it did not necessitate any perturbation, discretization or conversion while finding the solution for the nonlinear problems. The present analysis shows that FEKZ equation conspicuously depends on the time instance and history. These essential properties are effectively and systematically illustrated with the help of generalised calculus. More precisely, the considered nonlinear model can be effectively and accurately analysed and exemplified with the help of newly introduced and nurtured novel numerical methods illustrated in [65, 66], and we consider these methods for the future work to analyse the numerous class of nonlinear models. Finally, we can accomplish that the projected technique is more effective and extremely methodical while exemplifying the diverse and interesting class of complex phenomena defined with nonlinear problems existing in science and technology.