Introduction

Calculus of fractional order is pretty antique subject in mathematics. Fractional derivatives were debut in 1695, as in the question of the extension of meaning. Derivatives and integrals of arbitrary order afford more factual models of the real-world phenomenon [1], than classical calculus. During the twentieth century, a bulky amount of research on fractional calculus published by many pioneers includes Caputo [2], Miller and Ross [3], Podlubny [4], Liao [5], and others.

The problems relating to applications of fractional calculus are located in various connected branches of science and engineering, like finance [6], nanotechnology [7], electrodynamics [8], and many other fields. The analytical and numerical solution of fractional partial differential equations plays a vital role in describing the characters of nonlinear problems that arise in daily life.

In 1937, Fisher proposed a model for the temporal and spatial propagation of a virile gene in an infinite medium, called Fisher’s equation [9]. The simplest and classical case of Fisher’s equation so-called reaction diffusion equation is given by [10]

$$\frac{\partial u}{\partial t} = \lambda \frac{{\partial^{2} u}}{{\partial x^{2} }} + \mu u\left( {x,t} \right)\,\left( {1 - u\left( {x,t} \right)} \right),$$
(1)

which basically the Logistic equation and the conjunction of diffusion equation with diffusion factor \(\lambda\) and birth rate \(\mu\). Here, \(u\left( {x,t} \right)\) specifies the state evolution over the spatial–temporal domain characterized by the coordinates \(x\), \(t ,\) respectively. Fisher’s equation is widely used in chemical kinetics [11], Neolithic transitions [12], branching Brownian motion [13], epidemics and bacteria [14] and many other disciplines.

Many researchers studied various techniques like, Adomian decomposition method [15], homotopy perturbation Sumudu transform method [16], Haar wavelet method [17], optimal homotopy asymptotic method [17], homotopy perturbation method [18], Chebyshev spectral collocation method [19], and fractional natural decomposition method [20] to obtain numerical solutions for the Fisher’s equation of fractional order. Recently, Singh et al. [21] introduced and nurtured the new homotopy technique known as \(q\)-HATM to study nonlinear problems (including, classical and arbitrary order) arises in nature [22, 23]. This method is an elegant amalgamation of homotopy algorithm through Laplace transform.

Preliminaries

Here, we recall some definitions and properties of fractional calculus and Laplace transform, which are used in the sequel:

Definition 1

The fractional integral of a function \(f\left( t \right) \in C_{\mu } \left( {\mu \ge - 1} \right)\), of order \(\alpha > 0\) initially defined by Riemann–Liouville is represented as [4]

$$\begin{aligned} J^{\alpha } f\left( t \right) & = \frac{1}{{\Gamma \left( \alpha \right)}}\mathop \smallint \limits_{0}^{t} \left( {t - \vartheta } \right)^{\alpha - 1} f\left( \vartheta \right)d\vartheta , \\ J^{0} f\left( t \right) & = f\left( t \right). \\ \end{aligned}$$
(2)

Definition 2

The fractional derivative of \(f \in C_{ - 1}^{n}\) in the Caputo [2] sense is defined as

$$D_{t}^{\alpha } f\left( t \right) = \left\{ {\begin{array}{*{20}l} {\frac{{d^{n} f\left( t \right)}}{{dt^{n} }}, } & {\alpha = n \in N ,} \\ {\frac{1}{{\Gamma \left( {n - \alpha } \right)}}\mathop \smallint \limits_{0}^{t} \left( {t - \vartheta } \right)^{n - \alpha - 1} f^{\left( n \right)} \left( \vartheta \right)d\vartheta ,} & {n - 1 < \alpha < n ,n \in {\mathbb{N}}.} \\ \end{array} } \right.$$
(3)

Definition 3

The Laplace transform (LT) of a Caputo fractional derivative \(D_{t}^{\alpha } f\left( t \right)\) is represented as [2, 3]

$$L\left[ {D_{t}^{\alpha } f\left( t \right)} \right] = s^{\alpha } F\left( s \right) - \mathop \sum \limits_{r = 0}^{n - 1} s^{\alpha - r - 1} f^{\left( r \right)} \left( {0^{ + } } \right), \quad \left( {n - 1 < \alpha \le n} \right),$$
(4)

where \(F\left( s \right)\) represents the Laplace transform of the function \(f\left( t \right)\).

Fundamental idea of \(q\)-HATM

To present the fundamental idea of proposed method [24,25,26], we consider a general nonlinear non-homogeneous fractional partial differential equation of the form:

$$D_{t}^{\alpha } {\mathcal{U}}\left( {x,t} \right) + R {\mathcal{U}}\left( {x,t} \right) + N {\mathcal{U}}\left( {x,t} \right) = f\left( {x,t} \right),\quad n - 1 < \alpha \le n,$$
(5)

where \(D_{t}^{\alpha } {\mathcal{U}}\left( {x,t} \right)\) represents the fractional derivative of \({\mathcal{U}}\left( {x,t} \right)\) in the Caputo’s sense, \(R\) and \(N\) specifies the linear and nonlinear differential operator, respectively, and \(f\left( {x,t} \right)\) represents the source term. Now, by employing the LT on Eq. (5), we get

$$s^{\alpha } L\left[ {{\mathcal{U}}\left( {x,t} \right)} \right] - \mathop \sum \limits_{k = 0}^{n - 1} s^{\alpha - k - 1} {\mathcal{U}}^{\left( k \right)} \left( {x,0} \right) + L\left[ {R{\mathcal{U}}\left( {x,t} \right)} \right] + L\left[ {N{\mathcal{U}}\left( {x,t} \right)} \right] = L\left[ {f\left( {x,t} \right)} \right].$$
(6)

On simplifying Eq. (6), we have

$$L\left[ {{\mathcal{U}}\left( {x,t} \right)} \right] - \frac{1}{{s^{\alpha } }}\mathop \sum \limits_{k = 0}^{n - 1} s^{\alpha - k - 1} {\mathcal{U}}^{k} \left( {x,0} \right) + \frac{1}{{s^{\alpha } }}\left\{ {L\left[ {R{\mathcal{U}}\left( {x,t} \right)} \right] + L\left[ {N{\mathcal{U}}\left( {x,t} \right)} \right] - L\left[ {f\left( {x,t} \right)} \right]} \right\} = 0.$$
(7)

According to homotopy analysis method [5], here we define nonlinear operator as

$$\begin{aligned} N\left[ {\varphi \left( {x,t;q} \right)} \right] & = L\left[ {\varphi \left( {x,t;q} \right)} \right] - \frac{1}{{s^{\alpha } }}\mathop \sum \limits_{k = 0}^{n - 1} s^{\alpha - k - 1} \varphi^{\left( k \right)} \left( {x,t;q} \right)\left( {0^{ + } } \right) \\ & \quad + \frac{1}{{s^{\alpha } }}\left\{ {L\left[ {R\varphi \left( {x,t;q} \right)} \right] + L\left[ {N\varphi \left( {x,t;q} \right)} \right] - L\left[ {f\left( {x,t} \right)} \right]} \right\}, \\ \end{aligned}$$
(8)

where \(q \in \left[ {0,\frac{1}{n}} \right]\), and \(\varphi \left( {x,t;q} \right)\) is real function of \(x,\;t\) and \(q\).

We construct a homotopy for nonzero auxiliary function \(H\left( {x,t} \right)\) as follows:

$$\left( {1 - nq} \right)L\left[ {\varphi \left( {x, t;q} \right) - {\mathcal{U}}_{0} \left( {x,t} \right)} \right] = \hbar qH\left( {x,t} \right)N\left[ {\varphi \left( {x, t;q} \right)} \right],$$
(9)

where \(L\) be a symbol of the Laplace transform, \(q \in \left[ {0,\frac{1}{n}} \right] \left( {n \ge 1} \right)\) is the embedding parameter, \(\hbar \ne 0\) is an auxiliary parameter, \(\varphi \left( {x,t;q} \right)\) is an unknown function, and \({\mathcal{U}}_{0} \left( {x,t} \right)\) is an initial guess of \({\mathcal{U}}\left( {x,t} \right)\). The following results hold for \(q = 0\) and \(q = \frac{1}{n}\):

$$\varphi \left( {x,t;0} \right) = {\mathcal{U}}_{0} \left( {x,t} \right), \varphi \left( {x,t;\frac{1}{n}} \right) = {\mathcal{U}}\left( {x,t} \right),$$
(10)

respectively. Thus, by amplifying \(q\) from \(0\) to \(\frac{1}{n}\), the solution \(\varphi \left( {x,t;q} \right)\) converge from \({\mathcal{U}}_{0} \left( {x,t} \right)\) to the solution \({\mathcal{U}}\left( {x,t} \right)\). Expanding the function \(\varphi \left( {x,t;q} \right)\) in series form by employing Taylor theorem near to \(q\), one can get

$$\varphi \left( {x,t;q} \right) = {\mathcal{U}}_{0} \left( {x,t} \right) + \mathop \sum \limits_{m = 1}^{\infty } {\mathcal{U}}_{m} \left( {x,t} \right)q^{m} ,$$
(11)

where

$${\mathcal{U}}_{m} \left( {x,t} \right) = \frac{1}{m!}\frac{{\partial^{m} \varphi \left( {x, t;q} \right)}}{{\partial q^{m} }}|_{q = 0} .$$
(12)

On choosing the auxiliary linear operator, the initial guess \({\mathcal{U}}_{0} \left( {x,t} \right),\) the auxiliary parameter \(n, \hbar\) and \(H\left( {x,t} \right)\), the series (11) converges at \(q = \frac{1}{n}\); then it gives one of the solutions of the original nonlinear equation of the form

$${\mathcal{U}}\left( {x,t} \right) = {\mathcal{U}}_{0} \left( {x,t} \right) + \mathop \sum \limits_{m = 1}^{ \propto } {\mathcal{U}}_{m} \left( {x,t} \right)\left( {\frac{1}{n}} \right)^{m} .$$
(13)

Now, differentiating the zeroth order deformation Eq. (9) \(m\)-times with respect to \(q\) and then dividing by \(m!\) and finally taking \(q = 0\), which yields

$$L\left[ {{\mathcal{U}}_{m} \left( {x,t} \right) - \text{k}_{m} {\mathcal{U}}_{m - 1} \left( {x,t} \right)} \right] = \hbar H\left( {x,t} \right){\Re }_{m} \left( {{\vec{\mathcal{U}}}_{m - 1} } \right),$$
(14)

where the vectors are defined as

$${\vec{\mathcal{U}}}_{m} = \left\{ {{\mathcal{U}}_{0} \left( {x,t} \right),{\mathcal{U}}_{1} \left( {x,t} \right), \ldots ,{\mathcal{U}}_{m} \left( {x,t} \right)} \right\}.$$
(15)

By virtue of inverse Laplace transform on Eq. (14), we obtain the recursive equation as

$${\mathcal{U}}_{m} \left( {x,t} \right) = \text{k}_{m} {\mathcal{U}}_{m - 1} \left( {x,t} \right) + \hbar L^{ - 1} \left[ {H\left( {x,t} \right){\Re }_{m} \left( {{\vec{\mathcal{U}}}_{m - 1} } \right)} \right],$$
(16)

where

$${\Re }_{m} \left( {{\vec{\mathcal{U}}}_{m - 1} } \right) = \frac{1}{{\left( {m - 1} \right)!}}\frac{{\partial^{m - 1} N\left[ {\varphi \left( {x, t;q} \right)} \right]}}{{\partial q^{m - 1} }}|_{q = 0}$$
(17)

and

$$k_{m} = \left\{ {\begin{array}{*{20}c} {0, \quad m \le 1,} \\ {n, \quad m > 1.} \\ \end{array} } \right.$$
(18)

Finally, on solving Eq. (16) we obtain the components of the \(q\)-HATM series solution.

\(q\)-HATM solution for fractional Fisher’s equations

To demonstrate the efficiency and applicability of the proposed algorithm, we consider two examples as an illustration.

Example 4.1

Consider the nonlinear time-fractional Fisher’s equation [16, 20]:

$$D_{t}^{\alpha } u\left( {x,t} \right) = u_{xx} \left( {x,t} \right) + 6u\left( {x,t} \right)\left( {1 - u\left( {x,t} \right)} \right), \quad 0 < \alpha \le 1,$$
(19)

with initial condition

$$u\left( {x,0} \right) = \frac{1}{{\left( {1 + {\text{e}}^{x} } \right)^{2} }}.$$
(20)

Taking LT on Eq. (19) and then employing the condition given in Eq. (20), we have

$$L\left[ {u\left( {x,t} \right)} \right] - \frac{1}{s}\left\{ {\frac{1}{{\left( {1 + {\text{e}}^{x} } \right)^{2} }}} \right\} - \frac{1}{{s^{\alpha } }}L\left\{ {\frac{{\partial^{2} u}}{{\partial x^{2} }} + 6u - 6u^{2} } \right\} = 0.$$
(21)

Using the proposed algorithm, the nonlinear operator \(N\) to be define as

$$N\left[ {\varphi \left( {x,t;q} \right)} \right] = L\left[ {\varphi \left( {x,t;q} \right)} \right] - \frac{1}{s}\left\{ {\frac{1}{{\left( {1 + {\text{e}}^{x} } \right)^{2} }}} \right\} - \frac{1}{{s^{\alpha } }}L\left\{ {\frac{{\partial \varphi \left( {x,t;q} \right)}}{\partial x} + 6\varphi \left( {x,t;q} \right) - 6\varphi^{2} \left( {x,t;q} \right)} \right\}.$$
(22)

By adopting the foregoing procedure of \(q\)-HATM, the deformation equation of \(m\)th order at \(H\left( {x,t} \right) = 1\) is given as

$$L\left[ {u_{m} \left( {x,t} \right) - k_{m} u_{m - 1} \left( {x,t} \right)} \right] = h{\Re }_{m} \left[ {\vec{u}_{m - 1} } \right],$$
(23)

where

$$\begin{aligned} {\Re }_{m} \left[ {\vec{u}_{m - 1} } \right] & = L\left[ {u_{m - 1} \left( {x,t} \right)} \right] - \left( {1 - \frac{{k_{m} }}{n}} \right)\frac{1}{s}\left[ {\frac{1}{{\left( {1 + {\text{e}}^{x} } \right)^{2} }}} \right] \\ & \quad - \frac{1}{{s^{\alpha } }}L\left\{ {\frac{{\partial^{2} u_{m - 1} }}{{\partial x^{2} }} + 6u_{m - 1} - \mathop \sum \limits_{i = 0}^{m - 1} u_{i} u_{m - 1 - i} } \right\}. \\ \end{aligned}$$
(24)

By plugging inverse Laplace transform on both sides of Eq. (23), we get

$$u_{m} \left( {x,t} \right) = k_{m} u_{m - 1} \left( {x,t} \right) + \hbar L^{ - 1} \left\{ {{\Re }_{m} \left[ {\vec{u}_{m - 1} } \right]} \right\}.$$
(25)

On solving the forgoing equations systematically, we arrive at

$$\begin{aligned} u_{0} \left( {x,t} \right) & = \frac{1}{{\left( {1 + {\text{e}}^{x} } \right)^{2} }} , \\ u_{1} \left( {x,t} \right) & = \frac{{ - 10\hbar {\text{e}}^{x} t^{\alpha } }}{{\left( {1 + {\text{e}}^{x} } \right)^{3} \Gamma \left[ {\alpha + 1} \right]}} , \\ u_{2} \left( {x,t} \right) & = \frac{{ - 10\left( {n + \hbar } \right)h {\text{e}}^{x} t^{\alpha } }}{{\left( {1 + {\text{e}}^{x} } \right)^{3 }\Gamma \left[ {\alpha + 1} \right]}} + \frac{{50\hbar^{2} {\text{e}}^{x} \left( { - 1 + 2{\text{e}}^{x} } \right)t^{2\alpha } }}{{\left( {1 + {\text{e}}^{x} } \right)^{4} \Gamma \left[ {2\alpha + 1} \right]}} , \\ u_{3} \left( {x,t} \right) & = \frac{{ - 10\left( {n + \hbar } \right)^{2} h {\text{e}}^{x} t^{\alpha } }}{{\left( {1 + {\text{e}}^{x} } \right)^{3} \Gamma \left[ {\alpha + 1} \right]}} + \frac{{100\left( {n + \hbar } \right)\hbar^{2} {\text{e}}^{x} \left( { - 1 + 2{\text{e}}^{x} } \right)t^{2\alpha } }}{{\left( {1 + {\text{e}}^{x} } \right)^{4}\Gamma \left[ {2\alpha + 1} \right]}} \\ & \quad - \frac{{50\hbar^{3} {\text{e}}^{x} \left( {\left( {20{\text{e}}^{3x} - 15{\text{e}}^{2x} - 6{\text{e}}^{x} + 5} \right)\Gamma \left[ {\alpha + 1} \right]^{2} - 12{\text{e}}^{x}\Gamma \left[ {2\alpha + 1} \right]} \right)t^{3\alpha } }}{{\left( {1 + {\text{e}}^{x} } \right)^{6 }\Gamma \left[ {\alpha + 1} \right]^{2 }\Gamma \left[ {3\alpha + 1} \right]}}, \\ & \vdots . \\ \end{aligned}$$

In this manner, the rest of the iterative components can be obtained. Then, the family of \(q\)-HATM series solution of Eq. (19) is given by

$$u\left( {x,t} \right) = u_{0} \left( {x,t} \right) + \mathop \sum \limits_{m = 1}^{\infty } u_{m} \left( {x,t} \right)\left( {\frac{1}{n}} \right)^{m} .$$
(26)

If we set \(\alpha = 1,\; \hbar = - 1\) and \(n = 1\), then the obtained solution \(\mathop \sum \nolimits_{m = 1}^{N} u_{m} \left( {x,y,t} \right)\left( {\frac{1}{n}} \right)^{m}\) converges to the exact solution \(u\left( {x,t} \right) = \frac{1}{{\left( {1 + {\text{e}}^{x - 5t} } \right)^{2} }}\) of the classical order Fisher’s equation as \(N \to \infty .\)

Example 4.2

Consider the one-dimensional generalized fractional order Burgers–Fisher equation [17] at \(\eta = 1,\; \mu = 1\) and \(\beta = 0.01\):

$$D_{t}^{\alpha } u = \frac{{\partial^{2} u}}{{\partial x^{2} }} - \xi \left( {u\frac{\partial u}{\partial x} + u\left( {u - 1} \right)} \right), \quad 0 < \alpha \le 1,$$
(27)

with initial conditions

$$u\left( {x,0} \right) = \frac{1}{2} + \frac{1}{2}{ \tanh }\left( {\frac{ - \xi x}{4}} \right).$$
(28)

By performing LT on both sides of Eq. (27) and then make use of conditions provided in Eq. (28), we have

$$L\left[ {u\left( {x,t} \right)} \right] - \frac{1}{s}\left( {\frac{1}{2} + \frac{1}{2}{ \tanh }\left( {\frac{ - \xi x}{4}} \right)} \right) - \frac{1}{{s^{\alpha } }}L\left\{ {\frac{{\partial^{2} u}}{{\partial x^{2} }} - \xi \left( {u\frac{\partial u}{\partial x} + u\left( {u - 1} \right)} \right)} \right\} = 0.$$
(29)

The nonlinear operator \(N\) to be define as

$$\begin{aligned} N\left[ {\varphi \left( {x,t;q} \right)} \right] & = L\left[ {\varphi \left( {x,t;q} \right)} \right] - \frac{1}{s}\left( {\frac{1}{2} + \frac{1}{2}{ \tanh }\left( {\frac{ - \xi x}{4}} \right)} \right) \\ & \quad + \frac{1}{{s^{\alpha } }}L\left\{ {\frac{{\partial^{2} \varphi \left( {x,t;q} \right)}}{{\partial x^{2} }} - \xi \left( {\varphi \left( {x,t;q} \right)\frac{{\partial \varphi \left( {x,t;q} \right)}}{\partial x} + \varphi \left( {x,t;q} \right)\left( {\varphi \left( {x,t;q} \right) - 1} \right)} \right)} \right\}. \\ \end{aligned}$$
(30)

By exercising with this numerical procedure, one can get the deformation equation of the \(m\)th order for \(H\left( {x,t} \right) = 1\), as

$$L\left[ {u_{m} \left( {x,t} \right) - k_{m} u_{m - 1} \left( {x,t} \right)} \right] = h{\Re }_{m} \left[ {\vec{u}_{m - 1} } \right],$$
(31)

where

$$\begin{aligned} {\Re }_{m} \left[ {\vec{u}_{m - 1} } \right] & = L\left[ {u_{m - 1} \left( {x,t} \right)} \right] - \left( {1 - \frac{{k_{m} }}{n}} \right)\frac{1}{s}\left( {\frac{1}{2} + \frac{1}{2}\tan h\left( {\frac{ - \xi x}{4}} \right)} \right) \\ & \quad + \frac{1}{{s^{\alpha } }}L\left\{ {\frac{{\partial^{2} u_{m - 1} }}{{\partial x^{2} }} - \xi \left( {\mathop \sum \limits_{i = 0}^{m - 1} u_{i} \frac{{\partial u_{m - 1 - i} }}{\partial x} + \mathop \sum \limits_{i = 0}^{m - 1} u_{i} u_{m - 1 - i} - 1} \right)} \right\} \\ \end{aligned}$$
(32)

By applying inverse Laplace transform on Eq. (31), we get

$$u_{m} \left( {x,t} \right) = k_{m} u_{m - 1} \left( {x,t} \right) + \hbar L^{ - 1} \left\{ {{\Re }_{m} \left[ {\vec{u}_{m - 1} } \right]} \right\}.$$
(33)

On solving above equation, we have

$$\begin{aligned} u_{0} \left( {x,t} \right) & = \frac{1}{2} + \frac{1}{2}{ \tanh }\left( {\frac{ - \xi x}{4}} \right), \\ u_{1} \left( {x,t} \right) & = - \frac{{h\xi \left( {4 + \xi } \right){\text{sech}}^{2} \left( {\frac{ - \xi x}{4}} \right)t^{\alpha } }}{{16 \Gamma \left[ {\alpha + 1} \right]}}, \\ u_{2} \left( {x,t} \right) & = - \frac{{\left( {n + h} \right)\left( {4 + \xi } \right)h \xi {\text{sech}}^{2} \left( {\frac{ - \xi x}{4}} \right)t^{\alpha } }}{{16 \Gamma \left[ {\alpha + 1} \right]}} - \frac{{\left( {4 + \xi } \right)^{2} h^{2} \xi^{2} \sec h^{2} \left( {\frac{ - \xi x}{4}} \right)\tanh \left( {\frac{ - \xi x}{4}} \right)t^{2\alpha } }}{{64\Gamma \left[ {2\alpha + 1} \right]}}, \\ u_{3} \left( {x,t} \right) & = - \frac{{\left( {n + h} \right)^{2} \left( {4 + \xi } \right)h \xi {\text{sech}}^{2} \left( {\frac{ - \xi x}{4}} \right)t^{\alpha } }}{{16\Gamma \left[ {\alpha + 1} \right]}} - \frac{{\left( {n + h} \right)\left( {4 + \xi } \right)^{2} h^{2} \xi^{2} {\text{sech}}^{2} \left( {\frac{ - \xi x}{4}} \right)\tanh \left( {\frac{ - \xi x}{4}} \right)t^{2\alpha } }}{{32\Gamma \left[ {2\alpha + 1} \right]}}, \\ & \quad - \frac{{\left( {4 + \xi } \right)^{2} h^{3} \xi^{3} {\text{sech}}^{4} \left( {\frac{ - \xi x}{4}} \right)t^{3\alpha } }}{{512 \Gamma \left[ {1 + \alpha } \right]^{2 }\Gamma \left[ {1 + 3\alpha } \right]}}\left( {\Gamma \left[ {1 + 2\alpha } \right]\left( { - 2 + \xi \tanh \left( {\frac{\xi x}{4}} \right)} \right)} \right. \\ & \quad + \,\left. {\Gamma \left[ {1 + \alpha } \right]^{2} \left( {\left( {4 + \xi } \right){ \cosh }\left( {\frac{ - \xi x}{4}} \right) - 2\left( {2 + \xi + \xi \tanh \left( {\frac{\xi x}{4}} \right)} \right)} \right)} \right), \\ & \vdots . \\ \end{aligned}$$

In this pattern, remaining iterative components can be derived. Finally, the group of \(q\)-HATM series solution of Eq. (27) is given by

$$u\left( {x,t} \right) = u_{0} \left( {x,t} \right) + \mathop \sum \limits_{m = 1}^{\infty } u_{m} \left( {x,t} \right)\left( {\frac{1}{n}} \right)^{m} .$$
(34)

Exact solution of Eq. (27) at \(\alpha = 1\) is given by [17]

$$u\left( {x,t} \right) = \frac{1}{2} + \frac{1}{2}\tanh \left[ {\frac{ - \xi }{4}\left( {x - \left( {\frac{\xi }{2} + \frac{2\beta }{\xi } } \right)t} \right)} \right].$$

Numerical results and discussion

In order to verify whether the proposed algorithm leads to greater accuracy, the numerical solutions have been evaluated. From results, we can certainly conclude that the proposed technique provides remarkable exactness in comparison with the method available in the literature [16, 17].

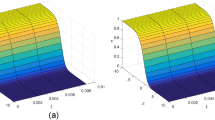
Figure 1 explores the comparison of \(q\)-HATM solution with exact solution and absolute error for Example 4.1. Figure 2 cites the action of solution obtained for Eq. (19) with distinct Brownian motion. Figure 3 depicts the \(q\)-HATM solution for different values of auxiliary parameter \(\hbar\) which helps us to control and adjust the convergence region. Figures 4, 5 and 6 explore the role of \(n\) with respect to \(\hbar\) in \(q\)-HATM solution. In Table 1, we present the comparison between the results obtained by the ADM [15], HPSTM [16] and proposed method with exact solution. Further, it can be observed from Table 2, the absolute error is very tiny.

Fig. 1
figure 1

a Surface of approximate solution. b Surface of exact solution. c Surface of absolute error \(= \left| {u_{{{\text{exa}} .}} - u_{{{\text{app}} . }} } \right|\) at \(\hbar = - 1\), \(n = 1\) and \(\alpha = 1\) for Example 4.1

Full size image
Fig. 2
figure 2

Plot of q-HATM solution \(u\left( {x,t} \right)\) with respect to \(t\) when \(n = 1, \;\hbar = - 1\) and \(x = 0.5\) with various values of \(\alpha\) for Example 4.1

Full size image
Fig. 3
figure 3

Plot of q-HATM solution \(u\left( {x,t} \right)\) at \(x = 1, \;n = 1 \;{\text{and}}\; \alpha = 1\) with diverse values of \(\hbar\) for Example 4.1

Full size image
Fig. 4
figure 4

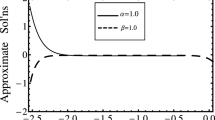
\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(x = 0.1, \;t = 0.01\) and \(n = 1\) with various values of \(\alpha\) for Example 4.1

Full size image
Fig. 5
figure 5

\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(x = 0.1, \;t = 0.01\) and \(n = 2\) with diverse values of \(\alpha\) for Example 4.1

Full size image
Fig. 6
figure 6

\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(x = 0.1,\; t = 0.01\) and \(n = 3\) with various values of \(\alpha\) for Example 4.1

Full size image
Table 1 Description of numerical solutions derived from ADM [15], HPSTM [16] and present method with classical solution at \(\alpha = 1, \;h = - 1, \;n = 1\) and \(t = 0.001\) with diverse values of \(x\) for Example 4.1
Full size table
Table 2 Error analysis for Example 4.1 at \(\alpha = 1, \;h = - 1, \;n = 1\) and \(t = 0.001\)
Full size table

Moreover, Fig. 7 cites the nature of \(q\)-HATM solution in comparison with exact solution for Example 4.2; in particular Fig. 7c revels the efficiency of proposed technique in terms of absolute error. Figure 8 explores the validity of Brownian motion, i.e. \(\alpha = 0.90, 0.75, 0. 50\). Figure 9 depicts the \(q\)-HATM solution for different values of auxiliary parameter \(\hbar\) which helps us to control and adjust the convergence region. Lastly, Figs. 10, 11 and 12 represent \(\hbar\)-curves and the horizontal line illustrates the range of convergence for Eq. (27). Further, the efficiency of proposed scheme is drowned in terms of numerical simulations for Example 4.2 which is shown in Table 3 and it clear that the proposed method is very accurate.

Fig. 7
figure 7

a Surface of approximate solution. b Surface of exact solution. c Surface of absolute error \(= \left| {u_{{{\text{exa}} .}} - u_{{{\text{app}} . }} } \right|\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;n = 1, \; \hbar = - 1 \;{\text{and}}\; \alpha = 1\) for Example 4.2

Full size image
Fig. 8
figure 8

Plot of q-HATM solution \(u\left( {x,t} \right)\) with respect to \(t\) when \(\eta = 1,\mu = 1,\xi = 0.01,\beta = 0.01,n = 1, \hbar = - 1\) and \(x = 0.5\) with diverse values of \(\alpha\) for Example 4.2

Full size image
Fig. 9
figure 9

Plot of q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;x = 1, \;\alpha = 1\; {\text{and}}\; n = 5\) with diverse values of \(\hbar\) for Example 4.2

Full size image
Fig. 10
figure 10

\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;n = 1,\;t = 0.01\) and \(\varvec{ }x = 0.5\) with diverse values of \(\alpha\) for Example 4.2 \(.\)

Full size image
Fig. 11
figure 11

\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;x = 0.5,\; t = 0.01\) and \(n = 2\) with diverse values of \(\alpha\) for Example 4.2

Full size image
Fig. 12
figure 12

\(\hbar\)-curve drown for the q-HATM solution \(u\left( {x,t} \right)\) at \(\eta = 1,\;\mu = 1,\;\xi = 0.01,\;\beta = 0.01, \;x = 0.5, \;t = 0.01\) and \(n = 3\) with diverse values of \(\alpha\) for Example 4.2

Full size image
Table 3 Description of numerical solutions derived from Haar wavelet method [17], OHAM [17] and present method with exact solution at \(\alpha = 1,\; h = - 1, \;\xi = 0.01\) and \(n = 1\) (Example 4.2)
Full size table

Conclusion

In this study, the \(q\)-homotopy analysis transform method is employed profitably to find the solution for nonlinear time-fractional Fisher’s equation. Two examples are carried out in order to validate and illustrate the efficiency of the method. The results reveal the complete reliability and wide applicability of the proposed technique. Compared to other numerical techniques, the proposed technique requires less amount of computational overhead. Moreover, the method manipulates and controls the series solution, which rapidly converges to the exact solution very efficiently in a short admissible domain. The results obtained, using the \(q\)-HATM, were in good record with results already available in the literature [15,16,17, 27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56].