Fourier pseudo-spectral method for the extended Fisher-Kolmogorov equation in two dimensions

Abstract

In the study of pattern formation in bi-stable systems, the extended Fisher-Kolmogorov (EFK) equation plays an important role. In this paper, a Fourier pseudo-spectral method for solving the EFK equation in two space dimensions is presented. Prior bounds are proved using Lyapunov function. Further, optimal error estimates are established for the semi-discrete scheme. Finally, a fully discrete scheme based on Crank-Nicolson method is proposed, and related optimal error estimates are derived and some numerical experiments are presented.

1 Introduction

In this paper, we consider the following extended Fisher-Kolmogorov (EFK) equation:

$$ u_{t}+\gamma\Delta^{2} u-\Delta u+f(u)=0, \quad \mbox{in } \Omega\times(0,T], $$

(1.1)

where $f(u)=u^{3}-u$, Ω is a bounded domain in $\mathbb{R}^{2}$ with boundary ∂Ω, γ is a positive constant. On the basis of physical considerations, equation (1.1) is supplemented with the following boundary conditions:

$$ u=0, \qquad \Delta u=0,\quad \mbox{in } \partial\Omega\times(0,T], $$

(1.2)

and the initial condition

$$ u(x,y,0)=u_{0}(x,y),\quad \mbox{in } \Omega. $$

(1.3)

When $\gamma=0$ in (1.1), we obtain the standard Fisher-Kolmogorov equation, which is a kind of classical second-order diffusion equation (see [1, 2] and so on). However, by adding a stabilizing fourth order derivative term to the Fisher-Kolmogorov equation, Coullet et al. [3], Dee and van Saarloos [4–6] proposed (1.1) and called the model the extended Fisher-Kolmogorov equation. Equation (1.1) occurs in a variety of applications like pattern formation in bi-stable systems [7], propagation of domain walls in liquid crystals [8], traveling waves in reaction diffusion systems [9] and a mesoscopic model of a phase transition in a binary system near the Lipschitz point [10].

Regarding computational studies, there are some numerical experiments conducted in [4] without any convergence analysis. In [11], Danumjaya and Pani studied the convergence of a numerical solution of (1.1) using the second-order splitting combined with orthogonal cubic spline collocation method. In [12], a finite element Galerkin method for the two-dimensional EFK equation (1.1) and optimal error estimates are derived. In [13], Khiari and Omrani studied the finite difference scheme for the EFK equation in two dimensions.

In this paper, we consider the Fourier pseudo-spectral method for problem (1.1)-(1.3). In Section 2, some basic results and definitions are recalled. In Section 3, prior bounds and optimal error estimates for semi-discrete scheme are proved. In Section 4, a fully discrete scheme based on the Crank-Nicolson method is proposed, and related theoretical results are proved. Finally, in Section 5, some numerical experiments are presented to confirm our results.

2 Preliminaries

In this section, we recall some basic results as regards the Fourier pseudo-spectral method, which will be used throughout this paper.

Let $\Omega=[0,\pi]\times[0,\pi]$, $2N_{1}$, $2N_{2}$ be any positive integers, in the continuation of this paper. Let $N_{1}=N_{2}=N$, then $h=\frac{\pi}{2N}$, $x_{i}=ih$, $y_{j}=jh$, $i,j\in\Lambda$, where $\Lambda=\{ 1,\ldots,2N-1\}$. Denote

$$\begin{aligned}& H_{0}^{2}(\Omega):=\biggl\{ u\in H^{2}, u|_{\partial\Omega}=\frac{\partial u}{\partial n}\bigg|_{\partial\Omega}=0\biggr\} , \\& H_{E}^{2}(\Omega):=\bigl\{ u\in H^{2}, u|_{\partial\Omega}=0\bigr\} . \end{aligned}$$

For the purpose of this article, we introduce the inner product in $C^{\infty}(\Omega)$ as

$$(f,g)_{m}=\sum_{\alpha\leq m}\bigl(D^{\alpha}f,D^{\alpha}g \bigr), $$

the associated $H^{m}$ norm is $\|f\|_{m}=\sqrt{\sum_{\alpha\leq m}\| D^{\alpha}f\|^{2}}$, and the $H^{m}$ semi-norm is defined as $|f|_{m}=\sqrt {\sum_{\alpha= m}\|D^{\alpha}f\|^{2}}$.

For any integer $2N>0$, we introduce the finite dimensional subspace of $H_{0}^{2}(\Omega)$

$$S_{N}=\operatorname{span}\{\sin k_{1}x \sin k_{2}y,k_{1},k_{2}\in\Lambda\}. $$

Let $P_{N}:L^{2}(\Omega)\rightarrow S_{N}$ be an orthogonal projecting operator which satisfies

$$(P_{N}u,v)=(u,v),\quad \forall v\in S_{N}. $$

For the operator $P_{N}$, we have the following results (see [14–16]).

Lemma 2.1

$P_{N}$ commutes with derivation on $H_{E}^{2}(\Omega)$, i.e.,

$$\Delta(P_{N}u)=P_{N}\Delta u,\quad \forall u\in H_{E}^{2}(\Omega). $$

Using the same methods [14, 16] as previously, we can obtain the following result for problem (1.1)-(1.3).

Lemma 2.2

For any real $0\leq\mu\leq\delta$, there is a constant C such that

$$\| u-P_{N}u\|_{\mu}\leq CN^{\mu-\delta}| u|_{\delta}, \quad \forall u\in H^{\delta}(\Omega), $$

where $| u|_{\delta}^{2}=\sum_{\alpha=\delta}\|D^{\alpha}f\|_{0}^{2}$.

We introduce the discrete $L^{2}$ inner product

$$(u,v)_{h}=\frac{\pi^{2}}{(2N-1)^{2}}\sum_{i,j\in\Lambda }u(x_{i},y_{j})v(x_{i},y_{j}), \quad u,v\in S_{N}. $$

For $u\in S_{N}$, the discrete $L^{2}$-norm is defined as

$$\| u\|_{h}=\sqrt{(u,u)_{h}}. $$

Demonstrating the discrete inner product is equivalent to the continuous case; we introduce the following lemma first.

Lemma 2.3

For $k, l\in\Lambda$, we have

$$(\cos kx \cos ly,1)_{h}=0. $$

Proof

Note that

$$\begin{aligned}& (\cos kx \cos ly,1)_{h} \\& \quad =\frac{\pi^{2}}{(2N-1)^{2}}\sum_{i,j\in\Lambda}\cos kx_{i} \cos ly_{j} \\& \quad =\frac{\pi^{2}}{(2N-1)^{2}}\sum_{i\in\Lambda}\cos kx_{i} \sum_{j\in\Lambda }\cos ly_{j} \\& \quad =\frac{\pi^{2}}{(2N-1)^{2}}\sum_{i\in\Lambda}\cos kx_{i} \sum_{j=1}^{N-1}\biggl(\cos ly_{j}+\cos \frac{\pi}{2}+\cos (\pi-ly_{j})\biggr) \\& \quad =\frac{\pi^{2}}{(2N-1)^{2}}\sum_{i\in\Lambda}\cos kx_{i} \sum_{j=1}^{N-1}(\cos ly_{j}+0-\cos ly_{j}) \\& \quad =0. \end{aligned}$$

Hence, the proof is complete. □

Lemma 2.4

For $u_{h}, v_{h}\in S_{N}$, we have

$$(u_{h},v_{h})_{h}=(u_{h},v_{h}). $$

Proof

For any $k_{1}, k_{2}, l_{1}, l_{2}\in\Lambda$, the following equalities hold:

$$\begin{aligned}& ( \sin k_{1}x_{i}\sin l_{1}y_{j},\sin k_{2}x_{i}\sin l_{2}y_{j})_{h} \\& \quad =\frac{\pi^{2}}{(2N-1)^{2}}\sum_{i,j\in\Lambda}\sin k_{1}x_{i}\sin l_{1}y_{j} \sin k_{2}x_{i}\sin l_{2}y_{j} \\& \quad =\frac{\pi^{2}}{4(2N-1)^{2}}\sum_{i,j\in\Lambda}\bigl[\cos (k_{1}-k_{2})x_{i}-\cos (k_{1}+k_{2})x_{i} \bigr] \bigl[\cos (l_{1}-l_{2})y_{j}-\cos (l_{1}+l_{2})y_{j}\bigr]. \end{aligned}$$

By using Lemma 2.3, we can get the following equality:

$$(\sin k_{1}x\sin l_{1}y,\sin k_{2}x\sin l_{2}y)_{h}= \textstyle\begin{cases} \frac{\pi^{2}}{4}, & k_{1}=k_{2}\text{ and } l_{1}=l_{2}, \\ 0, & \text{others} . \end{cases} $$

Hence, the proof is complete. □

Define $I_{N}:L^{2}(\Omega)\rightarrow S_{N}$ be an interpolation operator which satisfies

$$I_{N}u(x_{i},y_{j})=u(x_{i},y_{j}). $$

From [16–18], we have the following results on $I_{N}$.

Lemma 2.5

For the operator $I_{N}$, we have

• $I_{N}u=u$, $u\in S_{N}$,

• $(I_{N}u,I_{N}v)=(u,v)_{h}$, $u,v\in C^{0}(\Omega)$,

• $\| I_{N}(uv)\|\leq\| u\|_{\infty}\| I_{N}v\|$, $u,v\in C^{0}(\Omega)$,

• $(I_{N}u,v)_{h}=(u,v)_{h}$, $\forall v\in S_{N}$, $\forall u\in C^{0}(\Omega)$,

• for any real $0\leq\mu\leq\delta$, $\delta>\frac{1}{2}$, there is a constant C such that

  $$\| u-I_{N}u\|_{\mu}\leq CN^{\mu-\delta}| u|_{\delta}, \quad \forall u\in H^{\delta}(\Omega). $$

The following lemma is useful in our analysis.

Lemma 2.6

see [19]

There exist two positive constants $C_{1}$ and $C_{2}$, which may depend on Ω such that

$$C_{1}\| v\|_{2}\leq\bigl(\|\Delta v\|^{2}\| v \|_{1}^{2}\bigr)^{1/2}\leq C_{2}\| v \|_{2},\quad \forall v\in H^{2}(\Omega). $$

3 Semi-discrete approximation

In this section, we consider the semi-discrete approximation for problem (1.1)-(1.3). We first give the weak formulation of problem (1.1)-(1.3)

$$ \textstyle\begin{cases} (u_{t},v)+\gamma(\Delta u,\Delta v)-(\Delta u,v)+(f(u),v)=0,\quad \forall v\in H_{0}^{2}(\Omega), \\ u(x,y,0)=u_{0}(x,y). \end{cases} $$

(3.1)

Define the Fourier pseudo-spectral approximation: Find

$$u_{h}(t)=\sum_{i,j\in\Lambda}a_{i,j}(t) \sin(ix)\sin(jy)\in S_{N} $$

such that

$$ \begin{aligned} &(u_{ht},v)_{h}+\gamma(\Delta u_{h},\Delta v)_{h}-(\Delta u_{h},v)_{h}+ \bigl(f(u_{h}),v\bigr)_{h}=0, \quad \forall v\in S_{N}, \\ &\bigl(u_{h}^{0}(x,y),v\bigr)=\bigl(u_{0}(x,y),v \bigr). \end{aligned} $$

(3.2)

According to the definition of discrete inner product and properties of $I_{N}$, we can rewrite (3.2) in the form of

$$ (u_{ht},v)+\gamma(\Delta u_{h},\Delta v)-( \Delta u_{h},v)+\bigl(I_{N}f(u_{h}),v\bigr)=0, \quad \forall v\in S_{N}. $$

(3.3)

Furthermore, we get

$$ u_{ht}+\gamma\Delta^{2}u_{h}-\Delta u_{h}+I_{N}f(u_{h})=0. $$

(3.4)

For the solution of scheme (3.2), we have the following prior bounds.

Theorem 3.1

Let $u(0)\in H_{E}^{2}(\Omega)$, then there exists a unique solution $u_{h}(t)\in S_{N}$ for problem (3.2), such that

$$ \bigl\Vert u_{h}(t) \bigr\Vert _{2}\leq C \bigl(\gamma, \Vert u_{0} \Vert _{2,h}\bigr),\quad 0\leq t \leq T. $$

(3.5)

Proof

The equations of problem (3.2) are ordinary differential equations. According to ODE theory, there exists a unique local solution for problem (3.2) in the temporal interval $[0,t_{n})$. If (3.5) holds, using the extension theorem, we can obtain the existence of a global solution. So, we only need to prove (3.2).

Setting $v = u_{h}$ in (3.3), we can obtain

$$\frac{1}{2}\frac{d}{dt}\| u_{h}\|^{2}+\gamma\| \Delta u_{h}\|^{2}+\|\nabla u_{h}\|^{2}+ \bigl(I_{N}f(u_{h}),u_{h}\bigr)=0. $$

Using Lemma 2.3, we have

$$\frac{1}{2}\frac{d}{dt}\| u_{h}\|^{2}+\gamma\| \Delta u_{h}\|^{2}+\|\nabla u\|^{2}+ \bigl(u_{h}^{3},u_{h}\bigr)_{h}=\| u_{h}\|^{2}. $$

Note that

$$\bigl(u_{h}^{3},u_{h}\bigr)_{h}\geq0. $$

Hence,

$$\frac{1}{2}\frac{d}{dt}\| u_{h}\|^{2}\leq\| u_{h}\|^{2}. $$

We can obtain

$$ \bigl\Vert u_{h}(t) \bigr\Vert ^{2}\leq e^{2t} \bigl\Vert u_{h}(0) \bigr\Vert ^{2}, \quad 0\leq t\leq T. $$

(3.6)

We may define a Lyapunov function

$$ E_{h}(t)=\frac{\gamma}{2}\|\Delta u_{h} \|^{2}+\frac {1}{2}\|\nabla u_{h}\|^{2}+ \bigl(H(u_{h}),1\bigr)_{h}, $$

(3.7)

where $H(u_{h})=\frac{1}{4}(1-u_{h}^{2})^{2}$. Noticing that $H'(u_{h})=f(u_{h})$. It is also seen that

$$\begin{aligned} \frac{dE_{h}(t)}{dt}&=\gamma(\Delta u_{h},\Delta u_{ht})_{h}+( \nabla u_{h},\nabla u_{ht})_{h}+ \bigl(f(u_{h}),u_{h,t}\bigr)_{h} \\ &=\bigl(\gamma\Delta^{2}u_{h}-\Delta u_{h}+f(u_{h}),u_{ht} \bigr)_{h} \\ &=-\| u_{ht}\|_{h}^{2} \\ &\leq0. \end{aligned}$$

Therefore,

$$E_{h}(t)\leq E_{h}(0), $$

that is,

$$\begin{aligned}& \frac{\gamma}{2}\bigl\| \Delta^{2}u_{h}\bigr\| ^{2}+ \frac{1}{2}\| \nabla u_{h}\|^{2}+I_{N}H(u_{h}) \\& \quad \leq\frac{\gamma}{2}\bigl\| \Delta^{2}u_{0} \bigr\| ^{2}+\frac {1}{2}\|\nabla u_{0}\|^{2}+I_{N}H(u_{0}). \end{aligned}$$

Since $H(u_{h})\geq0$, we have

$$ \bigl\Vert \Delta^{2}u_{h} \bigr\Vert ^{2}\leq \bigl\Vert u_{h}(0) \bigr\Vert _{2}^{2}. $$

(3.8)

We also have

$$ \|\nabla u_{h}\|^{2}=-(\Delta u_{h},u_{h})\leq\frac {1}{2}\|\Delta u_{h} \|^{2}+\frac{1}{2}\| u_{h}\|^{2}. $$

(3.9)

Combining (3.6), (3.8) and (3.9), we complete the proof. □

Now, we consider the error estimates for the semi-discrete pseudo-spectral solution. According to the properties of $P_{N}$, we only need to analyze the error between $P_{N}u$ and $u_{h}$. Denote $\eta (t)=u-P_{N}u$ and $\theta(t)=P_{N}u-u_{h}$. Therefore

$$ u-u_{h}=u-P_{N}u+P_{N}u-u_{h}= \eta(t)+\theta(t). $$

(3.10)

By Lemma 2.1, we can rewrite (3.1) as

$$ (P_{N}u_{t},v)+\gamma(\Delta u,\Delta v)-( \Delta u,v)+\bigl(P_{N}u^{3},v\bigr)-(u,v)=0,\quad \forall v \in S_{N}. $$

(3.11)

Let u be the solution of (3.10), $u_{h}$ be the solution of (3.3). Subtracting (3.3) from (3.10), we find

$$ (\theta_{t},v)+\gamma(\Delta\theta,\Delta v)- (\Delta \theta,v)+\bigl(P_{N}u^{3}-I_{N}u_{h}^{3}, \theta\bigr)-(\theta,v)=0. $$

(3.12)

To estimate θ, we give the following lemma.

Lemma 3.2

Let u be the solution of (3.1), $u_{h}$ be the solution of (3.3). If $u\in L^{\infty}([0,T]; W^{2,\infty})$, then there exists a constant $C=C(\|u\|_{L^{\infty}([0,T],W^{2,\infty})},\gamma)$ such that

$$ \bigl\Vert \theta(t) \bigr\Vert \leq C\bigl( \bigl\Vert \theta(0) \bigr\Vert +h^{2}\bigr). $$

(3.13)

Proof

Taking in (3.12) the inner product with θ, we have

$$\frac{1}{2}\frac{d}{dt}\|\theta\|^{2}+\gamma\|\Delta \theta\|^{2}-(\Delta\theta,\theta)-\|\theta\| ^{2}+ \bigl(P_{N}u^{3}-I_{N}u_{h}^{3}, \theta\bigr)=0. $$

Furthermore

$$ \frac{d}{dt} \Vert \theta \Vert ^{2}+\gamma \Vert \Delta\theta \Vert ^{2}\leq \biggl(\frac{1}{\gamma}+3 \biggr) \Vert \theta \Vert ^{2}+ \bigl\Vert P_{N}u^{3}-I_{N}u_{h}^{3} \bigr\Vert ^{2}. $$

(3.14)

So in the next step, we need to estimate $\| P_{N}u^{3}-I_{N}u_{h}^{3}\|$. Note that

$$ P_{N}u^{3}-I_{N}u_{h}^{3}=P_{N}u^{3}-I_{N}(P_{N}u)^{3}+I_{N}(P_{N}u)^{3}-I_{N}u_{h}^{3}. $$

(3.15)

Applying the properties of $P_{N}$ and $I_{N}$, on the one hand,

$$\begin{aligned}& \bigl\Vert P_{N}u^{3}-I_{N}(P_{N}u)^{3} \bigr\Vert \\& \quad = \bigl\Vert P_{N}u^{3}-u^{3}+u^{3}-I_{N}u^{3}+I_{N}u^{3}-I_{N}(P_{N}u)^{3} \bigr\Vert \\& \quad \leq \bigl\Vert P_{N}u^{3}-u^{3} \bigr\Vert + \bigl\Vert u^{3}-I_{N}u^{3} \bigr\Vert + \bigl\Vert I_{N}u^{3}-I_{N}(P_{N}u)^{3} \bigr\Vert \\& \quad \leq \bigl\Vert P_{N}u^{3}-u^{3} \bigr\Vert + \bigl\Vert u^{3}-I_{N}u^{3} \bigr\Vert + \bigl\Vert I_{N}{\bigl((u-P_{N}u) \bigl(u^{2}+(P_{N}u)^{2}+uP_{N}u\bigr) \bigr)} \bigr\Vert \\& \quad \leq Ch^{2}| u^{3}|_{2}+ \bigl\Vert I_{N}(u-P_{N}u) \bigr\Vert \bigl\Vert u^{2}+uP_{N}u+(P_{N}u)^{2} \bigr\Vert _{\infty}\\& \quad \leq Ch^{2} \Vert u \Vert _{2}^{3}+C \Vert u \Vert _{\infty}^{2} \Vert u-P_{N}u \Vert \\& \quad \leq Ch^{2} \Vert u \Vert _{2}^{3}+Ch^{2} \Vert u \Vert _{\infty}^{2}| u|_{2}, \end{aligned}$$

and on the other hand,

$$\begin{aligned}& \bigl\Vert I_{N}(P_{N}u)^{3}-I_{N}u_{h}^{3} \bigr\Vert \\& \quad = \bigl\Vert I_{N}\bigl((P_{N}u)^{3}-u_{h}^{3} \bigr) \bigr\Vert \\& \quad = \bigl\Vert I_{N}(\theta) \bigl((P_{N}u)^{2}+u_{h}^{2}+P_{N}uu_{h} \bigr) \bigr\Vert \\& \quad \leq \bigl\Vert (P_{N}u)^{2}+u_{h}^{2}+P_{N}uu_{h} \bigr\Vert _{\infty} \Vert I_{N}\theta \Vert \\& \quad \leq C \Vert u \Vert _{\infty}^{2} \Vert \theta \Vert . \end{aligned}$$

Combining the above two results gives

$$ \bigl\Vert P_{N}u^{3}-I_{N}u_{h}^{3} \bigr\Vert \leq C\bigl( \Vert \theta \Vert +h^{2}\bigr). $$

(3.16)

Plugging (3.16) into (3.14) and using Gronwall’s inequality, we complete the proof. □

Applying Lemma 3.2, we have the following theorem.

Theorem 3.3

Let u be the solution of (3.1), $u_{h}$ be the solution of (3.3). If $u\in L^{\infty}([0,T]; W^{2,\infty})$, then there exists a constant $C=C(\gamma,\| u\|_{L^{\infty}([0,T];W^{2,\infty})})$ such that

$$\bigl\Vert u(t)-u_{h}(t) \bigr\Vert \leq Ch^{2}+C \bigl\Vert P_{N}u^{0}-u_{h}^{0} \bigr\Vert ,\quad 0\leq t\leq T. $$

Proof

Using the equality (3.10) and Lemma 3.2, we obtain

$$\begin{aligned} \Vert u-u_{h} \Vert &\leq \bigl\Vert \eta(t) \bigr\Vert + \bigl\Vert \theta (t) \bigr\Vert \\ &\leq Ch^{2} \Vert u \Vert _{2}+C\bigl(h^{2}+ \bigl\Vert P_{N}u^{0}-u_{h}^{0} \bigr\Vert \bigr). \end{aligned}$$

This completes the proof. □

4 Full-discrete approximation

In this section, we discretize the semi-discrete equation (3.2) in the temporal direction using Crank-Nicolson scheme. For any given positive integer M, let $\tau=T/M$ be the time step.

Define the net function $U_{i,j}^{n} = U(x_{i},y_{j}, t_{n})$ for $t_{n} = n\tau$, $n = 1,\ldots,M$, and $U^{n+1/2}=\frac{U^{n}+U^{n+1}}{2}$. The full-discrete pseudo-spectral scheme for problem (1.1)-(1.3) reads: find $U^{n}\in S_{N}$, $n=1,\ldots,M$ such that

$$ \textstyle\begin{cases} (\frac{U^{n+1}-U^{n}}{\tau},v)_{h}+\gamma(\Delta U^{n+1/2},\Delta v)_{h}-(\Delta U^{n+1/2},v)_{h}+(\tilde{f}(U^{n},U^{n+1}),v)_{h}=0, \\ (U^{0},v)_{h}=(u^{0}(\cdot),v)_{h}, \quad \forall v\in S_{N}. \end{cases} $$

(4.1)

Here

$$\tilde{f}\bigl(U^{n},U^{n+1}\bigr)= \textstyle\begin{cases} \frac{H(U^{n+1})-H(U^{n})}{U^{n+1}-U^{n}}, & U^{n+1}\neq U^{n}, \\ H'(U^{n+1/2}), & U^{n+1}= U^{n}, \end{cases} $$

and

$$H(V)=\frac{1}{4}\bigl(1-V^{2}\bigr)^{2}. $$

Observe that

$$ \tilde{f}\bigl(U^{n},U^{n+1}\bigr)= \frac {1}{4}{\bigl[\bigl(U^{n+1}\bigr)^{3}+ \bigl(U^{n+1}\bigr)^{2}U^{n}+\bigl(U^{n} \bigr)^{3}+\bigl(U^{n}\bigr)^{2}U^{n+1} \bigr]} -\frac{1}{2}\bigl(U^{n}+U^{n+1}\bigr). $$

(4.2)

According to Lemma 2.3, (4.1) is equivalent to

$$ \textstyle\begin{cases} (\frac{U^{n+1}-U^{n}}{\tau},v)+\gamma(\Delta U^{n+1/2},\Delta v)-(\Delta U^{n+1/2},v)+(I_{N}\tilde{f}(U^{n},U^{n+1}),v)=0, \\ U^{0}=u_{h}^{0}, \quad \forall v\in S_{N}. \end{cases} $$

(4.3)

For the solution of scheme (4.3), we have the following prior bounds.

Theorem 4.1

Let $U^{0}\in S_{N}$, then there exists a unique solution $U^{0}(t)\in S_{N}$ for problem (4.3), such that

$$ \bigl\Vert U^{n} \bigr\Vert _{2}\leq C\bigl(\gamma, \Vert u_{0} \Vert _{2,h}\bigr),\quad 0\leq t\leq T. $$

(4.4)

Proof

Taking in (4.3) the inner product with $U^{n+1/2}$, we obtain

$$\begin{aligned}& \frac{1}{2\tau}\bigl( \bigl\Vert U^{n+1} \bigr\Vert ^{2}- \bigl\Vert U^{n} \bigr\Vert ^{2}\bigr)+ \gamma \bigl\Vert \Delta U^{n+1/2} \bigr\Vert ^{2}+ \bigl\Vert \nabla U^{n+1/2} \bigr\Vert ^{2} \\& \quad {}+\frac{1}{2}\bigl(\bigl({\bigl(U^{n} \bigr)}^{2}+{\bigl(U^{n+1}\bigr)}^{2}\bigr) \bigl(U^{n+1/2}\bigr)^{2},1\bigr)_{h}- \bigl\Vert U^{n+1/2} \bigr\Vert ^{2}=0. \end{aligned}$$

Applying the Cauchy inequality to the last term yields

$$\begin{aligned}& \frac{1}{2\tau}\bigl( \bigl\Vert U^{n+1} \bigr\Vert ^{2}- \bigl\Vert U^{n} \bigr\Vert ^{2}\bigr)+ \gamma \bigl\Vert \Delta U^{n+1/2} \bigr\Vert ^{2}+ \bigl\Vert \nabla U^{n+1/2} \bigr\Vert ^{2} \\& \quad {}+\frac{1}{2}\bigl(\bigl({U^{n}}^{2}+{ \bigl(U^{n+1}\bigr)}^{2}\bigr) \bigl(U^{n+1/2} \bigr)^{2},1\bigr)_{h}\leq\frac {1}{2} \bigl\Vert U^{n+1} \bigr\Vert ^{2}+\frac{1}{2} \bigl\Vert U^{n} \bigr\Vert ^{2}. \end{aligned}$$

It follows from the above result that

$$ \frac{1-\tau}{2\tau} \bigl\Vert U^{n+1} \bigr\Vert ^{2} \leq\frac{1+\tau}{2\tau} \bigl\Vert U^{n} \bigr\Vert ^{2}. $$

(4.5)

Then we can get

$$ \bigl\Vert U^{n+1} \bigr\Vert ^{2}\leq C(T) \bigl\Vert U^{0} \bigr\Vert ^{2}. $$

(4.6)

As in (3.7), we define the Lyapunov function

$$E\bigl(U^{n}\bigr)=\frac{\gamma}{2} \bigl\Vert U^{n} \bigr\Vert ^{2}+\frac{1}{2} \bigl\Vert \nabla U^{n} \bigr\Vert ^{2}+\bigl(H\bigl(U^{n}\bigr),1 \bigr)_{h}. $$

Setting $v=U^{n+1}-U^{n}$ in (4.2) gives

$$\begin{aligned}& \frac{1}{\tau} \bigl\Vert U^{n+1}-U^{n} \bigr\Vert ^{2}+\frac{\gamma }{2}\bigl( \bigl\Vert \Delta U^{n+1} \bigr\Vert - \bigl\Vert \Delta U^{n} \bigr\Vert ^{2} \bigr)+\frac{1}{2} \bigl( \bigl\Vert \nabla U^{n+1} \bigr\Vert ^{2}- \bigl\Vert \nabla U^{n} \bigr\Vert ^{2}\bigr) \\& \quad {}+ \bigl(H\bigl(U^{n+1}\bigr)-H\bigl(U^{n}\bigr),1 \bigr)_{h}=0. \end{aligned}$$

(4.7)

According to the definition of $E(U^{n})$ and (4.7), we obtain

$$E\bigl(U^{n+1}\bigr)-E\bigl(U^{n}\bigr)=-\frac{1}{\tau} \bigl\Vert U^{n+1}-U^{n} \bigr\Vert ^{2}\leq0. $$

For Theorem 3.1, we complete the proof. □

We now consider the error estimate for the full-discrete pseudo-spectral solution. It follows from (3.1) and (4.1) that

$$\begin{aligned}& \bigl(P_{N}u_{t}(t_{n+1/2})+\gamma P_{N}\Delta^{2}u(t_{n+1/2})-P_{N}\Delta u(t_{n+1/2})+P_{N}f\bigl(u(t_{n+1/2})\bigr),v \bigr)=0, \end{aligned}$$

(4.8)

$$\begin{aligned}& \bigl(U^{n+1/2}+\gamma\Delta^{2}U^{n+1/2}- \Delta U^{n+1/2}+I_{N}\tilde {f}\bigl(U^{n},U^{n+1} \bigr),v \bigr)=0. \end{aligned}$$

(4.9)

Let $u^{n+1}=u(\cdot,t_{n+1})$ be the solution of (4.8), and $U^{n+1}$ be the solution of (4.9). Denote $\eta^{n}=u^{n}-P_{N}u^{n}$ and $\theta^{n}=P_{N}u^{n}-U^{n}$, we have

$$ u^{n}-U^{n}=u^{n}-P_{N}u^{n}+P_{N}u^{n}-U^{n}= \eta^{n}+\theta^{n}. $$

(4.10)

To estimate $\theta^{n}$, we need the following lemmas.

Lemma 4.2

Let $u^{n}$ be the solution of (4.8), and $U^{n}$ be the solution of (4.8). If $u\in L^{\infty}([0,T];W^{2,\infty})$. we have

$$\biggl(\frac{\partial u(t_{n+1/2})}{\partial t}-\frac{U^{n+1}-U^{n}}{\tau },v \biggr)=\tau^{2} \biggl(\frac{u_{ttt}(\xi^{n})}{24},v \biggr)+\frac{1}{ \tau} \bigl(\theta^{n+1}- \theta^{n},v \bigr), $$

where $t_{n}\leq\xi^{n}\leq t_{n+1}$.

Proof

Using the definition of $P_{N}$, we have

$$\begin{aligned}& \biggl(\frac{\partial u(t_{n+1/2})}{\partial t}-\frac{U^{n+1}-U^{n}}{\tau},v\biggr) \\& \quad =\biggl(\frac{\partial u(t_{n+1/2})}{\partial t}-\frac{u^{n+1}-u^{n}}{\tau },v\biggr)+\frac{1}{\tau} \bigl(\bigl(u^{n+1}-u^{n}\bigr)-\bigl(U^{n+1}-U^{n} \bigr),v\bigr) \\& \quad =\biggl(\frac{\partial u(t_{n+1/2})}{\partial t}-\frac{u^{n+1}-u^{n}}{\tau },v\biggr)+\frac{1}{\tau} \bigl(\theta^{n+1}-\theta^{n},v\bigr). \end{aligned}$$

Making use of the Taylor expansion, we find

$$u(t_{n+1})-u(t_{n})=\frac{\partial u(t_{n+1/2})}{\partial t}+\frac{\tau ^{3}}{24}u_{ttt} \bigl(\xi^{n}\bigr),\quad t_{n}\leq\xi^{n}\leq t_{n+1}. $$

Combing the above two results, we complete this proof. □

Lemma 4.3

Let $u^{n}$ be the solution of (4.8), $U^{n}$ be the solution of (4.9). If $u\in L^{\infty}([0,T]; W^{2,\infty})$ and $u_{t},u_{tt},u_{ttt}\in L^{\infty}([0,T];H^{2})$, then there exists a constant $C=(C(u)_{L^{\infty}([0,T];W^{2,\infty})}, \gamma)$ such that

$$ \bigl\Vert P_{N}f\bigl(u(t_{n+1/2}) \bigr)-I_{N}\tilde{f}\bigl(U^{n},U^{n+1}\bigr) \bigr\Vert \leq C\bigl(h^{2}+\tau^{2}+ \bigl\Vert \theta^{n+1/2} \bigr\Vert \bigr). $$

(4.11)

Proof

Note that

$$\begin{aligned}& \bigl\Vert P_{N}f\bigl(u(t_{n+1/2})\bigr)-I_{N} \tilde{f}\bigl(U^{n},U^{n+1}\bigr) \bigr\Vert \\& \quad \leq \bigl\Vert P_{N}f\bigl(u(t_{n+1/2})\bigr)-f \bigl(u(t_{n+1/2})\bigr) \bigr\Vert + \bigl\Vert f\bigl(u(t_{n+1/2}) \bigr)-\tilde{f}\bigl(U^{n},U^{n+1}\bigr) \bigr\Vert \\& \qquad {}+ \bigl\Vert \tilde {f}\bigl(U^{n},U^{n+1}\bigr)-I_{N} \tilde{f}\bigl(U^{n},U^{n+1}\bigr) \bigr\Vert \\& \quad \leq Ch^{2} \bigl\vert f\bigl(u(t_{n+1/2})\bigr) \bigr\vert _{2}+ \bigl\Vert f\bigl(u(t_{n+1/2})\bigr)-\tilde {f} \bigl(U^{n},U^{n+1}\bigr) \bigr\Vert +Ch^{2} \bigl\vert \tilde{f}\bigl(U^{n},U^{n+1}\bigr) \bigr\vert _{2}. \end{aligned}$$

By Lemma 4.2 and Sobolev’s embedding theorem, we get

$$\bigl\vert \tilde{f}\bigl(U^{n},U^{n+1}\bigr) \bigr\vert _{2}\leq C \bigl\Vert U^{0} \bigr\Vert _{2}. $$

So we just need to estimate $\| f(u(t_{n+1/2}))-\tilde {f}(U^{n},U^{n+1})\|$.,

$$\begin{aligned}& \bigl\Vert f\bigl(u(t_{n+1/2})\bigr)-\tilde{f}\bigl(U^{n},U^{n+1} \bigr) \bigr\Vert \\& \quad \leq \bigl\Vert f\bigl(u(t_{n+1/2})\bigr)-f\bigl(u^{n+1/2} \bigr) \bigr\Vert + \bigl\Vert f\bigl(u^{n+1/2}\bigr)-\tilde{f} \bigl(u(t_{n}),u(t_{n+1})\bigr) \bigr\Vert \\& \qquad {}+ \bigl\Vert \tilde{f}\bigl(u(t_{n}),u(t_{n+1}) \bigr)-\tilde {f}\bigl(U^{n},u(t_{n+1})\bigr) \bigr\Vert \\& \qquad {}+ \bigl\Vert \tilde{f}\bigl(U^{n},u(t_{n+1})\bigr)-\tilde{f} \bigl(U^{n},U^{n+1}\bigr) \bigr\Vert \\& \quad = \Vert E_{1} \Vert + \Vert E_{2} \Vert + \Vert E_{3} \Vert + \Vert E_{4} \Vert . \end{aligned}$$

We now estimate them term by term. Using the smoothness of f, and the boundedness of $\| u\|_{L^{\infty}}$, we estimate $E_{1}$ as

$$\Vert E_{1} \Vert \leq C \bigl\Vert u(t_{n+1/2})-u^{n+1/2} \bigr\Vert \leq C\tau^{2} \Vert u_{tt} \Vert _{L^{\infty}}. $$

According to the definition of $f(\cdot)$ and $\tilde{f}(\cdot,\cdot)$, we derive the bound for $E_{2}$:

$$\Vert E_{2} \Vert = \frac{1}{8} \bigl\Vert (u_{n+1}-u_{n}) (u_{n+1}+u_{n}) (u_{n}-u_{n+1}) \bigr\Vert \leq C\tau^{2} \Vert u_{t} \Vert _{L^{\infty}}. $$

Similarly, we easily derive the following estimates:

$$\begin{aligned} \Vert E_{3} \Vert &=\frac{1}{4} \bigl\Vert \bigl(u(t_{n})-U^{n}\bigr) \bigl(u^{2}(t_{n})+{U^{n}}^{2}+ \bigl(U^{n}+u(t_{n+1})\bigr) \bigl(u(t_{n})+u(t_{n+1}) \bigr)\bigr) \bigr\Vert \\ &\leq C \bigl\Vert u(t_{n})-U^{n} \bigr\Vert \leq C \bigl( \Vert \eta_{n} \Vert + \Vert \theta_{n} \Vert \bigr) \end{aligned}$$

and

$$\Vert E_{4} \Vert \leq C \bigl\Vert u(t_{n+1})-U^{n+1} \bigr\Vert \leq C\bigl( \Vert \eta_{n+1} \Vert + \Vert \theta_{n+1} \Vert \bigr). $$

Combining the above estimates gives the result. □

Theorem 4.4

Let u be the solution of (4.8), $U^{n}$ be the solution of (4.9). If $u_{0}\in H^{2}$, $u\in L^{\infty}([0,T];W^{2,\infty})$, $u_{t},u_{tt},u_{ttt}\in L^{\infty}([0,T];H^{2})$, then there exists a constant C such that

$$ \bigl\Vert \theta^{n} \bigr\Vert \leq C\bigl( \bigl\Vert \theta^{0} \bigr\Vert +h^{2}+\tau^{2} \bigr). $$

(4.12)

Proof

Combining (4.8) and (4.9), setting $v=\theta^{n+1/2}$, we obtain

$$\begin{aligned}& \tau^{2}\biggl(\frac{u_{ttt}(\xi^{n})}{24},\theta^{n+1/2}\biggr)+ \frac{1}{\tau }\bigl( \bigl\Vert \theta^{n+1} \bigr\Vert ^{2}- \bigl\Vert \theta^{n} \bigr\Vert ^{2} \bigr)+\gamma \bigl\Vert \Delta\theta^{n+1/2} \bigr\Vert ^{2}+ \bigl\Vert \nabla\theta^{n+1/2} \bigr\Vert ^{2} \\& \quad {}+\bigl(P_{N} f\bigl(u(t_{n+1/2})\bigr)^{3}-I_{N} \tilde{f}\bigl(U^{n},U^{n+1}\bigr)^{3},\theta ^{n+1/2}\bigr)=0. \end{aligned}$$

Using Lemma 4.3 to the above equality gives

$$\begin{aligned}& \bigl( \bigl\Vert \theta^{n+1} \bigr\Vert ^{2}- \bigl\Vert \theta^{n} \bigr\Vert ^{2}\bigr)+\tau \gamma \bigl\Vert \Delta\theta^{n+1/2} \bigr\Vert ^{2}+\tau \bigl\Vert \nabla\theta^{n+1/2} \bigr\Vert ^{2} \\& \quad \leq\tau \bigl\Vert \theta^{n+1/2} \bigr\Vert ^{2}+ \tau^{3} \biggl\Vert \frac {u_{ttt}(\xi^{n})}{24} \biggr\Vert \bigl\Vert \theta^{n+1/2} \bigr\Vert \\& \qquad {}+\tau \bigl\Vert P_{N} f \bigl(u(t_{n+1/2})\bigr)^{3}-I_{N} \tilde{f} \bigl(U^{n},U^{n+1}\bigr)^{3} \bigr\Vert \bigl\Vert \theta ^{n+1/2} \bigr\Vert \\& \quad \leq\frac{\tau}{2}\bigl( \bigl\Vert \theta^{n+1} \bigr\Vert ^{2}+ \bigl\Vert \theta ^{n} \bigr\Vert ^{2}\bigr) +\tau^{3}\biggl(\frac{1}{2} \biggl\Vert \frac{u_{ttt}(\xi^{n})}{24} \biggr\Vert ^{2}+\frac {1}{4}\bigl( \bigl\Vert \theta^{n+1} \bigr\Vert ^{2} + \bigl\Vert \theta^{n} \bigr\Vert ^{2}\bigr)\biggr) \\& \qquad {}+\tau\biggl(\frac{1}{2} \bigl\Vert P_{N} f \bigl(u(t_{n+1/2})\bigr)^{3}-I_{N} \tilde{f} \bigl(U^{n},U^{n+1}\bigr)^{3} \bigr\Vert ^{2}+\frac{1}{4}\bigl( \bigl\Vert \theta^{n+1} \bigr\Vert ^{2} + \bigl\Vert \theta^{n} \bigr\Vert ^{2}\bigr)\biggr). \end{aligned}$$

Using Lemma 4.3, we have

$$\begin{aligned} \bigl\Vert \theta^{n+1} \bigr\Vert ^{2}&\leq\bigl(1+C( \tau) \bigl\Vert \theta ^{n} \bigr\Vert ^{2}\bigr) +C \biggl\{ \tau\bigl(h^{2}+\tau^{2}+ \bigl\Vert \theta^{n+1} \bigr\Vert ^{2}+ \bigl\Vert \theta ^{n} \bigr\Vert ^{2}\bigr)+\tau^{3} \biggl\Vert \frac{u_{ttt}(\xi^{n})}{24} \biggr\Vert ^{2}\biggr\} \\ &\leq C \Biggl\{ \bigl\Vert \theta^{0} \bigr\Vert ^{2}+ \tau\sum_{j=0}^{n}\bigl( \bigl\Vert \theta^{j} \bigr\Vert ^{2}+ h^{2}+ \tau^{2}\bigr)+\tau^{3}\sum_{j=0}^{n} \bigl\Vert u_{ttt}\bigl(\xi^{j}\bigr) \bigr\Vert ^{2} \Biggr\} . \end{aligned}$$

By applying the discrete Gronwall inequality to the above result gives

$$\bigl\Vert \theta^{n} \bigr\Vert \leq C\bigl( \bigl\Vert \theta^{0} \bigr\Vert +h^{2}+\tau^{2}\bigr). $$

This completes the proof. □

Theorem 4.5

Let u be the solution of (3.1), $U^{n}$ be the solution of (4.1). If $u_{0}\in H^{2}$, $u\in L^{\infty}([0,T];W^{2,\infty})$, $u_{t},u_{tt},u_{ttt}\in L^{\infty}([0,T];H^{2})$, then there exists a constant $C=C(\gamma, \| u\|_{L^{\infty}([0,T];W^{2,\infty })})$ for τ small enough such that

$$\bigl\Vert u^{n}-U^{n} \bigr\Vert \leq C \bigl(h^{2}+\tau^{2}\bigr). $$

Proof

Using (4.12) and Theorem 4.1, we obtain

$$\begin{aligned} \bigl\Vert u^{n}-U^{n} \bigr\Vert &\leq \bigl\Vert \eta^{n} \bigr\Vert + \bigl\Vert \theta ^{n} \bigr\Vert \\ &\leq Ch^{2} \bigl\Vert u^{n} \bigr\Vert _{2}+C\bigl(h^{2}+\tau^{2}+ \bigl\Vert P_{N}u^{0}-U^{0} \bigr\Vert \bigr) \\ &\leq C\bigl(h^{2}+\tau^{2}\bigr). \end{aligned}$$

 □

5 Numerical results

In this section, two examples are presented to illustrate the effectiveness of the pseudo-spectral scheme (4.1). The Crank-Nicolson scheme is a typical difference scheme, we get nonlinear equations during each iteration in t. To compute the approximate solution, we use the Newton iterative method in each iteration. Set $\Omega=(0,\pi )\times(0,\pi)$ and $T=1$ in this section.

5.1 Example 1

We consider the following nonlinear inhomogeneous extended Fisher-Kolmogorov (EFK) equation:

$$u_{t}+\gamma\Delta^{2}u-\nabla u+f(u)=g(x,y,t), \quad \mbox{in }\Omega\times(0,T], $$

with the initial condition

$$u(x,y,0)=\sin(x)\sin(y), \quad \mbox{in }\Omega, $$

subject to the initial boundary conditions

$$u=0, \qquad \Delta u=0,\quad (x,y,t)\in\partial\Omega\times(0,T], $$

where $f(u)=u^{3}-u$, $g(x,y,t)=4\gamma \sin(x)\sin(y)e^{-t}+[\sin(x)\sin(y)e^{-t}]^{3}$. The exact solution of the problem is

$$u(x,y,t)=\sin(x)\sin(y)e^{-t}. $$

The profile of the exact solution is given in Figure 1, the behavior of the approximate solution is shown in Figure 2. The variation of the $L_{\infty}$-errors for different times is presented in Figure 3.

Figure 1

The profile of the exact solution for the EFK equation with $\pmb{\gamma=0.01}$ at $\pmb{t=T=1}$ .

Figure 2

The profile of the numerical solution for the EFK equation with $\pmb{\gamma=0.01}$ at $\pmb{t=T=1}$ .

Figure 3

The profile of the variation of $\pmb{L_{\infty}}$ -errors for different times with $\pmb{\gamma=0.01}$ at $\pmb{t=T=1}$ .

It shows the $L_{\infty}$-errors to be increasing along with the increase of time, and the increasing rates decline gradually with time increasing.

5.2 Example 2

We consider the following problem for the EFK equation:

$$u_{t}+\gamma\Delta^{2}u-\nabla u+f(u)=0,\quad \mbox{in } \Omega\times(0,T], $$

with the initial condition

$$u(x,y,0)=\sin(x)\sin(y), \quad \mbox{in } \Omega, $$

subject to the initial boundary conditions

$$u=0,\qquad \Delta u=0, \quad (x,y,t)\in\partial\Omega\times(0,T], $$

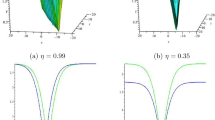
where $f(u)=u^{3}-u$. The profile of the approximate solution of the equation is given in Figure 4. In addition, Figure 5 represents the Lyapunov functional as it decreases.

Figure 4

The profile of the numerical solution for the EFK equation with $\pmb{\gamma=0.01}$ at $\pmb{t=T=1}$ .

Figure 5

The profile of the Lyapunov functional with $\pmb{\gamma =0.01}$ at $\pmb{n=0,\ldots,100}$ .

Now, we consider the $L_{\infty}$-errors for different τ with fixed $h=\frac{\pi}{20}$. Since there is no exact solution for this problem to the best of our knowledge, we take the numerical solution u with $h=\frac{\pi}{20}$, $\tau=\frac{1}{200}$ as the ‘exact solution’. $L_{\infty}$-errors are showed in Table 1 for different time steps at $x=\frac{\pi}{4}$, $y=\frac{\pi}{4}$.

Table 1 $\pmb{L_{\infty}}$ -errors for different time steps at $\pmb{x=\frac{\pi }{4}}$ , $\pmb{y=\frac{\pi}{4}}$

It is easy to see that the fourth column $\frac{\operatorname{err}(\frac {\pi}{4}, \frac{\pi}{4}, \tau)}{\tau}$ and the fifth column $\frac {\operatorname{err}(\frac{\pi}{4}, \frac{\pi}{4}, \tau)}{\tau^{2}}$ is monotone decreasing along with the time step’s waning. That means the order of convergence for time is better than $O(\tau^{2})$, so the numerical result is better than the theoretical result. The reason may be the existence of a nonlinear term or the limit of the theoretical proof tool.

We also consider the $L_{\infty}$-errors for the different h with fixed $\tau=0.005$. In this situation, we take the numerical solution u with $h=\frac{\pi}{60}$, $\tau=\frac{1}{100}$ as the ‘exact solution’. $L_{\infty}$-errors are showed in Table 2 for different space steps at $t=0.3$.

Table 2 $\pmb{L_{\infty}}$ -errors for different space steps at $\pmb{t=0.3}$

In Table 2, the fifth column is not monotone increasing along with the space step’s waning all the time, but it tends to be monotone decreasing when the space subdivision is small enough. That means the accuracy in space is better than the theoretical result.

In summary, the spatial accuracy of the Fourier pseudo-spectral scheme is of second order, and the time accuracy is better than the second order. The results indicate this numerical scheme is efficient and its computational accuracy is slightly better than the theoretical precision.

Remark 5.1

At the reviewer’s suggestion, we considered the relations between $L_{\infty}$-error and γ with numerical experiments. We find the $L_{\infty}$-error is decreasing along with the decrease of γ, which is the coefficient of the fourth order term. For the general fourth order nonlinear parabolic equations, the $L_{\infty}$-errors should have become bigger with the decrease of γ. Because we need to balance the nonlinear term with the fourth order term in the estimation of the errors, the errors is proportional to the inverse of γ. Compared with the general case, the numerical results are reversed in EFK equation. One of the reasons maybe is that we get the theoretical results by the Lyapunov function, so the estimated coefficients are irrelevant to γ. As for the lack of theoretical basis, we mention it as an open problem and will continue to study it.