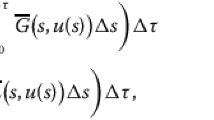Abstract
In this paper, we establish some new nonlinear retarded Volterra–Fredholm type integral inequalities on time scales. Our results not only generalize and extend some known integral inequalities, but also provide a handy and effective tool for the study of qualitative properties of solutions of some Volterra–Fredholm type dynamic equations.
Similar content being viewed by others
1 Introduction
In recent years, there exist a large number of published papers on the theory of time scales which was introduced by Stefan Hilger [1] in his Ph.D. thesis in 1988 in order to unify and extend the difference and differential calculus in a consistent way, for instance, [2–16] and the references therein. In particular, many scholars attached great importance to the study of dynamic inequalities on time scales (see, e.g., [17–31] and the references therein), which extended some discrete and continuous inequalities (see [32–36] and the references therein).
In 2013, the authors in [22] established and applied the following useful linear Volterra–Fredholm type integral inequality on time scales:
where \(I=[t_{0},\alpha]\cap\mathbb{T}\), \(t_{0}\in\mathbb{T}\), \(\alpha\in \mathbb{T}\), \(\alpha>t_{0}\), \(u_{0}\) is a nonnegative constant, u, f, g, and h are nonnegative rd-continuous functions defined on I.
In 2014, the authors in [27] investigated the nonlinear Volterra–Fredholm type integral inequality on time scales
where \(I=[t_{0},\alpha]\cap\mathbb{T}\), \(t_{0}\in\mathbb{T}\), \(\alpha\in \mathbb{T}\), \(\alpha>t_{0}\), u, \(f_{1}\), \(f_{2}\), \(f_{3}\) are rd-continuous functions defined on I, \(f_{1}\), \(f_{2}\), \(f_{3}\) are nonnegative, \(w\in C(\mathbb{R}_{+}, \mathbb{R}_{+})\) is a nondecreasing function with \(w(u)>0\) for \(u>0\), and k is a nonnegative constant.
Very recently, the author in [29] discovered the retarded Volterra–Fredholm type integral inequality on time scales
where \(I=[t_{0},T]\cap\mathbb{T}\), \(t_{0}\in\mathbb{T}\), \(T\in\mathbb{T}\), \(T>t_{0}\), \(\alpha:I\rightarrow I\) is continuous and strictly increasing satisfying \(\alpha(t)\leq t\), \(\alpha^{\Delta}\) is rd-continuous, u, a, b, f, and \(g: I\rightarrow\mathbb{R}_{+}\) are rd-continuous functions and a is nondecreasing.
Inspired by the ideas employed in [22, 27, 29], here we obtain some new nonlinear Volterra–Fredholm type integral inequalities on time scales. Our results not only generalize and extend the results of [22, 27] and some known integral inequalities but also provide a handy and effective tool for the study of qualitative properties of solutions of some complicated Volterra–Fredholm type dynamic equations.
2 Preliminaries
For an excellent introduction to the calculus on time scales, we refer the reader to [5] and [6].
In what follows, we always assume that \(\mathbb{R}\) denotes the set of real numbers, \(\mathbb{R}_{+}=[0,\infty)\), \(\mathbb{Z}\) denotes the set of integers, and \(\mathbb{T}\) is an arbitrary time scale (nonempty closed subset of \(\mathbb{R}\)), \(\mathcal{R}\) denotes the set of all regressive and rd-continuous functions, \(\mathcal{R}^{+}=\{p\in\mathcal{R}:1+\mu (t)p(t)>0, \mbox{for all } t\in\mathbb{T}\}\), \(I=[t_{0},T]\cap\mathbb{T}^{\kappa}\), where \(t_{0}\in\mathbb{T}^{\kappa}\), \(T\in\mathbb{T}^{\kappa}\), \(T>t_{0}\). The set \(\mathbb{T}^{\kappa}\) is defined as follows: If \(\mathbb{T}\) has a maximum m and m is left-scattered, then \(\mathbb{T}^{\kappa}=\mathbb{T}-\{m\}\). Otherwise \(\mathbb{T}^{\kappa}=\mathbb{T}\). The graininess function \(\mu: \mathbb {T}\rightarrow[0,\infty)\) is defined by \(\mu(t):=\sigma(t)-t\), the forward jump operator \(\sigma: \mathbb{T}\rightarrow\mathbb{T}\) by \(\sigma(t):=\inf\{s\in\mathbb{T}: s>t\}\), and the “circle plus” addition ⊕ defined by \((p\oplus q)(t):=p(t)+q(t)+\mu(t)p(t)q(t)\) for all \(t\in\mathbb {T}^{\kappa}\).
We give the following lemmas in order to use them in our proofs. One can find details in [5].
Lemma 2.1
([5, Theorem 1.16])
Assume that \(f:\mathbb{T}\rightarrow\mathbb{R}\) is a function and let \(t\in\mathbb{T}\). If f is differentiable at t, then
Lemma 2.2
([5, Theorem 1.98])
Assume that \(\nu:\mathbb {T}\rightarrow\mathbb{R}\) is a strictly increasing function and \(\widetilde{\mathbb{T}}:=\nu(\mathbb{T})\) is a time scale. If \(f: \mathbb{T}\rightarrow\mathbb{R}\) is an rd-continuous function and ν is differentiable with rd-continuous derivative, then for \(a, b\in \mathbb{T}\),
Lemma 2.3
([29])
Let \(\alpha:I\rightarrow I\) be a continuous and strictly increasing function such that \(\alpha(t)\leq t\), and \(\alpha^{\Delta}\) is rd-continuous. Assume that \(f: I\rightarrow\mathbb{R}\) is an rd-continuous function, then
implies
Lemma 2.4
([5, Theorem 1.117])
Suppose that for each \(\varepsilon>0\) there exists a neighborhood U of t, independent of \(\tau\in[t_{0},\sigma(t)]\), such that
where \(w: \mathbb{T}\times\mathbb{T}^{\kappa}\rightarrow\mathbb{R}_{+}\) is continuous at \((t,t)\), \(t\in\mathbb{T}^{\kappa}\) with \(t>t_{0}\), and \(w^{\Delta}_{t}(t,\cdot)\) are rd-continuous on \([t_{0},\sigma(t)]\). Then
implies
Lemma 2.5
([5, Theorem 6.1])
Suppose that y and f are rd-continuous functions and \(p\in\mathcal {R}^{+}\). Then
implies
Lemma 2.6
Let \(m\geq n\geq0\), \(m\neq0\), and \(a\geq0\), then
for any \(k>0\).
Proof
Set \(F(x)={\frac{n}{m}}x^{n-m}a^{m}+\frac{m-n}{m}x^{n}\), \(x>0\). It is seen that \(F(x)\) obtains its minimum at \(x_{0}=a\). Hence we get (2.5) holds for any \(k>0\). □
Throughout this paper, we assume that:
- (\(\mathrm{H}_{1}\)):
-
\(\alpha:I\rightarrow I\) is continuous and strictly increasing satisfying \(\alpha(t)\leq t\) and \(\alpha^{\Delta}\) is rd-continuous.
- (\(\mathrm{H}_{2}\)):
-
\(\beta, \gamma:I\rightarrow I\) are continuous satisfying \(\beta (t)\leq t\) and \(\gamma(t)\leq t\).
- (\(\mathrm{H}_{3}\)):
-
\(u, a, b: I\rightarrow\mathbb{R}_{+}\) are rd-continuous functions, a is nondecreasing, and \(b^{\Delta}(t)\geq0\).
- (\(\mathrm{H}_{4}\)):
-
\(f_{i}\ (i=1,2,3,4,5,6), g_{i}\ (i=1,2,3): I\rightarrow\mathbb{R}_{+}\) are rd-continuous functions.
- (\(\mathrm{H}_{5}\)):
-
\(v, w: \mathbb{T}\times\mathbb{T}^{\kappa}\rightarrow\mathbb {R}_{+}\) is continuous at \((t,t)\), \(t\in\mathbb{T}^{\kappa}\) with \(t>t_{0}\).
- (\(\mathrm{H}_{6}\)):
-
\(m, n: \mathbb{T}\times\mathbb{T}^{\kappa}\rightarrow\mathbb {R}_{+}\) is continuous at \((t,t)\), \(t\in\mathbb{T}^{\kappa}\) with \(t>t_{0}\).
3 Main results
Theorem 3.1
Assume that (\(\mathrm{H}_{1}\))–(\(\mathrm{H}_{4}\)) hold, \(0\leq p\leq1\), \(0\leq q\leq1\), \(0\leq r\leq1\) are constants, and \(\mu(t)A(t)<1\). Suppose that u satisfies
If there exist positive constants \(k_{i}\) (\(i=1,2,3\)) such that
then
where
Proof
Denote
Then z is nondecreasing on I. From (3.1) and (3.9) we have
Now using Lemma 2.6 for \(a=u(s)+f_{i}(s)\int_{\alpha(t_{0})}^{s}g_{j}(\tau )u(\tau)\Delta\tau\), \(i=2,4,6\), and \(j=i/2\) with \(m=1\) and \(n=p,q,r\) for any \(k_{1}, k_{2}, k_{3}>0\), respectively, we have
Now using (3.4) and (3.5) and (3.10) we get
Since \(V(t)\) is nondecreasing on I, then for \(t\in I\), from the above inequality we have
Let
Then (3.13) can be restated as
Set
Then \(w(t)\) is nondecreasing, and from (3.15) and (3.16) we obtain
Using Lemma 2.3, taking delta derivative of (3.16), and from (3.17), we have
where \(A(t)\) and \(C(t)\) are defined as in (3.6) and (3.8). From (3.7), we get
and from (3.18), (3.19), and Lemma 2.1, we have
which yields
i.e.,
Note that w is rd-continuous and \(B\oplus C\in\mathcal{R}^{+}\), from Lemma 2.5, (3.16), and (3.22), we obtain
From (3.17) and (3.23), we have
Using (3.24) on the right–hand side of (3.14) and according to (3.2), we obtain
From (3.24) and (3.25), we obtain
Noting (3.10), we get the desired inequality (3.3). This completes the proof. □
If we take \(p=q=r=1\), we can get the following corollary.
Corollary 3.1
Assume that (\(\mathrm{H}_{1}\))–(\(\mathrm{H}_{4}\)) hold. Suppose that u satisfies
If
then
where
Theorem 3.2
Assume that (\(\mathrm{H}_{1}\))–(\(\mathrm{H}_{4}\)) hold, \(0\leq q_{i}\leq l\), \(0\leq r_{i}\leq l\), \(l\neq0\), and \(0\leq\theta_{i}\leq1\) (\(i=1,2,3\)) are constants, and \(\mu(t)A(t)<1\). Suppose that u satisfies
If there exist positive constants \(k_{i}\) (\(i=1,2,\ldots,9\)) such that
then
where
Proof
Denote
Then z is nondecreasing on I. From (3.27) and (3.38) we have
Using Lemma 2.6, we obtain
Using (3.30), (3.31), (3.35)–(3.37), and (3.39), we get
It is similar to the proof of Theorem 3.1, we get
Then, using \(u^{l}(t)\leq z(t)\), we have (3.29). This completes the proof. □
Remark 3.1
If we take \(a(t)\equiv u_{0}\), \(b(t)\equiv1\), \(\alpha (t)\equiv t\), \(\beta(t)\equiv t\), \(f_{2}(t)\equiv1\), and \(f_{4}(t)=f_{5}(t)\equiv0\), then Corollary 3.1 reduces to [22, Theorem 2.2]. If we take \(a(t)\equiv k\), \(b(t)\equiv1\), \(\alpha(t)\equiv t\), \(\beta (t)\equiv t\), \(p=1\), \(q_{1}=r_{1}=q_{2}=r_{2}\), \(\theta_{1}=\theta_{2}=1\), \(f_{1}(t)=f_{3}(t)\), \(f_{2}(t)=f_{4}(t)\), \(g_{1}(t)=g_{2}(t)\), and \(f_{5}(t)\equiv0\), then Theorem 3.2 gives an exact estimation for the solution of (3.27) compared with the result of [27, Theorem 4].
Theorem 3.3
Assume that (\(\mathrm{H}_{1}\))–(\(\mathrm{H}_{3}\)), (\(\mathrm{H}_{5}\)), (\(\mathrm{H}_{6}\)) hold, \(0\leq p\leq1\), \(0\leq q\leq1\) are constants, \(\mu(t)\widetilde{A}(t)<1\), \(v_{t}^{\Delta}(t,s)\geq0\), \(w_{t}^{\Delta}(t,s)\geq0\) for \(t\geq s\) and (2.3) holds. Suppose that u satisfies
If there exist positive constants \(k_{i}\) (\(i=1,2\)) such that
then
where
Proof
Denote
Then z is nondecreasing on I. From (3.42) and (3.49), we have
Now, using Lemma 2.6 for \(a=v(t,s)u(s)+w(t,s)\int_{\alpha(t_{0})}^{\alpha (s)}f(\tau)u(\tau)\Delta\tau\), and \(m(T,s)u(s)+n(T,s)\int_{\beta(t_{0})}^{\beta(s)}g(\tau)u(\tau)\Delta \tau\) with \(m=1\) and \(n=p, q\) for any \(k_{1}, k_{2}>0\), respectively, we have
Now, using (3.45) and (3.46) and (3.51), we have
Since \(V(t)\) is nondecreasing on I, then for \(t\in I\), from the above inequality we have
Let
Then (3.53) can be restated as
Set
Then \(y(t)\) is nondecreasing, and from (3.55) and (3.56) we obtain
Using Lemma 2.3, taking the delta derivative of (3.56), and from (3.57), we have
where \(\widetilde{A}(t)\) and \(\widetilde{C}(t)\) are defined as in (3.47) and (3.48). It is similar to the proof of Theorem 3.1, we get (3.44). This completes the proof. □
Theorem 3.4
Assume that (\(\mathrm{H}_{3}\))–(\(\mathrm{H}_{5}\)) hold, \(0\leq q_{i}\leq l\), \(0\leq r_{i}\leq l\), \(l\neq 0\), \(0\leq\theta_{i}\leq1\) (\(i=1,2\)) are constants, and \(\mu(t)A(t)<1\), \(v_{t}^{\Delta}(t,s)\geq0\), \(w_{t}^{\Delta}(t,s)\geq0\) for \(t\geq s\). And assume (2.3) holds. Suppose that u satisfies
If there exist positive constants \(k_{i}\) (\(i=1,2,3,4,5,6\)) such that
then
where
Proof
Denote
Then z is nondecreasing on I. From (3.59) and (3.67) we have
Using Lemma 2.6, we obtain
Using (3.62), (3.63), (3.65), (3.66), (3.68), and (3.69), we get
Since \(F(t)\) is nondecreasing on I, then for \(t\in I\), from the above inequality we have
Let
Then (3.71) can be restated as
Set
Then \(N(t)\) is nondecreasing, and from (3.73) and (3.74) we obtain
Taking the delta derivative of (3.74) and from (3.75), we get
Let
Obviously,
From Lemma 2.4, (3.77), and (3.78), we obtain
It is easy to see that \(A\in\mathcal{R}^{+}\). Therefore, from Lemma 2.5 and the above inequality, we have
Combining (3.78) and (3.79), we get
Setting \(t=\tau\) in (3.80), integrating it from \(t_{0}\) to t, we easily obtain
From (3.75) and (3.82), we have
Using (3.83) on the right-hand side of (3.72) and according to (3.60), we obtain
From (3.83) and (3.84), we obtain
Then using (3.68), we have (3.61). This completes the proof. □
Remark 3.2
If we take \(l=q_{1}=r_{1}=\theta_{1}=1\), and \(f_{2}(t)\equiv 0\), then Theorem 3.4 reduces to [28, Theorem 3.2].
4 Applications
In this section, we will present some simple applications for our results. First, we consider the following Volterra–Fredholm type dynamic integral equation:
on time scales \(\mathbb{T}=q^{\mathbb{N}_{0}}\), where \(q^{\mathbb{N}_{0}}=\{ q^{n}: n\in\mathbb{N}_{0}, q>1\}\), and \(I=[1,T]\cap q^{\mathbb{N}_{0}}\), \(T=q^{N}\), N is some positive integer and \(K_{0}\in\mathbb{R}\).
The following theorem gives the bound on the solution of Eq. (4.1).
Theorem 4.1
Suppose that u is a solution of Eq. (4.1) on I. If there exist positive constants \(k_{1}\) and \(k_{2}\) such that
then
Proof
From (4.1), we get
Take \(t_{0}=1\), \(a(t)=|K_{0}|\), \(b(t)=1\), \(f_{1}(t)=\frac{2}{t}\), \(f_{2}(t)=f_{4}(t)=\frac{t^{2}}{t+1}\), \(f_{3}(t)=\frac{3}{2t}\), \(f_{5}(t)=f_{6}(t)\equiv0\), \(g_{1}(t)=g_{2}(t)=\frac{1+q}{q^{2}t^{3}}\), \(\alpha (t)=t\), \(\beta(t)=t\), \(p=\frac{1}{2}\), and \(q=\frac{1}{3}\) in Theorem 3.1, on the basis of a straightforward computation, we have
Using Theorem 3.1, we obtain the desired inequality (4.3). □
Secondly, we consider the following retarded Volterra–Fredholm type dynamic integral equation on \(\mathbb{R}\):
where \(I=[0,T]\), T is some positive real number and \(K_{0}\in\mathbb{R}\).
The next result also deals with the boundedness of the solutions of Eq. (4.5).
Theorem 4.2
Suppose that u is a solution of Eq. (4.5) on I. If there exist positive constants \(k_{1}\) and \(k_{2}\) such that
then
Proof
From (4.5), we have
Take \(t_{0}=0\), \(a(t)=|K_{0}|\), \(b(t)=1\), \(f_{1}(t)=\frac{3t}{1+3t}\), \(f_{2}(t)=\frac {1}{t^{4}}\), \(f_{3}(t)=e^{-t}\), \(f_{4}(t)\equiv1\) \(f_{5}(t)=f_{6}(t)\equiv0\), \(g_{1}(t)=t^{2}\), \(g_{2}(t)\equiv1\), \(\alpha (t)=\frac{t}{2}\), \(\beta(t)=\frac{t}{3}\), \(p=\frac{1}{2}\), and \(q=\frac {1}{3}\) in Theorem 3.1, on the basis of a straightforward computation, we obtain
Using Theorem 3.1, we obtain the desired inequality (4.7). □
5 Conclusions
In this paper, we have established some new retarded Volterra–Fredholm type integral inequalities on time scales, which extend some known inequalities and provide a handy tool for deriving bounds of solutions of retarded dynamic equations on time scales. Unlike some existing results in the literature, the integral inequalities considered in this paper involve the power nonlinearity, which results in difficulties in the estimation on the explicit bounds of unknown function \(u(t)\). We establish an inequality to overcome the difficulties, which can be used as a handy tool to solve the similar problems.
References
Hilger, S.: Ein Maßkettenkalkül mit Anwendung auf Zentrumsmanningfaltigkeiten. Ph.D. thesis, Universität Würzburg (1988)
Adivar, M., Raffoul, Y.N.: Existence results for periodic solutions of integro-dynamic equations on time scales. Ann. Mat. Pura Appl. 188, 543–559 (2009)
Atici, F.M., Biles, D.C., Lebedinsky, A.: An application of time scales to economics. Math. Comput. Model. 43, 718–726 (2006)
Bi, L., Bohner, M., Fan, M.: Periodic solutions of functional dynamic equations with infinite delay. Nonlinear Anal. 68, 170–174 (2008)
Bohner, M., Peterson, A.: Dynamic Equations on Time Scales: An Introduction with Applications. Birkhäuser, Boston (2001)
Bohner, M., Peterson, A.: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston (2003)
Dogan, A.: On the existence of positive solutions of the p-Laplacian dynamic equations on time scales. Math. Methods Appl. Sci. 40, 4385–4399 (2017)
Dogan, A.: Positive solutions of the p-Laplacian dynamic equations on time scales with sign changing nonlinearity. Electron. J. Differ. Equ. 2018, 39 (2018)
Erbe, L., Jia, B.G., Peterson, A.: Belohorec-type oscillation theorem for second order sublinear dynamic equations on time scales. Math. Nachr. 284, 1658–1668 (2011)
Erbe, L., Jia, B.G., Peterson, A.: On the asymptotic behavior of solutions of Emden–Fowler equations on time scales. Ann. Mat. Pura Appl. 191, 205–217 (2012)
Federson, M., Mesquita, J.G., Slavik, A.: Measure functional differential equations and functional dynamic equations on time scales. J. Differ. Equ. 252, 3816–3847 (2012)
Karpuz, B.: Volterra theory on time scales. Results Math. 65, 263–292 (2014)
Slavik, A.: Averaging dynamic equations on time scales. J. Math. Anal. Appl. 388, 996–1012 (2012)
Feng, Q.H., Meng, F.W.: Oscillation results for a fractional order dynamic equation on time scales with conformable fractional derivative. Adv. Differ. Equ. 2018, 193 (2018)
Liu, H.D., Ma, C.Q.: Oscillation criteria for second-order neutral delay dynamic equations with nonlinearities given by Riemann–Stieltjes integrals. Abstr. Appl. Anal. 2013, Article ID 530457 (2013)
Liu, H.D., Ma, C.Q.: Oscillation criteria of even order delay dynamic equations with nonlinearities given by Riemann–Stieltjes integrals. Abstr. Appl. Anal. 2014, Article ID 395381 (2014)
Agarwal, R.P., Bohner, M., Peterson, A.: Inequalities on time scales: a survey. Math. Inequal. Appl. 4, 535–557 (2001)
Anderson, D.R.: Nonlinear dynamic integral inequalities in two independent variables on time scale pairs. Adv. Dyn. Syst. Appl. 3, 1–13 (2008)
Bohner, E.A., Bohner, M., Akin, F.: Pachpatte inequalities on time scale. J. Inequal. Pure Appl. Math. 6(1), Article 6 (2005)
Pachpatte, D.B.: Explicit estimates on integral inequalities with time scale. J. Inequal. Pure Appl. Math. 7, Article ID 143 (2006)
Saker, S.H.: Some nonlinear dynamic inequalities on time scales. Math. Inequal. Appl. 14, 633–645 (2011)
Meng, F.W., Shao, J.: Some new Volterra–Fredholm type dynamic integral inequalities on time scales. Appl. Math. Comput. 223, 444–451 (2013)
Du, L.W., Xu, R.: Some new Pachpatte type inequalities on time scales and their applications. J. Math. Inequal. 6(2), 229–240 (2012)
Feng, Q.H., Meng, F.W., Zheng, B.: Gronwall–Bellman type nonlinear delay integral inequalities on time scale. J. Math. Anal. Appl. 382, 772–784 (2011)
Liu, H.D., Meng, F.W.: Nonlinear retarded integral inequalities on time scales and their applications. J. Math. Inequal. 12(1), 219–234 (2018)
Wang, J.F., Meng, F.W., Gu, J.: Estimates on some power nonlinear Volterra–Fredholm type dynamic integral inequalities on time scales. Adv. Differ. Equ. 2017, 257 (2017)
Gu, J., Meng, F.W.: Some new nonlinear Volterra–Fredholm type dynamic integral inequalities on time scales. Appl. Math. Comput. 245, 235–242 (2014)
Li, W.N., Sheng, W.H.: Some Gronwall type inequalities on time scales. J. Math. Inequal. 4(1), 67–76 (2010)
Liu, H.D.: A class of retarded Volterra–Fredholm type integral inequalities on time scales and their applications. J. Inequal. Appl. 2017, 293 (2017)
Wang, T.L., Xu, R.: Bounds for some new integral inequalities with delay on time scales. J. Math. Inequal. 6(3), 355–366 (2012)
Wang, T.L., Xu, R.: Some integral inequalities in two independent variables on time scales. J. Math. Inequal. 6(1), 107–118 (2012)
Feng, Q.H., Meng, F.W., Zhang, Y.M.: Some new finite difference inequalities arising in the theory of difference equations. Adv. Differ. Equ. 2011, 21 (2011)
Liu, H.D., Meng, F.W.: Some new generalized Volterra–Fredholm type discrete fractional sum inequalities and their applications. J. Inequal. Appl. 2016, 213 (2016)
Li, L.Z., Meng, F.W., He, L.L.: Some generalized integral inequalities and their applications. J. Math. Anal. Appl. 372(1), 339–349 (2010)
Li, L.Z., Meng, F.W., Ju, P.J.: Some new integral inequalities and their applications in studying the stability of nonlinear integro-differential equations with time delay. J. Math. Anal. Appl. 377(2), 853–862 (2011)
Feng, Q.H., Meng, F.W., Fu, B.S.: Some new generalized Volterra–Fredholm type finite difference inequalities involving four iterated sums. Appl. Math. Comput. 219(15), 8247–8258 (2013)
Acknowledgements
The author is indebted to the anonymous referees for their valuable suggestions and helpful comments which helped improve the paper significantly.
Funding
This research was supported by A Project of Shandong Province Higher Educational Science and Technology Program (China) (Grant No. J14LI09), and the Natural Science Foundation of Shandong Province (China) (Grant No. ZR2018MA018), and the National Natural Science Foundation of China (Grant No. 11671227).
Author information
Authors and Affiliations
Contributions
HDL organized and wrote this paper. Further, he examined all the steps of the proofs in this research. The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that there is no conflict of interests regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, H. On some nonlinear retarded Volterra–Fredholm type integral inequalities on time scales and their applications. J Inequal Appl 2018, 211 (2018). https://doi.org/10.1186/s13660-018-1808-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13660-018-1808-6