Abstract
In this work, we investigate the result of dissipative analysis for Takagi–Sugeno fuzzy Markovian jumping neural networks with impulsive perturbations via delay partition approach. By using the Lyapunov–Krasovskii functional and delay partition approach, we derive a set of delay-dependent sufficient criteria for obtaining the required results. Furthermore, we restate the obtained sufficient conditions in the form of linear matrix inequalities (LMIs), which can be checked by the standard MATLAB LMI tool box. The main advantage of this work is reduced conservatism, which is mainly based on the delay partition approach. Finally, we provide numerical examples with simulations to demonstrate the applicability of the proposed method.
Similar content being viewed by others
1 Introduction
In the last twenty years, neural networks have received increasing consideration because of their applications in various fields such as signal processing, pattern recognition, optimization problems, associative memories, and so on [1, 9, 30, 31, 42, 43]. In particular, the stability theory of neural networks has become an important topic in both theory and practice, since stability is one of the major problems related to neural network dynamic behaviors. Besides, time-delays are frequently encountered in hardware implementation of neural networks, since time-delays are the source of generation of instability and poor performance. Hence the stability analysis of neural networks with time delay have obtained remarkable consideration in recent years [12, 35, 42, 43].
In practice, most of the neural networks are represented by nonlinear models, so it is important and necessary to design an appropriate neural network approach for nonlinear systems. In this relation, the Takagi–Sugeno (T–S) fuzzy model can provide an effective approach for complex nonlinear systems in terms of fuzzy sets and linear input–output variables [21, 24]. The main advantage of this T–S fuzzy model is easy to analyze and design linear systems to nonlinear systems. Thus, many authors extended the T–S fuzzy models to describe different types of neural networks with time delays to establish the stability of the concerned network models [5, 25]. Very recently, Shen et al. [27] obtained an asynchronous state estimation for fuzzy Markovian jumping neural networks with uncertain measurements in a finite time interval. Based on the Lyapunov stability theory and Wirtinger-based integral inequality, sufficient conditions were constructed in [4] to ensure that the state estimation error system is robustly stable along with a guaranteed dissipative performance of T–S fuzzy neural networks.
On the other side, Markovian jump systems (MJSs), as a certain class of switched systems consisting of an indexed family of subsystems and a set of Markovian chains, have received increasing attention [18, 19]. Due to the presence of sudden variation, random component failures, and abrupt environment changes in dynamic systems, by MJSs we can model aircraft control, solar receiver control, manufacturing systems, networked control systems, power systems, and other practical systems [15, 26, 32]. During the past few years, MJSs have been used to various disciplines of science and engineering fields, and a great number of results have been obtained in [2, 3, 10, 12, 13, 29]. Based on a generalized double integral inequality, dissipativity conditions were proposed under the consideration of free-matrix-based integral inequality and Finsler’s lemma approach in [12]. In [13] the authors studied the problem of passivity and dissipativity analysis of Markovian jump neural networks including two types of additive time-varying delays. In [29] the results on dissipativity-based Markovian jump neural networks are established using some generalized integral inequalities. Stability analysis of neural models with Markovian jump limitations and delay constants are derived using reciprocally convex approach in [3].
On the other hand, dissipativity is an important concept of dynamical systems, which is closely related with the intuitive phenomenon of loss or dissipation of energy. Moreover, dissipativity theory gives a framework for the control design and stability analysis of practical control systems under an input–output energy-related consideration. Based on the framework of dissipativity, many problems were investigated for continuous-time neural networks [12, 13, 23, 35, 37, 41] and discrete-time neural networks [17], but there appeared a few works based on the dissipativity concept of T–S fuzzy neural networks [11, 14]. Also, it is well known that impulsive effects are used to express the dynamical models in many areas such as medicine, biology, economics, and telecommunications. Roughly speaking, the states of neural networks often undergo rapid disruption and sudden changes at certain moments of time, which leads to impulsive effects. Thus impulses should be taken into account while studying the dissipativity of neural networks and the corresponding issues studied in the literature [20, 22, 44]. However, up to now, the results of dissipativity analysis of Markovian jumping T–S fuzzy neural networks together with impulsive effects have not yet been reported, which is still an open challenge. All this motivated us to consider a new set of dissipative conditions for fuzzy Markovian jumping neural networks with impulsive control via delay partitioning approach.
The main contributions of this paper are summarized as follows:
-
(i)
Uncertain parameters, Markovian jumping, nonlinearities, time-delay, dissipative conditions and impulsive perturbations are considered in the framework of stability analysis and designing Takagi–Sugeno fuzzy neural networks.
-
(ii)
By employing a proper Lyapunov–Krasovskii functional the asymptotic stability of addressed neural networks is checked via some less conservative stability conditions.
-
(iii)
Some novel uncertain parameters are initially handled in the Lyapunov–Krasovskii functional, which ensures sufficient conditions for asymptotic stability of designed neural networks.
-
(iv)
The importance of the proposed algorithm is illustrated by numerical examples.
2 Problem formulation
Let \(\{r(t),t\geq 0\}\) be a right-continuous Markovian process taking values in the finite space \(S=\{1,2,\ldots,s\}\) with generator \(\varGamma =(\pi _{ij})\) (\(i,j\in S\)) given by
where \(\Delta t\geq 0\), \(\lim_{\Delta t\rightarrow 0}(o(\Delta t)/ \Delta t)=0\), \(\pi _{ij}\geq 0\) for \(j\neq i\) is the transition rate from mode i to mode j at time \(t+\Delta t\), and \(\pi _{ii}=- \sum_{j=1,j\neq i}^{N} \pi _{ij}\).
Consider the neural networks of Markovian jumping parameters with mixed interval time-varying delays of the following form:
where \(i=1,2,\ldots,n\), \(v_{i}(t)\) is the state of the ith neuron, \(a_{i}(r(t))>0\) denotes the rate with which the cell i resets its potential to the resting states when isolated from the other cells and inputs, \(w_{1ij}(r(t))\), \(w_{2ij}(r(t))\) and \(w_{3ij}(r(t))\) are the connection weights at the time t, \(u(t)=[u_{1}(t),u_{2}(t),\ldots, u_{n}(t)]^{T}\) is the external input, \(y(t)=[y_{1}(t), y_{2}(t),\ldots, y_{n}(t)]\) is the output, \(I_{k}(r(t))(\cdot )\) is a constant real matrix at the time moments \(t_{k}\), and \(f_{i}(\cdot )\) stands for the signal function of the ith neuron. In addition, we suppose that the discrete delay \(\tau (t)\) and distributed delay \(d(t)\) satisfy
where \(\tau _{1}\), \(\tau _{2}\), d, \(\mu _{1}\), \(\mu _{2}\) are constants. We consider system (1) together with the initial condition \(v(s)=\psi (s)\), \(s\in [-\max \{\tau _{2},d\},0]\).
Then we rewrite model (1) as
where \(v(t)=[v_{1}(t),v_{2}(t),\ldots, v_{n}(t)]^{T}\), \(A= \operatorname{diag}(a_{1}(r(t)),\ldots,a_{n}(r(t)))\), \(W_{1}=(w_{1ij}(r(t)))_{m \times n}\), \(W_{2}=(w_{2ij}(r(t)))_{m \times n}\), \(W_{3}=(w_{3ij}(r(t)))_{m \times n}\), and \(f(\cdot )=(f _{1}(\cdot ),f_{2}(\cdot ),\ldots,f_{n}(\cdot ))^{T}\).
Let \(v^{*}=(v_{1}^{*},v_{2}^{*},\ldots,v_{n}^{*})\) be the equilibrium points of system (3). We can obtain from (3) that in terms of the transformations \(x(\cdot )=v(\cdot )-v^{*}\) and \(f(x(t))=f(x(t)+v ^{*})-f(v^{*})\), system (3) can be written as
where \(x(t)=[x_{1}(t),x_{2}(t),\ldots, x_{n}(t)]^{T}\), \(f(\cdot )=(f _{1}(\cdot ), f_{2}(\cdot ),\ldots, f_{n}(\cdot ))^{T}\).
Further, we express the Markovian jumping neural network with impulsive control by a T–S fuzzy model. We represent the ith rule of this T–S fuzzy model in the following form:
where \(M_{ij}\) are fuzzy sets, \((v_{1}(t),v_{2}(t),\ldots,v_{j}(t))^{T}\) represents the premise variable vector, \(x(t)\) denotes the state variable, and r is the number of IF–THEN rules. It is known that system (5) has a unique global solution on \(t\geq 0\) with initial values \(\psi _{x} \in \mathcal{C}([-\max \{\tau _{2},d\},0];\mathbb{R}^{n})\). For convenience, \(r(t)=i\), where \(i\in s\), and in the upcoming discussion, we represent the system matrices associated together with the ith mode by \(A_{i}(r(t))=A_{i}\), \(W_{1i}(r(t))=W_{1i}\), \(W_{2i}(r(t))=W_{2i}\), \(W_{3i}(r(t))=W_{3i}\).
Then the state equation is as follows:
where \(\lambda _{i}(v(t)) = \frac{\beta _{i}(v(t))}{\sum_{i=1}^{r} \beta _{i}(v(t))}\), \(\beta _{i}(v(t)) = \prod_{j=1}^{p} M_{ij}(v_{j}(t)) \), and \(M_{ij}(\cdot )\) is the degree of the membership function of \(M_{ij}\). Further, we assume that \(\beta _{i}(v(t)) \geq 0\), \(i = 1,2,\ldots, r\), and \(\sum_{i=1}^{r} \beta _{i}(v(t)) > 0 \) for all \(v(t)\). Therefore \(\lambda _{i}(v(t))\) satisfy \(\lambda _{i}(v(t)) \geq 0\), \(i = 1,\ldots, r\), and \(\sum_{i=1}^{r} \lambda _{i}(v(t)) = 1 \) for any \(v(t)\).
Based on the previous simple transformation, we can equivalently rewrite model (6) as follows:
The following assumptions are needed to prove the required result.
Assumption (H1)
([9])
For all \(j\in {1,2,\ldots,n}\), \(f_{j}(0)=0\), and there exist constants \(F_{j}^{-}\) and \(F_{j}^{+}\) such that
for all \(\alpha _{1},\alpha _{2}\in \mathbb{R}\) and \(\alpha _{1} \neq \alpha _{2}\).
Assumption (H2)
The impulsive times \(t_{k}\) satisfy \(0=t_{0}< t_{1}<\cdots <t_{k} \rightarrow \infty \) and \(\inf_{k\in Z_{+}}\{t_{k}-t_{k-1}\}>0\).
The energy function E associated with system (7) is represented by
where
The following definitions and lemmas are needed to prove our results.
Definition 1
Given some value \(\vartheta >0\), real constant matrices \(\mathcal{Q}=\mathcal{Q}^{T} \) and \(\mathcal{R}=\mathcal{R}^{T}\), and a matrix \(\mathcal{S}\), the considered model (7) is \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative for any \(T \geq 0\). Under the zero initial condition, the following condition is holds:
Definition 2
The proposed neural network model (7) is called passive if there exists a scalar \(\gamma \geq 0\) such that the following inequality holds for all \(t_{f}\geq 0\) under the zero initial condition:
Lemma 2.1
([7])
For any vectors \(\tau (t)\geq 0\) and positive-definite matrix \(Q\in R^{n \times n}\), we have the following inequalities:
where M and N are free weighting matrices of appropriate dimensions, and
3 Main results
In this section, we establish a dissipativity condition for fuzzy impulsive Markovian jumping neural networks (7) with both discrete and distributed time delays. Under a Lyapunov functional and delay fractionizing approach, in the following theorem, we provide a new set of novel delay-dependent dissipative conditions with impulsive perturbations. For presentation convenience, we denote
Theorem 3.1
Under Assumptions (H1) and (H2), for given scalars \(\tau _{1}\), \(\tau _{2}\), d, \(\mu _{1}\), and \(\mu _{2}\), the neural network described by (7) is strictly \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative if there exist positive definite matrices \(P_{1i}\), \(P_{i}\) (\(i=2,\ldots,4\)), Q, R, \(S_{i}\) (\(i=1,2,\ldots,7\)), \(T_{i}\) (\(i=1,2\)), positive diagonal matrices \(U_{1}\), \(U_{2}\), and matrices O, \(L_{i}\), \(M_{i}\), \(V _{i}\) (\(i=1,2\)) of appropriate dimensions such that the following LMIs hold:
and
where
Proof
To obtain dissipativity criteria for the fuzzy Markovian jumping impulsive neural networks (7), we examine the Lyapunov–Krasovskii functional
where
with
For \(t=t_{k}\), we have
Based on the assumptions and conditions, we know that \(I_{ik}\) is a constant matrix at the moment \(t_{k}\) and in the mode i for \(i\in S\), \(k\in N\). So
For \(t\in [t_{k-1}, t_{k}]\), by (17) we obtain that the weak infinitesimal generator \(\mathcal{L}V(t,x(t),i)\) satisfies
Note that
Using Lemma 2.1, we obtain
Applying the lemma in [8] and the Newton–Leibniz formula
we have
Note that
The lemma in [6] gives
Since \(\tau _{2}-\tau (t) \leq \tau _{2}-\tau _{1}\), we have
and thus
Similarly, we have
and
For positive diagonal matrices \(U_{1}\) and \(U_{2}\), it follows from Assumption (H1) that
On the other side, for any matrix O of appropriate dimensions, from system (7) we have
Combining (18)–(37), we can obtain
By the conditions of Theorem 3.1, if \(\zeta (t)\neq 0\), then we have
For \(t\in [t_{k-1},t_{k}]\), in view of (16) and (39), we have
By a similar proof and mathematical induction we can ensure that (40) is true for all i, j, \(r(0)=i_{0}\in S\), \(k\in N\):
It follows from (38) that
Let
Then, applying the lemma in [8] to (43), we obtain the following inequalities:
Using Schur complements on (44)–(45), we obtain the LMIs of Theorem 3.1. Since \(\varPhi _{i} < 0\), we easily get
Integrating this inequality from 0 to T and using the zero initial conditions, we get
for all \(T \geq 0\). Hence, if condition (11) holds, then the proposed model (7) is \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative in the sense of Definition 1. □
Remark 1
The LKF \(V_{3}(t,x(t),i)\) plays a important role in reducing the conservativity of time-varying delay system, whereas in the derivative of \(\dot{V}_{3}(t,x(t),i)\), the cross terms \(-\int _{t- \frac{\tau _{a}}{N}}^{t} \dot{x}^{T}(s)S_{1}\dot{x}(s)\,ds\), \(-\int _{t-\tau (t)}^{t-\tau _{a}} \dot{x}^{T}(s)S_{2}\dot{x}(s)\,ds\), and \(-\int _{t-\tau _{2}}^{t-\tau (t)} \dot{x}^{T}(s)S_{2}\dot{x}(s)\,ds\) are defined as follows:
Finally, to reduce the conservatism of the constructed dissipativity conditions, the convexity of the matrix function for cross term is applied. This treatment involved in our paper is different from the approaches used in [12, 35, 37, 41] and may ensure a better feasible region for dissipativity conditions. Thus, using a tighter bounding of the time derivative of LKF and a low number of slack variables, the considered dissipativity condition is less conservative than that in [12, 35, 37, 41].
Remark 2
Very recently, many researchers endeavor to focus on how to reduce conservatism of dissipativity condition for neural network delay systems. A free-matrix-based integral inequality technique is constructed by using a set of slack variables, which can be solved via convex optimization algorithms [37]. Therefore, some improved dissipativity criteria for delayed neural networks are investigated in [35, 41] using the LKF approach. In [12] the authors developed the Wirtinger double integral inequality, which was used to analyze the dissipativity behavior of continuous-time neural networks involving Markovian jumping parameters under Finsler’s lemma approach. Using a delay fractioning approach, the designed dissipativity condition is much less conservative than those in the existing works, and the derived results can ensure the dissipativity of the proposed delayed neural networks. Hence the delay-partitioning method is widely applied and exposes the potential of reducing the conservatism. However, to the best of authors’ knowledge, dissipativity analysis of fuzzy Markovian jumping neural network with discrete and distributed time varying delays and impulses has not been investigated yet, and it shows the effectiveness of our developed methods.
Remark 3
Consider the Markovian jumping neural network without fuzzy and impulsive effects of the following form:
Due to Theorem 3.1, we obtain a corollary for the dissipativity analysis of Markovian jumping neural networks (48).
Corollary 3.2
Under Assumption (H1) and given scalars \(\tau _{1}\), \(\tau _{2}\), d, \(\mu _{1}\), and \(\mu _{2}\), the neural network model (48) is strictly \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative if there exist positive definite matrices \(P_{1i}\), \(P_{i}\) (\(i=2,\ldots,4\)), Q, R, \(S_{i}\) (\(i=1,2,\ldots,7\)), \(T_{i}\) (\(i=1,2\)), positive diagonal matrices \(U_{1}\), \(U_{2}\), and matrices O, \(L_{i}\), \(M_{i}\), \(V_{i}\) (\(i=1,2\)) of appropriate dimensions such that the following LMIs hold:
Proof
The proof is similar to that of Theorem 3.1 and therefore is omitted. □
Remark 4
When Markovian jumping parameters are not taken, that is, the Markov chain \(\{r(t),t\geq 0\}\) only takes a unique value 1 (i.e., \(S=1\)), then system (48) becomes the following neural network model:
For system (51), we obtain the following corollary by Theorem 3.1 and Corollary 3.2.
Corollary 3.3
Based on Assumption (H1) and given scalars \(\tau _{1}\), \(\tau _{2}\), d, \(\mu _{1}\), and \(\mu _{2}\), the neural network (51) is strictly \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative if there exist positive definite matrices \(P_{1}\), \(P_{i}\) (\(i=2,\ldots,4\)), Q, R, \(S_{i}\) (\(i=1,2,\ldots,7\)), \(T_{i}\) (\(i=1,2\)), positive diagonal matrices \(U_{1}\), \(U_{2}\), and matrices O, \(L_{i}\), \(M_{i}\), \(V_{i}\) (\(i=1,2\)) of appropriate dimensions such that the following LMIs hold:
and
where
Proof
To prove the dissipativity criteria for the recurrent neural networks (51), we define the following Lyapunov–Krasovskii functional:
where
Then, using the same proof as in Theorem 3.1, we get the result. □
Remark 5
If the distributed delay is not considered in system (51), then the recurrent neural network is rewritten as
The dissipative condition of delayed neural network (55) is constructed as follows.
Corollary 3.4
Under Assumption (H1) and given scalars \(\tau _{1}\), \(\tau _{2}\), and \(\mu _{1}\), the neural network (55) is \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative if there exist positive definite matrices \(P_{1}\), \(P_{i}\) (\(i=2,\ldots,3\)), Q, R, \(S_{i}\) (\(i=1,2,\ldots,6\)), \(T _{i}\) (\(i=1,2\)), positive diagonal matrices \(U_{1}\), \(U_{2}\), and matrices O, \(L_{i}\), \(M_{i}\), \(V_{i}\) (\(i=1,2\)) of appropriate dimensions such that the following LMIs hold:
and
where
and the other elements are as in Corollary 3.3.
Proof
This proof is similar to that of Corollary 3.3 and therefore is omitted. □
Remark 6
As a particular case of dissipativity, we get passivity criteria for system (55) by taking \(\mathcal{Q} = 0\), \(\mathcal{S} = I\), and \(\mathcal{R} =2\gamma I\) in Corollary 3.4. The following corollary can obtained from Corollary 3.4 and describes the passivity conditions for system (55).
Corollary 3.5
Under Assumption (H1) and given scalars \(\tau _{1}\), \(\tau _{2}\), and \(\mu _{1}\), the neural network (55) is passive if there exist positive definite matrices \(P_{1}\), \(P_{i}\) (\(i=2,\ldots,3\)), Q, R, \(S _{i}\) (\(i=1,2,\ldots,6\)), \(T_{i}\) (\(i=1,2\)), positive diagonal matrices \(U_{1}\), \(U_{2}\), and matrices O, \(L_{i}\), \(M_{i}\), \(V_{i}\) (\(i=1,2\)) of appropriate dimensions such that the following LMIs hold:
and
where
Proof
The proof directly follows from Corollary 3.4. □
4 Numerical examples
In this section, we analyze several numerical examples to exploit the effectiveness of the proposed methods.
Example 1
Consider the fuzzy impulsive neural network (7) with two-mode Markovian jumping process with the following parameters:
-
Mode 1:
-
Mode 2:
We choose
We consider the activation functions \(f_{1}(x) = f_{2}(x) = \tanh (x)\). Assumption (H1) is satisfied with \(F_{1}^{-}=0\), \(F_{1}^{+}=1\), \(F _{2}^{-}=0\), and \(F_{2}^{+}=1\). Thus
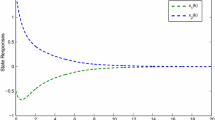
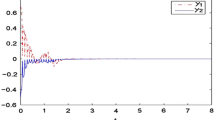
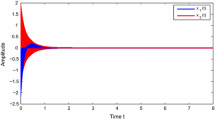
Let \(r(t)\) be a right-continuous Markov chain taking values in \(S = \{1, 2\}\) with generator , and let the membership functions for rules 1 and 2 be \(\mu _{1}(\theta (t))=\sin ^{2}(x_{1}-0.5)\) and \(\mu _{2}(\theta (t))= \cos ^{2}(x_{1}-0.5)\). Then via the Matlab LMI control toolbox, for \(N=2\), we can see that the LMIs given in Theorem 3.1 are feasible. Thus we observe from Theorem 3.1 that the neural network (7) subject to leakage delays and impulsive effect is dissipative. The simulation results for the state responses of system (7) with two Markovian jumping modes (\(i = 1,2\)) are given in Fig. 1. Also, Fig. 2 illustrates the mode transition rates. In Table 1, we mention the maximum allowable upper bound for delays \(\tau _{2}=d\) with different values of \(\mu _{1}\), \(\mu _{2}\).
Example 2
Consider the Markovian jumping neural network (48) with parameters
and the activation function \(f_{1}(x) = f_{2}(x) = \tanh (x)\). Choosing \(N=2\), \(\mu _{1}=0.5\), and \(\mu _{2}=0.1\) and using Matlab LMI toolbox and Corollary 3.2, we obtained the maximum allowable upper bound of \(\tau _{2}\) and d for various values of \(\tau _{1}\) listed in Table 2. This implies that the Markovian jumping neural network (48) is dissipative in the sense of Definition 1.
Example 3
Consider the neural network (51) with the following parameters:
For this neural network, we would like to have the dissipativity for the allowable maximum time delay value of \(\tau _{2}\) and d for different values of μ and given \(\tau _{1}\). We can see from Table 3 that the condition presented in Corollary 3.3 still ensures the dissipativity of this model. The results in [12, 35, 37, 41] are not applicable to this system as the time-varying distributed delay is involved in this system.
Example 4
Consider the neural networks (55) with the following coefficient matrices:
Here we choose \(F_{1}^{-}=-0.1\), \(F_{1}^{+}=0.9\), \(F_{2}^{-}=-0.1\), and \(F_{2}^{+}=0.9\). Thus
We assume that \(\tau _{1}=0\) and \(\tau _{2}=0.4\) for different values of \(\mu _{1}\). The optimum dissipativity performances γ are calculated by the methods in Corollary 3.4 and are listed in Table 4. We can observe that our considered dissipativity condition provides a less conservative result in comparison to the existing works [12, 35, 37, 41].
Example 5
Consider the neural networks (55) with the following parameters:
Moreover, the activation function is chosen as \(g_{i}(x_{i})=0.5( \vert x_{i}+1 \vert - \vert x_{i}-1 \vert )\), \(i=1,2\). The allowable upper bounds of \(\tau _{2}\) when \(\tau _{1}=0\) for various values of \(\mu _{1}\) obtained by Corollary 3.5 are listed in Table 5. We easily see that the obtained passivity-based results in our work are more general than the others [25, 36, 39, 42].
Example 6
Consider the neural networks (55), with the following parameters:
\(F_{1}^{-}=F_{2}^{-}=0\), and \(F_{1}^{+}=F_{2}^{+}=1\). For different values of \(\mu _{1}\), the allowable upper bounds of \(\tau _{2}\) when \(\tau _{1}=0\) computed by Corollary 3.5 and with the results presented in [16, 35, 37, 38, 40, 41] are listed in Table 6.
Example 7
Consider the neural networks (55) with the following parameters studied in [13, 28, 30, 33, 34].
\(f_{1}(x) = 0.3\tanh (x)\), \(f_{2}(x) = 0.8 \tanh (x)\), \(F_{1}^{-}=F_{2} ^{-}=0\), \(F_{1}^{+}=0.3\), and \(F_{2}^{+}=0.8\). By using Corollary 3.5 and solving MATLAB LMI tool box the corresponding results for the maximum allowable upper bounds of \(\tau _{2}\) for different values of \(\mu _{1}\) when \(\tau _{1}=0\) are computed and listed in Table 7. We can observe from Table 7 that the passivity condition proposed in this paper provides less conservative results than the others [13, 28, 30, 33, 34].
5 Conclusion
In this paper, we have studied the problem of dissipative conditions for Takagi–Sugeno fuzzy Markovian jumping neural networks with impulsive perturbations using the delay partition method. By constructing a proper LKF and LMI approach together with delay fractioning approach, we have established a set of sufficient conditions ensuring that the considered fuzzy Markovian neural networks are \((\mathcal{Q}, \mathcal{S}, \mathcal{R})\)–ϑ-dissipative. Finally, several numerical examples are given to illustrate the effectiveness of the proposed dissipative theory. Moreover, our results show that the developed method yields less conservative results than some other works. Furthermore, the problem of finite-time extended dissipative conditions for stochastic T–S fuzzy singular Markovian jump systems with randomly occurring uncertainties and time delay using the delay portioning approach is an untreated work and will be the topic of our future work.
References
Bao, H., Park, J.H., Cao, J.: Exponential synchronization of coupled stochastic memristor-based neural networks with time-varying probabilistic delay coupling and impulsive delay. IEEE Trans. Neural Netw. Learn. Syst. 27, 190–201 (2016)
Boyd, S., Ghaoui, L.E., Feron, E., Balakrishnan, V.: Linear Matrix Inequalities in Systems and Control Theory. SIAM, Philadelphia (1994)
Chen, G., Xia, J., Zhuang, G.: Delay-dependent stability and dissipativity analysis of generalized neural networks with Markovian jump parameters and two delay components. J. Franklin Inst. 353, 2137–2158 (2016)
Choi, H.D., Ahn, C.K., Shi, P., Lim, M.T., Song, M.K.: \(L_{2}\)–\(L_{\infty }\) filtering for Takagi–Sugeno fuzzy neural networks based on Wirtinger-type inequalities. Neurocomputing 153, 117–125 (2015)
Jian, J., Wan, P.: Global exponential convergence of fuzzy complex-valued neural networks with time-varying delays and impulsive effects. Fuzzy Sets Syst. 338, 23–39 (2018)
Kwon, O.M., Park, J.H., Lee, S.M., Cha, E.J.: New augmented Lyapunov–Krasovskii functional approach to stability analysis of neural networks with time-varying delays. Nonlinear Dyn. 76, 221–236 (2014)
Lakshmanan, S., Senthilkumar, T., Balasubramaniam, P.: Improved results on robust stability of neutral systems with mixed time-varying delays and nonlinear perturbations. Appl. Math. Model. 35, 5355–5368 (2011)
Liu, J., Gu, Z., Tian, E.: A new approach to \(H_{\infty }\) filtering for linear time-delay systems. J. Franklin Inst. 349, 184–200 (2012)
Liu, Y., Wang, Z., Liu, X.: Global exponential stability of generalized recurrent neural networks with discrete and distributed delays. Neural Netw. 19(5), 667–675 (2006)
Maharajan, C., Raja, R., Cao, J., Ravi, G., Rajchakit, G.: Global exponential stability of Markovian jumping stochastic impulsive uncertain BAM neural networks with leakage, mixed time delays, and α-inverse Hölder activation functions. Adv. Differ. Equ. 2018, 113 (2018)
Muralisankar, S., Gopalakrishnan, N., Balasubramaniam, P.: An LMI approach for global robust dissipativity analysis of T–S fuzzy neural networks with interval time-varying delays. Expert Syst. Appl. 39, 3345–3355 (2012)
Nagamani, G., Joo, Y.H., Radhika, T.: Delay-dependent dissipativity criteria for Markovian jump neural networks with random delays and incomplete transition probabilities. Nonlinear Dyn. 91, 2503–2522 (2018)
Nagamani, G., Radhika, T.: Dissipativity and passivity analysis of Markovian jump neural networks with two additive time-varying delays. Neural Process. Lett. 44, 571–592 (2016)
Pan, Y., Zhou, Q., Lu, Q., Wu, C.: New dissipativity condition of stochastic fuzzy neural networks with discrete and distributed time-varying delays. Neurocomputing 162, 267–272 (2015)
Pandiselvi, S., Raja, R., Zhu, Q., Rajchakit, G.: A state estimation \(H_{\infty }\) issue for discrete-time stochastic impulsive genetic regulatory networks in the presence of leakage, multiple delays and Markovian jumping parameters. J. Franklin Inst. 355, 2735–2761 (2018)
Radhika, T., Nagamani, G., Zhu, Q., Ramasamy, S., Saravanakumar, R.: Further results on dissipativity analysis for Markovian jump neural networks with randomly occurring uncertainties and leakage delays. Neural Comput. Appl. 23, 1–15 (2018)
Raja, R., Karthik Raja, U., Samidurai, R., Leelamani, A.: Dissipativity of discrete-time BAM stochastic neural networks with Markovian switching and impulses. J. Franklin Inst. 350, 3217–3247 (2013)
Raja, R., Karthik Raja, U., Samidurai, R., Leelamani, A.: Improved stochastic dissipativity of uncertain discrete-time neural networks with multiple delays and impulses. Int. J. Mach. Learn. Cybern. 6, 289–305 (2015)
Raja, R., Sakthivel, R., Marshal Anthoni, S.: Dissipativity of discrete-time BAM stochastic neural networks with Markovian switching and impulses. J. Franklin Inst. 350, 3217–3247 (2011)
Raja, R., Zhu, Q., Senthilraj, S., Samidurai, R.: Improved stability analysis of uncertain neutral type neural networks with leakage delays and impulsive effects. Appl. Math. Comput. 266, 1050–1069 (2015)
Sakthivel, R., Saravanakumar, T., Ma, Y.-K., Marshal Anthoni, S.: Finite-time resilient reliable sampled-data control for fuzzy systems with randomly occurring uncertainties. Fuzzy Sets Syst. 329, 1–18 (2107)
Sakthivel, R., Saravanakumar, T., Sathishkumar, M.: Non-fragile reliable control synthesis of the sugarcane borer. IET Syst. Biol. 11, 139–143 (2017)
Saravanakumar, T., Sakthivel, R., Selvaraj, P., Marshal Anthoni, S.: Dissipative analysis for discrete-time systems via fault-tolerant control against actuator failures. Complexity 21, 579–592 (2016)
Senan, S.: An analysis of global stability of Takagi–Sugeno fuzzy Cohen–Grossberg neural networks with time delays. Neural Process. Lett. 10, 1–12 (2018)
Senthilraj, S., Raja, R., Zhu, Q., Samidurai, R.: Effects of leakage delays and impulsive control in dissipativity analysis of Takagi–Sugeno fuzzy neural networks with randomly occurring uncertainties. J. Franklin Inst. 354, 3574–3593 (2017)
Senthilraj, S., Raja, R., Zhu, Q., Samidurai, R., Yao, Z.: Delay-interval-dependent passivity analysis of stochastic neural networks with Markovian jumping parameters and time delay in the leakage term. Nonlinear Anal. Hybrid Syst. 22, 262–275 (2016)
Shen, H., Xiang, M., Huo, S., Wu, Z.G., Park, J.H.: Finite-time \(H_{\infty }\) asynchronous state estimation for discrete-time fuzzy Markov jump neural networks with uncertain measurements. Fuzzy Sets Syst. 356, 113–128 (2019)
Shi, K., Zhong, S., Zhu, H., Liu, X., Zeng, Y.: New delay-dependent stability criteria for neutral-type neural networks with mixed random time-varying delays. Neurocomputing 168, 896–907 (2015)
Shu, Y., Liu, X.G., Qiu, S., Wang, F.: Dissipativity analysis for generalized neural networks with Markovian jump parameters and time-varying delay. Nonlinear Dyn. 89, 2125–2140 (2017)
Song, Q.: Exponential stability of recurrent neural networks with both time-varying delays and general activation functions via LMI approach. Neurocomputing 71, 2823–2830 (2008)
Song, Q., Yan, H., Zhao, Z., Liu, Y.: Global exponential stability of complex-valued neural networks with both time-varying delays and impulsive effects. Neural Netw. 79, 108–116 (2016)
Sowmiya, C., Raja, R., Cao, J., Rajchakit, G., Alsaedi, A.: Enhanced robust finite-time passivity for Markovian jumping discrete-time BAM neural networks with leakage delay. Adv. Differ. Equ. 2017, 318 (2017)
Sun, J., Liu, G.P., Chen, J., Rees, D.: Improved stability criteria for neural networks with time-varying delay. Phys. Lett. A 373, 342–348 (2009)
Tian, J., Zhong, S.: Improved delay-dependent stability criterion for neural networks with time-varying delay. Appl. Math. Comput. 217, 10278–10288 (2011)
Wu, Z., Park, J., Su, H., Chu, J.: Robust dissipativity analysis of neural networks with time-varying delay and randomly occurring uncertainties. Nonlinear Dyn. 69, 1323–1332 (2012)
Xu, S., Zheng, W.X., Zou, Y.: Passivity analysis of neural networks with time-varying delays. IEEE Trans. Circuits Syst. II, Express Briefs 56(4), 325–329 (2009)
Zeng, H.B., He, Y., Shi, P., Wu, M., Xiao, S.P.: Dissipativity analysis of neural networks with time-varying delays. Neurocomputing 168, 741–746 (2015)
Zeng, H.B., He, Y., Wu, M., Xiao, H.Q.: Improved conditions for passivity of neural networks with a time-varying delay. IEEE Trans. Cybern. 44, 785–792 (2014)
Zeng, H.B., He, Y., Wu, M., Xiao, S.P.: Passivity analysis for neural networks with a time-varying delay. Neurocomputing 74, 730–734 (2011)
Zeng, H.B., Park, J.H., Shen, H.: Robust passivity analysis of neural networks with discrete and distributed delays. Neurocomputing 149, 1092–1097 (2015)
Zeng, H.B., Park, J.H., Xia, J.W.: Further results on dissipativity analysis of neural networks with time-varying delay and randomly occurring uncertainties. Nonlinear Dyn. 79, 83–91 (2015)
Zhang, B., Xu, S., Lam, J.: Relaxed passivity conditions for neural networks with time-varying delays. Neurocomputing 142, 299–306 (2014)
Zhang, C.K., He, Y., Jiang, L., Lin, W.J., Wu, M.: Delay-dependent stability analysis of neural networks with time-varying delay: a generalized free-weighting-matrix approach. Appl. Math. Comput. 294, 102–120 (2017)
Zhu, J., Sun, J.: Stability of quaternion-valued impulsive delay difference systems and its application to neural networks. Neurocomputing 284, 63–69 (2018)
Acknowledgements
The authors express their sincere gratitude to the editors for the careful reading of the original manuscript.
Availability of data and materials
Data sharing not applicable to this paper as no data sets were generated or analyzed during the current study.
Funding
This work was jointly supported by the National Natural Science Foundation of China (61773217) and the Construct Program of the Key Discipline in Hunan Province.
Author information
Authors and Affiliations
Contributions
All three authors contributed equally to this work. They all read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Nirmala, V.J., Saravanakumar, T. & Zhu, Q. Dissipative criteria for Takagi–Sugeno fuzzy Markovian jumping neural networks with impulsive perturbations using delay partitioning approach. Adv Differ Equ 2019, 140 (2019). https://doi.org/10.1186/s13662-019-2085-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2085-5