Abstract
In this paper, considering the impact of stochastic environment noise on infection rate, a stochastic SIS epidemic model with nonlinear incidence rate is proposed and analyzed. Firstly, for the corresponding deterministic system, the threshold which determines the extinction or permanence of the disease is obtained by analyzing the stability of the equilibria. Then, for the stochastic system, the global dynamics is investigated by using the theory of stochastic differential equations; especially the threshold dynamics is explored when the stochastic environment noise is small. The results show that the condition for the epidemic disease to go to extinction in the stochastic system is weaker than that of the deterministic system, which implies that stochastic noise has a significant impact on the spread of infectious diseases and the larger stochastic noise is conducive to controlling the epidemic diseases. To illustrate this phenomenon, we give some computer simulations with different intensities of the stochastic noise.
Similar content being viewed by others
1 Introduction
Infectious diseases are the public enemy of mankind and have brought great catastrophe to mankind. Authors were committed to finding ways to control infectious diseases from pathology, epidemiology, culture and other aspects. The mathematical modeling method is considered as an effective method to understand the development and evolution of variables [1,2,3,4,5,6,7,8,9,10,11,12,13]. Mathematical models have been used to study the spread and evolution of infectious diseases in the human population. For example, Bernoulli in 1760 proposed the first mathematical model in epidemiology, for studying the spread and inoculation of smallpox. By classifying human populations into three separate categories: the susceptible S, the infected I and the removed R, Kermack and McKendrick [14] in 1927 proposed a well-known compartmental model. It is assumed in the model that the susceptible class can transform into the infective class through the contact with infected persons, and the infectives can be recovered through treatment so that have permanent immunity. Therefore, it is now well known as the SIR model, which has been widely studied by [15,16,17,18,19,20]. However, some research showed that some diseases, such as influenza [21], viral diarrhea [22] and hand, foot and mouth disease [23], the immunity gained after an illness is temporary, then part of the recovered can transfer to the susceptible population again, this model is known as the SIS model [24].
Many researchers pay special attention to the incidence rate of infectious diseases. A nonlinear incidence rate plays an important role in the evolution of infectious diseases, because epidemic models described by nonlinear incidence rates may be more suitable and realistic, which also exhibit much richer dynamics. For example, the standard incidence rate \(\beta \frac{SI}{N}\) or the bilinear incidence rate \(\beta SI\) is proposed and used in reference [25,26,27,28]. And saturation infection rate \(\frac{\beta SI}{1+\alpha I}\) is used in reference [29]. A special non-monotone with the form \(\beta S^{p} I^{q}\) is proposed and investigated by Severo [30], Liu et al. [31], Hethcote et al. [32], and Y. Li and Muldowney [33]. About more general forms of incidence functions, please see Pugliese [34], Thieme [35], Korobeinikov [36], Ruan and Wang [37] and Huang [38].
Motivated by the previous work, we pay special attention to the following model which is an improved case of Liu et al. [31]:
where Λ is the recruitment rate of the population including the birth and migration. α is mortality due to illness. p is positive integer. The biological significance of other parameters please see Liu et al. [31].
Generally in the dynamic modeling of infectious diseases, we will first consider a deterministic model, however, considering the real world is filled with random and unpredictable, using stochastic model to model the dynamic of infectious diseases is more practical. Different stochastic disturbance approaches have been introduced into epidemic models. On the whole, there are four common random stochastic approaches. The first one is to introduce the parameters’ disturbance to a deterministic system (see, e.g., [39,40,41,42,43,44,45,46,47]), the second one is to investigate the stochasticity by using the method of time Markov chains (see, e.g., [48,49,50,51,52]). The third one is to consider Lévy jump noise (see, e.g., [53,54,55]). The fourth one is to study stochastic disturbance around the positive equilibria of a deterministic system (see, e.g., [56, 57]). Similar ideas have also been used in other modeling and analysis, for example [58,59,60,61,62].
In the spread progress of infectious diseases, the transmission coefficient is often subject to interference from the environment. Mathematically, this interference from the environment can be described as a standard Brownian motion simply. In this paper, based on model (1), we assume that the nonlinear incidence rate is perturbed by white noise so that
where \(B(t)\) is a standard Brownian motion with intensity \(\sigma>0\). Then the resultant model takes the following form:
Our main objective in the rest of present paper is to attempt to establish the threshold dynamics of system (3) similar to the deterministic system.
2 Preliminaries
Throughout this paper, we let \(\mathbb{R}^{d}\): the d-dimensional Euclidean space. \(\mathbb{R}^{d}_{+}:= \{x\in\mathbb{R}^{d}: x_{i} > 0, 1\leq i\leq d\}\), i.e. the positive cone.
Let \((\varOmega,\mathcal{F}, \mathcal{P})\) be the complete probability space adapted to the filtration \(\{\mathcal{F}\}_{t\geq0}\) and \(\{B_{t}\} _{t\geq0}\) is a one-dimensional Brownian motion defined on it. \(\mathcal {L}^{1}(\mathbb{R}_{+};\mathbb{R}^{d})\) is the family of all \(\mathbb {R}^{d}\)-valued measurable \(\{\mathcal{F}_{t}\}\)-adapted processes \(f=\{f(t)\}_{t\geq0}\) and
Let \(C^{2,1}(\mathbb{R}^{d} \times\mathbb{R}_{+};\mathbb{R})\) denote the family of all real-valued functions \(V(x,t)\) defined on \(\mathbb{R}^{d} \times\mathbb{R}_{+}\) such that they are twice continuously differentiable in x and once in t. We set
Clearly, when \(V\in C^{2,1}(R\times R_{+}; R)\), we have \(V_{x}=\frac {\partial V}{\partial x}, V_{xx}=\frac{\partial^{2} V}{\partial x^{2}}\).
Lemma 2.1
(The one-dimensional Itô’s formula [63])
Let \(x(t)\) be an Itô’s process on \(t\geq0\) with the stochastic differential
where \(f\in\mathcal{L}^{1}(\mathbb{R}_{+};\mathbb{R})\) and \(g\in\mathcal {L}^{2}(\mathbb{R}_{+};\mathbb{R})\). Let \(V\in C^{2,1}(\mathbb{R}^{d} \times \mathbb{R}_{+};\mathbb{R})\). Then \(V(x(t),t)\) is again an Itô’s process with the stochastic differential given by
Let f be an integrable function on \([0,+\infty)\), define \(\langle f(t)\rangle=\frac{1}{t}\int_{0}^{t}f(\theta)\,d\theta\). Then we have the following definition [43].
Definition 2.1
For system (3),
-
(i)
the diseases \(I(t)\) is said to be extinctive if \(\lim_{t\rightarrow+\infty}I(t)=0\);
-
(ii)
the diseases \(I(t)\) is said to be permanent in mean if there exists a positive constant λ such that \(\liminf_{t\rightarrow+\infty}\langle I(t)\rangle\geq\lambda\).
By using the methods from Lahrouz and Omari [42], we can prove the following lemma.
Lemma 2.2
For any initial value \((S_{0}, I_{0})\in R^{2}_{+}\), there exists a unique solution \((S(t), I(t))\) to system (3) on \(t\geq0\), and the solution will remain in \(R^{2}_{+}\) with probability one, namely, \((S(t), I(t))\in R^{2}_{+}\) for all \(t\geq0\) almost surely.
Proof
Firstly, we know that, for any initial value \((S_{0}, I_{0})\in R^{2}_{+}\), because the coefficients of system (3) are locally Lipschitz continuous, then there exists a unique local solution on \([0,\tau _{\epsilon})\) where \(\tau_{\epsilon}\) is the explosion time. To prove this solution is global, we need to show \(\tau_{\epsilon}=\infty\) almost surely. To do it, let \(\epsilon_{0}>0\) such that \(S_{0} > \epsilon_{0}, I_{0} >\epsilon_{0}\). For any positive ϵ, which satisfies \(\epsilon\leq\epsilon_{0}\), define the stopping time \(\tau _{\epsilon}\) by
with the traditional setting \(\inf\varnothing= \infty\), where ∅ denotes the empty set. Clearly, \(\tau_{\epsilon}\) is increasing as \(\epsilon\rightarrow0\). Set \(\tau_{0} = \lim_{\epsilon\rightarrow0}\), then \(\tau_{0}\leq\tau_{\epsilon}\) a.s, hence we only need to prove \(\tau_{0} =\infty\) a.s. Otherwise, then there exist a pair of constants \(T > 0\) and \(\delta\in(0, 1)\) such that \(P\{\tau_{0}\leq T\} > \delta\). Hence there exists a positive constant \(\epsilon_{1}\leq\epsilon_{0}\) such that \(P\{\tau_{0}\leq T\} > \delta\) for any positive \(\epsilon\leq\epsilon_{1}\).
Define \(C^{2}\) function \(N: R^{2}_{+}\rightarrow R^{2}_{+}\) by \(N(t) = S(t)+I(t)\). Obviously, \(N(t)\) satisfies
After a simple calculation, it easy to see that, for all \(t <\tau _{\epsilon}\),
Define a function \(V: R^{2}_{+}\rightarrow R^{2}_{+}\) by
Obviously, V is positive definite. Using Itô’s formula, we get
where
Then we have
Thus,
Integrating both sides from 0 to \(\tau_{\epsilon}\wedge T\), and then taking expectations, yields
Set \(\varOmega_{e} = \{\tau_{e}\leq T\}\) for any positive \(\epsilon\leq \epsilon_{1}\) and then \(P(\varOmega_{E}) >\delta\). Note that, for every \(\omega \in\varOmega_{\epsilon}\), there is at least one of \(S(\tau_{\epsilon}, \omega), I(\tau_{\epsilon}, \omega)\) equals ϵ, then
Thus,
where \(I_{\varOmega_{\epsilon}}\) is the indicator function of \(\varOmega_{e}\). Letting \(\epsilon\rightarrow0\) leads to the contradiction \(\infty> V (S_{0}, I_{0}) + C_{2}T =\infty\). Thus, we must have \(\tau_{\epsilon}=\infty\) almost surely. The proof of Lemma 2.2 is completed. □
By using the methods from Ji et al. [64], we can prove the following lemma and remark.
Lemma 2.3
For any initial value \((S_{0}, I_{0})\in\overline{R}^{2}_{+}\), there exists a unique solution \((S(t), I(t))\) to system (3) on \(t\geq0\), and the solution will remain in \(\overline{R}^{2}_{+}\) with probability 1, namely, \((S(t), I(t))\in\overline{R}^{2}_{+}\) for all \(t\geq0\) a.s.
Remark 2.1
In fact, from system (3), we have
Then we have
If \(S_{0}+I_{0}\leq\frac{\varLambda}{\mu}\) then \(S(t)+I(t)\leq\frac{\varLambda }{\mu}\). Therefore, the region
is an invariant set, then, from now on, we always assume the initial value \((S(0),I(0))\in\varGamma\).
By using the methods from Meng et al. [43], we can prove the following lemma.
Lemma 2.4
Let \((S(t), I(t))\) be a solution of system (3) with initial value \((S(0), I(0))\in R^{2}_{+}\). Then
Proof
Let \(Z(t)=\int_{0}^{t}\sigma S^{p}(\tau)\,dB(\tau)\) and \(\theta>2\). By the Burkholder–Davis–Gundy inequality in [63] and Lemma 2.1, we have
where \(M_{\theta}=\sigma^{\theta} (\frac{\varLambda}{\mu} )^{p\theta}\). Then, for any \(0<\varepsilon<\frac{\theta}{2}-1\),
By Doob’s martingale inequality and the Borel–Cantelli lemma in [63], for almost all \(\omega\in\varOmega\), we get
holds for all but finitely many k. Thus, there exists a positive \(k_{0}(\omega)\), for almost all \(\omega\in \varOmega\), for which (4) holds when \(k\geq k_{0}(\omega)\). Hence, if \(k\geq k_{0}(\omega)\) and \(k\delta\leq t\leq(k+1)\delta\), then, for almost all \(\omega\in\varOmega\),
So, we have
Then, for the above ε, there exist a constant \(T(\omega)\) and a set \(\varOmega_{\epsilon}\), such that \(\mathbb{P}(\varOmega_{\epsilon })\geq1-\epsilon\) and for \(t\geq T(\omega)\), \(\omega\in\varOmega_{\epsilon}\),
Then we have
i.e.
This completes the proof of Lemma 2.4. □
3 Dynamics of the deterministic system
It is easy to see that the equilibrium of system (1) satisfies
resulting at most two equilibria: \(E_{0} (\frac{\varLambda}{\mu}, 0 ), E^{*} (S^{*}, I^{*} )\), where
From the expressions of \(I^{*}\), we know if
system (1) has unique positive equilibrium \(E^{*}\). Regarding the stability of these equilibria, we have the following theorem.
Theorem 3.1
Define
Then, for system (1), we have
-
(i)
if \(\mathcal{R}<1\), it has a unique stable ‘diseases-extinction’ equilibrium point \(E_{0}\), which implies the extinction of the diseases;
-
(ii)
if \(\mathcal{R}>1\), it has a stable positive equilibrium \(E^{*}\), which implies the permanence of the disease.
Proof
The Jacobian of the linearization system of the system (1) at \(E_{0}\) gives
which has the following eigenvalues:
Since \(\mu>0\), resulting \(\lambda_{1}<0\), according to the stability theory, \(E_{0}\) is stable if and only if \(\lambda_{2}<0\), i.e., \(\mathcal{R}<1\).
At \(E^{*}\) the Jacobian takes the form of
and the eigenvalues of matrix \(J_{1}\) satisfy
This implies \(\lambda_{1}\) and \(\lambda_{2}\) have negative real parts. Thus the equilibrium \(E^{*}\) is stable. □
4 Dynamics of the stochastic system
In this section, we try to explore the conditions leading to the extinction and persistence of the infectious disease.
4.1 Extinction
Let us introduce
where \(\mathcal{R}\) is given as in (6). Then we have the following.
Theorem 4.1
For system (3),
-
(i)
If \(\sigma^{2}>\max\{\beta (\frac{\mu}{\varLambda} )^{p},\frac{\beta^{2}}{2(\mu+\alpha+\gamma)}\}\), then the infectious disease of system (3) goes to extinction almost surely.
-
(ii)
If \(\sigma^{2}<\beta (\frac{\mu}{\varLambda} )^{p}\), then the infectious disease of system (3) goes to extinction almost surely for \(\mathcal{R}^{*}<1\).
Moreover, \(\lim_{t\rightarrow+\infty}S(t)=\frac{\varLambda}{\mu}\), almost surely.
Proof
Let \((S(t), I(t))\) be a solution of system (3) with initial value \((S(0), I(0)) \in R^{2}_{+}\). Applying Itô’s formula to system (3) results in
Integrating both sides of (7) from 0 to t gives
where
known as the local continuous martingale and \(M(0)=0\).
Consider the quadratic function
It is easy to verify that when \(\sigma^{2}>\sigma_{1}=\beta (\frac{\mu }{\varLambda} )^{p}\), \(g(z)\) reaches its maximum value \(g_{\max}=\frac {\beta^{2}}{2\sigma^{2}}\) at \(z = \frac{\beta}{\sigma^{2}}\); and when \(\sigma ^{2}<\sigma_{1}\), its maximum value \(g_{\max}= (\frac{\varLambda}{\mu} )^{p} (\beta-\frac{\sigma^{2}}{2} (\frac{\varLambda}{\mu} )^{p} )\) is achieved at \(z = (\frac{\varLambda}{\mu} )^{p}\). Then in (8), noticing \(S^{p}(t)\in [0, (\frac {\varLambda}{\mu} )^{p} ]\), we have two cases to discuss, depending on whether \(\sigma^{2}>\beta (\frac{\mu}{\varLambda} )^{p}\).
Case I: \(\sigma^{2}>\beta (\frac{\mu}{\varLambda} )^{p}\). In this case, we can easily see from (8) that
Dividing both sides of (10) by \(t>0\), we have
and by Lemma 2.4, we have
almost surely. Then taking the limit superior on both sides of (11) leads to
almost surely, when \(\sigma^{2}>\max\{\beta (\frac{\mu}{\varLambda} )^{p},\frac{\beta^{2}}{2(\mu+\alpha+\gamma)}\}\), which implies \(\lim_{t\rightarrow+\infty}I(t)=0\).
Case II: \(\sigma^{2}<\beta (\frac{\mu}{\varLambda} )^{p}\). In this case, we can similarly have
Dividing both sides of (12) by \(t>0\), we have
Taking the superior limit on both sides of (13) leads to
almost surely. Then when \(\mathcal{R}^{*}<1\), we have
almost surely, which implies \(\lim_{t\rightarrow+\infty}I(t)=0\).
Next, we prove the last conclusion. Given \(0<\varepsilon\ll1\), since \(\lim_{t\rightarrow+\infty}I(t)=0\), we have \(0< I(t)<\varepsilon\) for t large enough. By the first equation of system (3), we have
Then when \(\varepsilon\rightarrow0\) we have
almost surely. On the other hand from Remark 2.1, we have
almost surely. Let \(\varepsilon\rightarrow0\). Then one has
almost surely. From (14) and (15), we have
almost surely. This completes the proof of Theorem 4.1. □
Remark 4.1
Theorem 4.1 shows that when \(\mathcal{R}^{*}<1\), the infectious disease of system (3) dies out almost surely, that is to say, large white noise stochastic disturbance can lead to epidemic extinction.
Remark 4.2
Note that \(\mathcal{R}^{*}=\mathcal{R}-\frac{\sigma^{2} (\frac{\varLambda }{\mu} )^{2p}}{2(\mu+\alpha+\gamma)}\). Obviously, \(\mathcal{R}<1\) leads to \(\mathcal{R}^{*}<1\), while the other side is not true. This implies that the condition for \(I(t)\) going to extinction in the deterministic system is stronger than its stochastic counterpart due to the effect of the white noise disturbance.
4.2 Permanence in mean
Integrating from 0 to t and dividing by t on both sides of system (3) yields
Then one can get
Applying Itô’s formula gives
Integrating from 0 to t and dividing by t on both sides of (16) yields
by using Hölder’s inequality, we have
In (18), let \(a=\frac{\varLambda}{\mu}-\frac{\varTheta(t)}{\mu}, b=\frac{\mu+\alpha}{\mu}\langle I(t)\rangle\). Then according the number p being odd, there are two cases we should discuss.
Case I. When p is an even number, let \(p=2n, n\in N\). Then we have
Case II. When p is an odd number, let \(p=2n-1,n\in N\). Then
where \(b=\frac{\mu+\alpha}{\mu}\langle I(t)\rangle<\frac{\varLambda(\mu +\alpha)}{\mu^{2} }\) is used. Then we have
where
The inequality (19) can be rewritten as
By Lemma 2.4, we get \(\lim_{t\rightarrow+\infty}\frac{M(t)}{t}=0\) almost surely. According to Remark 2.1, one sees that \(I(t)\leq\frac{\varLambda }{\mu}\). Thus one has \(\lim_{t\rightarrow+\infty}\frac{I(t)}{t}=0\) and \(\lim_{t\rightarrow +\infty}\frac{\ln I(t)}{t}=0\) almost surely as \(I(t)\geq1\), and \(\lim_{t\rightarrow+\infty}\varTheta(t)=0\) almost surely. Taking the inferior limit of both sides of (20) yields
Let \(\Delta=\max\{\Delta_{i}, i=1,2\}\). We have
Thus, we get the permanence theorem as follows.
Theorem 4.2
If \(\mathcal{R}^{*}>1\), then the infectious disease I is permanent in mean, moreover, I satisfies
Remark 4.3
Theorem 4.1 and Theorem 4.2 show that the condition for the disease to go to extinction or permanence strongly depends on the intensity of white noise disturbances. And small white noise disturbances will be beneficial to long-term prevalence of the disease, conversely, large white noise disturbances may cause the epidemic disease to die out.
5 Numerical simulation
In the following, by employing the Euler Maruyama (EM) method [63, 65], we make some numerical simulations to illustrate the extinction and persistence of the diseases in stochastic system and corresponding deterministic system for comparison.
We set parameters as \(\mu=0.2, \beta=0.5, \gamma=0.79, \alpha=0.4, p=2\), in system (1). Then we obtain
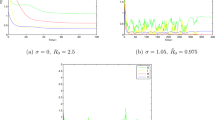
If \(\varLambda=0.25\), by simple calculation, we have \(\mathcal {R}=0.5621<1\), then according to Theorem 3.1, system (21) has a unique stable ‘diseases-extinction’ equilibrium point \(E_{0}(1.25,0)\), which implies the disease goes to extinction (see Fig. 1). If \(\varLambda=0.45\), we have \(\mathcal {R}=1.8210>1\). Then according Theorem 3.1, system (21) has a unique stable positive equilibrium \(E^{*}(1.6673, 0.1942)\), which implies that the disease of system (21) is permanent (see Fig. 2).
Next, to show the effect of stochastic perturbation on the spread of the disease, based on the deterministic system with persistent disease (see Fig. 2), we consider the stochastic system as follows:
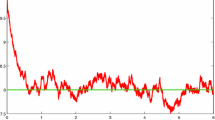
First, we let \(\sigma=0.4\), the condition I in Theorem 4.1 is satisfied, the by Theorem 4.1, the disease will die out under a large white noise perturbation (see Fig. 3). If let \(\sigma =0.3\), by a direct calculation, we get \(\mathcal{R}^{*}=0.9913<1\), obviously, the condition II in Theorem 4.1 is satisfied, the by Theorem 4.1, the disease will die out under a large white noise perturbation (see Fig. 4). While if we let \(\sigma=0.1\), by a direct calculation, we have \(\mathcal {R}^{*}=1.7289>1\), then the disease is persistent by Theorem 4.2 (see Fig. 5). Moreover, Fig. 5 shows the solution of the stochastic system oscillate around the positive equilibrium of the deterministic system.
6 Conclusion
The aim of this paper is to make contributions to understand the dynamics of SIS epidemic models with nonlinear incidence rate. First, we expand a deterministic SIS epidemic model by introducing the extra mortality. For the modified system, by analyzing the stability of equilibria, we define a threshold which determines the extinction and permanence of the epidemic disease. Second, we establish a stochastic system by introducing the white noise disturbance into the deterministic system. For the stochastic system, we define a new threshold associated with its deterministic counterpart and analyze the dynamics of the system based on the new threshold by using the theory of stochastic differential equations. Our results show that there exists a significant difference of threshold of the stochastic system from its deterministic counterpart. The difference caused by the introduction of stochastic white noise makes the extinction conditions of the diseases in the stochastic system are weaker than that of the corresponding deterministic model. However, in the present model, the nonlinear incidence rate takes the form \(\beta S^{p}(t)I(t)\), which is a special case of the nonlinear incidence rate \(\beta S^{p}(t)I^{q}(t)\) with \(q=1, p\in N\), for the more general case \(p, q\in R^{+}\), we do not give an effective analysis method at present. The analysis of this scheme in such case is left to our further study.
References
Zou, Y., He, G.: On the uniqueness of solutions for a class of fractional differential equations. Appl. Math. Lett. 74, 68–73 (2017)
Zhang, T., Liu, X., Meng, X., Zhang, T.: Spatio-temporal dynamics near the steady state of a planktonic system. Comput. Math. Appl. 75(12), 4490–4504 (2018)
Tao, M., Dong, H.: Algebro-geometric solutions for a discrete integrable equation. Discrete Dyn. Nat. Soc. 2017, Article ID 5258375 (2017)
Zhuo, X.: Global attractability and permanence for a new stage-structured delay impulsive ecosystem. J. Appl. Anal. Comput. 8(2), 457–470 (2018)
Zhang, X., Liu, L., Wu, Y., Cui, Y.: Entire blow-up solutions for a quasilinear p-Laplacian Schrodinger equation with a non-square diffusion term. Appl. Math. Lett. 74, 85–93 (2017)
Liu, Y., Dong, H., Zhang, Y.: Solutions of a discrete integrable hierarchy by straightening out of its continuous and discrete constrained flows. Anal. Math. Phys. (2018). https://doi.org/10.1007/s13324-018-0209-9
Zhang, T., Zhang, T., Meng, X.: Stability analysis of a chemostat model with maintenance energy. Appl. Math. Lett. 68, 1–7 (2017)
Wang, J., Cheng, H., Meng, X., Pradeep, B.S.A.: Geometrical analysis and control optimization of a predator–prey model with multi state-dependent impulse. Adv. Differ. Equ. 2017, 252 (2017)
Zuo, M., Hao, X., Liu, L., Cui, Y.: Existence results for impulsive fractional integro-differential equation of mixed type with constant coefficient and antiperiodic boundary conditions. Bound. Value Probl. 2017, 161 (2017)
Wang, J., Cheng, H., Li, Y., Zhang, X.: The geometrical analysis of a predator–prey model with multi-state dependent impulses. J. Appl. Anal. Comput. 8(2), 427–442 (2018)
Zhang, T., Ma, W., Meng, X.: Global dynamics of a delayed chemostat model with harvest by impulsive flocculant input. Adv. Differ. Equ. 2017(1), 115 (2017)
Wang, W., Ma, W., Lai, X.: Repulsion effect on superinfecting virions by infected cells for virus infection dynamic model with absorption effect and chemotaxis. Nonlinear Anal., Real World Appl. 33, 253–283 (2017)
Fan, X., Song, Y., Zhao, W.: Modeling cell-to-cell spread of HIV-1 with nonlocal infections. Complexity 2018, Article ID 2139290 (2018)
Kermack, W.O., McKendrick, A.G.: A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 115(772), 700–721 (1927)
Zhang, T., Meng, X., Zhang, T., Song, Y.: Global dynamics for a new high-dimensional SIR model with distributed delay. Appl. Math. Comput. 218(24), 11806–11819 (2012)
Meng, X., Chen, L., Wu, B.: A delay SIR epidemic model with pulse vaccination and incubation times. Nonlinear Anal., Real World Appl. 11(1), 88–98 (2010)
Zhang, T., Meng, X., Zhang, T.: Global analysis for a delayed SIV model with direct and environmental transmissions. J. Appl. Anal. Comput. 6(2), 479–491 (2016)
Li, K., Li, J., Wang, W.: Epidemic reaction-diffusion systems with two types of boundary conditions. Electron. J. Differ. Equ. 2018, 170 (2018)
Wang, W., Zhang, T.: Caspase-1-mediated pyroptosis of the predominance for driving CD4+ T cells death: a nonlocal spatial mathematical model. Bull. Math. Biol. 80(3), 540–582 (2018)
Li, F., Meng, X., Wang, X.: Analysis and numerical simulations of a stochastic SEIQR epidemic system with quarantine-adjusted incidence and imperfect vaccination. Comput. Math. Methods Med. 2018, Article ID 7873902 (2018)
Webster, R.G., Bean, W.J., Gorman, O.T., Chambers, T.M., Kawaoka, Y.: Evolution and ecology of influenza a viruses. Microbiol. Rev. 56(1), 152–179 (1992)
Finkbeiner, S.R., Allred, A.F., Tarr, P.I., Klein, E.J., Kirkwood, C.D., Wang, D.: Metagenomic analysis of human diarrhea: viral detection and discovery. PLOS Pathogens 4(2), 1–9 (2008)
Chan, L.G.: Deaths of children during an outbreak of hand, foot, and mouth disease in Sarawak, Malaysia: clinical and pathological characteristics of the disease. Clin. Infect. Dis. 31(3), 678–683 (2000)
Kermack, W.O., McKendrick, A.G.: A contribution to the mathematical theory of epidemics. ii. the problem of endemicity. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 138(834), 55–83 (1932)
Zhang, T., Meng, X., Zhang, T.: Global dynamics of a virus dynamical model with cell-to-cell transmission and cure rate. Comput. Math. Methods Med. 2015, Article ID 758362 (2015)
Li, J., Ma, Z., Zhou, Y.: Global analysis of SIS epidemic model with a simple vaccination and multiple endemic equilibria. Acta Math. Sci. 26(1), 83–93 (2006)
Miao, A., Zhang, T., Zhang, J., Wang, C.: Dynamics of a stochastic SIR model with both horizontal and vertical transmission. J. Appl. Anal. Comput. 2018(4), 1108–1121 (2018)
Song, Y., Miao, A., Zhang, T.: Extinction and persistence of a stochastic SIRS epidemic model with saturated incidence rate and transfer from infectious to susceptible. Adv. Differ. Equ. 2018(1), 293 (2018)
Zhang, T., Meng, X., Song, Y., Zhang, T.: A stage-structured predator–prey si model with disease in the prey and impulsive effects. Math. Model. Anal. 18(4), 505–528 (2013)
Severo, N.C.: Generalizations of some stochastic epidemic models. Math. Biosci. 4, 395–402 (1969)
Liu, W., Hethcote, H.W., Levin, S.A.: Dynamical behavior of epidemiological models with nonlinear incidence rates. J. Math. Biol. 25(4), 359–380 (1987)
Hethcote, H.W., Lewis, M.A., van den Driessche, P.: An epidemiological model with a delay and a nonlinear incidence rate. J. Math. Biol. 27(1), 49–64 (1989)
Li, M.Y., Muldowney, J.S.: Global stability for the SEIR model in epidemiology. Math. Biosci. 125(2), 155–164 (1995)
Pugliese, A.: Population models for diseases with no recovery. J. Math. Biol. 28(1), 65–82 (1990)
Thieme, H.R.: Persistence under relaxed point-dissipativity (with application to an endemic model). SIAM J. Math. Anal. 24(2), 407–435 (1993)
Korobeinikov, A.: Global properties of infectious disease models with nonlinear incidence. Bull. Math. Biol. 69(6), 1871–1886 (2007)
Ruan, S., Wang, W.: Dynamical behavior of an epidemic model with a nonlinear incidence rate. J. Differ. Equ. 188(1), 135–163 (2003)
Huang, G., Takeuchi, Y., Ma, W., Wei, D.: Global stability for delay SIR and SEIR epidemic models with nonlinear incidence rate. Bull. Math. Biol. 72(5), 1192–1207 (2010)
Miao, A., Wang, X., Zhang, T., Wang, W., Pradeep, B.G.S.A.: Dynamical analysis of a stochastic SIS epidemic model with nonlinear incidence rate and double epidemic hypothesis. Adv. Differ. Equ. 2017, 226 (2017)
Miao, A., Zhang, J., Zhang, T., Pradeep, B.G.S.: Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination. Comput. Math. Methods Med. 2017, Article ID 4820183 (2017)
Qi, H., Liu, L., Meng, X.: Dynamics of a non-autonomous stochastic SIS epidemic model with double epidemic hypothesis. Complexity 2017, Article ID 4861391 (2017)
Lahrouz, A., Omari, L.: Extinction and stationary distribution of a stochastic SIRS epidemic model with non-linear incidence. Stat. Probab. Lett. 83(4), 960–968 (2013)
Meng, X., Zhao, S., Feng, T., Zhang, T.: Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis. J. Math. Anal. Appl. 433(1), 227–242 (2016)
Liu, Q., Jiang, D., Shi, N., Hayat, T., Alsaedi, A.: Stationary distribution and extinction of a stochastic SIRS epidemic model with standard incidence. Phys. A, Stat. Mech. Appl. 469, 510–517 (2017)
Leng, X., Feng, T., Meng, X.: Stochastic inequalities and applications to dynamics analysis of a novel SIVS epidemic model with jumps. J. Inequal. Appl. 2017(1), 138 (2017)
Zhang, S., Meng, X., Wang, X.: Application of stochastic inequalities to global analysis of a nonlinear stochastic SIRS epidemic model with saturated treatment function. Adv. Differ. Equ. 2018(1), 50 (2018)
Meng, X., Li, F., Gao, S.: Global analysis and numerical simulations of a novel stochastic eco-epidemiological model with time delay. Appl. Math. Comput. 339, 701–726 (2018)
Gray, A., Greenhalgh, D., Mao, X., Pan, J.: The SIS epidemic model with Markovian switching. J. Math. Anal. Appl. 394(2), 496–516 (2012)
Cai, Y., Kang, Y., Banerjee, M., Wang, W.: A stochastic SIRS epidemic model with infectious force under intervention strategies. J. Differ. Equ. 259(12), 7463–7502 (2015)
Bian, F., Zhao, W., Song, Y., Yue, R.: Dynamical analysis of a class of prey-predator model with Beddington–Deangelis functional response, stochastic perturbation, and impulsive toxicant input. Complexity 2017, Article ID 3742197 (2017)
Zhang, X., Jiang, D., Alsaedi, A., Hayat, T.: Stationary distribution of stochastic SIS epidemic model with vaccination under regime switching. Appl. Math. Lett. 59, 87–93 (2016)
Yu, X., Yuan, S., Zhang, T.: Persistence and ergodicity of a stochastic single species model with Allee effect under regime switching. Commun. Nonlinear Sci. Numer. Simul. 59, 359–374 (2018)
Zhang, X., Jiang, D., Hayat, T., Ahmad, B.: Dynamics of a stochastic SIS model with double epidemic diseases driven by Lévy jumps. Phys. A, Stat. Mech. Appl. 471, 767–777 (2017)
Zhou, Y., Yuan, S., Zhao, D.: Threshold behavior of a stochastic SIS model with jumps. Appl. Math. Comput. 275, 255–267 (2016)
Zhao, Y., Yuan, S., Zhang, Q.: The effect of Lévy noise on the survival of a stochastic competitive model in an impulsive polluted environment. Appl. Math. Model. 40(17), 7583–7600 (2016)
Beretta, E., Kolmanovskii, V., Shaikhet, L.: Stability of epidemic model with time delays influenced by stochastic perturbations. Math. Comput. Simul. 45(3), 269–277 (1998)
Chang, Z., Meng, X., Zhang, T.: A new way of investigating the asymptotic behaviour of a stochastic SIS system with multiplicative noise. Appl. Math. Lett. 87, 80–86 (2019)
Liu, L., Meng, X.: Optimal harvesting control and dynamics of two-species stochastic model with delays. Adv. Differ. Equ. 2017, 18 (2017)
Lv, X., Wang, L., Meng, X.: Global analysis of a new nonlinear stochastic differential competition system with impulsive effect. Adv. Differ. Equ. 2017, 296 (2017)
Liu, G., Wang, X., Meng, X., Gao, S.: Extinction and persistence in mean of a novel delay impulsive stochastic infected predator–prey system with jumps. Complexity 2017, Article ID 1950970 (2017)
Feng, T., Meng, X., Liu, L., Gao, S.: Application of inequalities technique to dynamics analysis of a stochastic eco-epidemiology model. J. Inequal. Appl. 2016(1), 327 (2016)
Zhang, S., Meng, X., Feng, T., Zhang, T.: Dynamics analysis and numerical simulations of a stochastic non-autonomous predator–prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 26, 19–37 (2017)
Mao, X.: Stochastic Differential Equations and Applications, 2nd edn. Horwood, Chichester (2008)
Ji, C., Jiang, D., Shi, N.: The behavior of an SIR epidemic model with stochastic perturbation. Stoch. Anal. Appl. 30(5), 755–773 (2012)
Kloeden, P.E., Platen, E.: Higher-order implicit strong numerical schemes for stochastic differential equations. J. Stat. Phys. 66(1), 283–314 (1992)
Availability of data and materials
Data sharing not applicable to this article as all data sets are hypothetical during the current study.
Funding
This work is supported by Shandong Provincial Natural Science Foundation of China (No. ZR2015AQ001), the National Natural Science Foundation of China (No. 11371230), SDUST Research Fund (2014TDJH102) and SDUST Innovation Fund for Graduate Students (SDKDYC180348).
Author information
Authors and Affiliations
Contributions
NG and YS designed the study and carried out the analysis. NG, YS and XW contributed to writing the paper. JL performed numerical simulations. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gao, N., Song, Y., Wang, X. et al. Dynamics of a stochastic SIS epidemic model with nonlinear incidence rates. Adv Differ Equ 2019, 41 (2019). https://doi.org/10.1186/s13662-019-1980-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1980-0