1 Introduction

Infectious diseases have always threatened the health of human beings and have brought enormous disasters to human beings. In order to protect human life and control the prevalence of infectious diseases, researchers have used various methods, such as pathology, virology, epidemiology, and culture, to study the evolution of infectious diseases [1–4]. Mathematical modeling method is considered as a very useful method which was firstly proposed by D. Bernoulli in 1760 for investigating the spread of smallpox [5]. And in 1906, W.H. Hamer constructed and discussed a mathematical model to explain the recurrent epidemic of measles [6]. In 1911, R.A. Ross proposed a differential equation model to investigate the spread of malaria [7]. In 1927, W.O. Kermack and A.G. McKendrick proposed the classical epidemic model known as SIR model [8], in which the total population size is divided into three disjoint classes, namely the susceptible class (S), the infective class (I), and the recovery class (R). SIR models have been investigated by many scholars, e.g., [9–13]. In the SIR model, the susceptible can be infected, and the infected can be recovered and immunized for life. However, it is well known that for some epidemic diseases, such as meningitis, plague, venereal diseases, malaria, and sleeping sickness [14], the recovery does not produce lifelong immunity, thus the individual is transferred from the susceptible person to the infected person and then returns to the susceptible class upon recovery, then the model is identified as SIS model, e.g., [15–19]. While for some epidemic diseases, such as smallpox, tetanus, cholera, influenza, and typhoid fever, the recovery can produce temporary immunity, recovery may lose immunity after some time and back to the susceptible class. This model is known as SIRS model. SIS and SIRS models have been extensively investigated by many authors, e.g., [20–26].

Recently, Li et al. [27] considered both transfer from the infectious to the susceptible and transfer from the recovery to the susceptible and proposed an SIRS epidemic model with nonlinear transmission rate as follows (see Fig. 1):

$$ \textstyle\begin{cases} { \dot{S}(t)=\Lambda-\mu S(t)-S(t)f(I(t))+r_{1} I(t)+\delta R(t)},\\ {\dot{I}(t)=S(t)f(I(t))-(\mu+r_{1}+r_{2}+\alpha)I(t),}\\ {\dot{R}(t)=r_{2}I(t)-(\mu+\delta)R(t),} \end{cases} $$
(1.1)

where Λ is the birth rate, μ is the natural mortality rate, \(r_{1}\) is the transfer rate from the infective individuals to the susceptible individuals, \(r_{2}\) is the recovery rate of the infective individuals, α is the mortality due to illness, δ is the rate at which the recovered individuals loss of immunity and return to the susceptible individuals. f is a real locally Lipschitz function on \(R^{+} = [0,\infty)\) satisfying (i) \(f(0) = 0\) and \(f(I) > 0\) for \(I > 0\); (ii) \(f(I)/I\) is continuous and monotonously nonincreasing for \(I > 0\) and \(\lim_{I\rightarrow0^{+}}f(I)/I\) exists, denoted by β with \(\beta> 0\).

Figure 1
figure 1

The process diagram for SIRS model

Full size image

By using LaSalle’s invariance principle and Lyapunov direct method, a threshold dynamics determined by the basic reproduction number \(R_{0}=\frac{\Lambda\beta}{\mu(\mu+ r_{1} + r_{2} + \alpha)} \) was established, i.e., if \(R_{0}<1\), the infection-free equilibrium \(E_{0} = (\Lambda/\mu, 0, 0)\) is globally asymptotically stable, while if \(R_{0} > 1\), the endemic equilibrium \(E^{*} = (S^{*}, I^{*}, R^{*})\) is globally asymptotically stable.

As we all know, real life is filled with randomness and unpredictability. Stochastic models can better conform to the actual situation, therefore many scholars have done a lot of research on the randomness of biological models; e.g., in references [28–38], the authors considered the stochastic effect in population dynamical system, and in references [39–42], the authors investigated the stochastic stability. Inevitably, the spread of the diseases is affected by random factors. Generally speaking, a stochastic model constructed by different way will have different effect on a population dynamical system. For instance, references [43–49] studied a class of stochastic epidemic systems in which incidence rate β subjects to stochastic white noise disturbance. In references [50–55], the authors considered a class of stochastic systems of infectious diseases in which stochastic interference is assumed to be proportional to the variable. And references [56–58] investigated the stochastic epidemic model thought the Markov transformation.

In this paper, motivated by the previous work, we consider the incidence rate β in model (1.1) subject to stochastic white noise disturbance, i.e., \(\beta\rightarrow\beta+ \sigma\,\mathrm{d}{B}(t)\), and build the following system:

$$ \textstyle\begin{cases} { d{S}(t)= (\Lambda-\mu S(t)-\frac{\beta S(t)I(t)}{1+aI(t)}+r_{1} I(t)+\delta R(t) )\,dt-\frac{\sigma S(t)I(t)}{1+aI(t)}\,dB(t) },\\ {d{I}(t)= (\frac{\beta S(t)I(t)}{1+aI(t)}-(\mu+r_{1}+r_{2}+\alpha)I(t) )\,dt+\frac{\sigma S(t)I(t)}{1+aI(t)}\,dB(t),}\\ {d{R}(t)= (r_{2}I(t)-(\mu+\delta)R(t) )\,dt,} \end{cases} $$
(1.2)

where \(B(t)\) is a standard Brownian motion with intensity \(\sigma^{2}>0\).

Our main purpose is to explore the threshold value associated with epidemic spread and try to establish the threshold dynamics of system (1.2). In Sect. 2, we give some notation and auxiliary results. And a completely qualitatively analysis for the threshold dynamics of system (1.2) is showed in Sect. 3. In Sect. 4, we give a brief conclusion and some numerical simulations to verify the main results.

2 Preliminaries

Throughout this paper, we let \(\mathbb{R}^{d}\): the d-dimensional Euclidean space. \(\mathbb{R}^{d}_{+}:= \{x\in\mathbb{R}^{d} : x_{i} > 0, 1\leq i\leq d\}\), i.e., the positive cone.

Let \((\Omega,\mathcal{F}, \mathcal{P})\) be a complete probability space adapted to the filtration \(\{\mathcal{F}\}_{t\geq0}\) and \(\{B_{t}\}_{t\geq 0}\) is a one-dimensional Brownian motion defined on it. \(\mathcal {L}^{1}(\mathbb{R}_{+};\mathbb{R}^{d})\) is the family of all \(\mathbb {R}^{d}\)-valued measurable \(\{\mathcal{F}_{t}\}\)-adapted processes \(g=\{g(t)\}_{t\geq0}\) and

$$P \biggl[ \int_{0}^{T} \bigl\vert g(t) \bigr\vert \,dt< \infty \text{ for all } T>0 \biggr]=1. $$

By using the methods from [59] and [60], we can prove the following lemma.

Lemma 2.1

For any given initial value \((S(0),I(0),R(0))\in{R}^{3}_{+}\), system (1.2) has a unique positive solution \((S(t), I(t), R(t))\in{R}^{3}_{+} \) on \(t\geq0\), almost surely.

Lemma 2.2

The region

$$\Gamma= \biggl\{ \bigl(S(t), I(t), R(t)\bigr) \in{R}^{3}_{+}: S(t) > 0, I(t) \geq0, R(t) > 0, S(t) + I(t) + R(t) \leq\frac{\Lambda}{\mu}\biggr\} $$

is a positively invariant set for system (1.2).

Proof

Let \(N(t)=S(t)+I(t)+ R(t)\), by system (1.2), we obtain

$$\frac{\mathrm{d}N(t)}{\mathrm{d}t}\leq\Lambda-\mu N(t). $$

This implies that

$$N(t)\leq\frac{\Lambda}{\mu}+ \biggl(N(0)-\frac{\Lambda}{\mu} \biggr)e^{-\mu t}. $$

Then, if we denote \(\Gamma=\{(S(t), I(t), R(t))\in R_{+}^{3}:S(t), I(t), R(t)\leq\frac{\Lambda}{\mu}, t\geq0\}\), we have \(S(t)+I(t)+ R(t)\leq \frac{\Lambda}{\mu}\). Thus, the region Γ is positively invariant. □

By using the methods from Meng et al. [45], we can prove the following lemma.

Lemma 2.3

For any given initial value \((S(0), I(0), R(0))\in R^{3}_{+}\), the solution \((S(t), I(t), R(t))\) of system (1.2) has the following properties:

$$\lim_{t\rightarrow+\infty}\frac{1}{t} \int_{0}^{t}\frac{\sigma S(\tau )}{1+aI(\tau)}\,\mathrm{d}B(\tau)=0,\quad \lim_{t\rightarrow+\infty}\frac {1}{t} \int_{0}^{t}\sigma S(\tau)\,\mathrm{d}B(\tau)=0 $$

almost surely.

3 A threshold dynamics

In this section, we try our best to find the threshold that determines the spread of the disease.

3.1 Extinction

Definition 3.1

For system (1.2), the infected individuals \(I(t)\) are said to be extinctive if \(\lim _{t\rightarrow+\infty} I(t)=0\), almost surely.

Let us introduce

$$ {\widetilde{R}_{0}}=R_{0}-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}(\mu+r_{1}+r_{2}+\alpha).} $$

Then we have the following.

Theorem 3.2

If \(\sigma^{2}>\max\{\frac{\beta\mu}{\Lambda},\frac{\beta^{2}}{2(\mu +r_{1}+r_{2}+\alpha)}\}\) or \(\sigma^{2}<\frac{\beta\mu}{\Lambda}\) and \({\widetilde{R}_{0}}<1\), then the infected individuals of system (1.2) tend to zero exponentially almost surely.

Proof

Assume that \((S(t), I(t),R(t))\) is a solution of system (1.2) satisfying the initial value \((S(0), I(0), R(0)) \in R^{3}_{+}\). According to Itô’s formula, we have

$$ \mathrm{d}\ln I(t)= \biggl(\frac{\beta S(t)}{1+aI(t)}-( \mu+r_{1}+r_{2}+\alpha)-\frac{\sigma^{2}S^{2}(t)}{2(1+a I(t))^{2}} \biggr)\,\mathrm{d}t+ \frac{\sigma S(t)}{1+aI(t)}\,\mathrm{d}B(t). $$
(3.1)

Integral on both sides of system (3.1) from 0 to t shows

$$ \ln I(t)= \int_{0}^{t} \biggl(\frac{\beta S(\tau)}{1+aI(\tau)}- \frac{\sigma^{2}S^{2}(\tau)}{2(1+a I(\tau))^{2}} \biggr)\,\mathrm{d}\tau-(\mu+r_{1}+r_{2}+ \alpha)t+M_{1}(t)+\ln I(0), $$
(3.2)

where \(M_{1}(t)=\int_{0}^{t}\frac{\sigma S(\tau)}{1+aI(\tau)}\,\mathrm{d}B(\tau)\) and \(M_{1}(t)\) is the local continuous martingale with \(M_{1}(0)=0\). Next, we have two cases to be discussed, depending on whether \(\sigma^{2}>\frac{\beta\mu}{\Lambda}\).

If \(\sigma^{2}>\frac{\beta\mu}{\Lambda}\), we can easily see from (3.2) that

$$ \ln I(t)\leq \biggl(\frac{\beta^{2}}{2\sigma^{2}}-(\mu+r_{1}+r_{2}+ \alpha) \biggr)t+M_{1}(t)+\ln I(0). $$
(3.3)

Dividing both sides of (3.3) by \(t>0\), one gets

$$ \frac{\ln I(t)}{t}\leq- \biggl(\mu+r_{1}+r_{2}+ \alpha-\frac{\beta^{2}}{2\sigma^{2}} \biggr)+\frac{M_{1}(t)}{t}+\frac{\ln I(0)}{t}. $$
(3.4)

Since \(\limsup_{t\rightarrow\infty}\frac{\langle M_{1}(t),M_{1}(t)\rangle _{t}}{t}<\sigma^{2}<\infty\) almost surely, by Lemma 2.3, one can obtain that

$$\lim_{t\rightarrow+\infty}\frac{M_{1}(t)}{t}=0 $$

almost surely. Then, taking the limit superior on both sides of (3.4), we get

$$ \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t}\leq- \biggl( \mu+r_{1}+r_{2}+\alpha-\frac{\beta^{2}}{2\sigma^{2}} \biggr)< 0, $$

when \(\sigma^{2}>\frac{\beta^{2}}{2(\mu+r_{1}+r_{2}+\alpha)}\), which implies \(\lim_{t\rightarrow+\infty}I(t)=0\) almost surely.

If \(\sigma^{2}<\frac{\beta\mu}{\Lambda}\), similarly, one can have that

$$ \ln I(t)\leq \biggl(\frac{\beta\Lambda}{\mu}-\frac{\sigma ^{2}\Lambda^{2}}{2\mu^{2}}-( \mu+r_{1}+r_{2}+\alpha) \biggr)t+M_{1}(t)+\ln I(0). $$
(3.5)

Dividing both sides of (3.5) by \(t>0\), we obtain

$$ \begin{aligned}[b] \frac{\ln I(t)}{t}&\leq( \mu+r_{1}+r_{2}+ \alpha) \biggl[\frac{\beta\Lambda}{\mu(\mu+r_{1}+r_{2}+\alpha)}- \frac{\sigma ^{2}\Lambda^{2}}{2\mu^{2}(\mu+r_{1}+r_{2}+\alpha)}-1 \biggr] \\ &\quad{}+\frac{M_{1}(t)}{t}+\frac{\ln I(0)}{t}. \end{aligned} $$
(3.6)

By taking the superior limit on both sides of (3.6), one can have that

$$ \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t}\leq(\mu+r_{1}+r_{2}+ \alpha) ({\widetilde{R}_{0}}-1). $$

Then when \({\widetilde{R}_{0}}<1\), we get

$$ \limsup_{t\rightarrow+\infty}\frac{\ln I(t)}{t}< 0, $$

which implies \(\lim_{t\rightarrow+\infty}I(t)=0\) almost surely. The proof of Theorem 3.2 is completed. □

Remark 3.3

By Theorem 3.2, we get if \(\sigma^{2}>\max\{\frac{\beta\mu}{\Lambda },\frac{\beta^{2}}{2(\mu+r_{1}+r_{2}+\alpha)}\}\), then the infectious disease of system (1.2) goes to extinction almost surely, namely large white noise stochastic disturbance is conducive to control infectious disease. When the white noise is small and \({\widetilde{R}_{0}}<1\), the infectious disease of system (1.2) also goes to extinction almost surely, then \({\widetilde{R}_{0}}\) is the threshold associated with the extinction of infectious disease.

3.2 Persistence in mean

Definition 3.4

For system (1.2), the infected individuals \(I(t)\) are said to be persistent in mean if \(\liminf _{t\rightarrow+\infty}\langle I(t)\rangle>0\), almost surely, where \(\langle I(t)\rangle\) is defined as \(\frac{1}{t}\int_{0}^{t}I(\tau )\,\mathrm{d}\tau\).

Theorem 3.5

If \({\widetilde{R}_{0}}>1\), then the infected individuals \(I(t)\) are persistent in mean, and

$$ \liminf_{t\rightarrow+\infty} \bigl\langle I(t) \bigr\rangle \geq \frac{(\mu+r_{1}+r_{2}+\alpha)}{\beta(\frac{\mu+\alpha}{\mu}+\frac{r_{2}}{\mu +\delta} )+a(\mu+r_{1}+r_{2}+\alpha)}({\widetilde{R}_{0}}-1), $$

almost surely.

Proof

Integral on both sides of system (1.2) from 0 to t yields

$$ \begin{aligned} \Theta(t)&\triangleq\frac{S(t)-S(0)}{t}+ \frac{I(t)-I(0)}{t}+ \frac{\delta}{\mu+\delta}\frac{R(t)-R(0)}{t} \\ &=\Lambda-\mu \bigl\langle S(t) \bigr\rangle - \biggl(\mu+\alpha+ \frac{\mu r_{2}}{\mu+\delta} \biggr) \bigl\langle I(t) \bigr\rangle . \end{aligned} $$

Then we obtain

$$ \begin{aligned} \bigl\langle S(t) \bigr\rangle =\frac{\Lambda}{\mu}- \biggl( \frac{\mu+\alpha}{\mu}+\frac{r_{2}}{\mu+\delta} \biggr) \bigl\langle I(t) \bigr\rangle - \frac{\Theta(t)}{\mu}. \end{aligned} $$

Using Itô’s formula gives

$$ \begin{aligned}[b] \mathrm{d} \bigl(\ln I(t)+aI(t) \bigr)&= \biggl[ \beta S(t)-(\mu+r_{1}+r_{2}+\alpha)-a( \mu+r_{1}+r_{2}+ \alpha)I(t) \\ &\quad{}-\frac{\sigma^{2}S^{2}(t)}{2(1+aI(t))^{2}} \biggr]\,\mathrm{d}t+\sigma S(t)\,\mathrm{d}B(t) \\ & \geq \biggl[\beta S(t)-(\mu+r_{1}+r_{2}+\alpha)-a( \mu+r_{1}+r_{2}+\alpha)I(t) \\ &\quad{}-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}} \biggr]\,\mathrm{d}t+\sigma S(t)\,\mathrm{d}B(t). \end{aligned} $$
(3.7)

Integral on both sides of system (1.2) from 0 to t and dividing by t (\(t>0\)) yields

$$ \begin{aligned}[b] &\frac{\ln I(t)-\ln I(0)}{t}+a \frac{I(t)-I(0)}{t} \\ &\quad\geq\beta \bigl\langle S(t) \bigr\rangle -a(\mu+r_{1}+r_{2}+ \alpha) \bigl\langle I(t) \bigr\rangle - \biggl[\mu+r_{1}+r_{2}+ \alpha+\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}} \biggr]+\frac{M_{2}(t)}{t}, \\ &\quad\geq\frac{\beta\Lambda}{\mu}-\beta \biggl(\frac{\mu+\alpha}{\mu }+\frac{r_{2}}{\mu+\delta} \biggr) \bigl\langle I(t) \bigr\rangle -a(\mu+r_{1}+r_{2}+ \alpha) \bigl\langle I(t) \bigr\rangle \\ &\qquad{}-(\mu+r_{1}+r_{2}+\alpha)-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}}+ \frac{M_{2}(t)}{t}-\frac{\beta\Theta(t)}{\mu}, \end{aligned} $$
(3.8)

where \(M_{2}(t)=\int_{0}^{t}\sigma S(\tau)\,\mathrm{d}B(\tau)\) and \(M_{2}(t)\) is the local continuous martingale with \(M_{2}(0)=0\). From (3.8), we obtain

$$\begin{aligned} \bigl\langle I(t) \bigr\rangle \geq& \frac{1}{\beta(\frac {\mu+\alpha}{\mu}+\frac{r_{2}}{\mu+\delta} )+a(\mu+r_{1}+r_{2}+\alpha)} \biggl[ \frac{\beta\Lambda}{\mu}-(\mu+r_{1}+r_{2}+\alpha) \\ &{}-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}}-\frac{\beta\Theta(t)}{\mu}+\frac {M_{2}(t)}{t}- \frac{\ln I(t)-\ln I(0)}{t}-\frac{a(I(t)-I(0))}{t} \biggr] \\ \geq& \textstyle\begin{cases} \frac{1}{\beta(\frac{\mu+\alpha}{\mu}+\frac{r_{2}}{\mu +\delta} )+a(\mu+r_{1}+r_{2}+\alpha)} [ \frac{\beta\Lambda}{\mu}-(\mu+r_{1}+r_{2}+\alpha)\\ \quad{}-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}}-\frac{\beta\Theta(t)}{\mu }+\frac{M_{2}(t)}{t}+\frac{\ln I(0)}{t}-\frac{a(I(t)-I(0))}{t} ], &0< I_{1}(t)< 1;\\ \frac{1}{\beta(\frac{\mu+\alpha}{\mu}+\frac{r_{2}}{\mu+\delta} )+a(\mu +r_{1}+r_{2}+\alpha)} [ \frac{\beta\Lambda}{\mu}-(\mu+r_{1}+r_{2}+\alpha)\\ \quad{}-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}}-\frac{\beta\Theta(t)}{\mu }+\frac{M_{2}(t)}{t}-\frac{\ln I(t)-\ln I(0)}{t}-\frac{a(I(t)-I(0))}{t} ], &1\leq I_{1}(t). \end{cases}\displaystyle \end{aligned}$$
(3.9)

Since both \(I(t)\leq1\) and \(R(t)\leq1\), then one has \(\lim_{t\rightarrow+\infty}\frac{R(t)}{t}=0\), \(\lim_{t\rightarrow+\infty }\frac{\ln I(t)}{t}=0\) and \(\lim_{t\rightarrow+\infty}\Theta(t)=0\) almost surely. Note that \(\lim_{t\rightarrow+\infty}\frac{M_{2}(t)}{t}=0\) almost surely, we obtain

$$ \begin{aligned} &\liminf_{t\rightarrow+\infty} \bigl\langle I(t) \bigr\rangle \\ &\quad\geq\frac{(\mu+r_{1}+r_{2}+\alpha)}{\beta(\frac{\mu+\alpha}{\mu }+\frac{r_{2}}{\mu+\delta} )+a(\mu+r_{1}+r_{2}+\alpha)}\\ &\qquad {}\times \biggl(\frac{\beta \Lambda}{\mu(\mu+r_{1}+r_{2}+\alpha)}-\frac{\sigma^{2}\Lambda^{2}}{2\mu^{2}(\mu +r_{1}+r_{2}+\alpha)}-1 \biggr) \\ &\quad =\frac{(\mu+r_{1}+r_{2}+\alpha)}{\beta(\frac{\mu+\alpha}{\mu}+\frac {r_{2}}{\mu+\delta} )+a(\mu+r_{1}+r_{2}+\alpha)}({\widetilde{R}_{0}}-1) \end{aligned} $$

almost surely. This completes the proof of Theorem 3.5. □

Remark 3.6

Theorems 3.2 and 3.5 show that the condition for the disease to die out or persist depends on the intensity of white noise disturbances strongly and small white noise disturbances will be beneficial to long-term prevalence of the disease; conversely, large white noise disturbances may cause the epidemic disease to die out.

4 Conclusion and numerical simulation

This paper proposed a SIRS model with the special transfer from infectious, stochastic effect to the spread of the infectious disease is discussed. The threshold dynamics is explored when the noise is small. Our results show that dynamics of stochastic system is different with the deterministic case due to the effect of stochastic perturbation, large noise can cause the infectious disease to tend to zero exponentially, which is propitious to epidemic diseases control.

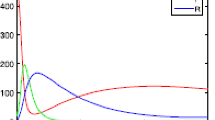
In the following, by employing the Euler–Maruyama (EM) method [61], we make some numerical simulations to illustrate the extinction and persistence of the diseases in the stochastic system and the corresponding deterministic system for comparison. First, we set parameters as \(\Lambda=2\), \(\alpha=0.2\), \(\beta=1\), \(a=1\), \(\mu =1\), \(r_{1}=0.9\), \(r_{2}=0.9\), \(\delta=0.1\) in system (1.1). A simple computation shows that \(R_{0}=0.6667<1\), then system (1.1) has a stable disease-free equilibrium \(E_{0}(2,0,0)\) (see Fig. 2). If we choose \(\beta=2\), in this case, \(R_{0}=1.3333>1\), then system (1.1) has a stable infection equilibrium \(E^{*}(1.7132,0.1421,0.1163)\) (see Fig. 3).

Figure 2
figure 2

Time series for \(S(t)\), \(I(t)\), \(R(t)\) of the deterministic SIR system with \(\beta=1\), \(\Lambda=2\), \(\alpha=0.2\), \(a=1\), \(\mu =1\), \(r_{1}=0.9\), \(r_{2}=0.9\), \(\delta=0.1\), where \({R}_{0}=0.6667<1\)

Full size image
Figure 3
figure 3

Time series for \(S(t)\), \(I(t)\), \(R(t)\) of the deterministic SIR system with \(\beta=2\), \(\Lambda=2\), \(\alpha=0.2\), \(a=1\), \(\mu =1\), \(r_{1}=0.9\), \(r_{2}=0.9\), \(\delta=0.1\), where \({R}_{0}=1.3333>1\)

Full size image

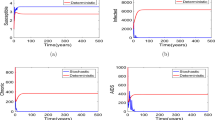
Next, let the intensity of noise \(\sigma=1.2\), a simple computation shows that the condition \(\sigma^{2}>\max\{\frac{\beta\mu}{\Lambda},\frac {\beta^{2}}{2(\mu+r_{1}+r_{2}+\alpha)}\}\) holds, then by Theorem 3.2, the disease dies out under a large white noise perturbation (see Fig. 4). On the other hand, if we reduce the intensity of noise σ to 1, in this case, we have \(\sigma^{2}<\frac{\beta\mu }{\Lambda}\) and \(\widetilde{R}_{0}=0.9067<1\), then by Theorem 3.2, the disease dies out (see Fig. 5). And if we decrease the intensity of noise σ from 1 to 0.2, by calculation we have \(\widetilde{R}_{0}=1.1667>1\), then by Theorem 3.5 the disease is persistent (see Fig. 6).

Figure 4
figure 4

Comparison of the deterministic system and the stochastic system, with \(\Lambda=2\), \(\alpha=0.2\), \(\beta=2\), \(a=1\), \(\mu =1\), \(r_{1}=0.9\), \(r_{2}=0.9\), \(\delta=0.1\), \(\sigma=1.2\), where \({R}_{0}=1.3333>1\)

Full size image
Figure 5
figure 5

Comparison of the deterministic system and the stochastic system, with \(\Lambda=2\), \(\alpha=0.2\), \(\beta=2\), \(a=1\), \(\mu =1\), \(r_{1}=0.9\), \(r_{2}=0.9\), \(\delta=0.1\), \(\sigma=0.8\), where \({R}_{0}=1.3333>1\), \(\widetilde{R}_{0}=0.9067<1\)

Full size image
Figure 6
figure 6

Comparison of the deterministic system and the stochastic system, with \(\Lambda=2\), \(\alpha=0.2\), \(\beta=2 \), \(a=1\), \(\mu =1\), \(r_{1}=0.9\), \(r_{2}=0.9\), \(\delta=0.1\), \(\sigma=0.5\), where \({R}_{0}=1.3333>1\), \(\widetilde{R}_{0}=1.1667>1\)

Full size image