Abstract
In this paper, two stochastic SIRS epidemic models with standard incidence were proposed and investigated. For the non-autonomous periodic model, the sufficient criteria for extinction of the disease are obtained firstly. Then we show that the stochastic system has at least one nontrivial positive T-periodic solution under some conditions. For the model that are both disturbed by the white noise and telephone noise, we construct a suitable Lyapunov functions to verify the existence of a unique ergodic stationary distribution. Meanwhile, the sufficient condition for the extinction of the disease is also established. Finally, examples are introduced to illustrate the theoretical analysis.
Similar content being viewed by others
1 Introduction
In the natural world, various systems are inevitably affected by the random factors [1,2,3]. Stochastic differential equations are important tools for studying random phenomena (see e.g. [4,5,6,7,8,9,10,11]). May [12] has pointed out that because of the continuous interference of the environment, the biological parameters in the ecosystem such as birth rates, intraspecific competition coefficients, death rates and other parameters may have some degree of random fluctuation. Parameter perturbation induced by white noise is an important and common form to describe the effect of stochasticity [13,14,15,16,17]. In recent years, many famous susceptible–infected–recovered–susceptible stochastic models have been formulated (see e.g. [18,19,20,21,22,23,24]). In [25], a stochastic SIRS model with environment noise was proposed as follows:
where \(B_{i}(t)\), denoting the white noise, are independent standard Brownian motions, \(\sigma_{i}^{2}\) are the intensities of the white noise, \(i=1,2,3\). For the meaning of detailed parameters, please see [25]. By using stochastic Lyapunov functions, the authors proved that the system (1) has a unique global positive solution for any initial value \((S(0),I(0),R(0))\in\mathbb{R}_{+}^{3}\) and also has an ergodic stationary distribution under some conditions.
In fact, owing to the season alternation, the life cycle of the individual, the mating habits, the food supply and so on, the birth rate, incidence rate of disease and other parameters in system (1) will exhibit more or less periodicity rather than being constant [26,27,28,29,30]. So it is more realistic to discuss the model (1) with periodic coefficients. In 2003, Greenhalgh and Moneim [31] studied a SIRS epidemic model with general seasonal variation in the contact rate. In 2009, Martcheva [32] studied a non-autonomous multi-strain SIS epidemic model with periodic coefficients. In 2015, Lin et al. [33] proposed a stochastic SIR epidemic model with seasonal variation and analyzed the existence of a nontrivial positive periodic solution. Motivated by the above work, we shall investigate the stochastic non-autonomous SIRS epidemic model which takes the form as follows:
where \(A(t)\), \(d(t)\), \(\beta(t)\), \(\delta(t)\), \(\gamma(t)\), \(\alpha(t)\) and \(\sigma_{i}(t)\) stand for the continuous positive periodic functions of period T, \(i=1,2,3\). In this paper, we intend to prove the existence of nontrivial positive T-periodic solutions under sufficient conditions of system (2).
In the real world, besides white noise, the system may be disturbed by many other noises. For example, telephone noise often causes the system to switch from one state to another [34, 35]. Recently, a large number of researchers have widely concerned the stochastic models with regime switching (see e.g. [36,37,38,39,40]). In 1978, Slatkin [41] developed and analyzed a population model in a markovian environment. In 1999, Mao [42] investigated the stability of stochastic differential equations with markovian switching. In 2016, Zhao et al. [43] have studied a stochastic phytoplankton allelopathy model under regime switching. The telephone noise is usually described by Markov chains. Let \((r(t))_{t\geq0}\) be a continuous-time Markov chain taking values in a finite state space \(\mathbb{S}=\{1,2,\ldots,m\}\). Coupling the Markov chain \(r(t)\) into model (1), we get
When the model is affected by severe stochastic interference such as rainfall or nutrition, etc., the parameter switch one state \(r(t)=i\) into another state \(r(t)=j\) and it will switch into the next regime until the next major environmental change. For any \(k\in\mathbb{S}\), \(A(k)\), \(d(k)\), \(\beta(k)\), \(\delta(k)\), \(\gamma(k)\), \(\alpha(k)\) and \(\sigma_{i}(k)\) (\(i=1,2,3\)) are positive constants. Another goal of this paper is to prove the existence of a unique ergodic stationary distribution of the positive solution to the system (3).
This paper is arranged as follows. In Sect. 2, we give some basic knowledge which are used in this paper. In Sect. 3, for the system (2), the criteria for extinction of the disease are obtained and then we show that the system has at least one nontrivial positive T-periodic solution under some conditions. In Sect. 4, for the system (3), we proposed a sufficient condition of the disease extinction. Meanwhile, the existence of a unique ergodic stationary distribution is proved. Finally, we conclude the main result briefly and make some numerical simulations in Sect. 5.
2 Preliminaries
In this paper, let \((\varOmega,\mathcal{F}, \{\mathcal{F}\}_{t\geq0}, \mathbb{P})\) be a complete probability space and let \(r(t)\), \(t\geq0\) be a right-continuous Markov chain on Ω taking values in the finite state space \(\mathbb{S}=\{1,2,\ldots,m\}\). For each vector \(g=(g(1),\ldots, g(m))\), set \(\hat{g}=\min_{k\in\mathbb{S}}\{g(k)\}\) and \(\check{g}=\max_{k\in\mathbb{S}}\{g(k)\}\). Supposed that the generator \(\varGamma=(q_{ij})_{m\times m}\) of the Markov chain is given by
where \(\Delta t>0\), \(q_{ij}>0\), \(i\neq j\) is the transition rate from state i to j while \(\sum_{j=1}^{m}q_{ij}=0\). Suppose further that the Markov chain \(r(t)\) is irreducible and has a unique stationary distribution \(\pi=(\pi_{1},\pi_{2},\ldots,\pi_{m})\), which is the solution of the system of linear equations \(\pi\varGamma=0\) subject to \(\sum_{h=1}^{m}\pi_{h}=1\) and \(\pi_{h}>0\) for all \(h\in\mathbb{S}\). For any vector \(\varpi=(\varpi(1),\varpi(2),\ldots,\varpi(m))^{T}\), we have
Consider the following equation:
where functions f and g are T-periodic in t.
Lemma 2.1
([37])
Assume that system (4) has a unique global solution. If there has a function \(V(t,x)\in C^{2}\) which is T-periodic in t such that
and
where we define the operator L by
Then for system (4) there exists a T-periodic solution.
Lemma 2.2
The following differential equations:
have a unique positive T-periodic solution \((m_{1}(t),m_{2}(t))^{T}\), where \(d(t)\), \(\delta(t)\) are continuous, positive and non-constant functions of period T.
The proof is similar to Lemma 3.1 in Liu et al. [28], here we omit it.
Now we are in the position to give some results of the stationary distribution for stochastic system under regime switching. Let \((X(t),r(t))\) be the diffusion process defined by the equation as follows:
where \(B(\cdot)\) denotes the p-dimensional Brownian motion and \(r(\cdot)\) is the right-continuous Markov chain in the above discussion, and \(b(\cdot, \cdot): \mathbb{R}^{n}\times\mathbb {S}\rightarrow\mathbb{R}^{n}\), \(\tau(\cdot,\cdot):\mathbb{R}^{n}\times \mathbb{S}\rightarrow\mathbb{R}^{n\times p}\), satisfying \(\tau(x,k)\tau ^{T}(x,k)=(d_{ij}(x,k))_{n\times n}\triangleq D(x,k)\). For any \(k\in \mathbb{S}\), let \(V(\cdot,k)\) be any twice continuously differentiable function, the operator \(\mathcal{L}\) is defined
Lemma 2.3
([37])
Assume that system (8) satisfies the conditions as follows:
-
(i)
\(q_{ij}>0\) for each \(i\neq j\);
-
(ii)
for any \(k\in\mathbb{S}\), \(D(x,k)=(d_{ij}(x,k))_{n\times n}\) is symmetric and obey
$$ \kappa_{0}|\xi|^{2}\leq\bigl\langle D(x,k)\xi,\xi\bigr\rangle \leq\kappa_{0}^{-1}|\xi |^{2} \quad \textit{for all }\xi\in\mathbb{R}^{n}, $$with some constant \(\kappa_{0}\in(0,1]\) for any \(x\in\mathbb{R}^{n}\);
-
(iii)
there exists a nonempty open set \(\mathcal{D}\) with compact closure, and for any \(k\in\mathbb{S}\), there is a nonnegative function \(V(\cdot,k):\mathcal{D}^{C}\rightarrow\mathbb{R}\) such that
$$\mathcal{L}V(x,k)\leq-1\quad \textit{for any }(x,k)\in\mathcal{D}^{C} \times\mathbb{S}. $$
Then \((X(t),r(t))\) of system (8) is positive recurrent and ergodic. Moreover, the system has a unique stationary distribution \(\mu (\cdot,\cdot)\) such that, for any Borel measurable function \(f(\cdot ,\cdot):\mathbb{R}^{n}\times\mathbb{S}\rightarrow\mathbb{R}\) satisfying
we have
3 Extinction of the disease and the periodic solution for system (2)
For the non-autonomous stochastic system (2), we investigate the extinction criteria of the disease, firstly. Define \(R_{1}(t)=\beta(t)-(\gamma(t)+d(t)+\alpha(t)+\frac{\sigma_{2}^{2}(t)}{2})\) and \(\langle f\rangle_{T}=\frac{1}{T}\int_{0}^{T}f(s)\,ds\), where f is an integral function on \([0,+\infty)\). Then we have the following conclusion.
Theorem 3.1
The disease \(I(t)\) will go to extinction exponentially almost surely when \(\langle R_{1}(t)\rangle_{T}<0\).
Proof
Applying the generalized Itô formula to model (2) yields
Let \(M(t):=\int_{0}^{t}\sigma_{2}(t)\,dB_{2}(t)\), based on the strong law of large numbers for martingales (see [44]), then \(\lim_{t\rightarrow\infty}\frac{M(t)}{t}=0\) a.s. Thus,
therefore
□
Next, we consider the existence of nontrivial positive T-periodic solution of system (2). To simplify, we denote \(g^{u}=\sup_{t\in[0,+\infty)}g(t)\), \(g^{l}=\inf_{t\in[0,+\infty)}g(t)\), where g is a bounded function on \([0,+\infty)\).
Define
where \(m_{1}(t)\) is the solution of system (7). Then we get the following theorem.
Theorem 3.2
If \(\langle R_{2}(t)\rangle_{T}>0\), then system (2) admits at least one positive T-periodic solution.
Proof
To prove Theorem 3.2, we should construct a \(C^{2}\)-function \(V(t,x)\) which is T-periodic in t and a closed set \(U\in\mathbb {R}_{+}^{3}\) satisfy the conditions in Lemma 2.1.
Take \(0<\theta<\min \{\frac{2d^{l}}{(\sigma_{1}^{2})^{u}\vee(\sigma _{2}^{2})^{u}\vee(\sigma_{3}^{2})^{u}},1 \}\) and \(K>0\) such that
where
Define
where \(V_{1}=\frac{1}{\theta+1}(S+I+R)^{\theta+1}\), \(V_{2}=-\ln S-\ln I-m_{1}(t)(S+I)-m_{2}(t)R+S+I+R-\omega(t)\), \(V_{3}=-\ln S\), \(V_{4}=-\ln R\), \(m_{1}(t)\), \(m_{2}(t)\) are given in Lemma 2.2, \(\omega(t)\) is a T-periodic function defined on \([0,+\infty)\) satisfying \(\omega'(t)=\langle R_{2}(t)\rangle_{T}-R_{2}(t)\) and \(\omega (0)=0\). Obviously, \(V(S,I,R,t)\) is T-periodic in t and
where \(U_{k}=(\frac{1}{k}, k)\times(\frac{1}{k}, k)\times(\frac{1}{k}, k)\). Therefore, condition (i) of Lemma 2.1 is satisfied. Next, we prove that condition (ii) of Lemma 2.1 is true.
Using Itô’s formula, we get
and
Hence
Define a bounded closed set
where \(\varepsilon>0\) is small enough. In the set \(\mathbb {R}_{+}^{3}\backslash U_{\varepsilon}\), one can choose ε sufficiently small and satisfying
where K̃ is a positive constant which of the following can be found in Eq. (18). For convenience, one can divide \(U_{\varepsilon}^{C}\) into the following six domains:
Clearly, \(U_{\varepsilon}^{C}=U_{1}\cup\cdots\cup U_{6}\). Now we show that \(LV(S,I,R,t)\leq-1\) on \(U_{\varepsilon}^{C}\times\mathbb{R}\), which is equivalent to prove it on these six domains.
Case 1. If \((S,I,R,t)\in U_{1}\times\mathbb{R}\), from (11), we get
where
Case 2. If \((S,I,R,t)\in U_{2}\times\mathbb{R}\), from (12), one can see that
Case 3. If \((S,I,R,t)\in U_{3}\times\mathbb{R}\), from (13), one can derive that
Case 4. If \((S,I,R,t)\in U_{4}\times\mathbb{R}\), from (14), we get
Case 5. If \((S,I,R,t)\in U_{5}\times\mathbb{R}\), (15) implies that
Case 6. If \((S,I,R,t)\in U_{6}\times\mathbb{R}\), from (16), one obtains
By (17), (19), (20), (21), (22) and (23), one can get
So, condition (ii) for Lemma 2.1 is true. By Lemma 2.1, Theorem 3.2 is proved. □
4 Extinction of the disease and the ergodic stationary distribution for system (3)
For the system with regime switching, we will explore the extinction of the disease and the existence of an ergodic stationary distribution. Let \((S(t),I(t),R(t),r(t))\) be the solution of system (3) with initial value \((S(0),I(0),R(0),r(0))\in\mathbb {R}_{+}^{3}\times\mathbb{S}\).
Define
then we have the following.
Theorem 4.1
If \(R_{1}^{*}<1\), then \(\lim_{t\rightarrow\infty}I(t)=0\) a.s.
Proof
By Itô’s formula, we get
Integrating both sides of Eq. (24) leads to
From the ergodic property of \(r(t)\), one can get
So, (25) implies that
Hence we have
□
Next, we shall establish sufficient conditions for the existence of an ergodic stationary distribution of system (3).
Let
where \(c_{1}(k)\) is the solution of the following linear system:
By the literature [34], system (26) has a unique solution
Then we have
Theorem 4.2
If \(R_{2}^{*}>1\), then system (3) has a unique ergodic stationary distribution.
Proof
To prove Theorem 4.2, we just have to verify that conditions (i), (ii) and (iii) in Lemma 2.3 be satisfied. First, assumption \(q_{ij}>0\) for \(i\neq j\) in Sect. 2 implicates that the condition (i) holds. Second, the diffusion matrix \(D(S,I,R,k)=\operatorname{diag}\{\sigma_{1}^{2}(k)S^{2}, \sigma_{2}^{2}(k)I^{2}, \sigma _{3}^{2}(k)R^{2}\}\) of model (3) is positive definite, which shows that condition (ii) in Lemma 2.3 is satisfied. Next, we will show condition (iii) is satisfied by constructing suitable Lyapunov function. Let us define
where \(c_{1}(k)\), \(c_{2}(k)\) are the solution of the system (26), \(\xi\in(0,1)\) and \(M>0\) satisfy \(\rho:=\hat{d}-\frac{\xi }{2}(\check{\sigma}_{1}^{2}\vee\check{\sigma}_{2}^{2}\vee\check{\sigma }_{3}^{2})>0\), and \(E+2\check{d}+\check{\beta}+\check{\delta}+\frac{\check {\sigma}_{1}^{2}+\check{\sigma}_{3}^{2}}{2}-M\varSigma_{k=1}^{m}\pi _{k}(\gamma(k)+d(k)+\alpha(k)+\frac{\sigma_{2}^{2}(k)}{2})(R_{2}^{*}-1)\leq -2\), E and \(\omega(k)\) will be defined later.
Denote
Applying the generalized Itô formula, we have
where \(E=\sup_{S+I+R\in\mathbb{R}_{+}}\{\check{A}(S+I+R)^{\xi}-\frac {\rho}{2}(S+I+R)^{\xi+1}\}\). Furthermore,
where
Let \(\omega=(\omega(1),\omega(2),\ldots,\omega(m))^{T}\) be the following Poisson system’s solution:
where \(\tilde{R}_{0}=(R_{01},R_{02},\ldots R_{0m})^{T}\). This shows that
Substituting this equality into (27), one has
and
Consequently, one can get
Consider the bounded open set \(D= (\frac{1}{\eta}, \eta )\times (\frac{1}{\eta}, \eta )\times (\frac{1}{\eta}, \eta )\subset\mathbb{R}_{+}^{3}\), where η is a positive number. From the discussing above, we derive that, for a sufficiently large η,
By virtue of Lemma 2.3, one can see that system (3) has a solution which is a stationary Markov process. The proof is completed. □
5 Conclusions and numerical simulations
In this paper, we proposed a stochastic non-autonomous SIRS epidemic model with periodic coefficients (model (2)), and a stochastic epidemic model perturbed by telegraph noise (model (3)). Then the dynamic behaviors of the two models are studied.
Firstly, for system (2), there are the following properties:
-
(1)
If \(\langle R_{1}(t)\rangle_{T}<0\), then the disease will go to extinction almost surely.
-
(2)
If \(\langle R_{2}(t)\rangle_{T}>0\), then system (2) has at least one positive T-periodic solution.
Secondly, system (3) possesses the following properties:
-
(1)
If \(R_{1}^{*}<1\), the disease \(I(t)\) will go to extinction exponentially with probability 1.
-
(2)
If \(R_{2}^{*}>1\), then the solution of system (3) has a unique ergodic stationary distribution.
To verify the correctness of the theoretical analysis, we will give some examples with computer simulations.
Example 1
First, we consider system (2) and let
Case (a). Simple calculation shows that
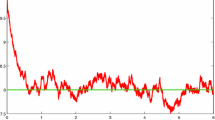
From Theorem 3.1, we know that the disease goes to extinction (see Fig. 1).
Case (b). We only change the intensity of the noise \(\sigma _{2}(t)=0.1\sin t+0.2\). Then direct computation leads to \(\langle R_{2}(t)\rangle_{T}=0.2573>0\). From Theorem 3.2, we can see that system (2) has at least one positive T-periodic solution (see Fig. 2).
Example 2
In model (3), if the Markov chain \(r(t)\) take values in \(\mathbb{S}=\{1,2\}\) with the generator
Then the unique stationary distribution of \(r(t)\) is \((\pi_{1},\pi _{2})= (\frac{1}{2},\frac{1}{2} )\). Choose parameters
Case (a). By direct calculation, we get \(R_{1}^{*}=0.5678<1\). Then from Theorem 4.1, we know the disease \(I(t)\) finally go to extinction (see Fig. 3).
Case (b). We only change the intensity of the noise \(\sigma_{2}(1)=0.15\), \(\sigma_{2}(2)=0.2\). Then we have \(R_{2}^{*}=2.0560>1\), one can derived that model (3) has a unique stationary distribution. Figure 4(a) shows the Markov chain switching process and Fig. 4(b) shows the process of changing system variables over time. From Fig. 4(c), Fig. 4(d) and Fig. 4(e), we can see system (3) has a stationary distribution.
Computer simulation of a single path of Markov chain \(r(t)\) and its corresponding solutions \((S(t),I(t),R(t))\) for the system (3). The last three pictures are the histograms of the path
References
Miao, A., Wang, X., Zhang, T., Wang, W., Pradeep, B.G.S.A.: Dynamical analysis of a stochastic SIS epidemic model with nonlinear incidence rate and double epidemic hypothesis. Adv. Differ. Equ. 2017(1), 226 (2017)
Li, F., Meng, X., Wang, X.: Analysis and numerical simulations of a stochastic SEIQR epidemic system with quarantine-adjusted incidence and imperfect vaccination. Comput. Math. Methods Med. 2018, Article ID 7873902 (2018)
Zhang, T., Meng, X., Zhang, T.: Global dynamics of a virus dynamical model with cell-to-cell transmission and cure rate. Comput. Math. Methods Med. 2015, Article ID 758362 (2015)
Li, X., Lin, X., Lin, Y.: Lyapunov-type conditions and stochastic differential equations driven by G-Brownian motion. J. Math. Anal. Appl. 439(1), 235–255 (2016)
Meng, X., Li, F., Gao, S.: Global analysis and numerical simulations of a novel stochastic eco-epidemiological model with time delay. Appl. Math. Comput. 339, 701–726 (2018)
Zhang, T., Liu, X., Meng, X., Zhang, T.: Spatio-temporal dynamics near the steady state of a planktonic system. Comput. Math. Appl. 75(12), 4490–4504 (2018)
Jiang, Z., Zhang, W., Zhang, J., Zhang, T.: Dynamical analysis of a phytoplankton–zooplankton system with harvesting term and Holling III functional response. Int. J. Bifurc. Chaos 28(13), 1850162 (2018)
Liu, L., Meng, X.: Optimal harvesting control and dynamics of two-species stochastic model with delays. Adv. Differ. Equ. 2017(1), 18 (2017)
Miao, A., Zhang, J., Zhang, T., Pradeep, B.G.S.A.: Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination. Comput. Math. Methods Med. 2017, Article ID 4820183 (2017)
Liu, X., Li, Y., Zhang, W.: Stochastic linear quadratic optimal control with constraint for discrete-time systems. Appl. Math. Comput. 228, 264–270 (2014)
Lin, X., Zhang, R.: \(\mathrm{H}_{\infty}\) control for stochastic systems with Poisson jumps. J. Syst. Sci. Complex. 24(4), 683–700 (2011)
May, R.M.: Stability and Complexity in Model Ecosystems. Princeton University Press, Princeton (2001)
Qi, H., Liu, L., Meng, X.: Dynamics of a non-autonomous stochastic SIS epidemic model with double epidemic hypothesis. Complexity 2017, Article ID 4861391 (2017)
Fan, X., Song, Y., Zhao, W.: Modeling cell-to-cell spread of HIV-1 with nonlocal infections. Complexity 2018, Article ID 2139290 (2018)
Chi, M., Zhao, W.: Dynamical analysis of multi-nutrient and single microorganism chemostat model in a polluted environment. Adv. Differ. Equ. 2018(1), 120 (2018)
Leng, X., Feng, T., Meng, X.: Stochastic inequalities and applications to dynamics analysis of a novel SIVS epidemic model with jumps. J. Inequal. Appl. 2017, 138 (2017)
Liu, G., Wang, X., Meng, X.: Extinction and persistence in mean of a novel delay impulsive stochastic infected predator-prey system with jumps. Complexity 2017, Article ID 1950970 (2017)
Zhao, W., Li, J., Meng, X.: Dynamical analysis of sir epidemic model with nonlinear pulse vaccination and lifelong immunity. Discrete Dyn. Nat. Soc. 2015, Article ID 848623 (2015)
Miao, A., Zhang, T., Zhang, J., Wang, C.: Dynamics of a stochastic SIR model with both horizontal and vertical transmission. J. Appl. Anal. Comput. 2018(4), 1108–1121 (2018)
Song, Y., Miao, A., Zhang, T.: Extinction and persistence of a stochastic SIRS epidemic model with saturated incidence rate and transfer from infectious to susceptible. Adv. Differ. Equ. 2018(1), 293 (2018)
Zhang, S., Meng, X., Wang, X.: Application of stochastic inequalities to global analysis of a nonlinear stochastic SIRS epidemic model with saturated treatment function. Adv. Differ. Equ. 2018(1), 50 (2018)
Zhong, X., Guo, S., Peng, M.: Stability of stochastic SIRS epidemic models with saturated incidence rates and delay. Stoch. Anal. Appl. 35(1), 1–26 (2016)
Chang, Z., Meng, X., Zhang, T.: A new way of investigating the asymptotic behaviour of a stochastic sis system with multiplicative noise. Appl. Math. Lett. 87, 80–86 (2019)
Qi, H., Leng, X., Meng, X., Zhang, T.: Periodic solution and ergodic stationary distribution of SEIS dynamical systems with active and latent patients. Qual. Theory Dyn. Syst. (2018). https://doi.org/10.1007/s12346-018-0289-9
Liu, Q., Jiang, D., Shi, N., Hayat, T., Alsaedi, A.: Stationary distribution and extinction of a stochastic SIRS epidemic model with standard incidence. Phys. A, Stat. Mech. Appl. 469, 510–517 (2017)
Zhang, S., Meng, X., Feng, T., Zhang, T.: Dynamics analysis and numerical simulations of a stochastic non-autonomous predator–prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 26, 19–37 (2017)
Yu, X., Yuan, S., Zhang, T.: The effects of toxin-producing phytoplankton and environmental fluctuations on the planktonic blooms. Nonlinear Dyn. 91(3), 1653–1668 (2018)
Liu, Q., Jiang, D., Shi, N., Hayat, T., Alsaedi, A.: Nontrivial periodic solution of a stochastic non-autonomous SISV epidemic model. Phys. A, Stat. Mech. Appl. 462, 837–845 (2016)
Zhang, T., Meng, X., Zhang, T.: Global analysis for a delayed SIV model with direct and environmental transmissions. J. Appl. Anal. Comput. 6(2), 479–491 (2016)
Zhang, T., Meng, X., Song, Y., Zhang, T.: A stage-structured predator–prey SI model with disease in the prey and impulsive effects. Math. Model. Anal. 18(4), 505–528 (2013)
Greenhalgh, D., Moneim, I.A.: SIRS epidemic model and simulations using different types of seasonal contact rate. Syst. Anal. Model. Simul. 43(5), 573–600 (2003)
Martcheva, M.: A non-autonomous multi-strain SIS epidemic model. J. Biol. Dyn. 3(2–3), 235–251 (2009)
Lin, Y., Jiang, D., Liu, T.: Nontrivial periodic solution of a stochastic epidemic model with seasonal variation. Appl. Math. Lett. 45, 103–107 (2015)
Yu, X., Yuan, S., Zhang, T.: Persistence and ergodicity of a stochastic single species model with Allee effect under regime switching. Commun. Nonlinear Sci. Numer. Simul. 59, 359–374 (2018)
Xu, C., Yuan, S., Zhang, T.: Average break-even concentration in a simple chemostat model with telegraph noise. Nonlinear Anal. Hybrid Syst. 29, 373–382 (2018)
Liu, M., Wang, K.: Persistence and extinction of a stochastic single-specie model under regime switching in a polluted environment. J. Theor. Biol. 264(3), 934–944 (2010)
Bian, F., Zhao, W., Song, Y., Yue, R.: Dynamical analysis of a class of prey–predator model with Beddington–DeAngelis functional response, stochastic perturbation, and impulsive toxicant input. Complexity 2017, Article ID 3742197 (2017)
Zhang, X., Jiang, D., Alsaedi, A., Hayat, T.: Stationary distribution of stochastic SIS epidemic model with vaccination under regime switching. Appl. Math. Lett. 59, 87–93 (2016)
Liu, Q., Jiang, D., Shi, N.: Threshold behavior in a stochastic SIQR epidemic model with standard incidence and regime switching. Appl. Math. Comput. 316, 310–325 (2018)
Settati, A., Lahrouz, A.: Stationary distribution of stochastic population systems under regime switching. Appl. Math. Comput. 244, 235–243 (2014)
Slatkin, M.: The dynamics of a population in a Markovian environment. Ecology 59(2), 249–256 (1978)
Mao, X.: Stability of stochastic differential equations with Markovian switching. Stoch. Process. Appl. 79(1), 45–67 (1999)
Zhao, Y., Yuan, S., Zhang, T.: The stationary distribution and ergodicity of a stochastic phytoplankton allelopathy model under regime switching. Commun. Nonlinear Sci. Numer. Simul. 37, 131–142 (2016)
Liptser, R.S.: A strong law of large numbers for local martingales. Stochastics 3(1–4), 217–228 (1980)
Acknowledgements
The authors thank the editors and the anonymous referees for their careful reading and valuable comments.
Availability of data and materials
Data sharing not applicable to this article as all data sets are hypothetical during the current study.
Funding
This work is supported by SDUST Research Fund (2014TDJH102).
Author information
Authors and Affiliations
Contributions
All authors worked together to produce the results and read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, W., Liu, J., Chi, M. et al. Dynamics analysis of stochastic epidemic models with standard incidence. Adv Differ Equ 2019, 22 (2019). https://doi.org/10.1186/s13662-019-1972-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1972-0