Delay-induced Hopf bifurcation in a diffusive Holling–Tanner predator–prey model with ratio-dependent response and Smith growth

Abstract

In this paper, we study a diffusion Holling–Tanner predator–prey model with ratio-dependent functional response and Simth growth subject to a homogeneous Neumann boundary condition. Firstly, we use iteration technique and eigenvalue analysis to get the local stability and a Hopf bifurcation at the positive equilibrium. Secondly, by choosing the constant related to delay as bifurcation parameter we obtain periodic solutions near the positive equilibrium. Besides, by using center manifold theory and normal form theory we reflect the stability with Hopf bifurcating periodic solution and bifurcating direction.

1 Introduction

Mathematical ecology is a fast and active branch of biomathematics, and the dynamics of biological models are very rich. Thus it is very important for research. The predator–prey model is a very important population dynamics model. It is mainly reflected the factors influencing on the model in the functional response, based on ratio, age, or gender structure, reaction–diffusion, etc. The results of the study are mainly reflected in the stability of the equilibrium point, periodic solution, almost periodic solution, limit cycle, Hopf bifurcation, etc. The functional response is a very important factor to predator–prey model [1–5], It can be divided into several types, such as Hassell–Varley type, Holling types, Beddington–DeAngelies type, Crowley–Martin type, and so on.

In recent years, many authors investigate the diffusive predator–prey model with logistic prey growth rate [6–10] or strong Allee effect in prey [11]. It came out that this assumption is not realistic for a food-limited population under the effect of environmental toxicants. Thus the population dynamics growth restriction is based on the unused available resources [12–16]. This model, also known as the Holling–Tanner model, has been studied for both its mathematical properties and its efficacy for describing real ecological systems such as mite/spider mite, lynx/hare, sparrow/sparrow hawk, and so one by Holling [2], Tanner [3] and Wollkind, Collings, and Logan [4].

In particular, Yue and Wang [16] studied the stability and Hopf bifurcation of a diffusive Holling–Tanner predator–prey model with smith growth subject to Neumann boundary condition:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=d_{1}\Delta u(x,t)+\frac{u(x,t) ( 1-u(x,t) ) }{1+cu(x,t)}- \frac{\beta u(x,t)v(x,t)}{\alpha v(x,t)+u(x,t)},&x\in (0,\pi),t>0, \\ \frac{\partial v(x,t)}{\partial t}=d_{2}\Delta v(x,t)+\delta v(x,t) ( 1-\frac{\eta v(x,t)}{u(x,t)} ), & x\in (0,\pi),t>0, \\ u_{x}(0,t)=u_{x}(\pi,t)=v_{x}(0,t)=v_{x}(\pi,t)=0, & t\geq 0, \\ u(x,0)=u_{0}(x)\geq 0,\qquad v(x,0)=v_{0}(x)\geq 0, & x\in (0,\pi). \end{cases} $$

(1.1)

In realistic systems, delay exists everywhere. We have obtained many interesting conclusions since time delays may have very complex influence on the dynamical behaviors of systems. In the survey papers [12, 17–19], the authors deduced that delay difference equations are much more complicated than ordinary differential equations, because time delay can lead to unstable equilibrium and induce bifurcation. Many results on the Hopf bifurcation of diffusion system can be found in [20–27]. The Hopf bifurcation of the diffusive predator–prey system with delay subject to homogeneous Neumann boundary conditions was studied in [20–23]. The Hopf bifurcation for a delayed predator–prey diffusion system with Dirichlet boundary condition wasonsidered in [24]. The Hopf bifurcation for a predator-prey model with age structure was studied in [27].

Chen et al. [20] have considered a delayed diffusive Leslie–Gower predator–prey system with homogeneous Neumann boundary conditions

$$\begin{aligned} \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=d_{1}\Delta u(x,t)+u(x,t) ( p- \alpha u(x,t)-v ( x,t-\tau_{1} ) ),& x\in (0,\pi),t>0, \\ \frac{\partial v(x,t)}{\partial t}=d_{2}\Delta v(x,t)+\mu v(x,t) ( 1-\frac{ v(x,t)}{u ( x,t-\tau_{2} ) } ), & x\in (0,\pi),t>0, \\ u_{x}(0,t)=u_{x}(\pi,t)=v_{x}(0,t)=v_{x}(\pi,t)=0, & t\geq 0, \\ u(x,t)=\phi (x,t)\geq 0, & (x,t)\in [0,\pi ]\times [-\tau_{2},0], \\ v(x,t)=\psi (x,t)\geq 0, & (x,t)\in [0,\pi ]\times [-\tau_{1},0]. \end{cases}\displaystyle \end{aligned}$$

Some related work considered the Hopf bifurcation in predator–prey models. According to the results of [20] and the analysis of the stability and bifurcation system (1.1) in [16], we mainly consider the dynamics of the following system:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=d_{1}\Delta u(x,t)+\frac{u(x,t) ( 1-u(x,t) ) }{1+cu(x,t)}-\frac{\beta u(x,t)v(x,t-\tau_{1})}{ \alpha v(x,t-\tau_{1})+u(x,t)}, &x\in (0,\pi),t>0, \\ \frac{\partial v(x,t)}{\partial t}=d_{2}\Delta v(x,t)+\delta v(x,t) ( 1-\frac{\eta v(x,t)}{u(x,t-\tau_{2})} ), & x\in (0,\pi),t>0, \\ u_{x}(0,t)=u_{x}(\pi,t)=v_{x}(0,t)=v_{x}(\pi,t)=0, & t\geq 0, \\ u(x,t)=\phi (x,t)\geq 0, & (x,t)\in [0,\pi ]\times [-\tau_{2},0], \\ v(x,t)=\psi (x,t)\geq 0, & (x,t)\in [0,\pi ]\times [-\tau_{1},0]. \end{cases} $$

(1.2)

As far as we know, there are no results on the Hopf bifurcation of system (1.2). In this paper, we investigate the stability of the positive equilibrium, delay-induced Hopf bifurcation, and the properties of Hopf bifurcation such as the direction of the bifurcation and stability of the bifurcating periodic solutions.

2 The stability of equilibrium and the existence of Hopf bifurcation

In this paper, we only investigate the effect of the delay on the stability of the positive equilibrium $E^{*}(u^{*},v^{*})$ of system (1.2), where

$$\begin{aligned} u^{*}=\frac{\alpha +\eta -\beta }{\alpha +\eta +\beta c},\qquad v^{*}=\frac{u ^{*}}{\eta }, \end{aligned}$$

under condition $(H)$: $\beta <\alpha +\eta$.

For simplicity, in this paper, we only study the case $\tau_{1}=\tau _{2}=\tau$. Let

$$\begin{aligned}& g^{(1)}(u,v)=\frac{u(x,t) ( 1-u(x,t) ) }{1+cu(x,t)}-\frac{ \beta u(x,t)v(x,t-\tau)}{\alpha v(x,t-\tau)+u(x,t)}, \\& g^{(2)}(u,v)=\delta v(x,t) \biggl( 1-\frac{\eta v(x,t)}{u(x,t-\tau)} \biggr). \end{aligned}$$

The linearization of (1.2) at the equilibrium $E^{*}$ is

$$\left(\begin{array}{c}\frac{\partial u(x,t)}{\partial t}\\ \frac{\partial v(x,t)}{\partial t}\end{array}\right)=D\mathrm{\Delta }\left(\begin{array}{c}u(x,t)\\ v(x,t)\end{array}\right)+A_0\left(\begin{array}{c}u(x,t)\\ v(x,t)\end{array}\right)+A_1\left(\begin{array}{c}u(x,t-\tau )\\ v(x,t-\tau )\end{array}\right),$$

(2.1)

where

$$\begin{array}{c}D\mathrm{\Delta }=\left(\begin{array}{cc}{d}_1\mathrm{\Delta }& 0\\ 0& d_2\mathrm{\Delta }\end{array}\right),A_0=\left(\begin{array}{cc}{b}_{11}& 0\\ 0& b_{22}\end{array}\right),\hfill \\ A_1=\left(\begin{array}{cc}0& b_{12}\\ b_{21}& 0\end{array}\right),\hfill \end{array}$$

with

$$\begin{aligned}& b_{11}=\frac{ ( 1-2u^{*} ) ( 1+cu^{*} ) -cu^{*} ( 1-u ^{*} ) }{ ( 1+cu^{*} ) ^{2}}-\frac{\alpha \beta v^{*2}}{ ( \alpha v^{*}+u^{*} ) ^{2}}, \\& b_{12}=\frac{-\beta u^{*2}}{ ( \alpha v^{*}+u^{*} ) ^{2}},\qquad b _{21}=\frac{\delta }{\eta }, \qquad b_{22}=-\delta. \end{aligned}$$

So, the characteristic equation of (2.1) is

$$ \operatorname{det}\bigl( \lambda I-M_{k}-A_{0}-A_{1}e^{-\lambda \tau } \bigr) =0, $$

(2.2)

where I is the $2\times 2$ identity matrix, and $M_{k}=-k^{2}\operatorname{diag}\{ d_{1},d_{2} \}$, $k\in N_{0}=\{0,1,2,3,\ldots \}$. This is

$$\begin{aligned}& \lambda^{2}+ \bigl[ ( d_{1}+d_{2} ) k^{2}- ( b_{11}+b_{22} ) \bigr] \lambda \\& \quad {}+ \bigl[ d_{1}d_{2}k^{4}-(b_{11}d_{2}+b_{22}d_{1})k^{2}+ \bigl( b _{11}b_{22}-b_{12}b_{21}e^{-2\lambda \tau } \bigr) \bigr] =0. \end{aligned}$$

(2.3)

When $\tau =0$, it becomes

$$ \lambda^{2}+T_{k}\lambda +D_{k}=0, $$

where

$$\begin{aligned}& T_{k}= ( d_{1}+d_{2} ) k^{2}- ( b_{11}+b_{22} ), \\& D_{k}=d_{1}d_{2}k^{4}- ( b_{11}d_{2}+b_{22}d_{1} ) k^{2}+ ( b_{11}b_{22}-b_{12}b_{21} ). \end{aligned}$$

When $\tau \neq 0$, assume that iω ($\omega >0$) is the root of (2.3). Then we have

$$\begin{aligned}& -\omega^{2}+i \bigl[ (d_{1}+d_{2})k^{2}- ( b_{11}+b_{22} ) \bigr] \omega \\& \quad {}+ \bigl[ d_{1}d_{2}k^{4}- ( b_{11}d_{2}+b_{22}d_{1} ) k ^{2}+ \bigl( b_{11}b_{22}-b_{12}b_{21}e^{-2i\omega \tau } \bigr) \bigr] =0. \end{aligned}$$

(2.4)

Separating the real and imaginary parts of (2.4), we get

$$ \textstyle\begin{cases} -\omega^{2}+d_{1}d_{2}k^{4}- ( b_{11}d_{2}+b_{22}d_{1} ) k^{2}+b _{11}b_{22}-b_{12}b_{21}\cos 2\omega \tau =0, \\ [ ( d_{1}+d_{2} ) k^{2}- ( b_{11}+b_{22} ) ] \omega +b_{12}b_{21}\sin 2\omega \tau =0, \end{cases} $$

(2.5)

which implies that

$$ \omega^{4}+P_{k}\omega^{2}+Q_{k}=0, $$

(2.6)

where

$$\begin{aligned}& P_{k}= \bigl[ d_{1}k^{2}-b_{11} \bigr] ^{2}+ \bigl[ d_{2}k^{2}-b_{22} \bigr] ^{2}, \\& Q_{k}=D_{k} \bigl[ d_{1}d_{2}k^{4}- ( b_{11}d_{2}+b_{22}d_{1} ) k ^{2}+ ( b_{11}+b_{22} ) \bigr] . \end{aligned}$$

For $0< k< N_{1}$, we can conclude that (2.6) has only one positive real root

$$ \omega_{k}=\sqrt{\frac{-P_{k}+\sqrt{P_{k}^{2}-4Q_{k}}}{2}},\quad k \in \{0,1,2, \ldots,N_{1}\}. $$

(2.7)

By (2.5) we obtain

$$ \tau_{k}^{j}=\tau_{k}^{0}+ \frac{\pi j}{\omega_{k}},\qquad \tau_{k}^{0}=\frac{1}{2 \omega_{k}} \arccos \frac{-\omega_{k}^{2}+d_{1}d_{2}k^{4}- ( b_{11}d _{2}+b_{22}d_{1} ) k^{2}+b_{11}b_{22}}{b_{12}b_{21}}, $$

(2.8)

for $k\in \{ 0,1,2,\ldots,N_{1} \}$.

Lemma 2.1

If condition $(H)$ hold, then

$$\begin{aligned} \tau_{N_{1}}^{j}\geq \tau_{k+1}^{j}\geq \tau_{k}^{j}\geq \cdots \geq \tau_{1}^{j} \geq \tau_{0}^{j} \end{aligned}$$

for $j\in N_{0}$.

Lemma 2.2

Let condition $(H)$ hold, $T_{k}>0$ and $D_{k}>0$ for $k\in N_{0}$, and let $\omega_{k}$ and $\tau_{k}^{j}$ be defined by (2.7) and (2.8), respectively. Then (2.2) has a pair of purely imaginary roots $i\omega_{k}$ for each $k\in \{ 0,1,2, \ldots,N_{1} \}$, and (2.2) has no purely imaginary roots for $k\geq N_{1}+1$.

Clearly, $\tau_{k}^{0}=\min_{j\in N_{0}} \{ \tau_{k}^{j} \}$, $k \in \{0,1,2,\ldots,N_{1}\}$, and from Lemmas 2.1 and 2.2 we know that $\tau_{0}^{0}=\min \{ \tau_{k}^{j}: 0\leq k\leq N_{1}, j\in N_{0} \}$. Denote $\tau^{*}=\tau_{0}^{0}$. Let $\lambda ( \tau)=\alpha (\tau)+i\delta (\tau)$ be the pair of roots of (2.2) near $\tau =\tau_{k}^{j}$ satisfying $\alpha ( \tau_{k}^{j} ) =0$ and $\delta ( \tau_{k}^{j} ) = \omega_{k}$. Then we have the following transversality condition.

Lemma 2.3

For $k\in \{0,1,2,\ldots,N_{1}\}$ and $j\in N_{0}$, $\frac{d \operatorname{Re}(\lambda)}{d \tau }|_{\tau =\tau_{k}^{j}}>0$.

Proof

Differentiating two sides of (2.2), we get

$$\operatorname{Re}\biggl( \frac{d\lambda }{d\tau } \biggr) ^{-1}=\operatorname{Re}\biggl[ \frac{(2\lambda +T_{k})e^{2\lambda \tau }}{-2a_{12}a_{21}\lambda }-\frac{\tau }{2 \lambda } \biggr] . $$

Thus, by (2.5) and (2.7) we have

$$\begin{aligned} \operatorname{Re}\biggl( \biggl( \frac{d\lambda }{d\tau } \biggr) ^{-1} \biggr) \bigg|_{\tau =\tau _{k}^{j}} =&\operatorname{Re}\biggl[ \frac{(2\lambda +T_{k})e^{2\lambda \tau }}{-a _{12}a_{21}\lambda }-\frac{\tau }{\lambda } \biggr] \bigg|_{\tau =\tau_{k} ^{j}} \\ =&\operatorname{Re}\biggl[ \frac{(2i\omega_{k}+T_{k})e^{2i\omega_{k}\tau_{k}^{j}}}{-ia _{12}a_{21}\omega_{k}}-\frac{\tau_{k}^{j}}{i\omega_{k}} \biggr] \\ =&\frac{T_{k}\sin 2\omega_{k}\tau_{k}^{j}-2\omega_{k}\cos 2\omega _{k}\tau_{k}^{j}}{a_{12}a_{21}\omega_{k}}=\frac{\omega_{k}^{2}+P_{k}}{ ( a_{12}a_{21} ) ^{2}}>0. \end{aligned}$$

From Lemmas 2.1–2.3 and from the qualitative theory of partial differential equations we obtain the following results. □

Theorem 2.1

Assume that condition $(H)$ holds and $\omega_{k}$ and $\tau_{k}^{j}$ are defined by (2.7) and (2.8), respectively. Denote the minimum of the critical values of delay by $\tau^{*}=\min_{k,j} \{ \tau_{k}^{j} \}$.

• (a) The positive equilibrium $( u^{*},v^{*} )$ of system (1.2) is asymptotically stable for $\tau \in ( 0,\tau^{*} )$ and unstable for $( \tau^{*},+\infty )$;

• (b) System (1.2) undergoes Hopf bifurcations near the positive equilibrium $( u^{*},v^{*} )$ at $\tau_{k}^{j}$ for $k\in \{ 0, 1, 2, \ldots, N_{1} \}$ and $j\in N_{0}$.

3 Direction of Hopf bifurcation and stability of bifurcating periodic solution

From Theorem 2.1 we know that model (1.2) undergoes Hopf bifurcations near $E^{*}$ at $\tau =\tau_{k}^{j}$ and that a family homogeneous and inhomogeneous periodic solutions bifurcate from $E^{*}$ of (1.2).

In this section, we investigate the stability of these Hopf bifurcations and bifurcating direction by using the normal formal theory of partial differential equation [21–23]. Without loss of generality, denote any of these critical values by $\tau_{0}$, at which the characteristic equation (1.2) has a pair of simple purely imaginary roots $i\omega _{0}$.

Setting $\tilde{u}(\cdot,t)=u(\cdot,\tau t)-u^{*}$, $\tilde{v}(\cdot,t)=v( \cdot,\tau t)-v^{*}$, $\tilde{U}(t)= ( \tilde{u}(\cdot,\tau t), \tilde{v}(\cdot,\tau t) )$, and $\mathcal{C}= C([-1,0],X)$, $X= \{ (u,v)\in W^{2,2}(0,\pi)|\frac{\partial u}{\partial x}=\frac{ \partial v}{\partial x}=0 \mbox{ at } x=0,\pi \}$ and then dropping the tildes for simplification of notation, system (1.2) can be written as the equation in the space $\mathcal{C}$:

$$ \frac{dU(t)}{dt}=\tau D_{0}\Delta U(t)+L(\tau) (U_{t})+ \tilde{G}(U _{t},\tau), $$

(3.1)

where for $\varphi = ( \varphi_{1},\varphi_{2} ) ^{T}\in \mathcal{C}$, $L(\mu)(\cdot):\mathcal{C}\rightarrow X$ and $\tilde{G}:\mathcal{C}\times R\rightarrow X$ are given by

$$\begin{array}{c}{D}_0\mathrm{\Delta }U=\left(\begin{array}{c}{d}_1\mathrm{\Delta }u\\ d_2\mathrm{\Delta }v\end{array}\right),L(\tau )\phi =\left(\begin{array}{cc}{b}_{11}{\phi }_1(0)& b_{12}{\phi }_2(-1)\\ b_{21}{\phi }_1(-1)& b_{22}{\phi }_2(0)\end{array}\right),\hfill \\ \tilde{G}(\phi ,\epsilon )=\tau \left(\begin{array}{c}{g}^{(1)}(\tau )\\ g^{(2)}(\tau )\end{array}\right)=\left(\begin{array}{c}{\sum }_{i+j+k+l\ge 2}\frac{1}{i!j!k!l!}{g}_{ijkl}^{(1)}{\phi }_1^i(0){\phi }_2^j(0){\phi }_1^k(-1){\phi }_2^l(-1)\\ {\sum }_{i+j+k+l\ge 2}\frac{1}{i!j!k!l!}{g}_{ijkl}^{(2)}{\phi }_1^i(0){\phi }_2^j(0){\phi }_1^k(-1){\phi }_2^l(-1)\end{array}\right)\hfill \end{array}$$

with $g_{ijkl}^{(n)}=\frac{\partial^{i+j+k+l}\tilde{g}^{(n)} ( u ^{*},v^{*},u^{*},v^{*} ) }{\partial u^{i} \partial v^{j} \partial w^{k}\partial s^{l}}$, $n=1,2$, and

$$\begin{aligned}& \tilde{g}^{(1)} ( u,v,w,s ) =\frac{ ( u+u^{*} ) ( 1- ( u+u^{*} ) ) }{1+c ( u+u^{*} ) }-\frac{\beta ( u+u^{*} ) ( s+v^{*} ) }{\alpha ( s+v^{*} ) + ( u+u^{*} ) }, \\& \tilde{g}^{(2)} ( u,v,w,s ) =\delta \bigl( v+v^{*} \bigr) \biggl( 1-\frac{\eta ( v+v^{*} ) }{ ( w+u^{*} ) } \biggr). \end{aligned}$$

By direct computation we obtain $g_{0200}=g_{0002}=g_{1100}=g_{1010}=g _{0011}=0$.

Setting $\tau =\tau_{0}+\varepsilon$, (3.1) is written as

$$ \frac{dU(t)}{dt}=\tau_{0} D_{0}\Delta U(t)+L( \tau_{0}) (U_{t})+ \tilde{G}(U_{t}, \varepsilon), $$

(3.2)

where

$$\begin{aligned} \tilde{G}(U_{t},\varepsilon)=\varepsilon D_{0}\Delta \varphi (0)+L( \varepsilon) (\varphi)+g(\varphi,\tau_{0}+\varepsilon) \quad \text{for } \varphi \in \mathcal{C}. \end{aligned}$$

So, $\varepsilon =0$ is the Hopf bifurcation value for (3.2), and $\Lambda_{0}= \{ -i\omega_{0}\tau_{0},i\omega_{0}\tau_{0} \}$ is the set of eigenvalues on the imaginary axis of the infinitesimal generator associated with the flow of the following linearized system of (3.2) at the origin:

$$\begin{aligned} \frac{dU(t)}{dt}=\tau_{0} D_{0}\Delta U(t)+L( \tau_{0}) (U_{t}). \end{aligned}$$

The eigenvalues of $\tau_{0}D_{0}\Delta$ on X are $\mu^{i}_{k}=-d _{i}\tau_{0}k^{2}$, $i=1,2$, $k\in N_{0}$, with the corresponding normalized eigenfunctions $\beta^{i}_{k}$, where

$${\beta }_k^1=\left(\begin{array}{c}{\gamma }_k(x)\\ 0\end{array}\right),{\beta }_k^2=\left(\begin{array}{c}0\\ {\gamma }_k(x)\end{array}\right),{\gamma }_k(x)=\frac{coskx}{{\parallel coskx\parallel }_{2,2}},k\in N_0.$$

Let $\mathbf{B}_{k}=\operatorname{span}\{ \langle v(\cdot),\beta_{k}^{i}\rangle \beta_{k}^{i}|v \in \mathcal{C},i=1,2 \}$. Then it is easy to verify that $L(\tau_{0})(\mathbf{B}_{k})\subset \operatorname{span}\{ \beta_{k}^{1},\beta _{k}^{2} \}$. Assume that $z_{t}(\theta)\in \mathcal{C}=C ( [-1,0],R ^{2} )$ and

$$z_t^T(\theta )\left(\begin{array}{c}{\beta }_k^1\\ {\beta }_k^2\end{array}\right)\in {\mathbf{B}}_k.$$

Then, the linear PDE restricted on $\mathbf{B}_{k}$ is equivalent to the following FDE on $\mathcal{C}=C ( [-1,0],R^{2} )$:

$$\dot{z}(t)=\left(\begin{array}{cc}{\mu }_k^1& 0\\ 0& {\mu }_k^2\end{array}\right)z(t)+L({\tau }_0)(z_t).$$

When $\tau =\tau_{0}$, define $\eta (\theta)\in BV ( [-1,0],R )$ such that

$$\begin{aligned} \mu_{k}\varphi (0)+L(\tau_{0})\varphi = \int_{-1}^{0}d\eta (\theta) \varphi (\theta) \end{aligned}$$

and the adjoint bilinear form on $\mathcal{C}^{*}\times \mathcal{C}$, $\mathcal{C}^{*}=C ( [0,1],R^{2*} )$ by

$$\begin{aligned} \bigl\langle \psi (s),\phi (\theta)\bigr\rangle =\psi (0)\phi (0)- \int_{-1} ^{0} \int_{0}^{\theta }\psi (\xi -\theta)\,d\eta (\theta)\phi (\xi)\,d\xi. \end{aligned}$$

Then, for (3.2) with fixed k, the dual bases $\Phi_{k}$ and $\Psi_{k}$ for its the eigenspace P and its dual space $P^{*}$ are given by

$$\begin{aligned} \Phi_{k}= \bigl( pe^{i\omega_{0}\tau_{0}\theta },\overline{p}e^{-i\omega _{0}\tau_{0}\theta } \bigr),\qquad \Psi_{k}=\operatorname{col}\bigl( q^{T}e^{-i\omega_{0} \tau_{0}s}, \overline{q}^{T}e^{i\omega_{0}\tau_{0}s} \bigr), \end{aligned}$$

where $\langle \Phi_{k},\Psi_{k}\rangle =I_{2}$, the $2\times 2$ identity matrix, and

$$p=\left(\begin{array}{c}{p}_1\\ p_2\end{array}\right)=\left(\begin{array}{c}1\\ \frac{i{\omega }_0+d_1{k}^2-b_{11}}{b_{12}}{e}^{i{\omega }_0{\tau }_0}\end{array}\right),q=\left(\begin{array}{c}{q}_1\\ q_2\end{array}\right)=D\left(\begin{array}{c}1\\ \frac{i{\omega }_0+d_1{k}^2-b_{11}}{b_{21}}{e}^{i{\omega }_0{\tau }_0}\end{array}\right),$$

with $D= ( 1+2\tau_{0} ( i\omega_{0}+d_{1}k^{2}-b_{11} ) +\frac{ ( i\omega_{0}+d_{1}k^{2}-b_{11} ) e^{2i\omega_{0}\tau_{0}}}{b _{12}b_{21}} ) ^{-1}$.

Following the standard procedure in [21, 23], especially [22], we can obtain the following normal form on the center manifold:

$$\dot{z}=Bz+\left(\begin{array}{c}{A}_{k1}{z}_1\epsilon \\ \overline{A_{k1}}{z}_2\epsilon \end{array}\right)+\left(\begin{array}{c}{A}_{k2}{z}_1^2{z}_2\\ \overline{A_{k2}}{z}_1{z}_2^2\end{array}\right)+O(|z|{\epsilon }^2+|z{|}^4),$$

(3.3)

where

$$\begin{aligned}& A_{k1}=-k^{2} ( d_{1}q_{1}p_{1}+d_{2}q_{2}p_{2} ) +i\omega _{0}q^{T}p, \\& A_{k2}=\frac{i}{2\omega_{0}\tau_{0}} \biggl( B_{k20}B_{k11}-2 \vert B_{k11} \vert ^{2}- \frac{1}{3} \vert B_{k02} \vert ^{2} \biggr) +\frac{1}{2} ( B_{k21}+D_{k21} ), \end{aligned}$$

with

$$\begin{aligned}& B_{k20}=\textstyle\begin{cases} \frac{\tau_{0}}{\sqrt{\pi }} ( c_{1}q_{1}+c_{2}q_{2} ), &k=0, \\ 0, & k\neq 0, \end{cases}\displaystyle \qquad B_{k11}=\textstyle\begin{cases} \frac{\tau_{0}}{\sqrt{\pi }} ( c_{3}q_{1}+c_{4}q_{2} ),& k=0, \\ 0, & k\neq 0. \end{cases}\displaystyle \\& B_{k02}= \textstyle\begin{cases} \frac{\tau_{0}}{\sqrt{\pi }} ( \overline{c_{1}}q_{1}+\overline{c _{2}}q_{2} ),& k=0, \\ 0, & k\neq 0, \end{cases}\displaystyle \qquad B_{k21}= \textstyle\begin{cases} \frac{\tau_{0}}{\pi }c_{5}, & k=0, \\ \frac{3\tau_{0}}{2\pi }c_{5},& k\neq 0, \end{cases}\displaystyle \end{aligned}$$

where

$$\begin{aligned}& c_{1} =g_{2000}^{(1)}p_{1}^{2}+2g_{1001}^{(1)}p_{1}p_{2}e^{-i\omega _{0}\tau_{0}}, \\& c_{2}=g_{0200}^{(2)}p_{2}^{2}+2g_{0110}^{(2)}p_{1}p _{2}e^{-i\omega_{0}\tau_{0}}+g_{0020}^{(2)}p_{1}^{2}e^{-2i\omega_{0} \tau_{0}}, \\& c_{3} =g_{0200}^{(1)} \vert p_{1} \vert ^{2}+2g_{1001}^{(1)}\operatorname{Re}\bigl\{ p_{1} \overline{p _{2}}e^{i\omega_{0}\tau_{0}} \bigr\} , \\& c_{4}=g_{0200}^{(2)} \vert p_{2} \vert ^{2}+2g _{0110}^{(2)}\operatorname{Re}\bigl\{ p_{1} \overline{p_{2}}e^{-i\omega_{0}\tau_{0}} \bigr\} +g _{0020}^{(2)} \vert p_{1} \vert ^{2}, \\& c_{5} =q_{1} \bigl( g_{3000}^{(1)}p_{1} \vert p_{1} \vert ^{2}+g_{2001}^{(1)} \bigl( p _{1}^{2}\overline{p_{2}}e^{i\omega_{0}\tau_{0}}+2 \vert p_{1} \vert ^{2}p_{2}e ^{-i\omega_{0}\tau_{0}} \bigr) \bigr) +q_{2} \bigl( g_{0210}^{(2)} \bigl( 2p _{1} \vert p_{2} \vert ^{2}e^{-i\omega_{0}\tau_{0}} \\& \hphantom{c_{5}=} {}+p_{2}^{2} \overline{p_{1}}e^{i\omega_{0}\tau_{0}} \bigr) +g _{0120}^{(2)} \bigl( p_{1}^{2}\overline{p_{2}}e^{-2i\omega_{0}\tau_{0}}+2 \vert p _{1} \vert ^{2}p_{2} \bigr) +f_{0030}^{(2)}p_{1} \vert p_{1} \vert ^{2}e^{-i\omega_{0} \tau_{0}} \bigr), \end{aligned}$$

and

$$\begin{aligned} D_{k21}= \textstyle\begin{cases} E_{0}, & k=0, \\ E_{0}+\frac{\sqrt{2}}{2}E_{2k}, &k\neq 0, \end{cases}\displaystyle \end{aligned}$$

where

$$E_j=\frac{2{\tau }_0}{\sqrt{\pi }}\left(\begin{array}{c}{S}_1{h}_{j11}^{(1)}(0)+\overline{S_1}{h}_{j20}^{(1)}(0)+S_2{h}_{j11}^{(2)}(-1)+\overline{S_2}{h}_{j20}^{(2)}(-1)+S_3{h}_{j11}^{(2)}(0)+\overline{S_3}{h}_{j20}^{(2)}(0)\\ S_4{h}_{j11}^{(1)}(-1)+\overline{S_4}{h}_{j20}^{(1)}(-1)+S_5{h}_{j11}^{(2)}(0)+\overline{S_5}{h}_{j20}^{(2)}(0)\end{array}\right)$$

with

$$\begin{aligned}& S_{1}=g_{2000}^{(1)}p_{1},\qquad S_{2}=g_{1001}^{(1)}p_{1},\qquad S_{3}=g_{1001} ^{(2)}p_{2}e^{-i\omega_{0}\tau_{0}}, \\& S_{4}=g_{0110}^{(2)}p_{2}+g_{0020}^{(2)}p_{1}e^{-i\omega_{0}\tau _{0}}, \qquad S_{5}=g_{0200}^{(2)}p_{2}+g_{0110}^{(2)}p_{1}e^{-i\omega_{0} \tau_{0}}, \end{aligned}$$

where $h_{k20}(\theta)$ and $h_{k11}(\theta)$ are determined by

$$\begin{aligned}& \textstyle\begin{cases} \dot{h}_{k20}(\theta)-2i\omega_{0}\tau_{0}h_{k20}(\theta)=\Phi_{k}( \theta) \big({\scriptsize\begin{matrix}{} B_{k20} \cr \overline{B_{k20}} \end{matrix}} \big) , \\ \dot{h}_{k20}(0)-L(\tau_{0})(h_{k20})=\tau_{0}c_{kj} \big({\scriptsize\begin{matrix}{} c_{1} \cr c_{2} \end{matrix}} \big) , \end{cases}\displaystyle \\& \textstyle\begin{cases} \dot{h}_{k11}(\theta)=2\Phi_{k}(\theta) \big({\scriptsize\begin{matrix}{} B_{k11} \cr \overline{B_{k11}} \end{matrix}} \big) , \\ \dot{h}_{k11}(0)-L(\tau_{0})(h_{k11})=2\tau_{0}c_{kj} \big({\scriptsize\begin{matrix}{} c_{1} \cr c_{2} \end{matrix}} \big) , \end{cases}\displaystyle \end{aligned}$$

with

$$\begin{aligned} c_{kj}=\textstyle\begin{cases} \frac{1}{\sqrt{\pi }}, & j=k=0, \\ \frac{1}{\sqrt{\pi }} , & j=0,k\neq 0, \\ \frac{1}{\sqrt{2\pi }}, & j=2k\neq 0, \\ 0 & \text{otherwise}. \end{cases}\displaystyle \end{aligned}$$

Through the change of variables $z_{1}=\omega_{1}-i\omega_{2}$, $z_{2}= \omega_{1}+i\omega_{2}$, and $\omega_{1}=\rho_{1}\cos \phi$, $\omega _{2}=\rho_{1}\sin \phi$, the normal form [20] becomes the following polar coordinate system:

$$\begin{aligned} \textstyle\begin{cases} \dot{\rho }=\kappa_{k1}\alpha \rho +\kappa_{k2}\rho^{3}+O ( \alpha ^{2}\rho + \vert (\rho,\alpha) \vert ^{4} ), \\ \dot{\phi }=-\omega_{0}\tau_{0}+O ( \vert (\rho,\alpha) \vert ), \end{cases}\displaystyle \end{aligned}$$

where $\kappa_{k1}=\operatorname{Re}A_{k1}$ and $\kappa_{k2}=\operatorname{Re}A_{k2}$. Thus, from [28] we see that the sign of $\kappa_{k1}\kappa_{k2}$ determines the direction of the bifurcation and the sign of $\kappa_{k2}$ determines the stability of the nontrivial periodic orbits and have following results.

• (a) When $\kappa_{k1}\kappa_{k2}<0$, system (1.2) undergoes Hopf bifurcation at the critical value $\tau =\tau^{*}$, which is a supercritical bifurcation. Moreover, if $\kappa_{k2}<0$, then the bifurcating periodic solution is stable; if $\kappa_{k2}>0$, then the bifurcating periodic solution is unstable.

• (b) When $\kappa_{k1}\kappa_{k2}>0$, system (1.2) undergoes Hopf bifurcation at the critical value $\tau =\tau^{*}$, which is a subcritical bifurcation. Moreover, if $\kappa_{k2}<0$, then the bifurcating periodic solution is stable; if $\kappa_{k2}>0$, then the bifurcating periodic solution is unstable.

4 Numerical simulations

In this section, we give some numerical simulations to support and extend our results by using the mathematical software Matlab.

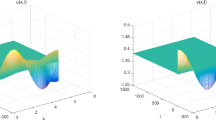
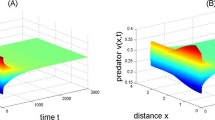
For system (1.2), we choose $d_{1}=0.2$, $d_{2}=1$, $\delta =2$, $\alpha =0.05$, $\beta =0.3$, $h=0.8$, $c=0.1$, and $(u(x,0),v(x,0))=(0.62+0.005\cos x,0.78+0.005 \cos x)$. Then, a series of calculations show that $(u^{*},v^{*})=(0.6250,0.7813)$ and $\tau^{*}=6.8222$. Hence $(0.6250,0.7813)$ is locally stable when $\tau \in [0,\tau^{*})$. When τ crosses through the critical $\tau^{*}$, $(0.6250,0.7813)$ loses its stability, Hopf bifurcation occurs, and a family of periodic solutions are bifurcation from $(0.6250,0.7813)$. The direction and stability of Hopf bifurcation can be determined by the signs $\kappa_{k1}$ and $\kappa_{k2}$; by the procedure of Sect. 3, $\kappa_{k1}=0.0150$ and $\kappa_{k2}=1.1544$. So, the Hopf bifurcation occurring at $\tau^{*}$ is subcritical, and the corresponding Hopf bifurcation periodic orbits are unstable. Taking $\tau =6.5<6.8222$, the numerical simulation results of system (1.2) are depicted Fig. 1. And taking $\tau =6.85>6.8222$, the numerical simulation results of system (1.2) are depicted Fig. 2, which is in agreement with the theoretical results.

Figure 1

The positive equilibrium $( u^{*},v^{*} ) =(0.6250,0.7813)$ of (1.2) is asymptotically stable when $\tau =6.5< 6.8222$. Here we set parameter values $d_{1}=0.2$, $d_{2}=1$, $\delta =2$, $\alpha =0.05$, $\beta =0.3$, $h=0.8$, $c=0.1$ and the initial value $(u(x,0),v(x,0))=(0.62+0.005\cos x,0.78+0.005\cos x)$

Figure 2

There exists unstable spatially homogenous periodic bifurcating from the positive equilibrium $( u^{*},v^{*} ) =(0.6250,0.7813)$ of (1.2) when $\tau =6.85>6.8222$. Here we set parameter values $d_{1}=0.2$, $d_{2}=1$, $\delta =2$, $\alpha =0.05$, $\beta =0.3$, $h=0.8$, $c=0.1$. (A)–(B) The initial value $(u(x,0),v(x,0))=(0.62+0.05\cos x,0.78+0.05\cos x)$; (C)–(D) The initial value $(u(x,0),v(x,0))=(0.62+0.05\sin x,0.78+0.05\sin x)$

5 Conclusions

This paper mainly consider about the effects of delay τ on dynamics of a diffusive predator-prey model with Simth growth rate under Neumann boundary conditions. Based on the analysis of the characteristic equations, we study the stability of the equilibrium and the existence of delay-induced Hopf bifurcations. Then, by the normal forms on the center manifold, we obtain the results determining the direction and stability of Hopf bifurcation. Finally, choosing the parameter values $d_{1}=0.2$, $d_{2}=1$, $\delta =2$, $\alpha =0.05$, $\beta =0.3$, $h=0.8$, $c=0.1$, we get the critical value of delay $\tau^{*}=6.8222$ with a direct computation. From Theorem 2.1 we know that the positive equilibrium $( u^{*},v^{*} ) =(0.6250,0.7813)$ is asymptotically stable for $\tau <\tau^{*}$ and unstable for $\tau >\tau^{*}$. So, system (1.2) undergoes Hopf bifurcation near the positive equilibrium $( u^{*},v ^{*} ) =(0.6250,0.7813)$ when the delay τ increasingly crosses through the critical value $\tau^{*}$.

For the predator–prey systems, pattern dynamics is also an interesting topic. Many authors have discussed the pattern dynamics of the diffusion equations [29–33]. In the next topics, we will discuss the pattern dynamics of a diffusive predator–prey model with Simth growth rate.