An optimal method for approximating the delay differential equations of noninteger order

Abstract

The main purpose of this paper is to use a method with a free parameter, named the optimal asymptotic homotopy method (OHAM), in order to obtain the solution of delay differential equations, delay partial differential equations, and a system of coupled delay equations featuring fractional derivative. This method is preferable to others since it has faster convergence toward homotopy perturbation method, and the convergence rate can be set as a controlled area. Various examples are given to better understand the use of this method. The approximate solutions are compared with exact solutions as well.

1 Introduction

Fractional arithmetic and fractional differential equations appeared in many disciplines, including medicine [1], economics [2], dynamical problems [3, 4], chemistry [5], mathematical physics [6], traffic model [7], fluid flow [8], and so on.

Scholars and researchers are invited to study books that have been written to better understand the concept of fractional arithmetic [9–11]. The fractional differential equations with delay in x are not very well realized. To find the approximate solution for delay differential equations with fractional derivative that we explore in this paper is presented as follows:

$$ D_{x}^{\alpha}u(x) + \mathfrak{A} \bigl(x, u(p_{0}x), u_{x}(p_{1}x), u_{xx}(p_{3}x), \ldots,u_{\underbrace{x\cdots x}_{{n} \text{ order}}}(p_{n}x) \bigr)=g(x) $$

(1.1)

with the initial conditions

$$ u_{x}(0)=\mu_{0},\qquad \ldots,\qquad u_{\underbrace{x\cdots x}_{{n} \text{ order}}}(0)= \mu_{n}, $$

where $\mu_{n}$ is a constant, $g(x)$ is a known analytic function, $0 \leq x \leq1$, $p_{j} \in\mathbb{R}$ for $j =0,1,2,\ldots,n$, $\mathfrak{A}$ is the differential operator, and $D_{x}^{\alpha}$ denotes the fractional Caputo derivative of order α given by

$$\begin{aligned} D_{x}^{\alpha}u(x)=\frac{1}{\Gamma(k+1-\alpha)} \int _{0}^{x}(x-s)^{k-\alpha}u^{(k+1)}(s) \,ds,\quad k< \alpha\leq k+1, k\in\mathbb{Z}^{+}. \end{aligned}$$

(1.2)

These equations for $\alpha=1$ appear in the mathematical and physical modeling of time-dependent process, and their goal is to determine the rate of change of the current situation in comparison with the former models. In particular, this conversion is basic when an ordinary differential equation is based on model failure. Among these types, there are pantograph differential equations , which have been of interest to many researchers. A pantograph is a machine that rolls up an electric current from upper lines for trams or electric trains. The term pantograph has been retrieved from its similarity to pantograph machines for drawings copying and writing [12–14]. About the existence of solutions for these equations, we can mention [15, 16].

The fractional differential equations with shrinking in x and delays in t are not very well realized. So we look for an approximate solution for delay differential equations with fractional derivative of the following form:

$$\begin{aligned}& D_{t}^{\alpha}u(x, t) + \mathfrak{A} \bigl(x, t, u(p_{0}x, q_{0}t), u_{x}(p_{1}x, q_{1}t), u_{xx}(p_{3}x, q_{3}t), \ldots,u_{\underbrace{x\cdots x}_{{n} \text{ order}}}(p_{n}x, q_{n}t) \bigr) \\& \quad =g(x,t) \end{aligned}$$

(1.3)

with the initial conditions

$$ u_{t}(x,0)=h_{0}(x), \ldots, u_{\underbrace{t\cdots t}_{{n} \text{ order}}}(x,0)=h_{n}(x), $$

where $g(x,t)$ is a known analytic function, $t>0$, $0 \leq x \leq 1$, $p_{j}, q_{j} \in\mathbb{R}$ for $j =0,1,2,\ldots,n$, $\mathfrak {A}$ is the partial differential operator, and $D_{t}^{\alpha}$ denotes the fractional Caputo derivative of order α given by

$$ D_{t}^{\alpha}u(x,t)=\frac{1}{\Gamma(k+1-\alpha)} \int _{0}^{t}(t-s)^{k-\alpha}u^{(k+1)}(x,s) \,ds,\quad k< \alpha\leq k+1, k\in\mathbb{Z}^{+}. $$

(1.4)

The delay differential equations (DDEs) and fractional delay differential equations (FDDEs) appear in modeling different problems in engineering and science such as biology models [17, 18], control theory [19, 20], oscillation theory [21, 22], delay systems [23, 24], and so on.

A number of papers that can be found in modeling, deploying and extending delay differential equations, delay partial differential equations, and fractional delay differential equations [25, 26].

It is difficult to derive the exact solution of most DDEs and FDDEs. Hence, a relatively large number of approximate solutions expressed by the scholars are not possible if they find the accurate analytical solutions with the existing procedures. Accordingly, for such differential equations, we have to consider some direct and iterative methods. Some of these techniques used by scholars include the finite difference method [27], the homotopy perturbation method (HPM) [28, 29], the differential transform method (DTM) [30, 31], Adomian’s decomposition method (ADM) [31], the optimal homotopy asymptotic method (OHAM) [32], the homotopy analysis method (HAM) [33–35], the variational iteration method (VIM) [36], and so on [37–40].

This paper is organized as follows. In Sect. 2, we give a description of OHAM. In Sect. 3, we express the convergence of OHAM. In Sect. 4, applications of OHAM to Eqs. (1.1) and (1.3) are illustrated, and some numerical examples are presented. Conclusions are drawn in Sect. 5.

2 Description of OHAM

The overall dimensions of the proposed approach [41] in this section are given and represented in the following differential equation:

$$\begin{array}{rll}& L(u(x,t))+N(u(x,t),u({\eta }_0(x),{\varsigma }_0(t)),u_x({\eta }_1(x),{\varsigma }_1(t)),\dots ,u_{{\underbrace{x\cdots x}}_{n\text{ order}}}({\eta }_n(x),{\varsigma }_n(t)))& \\ & +g(x,t)=0,x\in \mathrm{\Omega }\subseteq {\mathbb{R}}^n,t>0,\end{array}$$

(2.1)

with boundary condition

$$ B \biggl(u,\frac{\partial u}{\partial t} \biggr) =0,\quad t\in\Gamma, $$

(2.2)

where $L=D_{t}^{\alpha}$ is a linear operator, N is a nonlinear operator consisting of the space derivatives of integer order with respect to x along with delay functions, $u(x,t)$ is an unknown function, $g(x,t)$ is a known analytic function, B is a boundary operator, and Γ is the boundary of the domain Ω; also, $\eta_{j}(x)$ and $\varsigma_{j}(t)$ are delay functions. In this work, we consider $\eta_{j}(x)=p_{j} x$ and $\varsigma _{j}(t)=q_{j} t$ for $j=0,1,\ldots,n$.

According to OHAM, we concoct structural homotopy $v(x ,t;p):\Omega\times [0,1 ]\rightarrow\mathbb{R}$ that fulfills the conditions in the following equation:

$$\begin{aligned} &(1-p) L \bigl(v(x,t;p)-u_{0}(x,t) \bigr) \\ &\quad = H(p) (L \bigl(v(x,t;p) \bigr)+g(x,t) \\ &\qquad {}+N \bigl(u (x,t ),u \bigl(\eta_{0}(x),\varsigma_{0}(t) \bigr),u_{x} \bigl(\eta_{1}(x),\varsigma_{1}(t) \bigr),\ldots,u_{\underbrace {x\ldots x}_{{n} \text{ order}}} \bigl(\eta_{n}(x),\varsigma _{n}(t) \bigr) \bigr), \end{aligned}$$

(2.3)

where $p\in[0,1]$ is an infix parameter. The supporting function $H(p)$ is elected in the following display as a nonzero for $p \neq0$ and $H(0) =0$. When $p=0$ and $p=1$, we have $v(x,t;0)=u_{0}(x,t)$ and $v(x,t;1)=u(x,t)$.

Thus, when p varies from 0 to 1, the solution $v(x ,t;p)$ approaches from the initial guess $u_{0}(x,t)$ to exact solution $u(x,t)$; $u_{0}(x,t)$ obtained from (2.2) to (2.3) with $p=0$ giving

$$ L \bigl( u_{0}(x,t;0) \bigr)+g(x,t)=0. $$

(2.4)

The function $H(p)$ is assumed to be

$$ H(p)=p c_{1} + p^{2} c_{2} + p^{3} c_{3} + \cdots, $$

(2.5)

in which $c_{1}, c_{2}, c_{3}, \ldots$ are the convergence control parameters, which are unfamiliar and can be calculated. Another demonstration form $H(p)$ is offered by Herisanu and Marinca [41].

To compute the approximate solution, we expand $v(x,t;p,c_{i})$ in Taylor series around p:

$$ v(x,t;p,c_{i})= u_{0}(x,t)+\sum _{k=1}^{\infty}u_{k}(x,t;c_{i}) p^{k},\quad i=1,2,\ldots. $$

(2.6)

Define the vectors

$$\begin{aligned}& \vec{c}_{l}= \{c_{1},c_{2}, \ldots,c_{l} \}, \\& \vec{u}_{s}= \bigl\{ u_{0}(x,t),u_{1}(x,t; \vec{c}_{1}),\ldots,u_{s}(x,t;\vec {c}_{s}), \\& \hphantom{\vec{u}_{s}={}}(u_{0})_{x} \bigl(\eta_{1}(x), \varsigma_{1}(t) \bigr),(u_{1})_{x} \bigl(\eta _{1}(x),\varsigma_{1}(t);\vec{c}_{1} \bigr), \ldots,(u_{s})_{x} \bigl(\eta _{1}(x), \varsigma_{1}(t);\vec{c}_{s} \bigr) \\& \hphantom{\vec{u}_{s}={}}\vdots \\& \hphantom{\vec{u}_{s}={}}(u_{0})_{\underbrace{x\cdots x}_{{n} \text{ order}}} \bigl(\eta _{n}(x), \varsigma_{n}(t) \bigr),(u_{1})_{\underbrace{x\cdots x}_{ {n} \text{ order}}} \bigl( \eta_{n}(x),\varsigma_{n}(t);\vec{c}_{1} \bigr), \ldots ,(u_{s})_{\underbrace{x\cdots x}_{{n} \text{ order}}} \bigl(\eta _{n}(x), \varsigma_{n}(t);\vec{c}_{s} \bigr) \bigr\} . \end{aligned}$$

(2.7)

We consider the zero-order problem (2.4), the first-order equation

$$ L \bigl( u_{1}(x,t) \bigr)=c_{1} N_{0}(\vec{u}_{0})+g(x,t), $$

(2.8)

and the second-order equation

$$ L \bigl( u_{2}(x,t) \bigr)-L \bigl( u_{1}(x,t) \bigr)=c_{2} N_{0}(\vec {u}_{0})+c_{1} \bigl(L \bigl(u_{1}(x,t) \bigr)+N_{1} ( \vec{u}_{1} ) \bigr). $$

(2.9)

The equations in the general case $u_{k}(x,t)$ are

$$\begin{aligned} &L \bigl( u_{k}(x,t) \bigr)- L \bigl( u_{k-1}(x,t) \bigr) \\ &\quad =c_{k} N_{0} \bigl(u_{0} (x,t) \bigr) + \sum_{m=1}^{k-1}c_{m} \bigl(L \bigl(u_{k-m}(x,t) \bigr)+N_{k-m} ( \vec{u}_{k-1} ) \bigr), \end{aligned}$$

(2.10)

in which $k=2,3,\ldots$ , and $N_{m}$ is the coefficient at $p^{m}$ in the development of $N (v(x,t;p) )$ about the infix parameter p, and we have

$$ N \bigl(v(x,t;p,c_{i}) \bigr)=N_{0} \bigl(u_{0}(x,t) \bigr)+\sum_{m=1}^{\infty }N_{m} (\vec{u}_{m} )p^{m}. $$

(2.11)

We can see that the convergence of series (2.6) depends on the constants $c_{1},c_{2},\ldots$ . If it converges at $p=1$, we have

$$ \tilde{v}(x,t; c_{i})= u_{0}(x,t)+\sum _{k=1}^{m}u_{k}(x,t; c_{i}), \quad i=1,2, \ldots,m. $$

(2.12)

The following residual is the result obtained as a result of embedding (2.12) in (2.1):

$$\begin{aligned} \begin{aligned}[b] R(x,t;c_{i})&= L \bigl(\tilde{v}(x,t; p,c_{i}) \bigr) \\ &\quad {} +g(x,t)+N \bigl(\tilde{v}(x,t; p,c_{i}) \bigr),\quad i=1,2, \ldots,m. \end{aligned} \end{aligned}$$

(2.13)

If $R=0$, then ṽ is the exact solution of (2.1).

Using the method of least squares and knowing the exact solution of the problem, we can minimize the $L^{2}$-norm of the error $E v_{m}(c_{1}, c_{2}, c_{3},\ldots, c_{m})$. The $L^{2}$-norm of the error is

$$ \bigl\Vert E \widetilde{v}_{m}(c_{1},\ldots, c_{m}) \bigr\Vert _{2}= \biggl( \int_{\Omega} \int_{\Gamma} \widetilde{v}_{m}^{2}(x,t) \,dt \, dx \biggr)^{\frac{1}{2}}, $$

where $E \widetilde{v}_{m}(x,t)=|\widetilde{v}_{\mathrm{exact}}(x,t)-\widetilde{v}_{m}(x, t; c_{1},\ldots, c_{m})|$.

3 Convergence of OHAM

In this section, we consider the convergence of the OHAM.

Theorem 3.1

([42])

Let the solution components $u_{0},u_{1},u_{2}, \ldots$ , be defined as given in Eqs. (2.8)–(2.10). The series solution $\sum_{k=0}^{m-1}u_{k}(x,t)$ defined in (2.12) converges if there exists $0<\rho<1$ such that $\|u_{k+1}\| \leq\rho\|u_{k}\|$ for all $k\geq k_{0}$ for some $k_{0} \in\mathbb{N}$.

Proof

Consider the sequence $\{T_{n}\}_{n=0}^{\infty}$ defined as

$$\begin{aligned}& T_{0}=u_{0}, \\& T_{1}=u_{0}+u_{1}, \\& T_{2}=u_{0}+u_{1}+u_{2}, \\& \ldots, \\& T_{n}=u_{0}+u_{1}+u_{2}+ \cdots+u_{n}. \end{aligned}$$

Evidently, it is sufficient to show that the sequence $\lbrace T_{n} \rbrace_{n=0}^{\infty}$ in the Hilbert space $\mathbb {R}$ is a Cauchy sequence. To this end, consider

$$\begin{aligned} \|T_{n+1}-T_{n}\|&=\|u_{n+1}\| \\ &\leq\rho\|u_{n}\| \\ &\leq\rho^{2}\|u_{n-1}\| \\ &\quad \vdots \\ &\leq\rho^{n-k_{0}+1}\|u_{k_{0}}\|. \end{aligned}$$

Assuming that $n\geq m >k_{0}$, $n,m\in\mathbb{N}$, we have

$$\begin{aligned} \Vert T_{n}-T_{m} \Vert &= \bigl\Vert (T_{n}-T_{n-1})+(T_{n-1}-T_{n-2})+\cdots +(T_{m}-T_{m-1}) \bigr\Vert \\ &\leq \bigl\Vert (T_{n}-T_{n-1}) \bigr\Vert + \bigl\Vert (T_{n-1}-T_{n-2}) \bigr\Vert +\cdots+ \bigl\Vert (T_{m}-T_{m-1}) \bigr\Vert \\ &\leq \rho^{n-k_{0}} \Vert u_{k_{0}} \Vert +\rho^{n-k_{0}-1} \Vert u_{k_{0}} \Vert +\cdots +\rho^{m-k_{0}+1} \Vert u_{k_{0}} \Vert \\ &= \biggl(\frac{1-\rho^{n-m}}{1-\rho} \biggr)\rho^{m-k_{0}+1} \Vert u_{k_{0}} \Vert . \end{aligned}$$

Since $0<\rho<1$, we arrive at $\lim_{\substack{n\rightarrow\infty \\ m\rightarrow\infty} }\|T_{n}-T_{m}\|=0$. Therefore, in the Hilbert space $\mathbb{R}$, $\{T_{n}\}_{n=0}^{\infty}$ is a Cauchy sequence, and this implies that series solution converges to the series $\sum_{k=0}^{\infty}u_{k}(x,t)$. □

4 Test examples

To understand OHAM, in this section, we describe and then calculate some examples. These examples include delay differential equations, delay partial differential equations, and a system of coupled fractional delay equations with fractional derivative. In all these examples, we used the mathematical software Mathematica for calculations and graphs.

Test example 4.1

For the first example, we propose the FDDEs [43]

$$ D_{x}^{\alpha} u(x)+2 u \biggl(\frac{x}{2} \biggr) u \biggl(\frac {x}{2} \biggr)=1,\quad 0\leq x\leq1, 0< \alpha\leq1, $$

(4.1)

with the initial condition

$$ u(0)=0. $$

(4.2)

For $\alpha=1$, the exact solution of (4.1) is $u(x)=\sin(x)$.

Following the OHAM, according to what was formulated and presented in Sect. 2 for Eqs. (4.1)–(4.2), we get:

$$\begin{aligned}& u_{0}(x)=\frac{x^{\alpha}}{\Gamma(\alpha+1)}, \\& u_{1}(x)=\frac{2 c_{1}^{2} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma(\alpha+1) \Gamma(3 \alpha +1)}-\frac{2 c_{1} x^{\alpha}}{\Gamma(\alpha+1)}-\frac{2 x^{\alpha }}{\Gamma(\alpha+1)}, \\& u_{2}(x)=-\frac{2 x^{\alpha}}{\Gamma(\alpha+1)}-\frac{4 c_{1} x^{\alpha}}{\Gamma(\alpha+1)}-\frac{8 c_{1} \Gamma (\alpha +\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma(\alpha+1) \Gamma(3 \alpha+1)} \\& \hphantom{u_{2}(x)={}}{}- \frac{2 c_{1}^{2} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \alpha^{2} \Gamma(\alpha) \Gamma(3 \alpha )}-\frac{2 c_{1}^{2} x^{\alpha}}{\Gamma(\alpha+1)}+\frac{2^{5-4 \alpha } c_{1}^{3} \Gamma(4 \alpha) \Gamma (\alpha+\frac{1}{2} ) x^{5 \alpha}}{15 \sqrt{\pi} \alpha^{3} \Gamma(\alpha)^{2} \Gamma(3 \alpha) \Gamma(5 \alpha)} \\& \hphantom{u_{2}(x)={}}{}+ \frac{2 c_{1}^{3} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma(\alpha+1) \Gamma(3 \alpha+1)}+\frac {2 c_{2} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt {\pi} \Gamma(\alpha+1) \Gamma(3 \alpha+1)}, \\& \ldots. \end{aligned}$$

Then, considering the first three terms as estimates of solution for Eq. (4.1), we have

$$\begin{aligned} u(x) \approx& \frac{x^{\alpha}}{\Gamma(\alpha+1)} +\frac{2 c_{1}^{2} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma(\alpha+1) \Gamma(3 \alpha+1)}-\frac{2 c_{1} x^{\alpha }}{\Gamma(\alpha+1)}- \frac{2 x^{\alpha}}{\Gamma(\alpha +1)} \\ &{}-\frac{2 x^{\alpha}}{\Gamma(\alpha+1)}-\frac{4 c_{1} x^{\alpha }}{\Gamma(\alpha+1)}-\frac{8 c_{1} \Gamma (\alpha+\frac {1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma(\alpha+1) \Gamma(3 \alpha+1)}- \frac{2 c_{1}^{2} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \alpha^{2} \Gamma(\alpha) \Gamma(3 \alpha )} \\ &{}-\frac{2 c_{1}^{2} x^{\alpha}}{\Gamma(\alpha+1)}+\frac{2^{5-4 \alpha} c_{1}^{3} \Gamma(4 \alpha) \Gamma (\alpha +\frac{1}{2} ) x^{5 \alpha}}{15 \sqrt{\pi} \alpha^{3} \Gamma (\alpha)^{2} \Gamma(3 \alpha) \Gamma(5 \alpha)}+\frac{2 c_{1}^{3} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma(\alpha+1) \Gamma(3 \alpha+1)} \\ &{}+\frac{2 c_{2} \Gamma (\alpha+\frac{1}{2} ) x^{3 \alpha}}{\sqrt{\pi} \Gamma (\alpha+1) \Gamma(3 \alpha+1)}. \end{aligned}$$

(4.3)

According to least square method for the calculations of the constants $c_{1}$ and $c_{2}$, we get $c_{1}=-2.01508$, $c_{2}=7.91742$, which are called convergent control parameters.

In Table 1, we can see the estimated solutions toward $\alpha=1$, which are derived for various values of x applying OHAM. The $L^{2}$-norm of the error for Test example 4.1 of $\alpha=1$ is 0.00560315.

Table 1 Exact and approximate result of Test example 4.1 with various values of α

Test example 4.2

For the second example, we consider the FDDEs

$$ D_{x}^{\alpha} u(x)-2 u \biggl(\frac{x}{2} \biggr)+u(x)=-x^{2}-1,\quad 0\leq x\leq1, 2< \alpha\leq3, $$

(4.4)

with initial conditions

$$ u(0)=1, \qquad u^{\prime}(0)=-4,\qquad u^{\prime\prime}(0)=0. $$

(4.5)

With the help of the OHAM, according to what was formulated and presented in Sect. 2 for Eqs. (4.4)–(4.5), we get:

$$\begin{aligned}& u_{0}(x)=1-2 x^{2}-\frac{ (\alpha^{2}+3 \alpha+2 x^{2}+2 ) x^{\alpha}}{\Gamma(\alpha+3)} , \\& \begin{aligned} u_{1}(x)&=\frac{c_{1} x^{\alpha} (- (\alpha^{2}+3 \alpha+2 x^{2}+2 ) )}{\Gamma(\alpha+3)} \\ &\quad {}-\frac{c_{1} x^{\alpha} (2^{-\alpha} x^{\alpha} (2 (2^{\alpha}-2 ) (\alpha+1) (2 \alpha+1)+ (2^{\alpha +1}-1 ) x^{2} ) )}{\Gamma(2 \alpha+3)}, \end{aligned} \\& u_{2}(x)= -\frac{ (c_{1}^{2}+c_{1}+c_{2} ) x^{\alpha} (\alpha^{2}+3 \alpha+2 x^{2}+2 )}{\Gamma(\alpha+3)} \\& \hphantom{u_{2}(x)={}}{} -\frac{2^{-3 \alpha-1} c_{1}^{2} x^{3 \alpha} ( (-2^{\alpha +1}-2^{2 \alpha+1}+2^{3 \alpha+2}+1 ) x^{2} )}{\Gamma(3 \alpha+3)} \\& \hphantom{u_{2}(x)={}}{} - \frac{2^{-\alpha} (2 \alpha+3) (2 c_{1}^{2}+c_{1}+c_{2} ) x^{2 \alpha} ( (2^{\alpha+1}-1 ) x^{2} )}{\Gamma (2 \alpha+4)} \\& \hphantom{u_{2}(x)={}}{} - \frac{2^{-3 \alpha-1} (2 (-2^{\alpha+1}-2^{2 \alpha +1}+8^{\alpha}+4 ) (9 \alpha^{2}+9 \alpha+2 ) ) c_{1}^{2} x^{3 \alpha}}{\Gamma(3 \alpha+3)} \\& \hphantom{u_{2}(x)={}}{} - \frac{2^{-\alpha} (2 \alpha+3) (2 (2^{\alpha }-2 ) (2 \alpha^{2}+3 \alpha+1 ) ) (2 c_{1}^{2}+c_{1}+c_{2} ) x^{2 \alpha}}{\Gamma(2 \alpha+4)}, \\& \ldots. \end{aligned}$$

Then, considering the first three terms as estimates of solution for Eq. (4.4), we have

$$\begin{aligned} u(x) \approx & 1-2 x^{2}-\frac{ (\alpha^{2}+3 \alpha+2 x^{2}+2 ) x^{\alpha}}{\Gamma(\alpha+3)} \\ &{}+ \frac{c_{1} x^{\alpha} (- (\alpha^{2}+3 \alpha+2 x^{2}+2 ) )}{\Gamma(\alpha+3)} \\ &{}-\frac{c_{1} x^{\alpha} (2^{-\alpha} x^{\alpha} (2 (2^{\alpha}-2 ) (\alpha+1) (2 \alpha+1)+ (2^{\alpha +1}-1 ) x^{2} ) )}{\Gamma(2 \alpha+3)} \\ &{}-\frac{ (c_{1}^{2}+c_{1}+c_{2} ) x^{\alpha} (\alpha^{2}+3 \alpha+2 x^{2}+2 )}{\Gamma(\alpha+3)} \\ &{}- \frac{2^{-3 \alpha-1} c_{1}^{2} x^{3 \alpha} ( (-2^{\alpha+1}-2^{2 \alpha+1}+2^{3 \alpha+2}+1 ) x^{2} )}{\Gamma(3 \alpha+3)} \\ &{}-\frac{2^{-\alpha} (2 \alpha+3) (2 c_{1}^{2}+c_{1}+c_{2} ) x^{2 \alpha} ( (2^{\alpha+1}-1 ) x^{2} )}{\Gamma (2 \alpha+4)} \\ &{}- \frac{2^{-3 \alpha-1} (2 (-2^{\alpha+1}-2^{2 \alpha +1}+8^{\alpha}+4 ) (9 \alpha^{2}+9 \alpha+2 ) ) c_{1}^{2} x^{3 \alpha}}{\Gamma(3 \alpha+3)} \\ &{}-\frac{2^{-\alpha} (2 \alpha+3) (2 (2^{\alpha }-2 ) (2 \alpha^{2}+3 \alpha+1 ) ) (2 c_{1}^{2}+c_{1}+c_{2} ) x^{2 \alpha}}{\Gamma(2 \alpha+4)}. \end{aligned}$$

(4.6)

For the calculations of the constants $c_{1}$ and $c_{2}$, using the method of least squares, we have computed that

$$c_{1}=0,\qquad c_{2}=-0.970385. $$

In Table 2, we can see the estimated solutions for various values of α, which are derived for various values of x through applying OHAM. The $L^{2}$-norm of the error for Test example 4.2 with $\alpha=3$ is 0.00173416.

Table 2 Exact and approximate result of Test example 4.2 with various values of α

For $\alpha=3$, the approximate solution obtained by the proposed method corresponds to the exact solution $u(x)=1-2 x^{2}$.

Test example 4.3

For the third example, we offer the FDDEs [44]

$$ D^{\alpha}_{t}u(x,t)=u \biggl(x,\frac{t}{2} \biggr) u_{xx} \biggl(x,\frac {t}{2} \biggr)-u(x,t),\quad t>0, 0 \leq x\leq1, 0< \alpha\leq1, $$

(4.7)

with initial condition

$$ u(x,0)=x^{2}. $$

(4.8)

With attention to the OHAM, according to Sect. 2, for Eqs. (4.7)–(4.8), we get:

$$\begin{aligned}& u_{0}(x,t)=-\frac{c_{1} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha)} , \\& u_{1}(x,t)= -\frac{c_{1} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha )}-\frac{c_{1}^{2} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha)}+ \frac {\sqrt{\pi} 2^{2-3 \alpha} c_{1}^{2} x^{2} t^{2 \alpha}}{\alpha \Gamma (\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac{\sqrt{\pi } 4^{-\alpha} c_{1}^{2} x^{2} t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac{c_{2} x^{2} t^{\alpha }}{\alpha \Gamma(\alpha)}, \\& u_{2}(x,t)= \frac{\sqrt{\pi} 2^{2-3 \alpha} c_{1}^{2} x^{2} t^{2 \alpha }}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac{\sqrt{\pi} 4^{-\alpha} c_{1}^{2} x^{2} t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac {c_{1}^{2} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha)}- \frac{2 c_{1} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha)}-\frac{c_{2} x^{2} t^{\alpha }}{\alpha \Gamma(\alpha)}+x^{2}, \\& \ldots. \end{aligned}$$

Then, considering the first three terms as estimates of solution for Eq. (4.7), we have:

$$ u(x,t)\approx \frac{\sqrt{\pi} 2^{2-3 \alpha} c_{1}^{2} x^{2} t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac {1}{2} )}-\frac{\sqrt{\pi} 4^{-\alpha} c_{1}^{2} x^{2} t^{2 \alpha }}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}- \frac{c_{1}^{2} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha)}-\frac{2 c_{1} x^{2} t^{\alpha}}{\alpha \Gamma(\alpha)}-\frac{c_{2} x^{2} t^{\alpha }}{\alpha \Gamma(\alpha)}+x^{2}. $$

Using the method of least squares, we get

$$c_{1}=-1.25313, \qquad c_{2}=0.103091. $$

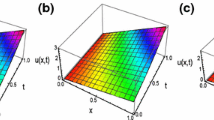
In Table 3, we can see the estimated solutions for various values of α, which are derived for various values of x and t in Fig. 1. We can see the exact and approximate answers featuring $\alpha=1$ through applying OHAM. The $L^{2}$-norm of the error for Test example 4.3 with $\alpha=1$ is 0.020451.

Figure 1

Comparison of the third-order approximate solution (4.7) with exact solution for $\alpha=1$

Table 3 Exact and approximate result of Test example 4.3 with various values of α

Toward $\alpha= 1$, the solution we have obtained is in accordance with the exact solution $u(x, t)=x^{2} \exp(t)$.

Test example 4.4

For the fourth instance, consider the FDDEs

$$\begin{aligned} D^{\alpha}_{t}u(x,t) =&u_{xx}(x,t)+u \biggl(x,\frac{t}{2} \biggr) u_{xx} \biggl(\frac{x}{2}, \frac{t}{2} \biggr) \\ &{}+2 u \biggl(\frac{x}{2},t \biggr), \quad t>0, 0\leq x\leq1, 1< \alpha\leq2, \end{aligned}$$

(4.9)

with initial conditions

$$ u(x,0)=x,\qquad u_{t}(x,0)=0. $$

(4.10)

Concerning the OHAM, according to what was formulated and presented in Sect. 2, for Eqs. (4.9)–(4.10), we get:

$$\begin{aligned}& u_{0}(x,t)=x , \\& u_{1}(x,t)= -\frac{c_{1} x t^{\alpha}}{\alpha \Gamma(\alpha)}, \\& u_{2}(x,t)= \frac{\sqrt{\pi} 4^{-\alpha} c_{1}^{2} x t^{2 \alpha }}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac{c_{1}^{2} x t^{\alpha}}{ (\alpha-\alpha^{2} ) \Gamma (\alpha)}-\frac{c_{1} x t^{\alpha}}{ (\alpha-\alpha^{2} ) \Gamma(\alpha)} \\& \hphantom{u_{2}(x,t)={}}{}- \frac{c_{1}^{2} x t^{\alpha}}{(\alpha-1) \Gamma (\alpha)}-\frac{c_{1} x t^{\alpha}}{(\alpha-1) \Gamma(\alpha )}-\frac{c_{2} x t^{\alpha}}{\alpha \Gamma(\alpha)}, \\& \ldots. \end{aligned}$$

Then, considering the first three terms as estimates of solution for Eq. (4.9) we have:

$$\begin{aligned} u(x,t) \approx& x-\frac{c_{1} x t^{\alpha}}{(\alpha-1) \Gamma(\alpha )}-\frac{c_{1} x t^{\alpha}}{\alpha \Gamma(\alpha)}- \frac{c_{1} x t^{\alpha}}{ (\alpha-\alpha^{2} ) \Gamma(\alpha )} \\ &{}-\frac{\sqrt{\pi} 4^{-\alpha} c_{1}^{2} x t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac {c_{1}^{2} x t^{\alpha}}{ (\alpha-\alpha^{2} ) \Gamma(\alpha )}+\frac{c_{1}^{2} x t^{\alpha}}{(\alpha-1) \Gamma(\alpha)}- \frac{c_{2} x t^{\alpha}}{\alpha \Gamma(\alpha)}. \end{aligned}$$

Using the method of least squares, by calculations we came to the following:

$$c_{1}=-1.03557,\qquad c_{2}=0.00250421. $$

In Table 4, we can see the estimated solutions toward various values of α, which are derived for various values of x and t by applying OHAM.

Table 4 Exact and approximate result of Test example 4.4 with various values of α

The $L^{2}$-norm of the error for Test example 4.4 with $\alpha=2$ is 0.000149502.

In Fig. 2, we can see the exact and approximate answers featuring $\alpha= 2$. For $\alpha= 2$, the exact solution with $u(x, t)=x \cosh(t)$ and the obtained approximate solution are consistent.

Figure 2

Comparison of the third-order approximate solution (4.9) with exact solution for $\alpha=2$

Test example 4.5

For the fifth instance, we consider the system of coupled FDDEs

$$ \textstyle\begin{cases} D^{\alpha}_{t}u(x,t)+v(x,t)-u_{xx}(x,t)+u v_{x} (\frac {x}{2},\frac{t}{2} )=\frac{1}{2} (t+3 x-2),\quad 0< \alpha\leq1, \\ D^{\alpha}_{t}v(x,t)-u (\frac{x}{2},\frac{t}{2} )+v_{xx} (\frac{x}{3},t )+v_{x} (\frac{x}{2},2 t )=\frac{1}{2} (t-x+3), \end{cases} $$

(4.11)

for $t>0$ and $0\leq x\leq1$ with initial conditions

$$ u(x,0)=x,\qquad v(x,0)=x. $$

(4.12)

For $\alpha=1$, the exact solutions are $u(x,t)=x - t$ and $v(x,t)=x + t$.

With respect to the OHAM, according to what was presented in Sect. 2, for Eqs. (4.11)–(4.12), considering the first two terms as estimates of solution for Eq. 4.11, we have:

$$\begin{aligned} u(x,t) \approx& x-\frac{11 t^{\alpha}}{\alpha \Gamma(\alpha )}+\frac{3 x t^{\alpha}}{2 \alpha \Gamma(\alpha)}+\frac{t^{\alpha +1}}{2 (\alpha^{2}+\alpha ) \Gamma(\alpha)}- \frac{10 t^{\alpha}}{\alpha \Gamma(\alpha)}-\frac{t^{\alpha+1}}{2 (\alpha^{2}+\alpha ) \Gamma(\alpha)} \\ &{}+\frac{c_{1} t^{\alpha+1}}{ (2 \alpha^{2}+2 \alpha ) \Gamma(\alpha)}-\frac{c_{1} t^{\alpha+1}}{2 (\alpha^{2}+\alpha ) \Gamma(\alpha)}-\frac{10 c_{1} t^{\alpha}}{\alpha \Gamma (\alpha)}+ \frac{3 c_{1} x t^{\alpha}}{2 \alpha \Gamma(\alpha )} \\ &{}+\frac{t^{\alpha+1}}{ (2 \alpha^{2}+2 \alpha ) \Gamma (\alpha)}-\frac{\sqrt{\pi} 4^{1-\alpha} c_{1} t^{2 \alpha}}{\alpha \Gamma (\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac{\sqrt{\pi } 2^{-3 \alpha-2} c_{1} x t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )} \\ &{}+\frac{\sqrt{\pi} 4^{-\alpha-1} c_{1} x t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha +\frac{1}{2} )}-\frac{2^{\alpha-3} c_{1} x \Gamma (\alpha +\frac{1}{2} ) t^{3 \alpha}}{\sqrt{\pi} \alpha^{2} \Gamma (\alpha) \Gamma(3 \alpha)}+ \frac{11\, 2^{-\alpha-2} c_{1} \Gamma(2 \alpha+1) t^{3 \alpha }}{\alpha^{2} \Gamma(\alpha)^{2} \Gamma(3 \alpha+1)} \\ &{}+\frac{3 c_{1} \Gamma(\alpha+2) t^{2 \alpha+1}}{2 \alpha \Gamma(\alpha) \Gamma (2 \alpha+3)}-\frac{2^{-\alpha-3} c_{1} \Gamma(2 \alpha+2) t^{3 \alpha+1}}{\alpha \Gamma(\alpha) \Gamma(\alpha+2) \Gamma(3 \alpha+2)} \end{aligned}$$

(4.13)

and

$$\begin{aligned} v(x,t) \approx& x+\frac{3 t^{\alpha}}{2 \alpha \Gamma(\alpha )}-\frac{x t^{\alpha}}{2 \alpha \Gamma(\alpha)}+\frac{t^{\alpha +1}}{2 (\alpha^{2}+\alpha ) \Gamma(\alpha)}- \frac {t^{\alpha+1}}{2 (\alpha^{2}+\alpha ) \Gamma(\alpha)} \\ &{}+ \frac{t^{\alpha+1}}{ (2 \alpha^{2}+2 \alpha ) \Gamma (\alpha)}+\frac{d_{1} t^{\alpha}}{2 \alpha \Gamma(\alpha)}-\frac {d_{1} x t^{\alpha}}{2 \alpha \Gamma(\alpha)}- \frac{d_{1} t^{\alpha +1}}{2 (\alpha^{2}+\alpha ) \Gamma(\alpha)} \\ &{}+\frac{d_{1} t^{\alpha+1}}{ (2 \alpha^{2}+2 \alpha ) \Gamma(\alpha)}-\frac{\sqrt{\pi} 2^{-\alpha-2} d_{1} t^{2 \alpha }}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}+\frac{11 \sqrt{\pi} 8^{-\alpha} d_{1} t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )} \\ &{}- \frac{3 \sqrt{\pi} 2^{-3 \alpha-2} d_{1} x t^{2 \alpha}}{\alpha \Gamma(\alpha) \Gamma (\alpha+\frac{1}{2} )}-\frac {2^{-\alpha-1} d_{1} \Gamma(\alpha+2) t^{2 \alpha+1}}{\alpha \Gamma (\alpha) \Gamma(2 \alpha+3)} . \end{aligned}$$

(4.14)

Substituting $x=0.5$ and $t=0.5$, we get $c_{1}=-0.705501$ and $d_{1}=-0.729647$.

In Table 5, we can see the estimated solutions toward $\alpha=1$ and $t=0.01$, which are derived for various values of x by applying OHAM.

Table 5 Exact and approximate result of Test example 4.5

5 Conclusion

We have successfully applied OHAM to obtain approximate solutions of the delay differential equations, delay partial differential equations, and a system of coupled fractional delay equations featuring fractional derivative. The result indicates that a few iterations of OHAM result in some useful solutions.

Finally, it should be added that the suggested technique has the potential to be practical in solving other similar nonlinear and linear problems in partial differential equations featuring fractional derivative.

Appendix:  Illustration of test example (4.1) in detail

Consider test example (4.1):

$$ D^{\alpha} u(x)+2 u \biggl(\frac{x}{2} \biggr) u \biggl(\frac {x}{2} \biggr)=1,\quad 0\leq x\leq1, 0< \alpha\leq1, $$

(A.1)

with initial condition

$$ u(0)=0. $$

(A.2)

Considering

$$ u(x,p)=u_{0}+ \sum_{i=1}^{\infty}u_{i}p^{i} $$

(A.3)

and

$$ H(p)=p c_{1}+ p^{2} c_{2}+ \cdots $$

(A.4)

and using of OHAM, for the first equation of (A.1), we get

$$\begin{aligned}& \bigl( D^{\alpha}u_{0}+ p D^{\alpha}u_{1}+ p^{2} D^{\alpha}u_{2}+ \cdots-1 \bigr) \\& \quad {}- \bigl(p D^{\alpha}u_{0}+p^{2} D^{\alpha}u_{1}+p^{3} D^{\alpha}u_{2}+\cdots -p \bigr) \\& \quad {}- \bigl( p c_{1}+ p^{2} c_{2}+ \cdots \bigr) \biggl( \bigl(D^{\alpha }u_{0}+ p D^{\alpha}u_{1}+p^{2} D^{\alpha}u_{2}+\cdots \bigr) \\& \quad {}+2 \biggl( u_{0} \biggl( \frac{x}{2} \biggr) +p u_{1} \biggl( \frac {x}{2} \biggr)+p^{2}u_{2} \biggl( \frac{x}{2} \biggr)+\cdots \biggr)^{2}-1 \biggr)=0. \end{aligned}$$

Equating the coefficients at different powers in p, we have the following differential equations:

$$\begin{aligned}& p^{0} \mbox{: } D^{\alpha} u_{0}=1, \\& p^{1} \mbox{: } D^{\alpha} u_{1}=2 c_{1} u_{0}^{2} \biggl( \frac{x}{2} \biggr), \\& p^{2} \mbox{: } D^{\alpha} u_{2}=(1+c_{1})D^{\alpha}u_{1}+2c_{1}u_{0} \biggl( \frac {x}{2} \biggr)u_{1} \biggl( \frac{x}{2} \biggr)+c_{2} D^{\alpha}u_{0}+2 c_{2} u_{0}^{2} \biggl( \frac{x}{2} \biggr), \\& p^{3} \mbox{: } D^{\alpha} u_{3}=D^{\alpha}u_{2}+c_{1} D^{\alpha}u_{2} +c_{2} D^{\alpha}u_{1} +c_{3} D^{\alpha}u_{0} \\& \hphantom{p^{3} \mbox{: } D^{\alpha} u_{3}={}}{}+4 c_{2} u_{0} \biggl( \frac{x}{2} \biggr)u_{1} \biggl( \frac{x}{2} \biggr)+4 c_{1} u_{0} \biggl( \frac{x}{2} \biggr)u_{2} \biggl( \frac{x}{2} \biggr) +2c_{1} u_{1} \biggl( \frac{x}{2} \biggr)+2c_{3} u_{0}^{2} \biggl( \frac {x}{2} \biggr), \\& \ldots. \end{aligned}$$