Skip to main content
SpringerLink
Log in

A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations

  • Original Paper
  • Published:
Numerical Algorithms Aims and scope Submit manuscript

Abstract

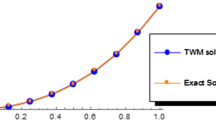
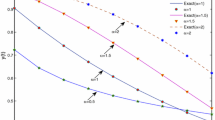
In this research, a Bernoulli wavelet operational matrix of fractional integration is presented. Bernoulli wavelets and their properties are employed for deriving a general procedure for forming this matrix. The application of the proposed operational matrix for solving the fractional delay differential equations is explained. Also, upper bound for the error of operational matrix of the fractional integration is given. This operational matrix is utilized to transform the problem to a set of algebraic equations with unknown Bernoulli wavelet coefficients. Several numerical examples are solved to demonstrate the validity and applicability of the presented technique.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Baillie, R.T.: Long memory processes and fractional integration in econometrics. J. Econ. 73, 5–59 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  2. Hall, M.G., Barrick, T.R.: From diffusion-weighted MRI to anomalous diffusion imaging. Magn. Reson. Med. 59, 447–455 (2008)

    Article  Google Scholar 

  3. Mandelbrot, B.: Some noises with 1/f spectrum, a bridge between direct current and white noise. IEEE Trans. Inform. Theory 13, 289–298 (1967)

    Article  MATH  Google Scholar 

  4. Povstenko, Y.Z.: Signaling problem for time-fractional diffusion-wave equation in a half-space in the case of angular symmetry. Nonl. Dyn. 55, 593–605 (2010)

    Article  MATH  Google Scholar 

  5. Engheta, N.: On fractional calculus and fractional multipoles in electromagnetism. IEEE. T. Antenn. Propag. 44, 554–566 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  6. Oldham, K.B.: Fractional differential equations in electrochemistry. Adv. Eng. Soft. 41, 9–12 (2010)

    Article  MATH  Google Scholar 

  7. Lederman, C., Roquejoffre, J.M., Wolanski, N.: Mathematical justification of a nonlinear integro-differential equation for the propagation of spherical flames. Annali di Matematica Pura ed Applicata 183, 173–239 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  8. Mainardi, F.: Fractional calculus: Some basic problems in continuum and statistical mechanics. In: Carpinteri, A., Mainardi, F. (eds.) Fractals and Fractional Calculus in Continuum Mechanics, pp 291–348. Springer, New York (1997)

  9. Rossikhin, Y.A., Shitikova, M.V.: Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Appl. Mech. Rev. 50, 15–67 (1997)

    Article  Google Scholar 

  10. He, J.H.: Some applications of nonlinear fractional differential equations and their approximations. Bull. Sci. Technol. 15, 86–90 (1999)

    Google Scholar 

  11. He, J.H.: Approximate analytical solution for seepage flow with fractional derivatives in porous media. Comput. Methods Appl. Mech. Eng. 167, 57–68 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  12. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  13. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, San Diego (2006)

    MATH  Google Scholar 

  14. Suarez, L., Shokooh, A.: An eigenvector expansion method for the solution of motion containing fractional derivatives. J. Appl. Mech. 64, 629–635 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  15. Abdulaziz, O., Hashim, I., Momani, S.: Solving systems of fractional differential equations by homotopy-perturbation method. Phys. Lett. A 372, 451–459 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. Odibat, Z., Momani, S.: Application of variational iteration method to nonlinear differential equations of fractional order. Int. J. Nonl. Sci. Numer. Simul. 1(7), 15–27 (2006)

    MathSciNet  Google Scholar 

  17. Momani, S., Odibat, Z.: Numerical comparison of methods for solving linear differential equations of fractional order. Chaos. Solitons. Fractals 31, 1248–1255 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  18. Daftardar-Gejji, V., Jafari, H.: Solving a multi-order fractional differential equation using adomian decomposition. Appl. Math. Comput. 189, 541–548 (2007)

    MathSciNet  MATH  Google Scholar 

  19. Meerschaert, M., Tadjeran, C.: Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 56, 80–90 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  20. Dubois, F., Mengue, S.: Mixed collocation for fractional differential equations. Numer. Algor. 34, 303–311 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  21. Saadatmandi, A., Dehghan, M.: A Legendre collocation method for fractional integro-differential equations. J. Vib. Control 17, 2050–2058 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  22. Bhrawy, A.H., Tharwat, M.M., Yildirim, A.: A new formula for fractional integrals of Chebyshev polynomials: application for solving multi-term fractional differential equations. J. Appl. Math. Model 37(6), 4245–4252 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. Saadatmandi, A.: Bernstein operational matrix of fractional derivatives and its applications. Appl. Math. Model 38(4), 1365–1372 (2014)

    Article  MathSciNet  Google Scholar 

  24. Rehman, M.ur., Ali Khan, R.: The Legendre wavelet method for solving fractional differential equations. Commun. Nonl. Sci. Numer. Simul. 16, 4163–4173 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ockendon, J.R., Tayler, A.B.: The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. Lond. Ser. A 322, 447–468 (1971)

    Article  Google Scholar 

  26. Ajello, W.G., Freedman, H.I., Wu, J.: A model of stage structured population growth with density depended time delay. SIAM. J. Appl. Math. 52, 855–869 (1992)

    Article  MathSciNet  Google Scholar 

  27. Sedaghat, S., Ordokhani, Y., Dehghan, M.: Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonl. Sci. Numer. Simul. 17, 4815–4830 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  28. Tohidi, E., Bhrawy, A.H., Erfani, K.: A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 37, 4283–4294 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  29. Yu, Z.H.: Variational iteration method for solving the multi-pantograph delay equation. Phys. Lett. A 372, 6475–6479 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  30. Wang, W.S., Li, S.F.: On the one-leg 𝜃—method for solving nonlinear neutral functional differential equations. Appl. Math. Comput. 193, 285–301 (2007)

    MathSciNet  Google Scholar 

  31. Evans, D.J., Raslan, K.R.: The Adomian decomposition method for solving delay differential equation. Int. J. comput. Math. 82, 49–54 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  32. Marzban, H.R., Razzaghi, M.: Solution of multi-delay systems using hybrid of block-pulse functions and Taylor series. Sound. Vib. 292, 954–963 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  33. Sadeghi Hafshejani, M., Karimi Vanani, S., Sedighi Hafshejani, J.: Numerical solution of delay differential equations using Legendre wavelet method. World Appl. Sci. 13, 27–33 (2011)

    Google Scholar 

  34. Saeed, U., Rehman, M.U.: Hermite wavelet method for fractional delay differential equations. J. Diff. Equa. 2014, 1–8 (2014)

    Article  Google Scholar 

  35. Yang, Y., Huang, Y.: Spectral-collocation methods for fractional pantograph delay-integrodifferential equations. Advan. Math. Phys. 2013, 1–14 (2013)

    MathSciNet  MATH  Google Scholar 

  36. Khader, M.M., Hendy, A.S.: The approximate and exact solutions of the fractional-order delay differential equations using Legendre seudospectral method. Int. J. pure. Appl. Math. 74, 287–297 (2012)

    MathSciNet  MATH  Google Scholar 

  37. Wang, Z.: A numerical method for delayed fractional-order differential equations. J. Appl. Math. 2013, 1–7 (2013)

    MathSciNet  Google Scholar 

  38. Moghaddam, B.P., Mostaghim, Z.S.: A numerical method based on finite difference for solving fractional delay differential equations. J. Taibah Univ. Sci. 7, 120–127 (2103)

    Article  Google Scholar 

  39. Yuanlu, L., Weiwei, Z.: Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 216, 2276–2285 (2010)

    MathSciNet  MATH  Google Scholar 

  40. Heydari, M.H., Hooshmandasl, M.R., Mohammadi, F., Cattani, C.: Wavelets method for solving systems of nonlinear singular fractional Volterra integro-differential equations. Commun. Nonl. Sci. Numer. Simul. 19, 37–48 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  41. Jafari, H., Yousefi, S.A., Firoozjaee, M.A., Momani, S., Khalique, C.M.: Application of Legendre wavelets for solving fractional differential equations. Comput. Math. Appl. 62, 1038–1045 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  42. Saeedi, H., Mohseni Moghadam, M.: Numerical solution of nonlinear Volterra integro-differential equations of arbitrary order by CAS wavelets. Appl. Math. Comput. 16, 1216–1226 (2011)

    MathSciNet  MATH  Google Scholar 

  43. Keshavarz, E., Ordokhani, Y., Razzaghi, M.: Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Model. 38, 6038–6051 (2014)

    Article  MathSciNet  Google Scholar 

  44. Balaji, S.: A new Bernoulli wavelet operational matrix of derivative method for the solution of nonlinear singular Lane-Emden type equations arising in astrophysics. J. Comput. Nonl. Dyn. 11, 051013 (2016)

    Article  Google Scholar 

  45. Tavassoli Kajani, M., Ghasemi, M., Babolian, E.: Numerical solution of linear integro-differential equation by using sine-cosine wavelets. Appl. Math. Comput. 180, 569–574 (2006)

    MathSciNet  MATH  Google Scholar 

  46. Mashayekhi, S., Ordokhani, Y., Razzaghi, M.: Hybrid functions approach for nonlinear constrained optimal control problems. Commun. Nonl. Sci. Numer. Simul. 17, 1831–1843 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  47. Kreyszig, E.: Introductory Functional Analysis with Applications. Wiley, New York (1978)

    MATH  Google Scholar 

  48. Keshavarz, E., Ordokhani, Y., Razzaghi, M.: A numerical solution for fractional optimal control problems via Bernoulli polynomials. J. Vib. Control., 1–15 (2015)

  49. Brunner, H., Huang, Q., Xies, H.: Discontinuous Galerkin methods for delay differential equations of pantograph type. SIAM J. Numer. Anal. 48, 1944–1967 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  50. Muroya, Y., Ishiwata, E., Brunner, H.: On the attainable order of collocation methods for pantograph integro-differential equations. J. Comput. Appl. Math. 152, 347–366 (2003)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Mathematical Sciences, Alzahra University, Tehran, Iran

    P. Rahimkhani & Y. Ordokhani

  2. Department of Computer Science, Faculty of Mathematical Sciences and Computer, Kharazmi University, Tehran, Iran

    E. Babolian

Authors
  1. P. Rahimkhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Y. Ordokhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. E. Babolian
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. Ordokhani.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Rahimkhani, P., Ordokhani, Y. & Babolian, E. A new operational matrix based on Bernoulli wavelets for solving fractional delay differential equations. Numer Algor 74, 223–245 (2017). https://doi.org/10.1007/s11075-016-0146-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11075-016-0146-3

Keywords

Search

Navigation