1 Introduction

From the pioneering work of Kermack and Mckendrick on SIR [1], many models for the transmission of infectious have descended (see [2–6]). Therefore, the ordinary threshold principle was for an SIR in a closed population, with no births and deaths. This assumption is just true for certain situations such as when the spread of disease is fast and the prevalence of the disease is brief. In order to make the model more realistic, more recent studies consider an epidemic model in a population with varying size (see [7–11]). In their paper [10], Gao and Hethcote assume that the total population is given by the following logistic equation:

$$ \frac{dN}{dt}=\biggl(b-\frac{arN}{K}\biggr)N-\biggl(\mu+ \frac{(1-a)rN}{K}\biggr)N, $$
(1)

where \(0< a<1\) is a convex combination constant and b and μ are the birth rate and death rate, \(r=b-\mu\) is the intrinsic growth rate, and \(K>0\) is the carrying capacity of the population. According to Zhou and Hethcote [9], when \(a=1\), (1) could be called a logistic birth model, and when \(a=0\), (1) could be called a logistic death model.

Zhang et al. mention an SIR model with logistic birth in [11]:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dS}{dt}=(b-r\frac{N}{K})N-\beta SI-\mu S,\\ \frac{dI}{dt}=\beta SI-\delta I,\\ \frac{dR}{dt}=\gamma I-\mu R. \end{array}\displaystyle \right . $$

Here \(N(t)=S(t)+I(t)+R(t)\) and \(\beta>0\) is the transmission coefficient, \(\delta=\alpha+\gamma+\mu\), and α is a non-negative constant and represents the death rate due to disease. \(\gamma>0\) is the rate constant for recovery. They use N as a variable in place of S; then the SIR model is described by the following system of differential equations:

$$ \left \{ \textstyle\begin{array}{@{}l} \frac{dI}{dt}=\beta I(N-I-R)-\delta I,\\ \frac{dR}{dt}=\gamma I-\mu R,\\ \frac{dN}{dt}=r(1-\frac{N}{K})N-\alpha I. \end{array}\displaystyle \right . $$
(2)

They showed that the region \(H=\{(I,R,N)\in\mathbb{R}_{+}^{3}: I+R\le N\le K \}\) is a positively invariant set with respect to (2). The disease-free \(E_{0}=(0,0,K)\) of the system (2) always exists, and if \(R_{0}=\frac{\beta K}{\delta}\le1\), the \(E_{0}\) is globally asymptotically stable in H. If \(R_{0}>1\), \(E_{0}\) is unstable and there is a unique endemic equilibrium \(E^{*}(I^{*}, R^{*}, N^{*})\), which is locally asymptotically stable and globally asymptotically stable when \(\alpha\le \min\{2\mu,\frac{1}{2}r\}\).

However, population systems are often subject to environmental noise (see [12, 13]), which is ignored by the deterministic models. Hence stochastic model has come to play an important role in infectious dynamics. Nowadays, the investigations of the epidemic models perturbed by the white noise have been engaging in a lot of attentions of many authors, and Beddington and May [14] assumed the environmental noise of the systems is proportional to the variables. Carletti [15] investigated stochastic perturbation around the positive equilibrium. Mao et al. [16–19] assumed the parameters in models are suffering stochastic perturbation.

Stochastic SIR models have been investigated in recent work. Tornatore et al. [17] proposed a stochastic SIR model with or without distributed time delay, they gave a sufficient condition for the asymptotic stability of the disease-free equilibrium. They only showed that the introduction of noise modifies the threshold of system for an epidemic to occur by numerical simulations. Lin and Jiang [18] considered a stochastic SIR model with perturbed disease transmission coefficient. They presented sufficient conditions for the disease to get extinct exponentially. In the case of persistence, they analyzed the long-time behavior of densities of the distributions of the solution and proved that the densities of the solution can converge in L1 to an invariant density under appropriate conditions. Also they found the support of the invariant density. Specially, when the intensity of white noise is relatively small, they gave a new threshold for an epidemic to occur. Ji et al. [19] discussed a two-group SIR model with the transmission parameter subject to white noise, while Yu et al. [20] investigated a two-group SIR model with stochastic perturbation around the positive equilibrium. But until now, few scholars have considered a stochastic SIR model with logistic growth.

In this paper, we consider the corresponding stochastic problem of a deterministic system by introducing noises in system (2). Here we assume that the disease transmission coefficient β is subject to environmental white noise, that is,

$$\beta\to\beta+\sigma \,dB(t). $$

Then \(\beta\, dt\to\beta \,dt+\sigma \,dB(t)\), where \(B(t)\) is a standard Brownian motion, \(\sigma^{2}>0\) is the intensity of environment white noise. Then model (2) becomes

$$ \left \{ \textstyle\begin{array}{@{}l} dI=[\beta(N-I-R)I-\delta I]\,dt+\sigma(N-I-R)I \,dB(t),\\ dR=(\gamma I-\mu R)\,dt,\\ dN=[r(1-\frac{N}{K})N-\alpha I]\,dt. \end{array}\displaystyle \right . $$
(3)

The aim of this paper is to discuss the dynamics of this stochastic SIR system. We show the solution of system (3) is positive and global. When \(R_{0}\le1\) we prove the disease-free equilibrium is stochastically asymptotically stable in the large, which is independent of the intensity of environmental white noise. When \(R_{0}>1\) we give the measurement of the difference between the solution and the endemic equilibrium of the deterministic model in a time average. The difference decreases with the decrease of the intensity of white noise. If the white noise is small and the death due to the disease is limited, the solution of (3) is going around the endemic equilibrium of the deterministic model for a long time. In this sense, we consider the disease to prevail.

Throughout this paper, let \((\varOmega ,\{\mathscr{F}_{t}\}_{t\ge0},P)\) be a complete probability space with a filtration \(\{\mathscr{F}_{t}\}_{t\ge 0}\) satisfying the usual conditions (i.e. it is right continuous and \(\mathscr{F}_{0}\)) that contains all P-null sets. Denote

$$\mathbb{R}^{3}_{+}=\bigl\{ x\in\mathbb{R}^{3}:x_{i}>0 \mbox{ for all } 1\le i\le3\bigr\} . $$

The remaining parts of this paper are as follows. In the next section we show the existence and uniqueness of a global positive solution of model (3). In Section 3, we analyze the stochastically asymptotic stability in the large of the disease-free equilibrium. In Section 4, we study the dynamics of system (3) around the endemic equilibrium of the deterministic model. Finally, in Section 5, numerical simulations are carried out.

2 Non-negative solutions

When we study a dynamical behavior, a global solution is important for the system. In this section, we show that the solution of (3) is global and nonnegative. As we know, for a stochastic differential equation to have a unique global (i.e., no explosion in a finite time) solution for any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and the local Lipschitz condition is a sufficient condition (see [21, 22]). Although the coefficients of system (3) satisfy local Lipschitz condition, they do not satisfy the linear growth condition, so the solution of system (3) may explode at a finite time. In this section, we will use the Lyapunov analysis method mentioned in [16] to show that the solution of system (3) is positive and global.

Theorem 1

There is a unique solution \((I(t),R(t),N(t))\) of system (3) on \(t\ge0\) for any initial value \((I(0),R(0),N(0))\in\mathbb{R}_{+}^{3}\), and the solution will remain in \(\mathbb{R}_{+}^{3}\) with probability 1, namely \((I(t),R(t),N(t))\in\mathbb{R}_{+}^{3}\) for all \(t\ge0\) almost surely.

Proof

Since coefficients of the equation are locally Lipschitz continuous for any initial value \((I(0),R(0),N(0))\in\mathbb{R}_{+}^{3}\), there is a unique local solution on \(t\in[0,\tau_{e})\), where \(\tau_{e}\) is the explosion time (see [21]). To show this solution is global, we need to show that \(\tau_{e}=\infty\) a.s. Let \(k_{0}>1\) be sufficiently large so that \(I(0)\), \(R(0)\), \(N(0)\) all lie within the interval \([\frac{1}{k_{0}},k_{0}]\). For each integer \(k\ge k_{0}\) define the stopping time

$$\tau_{k}=\inf\biggl\{ t\in[0,\tau_{e}):I(t)\notin\biggl( \frac{1}{k},k\biggr) \mbox{ or } R(t)\notin\biggl(\frac{1}{k},k \biggr) \mbox{ or } N(t)\notin\biggl(\frac{1}{k},k\biggr)\biggr\} , $$

where throughout this paper, we set \(\inf\emptyset=\infty\) (as usual ∅ denotes the empty set). Clearly, \(\tau_{k}\) is increasing as \(k\to\infty\). Set \(\tau_{\infty}=\lim_{k\to\infty}\tau_{k}\), whence \(\tau_{\infty}\le\tau _{e}\) a.s. If we can show that \(\tau_{\infty}=\infty\) a.s. then \(\tau _{e}=\infty\) and \((I(t),R(t),N(t))\in\mathbb{R}_{+}^{3}\) a.s. for all \(t\ge 0\). In other words, to complete the proof all we need to show is that \(\tau_{\infty}=\infty\) a.s. For if this statement is false, then there is a pair of constants \(T>0\) and \(\epsilon\in(0,1)\) such that

$$P\{\tau_{\infty}\le T\}>\epsilon. $$

Hence there is an integer \(k_{1}\ge k_{0}\) such that

$$ P\{\tau_{k}\le T\}>\epsilon\quad\mbox{for all } k\ge k_{1}. $$
(4)

Besides, for \(t\le\tau_{k}\), we can see

$$d(S+I+R)=dN=\biggl[rN\biggl(1-\frac{N}{K}\biggr)-\alpha I\biggr]\,dt\le \biggl[rN\biggl(1-\frac{N}{K}\biggr)\biggr]\,dt $$

and

$$\begin{aligned} N(t)&\le \left \{ \textstyle\begin{array}{@{}l@{\quad}l} K & \mbox{if }N(0)\le K,\\ N(0) & \mbox{if }N(0)> K, \end{array}\displaystyle \right . \\ &:=\bar{K}. \end{aligned}$$
(5)

Define a \(C^{2}\)-function \(V: \mathbb{R}_{+}^{3} \to\mathbb{\bar{R}}_{+}\) by

$$V(I,R,N)=I-1-\log I + R-1-\log R + N-1-\log N. $$

The non-negativity of this function can be seen from \(u-1+\log u\ge0\) \(\forall u>0\). Using Itô’s formula, we compute

$$dV:=LV\,dt+\sigma(I-1) (N-I-R)\,dB(t), $$

where

$$\begin{aligned}[b] LV ={}&\biggl(1-\frac{1}{I}\biggr)\bigl[\beta(N-I-R)I-\delta I\bigr]+ \frac{1}{2}\sigma^{2} (N-I-R)^{2} \\ &{} +\biggl(1-\frac{1}{R}\biggr) (\gamma I-\mu R)+\biggl(1- \frac{1}{N}\biggr)\biggl[rN\biggl(1-\frac {N}{K}\biggr)-\alpha I \biggr] \\ \le{}&\beta(N-I-R)I+\delta+\frac{1}{2}\sigma^{2}(N-I-R)^{2}+ \gamma I+\mu +rN+\alpha \\ \le{}&\mu+\alpha+\delta+\gamma\bar{K}+r\bar{K}+\beta\bar{K}^{2}+ \frac {1}{2}\sigma^{2}\bar{K}^{2} \\ :={}&\tilde{K}. \end{aligned} $$

Therefore,

$$\int_{0}^{\tau_{k}\land T}\,dV\bigl(I(t),R(t),N(t)\bigr)\le \int _{0}^{\tau_{k}\land T}\tilde{K}\,dt +\int_{0}^{\tau_{k}\land T} \sigma(I-1) (N-I-R)\,dB(t). $$

This implies that

$$\begin{aligned} & E\bigl[V\bigl(I(\tau_{k}\land T),R(\tau_{k} \land T),N(\tau_{k}\land T)\bigr)\bigr] \\ &\quad \le V\bigl(I(0),R(0),N(0)\bigr)+E \int_{0}^{\tau_{k}\land T} \tilde{K}\,dt \\ &\quad \le V\bigl(I(0),R(0),N(0)\bigr)+\tilde{K}T. \end{aligned}$$
(6)

Set \(\varOmega _{k}={\tau_{k}\le T}\) for \(k\ge k_{1}\) and by (4), \(P(\varOmega _{k})\ge\epsilon\). Note that for every \(\omega\in \varOmega _{k}\), there is at least one of \(I(\tau_{k},\omega)\), \(R(\tau_{k},\omega)\), \(N(\tau_{k},\omega)\) that equals k or \(\frac{1}{k}\), and hence \(V(I(\tau_{k}\land T),R(\tau_{k}\land T),N(\tau _{k}\land T))\) is no less than

$$k-1-\log k \quad\mbox{or} \quad\frac{1}{k}-1-\log\frac{1}{k}= \frac{1}{k}-1+\log k. $$

Consequently,

$$V\bigl(I(\tau_{k}\land T),R(\tau_{k}\land T),N( \tau_{k}\land T)\bigr)\ge(k-1-\log k)\land\biggl( \frac{1}{k}-1+\log k\biggr). $$

Then it follows from (4) and (6) that

$$\begin{aligned} & V\bigl(I(0),R(0),N(0)\bigr)+\tilde{K}T \\ &\quad \ge E\bigl[1_{\varOmega _{k(\omega)}}V\bigl(I(\tau_{k}\land T),R( \tau_{k}\land T),N(\tau _{k}\land T)\bigr)\bigr] \\ &\quad \ge\epsilon\biggl[(k-1-\log k)\land\biggl(\frac{1}{k}-1+\log k \biggr)\biggr], \end{aligned}$$

where \(1_{\varOmega _{k(\omega)}}\) is the indicator function of \(\varOmega _{k}\). Let \(k \to\infty\) lead to the contradiction \(\infty> V(I(0),R(0),N(0))+\tilde{K}T=\infty\). Therefore we shall have \(\tau_{\infty}=\infty\) a.s. □

Remark 1

Theorem 1 has shown that for any initial value \((I(0),R(0),N(0))\in \mathbb{R}^{3}_{+}\), system (3) has a unique global solution \((I(t),R(t),N(t))\in\mathbb{R}^{3}_{+}\) a.s., and by (5) if \(N(0)\le K\), then \(N(t)\le K\), so the region \(\varOmega ^{*}=\{(I,R,N)\in\mathbb{R}_{+}^{3}, I+R\le N\le K\}\) is a positively invariant set with respect to (3).

From now on, we always assume that \((I(0),R(0),N(0))\in \varOmega ^{*}\).

3 Stochastically asymptotical stability in the large of the disease-free equilibrium

Obviously, \(E_{0}=(0,0,K)\) which is called the disease-free equilibrium, is a solution of system (3). We divide this section into globally asymptotically stability at this point mainly by a stochastic Lyapunov function. First, we give a lemma (see [21]).

Consider the stochastic differential equation

$$ dx(t)=f\bigl(x(t),t\bigr)\,dt+g\bigl(x(t),t\bigr)\,dB(t) \quad \mbox{on } t\ge t_{0}. $$
(7)

Assume \(f(0,t)=0\) and \(g(0,t)=0\) for all \(t\ge t_{0}\). So \(x(t)\equiv0\) is a solution to (7), called the trivial solution or equilibrium position.

Lemma 1

If there exists a positive-definite decrescent radially unbounded function \(V(x,t)\in C^{2,1}(\mathbb{R}^{d}\times[t_{0},\infty);\mathbb{\bar{R}}_{+})\) such that \(LV(x,t)\) is negative-definite, then the trivial solution of (7) is stochastically asymptotically stable in the large.

Theorem 2

Assume \(R_{0}=\frac{\beta K}{\delta}\le1\), then the solution \((0,0,K)\) of system (3) is stochastically asymptotically stable in the large.

Proof

Let \(x=I\), \(y=R\), \(z=N-K\). Then \(x\ge0\), \(y\le0\), \(z\le0\) and system (3) becomes

$$ \left \{ \textstyle\begin{array}{@{}l} dx=(\beta(K+z-x-y)x-\delta x)\,dt+\sigma(K+z-x-y)x\,dB(t),\\ dy=(\gamma x-\mu y)\,dt,\\ dz=(-\frac{r}{K}z(K+z)-\alpha x)\,dt. \end{array}\displaystyle \right . $$
(8)

Define the stochastic Lyapunov function \(\mathbb{R} ^{3}\to\mathbb{\bar{R}}_{+}\):

$$V(x,y,z)=\frac{1}{\beta}x+\frac{1}{2\gamma}y^{2}+ \frac{1}{2\alpha}z^{2}. $$

Obviously, \(V(x,y,z)\) is positive-definite, decrescent and radially unbounded. By Itô’s formula, we compute

$$\begin{aligned} LV& =Kx+xz-x^{2}-xy-\frac{\delta}{\beta}x+xy-\frac{\mu}{\gamma}y^{2}- \frac {r}{\alpha K}z^{2}(K+z)-xz \\ & =\biggl(K-\frac{\delta}{\beta}\biggr)x-x^{2}-\frac{\mu}{\gamma}y^{2}- \frac{r}{\alpha K}z^{2}(K+z), \end{aligned}$$

according to the fact that \(R_{0}=\frac{\beta K}{\delta}\le1\) and \(K+z\ge0\), LV is negative-definite. By Lemma 1, we conclude that under the condition of \(R_{0}=\frac{\beta K}{\delta}\le1\), the trivial solution of system (8) is stochastically asymptotically stable in the large, i.e., the solution \((0,0,K)\) of system (3) is stochastically asymptotically stable in the large. □

Theorem 2 means that when \(R_{0}\le1\) the disease will die out after some period of time. This the phenomenon of interest to us studying an epidemic dynamical system. Another phenomenon we are interested in is when the disease will prevail and persist in a population, which will be discussed in the next section.

4 Asymptotic behavior around the endemic equilibrium of the deterministic model

Different from the deterministic system, there is no endemic equilibrium in system (3), so we cannot see whether the disease prevails through the endemic equilibrium. But (3) is a perturbation system of (2) which has an endemic equilibrium \(E^{*}\). We tend to study the behavior around \(E^{*}\) to reflect whether the disease will prevail.

Before proving the main theorem we put forward a lemma (see [21]).

Lemma 2

Let \(M=\{M_{t}\}_{t\ge0}\) be a real-valued continuous local martingale vanishing at \(t=0\). Then

$$\lim_{t\to\infty}\langle M,M\rangle_{t}=\infty \quad\textit{a.s.} \quad\Rightarrow \quad \lim_{t\to\infty } \frac{M_{t}}{\langle M,M\rangle_{t}}=0\quad\textit{a.s.} $$

and also

$$\limsup_{t\to\infty}\frac{\langle M,M\rangle_{t}}{t}< \infty \quad\textit{a.s.} \quad \Rightarrow\quad \lim_{t\to\infty}\frac{M_{t}}{t}=0\quad\textit{a.s.} $$

Theorem 3

Let \((I(t),R(t),N(t))\) be the solution of system (3) with any initial value \((I(0),R(0),N(0))\in\mathbb{R}_{+}^{3}\). If \(R_{0}>1\), \(\alpha <\frac{r}{2+(\frac{1}{1+\frac{\gamma}{\mu}})}\), then we have

$$\limsup_{t\to\infty}\frac{1}{t}\int_{0}^{t} \biggl[\bigl(I-I^{*}\bigr)^{2}+\frac{\mu}{\gamma }\bigl(R-R^{*} \bigr)^{2}+\biggl(-\frac{rN^{*}}{K\alpha}+1\biggr) \bigl(N-N^{*} \bigr)^{2}\biggr]\,ds\le\frac{K^{2}}{2\beta }I^{*}\sigma^{2}\quad\textit{a.s.}, $$

where \(E^{*}=(I^{*},R^{*},N^{*})\) is the endemic equilibrium of system (2).

Proof

Since \(E^{*}=(I^{*},R^{*},N^{*})\) is the endemic equilibrium of system (2), we have

$$ \beta\bigl(N^{*}-I^{*}-R^{*}\bigr)=\delta, \qquad \gamma I^{*}-\mu R^{*}=0, \qquad r \biggl(1-\frac {N^{*}}{K}\biggr)-\alpha\frac{I^{*}}{N^{*}}=0. $$
(9)

Define

$$\begin{aligned} V(I,R,N)& =\frac{1}{\beta}\biggl(I-I^{*}-I^{*}\ln\frac{I}{I^{*}}\biggr)+ \frac{1}{2\gamma }\bigl(R-R^{*}\bigr)^{2}+\frac{N^{*}}{\alpha} \biggl(N-N^{*}-N^{*}\ln\frac{N}{N^{*}}\biggr) \\ & :=V_{1}+V_{2}+V_{3}. \end{aligned}$$

Obviously, V is positive-definite. By Itô’s formula, we compute

$$dV:=(LV_{1}+LV_{2}+LV_{3})\,dt+\sigma\bigl(I-I^{*} \bigr) (N-I-R)\,dB(t), $$

where

$$\begin{aligned}& \begin{aligned}[b] LV_{1}& =\frac{1}{\beta}\biggl(1- \frac{I^{*}}{I}\biggr) \bigl(\beta(N-I-R)I-\delta I\bigr)+\frac {1}{2\beta} \sigma^{2}I^{*}(N-I-R)^{2} \\ & =\frac{1}{\beta}\bigl(I-I^{*}\bigr) \bigl(\beta(N-I-R)-\beta\bigl(N^{*}-I^{*}-R^{*} \bigr)\bigr)+\frac {1}{2\beta}\sigma^{2}I^{*}(N-I-R)^{2} \\ & =-\bigl(I-I^{*}\bigr)^{2}-\bigl(I-I^{*}\bigr) \bigl(R-R^{*}\bigr)+ \bigl(I-I^{*}\bigr) \bigl(N-N^{*}\bigr)+\frac{1}{2\beta}\sigma ^{2}I^{*}(N-I-R)^{2}, \end{aligned} \end{aligned}$$
(10)
$$\begin{aligned}& \begin{aligned}[b] LV_{2}& =\frac{1}{\gamma}\bigl(R-R^{*}\bigr) ( \gamma I-\mu R) \\ & =\frac{1}{\gamma}\bigl(R-R^{*}\bigr) \bigl(\gamma I-\mu R-\gamma I^{*}+\mu R^{*} \bigr) \\ & =\bigl(I-I^{*}\bigr) \bigl(R-R^{*}\bigr)-\frac{\mu}{\gamma}\bigl(R-R^{*} \bigr)^{2}, \end{aligned} \end{aligned}$$
(11)
$$\begin{aligned}& \begin{aligned}[b] LV_{3}& =\frac{N^{*}}{\alpha}\biggl(1- \frac{N^{*}}{N}\biggr)\biggl[rN\biggl(1-\frac{N}{K}\biggr)-\alpha I \biggr] \\ & =\frac{N^{*}}{\alpha}\bigl(N-N^{*}\bigr)\biggl[r\biggl(1-\frac{N}{K}\biggr)- \frac{\alpha I}{N}\biggr] \\ & =\frac{N^{*}}{\alpha}\bigl(N-N^{*}\bigr)\biggl[r\biggl(1-\frac{N}{K}\biggr)- \frac{\alpha I}{N}-r\biggl(1-\frac{N^{*}}{K}\biggr)+\frac{\alpha I^{*}}{N^{*}}\biggr] \\ & =\frac{N^{*}}{\alpha}\bigl(N-N^{*}\bigr)\biggl[-\frac{r}{K}\bigl(N-N^{*} \bigr)-\alpha\biggl(\frac {I}{N}-\frac{I^{*}}{N^{*}}\biggr)\biggr] \\ & =\frac{N^{*}}{\alpha}\bigl(N-N^{*}\bigr)\biggl[-\frac{r}{K}\bigl(N-N^{*} \bigr)-\frac{\alpha }{NN^{*}}\bigl(IN^{*}-IN+IN-I^{*}N\bigr)\biggr] \\ & =\frac{N^{*}}{\alpha}\biggl(-\frac{r}{K}+\frac{\alpha I}{NN^{*}}\biggr) \bigl(N-N^{*}\bigr)^{2}-\bigl(N-N^{*}\bigr) \bigl(I-I^{*}\bigr) \\ & \le\frac{N^{*}}{\alpha}\biggl(-\frac{r}{K}+\frac{\alpha }{N^{*}}\biggr) \bigl(N-N^{*}\bigr)^{2}-\bigl(N-N^{*}\bigr) \bigl(I-I^{*}\bigr), \end{aligned} \end{aligned}$$
(12)

where (9) is used in the upper equalities. So,

$$LV\le-\bigl(I-I^{*}\bigr)^{2}-\frac{\mu}{\gamma}\bigl(R-R^{*} \bigr)^{2}-\biggl(\frac{rN^{*}}{\alpha K}-1\biggr) \bigl(N-N^{*} \bigr)^{2}+\frac{K^{2}}{2\beta}I^{*}\sigma^{2} $$

and

$$\begin{aligned} dV\le{}&\biggl[-\bigl(I-I^{*}\bigr)^{2}-\frac{\mu}{\gamma}\bigl(R-R^{*} \bigr)^{2}-\biggl(\frac{rN^{*}}{\alpha K}-1\biggr) \bigl(N-N^{*} \bigr)^{2}+\frac{K^{2}}{2\beta}I^{*}\sigma^{2}\biggr]\,dt \\ &{}+\sigma\bigl(I-I^{*}\bigr) (N-I-R)\,dB(t). \end{aligned}$$

Note that \(E^{*}=(I^{*},R^{*},N^{*})\) is the endemic equilibrium of the system (2) and according to [11], \(N^{*}\) is the root of the following equation in the interval \((0,K)\):

$$\alpha-\frac{\alpha\delta}{\beta N}-r\biggl(1+\frac{\gamma}{\mu}\biggr) \biggl(1- \frac{N}{K}\biggr)=0, $$

i.e.

$$\frac{r}{K}\biggl(1+\frac{\gamma}{\mu}\biggr)N^{2}+\biggl[ \alpha-r\biggl(1+\frac{\gamma}{\mu }\biggr)\biggr]N-\frac{\alpha\delta}{\beta}=0. $$

Obviously,

$$ N^{*}>-\frac{\alpha-r(1+\frac{\gamma}{\mu})}{2\frac {r}{K}(1+\frac{\gamma}{\mu})}. $$
(13)

If \(\alpha<\frac{r}{2+(\frac{1}{1+\frac{\gamma}{\mu}})}\), then

$$ -\frac{\alpha-r(1+\frac{\gamma}{\mu})}{2\frac {r}{K}(1+\frac{\gamma}{\mu})}>\frac{\alpha}{\frac{r}{K}}. $$
(14)

By (13) and (14), we have

$$N^{*}>\frac{\alpha}{\frac{r}{K}}. $$

So,

$$\frac{rN^{*}}{\alpha K}-1>0. $$

Therefore,

$$\begin{aligned} &\int_{0}^{t}\biggl[\bigl(I-I^{*} \bigr)^{2}+\frac{\mu}{\gamma}\bigl(R-R^{*}\bigr)^{2}+\biggl( \frac{rN^{*}}{\alpha K}-1\biggr) \bigl(N-N^{*}\bigr)^{2}\biggr]\,ds \\ &\quad\le V(0)+\frac{K^{2}}{2\beta}I^{*}\sigma^{2}t+\int _{0}^{t}\sigma \bigl(I(s)-I^{*}\bigr) \bigl(N(s)-I(s)-R(s)\bigr)\,dB(s). \end{aligned}$$

Let

$$M_{t}=\int_{0}^{t}\sigma\bigl(I(s)-I^{*} \bigr) \bigl(N(s)-I(s)-R(s)\bigr)\,dB(s), $$

which is a real-valued continuous local martingale, \(M_{0}=0\), and

$$\begin{aligned} \frac{\langle M,M\rangle_{t}}{t}& =\frac{1}{t}\int_{0}^{t} \sigma ^{2}\bigl(I(s)-I^{*}\bigr)^{2}\bigl(N(s)-I(s)-R(s) \bigr)^{2}\,ds \\ & \le\bigl[K^{2}+2I^{*}K+\bigl(I^{*}\bigr)^{2} \bigr]K^{2}\sigma^{2}< \infty. \end{aligned}$$

Then by Lemma 2, we have

$$\lim_{t\to\infty}\frac{M_{t}}{t}=0 \quad\mbox{a.s.} $$

Hence,

$$\limsup_{t\to\infty}\frac{1}{t}\int_{0}^{t} \biggl[\bigl(I-I^{*}\bigr)^{2}+\frac{\mu}{\gamma }\bigl(R-R^{*} \bigr)^{2}+\biggl(-\frac{rN^{*}}{K\alpha}+1\biggr) \bigl(N-N^{*} \bigr)^{2}\biggr]\,ds\le\frac{K^{2}}{2\beta }I^{*}\sigma^{2} \quad\mbox{a.s.} $$

The proof is thus complete. □

Remark 2

Theorem 3 shows that if \(R_{0}>1\), \(\alpha<\frac{r}{2+(\frac{1}{1+\frac {\gamma}{\mu}})}\), the solution of system (3) goes around \(E^{*}\) for a long time while the intensity of the white noise is weak. Therefore according to [11], \(E^{*}\) is globally asymptotically stable when \(R_{0}>1\), \(\alpha\le\min\{2\mu,\frac{1}{2}r\}\). In this sense, as long as α is small properly, we consider the disease to prevail.

5 Numerical simulations

In this section, we make numerical simulations to illustrate our results by using Milstein’s higher order method [23]. We get the simulation figures with the initial value \((I(0),R(0),N(0))=(0.2,0.2,0.6)\) and time step \(\varDelta t=\frac {1}{2^{5}}\), and the parameters in (3) are given by

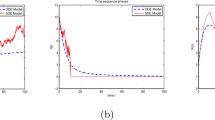
$$K=2,\qquad r=0.2,\qquad \mu=0.4,\qquad \alpha=0.05, \qquad\gamma=0.3. $$

First, we take \(\beta=0.3\), \(\sigma_{1}=0.5\), \(\sigma_{2}=0.8\); in this case, \(R_{0}=\frac{4}{5}<1\), and \(\beta=0.375\), such that \(R_{0}=1\). We find that these lines in Figure 1 and Figure 2 fit very well, which implies that the disease-free equilibrium \(E_{0}=(0,0,2)\) of system (3) is globally asymptotically stable.

Figure 1
figure 1

\(\pmb{E_{0}=(0,0,2)}\) of system ( 3 ) is globally asymptotically stable, when \(\pmb{R_{0}<1}\) .

Full size image
Figure 2
figure 2

\(\pmb{E_{0}=(0,0,2)}\) of system ( 3 ) is globally asymptotically stable, when \(\pmb{R_{0}=1}\) .

Full size image

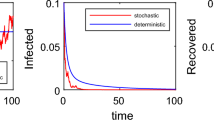
When \(\beta=0.5\), it is easy to check that \(R_{0}=\frac{4}{3}>1\). We choose \(\sigma_{1}=0.1\), \(\sigma_{2}=0.05\); the solution goes around the endemic equilibrium \(E^{*}\) for a long time, and the fluctuation decreases with the decreasing of white noise (see Figure 3). This result is consistent with the result of Theorem 3.

Figure 3
figure 3

The solution of system ( 3 ) is going around the endemic equilibrium of system ( 2 ).

Full size image