1 Introduction

In the last few decades, a special consideration has been paid to fractional differential equations (FDEs) due to their wide range applications into real world phenomena (see [1–4]). Various attempts have been made in order to present these phenomena in a superior way and to explore new fractional derivatives with different approaches such as Riemann–Liouville, Caputo, Hadamard, Hilfer–Hadamard, and Grünwald–Letnikov [5–11]. In fact, FDEs are nonlocal in nature, and they describe many nonlinear phenomena very precisely, so they have a huge impact on different disciplines of science like hydrodynamics, control theory, signal processing, and image processing. More applications in these multidisciplinary sciences can be traced in [12–15]. In literature, there exist many complex differential systems that cannot be solved analytically, and obtaining the solution of such a type of systems is a big challenge to mathematicians; therefore, in such a situation, a solution can be traced through its properties, which are known as qualitative properties. One of the interesting examples is to investigate the unique solution’s existence of an elliptic partial differential equation provided that there is a known average value [16]. In addition, another interesting example is the nonlinear problem of implicit FDEs with impulsive and integral boundary conditions which was investigated in [17] with the help of Schaefer’s fixed point theorem and Banach’s contraction principle. In fact, the qualitative properties like the existence and uniqueness theory for the solutions of fractional models with boundary value problem have attracted great attention among the researchers [18–27].

Another remarkable area which has recently received a considerable attention as one of the central topics in mathematical analysis is the stability of FDEs. In 1940, Ulam [28] initiated the stability of functional equations, which was improved by Hyers [29] in 1941 via Banach spaces. That is the reason why this stability is named Hyers–Ulam stability \((\mathcal{HUS})\). After that, Rassias [30] introduced the Hyers–Ulam–Rassias stability \((\mathcal{HURS})\) by generalizing the concept of \(\mathcal{HUS}\). Moreover, a number of mathematicians have spread the idea of \(\mathcal{HUS}\) to different classes of functional equations [31–33].

Abbas et al. [34] studied the Ulam stability and existence and uniqueness of solutions for the FDE

$$\begin{aligned} \textstyle\begin{cases} {}^{H}\mathcal{D}_{1^{+}}^{\alpha ,\beta }\mathtt{u}( \sigma )=f(\sigma ,\mathtt{u}(\sigma )),\quad \sigma \in [1,T], \\ {}^{H}\mathcal{I}_{1^{+}}^{\alpha ,1-\gamma }\mathtt{u}(1)=\phi , \end{cases}\displaystyle \end{aligned}$$

where \(0<\alpha <1\), \(0\leqslant \beta \leqslant 1\), \(\gamma =\alpha +\beta -\alpha \beta \), \(\phi \in \mathbb{R}\), \(T>1\), \({}^{H}\mathcal{D}_{1^{+}}^{\alpha ,\beta }(\cdot )\) and \({}^{H}\mathcal{I}_{1^{+}}^{\alpha ,1-\gamma }(\cdot )\) are the Hilfer–Hadamard fractional derivative and the Hadamard fractional integral, respectively.

Chalishajar et al. [35] studied the \(\mathcal{HUS}\) and the existence and uniqueness of solutions of

$$\begin{aligned} \textstyle\begin{cases} {}^{c}\mathcal{D}_{0^{+}}^{\alpha }\mathtt{u}(\sigma )= \phi _{1}(\sigma ,\mathtt{v}(\sigma )),\quad \alpha \in (1,2],\sigma \in [0,1], \\ {}^{c}\mathcal{D}_{0^{+}}^{\beta }\mathtt{v}(\sigma )=\phi _{2}( \sigma ,\mathtt{u}(\sigma )),\quad \beta \in (1,2],\sigma \in [0,1], \\ \mathfrak{p}\mathtt{u}(0)+\mathfrak{q}\mathtt{u}'(0)=\int _{0}^{1} \varphi _{1}(\mathtt{u}(s))\,ds,\quad\quad \mathfrak{p}\mathtt{u}(1)+ \mathfrak{q}\mathtt{u}'(1)=\int _{0}^{1}\varphi _{2}( \mathtt{u}(s))\,ds, \\ \widetilde{\mathfrak{p}}\mathtt{v}(0)+\widetilde{\mathfrak{q}} \mathtt{v}'(0)=\int _{0}^{1}\widetilde{\varphi }_{1}( \mathtt{v}(s))\,ds,\quad\quad \widetilde{\mathfrak{p}}\mathtt{v}(1)+ \widetilde{\mathfrak{q}}\mathtt{v}'(1)=\int _{0}^{1} \widetilde{\varphi }_{2}(\mathtt{v}(s))\,ds, \end{cases}\displaystyle \end{aligned}$$

where \({}^{c}\mathcal{D}_{0^{+}}^{(\cdot )}(\cdot )\) represents the fractional derivative in a Caputo sense, \(\mathfrak{p},\widetilde{\mathfrak{p}}>0\), \(\mathfrak{q}, \widetilde{\mathfrak{q}}\geqslant 0\), and \(\varphi _{1}\), \(\widetilde{\varphi }_{1}\), \(\varphi _{2}\), \(\widetilde{\varphi }_{2}\) are continuous functions.

In [36], the authors studied the \(\mathcal{HUS}\) and \(\mathcal{HURS}\) of Volterra integro-differential equation as follows:

$$\begin{aligned} \textstyle\begin{cases} {}^{H}\mathcal{D}_{0^{+}}^{\alpha ,\beta ;\psi } \mathtt{u}(\sigma )=f(\sigma ,\mathtt{u}(\sigma ))+\int _{0}^{ \sigma }\mathcal{K}(\sigma ,s,\mathtt{u}(\sigma ))\,ds,\quad \sigma \in \mathrm{J}=[0,T], \\ \mathcal{I}_{0^{+}}^{1-\gamma }\mathtt{u}(\sigma )| _{\sigma =0}= \mathtt{c}, \end{cases}\displaystyle \end{aligned}$$

where \(f(\sigma ,\mathtt{u})\) and \(\mathcal{K}(\sigma ,s,\mathtt{u})\) are the continuous functions with respect to σ, u on \(\mathrm{J}\times \mathbb{R}\), and σ, s, u on \(\mathrm{J}\times \mathrm{J}\times \mathbb{R}\), respectively, c is a given constant, \({}^{H}\mathcal{D}_{0^{+}}^{\alpha ,\beta ;\psi }(\cdot )\) is the Hilfer fractional derivative with ψ such that the fractional orders \(\alpha \in (0,1)\) and \(\beta \in [0,1]\), and \(\mathcal{I}_{0^{+}}^{1-\gamma }(\cdot )\) is the ψ-Riemann–Liouville fractional integral such that \(\gamma \in [0,1)\).

Dai et al. [37] studied the Caputo fractional derivative along with \(\mathcal{HUS}\) and \(\mathcal{HURS}\) for a class of FDEs of the following integral boundary condition:

$$\begin{aligned} \textstyle\begin{cases} \mathtt{u}'(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \mathtt{u}(\sigma )=\phi (\sigma ,\mathtt{u}(\sigma )),\quad \sigma \in [0,1], \\ \mathtt{u}(1)=\mathcal{I}_{0^{+}}^{\beta }\mathtt{u}(\eta )= \frac{1}{\Gamma (\beta )}\int _{0}^{\eta }(\eta -s)^{\beta -1} \mathtt{u}(s)\,ds, \end{cases}\displaystyle \end{aligned}$$

where \(\alpha \in (0,1)\), \(\beta >0\), \(\eta \in (0,1]\), \({}^{c}\mathcal{D}_{0^{+}}^{\alpha }(\cdot )\) represents the Caputo fractional derivative, \(\mathcal{I}_{0^{+}}^{\beta }(\cdot )\) represents the Riemann–Liouville fractional integral, \(\mathtt{u}\in \mathrm{C}^{1}[0,1]\), and \(\phi :[0,1]\times (-\infty ,\infty )\rightarrow (-\infty ,\infty )\) is a continuous function.

Motivated by the work introduced in [34–37], in this paper, we study the existence and uniqueness, \(\mathcal{HUS}\) and \(\mathcal{HURS}\) of the accompanying nonlinear FDE including Caputo fractional derivative. The proposed framework is as follows:

$$\begin{aligned} \textstyle\begin{cases} \mathtt{u}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \mathtt{u}(\sigma )=\phi (\sigma ,\mathtt{u}(\sigma )),\quad \sigma \in \mathrm{J}, \\ \mathtt{u}(0)=\sum_{i=0}^{k-2}\epsilon _{i}\mathtt{u}(\delta _{i}) \quad\quad \mathtt{u}(1)=\mathcal{I}_{0^{+}}^{\beta }\varphi (\eta , \mathtt{u}(\eta ))=\frac{1}{\Gamma (\beta )}\int _{0}^{\eta }( \eta -s)^{\beta -1}\varphi (s,\mathtt{u}(s))\,ds, \end{cases}\displaystyle \end{aligned}$$
(1)

where \(\mathrm{J}=[0,1]\), \({}^{c}\mathcal{D}_{0^{+}}^{\alpha }(\cdot )\) represents the Caputo fractional derivative of order α with \(1<\alpha <2\), \(\mathcal{I}_{0^{+}}^{\beta }(\cdot )\) is the Riemann–Liouville fractional integral of order β with \(\beta >1\), \(0<\eta \leqslant 1\) is a fixed real number, \(\epsilon _{i},\delta _{i}\geqslant 0\), \(i=1,2,\ldots ,k-2\), \(\mathtt{u}\in \mathrm{C}^{2}[0,1]\), and \(\phi ,\varphi :[0,1]\times (-\infty ,\infty )\rightarrow (-\infty , \infty )\) is a continuous function.

The article is organized as follows: In Sect. 2, we give some basic definitions and theorems associated with both fractional derivatives and integrals. The existence and uniqueness of solution, \(\mathcal{HUS}\), and \(\mathcal{HURS}\) to the considered system (1) are discussed in Sect. 3. A specific example is given in Sect. 4.

2 Fundamental results

Let \(\mathrm{C}^{2}[0,1]\) denote a set of differentiable functions and its derivatives that are continuous on \([0,1]\) with the norm

$$ \Vert \mathtt{u} \Vert =\max_{\sigma \in \mathrm{J}} \bigl\vert \mathtt{u}(\sigma ) \bigr\vert . $$

Definition 1

([38])

For any function u, the Riemann–Liouville integral for any noninteger arbitrary order α with \(\sigma >0\) is stated as follows:

$$ \mathcal{I}_{0^{+}}^{\alpha }\mathtt{u}(\sigma )= \frac{1}{\Gamma (\alpha )} \int _{0}^{\sigma }(\sigma -s)^{ \alpha -1} \mathtt{u}(s)\,ds. $$

Definition 2

([38])

For any function u, the Caputo derivative for any noninteger arbitrary order \(\alpha \in (p-1,p]\) with \(\sigma >0\) is stated as follows:

$$ {}^{c}\mathcal{D}_{0^{+}}^{\alpha }\mathtt{u}(\sigma )= \frac{1}{\Gamma (p-\alpha )} \int _{0}^{\sigma }(\sigma -s)^{p- \alpha -1}{ \mathtt{u}^{(p)}}(s)\,ds, $$

where \(p=[\alpha ]+1\), and \([\alpha ]\) denotes the integer part of α. Specifically, if u is defined on the interval J and \(1<\alpha \leqslant 2\), then

$$ {}^{c}\mathcal{D}^{\alpha }_{0^{+}}\mathtt{u}(\sigma )= \frac{1}{\Gamma (2-\alpha )} \int _{0}^{\sigma }(\sigma -s)^{1- \sigma } \mathtt{u}''(s)\,ds. $$

The Laplace transform of Caputo derivatives is

$$ \mathcal{L} \bigl\lbrace {}^{c}\mathcal{D}^{\alpha }_{0^{+}} \mathtt{u}( \sigma ) \bigr\rbrace (s)=s^{\alpha }\mathcal{U}(s)-\sum _{i=0}^{n-1}s^{ \alpha -k-1}\mathtt{u}^{(k)}(0), \quad \alpha \in (p-1,p], $$
(2)

where \(\mathcal{U}(s)\) is the Laplace transform of the function \(\mathtt{u}(\sigma )\).

Definition 3

The Mittag-Leffler (\(\mathcal{ML}\)) functions for arbitrary \(\varrho \in \mathbb{C}\) are

$$\begin{aligned}& \mathrm{E}_{\alpha }(\varrho )=\sum_{i=0}^{\infty } \frac{\varrho ^{i}}{\Gamma (\alpha i+1)},\quad \alpha \in \mathbb{C}, \Re (\alpha )>0, \\& \mathrm{E}_{\alpha ,\beta }(\varrho )=\sum_{i=0}^{\infty } \frac{\varrho ^{i}}{\Gamma (\alpha i+\beta )},\quad \alpha ,\beta \in \mathbb{C}, \Re (\alpha ),\Re (\beta )>0. \end{aligned}$$

The Laplace transforms of \(\mathcal{ML}\) functions are defined by

$$\begin{aligned}& \mathcal{L} \bigl\lbrace \mathrm{E}_{\alpha ,1} \bigl( \pm \lambda \sigma ^{ \alpha } \bigr) \bigr\rbrace (s)= \frac{s^{\alpha -1}}{(s^{\alpha }\mp \lambda )}, \quad \Re (\alpha )>0, \lambda \in \mathbb{R}, \\& \mathcal{L} \bigl\lbrace \sigma ^{\beta -1}\mathrm{E}_{\alpha ,\beta } \bigl( \pm \lambda \sigma ^{\alpha } \bigr) \bigr\rbrace (s)= \frac{s^{\alpha -\beta }}{(s^{\alpha }\mp \lambda )}, \quad \Re (\alpha ), \Re (\beta )>0, \lambda \in \mathbb{R}. \end{aligned}$$
(3)

Definition 4

([39])

A function u is said to be of exponential order if there are constants \(\tilde{M},\leftthreetimes >0\) with

$$ \bigl\vert \mathtt{u}(\sigma ) \bigr\vert \leqslant \tilde{M}e^{\leftthreetimes \sigma } \quad \text{for all } \sigma >0. $$

Theorem 5

([40] Krasnosel’skii fixed point theorem)

Let Λ be a closed convex and nonempty subset of a Banach space \(\mathfrak{X}\). Let \(\mathfrak{T}_{1}\), \(\mathfrak{T}_{2}\) be operators such that

  • \([\mathcal{A}_{1}]\) \(\mathfrak{T}_{1}\mathfrak{w}+\mathfrak{T}_{2}\mathfrak{x}\in \varLambda \) whenever \(\mathfrak{w},\mathfrak{x}\in \varLambda \);

  • \([\mathcal{A}_{2}]\) \(\mathfrak{T}_{1}\) is a completely continuous operator;

  • \([\mathcal{A}_{3}]\) \(\mathfrak{T}_{2}\) is a contractive operator.

Then there exists \(\mathfrak{y}\in \varLambda \) such that \(\mathfrak{y}=\mathfrak{T}_{1}\mathfrak{y}+\mathfrak{T}_{2} \mathfrak{y}\).

Theorem 6

([41] Generalized Banach’s fixed point theorem)

Let \((\mathfrak{X},d)\) be a generalized complete metric space. Assume that \(\mathfrak{T}:\mathfrak{X}\rightarrow \mathfrak{X}\) is a strictly contractive operator with Lipschitz constant \(\mathfrak{L}<1\). If there exists \(\kappa \geqslant 0\) such that \(d(\mathfrak{T}^{\kappa +1}\mathfrak{x},\mathfrak{T}^{\kappa } \mathfrak{x})<\infty \) for some \(\mathfrak{x}\in \mathfrak{X}\), then the following propositions hold:

  • \([\mathcal{A}_{1}]\) The sequence \(\lbrace \mathfrak{T}^{n}\mathfrak{x} \rbrace \) converges to a fixed point \(\tilde{\mathfrak{x}}\) of \(\mathfrak{T}\);

  • \([\mathcal{A}_{2}]\) The unique fixed point of \(\mathfrak{T}\) is \(\tilde{\mathfrak{x}}\in \tilde{\mathfrak{X}}= \lbrace \mathfrak{y}\in \mathfrak{X}:d(\mathfrak{T}^{\kappa }\mathfrak{x}, \mathfrak{y})<\infty \rbrace \);

  • \([\mathcal{A}_{3}]\) If \(\mathfrak{y}\in \tilde{\mathfrak{X}}\), then \(d(\mathfrak{y},\tilde{\mathfrak{x}})\leqslant \frac{1}{1-\mathfrak{L}}d(\mathfrak{T}\mathfrak{y},\mathfrak{y})\).

Theorem 7

([39])

The Laplace transform of any function u (\(\mathcal{L} \lbrace \mathtt{u}(\sigma ) \rbrace \)) exists and converges absolutely for \(\Re (s)>\leftthreetimes \) if u is of exponential order.

3 Main results

Here, we use assumptions for the existence and uniqueness of solution to the considered problem (1) under Krasnosel’skii and generalized Banach fixed point theorems. We also discuss the \(\mathcal{HUS}\) and \(\mathcal{HURS}\) for the solution of considered system (1). The following hypotheses need to hold for the upcoming results:

  • \([\mathcal{H}_{1}]\) Let \(\varphi ,\phi :\mathrm{J}\times (-\infty ,\infty )\rightarrow (- \infty ,\infty )\) be continuous, then there exist constants \({\mathcal{Q}_{\varphi },\mathcal{Q}_{\phi }}>0\) such that \(\sigma \in \mathrm{J}\) and \(\forall \mathfrak{h}_{1},\mathfrak{h}_{2}\in \mathbb{R}\)

    $$ \bigl\vert \varphi (\sigma ,\mathfrak{h}_{1})-\varphi (\sigma , \mathfrak{h}_{2}) \bigr\vert \leqslant \mathcal{Q}_{\varphi } \vert \mathfrak{h}_{1}-\mathfrak{h}_{2} \vert $$

    and

    $$ \bigl\vert \phi (\sigma ,\mathfrak{h}_{1})-\phi (\sigma , \mathfrak{h}_{2}) \bigr\vert \leqslant \mathcal{Q}_{\phi } \vert \mathfrak{h}_{1}-\mathfrak{h}_{2} \vert . $$

  • \([\mathcal{H}_{2}]\) There exist bounded functions \(\mathfrak{f}_{1},\mathfrak{g}_{1},\mathfrak{f}_{2},\mathfrak{g}_{2} \in \mathrm{C}^{2}[0,1]\) such that

    $$ \bigl\vert \varphi \bigl(\sigma ,\mathfrak{h}(\sigma ) \bigr) \bigr\vert \leqslant \mathfrak{f}_{1}( \sigma )+\mathfrak{g}_{1}(\sigma ) \bigl\vert \mathfrak{h}(\sigma ) \bigr\vert $$

    and \(\vert \phi (\sigma ,\mathfrak{h}(\sigma )) \vert \leqslant \mathfrak{f}_{2}( \sigma )+\mathfrak{g}_{2}(\sigma ) \vert \mathfrak{h}(\sigma ) \vert \) with \(\hat{\mathfrak{f}}_{1}=\sup_{\sigma \in \mathrm{J}}\mathfrak{f}_{1}( \sigma )\), \(\hat{\mathfrak{g}}_{1}=\sup_{\sigma \in \mathrm{J}}\mathfrak{g}_{1}( \sigma )\), \(\hat{\mathfrak{f}}_{2}=\sup_{\sigma \in \mathrm{J}}\mathfrak{f}_{2}( \sigma )\), and \(\hat{\mathfrak{g}}_{2}=\sup_{\sigma \in \mathrm{J}}\mathfrak{g}_{2}( \sigma )<1\).

3.1 Existence and uniqueness

Here, we examine the existence and uniqueness as follows.

Lemma 8

Let \(\mathtt{u}(\sigma )\in \mathrm{C}^{2}[0,1]\), \(1<\alpha <2\), \(\beta >1\). Also, let g be any continuous function and \(0<\eta \leqslant 1\), then the solution of

$$ \textstyle\begin{cases} \mathtt{u}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \mathtt{u}(\sigma )=\mathtt{g}(\sigma ),\quad \sigma \in [0,1], \\ \mathtt{u}(0)=\sum_{i=0}^{k-2}\epsilon _{i}\mathtt{u}(\delta _{i}), \quad\quad \mathtt{u}(1)=\mathcal{I}_{0^{+}}^{\beta }\varphi (\eta , \mathtt{u}(\eta ))=\frac{1}{\Gamma (\beta )}\int _{0}^{\eta }( \eta -s)^{\beta -1}\varphi (s,\mathtt{u}(s))\,ds, \end{cases} $$
(4)

is given by

$$\begin{aligned} \mathtt{u}(\sigma )={}& \int _{0}^{1}\mathbb{G}(\sigma ,s) \mathtt{g}(s) \,ds+ \frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds, \end{aligned}$$

where \(\mathbb{G}(\sigma ,s)\) is given by

$$ \mathbb{G}(\sigma ,s)= \textstyle\begin{cases} (\sigma -s)\mathrm{E}_{2-\alpha ,2} (- ( \sigma -s )^{2-\alpha } ) \\ \quad {} -(\vartheta _{1}\sigma +\vartheta _{3})(1-s)\mathrm{E}_{2- \alpha ,2} (- (1-s )^{2-\alpha } ),&0 \leqslant s\leqslant \sigma , \\ {-}(\vartheta _{1}\sigma +\vartheta _{3})(1-s)\mathrm{E}_{2-\alpha ,2} (- (1-s )^{2-\alpha } ),&\sigma \leqslant s \leqslant 1, \end{cases} $$
(5)

and

$$\begin{aligned}& \vartheta _{1}= \frac{1-\sum_{i=0}^{k-2}\epsilon _{i}}{1-\sum_{i=0}^{k-2}\epsilon _{i}+\sum_{i=0}^{k-2}\epsilon _{i}\delta _{i}}, \\& \vartheta _{2}= \frac{1}{1-\sum_{i=0}^{k-2}\epsilon _{i}+\sum_{i=0}^{k-2}\epsilon _{i}\delta _{i}}, \\& \vartheta _{3}= \frac{\sum_{i=0}^{k-2}\epsilon _{i}\delta _{i}}{1-\sum_{i=0}^{k-2}\epsilon _{i}+\sum_{i=0}^{k-2}\epsilon _{i}\delta _{i}}. \end{aligned}$$

Proof

Since \(\mathtt{u}(\sigma )\in \mathrm{C}^{2}[0,1]\), \(\mathtt{u}(\sigma )\) and \({}^{c}\mathcal{D}_{0^{+}}^{\alpha }\mathtt{u}(\sigma )\) are bounded. We have that \(\mathtt{u}''\) and \({}^{c}\mathcal{D}_{0^{+}}^{\alpha }\) are of exponential order, where \(\sigma \in \mathrm{J}\). Taking the Laplace transform of (4), by (2), we acquire

$$\begin{aligned} \begin{aligned} &s^{2}\mathcal{U}(s)-s\mathtt{u}(0)-\mathtt{u}'(0)+s^{\alpha } \mathcal{U}(s)-s^{\alpha -1}\mathtt{u}(0)-s^{\alpha -2} \mathtt{u}'(0)= \mathcal{G}(s), \\ &\mathcal{U}(s)=\frac{s^{-\alpha }}{1+s^{2-\alpha }}\mathcal{G}(s)+ \frac{1}{s} \mathtt{u}(0)+\frac{1}{s^{2}}\mathtt{u}(0). \end{aligned} \end{aligned}$$

Applying the inverse Laplace transform, by (3), we have

$$ \mathtt{u}(\sigma )= \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2- \alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr) \mathtt{g}(s)\,ds+\mathtt{u}(0)+\sigma \mathtt{u}'(0). $$
(6)

Further, we acquire

$$\begin{aligned}& \sum_{i=0}^{k-2}\epsilon _{i} \mathtt{u}(\delta _{i})=\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2- \alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr) \mathtt{g}(s)\,ds+\sum_{i=0}^{k-2} \epsilon _{i}\mathtt{u}(0)+\sum_{i=0}^{k-2} \epsilon _{i}\delta _{i}\mathtt{u}'(0), \\& \sum_{i=0}^{k-2}\epsilon _{i} \mathtt{u}(\delta _{i})=\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2- \alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr) \mathtt{g}(s)\,ds+\sum_{i=0}^{k-2} \epsilon _{i}\mathtt{u}(0)+\sum_{i=0}^{k-2} \epsilon _{i}\delta _{i}\mathtt{u}'(0). \end{aligned}$$

Applying the boundary conditions, we get

$$\begin{aligned} \mathtt{u}(0)={}&\vartheta _{2}\sum _{i=0}^{k-2}\epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds+ \frac{\vartheta _{3}}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{ \beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} -\vartheta _{3} \int _{0}^{1}(1-s)\mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds \end{aligned}$$
(7)

and

$$\begin{aligned} \mathtt{u}'(0)={}&{-}\vartheta _{2}\sum_{i=0}^{k-2}\epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds \\ &{}+ \frac{\vartheta _{1}}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{ \beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} -\vartheta _{1} \int _{0}^{1}(1-s)\mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds. \end{aligned}$$
(8)

Thus, substituting (7) and (8) into (6), we deduce that

$$\begin{aligned} \mathtt{u}(\sigma )={}&\frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds+ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds \\ & {} -(\vartheta _{1}\sigma +\vartheta _{3}) \int _{0}^{1}(1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \mathtt{g}(s)\,ds \\ ={}&\frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds \\ & {} -(\vartheta _{1}\sigma +\vartheta _{3}) \int _{\sigma }^{1}(1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \mathtt{g}(s)\,ds \\ & {} + \int _{0}^{\sigma } \bigl((\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr) \\ & {} -(\vartheta _{1}\sigma +\vartheta _{3}) (1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \bigr) \mathtt{g}(s)\,ds \\ ={}& \int _{0}^{1}\mathbb{G}(\sigma ,s)\mathtt{g}(s)\,ds+ \frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\mathtt{g}(s)\,ds. \end{aligned}$$

Hence, the proof is completed. □

Remark 1

Using the definition of \(\mathcal{ML}\) function, we obtain

$$ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\,ds=\sigma ^{3} \mathrm{E}_{2- \alpha ,4} \bigl(-\sigma ^{2-\alpha } \bigr), \quad (\sigma \in \mathrm{J},1< \alpha < 2), $$

this implies that the series is convergent. Thus, there exists a constant \(\mathrm{E}_{2-\alpha ,4}>0\) such that

$$ \biggl\vert \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\,ds \biggr\vert \leqslant \bigl\vert \mathrm{E}_{2-\alpha ,4} \bigl(-\sigma ^{2-\alpha } \bigr) \bigr\vert \leqslant \mathrm{E}_{2-\alpha ,4}. $$

Moreover, by the continuity of \(\mathcal{ML}\) function and (5), there exists a constant \(\aleph >0\) such that

$$ \int _{0}^{\sigma } \bigl\vert \mathbb{G}(\sigma ,s) \bigr\vert \,ds \leqslant \aleph ,\quad \sigma \in \mathrm{J}. $$

Theorem 9

Under hypotheses \([\mathcal{H}_{1}]\)–\([\mathcal{H}_{2}]\) and the inequality

$$ \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }\mathcal{Q}_{\varphi }}{\Gamma (\beta +1)}+ \aleph \mathcal{Q}_{\phi }< 1, $$

the given system (1) has a unique solution.

Proof

Using Lemma 8, the corresponding system (1) has the following solution:

$$\begin{aligned} \mathtt{u}(\sigma )={}& \int _{0}^{1}\mathbb{G}(\sigma ,s)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds+ \frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds, \end{aligned}$$

where \(\mathbb{G}(\sigma ,s)\) is given by (5).

Consider the operator \(\mathfrak{T}\) defined on \(\mathrm{C}^{2}[0,1]\) by

$$\begin{aligned} (\mathfrak{T}\mathtt{u} ) (\sigma )={}& \int _{0}^{1} \mathbb{G}(\sigma ,s)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds+ \frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds. \end{aligned}$$
(9)

Thus, we have \(\mathfrak{T}\mathtt{u}\in \mathrm{C}^{2}[0,1]\) for any \(\mathtt{u}\in \mathrm{C}^{2}[0,1]\). This proves that \(\mathfrak{T}\) maps \(\mathrm{C}^{2}[0,1]\) into itself.

Let \(\acute{\mathcal{B}}=\{\mathtt{u}\in \mathrm{C}^{2}[0,1]: \Vert \mathtt{u} \Vert <\epsilon \}\) and choose

$$ \epsilon > \frac{ (\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)}\hat{\mathfrak{f}}_{1}+\aleph \hat{\mathfrak{f}}_{2} )}{1- (\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)}\hat{\mathfrak{g}}_{1}+\aleph \hat{\mathfrak{g}}_{ 2} )}. $$

From (9), using \([\mathcal{H}_{2}]\) and for \(\mathtt{u}\in \acute{\mathcal{B}}\), we get

$$\begin{aligned}& \begin{aligned} \bigl\vert (\mathfrak{T}\mathtt{u} ) (\sigma ) \bigr\vert \leqslant{}& \int _{0}^{1} \bigl\vert \mathbb{G}(\sigma ,s) \bigr\vert \bigl\vert \phi \bigl(s, \mathtt{u}(s) \bigr) \bigr\vert \,ds+ \frac{ \vert (\vartheta _{1}\sigma +\vartheta _{3}) \vert }{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1} \bigl\vert \varphi \bigl(s,\mathtt{u}(s) \bigr) \bigr\vert \,ds \\ & {} +\vartheta _{2} \bigl\vert (1-\sigma ) \bigr\vert \sum _{i=0}^{k-2}\epsilon _{i} \int _{0}^{\delta _{i}} \bigl\vert (\delta _{i}-s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr) \bigr\vert \bigl\vert \phi \bigl(s,\mathtt{u}(s) \bigr) \bigr\vert \,ds \\ \leqslant{}&\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \bigl( \hat{\mathfrak{f}}_{1}+\hat{ \mathfrak{g}}_{1} \Vert \mathtt{u} \Vert \bigr)+\aleph \bigl( \hat{ \mathfrak{f}}_{2}+\hat{\mathfrak{g}}_{2} \Vert \mathtt{u} \Vert \bigr) \\ ={}& \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{\mathfrak{f}}_{1}+\aleph \hat{ \mathfrak{f}}_{2} \biggr)+ \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{ \mathfrak{g}}_{1}+\aleph \hat{\mathfrak{g}}_{2} \biggr) \Vert \mathtt{u} \Vert \\ \leqslant{}& \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{\mathfrak{f}}_{1}+\aleph \hat{\mathfrak{f}}_{2} \biggr)+ \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{ \mathfrak{g}}_{1}+\aleph \hat{\mathfrak{g}}_{2} \biggr) \epsilon \leqslant \epsilon \end{aligned} \\& \quad \implies \quad \Vert \mathfrak{T}\mathtt{u} \Vert \leqslant\epsilon ,\quad \mathtt{u}\in \acute{\mathcal{B}}. \end{aligned}$$

Hence, \(\mathfrak{T}\acute{\mathcal{B}}\subseteq \acute{\mathcal{B}}\).

Now, for any \(\mathtt{u}_{1},\mathtt{u}_{2}\in \mathrm{C}^{2}[0,1]\) and \(\sigma \in \mathrm{J}\), from (9), using \([\mathcal{H}_{1}]\), we have

$$\begin{aligned} { \bigl\vert (\mathfrak{T}\mathtt{u}_{1} ) (\sigma )- (\mathfrak{T} \mathtt{u}_{2} ) (\sigma ) \bigr\vert }\leqslant{}& \int _{0}^{1} \bigl\vert \mathbb{G}(\sigma ,s) \bigr\vert \bigl\vert \phi \bigl(s, \mathtt{u}_{1}(s) \bigr)-\phi \bigl(s,\mathtt{u}_{2}(s) \bigr) \bigr\vert \,ds \\ & {} +\frac{ \vert (\vartheta _{1}\sigma +\vartheta _{3}) \vert }{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1} \bigl\vert \varphi \bigl(s, \mathtt{u}_{1}(s) \bigr)-\varphi \bigl(s, \mathtt{u}_{2}(s) \bigr) \bigr\vert \,ds \\ & {} +\vartheta _{2} \Biggl\vert (1-\sigma )\sum _{i=0}^{k-2}\epsilon _{i} \Biggr\vert \int _{0}^{\delta _{i}} \bigl\vert (\delta _{i}-s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr) \bigr\vert \\ & {} \times \bigl\vert \phi \bigl(s,\mathtt{u}_{1}(s) \bigr)-\phi \bigl(s,\mathtt{u}_{1}(s) \bigr) \bigr\vert \,ds \\ \leqslant{}&\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }\mathcal{Q}_{\varphi }}{\Gamma (\beta +1)} \Vert \mathtt{u}_{1}- \mathtt{u}_{2} \Vert +\aleph \mathcal{Q}_{\phi } \Vert \mathtt{u}_{1}-\mathtt{u}_{2} \Vert \\ ={}& \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }\mathcal{Q}_{\varphi }}{\Gamma (\beta +1)}+ \aleph \mathcal{Q}_{\phi } \biggr) \Vert \mathtt{u}_{1}-\mathtt{u}_{2} \Vert . \end{aligned}$$

As \(\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }\mathcal{Q}_{\varphi }}{\Gamma (\beta +1)}+ \aleph \mathcal{Q}_{\phi }<1\), thus \(\mathfrak{T}\) is a contraction mapping. Hence, (1) has a unique solution. □

Theorem 10

Under hypotheses \([\mathcal{H}_{1}]\)–\([\mathcal{H}_{2}]\) and the inequality

$$ \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }\mathcal{Q}_{\varphi }}{\Gamma (\beta +1)}+ \aleph \mathcal{Q}_{\phi }< 1, $$
(10)

the given system (1) has at least one solution.

Proof

Let the operators \(\mathfrak{T}_{1}\) and \(\mathfrak{T}_{2}\) on \(\mathrm{C}^{2}[0,1]\) be defined by

$$\begin{aligned}& (\mathfrak{T}_{1}\mathtt{u}) (\sigma )=-(\vartheta _{1} \sigma + \vartheta _{3}) \int _{\sigma }^{1}(1-s)\mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr)\phi \bigl(s,\mathtt{u}(s) \bigr)\,ds, \\& \begin{aligned} (\mathfrak{T}_{2}\mathtt{u}) (\sigma )={}& \frac{(\vartheta _{1}\sigma +\vartheta _{3})}{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1}\varphi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{2}(1-\sigma )\sum_{i=0}^{k-2} \epsilon _{i} \int _{0}^{\delta _{i}}(\delta _{i}-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds \\ & {} + \int _{0}^{\sigma } \bigl((\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr) \\ & {} -(\vartheta _{1}\sigma +\vartheta _{3}) (1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds. \end{aligned} \end{aligned}$$

Let \(\mathfrak{S}_{\mathfrak{r}}=\{\mathtt{u}\in \mathrm{C}^{2}[0,1]: \Vert \mathtt{u} \Vert \leqslant \mathfrak{r}\}\) and choose

$$\begin{aligned} 0< \frac{ (\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)}\hat{\mathfrak{f}}_{1}+\aleph \hat{\mathfrak{f}}_{2} )}{1- (\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)}\hat{\mathfrak{g}}_{1}+\aleph \hat{\mathfrak{g}}_{2} )} \leqslant \mathfrak{ r}. \end{aligned}$$

For any \(\mathtt{u},\mathtt{v}\in \mathfrak{S}_{\mathfrak{r}}\), using \([\mathcal{H}_{1}]\)–\([\mathcal{H}_{2}]\), Remark 1, and the definitions of the operators \(\mathfrak{T}_{1}\) and \(\mathfrak{T}_{2}\), we get that

$$\begin{aligned} \Vert \mathfrak{T}_{1}\mathtt{u}+\mathfrak{T}_{2} \mathtt{v} \Vert \leqslant{}& \int _{0}^{1} \bigl\vert \mathbb{G}(\sigma ,s) \bigr\vert \bigl\vert \phi \bigl(s,\mathtt{v}(s) \bigr) \bigr\vert \,ds+ \frac{ \vert (\vartheta _{1}\sigma +\vartheta _{3}) \vert }{\Gamma (\beta )} \int _{0}^{\eta }(\eta -s)^{\beta -1} \bigl\vert \varphi \bigl(s,\mathtt{v}(s) \bigr) \bigr\vert \,ds \\ & {} +\vartheta _{2} \bigl\vert (1-\sigma ) \bigr\vert \sum _{i=0}^{k-2}\epsilon _{i} \int _{0}^{\delta _{i}} \bigl\vert (\delta _{i}-s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\delta _{i}-s )^{2-\alpha } \bigr) \bigr\vert \bigl\vert \phi \bigl(s, \mathtt{v}(s) \bigr) \bigr\vert \,ds \\ \leqslant{}&\frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \bigl( \hat{\mathfrak{f}}_{1}+\hat{ \mathfrak{g}}_{1} \Vert \mathtt{v} \Vert \bigr)+\aleph \bigl( \hat{ \mathfrak{f}}_{2}+\hat{\mathfrak{g}}_{2} \Vert \mathtt{v} \Vert \bigr) \\ ={}& \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{\mathfrak{f}}_{1}+\aleph \hat{ \mathfrak{f}}_{2} \biggr)+ \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{ \mathfrak{g}}_{1}+\aleph \hat{\mathfrak{g}}_{2} \biggr) \Vert \mathtt{v} \Vert \\ \leqslant{}& \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{\mathfrak{f}}_{1}+\aleph \hat{\mathfrak{f}}_{2} \biggr)+ \biggl( \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }}{\Gamma (\beta +1)} \hat{ \mathfrak{g}}_{1}+\aleph \hat{\mathfrak{g}}_{2} \biggr) \mathfrak{r}. \end{aligned}$$

Thus, we obtain \(\mathfrak{T}_{1}\mathtt{u}+\mathfrak{T}_{2}\mathtt{v}\in \mathfrak{S}_{\mathfrak{r}}\).

Using Theorem 9, the operator \(\mathfrak{T}_{2}\) is a contraction mapping.

By the continuity of \(\phi (\sigma ,\mathtt{u}(\sigma ))\), \(\mathtt{u}\in \mathfrak{S}_{\mathfrak{r}}\), and the two-parameter \(\mathcal{ML}\) function, the operator \(\mathfrak{T}_{1}\) is continuous.

Let \(\mathtt{u}\in \mathfrak{S}_{\mathfrak{r}}\), from \([\mathcal{H}_{2}]\) and Remark 1, we have

$$\begin{aligned} \bigl\vert \mathfrak{T}_{1}\mathtt{u}(\sigma ) \bigr\vert \leqslant \aleph \bigl( \hat{\mathfrak{f}}_{1}+\hat{ \mathfrak{g}}_{1} \Vert \mathtt{u} \Vert \bigr) \leqslant \acute{ \mathcal{C}}. \end{aligned}$$

Hence, \(\mathfrak{T}_{1}\) is uniformly bounded on \(\mathfrak{S}_{\mathfrak{r}}\).

Let \(\mathtt{u}\in \mathfrak{S}_{\mathfrak{r}}\) and \(\sigma _{1},\sigma _{2}\in \mathrm{J}\) such that \(\sigma _{1}<\sigma _{2}\),

$$\begin{aligned} \bigl\Vert (\mathfrak{T}_{1}\mathtt{u}) (\sigma _{1})-( \mathfrak{T}_{1} \mathtt{u}) (\sigma _{2}) \bigr\Vert ={}& \biggl\Vert (\vartheta _{1}\sigma _{1}+ \vartheta _{3}) \int _{\sigma _{1}}^{1}(1-s)\mathrm{E}_{2- \alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds \\ & {} -(\vartheta _{1}\sigma _{2}+\vartheta _{3}) \int _{\sigma _{2}}^{1}(1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \phi \bigl(s,\mathtt{u}(s) \bigr)\,ds \biggr\Vert \\ ={}& \biggl\Vert \vartheta _{1}\sigma _{1} \int _{\sigma _{1}}^{1}(1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \phi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} -\vartheta _{1}\sigma _{2} \int _{\sigma _{2}}^{1}(1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \phi \bigl(s,\mathtt{u}(s) \bigr)\,ds \\ & {} +\vartheta _{3} \int _{\sigma _{1}}^{\sigma _{2}}(1-s) \mathrm{E}_{2-\alpha ,2} \bigl(- (1-s )^{2-\alpha } \bigr) \phi \bigl(s,\mathtt{u}(s) \bigr)\,ds \biggr\Vert \\ \leqslant{}& \bigl[\vartheta _{1}(1-\theta )\mathrm{E}_{2-\alpha ,2} \bigl(- (1-\theta )^{2-\alpha } \bigr) \bigl(\sigma _{1} \vert 1- \sigma _{1} \vert -\sigma _{2} \vert 1-\sigma _{2} \vert \bigr) \\ & {} +\vartheta _{3}(1-\theta )\mathrm{E}_{2-\alpha ,2} \bigl(- (1- \theta )^{2-\alpha } \bigr) \vert \sigma _{2}-\sigma _{1} \vert \bigr] \bigl( \hat{\mathfrak{f}}_{1}+\hat{ \mathfrak{g}}_{1} \Vert \mathtt{u} \Vert \bigr), \end{aligned}$$

where \(\sigma _{1}<\theta <\sigma _{2}\). This implies that

$$\begin{aligned} \bigl\Vert (\mathfrak{T}_{1}\mathtt{u}) (\sigma _{1})-( \mathfrak{T}_{1} \mathtt{u}) (\sigma _{2}) \bigr\Vert \rightarrow 0\quad \text{as } \sigma _{1} \rightarrow \sigma _{2}. \end{aligned}$$

Therefore, \(\mathfrak{T}_{1}\) is relatively compact on \(\mathfrak{S}_{\mathfrak{r}}\). So, by Theorem 5 and Arzelà–Ascoli theorem, the operator \(\mathfrak{T}_{1}\) is compact on \(\mathfrak{S}_{r}\). Thus, system (1) has at least one solution on J. □

3.2 Ulam’s stability results

In this subsection, using the Banach fixed point theorem and Bielecki metric, we investigate \(\mathcal{HUS}\) and \(\mathcal{HURS}\) results in \(\mathrm{C}^{2}[0,1]\) for system (1).

Consider the space \(\mathrm{C}^{2}[0,1]\) endowed with the Bielecki metric:

$$\begin{aligned} d(\mathfrak{p},\mathfrak{q})=\sup_{\sigma \in \mathrm{J}} \frac{ \vert \mathfrak{p}(\sigma )-\mathfrak{q}(\sigma ) \vert }{\mathfrak{z}(\sigma )}, \quad \mathfrak{p},\mathfrak{q}\in \mathrm{C}^{2}[0,1], \end{aligned}$$

where \(\mathfrak{z}:\mathrm{J}\rightarrow (0,\infty )\). Obviously, \((\mathrm{C}^{2}[0,1],d)\) is a complete metric space.

The following Definitions 11 and 12 are adapted from [36].

Definition 11

If \(\hat{\mathfrak{u}}(\sigma ) \) is a continuously differentiable function satisfying

$$ \bigl\vert \hat{\mathfrak{u}}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \hat{\mathfrak{u}}( \sigma )-\phi \bigl(\sigma ,\hat{\mathfrak{u}}(\sigma ) \bigr) \bigr\vert \leqslant \rho ,\quad \sigma \in \mathrm{J}, $$

where \(\rho >0\), and there are a solution \(\mathtt{u}(\sigma )\) of (1) and a constant \(\wp >0\) independent of \(\hat{\mathfrak{u}}(\sigma )\) and \(\mathtt{u}(\sigma )\) such that

$$\begin{aligned} \bigl\vert \hat{\mathfrak{u}}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \wp \rho , \quad \sigma \in \mathrm{J}, \end{aligned}$$

then we say that (1) is \(\mathcal{HUS}\).

Definition 12

If \(\hat{\mathfrak{u}}(\sigma ) \) is a continuously differentiable function satisfying

$$ \bigl\vert \hat{\mathfrak{u}}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \hat{\mathfrak{u}}( \sigma )-\phi \bigl(\sigma ,\hat{\mathfrak{u}}(\sigma ) \bigr) \bigr\vert \leqslant \mathfrak{z}(\sigma ),\quad \sigma \in \mathrm{J}, $$

where \(\mathfrak{z}:\mathrm{J}\rightarrow [0,\infty )\) is a continuous function, and there are a solution \(\mathtt{u}(\sigma )\) of (1) and a constant \(\wp >0\) independent of \(\hat{\mathfrak{u}}(\sigma )\) and \(\mathtt{u}(\sigma )\) such that

$$\begin{aligned} \bigl\vert \hat{\mathfrak{u}}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \wp \mathfrak{z}(\sigma ),\quad \sigma \in \mathrm{J}, \end{aligned}$$

then we say that (1) is \(\mathcal{HURS}\).

Theorem 13

Let hypothesis \([\mathcal{H}_{1}]\) be satisfied. Moreover, let \(\mathfrak{z}:\mathrm{J}\rightarrow (0,\infty )\), and for any constant \(0\leqslant \mu <1\), we have

$$ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\mathfrak{z}(s)\,ds \leqslant \mu \mathfrak{z}(\sigma ). $$
(11)

If \(\hat{\mathfrak{u}}\in \mathrm{C}^{2}[0,1]\) satisfies

$$ \bigl\vert \hat{\mathfrak{u}}''( \sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \hat{ \mathfrak{u}}(\sigma )-\phi \bigl(\sigma ,\hat{\mathfrak{u}}(\sigma ) \bigr) \bigr\vert \leqslant \mathfrak{z}(\sigma ),\quad \sigma \in \mathrm{J}, $$
(12)

and \(\mathcal{Q}_{\phi }\mu <1\), then there exists a solution \(\mathtt{u}(\sigma )\) of (1) in \(\mathrm{C}^{2}[0,1]\) such that

$$\begin{aligned} \bigl\vert \hat{\mathfrak{u}}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \frac{\mu }{1-\mathcal{Q}_{\phi }\mu }\mathfrak{z}(\sigma ),\quad \sigma \in \mathrm{J}. \end{aligned}$$
(13)

This implies that under the above conditions, system (1) is \(\mathcal{HURS}\).

Proof

Using Lemma 8, the corresponding system (1) has the following solution:

$$ \mathtt{u}(\sigma )= \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2- \alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds+ \mathtt{u}(0)+\sigma \mathtt{u}'(0), $$
(14)

which follows from the proof of (6). We conclude that \(\mathtt{u}(\sigma ) \) satisfies (1) iff \(\mathtt{u}(\sigma ) \) satisfies (14).

Consider the operator \(\Omega :\mathrm{C}^{2}[0,1]\rightarrow \mathrm{C}^{2}[0,1]\) defined by

$$\begin{aligned}& (\Omega \mathtt{v}) (\sigma )= \int _{0}^{\sigma }(\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s,\mathtt{v}(s) \bigr)\,ds+ \mathtt{v}(0)+\sigma \mathtt{v}'(0),\\& \quad \sigma \in \mathrm{J}, \mathtt{v}\in \mathrm{C}^{2}[0,1]. \end{aligned}$$

Since ϕ and the two-parameter \(\mathcal{ML}\) function are continuous, this implies that the operator Ω is continuous.

From (11), for any \(\mathfrak{v},\mathfrak{w}\in \mathrm{C}^{2}[0,1]\), we obtain

$$\begin{aligned} d(\Omega \mathfrak{v},\Omega \mathfrak{w})&=\sup_{\sigma \in \mathrm{J}} \frac{ \vert \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} (- (\sigma -s )^{2-\alpha } ) [\phi (s,\mathfrak{v}(s))-\phi (s,\mathfrak{w}(s)) ]\,ds \vert }{\mathfrak{z}(\sigma )} \\ &\leqslant \mathcal{Q}_{\phi }\sup_{\sigma \in \mathrm{J}} \frac{ \vert \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} (- (\sigma -s )^{2-\alpha } ) \vert \mathfrak{v}(s)-\mathfrak{w}(s) \vert \,ds \vert }{\mathfrak{z}(\sigma )} \\ &=\mathcal{Q}_{\phi }\sup_{\sigma \in \mathrm{J}} \frac{ \vert \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} (- (\sigma -s )^{2-\alpha } )\mathfrak{z}(\sigma )\frac{ \vert \mathfrak{v}(s)-\mathfrak{w}(s) \vert }{\mathfrak{z}(\sigma )}\,ds \vert }{\mathfrak{z}(\sigma )} \\ &\leqslant \mathcal{Q}_{\phi }\mu d(\mathfrak{v},\mathfrak{w}). \end{aligned}$$

Since \(\mathcal{Q}_{\phi }\mu <1\), the operator Ω is strictly contractive.

Also, let \(\hat{\mathfrak{u}}\in \mathrm{C}^{2}[0,1]\) satisfy (12). Then, we get that \(\hat{\mathfrak{u}}\) satisfies the following inequality:

$$\begin{aligned} & \biggl\vert \hat{\mathfrak{u}}(\sigma )-\hat{ \mathfrak{u}}(0)-\sigma \hat{\mathfrak{u}}'(0)- \int _{0}^{\sigma }(\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s,\hat{\mathfrak{u}}(s) \bigr)\,ds \biggr\vert \\ &\quad \leqslant \biggl\vert \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2- \alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr) \mathfrak{z}(s)\,ds \biggr\vert . \end{aligned}$$
(15)

Using (11), (15), and the definition of the operator Ω, we get

$$\begin{aligned} \bigl\vert (\Omega \hat{\mathfrak{u}}) (\sigma )-\hat{\mathfrak{u}}(\sigma ) \bigr\vert &= \biggl\vert \hat{\mathfrak{u}}(0)+\sigma \hat{ \mathfrak{u}}'(0)+ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s,\hat{\mathfrak{u}}(s) \bigr)\,ds- \hat{\mathfrak{u}}(\sigma ) \biggr\vert \\ &\leqslant \biggl\vert \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2- \alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr) \mathfrak{z}(s)\,ds \biggr\vert \leqslant \mu \mathfrak{z}(\sigma ). \end{aligned}$$

Therefore, we conclude that

$$\begin{aligned} d(\Omega \hat{\mathfrak{u}},\hat{\mathfrak{u}})\leqslant \mu < \infty , \quad 0\leqslant \mu < 1. \end{aligned}$$
(16)

Using \([\mathcal{A}_{2}]\) of Theorem 6, there exists an element

$$\begin{aligned} \mathtt{u}\in \tilde{\mathrm{C}}[0,1]= \bigl\{ y\in \mathrm{C}^{2}[0,1]:d( \Omega \hat{\mathfrak{u}},y)< \infty \bigr\} \end{aligned}$$

such that \(\Omega \mathtt{u}=\mathtt{u}\) or, likewise,

$$ \mathtt{u}(\sigma )= \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2- \alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds+ \mathtt{u}(0)+\sigma \mathtt{u}'(0). $$

Since (14) is the likewise integral equation of (1), so \(\mathtt{u}(\sigma )\) is a solution of (1). Also, using \([\mathcal{A}_{3}]\) of heorem 6 and (16), we have

$$\begin{aligned} d(\hat{\mathfrak{u}},\mathtt{u})\leqslant \frac{1}{1-\mathcal{Q}_{\phi }\mu }d(\Omega \hat{ \mathfrak{u}}, \hat{\mathfrak{u}})\leqslant \frac{\mu }{1-\mathcal{Q}_{\phi }\mu }. \end{aligned}$$

By the definition of d, we get that (13) holds. □

Theorem 14

Let hypothesis \([\mathcal{H}_{1}]\) be satisfied, and let \(\mathfrak{z}:\mathrm{J}\rightarrow (0,\infty )\), and for any constant \(0\leqslant \mu <1\), we have

$$ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\mathfrak{z}(s)\,ds \leqslant \mu \mathfrak{z}(\sigma ) $$
(17)

and \(\mathcal{Q}_{\phi }\mu <1\). If \(\hat{\mathfrak{u}}\in \mathrm{C}^{2}[0,1]\) satisfies

$$ \bigl\vert \hat{\mathfrak{u}}''( \sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\alpha } \hat{ \mathfrak{u}}(\sigma )-\phi \bigl(\sigma ,\hat{\mathfrak{u}}(\sigma ) \bigr) \bigr\vert \leqslant \rho ,\quad \sigma \in \mathrm{J}, $$
(18)

where \(\rho >0\), then there exists a solution \(\mathtt{u}(\sigma )\) of (1) in \(\mathrm{C}^{2}[0,1]\) such that

$$\begin{aligned} \bigl\vert \hat{\mathfrak{u}}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \frac{\mathfrak{z}(1)\rho \mathrm{E}_{2-\alpha ,4}}{(1-\mathcal{Q}_{\phi }\mu )\mathfrak{z}(0)}, \quad \sigma \in \mathrm{J}. \end{aligned}$$
(19)

This implies that under the above conditions, system (1) is \(\mathcal{HUS}\).

Proof

The first segment of the proof is obtained by performing the same steps as in Theorem 13. Let the operator \(\Omega :\mathrm{C}^{2}[0,1]\rightarrow \mathrm{C}^{2}[0,1]\) be defined by

$$\begin{aligned}& (\Omega \mathtt{v}) (\sigma )= \int _{0}^{\sigma }(\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s,\mathtt{v}(s) \bigr)\,ds+ \mathtt{v}(0)+\sigma \mathtt{v}'(0), \\& \quad \sigma \in \mathrm{J}, \mathtt{v}\in \mathrm{C}^{2}[0,1]. \end{aligned}$$

For any \(\mathfrak{v},\mathfrak{w}\in \mathrm{C}^{2}[0,1]\), we have

$$\begin{aligned} d(\Omega \mathfrak{v},\Omega \mathfrak{w})\leqslant \mathcal{Q}_{\phi } \mu d(\mathfrak{v},\mathfrak{w}). \end{aligned}$$

Since \(\mathcal{Q}_{\phi }\mu <1\), from Theorem 13, this implies that the operator Ω is strictly contractive in \((\mathrm{C}^{2}[0,1],d)\).

Suppose that \(\hat{\mathfrak{u}}\in \mathrm{C}^{2}[0,1]\) satisfies (18). Using Remark 1, we get

$$\begin{aligned} & \biggl\vert \hat{\mathfrak{u}}(\sigma )-\hat{\mathfrak{u}}(0)-\sigma \hat{ \mathfrak{u}}'(0)- \int _{0}^{\sigma }(\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s,\hat{\mathfrak{u}}(s) \bigr)\,ds \biggr\vert \\ &\quad \leqslant \rho \biggl\vert \int _{0}^{\sigma }(\sigma -s) \mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\,ds \biggr\vert \leqslant \rho \mathrm{E}_{2-\alpha ,4},\quad \sigma \in \mathrm{J}. \end{aligned}$$

Now, by the definition of the operator Ω, we get

$$\begin{aligned} \bigl\vert (\Omega \hat{\mathfrak{u}}) (\sigma )-\hat{\mathfrak{u}}(\sigma ) \bigr\vert &= \biggl\vert \hat{\mathfrak{u}}(0)+\sigma \hat{ \mathfrak{u}}'(0)+ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2-\alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s,\hat{\mathfrak{u}}(s) \bigr)\,ds- \hat{\mathfrak{u}}(\sigma ) \biggr\vert \\ &\leqslant \rho \mathrm{E}_{2-\alpha ,4},\quad \sigma \in \mathrm{J}. \end{aligned}$$

Since \(\mathfrak{z}\) is a nondecreasing positive function, we have

$$\begin{aligned} d(\Omega \hat{\mathfrak{u}},\hat{\mathfrak{u}})=\sup _{\sigma \in \mathrm{J}} \frac{ \vert \Omega \hat{\mathfrak{u}}(\sigma )-\hat{\mathfrak{u}}(\sigma ) \vert }{\mathfrak{z}(\sigma )} \leqslant \frac{\rho \mathrm{E}_{2-\alpha ,4}}{\mathfrak{z}(0)}< \infty . \end{aligned}$$
(20)

Using \([\mathcal{A}_{2}]\) of Theorem 6, there exists an element

$$\begin{aligned} \mathtt{u}\in \tilde{\mathrm{C}}[0,1]= \bigl\{ y\in \mathrm{C}^{2}[0,1]:d( \Omega \hat{\mathfrak{u}},y)< \infty \bigr\} \end{aligned}$$

such that \(\Omega \mathtt{u}=\mathtt{u}\) or, likewise,

$$ \mathtt{u}(\sigma )= \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{2- \alpha ,2} \bigl(- (\sigma -s )^{2-\alpha } \bigr)\phi \bigl(s, \mathtt{u}(s) \bigr)\,ds+ \mathtt{u}(0)+\sigma \mathtt{u}'(0), $$

which implies \(\mathtt{u}(\sigma )\) is a solution of (1).

Thus, from \([\mathcal{A}_{3}]\) of Theorem 6 and (20), it follows that

$$\begin{aligned} d(\hat{\mathfrak{u}},\mathtt{u})\leqslant \frac{1}{1-\mathcal{Q}_{\phi }\mu }\sup _{\sigma \in \mathrm{J}} \frac{ \vert \Omega \hat{\mathfrak{u}}(\sigma )-\hat{\mathfrak{u}}(\sigma ) \vert }{\mathfrak{z}(\sigma )} \leqslant \frac{1}{1-\mathcal{Q}_{\phi }\mu } \frac{\rho \mathrm{E}_{2-\alpha ,4}}{\mathfrak{z}(0)}. \end{aligned}$$

By the definition of d, we get that

$$\begin{aligned} \bigl\vert \hat{\mathfrak{u}}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \frac{\mathfrak{z}(\sigma )\rho \mathrm{E}_{2-\alpha ,4}}{(1-\mathcal{Q}_{\phi }\mu )\mathfrak{z}(0)}, \quad \sigma \in \mathrm{J}. \end{aligned}$$
(21)

Therefore, (19) follows directly from (21). □

4 Illustrative example

Here, we provide an adequate problem to testify our results.

Example 1

Let

$$\begin{aligned} \textstyle\begin{cases} \mathtt{u}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{\frac{3}{2}} \mathtt{u}(\sigma )= \frac{1}{(8+\sigma ^{2})(1+ \vert \mathtt{u}(\sigma ) \vert )},\quad \sigma \in \mathrm{J}, \\ \mathtt{u}(0)=\sum_{i=0}^{4}\epsilon _{i}\mathtt{u}(\delta _{i}) \quad\quad \mathtt{u}(1)=\frac{1}{\Gamma (\frac{3}{2})}\int _{0}^{ \frac{1}{4}} (\frac{1}{4}-s )^{\frac{1}{2}} \frac{s^{2}+\mathtt{u}(s)}{60}\,ds, \end{cases}\displaystyle \end{aligned}$$
(22)

where \(\epsilon _{0}=\frac{9}{40}\), \(\epsilon _{1}=\frac{47}{200}\), \(\epsilon _{2}=\frac{49}{200}\), \(\epsilon _{3}=\frac{51}{200}\), \(\epsilon _{4}=\frac{53}{200}\), \(\delta _{0}=\frac{21}{40}\), \(\delta _{1}= \frac{107}{200}\), \(\delta _{2}=\frac{109}{200}\), \(\delta _{3}=\frac{111}{200}\), \(\delta _{4}=\frac{113}{200}\), and \(\mathtt{u}(\sigma )\in \mathrm{C}^{2}[0,1]\).

From system (1), we see that

$$\begin{aligned}& \alpha =\frac{3}{2},\quad\quad \beta =\frac{3}{2},\quad\quad \eta =\frac{1}{4},\\& \phi \bigl(\sigma ,\mathtt{u}(\sigma ) \bigr)= \frac{1}{(8+\sigma ^{2})(1+ \vert \mathtt{u}(\sigma ) \vert )},\quad\quad \varphi \bigl( \sigma ,\mathtt{u}(\sigma ) \bigr)= \frac{\sigma ^{2}+\mathtt{u}(\sigma )}{60}. \end{aligned}$$

Now, for all \(\mathfrak{h}_{1},\mathfrak{h}_{2}\in \mathbb{R}\) and \(\sigma \in \mathrm{J}\), we have

$$ \bigl\vert \varphi (\sigma ,\mathfrak{h}_{1})-\varphi (\sigma , \mathfrak{h}_{2}) \bigr\vert \leqslant \frac{1}{8} \vert \mathfrak{h}_{1}-\mathfrak{h}_{2} \vert $$

and

$$ \bigl\vert \phi (\sigma ,\mathfrak{h}_{1})-\phi (\sigma , \mathfrak{h}_{2}) \bigr\vert \leqslant \frac{1}{60} \vert \mathfrak{h}_{1}-\mathfrak{h}_{2} \vert . $$

These satisfy condition \([\mathcal{H}_{1}]\) with \(\mathcal{Q}_{\varphi }=\frac{1}{8}\) and \(\mathcal{Q}_{\phi }=\frac{1}{60}\).

Further, by Remark 1, we have

$$ \frac{(\vartheta _{1}+\vartheta _{3})\eta ^{\beta }\mathcal{Q}_{\varphi }}{\Gamma (\beta +1)}+ \aleph \mathcal{Q}_{\phi }= \frac{(-\frac{600}{1183}+\frac{1783}{1183})\frac{1}{4}^{\frac{3}{2}}\frac{1}{8}}{\Gamma (\frac{5}{2})}+ \frac{1}{60}=\frac{1}{48\sqrt{\pi }}+\frac{1}{60}< 1. $$

From Theorems 9 and 10, system (1) has a unique solution.

Next, we check the \(\mathcal{HUS}\) and \(\mathcal{HURS}\) for (22).

Letting \(\mathfrak{z}(\sigma )=e^{\sigma }\), by Remark 1, we obtain

$$ \int _{0}^{\sigma }(\sigma -s)\mathrm{E}_{\frac{1}{2},2} \bigl(- (\sigma -s )^{\frac{1}{2}} \bigr)e^{s}\,ds< 0.56e^{\sigma }, \quad \sigma \in \mathrm{J}. $$

Thus, \(\mathfrak{z}(\sigma )=e^{\sigma }\) satisfies (11) with \(\mu =0.56\) and \(\mathcal{Q}_{\phi }\mu =\frac{7}{750}<1\).

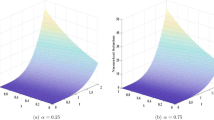
Hence, from Theorems 13 and 14, the given system (22) is \(\mathcal{HUS}\) and \(\mathcal{HURS}\). The \(\mathcal{HUS}\) and \(\mathcal{HURS}\) of (22) do not depend on the initial value condition. The solution \(\mathtt{u}(\sigma )\) of (22) with the given boundary conditions and initial value conditions \(\mathtt{u}(0)=0\) and \(\mathtt{u}'(0)=0\) is shown in Figs. 1 and 2, respectively.

Figure 1
figure 1

The solution \(\mathtt{u}(\sigma )\) of (22) with the given boundary conditions

Full size image
Figure 2
figure 2

The solution \(\mathtt{u}(\sigma )\) of (22) with the initial condition \(\mathtt{u}(0)=\mathtt{u}'(0)=0\)

Full size image

Now, we consider \(\mathtt{v}\in \mathrm{C}^{2}[0,1]\) as the solution of the following FDE:

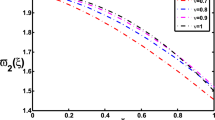
$$\begin{aligned} \textstyle\begin{cases} \mathtt{v}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{ \frac{3}{2}}\mathtt{v}(\sigma )= \frac{1}{(8+\sigma ^{2})(1+ \vert \mathtt{v}(\sigma ) \vert )}+\sigma ,\quad \sigma \in \mathrm{J}, \\ \mathtt{v}(0)=0,\quad \quad \mathtt{v}'(0)=0. \end{cases}\displaystyle \end{aligned}$$

We conclude that v satisfies (12). Therefore, we have

$$\begin{aligned} \bigl\vert \mathtt{v}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \frac{\mu }{1-\mathcal{Q}_{\phi }\mu }e^{\sigma }=0.565276e^{\sigma }, \quad \sigma \in \mathrm{J}; \end{aligned}$$

see Fig. 3.

Figure 3
figure 3

Functions \(\mathtt{v}(\sigma )-\mathtt{u}(\sigma )\), \(\mathtt{w}(\sigma )-\mathtt{u}(\sigma )\), and \(\pm 0.56e^{\sigma }\)

Full size image

On the other hand, we consider \(\mathtt{w}\in \mathrm{C}^{2}[0,1]\) as the solution of the following FDE:

$$\begin{aligned} \textstyle\begin{cases} \mathtt{w}''(\sigma )+{}^{c}\mathcal{D}_{0^{+}}^{ \frac{3}{2}}\mathtt{w}(\sigma )= \frac{1}{(8+\sigma ^{2})(1+ \vert \mathtt{w}(\sigma ) \vert )}+e^{\sigma },\quad \sigma \in \mathrm{J}, \\ \mathtt{w}(0)=0,\qquad \mathtt{w}'(0)=0, \end{cases}\displaystyle \end{aligned}$$

then w satisfies (12). Therefore, we have

$$\begin{aligned} \bigl\vert \mathtt{w}(\sigma )-\mathtt{u}(\sigma ) \bigr\vert \leqslant \frac{\mu }{1-\mathcal{Q}_{\phi }\mu }e^{\sigma }=0.565276e^{\sigma }, \quad \sigma \in \mathrm{J}; \end{aligned}$$

see Fig. 3.

5 Conclusion

Banach’s contraction principle and Krasnoselskii’s fixed point theorem have been successfully used in this work to accomplish the essential conditions for investigating the existence and uniqueness of solution of our proposed system. In this manner, under specific assumptions and conditions, the \(\mathcal{HUS}\) and \(\mathcal{HURS}\) results have been demonstrated to study the solution of our proposed system. An illustrative example is given at the end to apply our theoretical results and show its validity. Some possible future directions of our work can be dedicated to applying our obtained results to study some interesting and important phenomena in physics and engineering such as elastic beam equation and fluid flow problems. Now possible extensions and generalizations of our obtained results can also be our future directions.