Introduction

Since the development of application about micro/nano-electro-mechanical systems (M/NEMS) in chemical, medicine and mechanical engineering, fluid transmission at micro- and nanotubes or channels attracts lots of research interests. The key factor for the design and production of such fluid transmission structures is the fluid–structure interaction at the micro- or nanoscale, especially the dynamic behavior for fluid-conveying CNTs [1,2,3].

Theoretical analysis and experimental research are two general approaches for studying the dynamic characteristics of fluid-conveying CNTs. However, dynamic experimentation at the nanoscale is quite difficult to execute and control [2]; many theoretical and numerical methods have been employed, including molecular dynamics simulations (MD) [4, 5], classical elastic constitutive models [6], and small-scale elastic models such as the coupled stress model, nonlocal elastic model and elastic strain gradient model [7,8,9,10,11,12,13,14,15,16]. MD is the most reasonable approach because it calculates the interaction between all of the atoms in the system, but the application of MD is limited to some complex structures, such as fluid-conveying systems. Classical elastic models could provide reasonable results without complicated calculations. However, some dynamic properties predicted by classical models are inaccurate since the size effects at nano- and microscales are ignored. Therefore, continuum models based on small-scale theory are the most appropriate tool for analysis of micro- or nanoeffects on the mechanical properties of nanostructures. One of this continuum models is the nonlocal elastic model proposed by Eringen [17].

Since nonlocal constitutive equation is simple for calculation, many nonlocal continuum models have been established to study the dynamic properties of CNTs [8,9,10,11,12,13,14,15,16]. However, the nonlocal constitutive equation can only predict the scale effects of solids, when fluid flow inside CNT must be modeled by other theories, such as the slip boundary theory [14,15,16]. Thus, some unsatisfactory results are obtained, because slip boundary condition is inappropriate for liquids. Furthermore, the nonlocal constitutive equation for solids is also inadequate in some cases. For example, analyses of high-frequency wave propagation based on nonlocal beam and shell models are not accurate [10].

To correct the deficiencies of the nonlocal model, Lim and his colleagues developed a new constitutive equation that coupled two kinds of scale effect caused by stress nonlocality and strain gradients in a single combined equation [18]. By applying this new stress/strain equation, different kinds of nano- and micro-scale effects caused by strain and stress can be analyzed together, and many numerical results related to the dynamic behavior of nanostructures have been published on the basis of this coupling nonlocal strain gradient model.

Li C and his colleague employed the nonlocal strain gradient elastic models to predict the dynamic behaviors of nanostructures, and found the stress nonlocality causes a softening effect when the strain gradient leads to a stiffening result [19,20,21]. Li L et al. applied this new model to study the vibration behavior for fluid-filled nanotubes, while more exact results were obtained than other numerical simulation methods [22,23,24]. Zeighampour et al. established beam and shell models based on Lim’s theory [18] to investigate dynamic properties of double-walled fluid-conveying carbon nanotubes; while the slip boundary theory is employed to analyze the critical fluid velocity [25,26,27,28,29,30]. However, most of the numerical results obtained by these slip boundary models are not satisfactory, since the slip boundary condition is inappropriate for nano- or microscale liquid. To overcome this shortcomings, the authors simulated the nanoscale effects induced by fluid flow based on nonlocal fluid dynamics [17], while the dynamic nonlocal strain gradient beam models for fluid-conveying CNTs were developed [28, 29]. It was found the dynamic performances of fluid-conveying CNTs predicted by the new nonlocal fluid dynamic models agreed more closely with Monte Carlo simulation results than other continuum models, including slip boundary models [31, 32]. However, the beam models fail to analyze the CNTs with low slenderness ratios.

To predict dynamic properties of fluid-filled CNTs with low slenderness ratios, a nonlocal strain gradient shell model is developed to study the axisymmetric wave propagation characteristics. The equilibrium equation of axisymmetric wave motion in the fluid-conveying CNTs is obtained. The nanoscale effects leaded by fluid flow are simulated when using nonlocal fluid dynamics proposed by Eringen [17]. Thus the stress nonlocality and strain gradient induced by CNT and inner fluid are fully investigated.

Dynamic Model for a Fluid-Filled Nanotube

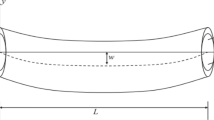
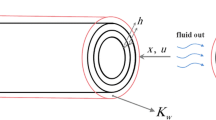
The fluid-conveying CNT is seen as a cylindrical shell in the Cartesian coordinate system, as indicated in Fig. 1, where fluid flow through the shell with uniform velocity U. The length and radius of CNT are L0 and R, respectively.

Fig. 1
figure 1

Shell model of fluid-conveying CNT in the Cartesian coordinate system

Full size image

According to Lim’s theory [18], the elastic constitutive relation of a fluid-filled membrane shell are shown in Eqs. (1–3) as follows [18]:

$$\left[ {1 - \left( {{\text{ea}}} \right)^{2} \nabla^{2} } \right]\sigma_{x} = \lambda \left( {1 - l^{2} \nabla^{2} } \right)\left( {\varepsilon_{x} + \varepsilon_{\theta } } \right) + 2\mu \left( {1 - l^{2} \nabla^{2} } \right)\varepsilon_{x} ,$$
(1)
$$\left[ {1 - \left( {ea} \right)^{2} \nabla^{2} } \right]\sigma_{\theta } = \lambda \left( {1 - l^{2} \nabla^{2} } \right)\left( {\varepsilon_{x} + \varepsilon_{\theta } } \right) + 2\mu \left( {1 - l^{2} \nabla^{2} } \right)\varepsilon_{\theta }$$
(2)
$$\tau_{x\theta } = 2\mu \varepsilon_{x\theta } ,$$
(3)

where \(\sigma_{x}\), \(\sigma_{\theta }\), and \(\tau_{x\theta }\) are stress components along different directions;\(\varepsilon_{x}\), \(\varepsilon_{\theta }\), and \(\varepsilon_{x\theta }\) are corresponding strain components; and \(\lambda\) and \(\mu\) denote elastic constants. The scale effects in Eqs. (1, 2) are calculated by the nonlocal parameter ea, and the strain gradient parameter \(l\). Thus the classical constitutive equations are obtained when \({\text{ea}} = l = 0\). The internal forces of the shell are obtained by integrating the stress tensor at the cross section of the shell as follows [33]:

$$N_{x} ,N_{\theta } ,N_{x\theta } ,N_{\theta x} = \int_{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-\nulldelimiterspace} 2}}}^{{{{ - h} \mathord{\left/ {\vphantom {{ - h} 2}} \right. \kern-\nulldelimiterspace} 2}}} {\left( {\sigma_{x} ,\sigma_{\theta } ,\tau_{x\theta } ,\tau_{\theta x} } \right)} {\text{d}}z,$$
(4)

where h stands for the thickness of wall for CNT. Substituting Eqs. (1–3) into Eq. (4) yields

$$\mu = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \upsilon } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {1 + \upsilon } \right)}},\lambda = {{E\upsilon } \mathord{\left/ {\vphantom {{E\upsilon } {\left( {1 - \upsilon^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - \upsilon^{2} } \right)}},\gamma = 2\varepsilon_{x\theta } ,$$
$$N_{x} - \left( {{\text{ea}}} \right)^{2} \frac{{\partial^{2} N_{x} }}{{\partial x^{2} }} = \frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\left[ {\varepsilon_{x} - l^{2} \frac{{\partial^{2} \varepsilon_{x} }}{{\partial x^{2} }} + \upsilon \left( {\varepsilon_{\theta } - l^{2} \frac{{\partial^{2} \varepsilon_{\theta } }}{{\partial x^{2} }}} \right)} \right],$$
(5)
$$N_{\theta } - \left( {{\text{ea}}} \right)^{2} \frac{{\partial^{2} N_{\theta } }}{{\partial x^{2} }} = \frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\left[ {\varepsilon_{\theta } - l^{2} \frac{{\partial^{2} \varepsilon_{\theta } }}{{\partial x^{2} }} + \upsilon \left( {\varepsilon_{x} - l^{2} \frac{{\partial^{2} \varepsilon_{x} }}{{\partial x^{2} }}} \right)} \right],$$
(6)
$$N_{x\theta } = N_{\theta x} = Gh\gamma ,$$
(7)

where \(\mu = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \upsilon } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {1 + \upsilon } \right)}},\lambda = {{E\upsilon } \mathord{\left/ {\vphantom {{E\upsilon } {\left( {1 - \upsilon^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - \upsilon^{2} } \right)}}\) and \(\gamma = 2\varepsilon_{x\theta }\). The parameters \(E\),\(\upsilon\) and \(\gamma\) stand for Young’s modulus, Poisson’s ratio and shear strain, respectively. Since the bending moments are negligible for a membrane cylindrical shell, the dynamic equilibrium equations for a fluid-conveying nanotube in the axial, circumferential and radial directions (\(x\), \(\theta\), and \(r\)) are [34]

$$\rho_{{\text{c}}} h\frac{{\partial^{2} u}}{{\partial t^{2} }} - \frac{{\partial N_{x} }}{\partial x} - \frac{1}{R}\frac{{\partial N_{\theta x} }}{\partial \theta } = 0,$$
(8)
$$\rho_{{\text{c}}} h\frac{{\partial^{2} v}}{{\partial t^{2} }} - \frac{1}{R}\frac{{\partial N_{\theta } }}{\partial \theta } - \frac{{\partial N_{x\theta } }}{\partial x} = 0,$$
(9)
$$\left( {\rho_{{\text{c}}} h + \frac{{\rho_{{\text{f}}} R}}{2}} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{N_{\theta } }}{R} + \rho_{{\text{f}}} \frac{R}{2}U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \rho_{{\text{f}}} RU\frac{{\partial^{2} w}}{\partial x\partial t} = 0,$$
(10)

where t stands for the variable of time, \(\rho_{f}\) and \(\rho_{{\text{c}}}\) are the mass density for fluid and CNT, respectively. Considering the geometric relationships under axisymmetric conditions (\({\partial \mathord{\left/ {\vphantom {\partial {\partial \theta = 0}}} \right. \kern-\nulldelimiterspace} {\partial \theta = 0}}\)), we have the following:

$${{\varepsilon_{x} = \partial u} \mathord{\left/ {\vphantom {{\varepsilon_{x} = \partial u} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}},{{\varepsilon_{\theta } = w} \mathord{\left/ {\vphantom {{\varepsilon_{\theta } = w} R}} \right. \kern-\nulldelimiterspace} R},{{\gamma = \partial v} \mathord{\left/ {\vphantom {{\gamma = \partial v} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}},$$
(11)

where \(u\), \(v\) and \(w\) are displacements in the x, θ, and r directions, respectively. Using Eq. (11), Eqs. (8–10) simplify to

$$\rho_{{\text{c}}} h\frac{{\partial^{2} u}}{{\partial t^{2} }} - \frac{{\partial N_{x} }}{\partial x} = 0,$$
(12)
$$\rho_{{\text{c}}} h\frac{{\partial^{2} v}}{{\partial t^{2} }} - \frac{{\partial N_{x\theta } }}{\partial x} = 0,$$
(13)
$$\left( {\rho_{{\text{c}}} h + \frac{{\rho_{{\text{f}}} R}}{2}} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{{N_{\theta } }}{R} + \rho_{{\text{f}}} \frac{R}{2}U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \rho_{{\text{f}}} RU\frac{{\partial^{2} w}}{\partial x\partial t} = 0.$$
(14)

Equations (12–14) are axisymmetric governing equations of motion for fluid-conveying CNTs based on membrane cylindrical shell theory. Here, the nanoscale effects contributed by CNTs are measured by stress nonlocallity and strain gradient, as shown in Eqs. (5–7). However, the scale effects leaded by fluid flow inside the CNTs are not negligible. Since slip boundary effect is inappropriate for liquids, the nonlocal fluid dynamic theory developed by Eringen is an acceptable option. According to nonlocal fluid dynamics principles, flow velocity,\(U\), inside a nanotube is calculated as follows [17]:

$$\eta \frac{{{\text{d}}U}}{{{\text{d}}r}}{ = }\frac{PR}{{Si(\lambda )}}\left\{ { - \frac{1}{\lambda }\sin \lambda \sin \lambda \overline{r} + \frac{1}{2}\overline{y} \left[ {Si\lambda (1 + \overline{r}) + Si\lambda (1 - \overline{r})} \right]} \right\},$$
(15)

where

$$Si(x) = \int_{0}^{x} {\frac{\sin t}{t}} {\text{d}}t,\lambda { = }\frac{R}{{({\text{ea}})_{f} }}, \overline{r} = \frac{r}{R}, 0 \le r \le R.$$
(16)

In Eqs. (15, 16), \(\eta\) is the fluid viscosity coefficient, P is the pressure gradient, and (ea)f stands for the nonlocal parameter for the fluid. Considering Eqs. (5–7), Eqs. (12–14) change as

$$\rho_{{\text{c}}} h\left[ {\frac{{\partial^{2} u}}{{\partial t^{2} }} - \left( {{\text{ea}}} \right)^{2} \frac{{\partial^{4} u}}{{\partial t^{2} \partial x^{2} }}} \right] = \frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\left[ {\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} - l^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }}} \right) + \frac{\upsilon }{R}\left( {\frac{\partial w}{{\partial x}} - l^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right)} \right],$$
(17)
$$\rho_{{\text{c}}} h\frac{{\partial^{2} v}}{{\partial t^{2} }} - Gh\frac{\partial v}{{\partial x}} = 0,$$
(18)
$$\begin{gathered} \left( {\rho_{{\text{c}}} Rh + \frac{{\rho_{{\text{f}}} R^{2} }}{2}} \right)\left[ {\left( {{\text{ea}}} \right)^{2} \frac{{\partial^{4} w}}{{\partial x^{2} t^{2} }} - \frac{{\partial^{2} w}}{{\partial t^{2} }}} \right] + \frac{1}{2}\rho_{{\text{f}}} R^{2} U^{2} \left[ {\left( {{\text{ea}}} \right)^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right] \hfill \\ + \rho_{{\text{f}}} RU\left[ {\left( {{\text{ea}}} \right)^{2} \frac{{\partial^{4} w}}{{\partial x^{3} \partial t}} - \frac{{\partial^{2} w}}{\partial x\partial t}} \right] = \frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\left[ {\frac{1}{R}\left( {w - l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \upsilon \left( {\frac{\partial u}{{\partial x}} - l^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }}} \right)} \right]. \hfill \\ \end{gathered}$$
(19)

Equations (15–19) are the governing equations of axisymmetric free vibration of fluid-conveying nanotubes on the basis of nonlocal fluid dynamic and nonlocal strain gradient. Obviously, Eq. (18) is not coupled with Eqs. (17, 19) in such a way because the torsional wave here is independent with the waves at longitudinal and radial direction. Now, if we only consider the axisymmetric wave motion governed by the coupled dynamic equations in terms of u and w, we yield the following expression [35]:

$$u = \overline{u}e^{{{\text{i}}\left( {kx - \omega t} \right)}} ,$$
(20)
$$w = \overline{w}e^{{{\text{i}}\left( {kx - \omega t} \right)}} ,$$
(21)

where \(i = \sqrt { - 1}\). Substituting Eqs. (20, 21) into Eqs. (17, 19), we obtain

$$\left\{ {\frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\left( {k^{2} + l^{2} k^{4} } \right) - \rho_{{\text{c}}} h\left[ {1 + \left( {{\text{ea}}} \right)^{2} k^{2} } \right]\omega^{2} } \right\}\overline{u} - {\text{i}}\frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\frac{\upsilon }{R}\left( {k + l^{2} k^{2} } \right)\overline{w} = 0,$$
(22)
$$\begin{gathered} \left\{ {\left( {\rho_{{\text{c}}} Rh + \frac{{\rho_{{\text{f}}} R^{2} }}{2}} \right)\left[ {\left( {{\text{ea}}} \right)^{2} k^{2} + 1} \right]\omega^{2} + \rho_{{\text{f}}} RU\left[ {\left( {{\text{ea}}} \right)^{2} k^{3} - k} \right]\omega } \right. \hfill \\ \left. { + \frac{1}{2}\rho_{{\text{f}}} R^{2} U^{2} \left[ {\left( {{\text{ea}}} \right)^{2} k^{4} + k^{2} } \right]} \right\}\overline{w} - {\text{i}}\frac{Eh\upsilon }{{1 - \upsilon^{2} }}\left( {l^{2} k^{3} + k} \right)\overline{u} = 0. \hfill \\ \end{gathered}$$
(23)

Equations (22, 23) can be expressed as following:

$$\left( {\begin{array}{*{20}c} {\Delta_{1} } & {\Delta_{2} } \\ {\Delta_{3} } & {\Delta_{4} } \\ \end{array} } \right)\left( \begin{gathered} {\overline{u}} \hfill \\ {\overline{w}} \hfill \\ \end{gathered} \right) = 0,$$
(24)

where

$$\Delta_{1} = \frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\left( {k^{2} + l^{2} k^{4} } \right) - \rho_{{\text{c}}} h\left[ {1 + \left( {{\text{ea}}} \right)^{2} k^{2} } \right]\omega^{2} ,$$
$$\Delta_{2} = - {\text{i}}\frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\frac{\upsilon }{R}\left( {k + l^{2} k^{2} } \right),$$
$$\Delta_{3} = - {\text{i}}\frac{Eh\upsilon }{{1 - \upsilon^{2} }}\left( {l^{2} k^{3} + k} \right),$$
$$\Delta_{4} = \left( {\rho_{{\text{c}}} Rh + \frac{{\rho_{{\text{f}}} R^{2} }}{2}} \right)\left[ {\left( {{\text{ea}}} \right)^{2} k^{2} + 1} \right]\omega^{2} + \rho_{{\text{f}}} RU\left[ {\left( {{\text{ea}}} \right)^{2} k^{3} - k} \right]\omega + \frac{1}{2}\rho_{{\text{f}}} R^{2} U^{2} \left[ {\left( {{\text{ea}}} \right)^{2} k^{4} + k^{2} } \right].$$

The existence of a non-zero solution for Eq. (24) requires

$$\left| {\begin{array}{*{20}c} {\Delta_{1} } & {\Delta_{2} } \\ {\Delta_{3} } & {\Delta_{4} } \\ \end{array} } \right| = 0$$
(25)

Employing the dimensionless form below:

$$\overline{U} = \left( {\frac{{\rho_{f} R}}{{{\text{Eh}}}}} \right)^{1/2} U;\xi { = }\frac{l}{{L_{0} }}\,;\xi_{s} { = }\frac{{({\text{ea}})_{s} }}{{L_{0} }};\xi_{f} { = }\frac{{({\text{ea}})_{f} }}{{L_{0} }};\Omega { \, = \, }\left( {\frac{{\rho_{f} R}}{{{\text{Eh}}}}} \right)^{1/2} \omega R; \, K = kR.$$

Equation (24) reduces into dimensionless form as follows:

$$\left| {\begin{array}{*{20}c} {\overline{\Delta }_{1} } & {\overline{\Delta }_{2} } \\ {\overline{\Delta }_{3} } & {\overline{\Delta }_{4} } \\ \end{array} } \right| = 0,$$
(26)

where

$$\overline{\Delta }_{1} = \frac{{{\text{Eh}}}}{{\left( {1 - \upsilon^{2} } \right)R^{2} }}\left( {K^{2} + \xi^{2} K^{4} } \right) - \frac{{\rho_{c} {\text{Eh}}^{2} }}{{\rho_{f} R^{3} }}\left( {1 + \xi_{c}^{2} K^{2} } \right)\Omega^{2} ,$$
$$\overline{\Delta }_{2} = - {\text{i}}\frac{{{\text{Eh}}}}{{1 - \upsilon^{2} }}\frac{\upsilon }{R}\left( {\frac{K}{R} + \xi^{2} K^{2} } \right),$$
$$\overline{\Delta }_{3} = - {\text{i}}\frac{Eh\upsilon }{{\left( {1 - \upsilon^{2} } \right)R}}\left( {\xi^{2} K^{3} + K} \right),$$
$$\begin{gathered} \overline{\Delta }_{4} = \left( {\frac{{\rho_{{\text{c}}} h}}{R} + \frac{{\rho_{{\text{f}}} }}{2}} \right)\frac{{{\text{Eh}}}}{{\rho_{{\text{f}}} R}}\left( {\xi_{{\text{c}}}^{2} K^{2} + 1} \right)\Omega^{2} + \frac{Eh}{{R^{2} }}\overline{U}\left( {\xi_{{\text{c}}}^{2} K^{3} - K} \right)\Omega \hfill \\ + \frac{Eh}{{2R}}\overline{U}^{2} \left( {\xi_{{\text{c}}}^{2} K^{4} + K^{2} } \right). \hfill \\ \end{gathered}$$

By solving Eq. (26), the influence of scale effects on dynamic behaviors such as axisymmetric wave propagation and damping can be investigated in detail.

Results and Discussion

The dynamic characteristics of fluid-conveying CNTs could be investigated based on Eqs. (23–28). Some physics constants and parameters are defined as P = 1 × 103 Pa m−1; R = 1 × 10−8 m; h = 0.045 × 10−9 m; μ = 1 × 106 Pa·s; L0 = 1 × 10−9 m; E = 1.0 × 1012 Pa; \(\rho_{f}\) = 1 × 103 kg·m−3; \(\rho_{{\text{c}}}\) = 2.27 × 103 kg·m−3 [31, 32].

Figure 2 indicates the relationship between the first-mode frequency, \(\Omega\), and \(\xi\) for different values of \(\xi_{{\text{c}}}\). Here, the value of \(\Omega\) decreases when \(\xi_{{\text{c}}}\) increases from 0.01 to 0.2 but increases when \(\xi\) increases from 0 to 0.2. Similar results are illustrated in Fig. 3, because the value of \(\Omega\) continues to increase with decreasing \(\xi_{{\text{c}}}\) but increases when \(\xi\) increases from 0.01 to 0.2. Thus, wave propagation at first mode is promoted by strain gradient effects and damped by nonlocal stress effects.

Fig. 2
figure 2

First-mode Ω vs \(\xi\) for different values of \(\xi_{{\text{c}}}\)

Full size image
Fig. 3
figure 3

First mode of Ω vs \(\xi_{{\text{c}}}\) for different values of \(\xi\)

Full size image

However, different results for the second-mode wave are indicated in Figs. 4 and 5. First, the value of \(\Omega\) keeps increasing when \(\xi_{{\text{c}}}\) rises from 0.01 to 0.09 in Fig. 4, but remains constant when \(\xi\) decreases from 0 to 0.2. Similar results are shown in Fig. 5, where \(\Omega\) increases when \(\xi_{{\text{c}}}\) changes from 0 to 0.09, but stays constant when \(\xi\) takes different values. Therefore, the strain gradient effects do not influence second-mode wave propagation, but nonlocal stress effects promote wave propagation.

Fig. 4
figure 4

Second-mode Ω vs \(\xi\) for different values of \(\xi_{{\text{c}}}\)

Full size image
Fig. 5
figure 5

Second-mode Ω vs \(\xi_{{\text{c}}}\) for different values of \(\xi\)

Full size image

Figures 6 and 7 show the dispersion relation for first-mode wave propagation that \(\Omega\) is a function of wavenumber K with different values of \(\xi_{{\text{c}}}\) and \(\xi\), respectively. The frequency grows with increasing wavenumber in Figs. 6 and 7, which agrees with classical theory. Similar to our previous results, the effects of strain gradient and stress nonlocality have contrary influences on the first-mode wave propagation, because \(\Omega\) keeps growing with increasing \(\xi\) in Fig. 6, and declines with increasing \(\xi_{{\text{c}}}\) as seen in Fig. 7.

Fig. 6
figure 6

First-mode Ω vs K for different values of \(\xi\)

Full size image
Fig. 7
figure 7

First-mode Ω vs K for different values of \(\xi_{{\text{c}}}\)

Full size image

The dispersion relation for the second-mode wave is shown in Fig. 8 with different \(\xi_{{\text{c}}}\). The wave frequency increases with wavenumber K initially, then decreases when K goes beyond a critical value. Thus, waves with large wavelength and low wavenumber are promoted, and waves with low wavelength and high wave number are damped. The critical value of K varies with \(\xi_{{\text{c}}}\) but remains between 2 and 3, as shown in Fig. 8. Additionally, Fig. 8 shows that waves decay more rapidly when \(\xi_{{\text{c}}}\) increases and nonlocal effects are more powerful, which cause a stronger wave-decay effect.

Fig. 8
figure 8

Second-mode Ω vs K with different values of \(\xi_{{\text{c}}}\)

Full size image

In addition to the effects dominated by strain gradient and stress nonlocality in CNTs, the results of the analysis for the nanoeffects contributed by inner fluid are also unnegligible. The influence of flow velocity U on the first-mode wave is illustrated in Figs. 9 and 10. Both figures indicate that the flow velocity, U, has no effect on the frequency, since \(\Omega\) remains constant when U changes from 0 to 100. Since U is function of \(\xi_{{\text{f}}}\) according to Eq. (15), the nonlocal effects induced by fluid flow only affect the flow velocity. Thus, the first-mode \(\Omega\) also stays constant for any value of \(\xi_{{\text{f}}}\), as shown in Fig. 11.

Fig. 9
figure 9

First-mode Ω vs U for different values of \(\xi\)

Full size image
Fig. 10
figure 10

First-mode Ω vs U for different values of \(\xi_{{\text{c}}}\)

Full size image
Fig. 11
figure 11

First-mode Ω vs \(\xi_{{\text{f}}}\) for different values of \(\xi_{{\text{c}}}\)

Full size image

However, the second-mode of \(\Omega\) is a function of U, as shown in Fig. 12. The value of \(\Omega\) continues to increase when U < 10, but decreases after U > 10. This outcome can be explained as the fluid flow with low velocity promotes the wave propagation, while flow with high velocity leads to wave damping.

Fig. 12
figure 12

Second-mode Ω vs U for different values of \(\xi_{{\text{c}}}\)

Full size image

Furthermore, the value of second-mode Ω only continues to decrease when \(\xi_{f}\) increases, as shown in Fig. 13. Moreover, Ω decreases sharply when \(\xi_{f} < 0.03\) initially, then decreases more slowly and approaches a constant value. In contrast to the effects of stress nonlocality on CNTs, the fluid nonlocality leads to wave damping. As discussed previously, the nonlocal effects of fluid flow only affect flow velocity. Thus, the flow velocity decreases with increasing \(\xi_{{\text{f}}}\), and lower velocities cause weaker vibrations and wave frequencies.

Fig. 13
figure 13

Second-mode Ω vs \(\xi_{{\text{f}}}\) for different values of \(\xi_{{\text{c}}}\)

Full size image

Conclusion

A shell model on the basis of nonlocal strain gradient theory is developed to simulate axisymmetric wave propagation in fluid-conveying CNTs when the nanofluid effect is measured by nonlocal fluid dynamics. By solving the governing equations of axisymmetric wave, the wave characteristics are analyzed in detail. The numerical results and wave behaviors are indicated as follows:

(1) The nonlocal stress effect induces the damping of first-mode waves but promotes second-mode wave propagation.

(2) The strain gradient effect promotes the propagation of the first-mode wave but has no influence on second-mode waves.

(3) The nonlocal fluid effect leads to the damping of second-mode waves but exerts no influence on first-mode waves.

Therefore, three kinds of scale effect exert different influences on axisymmetric wave characteristic of fluid-conveying CNTs. These numerical conclusions are meaningful for the design and processing of MEMS.