Size-dependent effects on critical flow velocity of a SWCNT conveying viscous fluid based on nonlocal strain gradient cylindrical shell model

Abstract

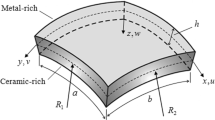
This article investigates vibration and instability analysis of a single-walled carbon nanotube (SWCNT) conveying viscous fluid flow. For this purpose, the first-order shear deformation shell model is developed in the framework of nonlocal strain gradient theory (NSGT) for the first time. The proposed model is a conveying viscous fluid in which the external force of fluid flow is applied by the modified Navier–Stokes relation and considering slip boundary condition and Knudsen number. The NSGT can be reduced to the nonlocal elasticity theory, strain gradient theory or the classical elasticity theory by inserting their specific nonlocal parameters and material length scale parameters into the governing equations. Comparison of above-mentioned theories suggests that the NSGT predicts the greatest critical fluid flow velocity and stability region. The governing equations of motion and corresponding boundary conditions are discretized using the generalized differential quadrature method. Furthermore, the effects of the material length scale, nonlocal parameter, Winkler elastic foundation and Pasternak elastic foundation on vibration behavior and instability of a SWCNT conveying viscous fluid flow with simply supported and clamped–clamped boundary conditions are investigated.

Appendix

$$\begin{aligned} \delta u: \, A_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + l^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }}} \right) + B_{11} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} + l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ + A_{12} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{1}{R}\frac{\partial w}{\partial x} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) \hfill \\ + B_{12} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ + \frac{{A_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ + \frac{{B_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ = (1 - \mu^{2} \nabla^{2} )\left( {I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right) \hfill \\ \end{aligned}$$

(30)

$$\begin{aligned} \delta v: \, \frac{{A_{12} }}{R}\left( {\frac{{\partial^{2} u}}{\partial x\partial \theta } + l^{2} \frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }}} \right) + \frac{{B_{12} }}{R}\left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ + \frac{{A_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} v}}{{\partial \theta^{2} }} + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }}} \right) \hfill \\ + \frac{{B_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} + \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial \theta^{4} }}} \right) \hfill \\ + A_{66} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ + B_{66} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } + \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ + \frac{{K_{\text{s}} A_{44} }}{R}\left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R} - l^{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right. \hfill \\ \left. { - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) = \left( {1 - \mu^{2} \nabla^{2} } \right)I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{1} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} \hfill \\ \end{aligned}$$

(31)

$$\begin{aligned} \delta w: \, \frac{{A_{12} }}{R}\left( {\frac{\partial u}{\partial x} + l^{2} \frac{{\partial^{3} u}}{{\partial x^{3} }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} u}}{{\partial x\partial \theta^{2} }}} \right) + \frac{{B_{12} }}{R}\left( {\frac{{\partial \psi_{x} }}{\partial x} + l^{2} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }}} \right) \hfill \\ + \frac{{A_{22} }}{R}\left( { - \frac{1}{R}\frac{\partial v}{\partial \theta } - \frac{w}{R} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} v}}{{\partial \theta^{3} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) \hfill \\ + \frac{{B_{22} }}{R}\left( { - \frac{1}{R}\frac{{\partial \psi_{\theta } }}{\partial \theta } + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} \psi_{\theta } }}{{\partial \theta^{3} }}} \right) \hfill \\ + K_{\text{s}} A_{55} \left( {\frac{{\partial \psi_{x} }}{\partial x} - \frac{{\partial^{2} w}}{{\partial x^{2} }} - l^{2} \frac{{\partial^{3} \psi_{x} }}{{\partial x^{3} }} - l^{2} \frac{{\partial^{4} w}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{x} }}{{\partial x\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ + \frac{{K_{\text{s}} A_{44} }}{R}\left( {\frac{{\partial \psi_{\theta } }}{\partial \theta } - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial v}{\partial \theta } - l^{2} \frac{{\partial^{3} \psi_{\theta } }}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} w}}{{\partial x^{2} \partial \theta^{2} }}} \right. \hfill \\ \left. { + \frac{{l^{2} }}{R}\frac{{\partial^{3} v}}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} \psi_{\theta } }}{{\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} w}}{{\partial \theta^{4} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} v}}{{\partial \theta^{3} }}} \right) - \rho_{\text{b}} h_{\text{f}} \left( {v_{x}^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) \hfill \\ + \frac{{\mu_{\text{f}} h_{\text{f}} }}{{R^{2} }}\left( {v_{x} \frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) - \frac{{2\mu_{\text{f}} h_{\text{f}} }}{{R^{2} }}\left( {v_{x} \frac{\partial w}{\partial x}} \right) + \mu_{\text{f}} h_{\text{f}} \left( {v_{x} \frac{{\partial^{3} w}}{{\partial x^{3} }}} \right) \hfill \\ + k_{\text{w}} w + k_{\text{p}} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{k_{\text{p}} }}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} = \left( {1 - \mu^{2} \nabla^{2} } \right)I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \rho_{\text{b}} h_{\text{f}} \left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + 2v_{x} \frac{{\partial^{2} w}}{\partial x\partial t}} \right) \hfill \\ - \frac{{\mu_{\text{f}} h_{\text{f}} }}{{R^{2} }}\left( {\frac{{\partial^{3} w}}{{\partial t\partial \theta^{2} }}} \right) + \frac{{2\mu_{\text{f}} h_{\text{f}} }}{{R^{2} }}\left( {\frac{\partial w}{\partial t}} \right) - \mu_{\text{f}} h_{\text{f}} \left( {\frac{{\partial^{3} w}}{{\partial x^{2} \partial t}}} \right) \hfill \\ \end{aligned}$$

(32)

$$\begin{aligned} \delta \psi_{x} : \, B_{11} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} - l^{2} \frac{{\partial^{4} u}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }}} \right) + D_{11} \left( {\frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} - l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ + B_{12} \left( {\frac{1}{R}\frac{{\partial^{2} v}}{\partial x\partial \theta } + \frac{1}{R}\frac{\partial w}{\partial x} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) \hfill \\ + D_{12} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } + \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ + \frac{{B_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} u}}{{\partial \theta^{2} }} + \frac{{\partial^{2} v}}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ + \frac{{D_{66} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} + \frac{{\partial^{2} \psi_{\theta } }}{\partial x\partial \theta } - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{2} \partial \theta^{2} }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ - K_{\text{s}} A_{55} \left( {\psi_{x} + \frac{\partial w}{\partial x} - l^{2} \frac{{\partial^{2} \psi_{x} }}{{\partial x^{2} }} - l^{2} \frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} \psi_{x} }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x\partial \theta^{2} }}} \right) \hfill \\ = (1 - \mu^{2} \nabla^{2} )\left( {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{x} }}{{\partial t^{2} }}} \right) \hfill \\ \end{aligned}$$

(33)

$$\begin{aligned} \delta \psi_{\theta } : \, \frac{{B_{12} }}{R}\left( {\frac{{\partial^{2} u}}{\partial x\partial \theta } - l^{2} \frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }}} \right) + \frac{{D_{12} }}{R}\left( {\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } - l^{2} \frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }}} \right) \hfill \\ + \frac{{B_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} v}}{{\partial \theta^{2} }} - \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} v}}{{\partial \theta^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }}} \right) \hfill \\ + \frac{{D_{22} }}{R}\left( {\frac{1}{R}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial \theta^{4} }}} \right) \hfill \\ + B_{66} \left( {\frac{1}{R}\frac{{\partial^{2} u}}{\partial x\partial \theta } - \frac{{\partial^{2} v}}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} u}}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} v}}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} u}}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} v}}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ + D_{66} \left( {\frac{1}{R}\frac{{\partial^{2} \psi_{x} }}{\partial x\partial \theta } - \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{4} \psi_{x} }}{{\partial x^{3} \partial \theta }} - l^{2} \frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{4} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{4} \psi_{x} }}{{\partial x\partial \theta^{3} }} - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{4} \psi_{\theta } }}{{\partial x^{2} \partial \theta^{2} }}} \right) \hfill \\ - K_{\text{s}} A_{44} \left( {\psi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta } - \frac{v}{R} - l^{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial x^{2} }} - \frac{{l^{2} }}{R}\frac{{\partial^{3} w}}{{\partial x^{2} \partial \theta }} + \frac{{l^{2} }}{R}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right. \hfill \\ \left. { - \frac{{l^{2} }}{{R^{2} }}\frac{{\partial^{2} \psi_{\theta } }}{{\partial \theta^{2} }} - \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{3} w}}{{\partial \theta^{3} }} + \frac{{l^{2} }}{{R^{3} }}\frac{{\partial^{2} v}}{{\partial \theta^{2} }}} \right) = \left( {1 - \mu^{2} \nabla^{2} } \right)I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \psi_{\theta } }}{{\partial t^{2} }} \hfill \\ \end{aligned}$$

(34)

The above parameters in Eqs. (30)–(34) are defined as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{22} } & {A_{66} } & {A_{44} } & {A_{55} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{22} } & {C_{66} } & {C_{44} } & {C_{55} } \\ \end{array} } \right\}} {\text{d}}z \hfill \\ \left\{ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {B_{22} } & {B_{66} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{22} } & {C_{66} } \\ \end{array} } \right\}} \, z{\text{d}}z \hfill \\ \left\{ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & {D_{22} } & {D_{66} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\left\{ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{22} } & {C_{66} } \\ \end{array} } \right\} \, } z^{2} {\text{d}}z \hfill \\ \left\{ {\begin{array}{*{20}c} {I_{0} } & {I_{1} } & {I_{2} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {\rho (z,T)\left\{ {\begin{array}{*{20}c} 1 & z & {z^{2} } \\ \end{array} } \right\}} \, z{\text{d}}z \hfill \\ \end{aligned}$$

(35)

And then, the boundary conditions can be explained as follows

$$\begin{aligned} C - C \hfill \\ \delta u\left| {_{x = 0,L} } \right. = 0 \hfill \\ \delta v\left| {_{x = 0,L} } \right. = 0 \hfill \\ \delta w\left| {_{x = 0,L} } \right. = 0 \hfill \\ \delta \psi_{x} \left| {_{x = 0,L} } \right. = 0 \hfill \\ \delta \psi_{\theta } \left| {_{x = 0,L} } \right. = 0 \hfill \\ S - S \hfill \\ \delta v\left| {_{x = 0,L} } \right. = 0 \hfill \\ \delta w\left| {_{x = 0,L} } \right. = 0 \hfill \\ (1 - l^{2} \nabla^{2} )\left( {A_{11} \frac{\partial u}{\partial x} + B_{11} \frac{{\partial \psi_{x} }}{\partial x} + A_{12} \left( {\frac{\partial v}{R\partial \theta } + \frac{w}{R}} \right) + B_{12} \frac{{\partial \psi_{\theta } }}{R\partial \theta }} \right)\;{\text{at}}\,x = 0,L \hfill \\ (1 - l^{2} \nabla^{2} )\left( {B_{11} \frac{\partial u}{\partial x} + D_{11} \frac{{\partial \psi_{x} }}{\partial x} + B_{12} \left( {\frac{\partial v}{R\partial \theta } + \frac{w}{R}} \right) + D_{12} \frac{{\partial \psi_{\theta } }}{R\partial \theta }} \right)\,{\text{at}}\,x = 0,L \hfill \\ \delta \psi_{\theta } \left| {_{x = 0,L} } \right. = 0 \hfill \\ \end{aligned}$$

(36)