Introduction

The optimal use of land and water for agriculture appears to be a vital and unavoidable task due to water and land limitations globally. Cropping pattern is one of the most influential factors in irrigation management which is in direct relationship with the optimal allocation of land and water resources. With regards to cropping patterns management, two questions must be answered: (1) “Which crop(s) should be planted?” and (2) “How much area should be allocated to each crop?” Optimal use of water resources and minimal damage to the environment should also be considered when providing answers to these questions. Therefore, the amount of irrigational water to be applied is usually determined as a by-product of cropping patterns optimization process.

A number of approaches including benefit-cost, functional, programming, and simulation are often used in order to determine the best cropping pattern and the amount of water to be allocated for each crop (Noory et al. 2012; Parsinejad et al. 2013; Sadegh and Kerachian 2011; Singh 2012). Meanwhile, the cost-benefit approach is quite popular, as most researchers aim at maximization of the expected net income resulting from the proposed pattern (Ghahraman and Sepaskhah 2002; Karamouz et al. 2008b). Nevertheless, a number of models are intended to maximize the net social benefits (Soltani et al. 2009).

In order to construct cropping pattern models, various modeling approaches have been employed, including linear (Faramarzi et al. 2010; Haddad et al. 2009; Kehkha et al. 2005; Ramezani Etedali et al. 2013; Salami et al. 2009; Soltani et al. 2009) and nonlinear models (Ghahraman and Sepaskhah 2002, 2004; Kiani 2009; Montazar and Rahimikob 2008). However, the high computational load associated with solving complex environmental and water resources models has led many researchers to use various types of Evolutionary Algorithms (EA) for such purposes (Afshar et al. 2009; Bazargan et al. 2011; Haddad et al. 2008; Monem and Namdarian 2005; Noory et al. 2011). Among EAs, Genetic Algorithm (GA) has been the most commonly applied EA within water resources planning and management literature, due to its great ability to solve nonlinear, non-convex, multimodal, and discrete problems for which deterministic search techniques incur difficulty or fail completely (Nicklow et al. 2009). To date, various contributions have been made to improve the efficiency and applicability of GA for agricultural water resources planning (Karamouz et al. 2008a, b; Malekmohammadi et al. 2009, 2011; Nagesh Kumar et al. 2006; Raju and Kumar 2004; Raju et al. 2012; Zahraie et al. 2003, 2008).

Despite their implications, however, the cropping pattern and water allocation optimization models tend to omit the existence of land parcels and consider the agricultural land as an entirety without any fragmentations. That is, the area under investigation is considered as one single piece of land with constant characteristics regardless of its extent (i.e., farm, plain, or region). Nevertheless, this simplification often results in neglecting a number of significant contributing factors, including land and water resources ownership, hydrological and agronomical characteristics of fields, and investment capabilities of farmers, which all vary from farm to farm. This is while most of the above-mentioned field data—e.g., ownership, location and area of parcels, availability of water resources to each, and the present cropping patterns—are routinely collected by agricultural management bodies in the form of multi-purpose cadaster data.

On the other hand, high computational load associated with incorporation of such a high level of details when providing decisions at farm level is a limiting factor in the development of farm-based cropping pattern and water allocation optimization models.

In this paper, we present a simulation–optimization framework which takes advantage of a novel algorithm, namely piece-wise genetic algorithm (PWGA), in order to model each farm separately and to support farm-based cropping pattern and conjunctive use decisions. The proposed framework is comprised of a groundwater modeling module taking advantage of unit response matrix in order to reduce the computational load, coupled with PWGA cropping pattern optimization algorithm. As it will be shown in the following, our proposed algorithm is able to address the problems arising from incorporation of high number of decision variables.

Materials and methods

Model formulation

A proper and realistic model for optimization of the cropping patterns and water allocation is a model that might optimally allocate land and water to various crops. In this vein, the main objective of the proposed model is to maximize the difference between gross benefit of crop production and all costs associated with agricultural activities. These costs are usually consist of the costs of planting, growing, and harvesting crops, in addition to the costs of applied irrigational water. Thus, the objective function of the optimization model could be defined as Eq. (1):

$$Maximize\,Z = B - C$$
(1)

where: Z = total net benefit of the cultivation plan during the planning horizon, B = sum of gross benefits resulting from cultivation plan, C = sum of costs associated with cultivation plan.

Nevertheless, the novelty of the approach lies in the way that the benefits and costs are calculated separately for each farm, instead of each crop. The model constraints are presented by Eqs. (2)–(18):

$$B = \mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{c = 1}^{Cr} (Y_{{a_{fc} }} \times Pr_{c} \times \alpha_{fc} \times A_{f} )$$
(2)
$$C = \mathop \sum \limits_{f = 1}^{F} \mathop \sum \limits_{c = 1}^{Cr} \left( {C_{cf} \times \alpha_{fc} \times A_{f} + \mathop \sum \limits_{t = 1}^{T} g_{fct} \times P_{g} + s_{fct} \times P_{s} } \right)$$
(3)

where: F = number of fields, Cr = number of crops, \(Y_{{a_{fc} }}\) = actual crop production per area of crop c in field f, \(Pr_{c}\) = market price of crop c, \(\alpha_{fc}\) = percentage of allocated area to specified crop c in field f, A f  = agricultural area in field f, \(C_{cf}\) = crop production cost of crop c in field f, T = number of time periods in planning horizon. \(g_{fct}\) = allocated groundwater during period t to crop c in field f. \(P_{g}\) = groundwater price per volume, \(S_{fct}\) = allocated surface water during period t to crop c in field f, \(P_{s}\) = surface water price per volume.

$$X_{fc} = \left\{ {\begin{array}{*{20}l} 1 & {crop \,c \,is \,planted \,in \,field \,f} \\ 0 & {otherwise} \\ \end{array} } \right\}$$
(4)
$$\mathop \sum \limits_{c = 1}^{Cr} \alpha_{fc} \le 1\,\;\forall \quad f$$
(5)
$$\mathop \sum \limits_{c = 1}^{Cr} X_{fc} \le 1\,\;\forall \quad f$$
(6)
$$0 \le \alpha_{fc} \le X_{fc}$$
(7)
$$0 \le s_{fct} \le (S_{max} )_{ft} X_{fc}\,\; \forall \quad f,c, t$$
(8)
$$0 \le \mathop \sum \limits_{c = 1}^{Cr} s_{fct} \le (S_{max} )_{ft} X_{fc} \,\;\forall \quad f, t$$
(9)
$$0 \le g_{fct} \le (G_{max} )_{ft} X_{fc} \,\;\forall \quad f,c, t$$
(10)
$$0 \le \mathop \sum \limits_{c = 1}^{Cr} g_{fct} \le (G_{max} )_{ft} x_{fc} \,\;\forall \quad f, t$$
(11)

where: X fc  = decision variable determining whether crop c is cultivated in field f, (S min ) ft and (S max ) ft  = minimum and maximum volume of available surface water for farm f during time-step t. (G min ) ft and (G max ) ft  = minimum and maximum volume of available groundwater for farm f during time-step t. It is worthy to note that Eq. 6 is intended to restrict the model to allocate each farm to one crop at a time. Nevertheless, by removing this constraint, the model would be able to plant each farm with multiple crops.

In order to calculate the amount of actual crop production (\(Y_{{a_{fc} }}\)), a production function developed by Doorenbos and Kassam (1979) and later extended by Ghahraman and Sepaskhah (2004) is used, as follows:

$$(Y_{a} )_{fc} = x_{fc} \times (Y_{p} )_{c} \left( {\mathop \prod \limits_{t = 1}^{T} \left[ {1 - K_{yt} \left( {1 - \frac{{(W_{a} )_{fct} }}{{(W_{p} )_{fct} }}} \right)} \right]} \right)\left\{ {\begin{array}{*{20}c} {\forall f = 1, \ldots ,F} \\ {\forall c = 1, \ldots ,C} \\ \end{array} } \right\}$$
(12)
$$wa_{fct} = 1000(s_{fct} + g_{fct} )/(\alpha_{fc} \times A_{f} )\forall \quad f,c, t$$
(13)
$$(W_{p} )_{fct} = \frac{{I_{fct} }}{{(E_{a} )_{f} }} \forall \quad f,c, t$$
(14)
$$I_{fct} = (ET_{a} )_{ct} - (P_{e} )_{t} \forall \quad f,c, t$$
(15)
$$0 \le 1 - \frac{{(W_{a} )_{fct} }}{{(W_{p} )_{fct} }} \le x_{ct} \forall \quad f,c, t$$
(16)

where: (Wa) fct  = depth of water applied to crop c in farm f during time-step t. (Wp) fct  = actual irrigation requirement of crop c in farm f during time-step t, \(I_{fct}\) = irrigation water requirement of crop c in period t, (Ea) f  = irrigation efficiency in farm f, \((ET_{a} )_{ct}\) = actual evapotranspiration of crop c in period t, \((P_{e} )_{t}\) = effective precipitation in period t, x ct  = maximum tolerance of crop c to deficit irrigation in period t.

Finally, the last constraint of the model restricts the model to maintain the groundwater drawdown at each well to a level lower than a preset boundary:

$$\Delta h_{kt} = P(g_{1,1} , g_{2,1} , \ldots ,g_{k,1} ,g_{1,2} , \ldots , g_{k,t} )$$
(17)
$$\Delta {\text{h}}_{kt} \le \left( {\Delta h} \right)_{allowable}$$
(18)

where: P = groundwater modeling function, g 1,1 to g k,t  = volumes of groundwater pumped from well 1 to k in period 1 to t, \(\Delta {\text{h}}_{kt}\) = calculated drawdown of well k in time-step t, \(\left( {\Delta h} \right)_{allowable}\) = maximum level of allowable groundwater table drawdown.

As it could clearly be seen in Eqs. (2)–(18), this optimization model allocates water from groundwater and surface resources to each of the farms separately. Besides, the cultivation fraction is exclusively addressed for each farm, in contrast to defining the cultivation fraction for each of the crops, which is general in cropping patterns optimization models.

Simulation–optimization framework

As demonstrated in Eq. (17), the proposed optimization model relies on a groundwater simulation model in order to calculate water table drawdown. MODFLOW is a widely recognized groundwater model (Harbaugh 2005) which has been frequently used in conjunction with conjunctive use optimization models (Bazargan-Lari et al. 2009; Karamouz et al. 2005; Khare et al. 2007; Safavi et al. 2010). However, the high computational load associated with the use of this model makes it difficult to couple it with iterative-based optimization algorithms. Larroque et al. (2008) and Alimohammadi et al. (2005) were among those who demonstrated that the use of Unit Response Matrix (URM) is an efficient way of incorporating groundwater models in optimization procedure, since URMs could significantly reduce the computational run-time.

Figure 1 illustrates the architecture of the proposed framework. As depicted in this figure, the base level of the framework is made up roughly of two types of data. The first strand is more or less related to farms characteristics, and could be supplied through agricultural cadaster or similar campaigns. The second strand, however, includes the data that are generic and could be associated with all farms (e.g., meteorological data, crop coefficients, and economic data). Further, the data nested in the base level of the framework supply all of the parameters presented in “Model formulation” (excluding the decision variables).

Fig. 1
figure 1

Architecutre of Farm-based cropping pattern and water allocation optimization model

Full size image

The next module of the framework is the GA-based optimization model, which is comprised of the optimization algorithms bearing the responsibility of searching for the optimal cropping pattern with regards to the parameters derived from data module and the groundwater model.

For the groundwater model, MODFLOW is used as the main groundwater simulation model. However, an embedded URM function is employed in conjunction with the optimization algorithm for calculating water table drawdown with respect to well discharge values. Based on the additively principle, the URM function for total of k wells is calculated as:

$$S\left( {k,t} \right) = \mathop \sum \limits_{t = 1}^{T} \mathop \sum \limits_{j = 1}^{k} \beta_{k} \left( {k,j,T - t + 1} \right)q\left( {j,t} \right)$$
(19)

where: S(k, t) = change of water table level at well k at the end of the time period of t, β k (k, j, T − t + 1) = the unit response coefficient, which is defined as the unit change of the water table at well k during t, due to the excitation (withdrawal/recharge) at well j during t.

β is a function of the distance between wells, the well diameters, the hydraulic conductivity of the aquifer, the recharge of the aquifer, boundary conditions, and the starting heads (Maddock 1972). The above equations could also be used for multi-aquifer systems (Yazicigil 1990).

Piece-wise genetic algorithm

Genetic algorithms are a strand of evolutionary algorithms that use a random search technique that “evolve” a potential solution for a given system using the genetic operators (Karamouz et al. 2007). GAs are usually characterized by: (1) generation of an initial population of potential solutions, each identified as a chromosome; (2) computation of the objective function value, or fitness metric of each solution and subsequent ranking of chromosomes according to this metric; (3) some aspect of chromosome ranking and selection of candidate solutions to participate in a mating operator, where information from two or more parent solutions are combined to create offspring solutions; and (4) mutation of each individual offspring to maintain diversity and prevent premature convergence to local optima. These elements are repeated in sequential generations until a suitable solution is obtained (Nicklow et al. 2009).

The general structure of chromosomes used in most cropping patterns optimization models is a vector consisting of the following decision variables: number of Cr variables, each representing the plantation fraction of a crop, followed by T sequences of St and Gt which form the water allocation scheme. Alternatively, St and Gt could exclusively be defined for each of the crops. However, the use of such vector-based approach would be problematic in detailed models, since the incorporation of decision variables for each farm would result in a rather large vector.

The proposed chromosome structure to curb this issue is a matrix-based chromosome, in which each row of the matrix encodes the decision variables corresponding to a farm. In such a structure, assuming that the farm decision variables consist of a crop choice variable, a crop plantation percentage variable, and 72 water allocation variables, each of which correspond to either surface water or groundwater decisions during 10 days, the chromosome would be a matrix of n × 74, instead of a relatively large vector of 1 × (n × 74) length.

GA operators

The use of matrix to encode chromosomes allows for easier handling of GA operations. For instance, two types of crossover operations are defined in PWGA, namely horizontal and vertical crossover operations (Fig. 2). In horizontal crossover, the chromosomes exchange some sequences of rows, while in the latter type columns are exchanged between parents to form offspring. In this context, the use of horizontal crossover provides higher chance of survival for relatively successful farm plans and has a tendency to repeatedly associate those plans with the same farms. That is, by doing this the farm decisions remain intact and are only exchanged between chromosomes. Therefore, any changes in farm decisions are solely achieved using mutations. Nevertheless, vertical crossovers tend to do a shuffle-like crossover during which the farm plans cannot be preserved. Therefore, due to its inherent randomness, this crossover operation has to be combined with fewer mutations.

Fig. 2
figure 2

Vertical and horizontal crossover operations in PWGA

Full size image

Handling the chromosomes as matrices also allows for more flexibility during mutations. In the present study, the mutation function performs mutations on each of the farm plans. That is, a random point is proposed for each row of the selected matrix. As the variables are comprised of integers and real numbers, a mutation is then performed on each selected element based on its nature and defined boundaries. Nevertheless, whether each of the farms should receive mutations and also the amount of mutation performed on each farm could easily be managed when using matrix chromosomes.

Variable concentration

As illustrated in Fig. 3, the first and second elements of the chromosome rows consist of the number of proposed crop (integer), followed by the plantation fraction (0 ≤ α ≤ 1). However, instead of variables S t and G t , the deficit irrigation fraction (x t) is used which is defined as:

Fig. 3
figure 3

Proposed chromosome structure for cropping pattern planning

Full size image
$$x_{t} = 1 - \left( {\frac{{\left( {Wa} \right)_{t} }}{{\left( {Wp} \right)_{t} }}} \right)$$
(20)

In this scheme, the use of deficit irrigation with 5 time-steps corresponding to 5 growth stages of crop Cf (Ghahraman and Sepaskhah 2004) reduces the number of decision variables from f × (2 + 72) to the far smaller value of f × (2 + 5). Based on Eq. (20), and given the fact that Wp is known, Wa could be derived from x t . Due to the low price of the surface waters and the critical condition of groundwater resources, the priority of each farm is to consume all of its surface resources and then try to reach the proposed deficit irrigation plan using groundwater resources (if any). Hence, the corresponding G t and S t could be evaluated for each farm, based on Cf, αf, and x 1 to x 5.

Stall handling

The proposed PWGA takes advantage of a semi-adaptive stall handling mechanism. In order to prevent premature convergence of the population and to avoid being trapped in local optima—as this is expectable due to the non-convex nature of the problem—the algorithm is able to increase the population diversity when a persistent stall occurs. To this end, the algorithm reduces the probabilities of crossover and elitism and increases the rate of mutations. In this context, elites are highly fit individuals reaching the next generation without participating in crossover or mutations. During the stall handling process, the increased randomness due to the increased probability of mutations helps to maintain population diversity. Nevertheless, the best solutions are still preserved, since few elites are still allowed to reach the next generations. Once the desired level of diversity is achieved, the crossover probability and the number of elites return to the previous state.

Case study

The study area is Mobarakabad district, settled on Qaderabad-Madarsoleiman plain in Fars province, Iran. As precipitation is limited due to the semi-arid climate of the central parts of Iran, a large portion of the irrigational water is withdrawn from the groundwater resources. Uncontrolled growth of the agricultural activities in the area has caused the water table to drop 1.2 m per annum (Pouyan-Shiraz-Consultants 2012).

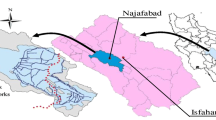
Figure 4 shows the location and the cropping pattern of Mobarakabad in 2007. The study area is comprised of 126 land parcels with 63 owners. The total cultivated area is 207.8 ha with an average of 1.647 ha per field (Ghasemi et al. 2010). The majority of the farms are under the cultivation of wheat. The only surface water resource is Mobarakabad aqueduct’s fountain which is located outside of the case study area and groundwater extraction is determined to not have any effects on it. One aqueduct and 17 wells supply the agricultural water in this area. The discharge of the aqueduct depends on climatic conditions and ranges from 20 l/s during droughts up to 150 l/s in wet years. The 10-day share of each field from surface water is currently determined based on the area of each field.

Fig. 4
figure 4

Location and cropping pattern of the study area (Mokhtarabad) in 2007

Full size image

In this study, various conditions are simulated by means of altering the model parameters. Further, the results acquired from PWGA are compared with those of the general plain-level optimization models run for the same conditions. To this end, the effects of wet, normal, and drought climatic conditions are simulated by altering the meteorological parameters and the availability of surface waters. Various levels of allowable groundwater table drawdown formed the second group of scenarios. Finally, various water prices were defined in order to investigate the effects of water price on the model’s output. However, since no water market was established between the farmers, the market price for groundwater was unknown. Thus, the base groundwater price was calculated as the sum of the fixed and variable annual costs of operating pumping wells. This value was determined to be 109.7 Rials/m3, and four water price scenarios included 100 and 200 % increase of the groundwater price (219.4 and 329.1 Rials/m3), in addition to 1000 and 2500 Rials/m3 fees.

Results and discussion

Cropping patterns optimization

The results for nine scenarios in both cases of using PWGA and the general form of cropping pattern optimization model which was solved using GA are provided in Table 1. As it could be seen at first glance, the net benefits resulting from more restrictive scenarios tend to be lower in comparison to those acquired from more permissive scenarios (e.g., ∆h ≤ 1 m in comparison with ∆h ≤ 3 m).

Table 1 Results of cropping pattern optimization, PWGA versus plain models
Full size table

Nevertheless, the most notable occurrence is the differences between the results of PWGA and the plain-level model. Table 1 clearly demonstrates that the plain-level model has a tendency to overestimate the net benefits in all of the nine cases. This is partially due to the fact that in contrast with the real-world situations, the plain model has been able to favorably allocate groundwater from all of the 17 wells to large areas of land. However, in real-world, the private ownership of the wells would limit the areas that enjoy using the groundwater resources. Moreover, given the current situation in the study area, the withdrawal rate of each farm from surface waters cannot exceed its predetermined share of water. Hence, the results acquired from PWGA could be considered as more realistic in comparison with those of the plain model.

Due to the spatial nature of the optimal decisions provided by PWGA, these results could easily be linked with spatial databases and be presented in the form of maps/spatial services. Figures 5 and 6 illustrate the proposed cropping pattern, and plantation fractions obtained for the first scenario (∆h ≤ 1 m).

Fig. 5
figure 5

Parcel-level optimal cropping pattern decisions for the study area (∆h ≤ 1 m)

Full size image
Fig. 6
figure 6

Optimal plantation fraction of Mokhtarabad farms (∆h ≤ 1 m)

Full size image

It is worthy to note that, due to the fact that a number of parameters are calculated for chromosomes during the optimization procedure, these parameters could also be extracted for each desired chromosome when required. These parameters include S t , G t , (Ya) f , Bf, C f , and ∆h k,t . That is to say, although the conjunctive use decisions are not directly incorporated as decision variables, they could be easily derived from the chromosomes. For instance, due to limited space in this paper, only the conjunctive use decisions obtained for farms 18 and 77 under the second scenario (∆h ≤ 2 m) are presented in Fig. 7.

Fig. 7
figure 7

Optimal conjunctive use decisions under ∆h ≤ 2 m scenario: a farm number 18 is planted with barley and has no access to groundwater; b farm number 77 is planted with watermelon and has access to groundwater

Full size image

Stall handling

Figure 8 illustrates the convergence process of PWGA populations and makes comparison between the algorithms in presence and absence of the stall handling code. As shown on the left side of Fig. 8, the mean fitness of the population rapidly approaches the best fitness, showing that the population is gradually dominated by highly fit individuals (premature convergence). In contrast, in case the stall handling mechanism is enabled, the mutation rate is increased and the mean fitness of the population drops when encountering a persistent stall. This increase has led to increase of the gene diversity within the population, and the algorithm could eventually find better solutions. The repetition of this process has contributed to a wavy form noticeable in mean fitness of the population, and an overall improvement in the algorithm’s efficiency.

Fig. 8
figure 8

The effects of absence/presence of stall handling code on PWGA performance

Full size image

Summary and conclusion

In this paper, a novel approach to cropping patterns and water allocation optimization was presented. The proposed model aimed at supporting optimal cropping pattern and conjunctive use decisions at land parcel level. For this purpose, a URM groundwater model is coupled with a modified genetic algorithm. The matrix-based genetic algorithm, namely PWGA, was used in order to tackle the large number of decision variables incorporated in such a detailed model. As expected, the use of PWGA showed that general cropping pattern optimization models tend to overestimate the optimal net benefits, due to having an unrealistic modeling approach to allocation of water resources.

The proposed PWGA algorithm provides superior capabilities for handling large numbers of decision variables, including the easier and more flexible crossover and mutation operations. Besides, the dimensions of the problem are reduced by condensation of the water allocation variables using a new approach.

The use of a semi-adaptive mechanism for handling persistent generation stalls has also improved the performance of the proposed optimization model in avoiding convergence to local optimums. Nevertheless, this mechanism could be further developed in such a way that the operation probabilities are dynamically determined for each generation, based on the diversity estimates obtained from the populations.

Although two crossover operations are presented in this paper, PWGA used in this study could only use one of the two types at a time. Nevertheless, the codes could be extended to perform both crossover operations simultaneously and with different probabilities. Furthermore, the authors did not incorporate any dynamism in severity of the mutation and/or crossover operations.

Finally, in the present study we only tried to maximize the overall net income of the plain by proposing decisions at land parcel level, while maintaining a certain level of groundwater exploitation. Nevertheless, the incorporation of cadastral data including detailed ownership data has made it possible to evaluate metrics regarding the equality of water usages, distribution of income, and many other factors for each of the proposed decision sets. The authors conclude that incorporation of such disparity metrics in the objective function would result in improving the applicability of the optimization model in real-world scenarios.