Introduction

Water is one of the most essential and valuable resources among the many natural resources found in the earth. It is necessary for human development, socio-economic development, and ecosystem diversity. It has been found in the surface and sub-surface in the earth. Surface water, which is found on the surface of the earth such as rivers, lakes, oceans while in sub-surface, water that find beneath the ground surface and collects in underground. During last decades, the requirement of water has been increased rapidly due to rise in the population and fast industrialization. To fulfill this additional water demand, dependability on the sub-surface water has been increased (Omar et al. 2019). At the same time, overexploitation and pollution in the natural water resources are also threatening to the ecosystems (Gupta et al. 2020). The combination of these two problems which have drawn the attention of many researchers working in the relative fields and forced them to search novel, multi-disciplinary approaches to address these vital issues. Thus, there is need of groundwater protection and management. A detailed knowledge of the characteristics of aquifers is essential for conservation and effective management of groundwater resources. The environment under the ground surface cannot easily examine or accessible. In that case, only the models help in understanding the groundwater system, simulating and predicting their behavior. The model is nothing but a representation of a complicated phenomenon as a mathematical equation (McGarity 1985). Models are developed to perform certain functions, as presented below:

  1. 1.

    Quantitative assessment of physical phenomena or processes occurring in an aquifer system.

  2. 2.

    Find out the major problems which need more research.

  3. 3.

    Selection of optimal sampling locations as well as enhance the field monitoring system

  4. 4.

    Design a groundwater remedial program for sustainable groundwater management.

Numerical flow models, used normally in the groundwater studies, are an effort to present the aquifer system processes by the mathematical equations. In terms of the flow of groundwater, there are mainly two governing processes, one is flow in response to the hydraulic potential gradients, and the loss/gain of groundwater from sinks or sources, recharges, or water extraction from the wells (National Research Council 1990; Parker 1991). Groundwater models play an important role in the evaluation of the quantity of groundwater as well as quality (ElKashouty 2021). These models can be used for issues ranging from calculations of overall water balance to problems of small-scale pollution (Hasan et al. 2021). The status of the different groundwater modeling systems that are being used is presented in Table 1 (Refsgaard 1996).

Table 1 Status of hydrological modeling systems (Refsgaard 1996)
Full size table

In the earlier period, models have also helped in decision support systems (DCS). In some cases, the model has been offered as the deciding criterion (Bauer et al. 2005). Development in the field of computational ability, software engineering and availability of computers helps in the groundwater model development stage, and it became an effective and efficient tool/method for groundwater assessment and management (Joshi and Gupta 2018). Groundwater model also helps in the assessment of the effects of groundwater management measures on the groundwater head and aquifer condition under various future scenarios (Baalousha 2009; Scibek et al. 2007). MODFLOW is a widely used user-friendly groundwater flow model around the world, which simulates groundwater by solving groundwater flow equations. MODFLOW is a computer code, primarily written in FORTRAN language, developed by USGS (United States Geological Survey) in the early 1980s. The source code of MODFLOW is free in public domain (McDonald and Harbaugh 2003). In the literature, so much work has been done on groundwater modeling based on MODFLOW code such as Ting et al. (1998), Nishikawa (1998), Heinzer and Hansen (1999), Tsou and Whittemore (2001), Asghar et al. (2002), Maxwell and Kollet (2008), Faunt et al. (2011), Wang et al. (2008), Umar et al. (2008), Wang et al. 2009, Lachaal et al. (2012), Panagopoulos (2012) and Gaur et al. (2021). A novel study was done by Gupta and Sharma in (2019) for a small region of Ajmer district, Rajasthan, India. They evaluate the groundwater resource vulnerability using three assessment criteria as quantitative, qualitative and socio-economic. These all studies are an example of the successful application of MODFLOW code in the field of groundwater.

An approach to the modeling

An accurate groundwater model presents the real condition of groundwater aquifer system under certain hydrological stresses. It can be easy, like one-dimensional analytical solution, or very complex three-dimensional multi-layered models (Olsthoorn 1985). There are lots of complexities associated with the groundwater flow modeling, and it is always suggested to start with a easy model. After successful conceptualization of the simple model, complexity in the model can be added step by step (Hill 2006). Apart from the modeling approach, there are other factors like initial head value (condition), boundary conditions, temporal and spatial discretization, and quality of gathered/collected data can affect the modeling outputs.

Conceptual model

The conceptual model can be defined as the thorough depiction of the groundwater aquifer system, which includes the interpretation of the hydrological and the geological conditions of the aquifer as well as information about the water budget. After the objective identification, it is the most important part and next step of the modeling. Conceptualization of the model requires good knowledge about the geology, hydrology of the concern area, boundary conditions and hydraulic properties of the aquifer, soil characteristics (Omar et al. 2021). An excellent conceptual model must portray the actuality in an easy manner that meets the modeling goals and management requirements (Bear and Verruijt 1987). The main issues involved in the conceptual model are:

  1. 1.

    Geometry (Horizontal & Vertical) of the Aquifer and model domain

  2. 2.

    Initial conditions as well as boundary conditions of the area

  3. 3.

    Aquifer properties like hydraulic conductivity (Kx, Ky and Kz), porosity, storativity, etc.

  4. 4.

    Recharge into the groundwater

  5. 5.

    Sources and sinks identification for discharge information

  6. 6.

    Water budgeting

After successful completion of the conceptual model, next step is setting up the numerical model. The numerical (mathematical) model presents the conceptual model in the form of complex equations of mathematics. These mathematical equations can be solved analytically or numerically. Figure 1 shows the adopted methodology for the groundwater flow model development and conceptualization.

Fig. 1
figure 1

Flowchart of methodology for preparation of the model

Full size image

A mathematical model is a set of partial differential equations (PDE) that represent the physical processes of groundwater flow in the aquifer system. A discretized numerical method has been used to find out the solution of the governing equations (Eq. 1) of the groundwater flow in the study. To derive mathematical equations describing the groundwater flow systems, the basic principles of mass conservation of liquid are used. The fundamental principle of conservation of mass (normally known as the continuity equation) is used in conjunction with the mathematical equations of related processes to derive the differential equations that depict the water flow.

The process of groundwater flow is controlled by Darcy’s law and the law of mass conservation. Darcy’s law can be described as the liquid flow through a permeable medium (porous media) and interrelated to the characteristics of that liquid, the properties of the permeable medium and the hydraulic gradient. By combining Darcy's law with the law of mass conservation, a common form of equation expressing the transient flow of compressed liquid in anisotropic, non-homogeneous aquifers can be obtained. The governing partial differential equation (PDE) for three-dimensional groundwater flow through a permeable medium for a confined aquifer has been given by equation number 01 (Reilly and Harbaugh 2004):

$$\frac{\partial }{\partial x}\left[ {K_{xx} \frac{\partial h}{{\partial x}}} \right] + \frac{\partial }{\partial y}\left[ {K_{yy} \frac{\partial h}{{\partial y}}} \right] + \frac{\partial }{\partial z}\left[ {K_{zz} \frac{\partial h}{{\partial z}}} \right] + W = S_{S} \frac{\partial h}{{\partial t}}$$
(1)

where Kxx, Kyy and Kzz are the hydraulic conductivity (HC) of the aquifer in all three directions (x, y and z) (LT−1). W is the volumetric flux (flow) per unit volume (T−1), Ss is the specific storage of aquifer’s porous material (L−1), h is the potentiometric head (L), t is the time (T).

Initial and boundary conditions

To get a distinctive answer of the partial differential equation (PDE) corresponding to a certain conceptual problem, further data about the physical state of the problem are requisite. This additional data can be supplied by initial and boundary conditions. Apart from mathematical constraint, boundary conditions also characterize the sources and sinks in the groundwater (Rushton and Redshaw 1979). For getting solution of transient-type problems, initial and boundary conditions are required, while for getting solution of steady-state type of problems, only boundary conditions must be specified (Omar et al. 2020). Improper boundary conditions identification may affect the solution and lead to inaccurate output of the model (Franke et al. 1987). Scientifically, the initial and boundary conditions take account of the geometry (type) of the boundary, and the starting values of the dependent (variable) or its derivative normal to the boundary.

In the groundwater flow model, boundary conditions symbolize the locations, where water flows into or out of the model area due to any external factors. River, evapotranspiration, recharge, wells and lakes are some general examples of the boundary conditions.

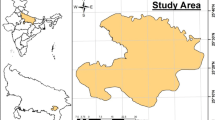
Study area

River Koshi originates from Tibet, at an altitude of over 7000 m above msl (mean sea level in the Himalayas. It is tributary of the Ganga River and joins it near Kursela (25 °24′43″N and 87 °15′32″E) in Katihar district, Bihar, India. The coordinates of the source point of the Koshi River are 26 °54′47″ N and 87 °09′25″E. The Koshi River has a total length of about 729 km, and it drains an area of approx 74,500 km2 in India, Tibet, and Nepal. The salient features of the Koshi river basin are presented in Table 2. Koshi River has three main tributaries as Sun Koshi in Nepal & its tributaries, Arun River in north of Mount Everest and Tamur River in eastern Nepal. After this confluence point, Koshi river flowing about 12 km through mountainous regions, it debouches into the plain area, near Chatra in Nepal. After this, Koshi River flows in the sandy alluvial plain areas of Nepal tarai about 50 km up to Hanuman Nagar. After that, it goes into Indian Territory and merges with the River Ganga near Kursela in Bihar. It has four tributaries in the right bank and two tributaries in the left bank, name mentioned in Table 2. Koshi River flows in the south-west direction from Chatra, to Galpaharia Nepal, and this westward movement of the river is controlled by the Mahabharat range. In this stretch, the river has been braided in several channels and expands over a width of 6 to 16 km. Braiding behavior of the river into several channels can be justified due to sediment (Fig. 2). After flowing about 100 km in sandy alluvial plain area, river takes a turn in eastward direction.

Table 2 Table salient features of the Koshi Basin
Full size table
Fig. 2
figure 2

Location of the study area with elevation level data

Full size image

Slope

Koshi River originates in mountainous regions, flowing through the plain areas and merges into the River Ganga. In this journey, river has varying slopes from steepest to relatively less steep slope. The bed gradient of the Koshi River from Chatra, Nepal to the point of confluence near Kursela in Bihar is presented in Table 3.

Table 3 Average bed gradient of Koshi River
Full size table

Hydrology and geology characteristics of the area

Based on the characteristics of soil, the drainage area of the Koshi River has been separated into three regions. One is upper basin, mid basin, and lower basin region. Upper basin zone lies totally in the mountainous region and soil of this zone can be classified as Brown Hill Soil, mountain-meadow soil and sub-mountain soil. The mid basin zone lies in Nepal and includes the area between the mountainous and plain portion of the basin in the foothills of the Himalaya, also known as the Terai area. Lower basin zone covers large inland delta formed by the enormous sand deposition by the Koshi River. Approx 25 MCM of sand and silt per year has been deposited in this zone. Upper and mid Koshi basin covers more than 85% of the total area and has relatively divergent features concerning the lower basin area. This upper basin is normally responsible for the hydraulic characterization and hydrological behavior of the Koshi River, whereas lower basin has small involvement to it. The geological nature of the Koshi River is unstable and subject to heavy erosion which eventually increases the soil sediment load in the river flow. The soil of the Koshi basin is of poorly graded type. The region near to the Koshi River has sandy loam type of soil, while the regions away from the Koshi possess sandy silt type of soil. In general, soils are coarse textured along the river course, whereas fine textured away from the river course and rivulets.

Data collection

The first point of the groundwater research involves collecting all the existing data related to the hydraulic and geological properties (hydrogeological) of the concerned area. This will consist of information on surface and sub-surface geology, aquifer characteristics and boundary conditions, water tables, irrigation pattern, precipitation, type of vegetation, land use and land cover type (LULC), groundwater quality, pumping characteristics, recharge, stream flows and soil type. Two types of hydrogeological data are required for the accurate groundwater flow model development. The first data describe physical framework of groundwater system, and the second data express its hydrological stress (Moore 1979).

In the physical framework, the basic data requirements are:

  1. 1.

    Geology—Geology data consist of fence diagram or cross section of the area showing the horizontal and vertical extent and boundaries of the system, geologic map.

  2. 2.

    Aquifer Characteristics—This consists of aquifer thickness (Isopach Maps), aquifer type, lateral extent and aquifer boundaries.

  3. 3.

    Topography—Topography data contain details of surface drainage system, surface water bodies, wetlands, extent and thickness of streams, springs and swamps (if any).

  4. 4.

    LULC—LULC data contain agricultural areas, their pattern, irrigation behavior, and recreational areas, etc.

  5. 5.

    Elevation Profile—Elevation data of the bottom of the aquifers and confining beds.

The basic data requisite under the hydrological framework are:

  1. 1.

    Discharge—Type and extent of the discharge areas, spatial (areal coverage) and temporal (time coverage) distribution of rate of discharge, groundwater pumping data, evapotranspiration rate.

  2. 2.

    Recharge—spatial (areal coverage) and temporal (time coverage) distribution of the recharge rate, type and extent of the recharge areas.

  3. 3.

    Water Table Elevation—Groundwater table and potentiometric data of aquifers.

  4. 4.

    Hydrograph of groundwater table and surface water (rivers, lakes, ponds, etc.) levels.

  5. 5.

    Conductivity (K)—Horizontal hydraulic conductivity (Kxx, Kyy) and vertical hydraulic conductivity (Kzz) of the aquifers, transmissivity distribution, conductivity values and their distribution for rivers, stream channels and lake sediments.

  6. 6.

    Groundwater and surface water interaction.

Different data have been collected from various government organizations and departments for the groundwater model development. The data include well (open well as well as dug well) data, borehole data, precipitation data, groundwater table data, river stage and river bed elevation data, river conductivity data, population (rural and urban separately) data, livestock data, etc. For the river cross section, different points were identified over the rivers, and an extensive field survey was done. In the field survey, DGPS (Differential Global Positioning System) and echo-sounder equipment were mainly used. DGPS was used to know the latitude, longitude and altitude (elevation) of the points, and echo-sounder gives the bottom elevation of the River bed. The echo-sounder device works on the sonar technique and is used to find out the water bodies depth by transmitting acoustic waves into the water. The time interval between pulse release and pulse come back is recorded, which is used together with the speed of sound in the water to measure the depth of water. Table 4 shows data used in the study and the source of that data. The DEM of study area is obtained with the help of SRTM data which is available at USGS site. DEM of the study area is demonstrated in Fig. 2.

Table 4 Data used in the study and the
Full size table

Methodology

To develop a groundwater flow model in MODFLOW, it is first essential to be familiar with the soil strata characteristics under the area. Fence diagram has been constructed based on the lithological data. Through the fence diagram, one gets to know about the horizontal and vertical disposition of the aquifers present in the study area as shown in Fig. 3. In the plain region, Koshi River brings heavy silt due to diminution in the silt carrying capacity of the river. That’s why top surface of area is alluvial soil. At some places, clay capping also found which is very thin (< 1 m to 5 m). Top surface layer is gray colored fine silty soil, whereas in the second layer, coarseness of the sand increases. The aquifer bottom is made up of relatively hard and impermeable bed. Thus, in this area, groundwater occurs under unconfined condition. Because of this unpredictability, for development of groundwater model, a multiple layers (three) conceptual model is used in the present study. After developing the individual soil strata of groundwater aquifer, the solid data were generated and interpolated into the MODFLOW program. Cross section of the solid data is shown in Fig. 4.

Fig. 3
figure 3

Fence diagram based on lithological log data

Full size image
Fig. 4
figure 4

Cross section of the solid data

Full size image

Well inventory

For observation data, the groundwater level from observation wells has been collected from the Central Groundwater Board (CGWB) website. This water level indicator shows drawdown in the well which vary place to place/location. The groundwater level lies between 1.8 m and 15 m below groundwater level (bgl) which varying spatially and temporally. These observation well data help in calibration of the model. Pumping wells are also taken into the consideration to include the effect of withdrawal in the model. For pumping well data, a survey was done in the study area, and location of each pumping well was marked using Differential Global Positioning System (DGPS). DGPS provides the latitude and longitude of each well along with elevation of the well from mean sea level (MSL). Discharge from each well was collected from the local person in conjunction with some other related information like fluctuation in the water level. Based on the value of withdrawal of water from the well, pumping rate was determined for each well. Pumping wells influence the groundwater level as withdrawal from the well increases. Well yield also varies according to the depth, up to a depth of 50 m yield of well is 480–960 m3/day and depth more than 100 m produces yield of 2400—4800 m3/hr.

Model development

In this paper, the groundwater flow model is envisaged as a three-layered aquifer system. The study area has been discretized into a 3-D (three-dimensional) square grid with single grid cell size of 100 m × 100 m. In the model, approximately 96,000 active grid cells were created for the numerical solution. These grid cells increase the complexity and computational runtime for the numerical flow models, as so many grid cells increase the simulation time but also provide more accurate model results. The hydraulic conductivity (K) of different locations was calculated based on the test samples collected. Twenty-five test samples have been collected from spatially distributed locations in the study area, and K values have been computed correspondingly. For the study area, the value of horizontal hydraulic conductivity (Kxx/Kyy) was found to be high due to the loose soil condition of the area. For the computation of vertical hydraulic conductivity (Kzz), the literature was reviewed, and according to McDonald and Harbaugh (1988), this was said to be one tenth of the horizontal hydraulic conductivity. Recharge to the groundwater was considered from the precipitation (majorly rainfall), seepage from the rivers, water bodies and return flow from the irrigation. Initial recharge value was taken as 10% of the total rainfall, and total rainfall for the study area has been collected from the IMD. Calculated recharge value was assigned to the top layer of the model. Specified flow boundary and no flow boundary have been considered in the study area.

Model calibration

After the model development, model has been run in the GMS (Groundwater Modeling System) software (Anon 2000). GMS has the capability to incorporate the geographic information system (GIS) layers in it. Results of the first model run may vary from the actual field conditions. This is because modeling is an attempt to simplify and approximations of the reality of the groundwater system. In approximation and mathematical modeling of the governing equations of groundwater flow errors are unavoidable. In the model calibration, an attempt has been made to adjust the parameters of model such as groundwater recharge, water discharge, aquifer hydraulic conductivity. The main purpose of model calibration is to allow the output of the simulated model to match the measurements in the real field conditions within an acceptable criterion. If the model calibration is successful, the model is very fine-tuned with the actual groundwater flow, and the groundwater level of the developed model is forced to match with the actual groundwater table. The calibration process is an important part of the model conceptualization; it makes the model predictive and makes the model to be valid for any flow condition not for a particular fixed defined conditions. For better understanding of the calibration process of the model, consider the observed groundwater head as (ho)i at the observation point i and the computed head at the same point is (hc)i. The root mean square error (RMSE) of the residual can be found here (Sun, et al., 2009):

$${\text{RMSE}} = \left[ {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {h_{o} - h_{c} } \right)^{2} } \right]^{1/2}$$
(2)

RMSE can be defined as the square root of the sum of the square of the differences between simulated and observed heads, divided by the number of observation wells. Thus, the main objective of the calibration should be to minimize the RMSE by optimization of the considered model parameters. To achieve this, accurate field data, proper aquifer characterization and enough data are required. This calibration can be done manually by changing the value of the parameters (trial and error adjustment) or automatically by the inbuilt available tools in the software. In GMS, there is an automated parameter estimation code available called PEST (Parameter Estimation Tool) (Doherty and Hunt 2010), and UCODE (Poeter and Hill 1999) may be used for the direct calibration. In this research, model calibration has been done considering the three model parameters, hydraulic conductivity (K) (Horizontal, Kxx, Kyy and Vertical, Kzz) and recharge rate (R). Values of these parameters have been varying in a phase manner and adjusted till the model simulated head, matched fairly reasonably with the observed head values. In calibration, various scenarios are also made.

Model validation

In modeling of the groundwater flow, the term “validation” is not justified Oreskes et al. (1994). In groundwater modeling, only approximation of the real field conditions has been done with the help of any mathematical model. After the model calibration, verification and validation of the model are another important part of model conceptualization. The main aim of the model validation is to ensure whether the calibrated model works perfectly on any other value of model parameters or not. If model validation is not done, it is possible that the model may provide the same values for the different sets of values. Good calibrated model does not mean that the model can predict the good water head (Reilly and Harbaugh 2004). In this present study, model has been validated for considering the three years data.

Sensitivity analysis

Sensitivity analysis helps to speed up the process of model calibration, that’s why it important. In groundwater flow modeling, there are large numbers of uncertain parameters. Along with this, there is another uncertainty associated with the field measurements. Handling these issues is time consuming and involves considerable effort. To cope up with these issues simultaneously, sensitivity analysis becomes important. Sensitivity analysis shows which parameter(s) have a greater impact on the model output. Parameters that have high impact on the model output have to be given the most attention in the calibration process as well as in the field data collection. In this study, for the sensitivity analysis, the most common method, i.e., finite difference approximation has been adopted. In this, observation has been made in the model output, while changing a certain model parameter. In GMS, this can be achieved by using PEST package.

Results and discussion

In this work, a transient three-layered groundwater flow model has been conceptualized and developed in GMS with the support of the ArcGIS. It is an attempt to match the computed head data with the observed hydraulic head data in MODFLOW code. Calibration of model has been made considering fifteen observation wells. In the calibration process, three model parameters has been taken into the consideration, and their value was adjusted during many sequential runs until the acceptable match between the observed and computed head contours was obtained. The accuracy of the developed model can be judged by comparing the root mean square error (RMSE). In a good calibrated and validated model, RMSE must be least. In this study, RMSE error comes out to be 0.254 m. This indicates an acceptable match between the computed head and observed head for the developed model.

Water budget

Normally, groundwater flow modeling programs generate water budgets for the concern area. In water budgeting, it computes the budget by tabulating the budget data that can be generated from MODFLOW using the cell-by-cell flow (ccf) option. A sub-region of the model for which it generates the water budget is named as a zone and is designated by a zone number. By just specifying the sub-regions, water budget can be calculated for that region. The groundwater budget has been calculated from the developed groundwater flow model for the area using zone budget tool.

In this study, recharge from the rainfall is 15,792,310.517 m3/day, and from other inflows, it is 129,457.268 m3/day. Outflow from the study area is 2,619,543.802 m3/day. And discharge from the well is 8,437,000 m3/day. The loss of groundwater in the form of evapotranspiration is 8,679.632 m3/day. The water budget results show that the total inflow into groundwater from various resources is higher than the outflow of water from the study area. But in recent years, due to mismanagement of the groundwater and increasing pollutants (contamination) in surface water, withdrawals (extraction of water from wells, tubewells, etc.) from groundwater have increased significantly. In the future, it is necessary and very important for water resource scientists and researchers to take this into account for the conservation and sustainable management of this water resource.

Conclusion

Water is essential for life and all living beings. It is found both inside the earth surface and on its surface. As a precious natural resource, it should be conserved by the people of all mankind. For groundwater management, the concept of groundwater flow numerical model is a good practice adopted by many hydrologists and researchers. Precisely modeling of groundwater system is a complex task, requires a lot of data, and has to deal with various unfamiliar and unpredictable hydro-geographical features. Over the decades, the groundwater flow model has proved to be a very useful tool in solving groundwater problems and decision making for appropriate management of the groundwater. For this reason, groundwater modeling is being used frequently nowadays. In this study, a three-dimensional multilayered transient groundwater flow model was conceptualized for the Koshi river basin. For the model development, different types of data have been collected from the various sources. After analysis, these data were provided as input to the model. In the model development, field data were also used for precise model simulation. Sensitivity analysis and model calibration were done for the developed groundwater flow model. With the help of observation data, model validation was also performed, and result of model validation shows that the computed values of the groundwater level are in good-fitness of the observed data, which indicate the model is reliable. Groundwater budgeting was also done for the study area, and result of this study suggests that the total inflow into the study area is more than the total outflow from the area. But, in recent times, it has been observed that due to the negligence and poor administration of the local authority, the groundwater has started depleting at some places in the study area. The main reason behind this situation is the overexploitation of the groundwater. Local people are exploiting the groundwater excessively, and for this, they are extracting groundwater from the aquifer by installing more and more wells, tubewells, etc. In order that there is no shortage of this natural water resource in the near future, it has to be conserved from now on, and for this, sustainable management and conservation of the groundwater are the only solution. Therefore, in order to preserve pure groundwater in future, groundwater resource development plans in the Koshi river basin should be taken into account.