Introduction

Knowledge about breeding patterns is essential to assess stocks and the reproductive potential of marine species (Costa and Soares-Gomes 2009; Naderi et al. 2018). Fecundity is a species-specific factor that allows to evaluate the reproductive potential and to estimate the future stock size of a given species or population (Anger and Moreira 1998; Hattori and Pinheiro 2003; Figueiredo et al. 2008). In most marine species fecundity is directly related to such biological characteristics of females as body size, maturation age, reproductive effort, and life expectancy (Pinheiro and Fransozo 1995; Llodra 2002; Pinheiro et al. 2003).

Carcinus maenas (Linnaeus 1758), the European green crab, is a widely distributed epibenthic species inhabiting both hard and soft intertidal habitats in coasts and estuaries (Baeta et al. 2005). Worldwide, it is one of the most ecologically prominent benthic predators in marine and estuarine intertidal areas (Waser et al. 2017). Despite its native spatial distribution being the Northeast Atlantic, from Mauritania to Norway, and including Iceland (Crothers 1967; Carlton and Cohen 2003; Rewitz et al. 2004; Young et al. 2017), during the last two centuries this species spread its geographic distribution settling in five major regions of the globe: Northeast, Northwest and Southwest of the Pacific Ocean, and Northwest and Southeast Atlantic Ocean (Thresher et al. 2000; Young and Elliott 2020).

Carcinus maenas can be found along the entire Portuguese coast, presenting a high population density in the largest estuaries and lagoons from the southeast to the northwest extremes (Elumalai et al. 2007; Amaral et al. 2009; Monteiro et al. 2021). Being a key epibenthic predator that affects estuarine ecological processes via trophic interactions, C. maenas is of utmost ecological importance (Kristensen et al. 2008; Amaral et al. 2009; Vermeiren and Sheaves 2014). Shifts in its populations and distributions can influence estuarine communities, which may lead to major effects on the ecosystem (Grosholz and Ruiz 1995; Vermeiren and Sheaves 2014). In North America, the increase in area occupied by the invasive C. maenas lead to a drastic reduction in the numbers of several native benthic species, such as Mya arenaria bivalve (Cohen et al. 1995) and American oysters (Crassostrea virginica) (Pickering et al. 2017), leading to potentially large economic losses (Leignel et al. 2014). For instance, in the Gulf of St. Lawrence the estimated economic losses in bivalve fisheries and aquaculture, due to C. maenas, varied between 42 and 109 million dollars (Colautti et al. 2006). Nowadays, these losses may persist, as C. maenas eradication effort was unsuccessful (Young and Elliott 2020). Still, the fishing sector adapted to the new reality by targeting C. maenas. Aside from its deleterious effect on other fisheries, C. maenas is also of high economic importance as harvested species, mainly in Europe. According to port landing data provided by the “Directorate-general for natural resources, safety and maritime services” (DGRM), this crab is fished along the entire Portuguese coast. C. maenas is sold as bait for octopus trap fishing, angling or sold fresh for human consumption in markets (Leitão et al. 2021). Amid the 1980s and 1990s, it was also exported to Spain, potentially for seafood broth (Gomes 1991).

In C. maenas, mating can only occur immediately after the moulting of the females while the exoskeleton is not completely calcified. In turn, males can mate with the fully consolidated exoskeleton (Crothers 1967; Reid and Naylor 1994). Males can recognize a moulting female by the pheromones released ahead of moulting (Eales 1974; Klassen and Locke 2007). The number of breeding seasons varies across different regions depending on the water temperature (Audet et al. 2008). In temperate waters there is only one reproductive period per year, whereas in warmer waters there are two (Lovell et al. 2007; Young and Elliott 2020). Along the Portuguese coast, the reproductive period occurs between October to June, when the water temperature stays below 23ºC, peaking during the cooler winter months (January and February) (Sprung 2001; Young and Elliott 2020). Temperature also affects the duration of the reproductive cycle of C. maenas, which has been observed to vary across systems (Hines et al. 2004). Therefore, regional patterns in the number of breeding periods (Young and Elliott 2020), size and number of eggs (Collin et al. 2018; Rodríguez-Félix et al. 2018), and time of the larval period (Nagaraj 1993; Spitzner et al. 2019) are found as result of environmental variability among areas.

Different populations display different conditions depending on such habitat characteristics as the physical environment or food availability (De Silva et al. 1998; Lloret et al. 2002). The quality of a given habitat has been shown to be related to marine species population conditions (De Silva et al. 1998; Lloret et al. 2002; Vieira et al. 2018), which in turn can be assessed by a variety of criteria ranging from morphometric and physiological measures to biochemical measures (Lloret et al. 2002; Vieira et al. 2018; Creed et al. 2019). Weight-length relationship data is routinely collected for marine species. This information has been used as an indicator of the environmental quality of marine habitats (Jisr et al. 2018) and used to determine body condition indices providing measures of relative assemblage integrity (Jisr et al. 2018).

Accessing reproductive parameters and the impacts upon them of environmental factors allows a better understanding of population fluctuations and fecundity. The objective of this research is to increase our understanding of environmental and regional processes affecting C. maenas fecundity. For that, we infer its allometry and size–fecundity relations in four lagoons and estuaries along the Portuguese coast.

Materials and Methods

Study Area and Sampling Procedures

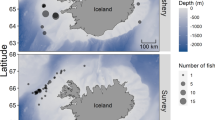
In order to assess intra-regional differences, the study was conducted in four coastal systems with different characteristics and at different latitudes along the Portuguese coast. In southern Portugal we sampled, Ria Formosa and Ria de Alvor, on the centre, Rio Sado and in northern Portugal, Ria de Aveiro (Fig. 1). Females were collected with traps between November 2019 and February 2020, in an intermediate stage of egg mass development (orange coloration). The number of egg-bearing females caught varied between 28 individuals in Ria Formosa and 51 in Ria de Aveiro (Table 1). These sample sizes were required to obtain a large range for the ovigerous females body size.

Fig. 1
figure 1

Geographical location of the different systems; at orange coloration Portugal and with green coloration the areas of study: Ria Formosa, Ria de Alvor, Rio Sado and Ria de Aveiro

Full size image
Table 1 Biometric data and fecundity of C. maenas along with four different systems of the Portuguese Coast. N, number of individuals; CW, carapace width; Fecundity, number of eggs; Mean SST, mean sea surface temperature (°C); mean salinity (PSU)
Full size table

The Ria Formosa is a highly productive shallow lagoon with a multi-inlet barrier island system that extends 55 km along south Portugal (Falcão and Vale 1990; Barbosa 2010). It is a mesotidal system with mean tidal range of approximately 2 m, varying from 1.5 m to 3.5 m, and dominated by the semi-diurnal component of the tide. Only 14% of the lagoon surface is permanently submersed (subtidal channels) and the intertidal area covers approximately 1/3 of the lagoon (Newton and Mudge 2003). The lagoon has an important ecological role as a breeding and nursery ground for economically valuable species (Ribeiro et al. 2008).

The Ria de Alvor is a coastal lagoon system (Duarte et al. 1999) between the cities of Lagos and Portimão that covers an area of 15 km2 (CCDRA 2004). Its tidal regime is mesotidal and semidiurnal, with an average tidal amplitude of 3.5 m. The water temperature oscillates between 16 Cº in Winter and 25 Cº in Summer. It is a system with an elevated hydrodynamics (Dias 1993) but also the most vulnerable and degraded system on the Algarve coast, because of human pressure (Duarte et al. 1999).

The Sado river estuary (hereafter named Rio Sado) is located on the western coast, being the second largest estuary in Portugal with an area of approximately 180 km2 (Ferreira et al. 2003). It is a mesotidal, well-mixed estuary (Bettencourt et al. 2004) with mean tidal range of approximately 1 m, varying from 0.6 m to 1.6 m. The exploitation of salt flats influences the water salinity inside the estuary (Gonçalves et al. 2015).

The Ria de Aveiro is a shallow coastal lagoon on the western coast of Portugal, with four main channels (LillebØ et al. 2015; Sousa et al. 2019). It is 1.3 km long, 350 m wide, 20 m deep (Dias and Lopes 2006). Its mesotidal regime has a tidal range between 0.6 m and 3.2 m (Dias et al. 1999).

Laboratory Procedures

The carapace width (CW), carapace length (CL), and carapace thickness (CT) was measured with a 0.01 mm precision vernier calliper. The total weight (TW) of specimens was measured with an analytical digital scale of a 0.0001 g precision. Three sub-samples of the egg mass were removed from each individual (Rodríguez-Félix et al. 2018). Each replicate weight (Wr) was measured and stored in a 4% formaldehyde solution diluted from 37% commercial formalin. The remaining egg mass was removed from the abdomen by carefully extracting the eggs from the pleopods and the females’ body weight (i.e., without eggs) was taken (in g). This allowed the calculation of the total egg mass weight (Wegg). The number of eggs in each subsample (n) was placed in a Bogorov counting chamber and counted under a Leica Stereoscope.

The fecundity (F) for each subsample was estimated by the gravimetry method using Eq. 1, where n is the number of eggs in the subsample, Wegg is the total egg weight, and Wr is the weight of the subsample:

$$F=\frac{n\cdot {w}_{egg}}{{w}_{r}}$$
(1)

The mean fecundity and the respective standard deviation of each egg-bearing female were calculated using the results of the three subsamples. Additionally, the minimum, maximum, and mean fecundity and respective standard deviation were calculated for each system.

The environmental data from each system, namely, annual mean temperature (ºC) and seawater salinity (PSU), were collected from Bio-ORACLE: Marine data layers for ecological modelling (https://www.bio-oracle.org/explore-data.php). Data were placed in the QGIS software and interpolated to the locations where the ovigerous females were collected.

Data Analysis

Carcinus maenas was tested for four relations among fecundity and morphometric variables: (i) egg count was regressed against CW by ordinary least squares (OLS); (ii) egg wet weight was regressed against egg count by principal component analysis (PCA); (iii) egg wet weight was regressed against body wet weight (i.e., weight of the body not considering the egg mass) by PCA; (iv) carapace width was tested as a predictor of its body wet weight. Because the CW-weight relation is allometric, the predictor and response were first plotted on a log-scale and then regressed by OLS. The use of PCA or OLS depended on the proportion between the error in the measurement of x and y variables, and on the intention of establishing a hierarchical relation or just testing correlations (Pearson 1901; Draper 1992; Smith 2009; Vieira et al. 2016). A probability level α < 0.05 was used in all analyses in order to reject the null hypothesis.

ANCOVA

The four abovementioned relations were further tested for the extra effect of the covariate “system” and hence, compared among four estuarine and lagoon systems in Portugal—Ria Formosa, Ria de Alvor, Rio Sado and Ria de Aveiro—applying an analysis of covariance (ANCOVA). These models take the form y = a + βx + ax + ε. Here, the response variable (y) was fecundity and the predictor (x) was a morphometric measure. The covariate (a) was “systems” with four levels corresponding to Ria Formosa, Ria de Alvor, Rio Sado and Ria de Aveiro. The covariate (a) is also known as the categorical independent variable. The error term (ε) within each system should tend to 0 and be similar among systems. The first step was to test that independent variables (predictor and covariate) were uncorrelated (ax≈0) and that there was indeed a response to a predictor—i.e., that there was a true xy correlation leading to a β significantly different from 0. Only in such case we proceeded to the second step, where it was tested whether systems had homogeneity of slopes. If (when) they did, we proceeded to the third and final step, where a pooled slope was applied to the systems to test the differences among intercepts i.e., among the levels of each system. This protocol was followed with the significances of slopes and pairwise differences between slopes and between intercepts being estimated by permutation tests with 1000 randomizations using the software by Vieira and Creed (2013a, b). The logarithm of CL and the logarithm of body wet weight (BWW) were regressed on each other using PCA. This is justified by (i) the absence of a hierarchical relation between variables, (ii) both variables measured with similar accuracy, and (iii) both variables have similar variances (Draper 1992; Smith 2009; Vieira et al. 2016). The EC was regressed on CW using OLS. The egg count (EC) was regressed on egg weight (EW) using OLS. The EW was regressed on BWW using OLS, yielding results identically to the application of PCA.

Results

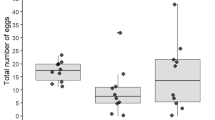
The CW of the 180 egg-bearing females varied between 26.96 and 61.25 mm, and the fecundity varied between 22121 and 408538 eggs/female (Table 1). All the extreme values were obtained from Ria de Aveiro, where, from the 51 females, the CW varied between 26.96 and 61.25 mm (mean = 43.14 mm), whereas the fecundity varied between 22121 and 408538 (mean = 173751). Among the 32 females sampled in Rio Sado, the CW varied between 32.63 and 51.95 mm (mean = 40.64 mm), whereas the fecundity varied between 31055 and 222333 eggs/female (mean = 94353). Among the 49 females sampled in the Ria de Alvor, the CW varied between 30.82 and 56.25 mm (mean = 45.18 mm), whereas the fecundity varied between 28452 and 361956 eggs/female (mean = 170269). Among the 28 females sampled in the Ria Formosa, the CW varied between 31.96 and 55.37 mm (mean = 45.68 mm), whereas the fecundity varied between 61151 and 249324 eggs/female (mean = 142250).

Carapace Width–Egg Counting Relationship

CW and egg counting (EC) were statistically significant correlated in all systems, with all CW-EC regressions yielding statistically significant slopes (Table 2 and Fig. 2a). Differences among slopes (EC) were observed between Ria de Alvor and both Rio Sado and Ria Formosa, but not observed for Ria de Aveiro (Table 3 and Fig. 2a). Hence, two separate groups were formed within which were tested for differences among intercepts. The first compared between Ria de Aveiro and Ria de Alvor (Table 2 and Fig. 2b), obtaining statistically significant different intercepts (Table 3). The second compared between Ria de Aveiro, Rio Sado and Ria Formosa (Table 2 and Fig. 2b), showing that intercepts were statistically significant different among all systems (Table 3). Overall, results show an isometric (linear) relation between CW and EC that changes with location. The highest fecundity was in Ria de Aveiro, then in Ria de Alvor and then, in equal terms, Rio Sado and Ria Formosa.

Table 2 Regression statistics for ANCOVA for all relations. For CW-EC relation two tests for differences among intercepts were performed: (est1) compared between Ria de Aveiro and Ria de Alvor, whereas (est2) compared among Ria de Aveiro, Rio Sado and Ria Formosa: For BWW-EW relation two tests for differences among intercepts were performed: (est1) compared between Ria de Aveiro and Ria de Alvor, whereas (est2) compared between Rio Sado and Ria Formosa. CW, carapace width; EC, egg counting, EW, egg weight; BWW, body wet weight; d.f., degrees of freedom; r, correlation coefficient; S, slopes; p, statistical value; Int, intercept
Full size table
Fig. 2
figure 2

Carcinus maenas egg count regressed against carapace width and compared among four lagoon and estuarine systems from Portugal. The ANCOVA protocol tested for a differences among slopes, and then for b differences among intercepts. Two tests for differences among intercepts were performed: (est1) compared between Ria de Aveiro and Ria de Alvor, whereas (est2) compared between Ria de Aveiro, Rio Sado and Ria Formosa

Full size image
Table 3 ANCOVA’s comparing each regression among four systems. Values are the significances of pair-wise differences between systems. The upper triangle has results for slopes and the lower triangle has results for intercepts. For CW-EC relation two tests for differences among intercepts were performed: (est1) compared between Ria de Aveiro and Ria de Alvor, whereas (est2) compared among Ria de Aveiro, Rio Sado and Ria Formosa. For BWW-EW relation, two tests for differences among intercepts were performed: (est1) compared between Ria de Aveiro and Ria de Alvor, whereas (est2) compared between Rio Sado and Ria Formosa. CW, carapace width; EC, egg counting; EW, egg weight; BWW, body wet weight
Full size table

Egg Counting and Egg Weight Relationship

Egg counting (EC) and egg weight (EW) were statistically significant correlated in all systems, with all EC-EW regressions yielding statistically significant slopes (Table 3 and Fig. 3a). Differences among slopes (EW) were observed between Ria de Alvor and Ria de Aveiro, but not for other comparisons (Table 3 and Fig. 3a). Therefore, we tested for differences among intercepts disregarding the Ria de Alvor vs Ria de Aveiro comparison. The pooled slope of 2.49 × 10–5 leads to significantly different intercepts (Table 2 and Fig. 3b) except between the Ria de Aveiro and Rio Sado intercepts (Table 3).

Fig. 3
figure 3

Carcinus maenas egg weight regressed against egg count and compared among four lagoon and estuarine systems from Portugal. The ANCOVA protocol tested for (a) differences among slopes, and then for (b) differences among intercepts

Full size image

Body Wet Weight–Egg Weight Relationships

BWW and egg weight (EW) were statistically significant correlated in all systems, with all BWW-EW regressions yielding statistically significant slopes (Table 2 and Fig. 4a). Differences among slopes (EW) were observed between Ria do Alvor and both Ria Formosa and Rio Sado (Table 3 and Fig. 4a). No statistically significant differences among slopes were observed between Ria de Alvor and Ria de Aveiro or between Rio Sado and Ria Formosa. Hence, two separate groups were formed within which differences among intercepts were tested. The first compared between Ria de Aveiro and Ria de Alvor (Table 2 and Fig. 4b), not revealing significant differences (Table 3). The second compared between Rio Sado and Ria Formosa, obtaining significantly different intercepts (Tables 2 and 3 and Fig. 4b). Results show an isometric (linear) relation between EW and BWW that changes with location. The highest fecundity was in the group containing Ria de Aveiro and Ria de Alvor, then, in Ria Formosa and finally in Rio Sado.

Fig. 4
figure 4

Carcinus maenas egg weight regressed against body wet weight and compared among four lagoon and estuarine systems from Portugal. The ANCOVA protocol tested for (a) differences among slopes, and then for (b) differences among intercepts. Two tests for differences among intercepts were performed: (est1) compared between Ria de Aveiro and Ria de Alvor, whereas (est2) compared between Rio Sado and Ria Formosa

Full size image

Carapace Width and Body Wet Weight Relationship

CW and BWW were statistically significant correlated in all systems, with all CW-BWW logarithm regressions yielding statistically significant slopes (Table 2 and Fig. 5a). However, no statistical differences among slopes were observed (Table 3 and Fig. 5a). Hence, a pooled slope of 3.0632 was applied and then tested for differences among intercepts. No statistical differences among intercepts were observed (Table 2 and Fig. 5b). These results prove that the allometric relation between CW and BWW follows the exponential form BWW = 1.62 × 10−4 × CW3.0632 for the four systems tested. The exponent ≈ 3 indicates that growth is nearly isometric, with C. maenas females preserving its shape throughout their lives.

Fig. 5
figure 5

Carcinus maenas body wet weight regressed against carapace width and compared among four lagoon and estuarine systems from Portugal. The ANCOVA protocol tested for (a) differences among slopes, and then for (b) differences among intercepts

Full size image

Discussion

The present work provided new information on the reproductive biology of C. maenas along the North-western Atlantic coast, uncovering important knowledge about a fecundity gradient across the Portuguese coast. Classified as one of the world’s 100 worst invaders by the International Union for Conservation of Nature (IUCN) (Lowe et al. 2000), C. maenas is the world’s most widely distributed intertidal crab, with several articles on its ecology and larval development (Young and Elliott 2020). Despite the large existing scientific knowledge on C. maenas, data on fecundity and breeding patterns of this species are still scarce, being restricted to two studies on non-native populations from the Northeast coast of North America (Audet et al. 2008; Griffen 2013).

The positive correlation between morphological parameters and fecundity (CW vs EC and BWW vs EW) shows that fecundity is proportional to body size, regardless of the systems. This relationship is explained by the abdomen carapace width: the larger the abdomen (CW) the higher the number of eggs a female (higher fecundity) can bear (Audet et al. 2008; Rodríguez-Félix et al. 2018). Our results are in line with other studies on marine species where an increase in the female body size also lead to an increase in their fecundity. Such were the cases for non-native populations of C. maenas (Audet et al. 2008; Griffen 2013), congeneric species Carcinus aestuarii (Baklouti et al. 2013) and other species of crabs (Rodríguez-Félix et al. 2018) and fishes (Quinn et al. 2011).

Several fecundity studies on Carcinus genus (C. maenas and C. aestuarii a congeneric species) showed that fecundity varies widely across regions (Table 4). The results obtained in our study are in line with the fecundity values recorded in non-native populations of Northeast coast of America (Audet et al. 2008; Griffen 2013). Comparing with the C. aestuarii populations, inhabiting in Mediterranean Sea, the fecundity calculated in our study for C. maenas was much higher (Table 4). The differences in fecundity within C. maenas populations or among C. maenas congeneric species are most likely explained by the sea surface difference across areas, for instance higher temperatures in the Mediterranean Sea are associated to low crabs’ fecundity (Table 4).

Table 4 Mean fecundity and respective carapace width (CW) range for various populations of C. maenas and the congeneric species Carcinus aestuarii
Full size table

However, this study confirmed the existence of regional differences in C. maenas fecundity associated to environmental gradients. Fecundity was higher in the systems with lower SST, which is in line with the fecundity of non-native C. maenas populations from the Northeast coast of North America (Audet et al. 2008; Griffen 2013), as well as the fecundity of other marine and crab species monitored along the North-Western coast of Iberia (Perez-Miguel et al. 2020). The exception to the temperature effect is the Rio Sado, with a possible reason being the lower salinity of this system compared to the other study areas analysed (Table 1). The reproduction period in Sado occurs between the months of October and May (Sprung 2001), coinciding with the rainy periods. In the Rio Sado, this period coincides with an increase in runoff leading to a decrease in the salinity. Hence, in Rio Sado fecundity is most likely affected by the combined effect of temperature and salinity. In fact, besides temperature, other hydrological features of the study systems aspects can affect the species physiological conditions (Young and Elliott 2020), size and number of eggs (Collin et al. 2018; Rodríguez-Félix et al. 2018) and duration of the larval period (Nagaraj 1993; Spitzner et al. 2019). Therefore, differences in fecundity among systems are also associated to the particular/regional hydrology. In decapoda, the reproductive effort can be influenced by changes in environmental conditions, such as salinity (Vernberg and Piyatiratitivorakul 1998), with trade-offs between survival and reproductive activity (Gelin et al. 2001).

Morphometric relationships have been used for a local and interregional morphological comparison of populations (Froese 2006), and also to evaluate environmental ecological status (Lloret et al. 2002). Morphometric condition indices can provide information on “well-being” for some marine species (Lambert and Dutil 1997), which in turn could imply something about local ecosystem conditions, for example food limitation (Shephard et al. 2015). In our study, the positive correlation among all morphological parameters (CW, BWW) and the nearly isometric exponent (≈3) of the CW vs BWW model demonstrates that females’ body mainly changed in size, roughly preserving the shape. No statistically significant differences were observed among the CW-BWW regressions performed for each studied system, indicating that, contrary to fecundity, the somatic growth of C. maenas is not affected by latitudinal or environmental conditions. Morphometric results on CW-BWW regressions suggest that all the studied systems are effectively at the same environmental quality status. The study of body condition assumes that heavier individuals of a given length class are in better condition (Jones et al. 1999). Condition indices have been used in aquaculture as indicators of the general “well-being or fitness” of the population in consideration (Bolger and Connolly 1989). The operationalisation’s level and type of the bioindicators used to assess population biological conditions, such as morphometric indicators, is shown by their inclusion, within the marine strategy framework directive in European Union (Shephard et al. 2015), where these have been proposed as environmental “surveillance indicators.”

Globally, many highly prized commercial species are under assessment, and substantial data exists to predict their status (EU Reg. 1543/2000; EU reg. 665/2008). Information collected at national or international level, e.g., Data Collection Regulation (DCR) and the Data Collection Framework (DCF) programs (EU reg. 665/2008), can now make better use of this information to implement routines which aim to assess environmental quality status based on populations data. However, multiple ecosystem pressures, and cumulative or synergistic responses, can make the use of biological indicators difficult. Therefore, it is necessary to consider multiple surveillance indicators in ecosystems ecological status shifts.