Archimedes Optimizer: Theory, Analysis, Improvements, and Applications

Abstract

The intricacy of the real-world numerical optimization tribulations has full-fledged and diversely amplified necessitating proficient yet ingenious optimization algorithms. In the domain wherein the classical approaches fall short, the predicament resolving nature-inspired optimization algorithms (NIOA) tend to hit upon an excellent solution to unbendable optimization problems consuming sensible computation time. Nevertheless, in the last few years approaches anchored in nonlinear physics have been anticipated, announced, and flourished. The process based on non-linear physics modeled in the form of optimization algorithms and as a subset of NIOA, in countless cases, has successfully surpassed the existing optimization methods with their effectual exploration knack thus formulating utterly fresh search practices. Archimedes Optimization Algorithm (AOA) is one of the recent and most promising physics optimization algorithms that use meta-heuristics phenomenon to solve real-world problems by either maximizing or minimizing a variety of measurable variables such as performance, profit, and quality. In this paper, Archimedes Optimization Algorithm (AOA) has been discussed in great detail, and also its performance was examined for Multi-Level Thresholding (MLT) based image segmentation domain by considering t-entropy and Tsallis entropy as objective functions. The experimental results showed that among recent Physics Inspired Optimization Algorithms (PIOA), the Archimedes Optimization Algorithm (AOA) produces very promising outcomes with Tsallis entropy rather than with t-entropy in both color standard images and medical pathology images.

1 Introduction

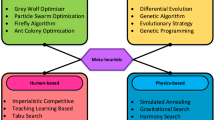
As the name suggests, meta-heuristics in computer science and mathematics are high-level processes or heuristic designs used to create algorithms that can nevertheless offer an adequate solution to an optimization issue, despite the limited processing capability. Most of the time use of conventional methods to optimize some problem takes a long time. Therefore compromising somewhat on the quality of the solution, which may not find the optimal solution, but we will find a solution that is sufficient for our needs, and we can do this very efficiently with a meta-heuristic algorithm. Among the various meta-heuristic algorithm some are inspired by our nature or mimic some behavior from our nature. Commonly, nature-inspired algorithms are employed to solve a variety of optimization challenges. There have been several meta-heuristics developed in the last three decades to help solve complicated and real-world problems in a variety of sectors. These meta-heuristics algorithms draw a huge amount of attention to researchers and scientists due to their complex problem-solving capability. Meta-heuristics algorithms can be used in many different fields, such as computer science, image processing, control systems, electrical engineering, different types of classification, etc. According to the No Free Lunch Theorem, “all optimization algorithms perform equally well when their performance is averaged across all possible problems”. That means one can’t say that one optimization is good for solving all types of optimization task. It is application dependent. So, the researcher tries to invent a new algorithm or improve the existing one according to their requirements. New NIOAs are always a good thing for the research field, as long as they solve problems quickly and effectively. One can classify these optimization problems according to the solution originated or the behavior of the algorithms. Figure 1 shows the classification of meta-heuristic algorithms.

Fig. 1

Classification of optimization methods

Image segmentation is the branch of digital image processing which primarily emphasizes on sectionalization of an image into numerous shares as per their features or properties basically for easier analysis of imagery. Various methods of segmentation are extensively employed [1, 2] namely thresholding-based, boundary-based, region-based, clustering-based [3, 4], and hybrid technique based, and amongst all the methods, thresholding-based is the most popular one. Multi-Level Thresholding (MLT) image segmentation has attained significant attention in quite a lot of image processing applications [5]. Nevertheless, the usage of traditional thresholding methods in determining the optimal threshold values (as a part of preprocessing step) is not just time-consuming but computationally demanding. This leads to the requirement of extension and attachment of certain procedures that might resolve the issue thus actuating the curiosity and interest in several academic scholars. Enormous research attempts are made during recent years toward solving real-world optimization problems with exceptionally towering dimensional search space, and rigorous constraints with nonlinear objective functions. More than a few mathematical elucidations rather than traditional optimization methods have been provided by a variety of researchers to work out the optimization problems however, the complexity of such mathematical solutions turned out to be very high requiring enormous computational time thereby proving to be ineffective in providing comprehensive solution in such circumstances. This pursuit consequently leads in the direction of the requirement for several modern technological optimization processes that would be proficient enough to accomplish the most favorable general yet thriving solution bearing in mind time, complexity, and other checks.

In light of this, NIOA [6] and their upgraded variations and subset whose solutions were based on chemical, physical, and biological phenomena in nature showed their usefulness in engineering optimization issues and also in resolving a number of MLT problems [7]. These nature-inspired solutions happen to be incredibly trendy as they offered to a large extent improved solutions in terms of efficiency and complexity than earlier methods. However, in recent years methodologies associated with nonlinear physics have flourished; therefore, across a wide range of applications, nonlinear procedures-based algorithms are more effective and versatile than other approaches published previously. Numerous global optimization strategies more notably; unique searching strategies based on various nonlinear physics phenomena are a popular current trend in NIOA design leading to the introduction of the Physics Inspired Optimization Algorithm (PIOA). The uniqueness of this method is that nonlinear processes [8] may perhaps be used as a brainwave for building up flourishing search algorithms that principally tag along with the nonlinear directives originated in natural systems [9]. Such approaches appear to be more challenging to develop than other search methodologies, since they need not only the use of a novel, natural nonlinear method as the searching basis, but also modeling an effective adaption of that procedure for addressing optimization issues. In order to build a completely new optimization algorithm following nonlinear processing modeling, this can be a challenging task and may require an expensive design method. In addition, this modeling may demand the tweaking of a set of algorithm parameters that are often connected with physical sub-processes inside the primary nonlinear process.

In this paper, a brief study has been performed on the Archimedes Optimization Algorithm (AOA) [10] which is a most recent and one of the most promising physics-inspired algorithm in the domain of optimization. This AOA is motivated by the physics phenomenon and here author evaluated, assessed, documented, and profoundly experimented with two types of images namely standard color images and pathology images by employing AOA. This paper mostly talks about AOA, its variations and improvements, and how Tsallis and t-entropy can be used to improve MLT image segmentation. Here, Tsallis and t-entropy are used as objective functions. Among all PIOA-based algorithms, AOA gives the best result in both Tsallis and t-entropy. But AOA with Tsallis entropy outperformed AOA with t-entropy in most of the cases with 4, 6, and 8 threshold values. Furthermore, we can conclude that AOA with Tsallis entropy gives superior results for medical pathology images rather than standard color images. Details discussion done in results section (Sect. 6) and conclusion section (Sect. 7). Several recently introduced Physics Inspired Optimization Algorithms (PIOA) have been included in Table 1 with Google Scholar Citation underlined (Dated: 17.07.2022).

Fig. 2

Year-wise AOA-based research work proposed

Table 1 Recently introduced Physics-Inspired Optimization Algorithms (PIOA)

In this paper, the author mainly concentrates on Archimedes Optimization Algorithm (AOA). The AOA is one of the most promising methods among the various PIOA-based optimization methods which is proposed in recent years (Fig. 2). This AOA-based method is widely used in the energy section, especially in the wind energy domain. The use of the AOA method in the image processing domain is surprisingly very low, though it performs very well in this domain. We have evaluated the performance of the AOA in the multi-level image segmentation domain in this paper in Sect. 6. Figure 4 represents the details analysis of the AOA method used in the different research fields. The author found most of the papers on AOA were published in different journals and only two papers were found which are published at the conference Fig. 3b.

Fig. 3

a AOA-based work published by different publishers. b Number of AOA-based work published in Journal Vs Conference

Fig. 4

Application area of AOA Vs number of paper published

Consequently, the following are the principal contributions of the paper:

• A very little effort was done before exploring AOA-based multi-level thresholding for image segmentation thereby this paper focuses on a brief study on AOA and the implementation and application of the seven recently developed PIOA in multi-level image segmentation domain.

• Only Differential Evolution (DE) has been used with t-entropy for Multi-Level Thresholding in the original finding paper of t-entropy [17]. This research work uses the Tsallis entropy and the newly constructed t-entropy as objective functions. As per the best of knowledge and research, t-entropy has not been utilized for Multi-Level Thresholding particularly with PIOA to date and this paper focuses on this as one of its main contributions.

• To explore the efficacy of the hitherto untested PIOA with Tsallis and t-entropy, a meticulous comparison analysis was conducted across two image kinds, namely standard color images and pathology images.

The paper’s remaining sections are organized as follows: The brief discussions on AOA and improvement and application area of AOA in recent years (2020–2022). Tsallis and t-entropy are presented in Sect. 5. Section 6 highlights the experimental results of recently developed PIOA in the field of MLT considering Tsallis entropy and t-entropy as objective functions. Lastly, Sect. 7 discusses the conclusion and future directions for study.

2 Methodology

For several decades, the natural phenomenon has been constantly borrowed bearing in mind its outstanding facts, functions, and phenomenon to resolve complex optimization difficulties. As with the physics-based algorithm, the motivations derived from physical laws are transformed into workable solutions and then evolve over time. To solve various optimization issues, in the last 3 years (2019 to 2021), some efficient Physics Inspired Optimization Algorithms (PIOA) have been introduced and this paper deals with the same, and also a comparative study has been done in the result section. The various PIOA have been listed in Table 1 and this section deals with the discussion on recent PIOA namely Archimedes Optimization Algorithm (AOA). Algorithm 1 is a summary of the overall approach to MLT utilizing NIOA, which is comprised of several phases (Fig. 5).

Fig. 5

General methodology for multilevel thresholding employing NIOA

2.1 Archimedes Optimization Algorithm (AOA)

Archimedes Optimization Algorithm [10] is a population-based PIOA algorithm that has been built upon the concept of the law of physics popularly recognized as the Archimedes principle. Archimedes’ principle basically elucidates the law of buoyancy which fundamentally elaborates the association amongst an object immersed in a fluid and buoyant force that is applied to it. However, if at all the weight of the object is superior to that of the weight of the displaced fluid, the object tends to sink else, the object will float above the fluid taken into consideration. In AOA, the population individuals of the algorithm are compared and considered as the immersed objects. Since all the population-based NIOA inaugurate its search process with an initial population known as candidate solutions that are associated with some random density, volume, and acceleration. Similarly, AOA also commences with a similar concept as that of the other existing population-based algorithm wherein each of the objects, $O_{i}$ that is immersed, with total population $N$ is initialized with a random search space position with lower bound $lb_{i }$ and upper bound $ub_{i }$ which basically is the fluid here as depicted Details algorithm steps are given below.

2.2 Algorithms Steps

In this section, we present the AOA algorithm’s mathematical formulations. Theoretically, AOA is a global optimization method because it consists of both exploration and exploitation phases. Pseudo-code of this algorithm presents in Sect. 2.3. The following are the AOA’s mathematical equation-based steps:

2.3 Step 1: The Initialization Phase

All the parameters of AOA are initialized with help of (1)

$$O_{i} = \, rand \, \times \, \left( {ub_{i} - \, lb_{i} } \right) \, + \, lb_{i} ; \, where \, i \, = \, 1, \, 2, \, 3, \, \ldots , \, N$$

(1)

Here, O_i is the $ith$ object within the $N$ (Population size). ub_i and lb_i is the upper bound and lower bounds in the search space respectively.

Each the $ith$ object’s volume (vol) and density (den) are initialized using the Eq. (2).

$$vol_{i} = \, rand$$

(2)

$$den_{i} = rand$$

(3)

$rand$ is a D dimensional vector, that generates random numbers between [0, 1] randomly.

Final initializes the acceleration (acc) of the $ith$ object using (4)

$$acc_{i} = \, lb_{i} + \, rand \, \times \, \left( {ub_{i} - \, lb_{i} } \right)$$

(4)

In the step 2, by analyzing the original population, the best fitness values are picked and assigned it to $Xbest, den_{best} , vol_{best}\, and\, acc_{best}$.

2.4 Step 2: Update the Volumes and Densities

For object $i$ the density and volume are updated according following Eq. (5) in $t + 1$ iteration.

$$\begin{gathered} den_{i}^{t + 1} = den^{i } + rand \times \left( {den_{best} - den_{i}^{t} } \right) \hfill \\ vol_{i}^{t + 1} = vol^{i } + rand \times \left( {vol_{best} - vol_{i}^{t} } \right) \hfill \\ \end{gathered}$$

(5)

The $vol_{best}$ and $den_{best}$ represent the best volume and density value which is found so far, $rand$ is the uniform distribution value between [0,1]. Transfer operator TF is utilized in AOA to transform search from exploration to exploitation, as mentioned by (6).

2.5 Step 3: Transfer Operator and Density Factor

At first, objects bump into each other, and then, after some time, they try to reach a state of equilibrium. Transfer operator $TF$ is used in AOA to convert search from exploration to exploitation, as stated by (6)

$$TF = \exp \left( {\frac{{t - t_{max} }}{{t_{max} }}} \right)$$

(6)

where transfer TF increases gradually over iteration until it reaches 1. Here $t_{max}$ represent the maximum iteration and $t$ is iteration number. In the same way, the density decreasing factor $d$ helps AOA with global-to-local searches (7)

$$d^{t + 1} = \exp \left( {\frac{{t_{max } - t}}{{t_{max} }}} \right) - \left( {\frac{1}{{t_{max} }}} \right)$$

(7)

$d^{t + 1}$ is the density of $t + 1$ iteration which decreases over time, and makes it possible to converge on a point. This density parameter plays a critical role to balance between exploitation and exploration in AOA.

2.6 Step 4.1: Exploration Phase (Collision Between Objects Occurs)

If the value of transfer operator $TF$ $\le$ 0.5 then there is a collision between object. Then select a random material ($mr$) and at iteration $t + 1$, update the object’s acceleration using (8).

$$acc_{i}^{t + 1} = \frac{{den_{mr} + vol_{mr} \times acc_{mr} }}{{den_{i}^{t + 1} \times vol_{i}^{t + 1} }}$$

(8)

Here, $acc_{i}^{t + 1}$, $den_{i}^{t + 1}$ and $vol_{i}^{t + 1}$ represent acceleration, density and volume of $ith$ object in $T + 1$ iteration. $den_{mr}$, $acc_{mr}$ and $vol_{mr}$ are the density, acceleration and volume of random material. The value of $TF$ ensure the exploration when it is $\le$ 0.5. When the value of $TF \le$ 0.5 then one third of the iteration are in exploration phase.

2.7 Step 4.2: Exploitation Phase (No Collision Between Objects)

By applying the $TF \ge$ 0.5 the exploration behavior changes to exploitation. That means there is no collision between object. Then the acceleration of $ith$ object in $T + 1$ iteration updated using following Eq. (9).

$$acc_{i}^{t + 1} = \frac{{den_{best} + vol_{best} \times acc_{best} }}{{den_{i}^{t + 1} \times vol_{i}^{t + 1} }}$$

(9)

$acc_{best}$ is the best object’s acceleration..

2.8 Step 4.3: Normalize Acceleration

When calculating percentage change, normalize the acceleration.

$$acc_{i - norm}^{t + 1} = u \times \frac{{acc_{i}^{t + 1} - \min \left( {acc} \right)}}{{\max \left( {acc} \right) - \min \left( {acc} \right)}} + l$$

(10)

where $u$ and $l$ represent the normalization range and are respectively set to 0.90 and 0.10. The $acc_{i - norm}^{t + 1}$ is responsible for calculating the percentage step change for each agent. The acceleration value will be high if the item $i$ is far from the global optimum. That means the object is in the exploration phase; otherwise, it will be in the exploration phase. In general, the acceleration factor starts with a large value and decreases with iteration.

2.9 Step 5: Update position

If $TF \le$ 0.5 (exploration phase), in next $t + 1$ iteration the $ith$ object position calculates by following Eq. (11)

$$x_{i}^{t + 1} = x_{i}^{t} + C_{1} \times rand \times acc_{i - norm}^{t + 1} \times d \times \left( {x_{rand} - x_{i}^{t} } \right)$$

(11)

Here, $C_{1}$ represent the constant value which is equal to 2.

Otherwise, $TF \ge$ 0.5 (exploitation) and update the position with the Eq. (12)

$$x_{i}^{t + 1} = x_{best}^{t} + F \times C_{2} \times rand \times acc_{i - norm}^{t + 1} \times d \times \left( {T \times x_{rand} - x_{i}^{t} } \right)$$

(12)

Here, $C_{2}$ represent the constant value which is equal to 6.$T$ goes up over time and is directly related to transfer operator. The value of $T$ defined by $T = C_{3} \times TF$.

The flat $F$ indicates a shift in motion direction by employing (13)

$$F = \left\{ {\frac{ + 1 if P \le 0.5}{{ - 1 if P \ge 0.5}}} \right\}$$

(13)

where $P = 2 \times rand - C_{4}$.

2.10 Step 6: Evaluation

Evaluate each item using the objective function $f$ and record the best solution so far. Assign $acc_{best}$, $vol_{best}$, $den_{best}$, $X_{best}$ (Fig. 6).

2.11 Pseudo Code of AOA

Fig. 6

Pseudo code of AOA

2.12 Time Complexity of AOA

The time complexity of AOA can be described as given below: Assuming the population size of the algorithm is $n$, the search space dimension is $d$, and the maximum number of iterations is $T$. $O\left( {nd} \right)$ is the calculation complexity for all of its components, including density, volume, acceleration, fitness value, and initialization. The exploration and exploitation phases update complexity are $O \left( {T \left( {1 + 2n + 2n\, log\, n} \right)} \right)$. So, applying the sum to all these complexities can be expressed as

$$O\left( {AOA} \right) = 5 \times O \left( {nd} \right) + O\left( { T \left( {1 + 2n + 2n\, log\, n} \right)} \right)$$

(14)

2.13 Merits and Limitations

Most of the nature-inspired optimization problems have some shortcomings. They trap into local optima. AOA suffers also same problem and because of that finding, the optimal solution goal is not achieved. This problem increases gradually when we move from unimodal to a multimodal or high-dimension complex problem. AOA is renowned for its efficiency, simplicity, and resilience, but it also has issues with premature and sluggish convergence, which causes it to become stuck in local minima. AOA generates a new solution based on the previous iteration. This phenomenon may reduce the algorithm coverage rate and might cover the whole search space effectively and it reduces the algorithm efficiency. So many researchers introduce various methods or adapt new parameters to balance between exploration and exploitation phase. All of the enhanced versions of AOA that which author found so far are discussed below.

3 Enhanced AOA Variants

There are a numerous number of physics-inspired based meta-heuristic algorithms proposed by various researchers. Each algorithm has its advantages and drawback. AOA is one of the new physis-inspired algorithms which become very popular within a very short period. Though it has also some drawbacks but most of the cases it gives us excellent results in various real-world applications. In the energy sector, it has made a significant impact. In a few cases, it is observed that it traps in local optima due to unbalancing of exploration and exploitation phase. So, some researchers tried to make this AOA better and more robust for their application. Sometimes an extra parameter is added [19] or a chaotic method is introduced inside the algorithm [21] or Levy Flight-based method is adopted [24] to avoid trapping into local optima. In most cases, researchers modified AOA according to their needs, and also they tried to modify the algorithm in such a way so that it can perform equally well for other applications. In this literature survey, we found that eight improvements to AOA have been proposed so far. A graph in Fig. 3b shows two things, i.e., the number of published papers in journals vs conferences and the number of improvement papers among the total proposed papers. Details study of all proposed improvement papers is given in Table 2.

Table 2 Improvements of AOA

4 Application of AOA

In the last twenty years, the nature-inspired optimization algorithm (NIOA) has been used in a wild variety of fields such as the energy sector, network sector, image processing field, artificial intelligence (AI), electronics sector, etc. In each sector, NIOA has put its remarkable footprint. In the last two decade, more than two hundred optimization algorithm has been proposed so far. Each algorithm has its flavor, which means the performance of these algorithms is application dependent. As previously said according to the free lunch theorem one cannot say that one algorithm gives the best result in all the fields. So, like other NIOA Archimedes Optimization Algorithm (AOA) is not the exception. This AOA has also some drawback which was discussed in the previous section and it is also been improved by many researchers. The researcher modifies the AOA according to its application area which is discussed in Table 2. From the literature survey of AOA, we can conclude that AOA has been widely used in the energy sector, especially in the wind energy domain [20, 26, 29]. AOA is also used in proton exchange membrane fuel cells [18, 21, 33] for parameter optimization. The application of AOA in the medical image domain is very little [34]. Only one paper we found where AOA has been applied in the medical image domain. In this paper, the author developed a model to detect and diagnose disease from chest X-rays. Though we found three papers in the image processing domain where AOA has been applied. Apart from medical images, AOA is also used to classify soybean plant disease [38] and Human facial analysis [35]. This paper AOA use here to determine the ideal facial area for gender recognition [35]. AOA has also been used in wireless sensor networks [22] and 5G cellular networks [46] to minimize traffic. Details study of the application area of AOA is discussed in Table 3.

Table 3 Application area of AOA

4.1 Paper Sources and Keywords

(A) Sources

The mentioned papers have been collected from the following sources:

• (i) SpringerLink—https://www.springerlink.com

• (ii) Google Scholar—https://scholar.google.com

• (iii) IEEE Xplore—https://ieeexplore.ieee.org

• (iv) ScienceDirect—https://www.sciencedirect.com

• (v) ACM Digital Library—https://dl.acm.org

• (vi) DBLP—https://dblp.uni-trier.de

• (vii) JOCA —http://www.joca.cn

• (viii) WILEY—https://www.wiley.com

• (ix) Taylor & Francis—https://www.tandfonline.com

(B) Keywords

Each of these above sources is queried with the following combinations of keywords:

KW1: Nature-Inspired Optimization Algorithms.

KW2: Image segmentation.

KW3: Hierarchical and Partitional clustering based image segmentation.

KW4: Nature Inspired Optimization Algorithm based image clustering.

KW5: Image segmentation medical image.

KW6: Image segmentation pathology image.

KW7: optimization.

KW8: Physics Inspired Optimization Algorithms.

KW9: Archimedes Optimization Algorithm.

KW10: Image segmentation using Swarm Intelligence algorithms.

KW11: Archimedes Optimization Algorithm improvement.

KW12: Multi-thresholding.

KW13: Archimedes Optimization Algorithm in Multi-thresholding.

5 AOA-Based Image Multi-level Thresholding

There are several computer vision applications in which image segmentation is a fundamental part of the process and thresholding is regarded as extremely important in this sector. Based on the number of threshold values one may classify two types of thresholding, namely bi-level and multi-level thresholding. From its name, one can say that when there is two threshold value then it is the bi-level threshold and when the threshold value is more than two it is said multi-level threshold. Multilevel Thresholding (MLT) segmentation algorithms have limits while looking for ideal thresholding values comprehensively to enhance the objective function, which also increases computing cost. In a nutshell, as the number of thresholds increases, MLT approaches become increasingly computationally difficult. Many scholars are drawn to a variety of methods that are inspired by nature or human behavior or physics phenomenon that may be used extensively to address this and other concerns with MLT.

In addition to that recently designed PIOA has also been utilized for MLT in the last 2 to 3 years. However, the effort is too little. For example, Dinkar et al. [50] suggested an Opposition-Based Laplacian Equilibrium Optimizer (OB-L-EO) in Image Segmentation using Multilevel Thresholding by utilizing Otsu’s interclass variance function over Standard Gray Scale Images and employing Berkeley Segmentation Dataset (BSD) and claims that the Proposed OB-L-EO is capable of exhibiting superior outcome in terms of maximizing variance and PSNR values thereby outperform other methods. Basset et al. [51] proposed an Equilibrium Optimization Algorithm (EOA) for multi-thresholding image segmentation by utilizing Kapur’s entropy over Standard Gray Scale Images and employing Berkeley Segmentation Dataset (BSD) and claims proposed EOA is capable of outperforming all other algorithms. However, EO failed to show its superiority over some algorithms in Standard values, and CPU time for the large threshold levels. Qi et al. [52] proposed Hybrid Equilibrium Optimizer Algorithm (HEOA) for multi-level image segmentation utilizing 3D Otsu over Standard Color Images, and Color Satellite Images using the CEC2015 dataset and claims that the proposed HEOA is capable of performing better (has the good optimal ability) than the other methods. However, it takes enormous time to iterate in order to find the best solution. On the other hand, this method has strong performance in wood fiber image segmentation thereby having a greater scope in the field of medical image segmentation, forest fire image segmentation, and so on. Rai et al. [7] also performed a comparative study among six NIOA called Archimedes Optimization Algorithm (AROA), Aquila Optimizer (AQO), Arithmetic Optimization Algorithm (AOA), Rat Swarm Optimization Algorithm (RSA), Particle Swarm Optimization (PSO), and Firefly Algorithm (FA) in satellite image MLT domain by considering Masi entropy as an objective function. Experimental results showed that AROA gave better results than other tested NIOA in terms of optimization ability, quality parameters, and execution time. Kurban et al. [53] also performed a comparative study among six novel NIOA such as Slime Mould Algorithm (SMA), Henry Gas Solubility Optimization (HGSO), turbulent flow of water-based Optimization (TFWO), Political Optimizer (PO), Marine Predators Algorithm (MPA) and Equilibrium Optimization (EO) for color image thresholding using Kapur and Otsu as objective functions. Comprehensive studies showed that MPA and TFWO produced better results than SMA, EO, PO, and HGSO for satellite images. Cuckoo search-based multi-level thresholding for lymphoblastic leukemia image segmentation proposed by Ray et al. [54]. The next section focuses mostly on the problem foundation and objective function for multi-level thresholding.

5.1 Problem Formulation of Multilevel Thresholding

In image segmentation, based on multiple thresholding [55, 56], the primary objective is to choose threshold values so that the segmented images possess the required characteristic. Here the threshold values are taken into account while constructing the objective function. By minimizing or maximizing of objective function with help of threshold value we can achieve our goal.

Suppose, an image $I$ have $L$ gray levels and which can be classified into $K$ number of classes i.e. ($C_{1, } C_{2} , \ldots , C_{i} , \ldots , C_{k}$) using ($K - 1$) number of thresholds which values are ($T = t_{1} , t_{2} , \ldots , t_{i} , \ldots ,t_{K - 1}$), where ($t_{1} < t_{2} < , \ldots , < t_{i} , \ldots , < t_{K - 1}$). Here, for an 8-bit image, $L$ = 256 and the grayscale levels fall between 0 and 255. So, a pixel with gray level $G$ belongs to the class $C_{i}$ if ($t_{i + 1} < G < t_{i}$) for $i = 1,2, \ldots ,K$. So, a single objective function can be written as

$$T^{\prime} = {\text{arg max}}/{\text{min}}_{0 \le T \le L - 1} \left\{ {F\left( T \right)} \right\}$$

(15)

Here thresholds T′ which optimizes the objective function ${\text{F}}\left( {\text{T}} \right)$. To get the segmented image $I$, the objective function $F\left( T \right)$ must satisfy the desired property. Following is a simple mathematical implementation of Tsallis entropy as an objective function in this study.

For multi-objective thresholding, $T^{\prime\prime}$ optimize the set of objective functions.

$$F\left( T \right) = \left( {F_{1} \left( T \right),F_{2} \left( T \right), \ldots , F_{j - 1} \left( T \right), \ldots , F_{n} \left( T \right)} \right), where\, n > 1$$

(16)

$$T^{\prime\prime} = {\text{arg max}}/{\text{min}}_{0 \le T \le L - 1} \left\{ {F\left( T \right)} \right\}$$

(17)

5.2 Objective Function

5.2.1 Tsallis Entropy as Objective Function

Constantin Tsallis introduced the Tsallis entropy as an extension of the Boltzmann–Gibbs entropy measure [57]. Using the entropy formula given in Eq. (18) Tsallis’ entropy measure may be expanded to a non-extensive system based on the idea of multi-fractal theory.

$$S_{q} = \frac{{1 - \mathop \sum \nolimits_{i = 1}^{k} \left( {p_{i} } \right)^{q} }}{q - 1}$$

(18)

where, $0 \le {\text{p}}_{{\text{i}}} \le 1$ represents the probability of the state i. In the case of a gray level image, It indicates the appearance of the ith gray level in a grayscale image. The Tsallis parameter $q$ represents the system under consideration’s non-extensivity. Using the pseudo-additivity entropy rule, it may be expressed as

$$S_{q} \left( {f + b} \right) = S_{q} \left( f \right) + S_{q} \left( b \right) + \left( {1 - q} \right).S_{q} \left( f \right).S_{q} \left( b \right)$$

(19)

Here, the threshold value ${\text{t}}$ separates the image’s foreground and background classes, which are represented by the, $f$ and $b$.

Here, classes $f$ and $b$ are used to represent the image’s foreground and background areas, which are separated from one another by the image’s threshold value (${\text{t}}$). Suppose,$\left\{ {\left( {{\text{p}}_{1} ,{\text{p}}_{2} , \ldots \ldots ,{\text{p}}_{{\text{L}}} } \right)|{\text{p}}_{{\text{i}}} \ge 0,{\text{i}} = 1,{ }2,...,{\text{L}}.;{\text{ L}} = {\text{number of discrete gray levels}};{ }\mathop \sum \limits_{{{\text{i}} = 1}}^{{\text{n}}} {\text{p}}_{{\text{i}}} = 1} \right\}$ is the probability distribution of the image’s gray-level intensities. The following equation represents the probability distribution of classes $f$ and $b$:

$$P_{f} = \frac{{p_{1} }}{{P^{f} }}, \frac{{p_{2} }}{{P^{f} }}, \ldots ., \frac{{p_{t} }}{{P^{f} }}\;{\text{and}}\;P_{b} = \frac{{p_{t + 1} }}{{P^{b} }}, \frac{{p_{t + 2} }}{{P^{b} }}, \ldots ., \frac{{p_{L} }}{{P^{b} }}$$

(20)

where,

$$P^{f} = \mathop \sum \limits_{i = 1}^{{t_{1} }} p_{i} ,\,{\text{and}}\;P^{b} = \mathop \sum \limits_{i = t + 1}^{L} p_{i}$$

(21)

Therefore, for each class, Tsallis entropy may be expressed as follows:

$$S_{q}^{f} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{i = 1}^{t} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{f} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P^{f} }$}}} \right)^{q} }}{q - 1},\;S_{q}^{b} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{i = t + 1}^{L} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{b} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P^{b} }$}}} \right)^{q} }}{q - 1}$$

(22)

Bilevel-thresholding maximizes the total of the information measures for the foreground and background. Therefore, the following formulation may be used to determine the appropriate threshold:

$$t_{opt} = {\text{Arg max}}\left[ {S_{q}^{f} \left( t \right) + S_{q}^{b} \left( t \right) + \left( {1 - q} \right).S_{q}^{f} \left( t \right).S_{q}^{b} \left( t \right)} \right]$$

(23)

Subject to the following constraints:

$$\left| {P^{f} + P^{b} } \right| - 1 < S < 1 - \left| {P^{f} + P^{b} } \right|,\;{\text{where,}}\;S\left( t \right) = S = S_{q}^{f} \left( t \right) + S_{q}^{b} \left( t \right) + \left( {1 - q} \right).S_{q}^{f} \left( t \right).S_{q}^{b} \left( t \right)$$

(24)

The following expression may be used to simply expand this approach to multi-level thinking:

$$\left( {t_{1} ,t_{2} , \ldots \ldots ,t_{m} } \right) = {\text{Arg max}}\left[ {S_{q}^{1} \left( t \right) + S_{q}^{2} \left( t \right) + \cdots + S_{q}^{M} \left( t \right) + \left( {1 - q} \right).S_{q}^{1} \left( t \right).S_{q}^{2} \left( t \right) \ldots ..S_{q}^{M} \left( t \right)} \right]$$

(25)

where,

$$S_{q}^{1} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{i = 1}^{{t_{1} }} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P^{1} }$}}} \right)^{q} }}{q - 1}{ },\;{\text{and}}\;S_{q}^{M} \left( t \right) = \frac{{1 - \mathop \sum \nolimits_{{i = t_{m} + 1}}^{L} \left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {P^{M} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${P^{M} }$}}} \right)^{q} }}{q - 1},\;{\text{And}}\;M = m + 1$$

(26)

Subject to the following constraints:

$$\left| {P^{1} + P^{2} } \right| - 1 < S^{1} < 1 - \left| {P^{1} + P^{2} } \right|, \left| {P^{2} + P^{3} } \right| - 1 < S^{2} < 1 - \left| {P^{2} + P^{3} } \right|\& \left| {P^{m} + P^{m + 1} } \right| - 1 < S^{M} < 1 - \left| {P^{m} + P^{m + 1} } \right|$$

(27)

where $P^{1} , P^{2}$ and $P^{m + 1}$ corresponding to $S^{1} , S^{2}$ and $S^{M}$ have been computed using $t_{1} , t_{2} , \ldots \ldots ,t_{m}$ respectively.

5.2.2 t-Entropy as Objective Function

In 2021, Chakraborty et al. introduced a new measure of entropy termed t-entropy [17]. Suppose there is an image $I$ which has a normalized histogram ${\varvec{p}} = \left( {p_{0} ,p_{2} ,p_{3} , \ldots ,p_{n} , \ldots ,p_{L - 1} } \right) | p_{i} \ge 0, i = 0,1,2, \ldots ,n,...L - 1;$ in where $L$ is the image’s number of gray levels and $\mathop \sum \limits_{i = 0}^{L - 1 } p_{i} = 1$, then t-entropy $\left( {H_{c} } \right)$ of the image is then calculated as follows:

$$H_{c} \left( {\varvec{p}} \right) = \mathop \sum \limits_{i = 0}^{L - 1} p_{i} \tan^{ - 1} \left( {\frac{1}{{p_{i}^{c} }}} \right) - \frac{\pi }{4}$$

(28)

where $c$ is a positive constant.

Assuming that the normalized histogram is divided into $K$ classes by $nt = K - 1$ thresholds(t), the entropy for each class may be determined as follows:

$$\begin{gathered} H_{c}^{1} \left( {th_{1} } \right) = \mathop \sum \limits_{i = 0}^{{th_{1} - 1}} \frac{{p_{i} }}{{w_{1} }}\tan^{ - 1} \left( {\frac{1}{{\left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {w_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${w_{1} }$}}} \right)^{c} }}} \right) - \frac{\pi }{4} \hfill \\ H_{c}^{2} \left( {th_{2} } \right) = \mathop \sum \limits_{{i = th_{1} }}^{{th_{2} - 1}} \frac{{p_{i} }}{{w_{2} }}\tan^{ - 1} \left( {\frac{1}{{\left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {w_{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${w_{2} }$}}} \right)^{c} }}} \right) - \frac{\pi }{4} \hfill \\ \vdots \hfill \\ \vdots \hfill \\ H_{c}^{K} \left( {th_{nt} } \right) = \mathop \sum \limits_{{i = th_{nt} }}^{L - 1} \frac{{p_{i} }}{{w_{nt} }}\tan^{ - 1} \left( {\frac{1}{{\left( {{\raise0.7ex\hbox{${p_{i} }$} \!\mathord{\left/ {\vphantom {{p_{i} } {w_{nt} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${w_{nt} }$}}} \right)^{c} }}} \right) - \frac{\pi }{4} \hfill \\ \end{gathered}$$

(29)

where,

$$w_{1} \left( {th_{1} } \right) = \mathop \sum \limits_{i = 0}^{{th_{1} - 1}} p_{i} , w_{2} \left( {th_{2} } \right) = \mathop \sum \limits_{{i = th_{1} }}^{{th_{2} - 1}} p_{i } , \ldots \; \ldots \; \ldots \; \ldots ,w_{K} \left( {th_{nt} } \right) = \mathop \sum \limits_{{i = th_{nt} }}^{L - 1} p_{i}$$

(30)

where, for ease of computation, two dummy thresholds $th_{0} = 0, th_{nt} = L - 1$ are introduced with $th_{0} < th_{1} < \ldots < th_{n - 1} < th_{nt}$. Then, the best threshold value may be determined by using this method.

$$\varphi \left( {th_{1} ,th_{2} , \ldots \ldots ,th_{nt} } \right) = {\text{Arg max}}\left( {\left[ {H_{c}^{1} \left( {th_{1} } \right) + H_{c}^{2} \left( {th_{2} } \right) + \ldots + H_{c}^{K} \left( {th_{nt} } \right)} \right]} \right)$$

(31)

For image segmentation based on multi-level thresholding-based, the positive constant $c$ had been evaluated over $\left[ {0.01, 20} \right]$ and determined to be optimal at $c = 0.1$.

6 Experimental Result

In this section, the author did a comparative study between AOA with six other PIOA with help of Tsallis entropy and t-entropy over standard pathology images and standard color images. The six PIOA’s experimental results in multi-threshold domains namely Nuclear Reaction Optimization (NRO), Atom Search Optimization (ASO), Equilibrium Optimizer (EO), Henry Gas Solubility Optimization (HGSO), Flow Direction Algorithm (FDA), Atomic Orbital Search (AOS) are compared with Archimedes Optimization Algorithm (AOA). The algorithms parameter values used in these seven algorithm are defined in Table 4. Each NIOA’s specifications are determined after extensive testing. Tsallis’ and t-entropy are used as objective functions in the experiment. To make fair comparisons amongst NIOA techniques, the optimization procedure for each of the evaluated objective functions uses $NFE \left( {\text{Number of Function Evaluations }} \right){ } = { }1000{ * }d{ }$ as the halting condition. This criterion has been established to promote consistency with earlier published studies. When evaluating the experiments, the number of threshold values (TH) set to 4, 6, and 8 is taken into account. In addition, FE is a key performance metric used to evaluate the NIOA’s efficiency. FE allows some technical variables, such as the computer system where experiments are performed and implemented, that affect CPU time, focusing exclusively on the algorithm’s ability to explore the solution space. Mean fitness $\left( {\overline{f}} \right)$ and standard deviation $\left( \sigma \right)$ have been used to figure out how well the PIOA can optimize. A number of other metrics were used to assess the efficiency of these PIOA-based models segmented data: the PSNR, QILV, and Feature Similarity Index, for example (FSIM). Within the realm of image segmentation, these parameters have a great deal. The list of segmentation quality metrics that are being employed is presented in Table 5. [2, 58]. The hardware and software requirements for the experiment include MatlabR2018b and Windows-10 operating system, × 64-based personal computer, Ryzen 5 central processing unit, and 16 gigabytes of RAM. A standard set of 100 color photos is used to test the suggested methods which are collected from [59] (https://lear.inrialpes.fr/~jegou/data.php). The renal pathology images are taken from [60] (https://tcgadata.nci.nih.gov/tcga/). Figure 7 depicts the original color standard picture and kidney pathology imaging.

Table 4 Parameter setting of the PIOA

Table 5 Three well-known performance parameters for the evaluation of the image segmentation methods

Fig. 7

Original image: a Standard Color Image; b Color Renal Pathology Image

6.1 Experimental Results of Standard Color Images over Tsallis Entropy

For the standard color picture, Fig. 8 shows the segmented results of Fig. 7a using Tsallis entropy as an objective function across 4, 6, and 8 thresholds using different PIOA (AOA, ASO, HGSO, EO, AOS, FDA and NRO). Table 6 compares numerically the aforementioned PIOAs using Tsallis entropy as the objective function across 4, 6, and 8 thresholds for a typical color image. Here standard deviation $\left( {\sigma_{f} } \right)$, fitness function $\left( {\overline{f}} \right)$, Computational time (Time (sec)), PSNR, FSIM and SSIM used as numerous parameters for performance evaluation of segmented image. With addition, the bold value in this table is represented the best performance value. Table 6 reveals that AOA achieves the best outcome across all threshold values (4, 6, and 8) for every parameter considered, but NRO achieves the lowest result across all evaluated PIOAs. From the same table, Table 6, we can conclude that when the number of thresholds increases, FSIM, PSNR, and SSIM values similarly increase for the objective function studied in this situation. The fitness value of AOA is compared to that of other PIOAs studied (Table 1) using a non-parametric significance test known as Wilcoxon’s rank test [61] that permits the estimation of differences between the outcomes of two related approaches. A p value of less than 0.05 (5 percent significance threshold) strongly supports the rejection of the null hypothesis, indicating that the results of the best algorithm differ statistically insignificantly from those of the other peer algorithms and that the difference is not attributable to random chance. Table 7 presents the pair-wise comparisons of PIOA (AOA vs. ASO; AOA vs. FDA; AOA vs. EO; AOA vs. HGSO; AOA vs. AOS; and AOA vs. NRO) based on Wilcoxon p-values for Standard Color images for Tsallis Entropy for 4, 6, and 8 thresholds. The fact that all Wilcoxon p-values collected and projected in Table 7 are less than 0.05 (5 percent significance threshold) with h = 1 is evidence against the null hypothesis, implying that the AOA fitness values for performance are statistically superior. This suggests that AOA combined with Tsallis entropy as an objective function is competent enough to produce consistent solutions regardless of the threshold settings.

Fig. 8

Segmented results of PIOA using Tsallis entropy over 4, 6, and 8 thresholds for Fig. 7a

Table 6 Numerical comparison of PIOA for Tsallis Entropy as objective function over standard color image

Table 7 Comparison among PIOA depending on Wilcoxon p values over Standard Color image for Tsallis Entropy

6.2 Experimental Results of Pathology Images over Tsallis Entropy

For the pathology images, Fig. 9 shows the segmented results of Fig. 7(b) using Tsallis entropy as an objective function across 4, 6, and 8 thresholds using different PIOA (AOA, ASO, HGSO, EO, AOS, FDA and NRO). Tsallis entropy is used as the objective function in the numerical comparison of various PIOAs for pathology images with 4, 6, and 8 thresholds in Table 8. Here standard deviation $\left( {\sigma_{f} } \right)$, fitness function $\left( {\overline{f}} \right)$, Computational time (sec), PSNR, FSIM and SSIM used as numerous parameters for performance evaluation of segmented image. With addition the bold value in this table is represented the best performance value. Table 8 reveals that AOA achieves the best outcome across all threshold values (4, 6, and 8) for every parameter considered, but NRO achieves the lowest result across all evaluated PIOAs. Table 8 further shows that when the number of thresholds increases, values for PSNR, FSIM, and SSIM likewise increase for the objective function studied in this situation. Table 9 displays the pair-wise comparisons of PIOA (AOA vs. ASO; AOA vs. FDA; AOA vs. EO; AOA vs. HGSO; AOA vs. AOS; and AOA vs. NRO) based on Wilcoxon p-values for Pathology images for Tsallis Entropy for 4, 6, and 8 thresholds. All of the Wilcoxon p-values found and shown in Table 9 are less than 0.05, which is the 5 percent significance level. This seems to show that the null hypothesis is not true, which means that the AOA fitness values for performance are statistically better. Lastly, it can be concluded that the AOA algorithm is better for both standard color images and pathology images in terms of the different performance parameters and takes less time to run.

Fig. 9

Segmented results of PIOA using Tsallis entropy over 4, 6, and 8 thresholds for Fig. 7b

Table 8 Numerical comparison of PIOA for Tsallis entropy as an objective function over Pathology Image

Table 9 Comparison among PIOA depending on Wilcoxon p values over Color Pathology Image for Tsallis Entropy

6.3 Results over t-Entropy for Standard Color Images

For the standard color images, Fig. 10 shows the segmented results of Fig. 7a using t-entropy as an objective function across 4, 6, and 8 thresholds using different PIOA (AOA, ASO, HGSO, EO, AOS, FDA and NRO). t-entropy is used as the objective function in the numerical comparison of various PIOAs for standard images with 4 and 8 thresholds in Table 10. Here standard deviation $\left( {\sigma_{f} } \right)$, fitness function $\left( {\overline{f}} \right)$, Computational time (sec), PSNR, FSIM and SSIM used as numerous parameters for performance evaluation of segmented image. With addition the bold value in this table is represented the best performance value. Table 10 shows clearly that AOA gets the best results over the threshold values of 4, 6 and 8 for all parameters except for $\sigma_{f}$. In terms of characteristics such as PSNR and SSIM, NRO is the poorest of the studied PIOAs, but it has the best standard deviation $\left( {\sigma_{f} } \right)$ value. In addition, for a given threshold value, NRO requires the most computational time. On the other hand, threshold value 8, NRO imparts the worst result amongst all the tested PIOA’s for the parameters namely computational time and FSIM whereas HGSO achieves the best standard deviation $\left( {\sigma_{f} } \right)$ value. Consequently, for threshold value 6, AOA achieves the best results for all parameters considered, whereas FDA achieves the poorest results among all examined PIOAs for the parameters FSIM, PSNR, and SSIM. Additionally, for the same, NRO requires the most computational time. Table 11 displays the pair-wise comparisons of PIOA (AOA vs. ASO; AOA vs. FDA; AOA vs. EO; AOA vs. HGSO; AOA vs. AOS; and AOA vs. NRO) based on Wilcoxon p-values for Standard Color images with t-entropy for 4, 6, and 8 thresholds. The Wilcoxon p-values obtained and projected in Table 11 for threshold number 8 are less than 0.05 (5 percent significance level) with h = 1, which is an evident proof against the null hypothesis, implying that the AOA fitness values for performance are statistically superior. Nonetheless, this is not the case for threshold values 4 and 6, since the Wilcoxon p-values obtained are more than 0.05 (5 percent significant level) in a few instances, as seen in the table.

Fig. 10

Segmented results of PIOA using t-entropy over 4, 6, and 8 thresholds for Fig. 7a

Table 10 Numerical comparison of PIOA for t-entropy as an objective function over a standard color image

Table 11 Comparison among PIOA depending on Wilcoxon p values over Standard Color image for t-entropy

6.4 Results over t-entropy for Pathology Images

Figure 11 illustrates the visual segmentation results of Fig. 7(b) utilizing several PIOA (AOA, ASO, HGSO, EO, AOS, FDA, and NRO) using t-entropy as the objective function across thresholds of 4, 6, and 8 for the Pathology picture. t-entropy is used as the objective function in the numerical comparison of various PIOAs for pathology images with 4 and 8 thresholds in Table 12. Here standard deviation $\left( {\sigma_{f} } \right)$, fitness function $\left( {\overline{f}} \right)$, Computational time (sec), PSNR, FSIM and SSIM used as numerous parameters for performance evaluation of segmented image. With addition the bold value in this table is represented the best performance value. For every parameter considered, results in Table 12 clearly show that AOA achieves the greatest results over threshold values of 6. NRO, on the other hand, is the worst PIOA in terms of all criteria except for PSNR, whereas FDA is the worst in terms of PSNR. On the other hand for threshold values 4 and 8, AOA accomplishes the best result for every parameter taken into account except for that of the standard deviation $\left( {\sigma_{f} } \right).$ FDA and NRO achieves the best standard deviation $\left( {\sigma_{f} } \right)$ values for threshold values 4 and 8 respectively. FDA performs worst for threshold values 4 and 8 in terms of FSIM, PSNR and SSIM nonetheless; NRO consumes the most computation time. Table 13 tabulates the pair-wise comparisons of PIOA (AOA vs. ASO; AOA vs. FDA; AOA vs. EO; AOA vs. HGSO; AOA vs. AOS; and AOA vs. NRO) based on Wilcoxon p-values for Standard Color images with t-entropy for 4, 6, and 8 thresholds. The Wilcoxon p-values obtained and predicted in Table 13 for threshold number 8 are less than 0.05 (5 percent significance level) with h = 1, indicating that the AOA performance fitness values are statistically better. Nonetheless, this is not the case for threshold values 4 and 6, since the Wilcoxon p-values obtained are more than 0.05 (5 percent significant level) in a few instances, as seen in the table.

Fig. 11

Segmented results of PIOA using t-entropy over 4, 6, and 8 thresholds for Fig. 7b

Table 12 Numerical comparison of PIOA fort-entropy as an objective function over Pathology Image

Table 13 Comparison among PIOA depending on Wilcoxon p values over Color Pathology Image for t-entropy

6.5 Discussion on the Performance Comparison Among Objective Functions

According to Table 6 and Table 10, it is clear that Tsallis and t-entropy, two famous objective functions for standard color pictures, outperform for every PIOA over characteristics such as fitness function $\left( {\overline{f}} \right)$, standard deviation $\left( {\sigma_{f} } \right)$, computational time (sec), FSIM, and PSNR for all PIOAs. Tsallis entropy, on the other hand, surpasses t-entropy in terms of SSIM for nt = 6 and 8; nevertheless, for nt = 4, t-entropy yields superior results. When utilizing Tsallis entropy to segment standard color images, different PIOA’s require almost half the computation time for different threshold values than using t-entropy as an objective function. It can be concluded and inferred from the experimental results that every PIOA combination with Tsallis entropy surpasses the PIOA combination with t-entropy in almost all circumstances and in almost all parameters. While this is true, the PIOA in combination with Tsallis entropy yields better results and is clearly superior as an objective function for any threshold value, it is clear by looking at Tables 8 and 12, which show that this is also true for every parameter evaluated in the scenario. This demonstrates that, despite the fact that t-entropy is a recently proposed notion that is rarely used in image segmentation, Tsallis entropy as an objective function gives an intriguing and unorthodox option for regular color image segmentation problems. Both Tsallis entropy and t-entropy as objective functions in association with various PIOA are more suited for pathology pictures than ordinary color images in general, according to this analysis. According to the tables described above, a further examination shows that the processing time rises, but the values for FSIM and PSNR and SSIM also increase as the number of thresholds grows for the objective function under consideration. For a typical color image and a pathologic image, Figs. 12 and 13 provide a visual comparison between Tsallis and t-entropy in terms of processing time, FSIM, PSNR, and SSIM. The average values of the computational time, FSIM, PSNR, and SSIM for the graphs have been computed by averaging the results of all the seven tested PIOA over all the tested standard color images and pathology images.

Fig. 12

Comparison among Tsallis and t-entropy over Standard Color Images

Fig. 13

Comparison among Tsallis and t-entropy over Color Pathology Images

7 Conclusion

In this paper, the author conducted a depth review of AOA which is a recent physics-inspired optimization problem. Along with AOA the author also presents several optimization techniques inspired by the non-linear physics phenomena applied over standard color and pathology images for MLT image segmentation problems. In this study, the author considers two significant objective functions i.e. Tsallis and t-entropy. An intense experiment has been carried out to demonstrate the significance of different PIOA in the field of MLT image segmentation and the comparison among the different methods namely AOA, ASO, HGSO, EO, AOS, FDA, and NRO has been carried forward to identify the appropriate one for the same. The performance of AOA along with several other PIOA are evaluated here with help of PSNR, FSIM, SSIM, standard deviation, fitness function, etc. Quite a few contributions have been projected in this paper as highlighted in the introduction section out of which, t-entropy for MLT predominantly with PIOA marks the key contribution. The results and core proclamation of this paper have been recapitulated as follows:

• (a) It is evident from the numerical results that AOA has shown its competence and accuracy above other PIOA’s signifying that AOA is the most suitable PIOA for the MLT image segmentation process of the standard color images as well as pathology images over the entire threshold’s values (4, 6, and 8) for every parameter taken into account with Tsallis’ entropy as objective function thus paving its way towards other realms of image processing with fastest execution time. On the other hand, NRO for the same scenario displayed the worst result.

• (b) Further, using t-entropy as the objective function, the experimental result generated showcased that for different performance parameters different PIOA has its own significance. Also, the performance of PIOA varied as per the different threshold values taken into account. However, from the overall analysis, it can be stated that AOA in most of the cases outperforms other PIOA’s considered in this paper.

• (c) In addition, every PIOA generates better results in terms of computational effort and quality parameters every time Tsallis’ entropy as the objective function is taken into account for both variants of imagery in comparison to that of the t-entropy taken under similar circumstances.

• (d) Each PIOA’s considered in this paper and highlighted in Table 1, consumes almost half of the computation time for different threshold values considering Tsallis entropy to segment the standard color images as compared to segmentation using t-entropy as an objective function. However, in general, it can be stated that the computation time consumed by different PIOA using Tsallis entropy is much lesser than consumed using t-entropy.

• (e) The experimental conclusion demonstrates that both objective functions studied in this research in relation to various PIOA are better suited for pathology images than the usual color image.

• (f) Even though as mentioned earlier that t-entropy is the newly established concept rarely employed in image segmentation, Tsallis entropy as an objective function proves its way towards flattering the researcher by becoming an interesting and unconventional preference/choice for standard color image and pathology image segmentation tasks.

• (g) As the number of thresholds rises, it is also shown that computation time increases, and PSNR and the other SSIM metrics do as well for both the objective function.

The experimental analysis unquestionably draws attention to the researcher to explore and examine AOA for MLT based image segmentation and broadly in the image processing domain [62]. This in turn leads to several research directions and challenges and the same has been brought to light below:

• (a) Two-Dimensional (2D) objective functions [7] like 2D Cross, 2D-Renyi, 2D Tsallis, 2D Otsu, etc., could be considered and applied over diverse PIOA in the domain of image segmentation making it a challenging task.

• (b) Other variants of images such as standard grayscale, satellite images, and other medical images such as MRI, CT, histology, etc., could be considered using the numerous PIOA experimented in this paper.

• (c) In addition, an improved variant of t-entropy or 2D t-entropy needs to be initiated and further applied in the domain of image segmentation to yield an exceptional outcome.

• (d) Last but not the least, initiating hybrid AOA or a hybrid PIOA to explore multi-objective MLT could be a striking work for the future (Table 14).

Table 14 Nomenclature