On the use of adjoint gradients for time-optimal control problems regarding a discrete control parameterization

Abstract

In this paper, we discuss time-optimal control problems for dynamic systems. Such problems usually arise in robotics when a manipulation should be carried out in minimal operation time. In particular, for time-optimal control problems with a high number of control parameters, the adjoint method is probably the most efficient way to calculate the gradients of an optimization problem concerning computational efficiency. In this paper, we present an adjoint gradient approach for solving time-optimal control problems with a special focus on a discrete control parameterization. On the one hand, we provide an efficient approach for computing the direction of the steepest descent of a cost functional in which the costs and the error in the final constraints reduce within one combined iteration. On the other hand, we investigate this approach to provide an exact gradient for other optimization strategies and to evaluate necessary optimality conditions regarding the Hamiltonian function. Two examples of the time-optimal trajectory planning of a robot demonstrate an easy access to the adjoint gradients and their interpretation in the context of the optimality conditions of optimal control solutions, e.g., as computed by a direct optimization method.

1 Introduction

Improving the performance of mechanical systems requires sophisticated optimization strategies to fulfill the high demands of current and future product requirements. In general, two problem formulations can be considered to describe various optimization applications: structural optimization of mechanical components and/or finding an optimal control for nonlinear dynamical systems [37]. The focus of this paper is on the latter problem and relates particularly with time-optimal controls.

Bobrow et al. [4] solved the time-optimal control problem for the case where the path is specified and the actuator torque limitations for the robot control are known. They computed the optimal control torques using a conventional linear feedback control system. Shin and McKay [35] used dynamic programming considering parametric functions to reduce the state space. Regarding the application to industrial robots, smooth trajectory planning is essential and has been presented, e.g., by Constantinescu and Craft [8] by using cubic splines to parameterize the state-space trajectory. Reiter et al. [31] proposed a time-optimal path tracking problem formulated as a nonlinear programming (NLP) problem solved by a multiple shooting method to account for the continuity required to respect the technological limits of real robots. Moreover, methods for the fast computation of optimal solutions to planning problems with changing parameters based on B-spline parameterization are presented in [30].

An alternative to the methods mentioned above is the use of indirect optimization methods avoiding the solution of a boundary value problem suffering from poor initial controls. The fundamental work by Bryson and Ho [6] shows how the gradient in an indirect optimization approach can be computed in a straightforward manner using adjoint variables. Optimal control problems can be solved iteratively with adjoint gradients using nonlinear optimization routines, as described in the sense of optimal control or parameter identification in multibody systems, e.g., in [23].

The adjoint method has been used by various authors [2, 14, 17] in different research areas. In the last few decades, the sensitivity analysis based on the adjoint method has become increasingly important [7, 26]. An extensive literature review in a more recent work [15] presents various gradient-based optimization methods, especially in design optimization of flexible multibody systems.

Moreover, since the adjoint method is computationally efficient, real-time applications and neural network applications can be addressed with the adjoint approach. For instance, physics-informed neural networks use partial differential equations in the cost functions to incorporate prior scientific knowledge. Previous research has shown that the discrete adjoint approach is efficient in application of neural networks [29]. Solvers capable of building efficient gradients are beneficial for training machine learning embedded cost functionals. Moreover, Gholami et al. [12] proposed an adjoint-based neural ordinary differential equation framework that provides unconditionally accurate gradients. Johnston and Patel [18] stated that adjoint methods are used in both control theory and machine learning to efficiently compute gradients of functionals.

In this paper, we concentrate on the efficient computation of gradients in optimal control problems and the role of adjoint variables in the optimization strategy. The proposed ideas can also be used in neural network approaches for the interpretation and evaluation of optimal solutions. In particular, we discuss a particular class of time-optimal control problems for dynamic systems involving final constraints. For such problems, Eichmeir et al. [10] recently presented an indirect gradient method to relate the control variations to the error of the given final constraints. In this paper, we extend the method to provide an exact gradient for discrete control parameterizations for direct or indirect optimization methods. For both methods, the Hamiltonian of the system can be determined and can then be considered for classical statements about optimality. To be more precise, we investigate the role of the adjoint variables in the verification of the optimality conditions of a solution derived by an arbitrary optimization approach, e.g., computed by a direct optimization method.

To this end, we discuss the time-optimal control problem of a two-arm robot. In a first example, the robot is formulated with rigid bodies. The advantage of the proposed approach, in particular, concerning computational effort, will be exploited in a second example of a flexible robotic system using the absolute nodal coordinate formulation (ANCF) for describing large deformations. Both examples are solved by a direct optimization method, and the evaluation of the optimality criteria regarding a Hamiltonian leads to an interpretation of the adjoint gradients. In addition, we performed a comparison of the number of function evaluations in a local minimum considering either numerical or analytical gradients, which shows the clear advantage of using adjoint gradients.

2 Time-optimal control problem

The aim of an optimal control problem is to find a control of a dynamical system to minimize certain performance measures. Let us consider the nonlinear dynamical system

$$ \dot{\mathbf{x}}(t) = \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)) \quad \text{with} \quad \mathbf{x}(0) = \mathbf{x}_{0}, $$

(1)

where $\mathbf{x}(t) \in \mathbb{R}^{n}$ and $\mathbf{u}(t) \in \mathbb{R}^{m}$ are the vectors of state and control variables, respectively. A performance measure might be the energy consumption or the operation time from initial to final state. The focus in this work will be on the latter.

We briefly discuss the time-optimal control problem [3, 6, 21]. The goal is to determine a final time $t_{f} = t_{f}^{*}$ and a control $\mathbf{u}(t) = \mathbf{u}^{*}$ such that the scalar cost functional

$$ J(\mathbf{x}(t),\mathbf{u}(t),t_{f}) = \int _{t_{0}}^{t_{f}} \Big[1 + P( \mathbf{x}(t),\mathbf{u}(t))\Big] \,\mathrm{d}t$$

(2)

is minimized while satisfying the final constraints

$$ \boldsymbol{\phi}(\mathbf{x}(t_{f}), t_{f}) = \mathbf{0} \in \mathbb{R}^{q}. $$

(3)

Note that the state variables $\mathbf{x}(t)$ and control $\mathbf{u}(t)$ are functions over the time interval $t\in [t_{0},\,t_{f}]$ in the cost functional and that inequality constraints for the state variables and control are accounted for using the penalty function $P(\mathbf{x},\mathbf{u})$. This means that a penalty term will be added to the final time $t_{f}$ in case of violating inequality constraints; see Eq. (2). The optimal control problem is defined by Eqs. (1)–(3) and can be solved by two different approaches. Direct methods transform the original infinite-dimensional optimization problem into a finite-dimensional one. The resulting NLP problem can be treated by well-known methods, e.g., the sequential quadratic programming (SQP) approach [24]. An optimal point is in accordance with the Karush–Kuhn–Tucker (KKT) conditions [19, 22], which are necessary optimality conditions for direct optimization methods. Contrary, indirect methods are based on the calculus of variations and the derived necessary optimality conditions. These explicit expressions result from Pontryagin’s minimum principle and are in the form of a two-point boundary value problem, which is usually hard to solve. Shooting methods, collocation methods, or gradient-based approaches can be used to solve the underlying two-point boundary value problem.

2.1 Direct optimization method

Direct methods transform the original infinite-dimensional optimization problem into a finite-dimensional one by a parameterization of the control $\mathbf{u}(t)$. In this paper, the control is discretized by a set of grid nodes $\bar{\mathbf{u}}$. Hence the set of optimization variables in time-optimal control problems is defined by $\mathbf{z}^{\mathsf{T}} = \left(t_{f},\, \bar{\mathbf{u}}^{\mathsf{T}} \right) \in \mathbb{R}^{z}$. The discretization of the control leads to an NLP problem of the form

$$ \begin{aligned}& \underset{\mathbf{z}}{\text{min}}~J(\mathbf{z}) \\& \text{s.t.}~\boldsymbol{\phi}(\mathbf{z}) = \mathbf{0}.\end{aligned}$$

(4)

Note that the NLP problem is defined by the optimization variables $\mathbf{z}$. To evaluate the cost functional and final constraints, the state variables $\mathbf{x}$ have to be computed with respect to the optimization variables $\mathbf{z}$. For solving the state equations in this step, a classical ordinary differential equation (ODE) solver can be used, e.g., an explicit Runge–Kutta solver. The NLP problem in Eq. (4) can be solved by classical direct optimization methods. The local optimality of direct methods is investigated by introducing the Lagrangian function

$$\mathcal{L}(\mathbf{z},\boldsymbol{\xi}) = J(\mathbf{z}) - \boldsymbol{\xi}^{\mathsf{T}}\boldsymbol{\phi}(\mathbf{z}), $$

(5)

where $\boldsymbol{\xi} \in \mathbb{R}^{q}$ is the Lagrange multiplier. The necessary first-order or KKT conditions of the optimization problem in Eq. (4) are formulated as

$$ \begin{pmatrix}\nabla _{\mathbf{z}} \mathcal{L}(\mathbf{z}^{*},\boldsymbol{\xi}^{*}) \\\nabla _{\boldsymbol{\xi}} \mathcal{L}(\mathbf{z}^{*}, \boldsymbol{\xi}^{*})\end{pmatrix}= \mathbf{0}. $$

(6)

One of the most powerful methods for finding a KKT point $\left(\mathbf{z}^{*}, \, \boldsymbol{\xi}^{*}\right)$ of the NLP problem is an SQP approach [16, 25, 28]. The basic idea of this approach is to replace the original NLP problem with a quadratic subproblem. The solution of this subproblem is then used in an iterative method to determine a KKT point satisfying Eq. (6). The quadratic approximation of the cost function and the linear approximation of the constraints lead to

$$ \begin{aligned}& \underset{\mathbf{d}_{k}}{\text{min}}~J(\mathbf{d}_{k}) \approx J( \mathbf{z}_{k}) + \nabla _{\mathbf{z}} J(\mathbf{z}_{k})^{\mathsf{T}} \mathbf{d}_{k} + \frac{1}{2}\mathbf{d}_{k}^{\mathsf{T}}\nabla ^{2}_{ \mathbf{z}\mathbf{z}}J(\mathbf{z}_{k})\mathbf{d}_{k} \\ & \text{s.t.}~\boldsymbol{\phi}(\mathbf{d}_{k}) \approx \boldsymbol{\phi}(\mathbf{z}_{k}) + \nabla _{\mathbf{z}} \boldsymbol{\phi}(\mathbf{z}_{k})^{\mathsf{T}} \mathbf{d}_{k}, \end{aligned} $$

(7)

where $\mathbf{d}_{k} = \mathbf{z} - \mathbf{z}_{k}$ is the minimizer of the quadratic subproblem. In analogy to Eq. (6), the KKT conditions regarding the quadratic-linear model result in the linear system

$$ \begin{pmatrix}\nabla ^{2}_{\mathbf{z}\mathbf{z}} \mathcal{L} & - \nabla _{ \mathbf{z}} \boldsymbol{\phi}(\mathbf{z}_{k}) \\\nabla _{\mathbf{z}} \boldsymbol{\phi}(\mathbf{z}_{k})^{\mathsf{T}} & \mathbf{0}\end{pmatrix}\begin{pmatrix}\mathbf{d}_{k} \\\boldsymbol{\xi}_{k}\end{pmatrix}=\begin{pmatrix}-\nabla _{\mathbf{z}} J(\mathbf{z}_{k}) \\-\boldsymbol{\phi}(\mathbf{z}_{k})\end{pmatrix} , $$

(8)

which is called the KKT system. The solution of this system is used to update the optimization variables

$$\mathbf{z}_{k+1} = \mathbf{z}_{k} + \alpha _{k}\mathbf{d}_{k} $$

(9)

for the $(k+1)$th iteration. The method is made more robust by using a step length control parameter $\alpha _{k}$. The factor is obtained by minimizing a proper merit function. For a detailed description and different variants of the basic SQP approach, we refer to [3, 24], which is quite standard and implemented in various codes in this way. One goal of the present paper is to derive adjoint gradients providing analytically given gradients for an SQP approach. Hence the following section is devoted to the derivation of analytically computed adjoint gradients of the Jacobians in Eq. (8). This approach is especially efficient in the case of a high number of optimization variables. Moreover, the indirect approach is used for the evaluation of the chosen parameterization of the control. The parameterization of the control is correctly chosen with respect to the problem formulation if the necessary optimality conditions based on indirect methods are sufficiently small; see Fig. 2 for a graphical validation in the scope of an example.

2.2 Adjoint gradient approach

In this section, we exploit the adjoint gradient approach to evaluate the necessary first-order conditions regarding the Hamiltonian function in an indirect optimization method. For this purpose, we briefly summarize the key idea and theory for determining time-optimal controls for dynamic systems regarding final constraints using an indirect method. Generally, indirect methods are based on optimality conditions and lead to solving the underlying two-point boundary value problem. Instead of solving the two-point boundary value problem, the optimization problem can also be addressed by a gradient-based method, e.g., the Kelley–Bryson method [5, 20]. The key idea is to find a variation of the control to produce the maximum local decrease of the cost functional. To find a minimum of the cost functional, we can simply walk a short distance along the negative gradient of the cost functional. We pursue this method to fulfill the necessary optimality conditions derived by the calculus of variations following the basic ideas in [3, 6, 21].

2.2.1 Combined adjoint gradient approach regarding final constraints

The adjoint gradient computation in the presence of final constraints has been presented in a recent work [10], and here we briefly summarize the main steps. To derive the adjoint and influence equations, the cost functional in Eq. (2) is extended by the state equations in Eq. (1) leading to

$$ \bar{J} = \int _{t_{0}}^{t_{f}} \Big[ 1 + P(\mathbf{x},\mathbf{u}) + \mathbf{p}^{\mathsf{T}} \big( \mathbf{f}(\mathbf{x},\mathbf{u}) - \dot{\mathbf{x}} \big) \Big]\mathrm{d}t $$

(10)

for any choice of the adjoint variables $\mathbf{p} \in \mathbb{R}^{n}$ in the cases where the state equations are satisfied. To compute the variation of the extended cost functional $\bar{J}$, we perform infinitesimal variations of the final time $\delta t_{f}$ and of the control $\delta \mathbf{u}$, which also cause a variation of the states $\delta \mathbf{x}$ due to the state equations. The resulting variation of $\bar{J}$ leads to a variation $\delta \dot{\mathbf{x}}$, which can be eliminated by integration by parts. Finally, the cost functional can be reduced to

$$ \delta \bar{J} = \int _{t_{0}}^{t_{f}} \Big( P_{\mathbf{u}} + \mathbf{p}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \Big) \delta \mathbf{u}\, \mathrm{d}t + (1 + P_{f}) \delta t_{f}$$

(11)

in the case where the adjoint variables fulfill the linear time-variant final value problem

$$ \dot{\mathbf{p}} = -P^{\mathsf{T}}_{\mathbf{x}} - \mathbf{f}_{ \mathbf{x}}^{\mathsf{T}} \mathbf{p} \quad \text{with} \quad \mathbf{p}(t_{f}) = \mathbf{0}, $$

(12)

which is solved backward in time. Note that to compute the adjoint system, the state equations must first be solved forward in time. The subscripts $\mathbf{u}$ and $\mathbf{x}$ denote the partial derivatives with respect to $\mathbf{u}$ and $\mathbf{x}$, and the subscript $f$ indicates the evaluation of quantities at time $t=t_{f}$.

The optimization problem in Eqs. (1)–(3) does not only consist of minimizing the cost functional, but in addition, the final constraints must be fulfilled. The variations of the cost functional and final constraints will lead to a combined gradient-based approach for updating the final time and controls. As a first step, the final constraints are extended with the state equations, leading to

$$\bar{\boldsymbol{\phi}} = \int _{t_{0}}^{t_{f}} \mathbf{R}^{ \mathsf{T}} \big( \mathbf{f}(\mathbf{x},\mathbf{u}) - \dot{\mathbf{x}} \big) \mathrm{d}t + \boldsymbol{\phi}(\mathbf{x}(t_{f}), t_{f}). $$

(13)

Proceeding exactly the same way as above, the variation for the extended final constraints is defined by

$$ \delta \bar{\boldsymbol{\phi}} =\int _{t_{0}}^{t_{f}} \mathbf{R}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \delta \mathbf{u} \, \mathrm{d}t + \mathit{\dot{\boldsymbol{\phi}}}_{f} \delta t_{f}, $$

(14)

where $\dot{\boldsymbol{\phi}}_{f}$ denotes the total time derivative of Eq. (3) evaluated at time $t=t_{f}$. The influence adjoint variables $\mathbf{R} \in \mathbb{R}^{n\times q}$ have to fulfill the matrix differential equation

$$ \dot{\mathbf{R}} = -\mathbf{f}^{\mathsf{T}}_{\mathbf{x}}\mathbf{R} \quad \text{with} \quad \mathbf{R}(t_{f}) = \boldsymbol{\phi}_{\mathbf{x}}^{\mathsf{T}}( \mathbf{x}(t_{f}),t_{f}), $$

(15)

in which one set of $n$ ordinary differential equations for each component of the final constraints $\boldsymbol{\phi}(\mathbf{x}(t_{f}),t_{f})=\mathbf{0}$ is solved backward in time.

A linear combination of the scalar $\delta \bar{J}$ and vector $\delta \bar{\boldsymbol{\phi}}$ needs the introduction of vector multipliers $\boldsymbol{\nu}\in \mathbb{R}^{q}$ resulting in

$$ \delta \bar{J} + \boldsymbol{\nu}^{\mathsf{T}}\delta \bar{\boldsymbol{\phi}} = \int _{t_{0}}^{t_{f}} \underbrace{\vphantom{\Big( 1 + P_{f} + \boldsymbol{\nu}^{\mathsf{T}} \dot{\boldsymbol{\phi}}_{f} \Big)}\Big[ P_{\mathbf{u}} + \Big(\mathbf{p}^{\mathsf{T}} + \boldsymbol{\nu}^{\mathsf{T}}\mathbf{R}^{\mathsf{T}}\Big) \mathbf{f}_{\mathbf{u}}\Big]}_{:= - \delta \mathbf{u}^{\mathsf{T}}} \delta \mathbf{u} \, \mathrm{d}t + \underbrace{\Big( 1 + P_{f} + \boldsymbol{\nu}^{\mathsf{T}} \dot{\boldsymbol{\phi}}_{f} \Big)}_{:= - \delta t_{f}}\delta t_{f}, $$

(16)

where $\boldsymbol{\nu}$ is a vector of multipliers to combine both sets of adjoint variables and is computed in such a way that the variations in the control and final time lead to a better approximation of the final constraints. The largest possible decrease of the combined variation is obtained if the variations $\delta \mathbf{u}$ and $\delta t_{f}$ are chosen in the appropriate descent directions in Eq. (16) for the optimal updates $\mathbf{u}_{\mathrm{new}}= \mathbf{u} + \delta \mathbf{u}$ and $t_{f,\,\mathrm{new}}= t_{f} + \delta t_{f}$. These updates always reduce the cost functional and final constraints within one iteration.

Moreover, the Hamiltonian for the time-optimal control problem in Eqs. (1)–(3) was formulated by

$$ \mathcal{H}(\mathbf{x}(t), \mathbf{u}(t), \boldsymbol{\lambda}(t)):= 1 + P(\mathbf{x}(t),\mathbf{u}(t)) + \boldsymbol{\lambda}(t)^{ \mathsf{T}} \mathbf{f}(\mathbf{x}(t),\mathbf{u}(t)), $$

(17)

in which $\boldsymbol{\lambda}(t) = \mathbf{p}(t) + \mathbf{R}(t) \boldsymbol{\nu}$ exploits the decoupling of boundary conditions of the state and adjoint equations by introducing a set of adjoint variables $\mathbf{p}$ and the so-called influence adjoint variables $\mathbf{R}$ for $q$ final constraints. The decoupling within the multiplier $\boldsymbol{\lambda}$ enables sequential integration of a new set of canonical equations forward and backward in time, depending on a putative optimal control history. The solution of the canonical (adjoint and influence) equations for $\mathbf{p}$ and $\mathbf{R}$ can be combined to determine the Hamiltonian in Eq. (17). A more elaborate derivation can be found in [10], supplemented with examples and convergence analysis.

2.2.2 Parameterization of control

The following adjoint gradient approach allows the consideration of final constraints and enables the use of various control parameterizations. Hence the infinite-dimensional optimal control problem is reduced to a finite-dimensional problem to reduce the complexity of the optimization task. As proposed for instance in [10], the variation $\delta \mathbf{u}$ can be defined as an explicit function in time by

$$ \delta \mathbf{u} := - P_{\mathbf{u}}^{\mathsf{T}} - \mathbf{f}_{ \mathbf{u}}^{\mathsf{T}} \big(\mathbf{p} + \mathbf{R}\boldsymbol{\nu}\big), $$

(18)

and only depends on the time discretization of the forward and backward solution. It has to be emphasized that this update $\delta \mathbf{u}$ is not yet dependent on the type of parameterization. To meet the restrictions of industrial applications, feasible control parameterizations have to be specified. However, the control function $\mathbf{u}(t)$ can be parameterized by grid nodes $\bar{\mathbf{u}}$ (see the Appendix for a cubic spline parameterization of the control) in the form

$$ \mathbf{u}(t) = \mathbf{C}(t)\, \bar{\mathbf{u}}, $$

(19)

leading to the variation of the control

$$ \delta \mathbf{u}(t) = \mathbf{C}(t)\,\delta \bar{\mathbf{u}}.$$

(20)

It has to be emphasized that any parameterization according to Eq. (19) can be used for the proposed gradient approach. Following the theory introduced in Section 2.2.1, the variation in Eq. (20) is inserted into Eq. (16). Since the variation $\delta \bar{\mathbf{u}}$ does not depend on time, we can rewrite the combined variation in the following form:

$$\delta J + \boldsymbol{\nu}^{\mathsf{T}}\delta \bar{\boldsymbol{\phi}} = \underbrace{\int _{t_{0}}^{t_{f}} \Big[\Big(P_{\mathbf{u}} + \boldsymbol{\lambda}^{\mathsf{T}}\mathbf{f}_{\mathbf{u}} \Big)\mathbf{C}\Big] \, \mathrm{d}t }_{:= -\delta \bar{\mathbf{u}}^{\mathsf{T}}} \delta \bar{\mathbf{u}} + \underbrace{\vphantom{\int _{t_{0}}^{t_{f}}}\Big( 1 + P_{f} + \boldsymbol{\nu}^{\mathsf{T}}\dot{\boldsymbol{\phi}}_{f} \Big)}_{:= -\delta t_{f}} \delta t_{f}. $$

(21)

Similarly to the previous section, the variations of the grid nodes $\delta \bar{\mathbf{u}}$ and final time $\delta t_{f}$ are defined by

$$\begin{aligned} \delta \bar{\mathbf{u}}&= -\kappa \, \int _{t_{0}}^{t_{f}} \mathbf{C}^{ \mathsf{T}} \Big( P_{\mathbf{u}}^{\mathsf{T}} + \mathbf{f}_{ \mathbf{u}}^{\mathsf{T}}\boldsymbol{\lambda}\Big) \, \mathrm{d}t, \end{aligned}$$

(22)

$$\begin{aligned} \delta t_{f}&=-\kappa \alpha \Big( 1 + P_{f} + \dot{\boldsymbol{\phi}}_{f}^{\mathsf{T}}\boldsymbol{\nu} \Big), \end{aligned}$$

(23)

so that the combined variation leads to the largest possible decrease. The scalar $\kappa$ is a sufficiently small step size, and the factor $\alpha$ can be used as a scaling factor if the magnitudes of the two latter variations differ dramatically. The choice of the vector of multipliers $\boldsymbol{\nu}$ is based on the reduction of the final constraints in every iteration with the updates $\delta \bar{\mathbf{u}}$ and $\delta t_{f}$, i.e.,

$$\delta \bar{\boldsymbol{\phi}}:=-\varepsilon \, \boldsymbol{\phi}_{f}, $$

(24)

choosing an appropriate update parameter $\varepsilon >0$, as shown in detail in [10]. This approach finally results in

$$\boldsymbol{\nu} = \mathbf{A}^{-1} \big( \varepsilon \, \boldsymbol{\phi}_{f} - \mathbf{b} \big), $$

(25)

where we use the abbreviations

$$\begin{aligned} \mathbf{A}&:= \kappa \, \int _{t_{0}}^{t_{f}} \mathbf{R}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \mathbf{C} \, \mathrm{d}t \int _{t_{0}}^{t_{f}} \mathbf{C}^{\mathsf{T}}\mathbf{f}_{\mathbf{u}}^{\mathsf{T}}\mathbf{R} \, \mathrm{d}t + \kappa \alpha \dot{\boldsymbol{\phi}}_{f} \dot{\boldsymbol{\phi}}_{f}^{\mathsf{T}}, \end{aligned}$$

(26)

$$\begin{aligned} \mathbf{b}&:= \kappa \, \int _{t_{0}}^{t_{f}} \mathbf{R}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \mathbf{C} \, \mathrm{d}t \int _{t_{0}}^{t_{f}} \mathbf{C}^{\mathsf{T}} \Big( P_{\mathbf{u}}^{\mathsf{T}} + \mathbf{f}_{\mathbf{u}}^{\mathsf{T}}\mathbf{p} \Big) \, \mathrm{d}t + \kappa \alpha \dot{\boldsymbol{\phi}}_{f} ( 1 + P_{f} ). \end{aligned}$$

(27)

This combined gradient approach enables the use of various parameterizations of the control, shown, e.g., in [10] for a bang-bang control. This paper investigates the combined gradient approach to evaluate necessary optimality conditions regarding the Hamiltonian function.

In case of using a direct optimization method, the corresponding analytically adjoint gradients can be used instead of numerically computed gradients because of the computational burden. To derive these adjoint gradients, the discrete control parameterization from Eq. (20) is inserted into the variation of the cost functional in Eq. (11) and into the variation of the final constraints in Eq. (14). Hence the analytically adjoint gradients are given by

$$\begin{aligned} \nabla _{\bar{\mathbf{u}}} \, J^{\mathsf{T}} =& \int _{t_{0}}^{t_{f}} \Big( P_{\mathbf{u}} + \mathbf{p}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \Big) \mathbf{C}\, \mathrm{d}t, \end{aligned}$$

(28)

$$\begin{aligned} \nabla _{\bar{\mathbf{u}}} \, \boldsymbol{\phi}^{\mathsf{T}} =& \int _{t_{0}}^{t_{f}} \mathbf{R}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \mathbf{C}\, \mathrm{d}t, \end{aligned}$$

(29)

and can be used instead of the numerical gradients in Eq. (8) in a direct optimization method. Note that the analytical gradients of $J$ and $\boldsymbol{\phi}$ with respect to $t_{f}$ cannot be simply given in a proper form and are therefore computed numerically in this case. It has to be emphasized that the size of the adjoint system does not increase with a larger number of grid nodes, which is not the case in the direct differentiation method or a numerical differentiation method. If (forward or backward) numerical differentiation is used, then the equations of motion have to be solved $(1+z)$ times to evaluate the numerical gradients, where $z$ is the number of optimization variables. Hence, the number of forward simulations grows linearly with the number of optimization variables.

Note that the variables $\kappa$, $\alpha$, and $\varepsilon$ are introduced here in accordance to the prework paper [10] but are not relevant in the discussion of the present paper, and therefore the variables are set to $\kappa = \alpha = \varepsilon = 1$. In this paper, the gradients in Eq. (28) and (29) are provided to a direct optimization method without using any user-defined scaling factors. Furthermore, the presented approach provides a new view of adjoint gradients in terms of the evaluation of optimality criteria using the Hamiltonian function.

3 Interpretation of the adjoint variables for optimality conditions

The decoupling of the gradients in Section 2.2 can lead to a new perspective on the adjoint variables in the evaluation and interpretation of Pontryagin’s principle. Bryson and Ho [6] derive the necessary optimality conditions using the calculus of variations. The minimization of the Hamiltonian must be addressed for restricted optimal controls problems according to Pontryagin’s minimal principle [21]. In this paper, we state the Hamiltonian as

$$ \mathcal{H}(\mathbf{x},\mathbf{u},\boldsymbol{\lambda}):= 1 + P( \mathbf{x},\mathbf{u}) + \boldsymbol{\lambda}^{\mathsf{T}} \mathbf{f}( \mathbf{x},\mathbf{u}), $$

(30)

in which the multiplier $\boldsymbol{\lambda}$ is computed by a linear combination of the adjoint variables

$$ \boldsymbol{\lambda} = \mathbf{p}+ \mathbf{R}\boldsymbol{\nu}. $$

(31)

Using the introduced Hamiltonian, we can formulate the necessary optimality conditions for time-optimal control problems. The derived variation in Eq. (22) can be rewritten in terms of the Hamiltonian as

$$\begin{aligned} \delta \bar{\mathbf{u}} = - \int _{t_{0}}^{t_{f}} \mathcal{H}_{ \bar{\mathbf{u}}}^{\mathsf{T}} \, \mathrm{d}t, \end{aligned}$$

(32)

where the partial derivative of the Hamiltonian with respect to the grid nodes $\bar{\mathbf{u}}$ is given by

$$\frac{\partial \mathcal{H}}{\partial \bar{\mathbf{u}}} = \frac{\partial \mathcal{H}}{\partial \mathbf{u}} \frac{\partial \mathbf{u}}{\partial \bar{\mathbf{u}}} = \Big( P_{ \mathbf{u}} + \boldsymbol{\lambda}^{\mathsf{T}}\mathbf{f}_{\mathbf{u}} \Big) \mathbf{C}. $$

(33)

In a similar manner, the variation in Eq. (23) can be reformulated as

$$\begin{aligned} \delta t_{f}= - \Big( \mathcal{H} + \boldsymbol{\phi}_{t}^{\mathsf{T}} \boldsymbol{\nu} \Big) \Big|_{t=t_{f}}, \end{aligned}$$

(34)

where the total time derivative of the final constraints is given by

$$\dot{\boldsymbol{\phi}}_{f} = \left ( \frac{\partial \boldsymbol{\phi}}{\partial \mathbf{x}} \frac{\partial \mathbf{x}}{\partial t} + \frac{\partial \boldsymbol{\phi} }{\partial t}\right )\biggl|_{t=t_{f}} = \Big( \mathbf{R}^{\mathsf{T}} \mathbf{f} + \boldsymbol{\phi}_{t} \Big) \Big|_{t=t_{f}}. $$

(35)

Note that the partial derivative of the constraints with respect to the states is expressed in terms of the influence adjoint variables given in the final condition in Eq. (15). In this paper, we use the adjoint gradients within the optimality conditions for other optimization methods relating to a Hamiltonian function. An optimal control parameterized by $\mathbf{u} = \mathbf{C}\,\bar{\mathbf{u}}$ must satisfy the necessary optimality conditions

$${\dot{\mathbf{x}}}^{\ast }=\phantom{-}{\mathcal{H}}_{\mathit{\lambda }}^{\mathsf{T}}({\mathbf{x}}^{\ast },{\mathbf{u}}^{\ast },{\mathit{\lambda }}^{\ast }),t\in [t_0,t_f],$$

(36)

$${\dot{\mathit{\lambda }}}^{\ast }=-{\mathcal{H}}_{\mathbf{x}}^{\mathsf{T}}({\mathbf{x}}^{\ast },{\mathbf{u}}^{\ast },{\mathit{\lambda }}^{\ast }),t\in [t_0,t_f],$$

(37)

$$\mathbf{0}={\int }_{t_0}^{t_f}{\mathcal{H}}_{\overline{\mathbf{u}}}^{\mathsf{T}}\mathrm{d}t,t\in [t_0,t_f],$$

(38)

$$0=\mathcal{H}({\mathbf{x}}^{\ast },{\mathbf{u}}^{\ast },{\mathit{\lambda }}^{\ast })+{\mathit{\varphi }}_t^{\mathsf{T}}{\mathit{\nu }}^{\ast },t=t_f,$$

(39)

fulfilling the boundary conditions

$$\begin{aligned} \mathbf{x}(t_{0}) & = \mathbf{x}_{0}, \\ \end{aligned}$$

(40)

$$\begin{aligned} \mathbf{x}(t_{f}) & = \mathbf{x}_{f}, \\ \end{aligned}$$

(41)

$$\begin{aligned} \boldsymbol{\lambda}(t_{f}) & = \boldsymbol{\lambda} _{f}. \end{aligned}$$

(42)

However, since the defined Hamiltonian is an autonomous system, $\frac{\mathrm{d}}{\mathrm{d} t}\mathcal{H}\left(\mathbf{x}^{*},\mathbf{u}^{*}, \boldsymbol{\lambda}^{*}\right) = \mathrm{0}$ only if an infinite number of grid nodes is used. In addition to the optimality conditions in Eq. (36)–(39), the optimal control history $\mathbf{u}^{*}$ can be evaluated in the particular case where the control appears linearly in the underlying state equation by introducing the switching function [27]

$$ h^{*}_{i}(t) = {\mathbf{f}^{\,*}_{u_{i}}}^{\mathsf{T}} \boldsymbol{\lambda}^{*}, \quad i=1,\,\dots ,\,m.$$

(43)

Following Pontryagin’s principle, three cases can be observed to express the optimal control

$$ u^{*}_{i}(t) := \left \{\textstyle\begin{array}{l@{\quad}l}u_{i,\mathrm{max}} \quad & \text{for} \quad h^{*}_{i} < 0, \\u_{i,\mathrm{min}} \quad & \text{for} \quad h^{*}_{i} > 0, \\\text{unspecified} \quad & \text{for} \quad h^{*}_{i} = 0, \end{array}\displaystyle \right . $$

(44)

where an infinite number of grid nodes $\hat{u}_{i}$ is assumed, and the dynamic behavior of the control is of the bang-bang type. Hence Eq. (43) and (44) can be used in a postprocessing step to relate the optimal control $u_{i}^{*}$ generated by a direct method with the switching functions $h_{i}$ to evaluate the solution in terms of an indirect method. If an infinite number of grid nodes is used, then the roots of the switching function exactly match the switching times of the control. Note that the optimization results of the direct approach may yield to so-called singular intervals, where the switching function is zero for a finite time interval, and Pontryagin’s principle does not provide any information on the optimal control. However, gradient-based optimization methods are appropriate to identify the control history of singular intervals [9].

3.1 Procedure for the use of the adjoint gradients

• 1. Select an initial final time $t_{f}$ and initial grid nodes $\bar{\mathbf{u}}$. In time-optimal control problems, it is numerically advantageous to use a normalized time domain $\tau =t/t_{f} \in [0,\,1]$. Derivatives with respect to the original time coordinate are given by $\mathrm{d}(\cdot )/\mathrm{d}t = 1/t_{f} \, (\cdot )'$, where the variable $(\cdot )$ is a function of the normalized time domain $\tau$.

• 2. Solve the state equations related to initial conditions

  $$ \mathbf{x}' = t_{f} \,\mathbf{f}(\mathbf{x},\mathbf{u}) \quad \text{with} \quad \mathbf{x}(0) = \mathbf{x}_{0}$$

  (45)

  using an ODE solver.

• 3. Compute the adjoint variables $\mathbf{p}(\tau )$ by solving the linear time-variant final value problem backward in time

  $$\mathbf{p}' = - t_{f} \Big( P^{\mathsf{T}}_{\mathbf{x}} + \mathbf{f}_{ \mathbf{x}}^{\mathsf{T}} \mathbf{p} \Big) \quad \text{with} \quad \mathbf{p}(1) = \mathbf{0}. $$

  (46)

• 4. Compute the adjoint variables $\mathbf{R}(\tau )$ using the matrix differential equation

  $$\mathbf{R}'= -t_{f}\,\mathbf{f}^{\mathsf{T}}_{\mathbf{x}}\mathbf{R} \quad \text{with} \quad \mathbf{R}(1) = \boldsymbol{\phi}_{\mathbf{x}}^{ \mathsf{T}}(\mathbf{x}(1),1). $$

  (47)

• 5. Compute the adjoint gradients of the cost functional and the final constraints

  $$ \nabla _{\bar{\mathbf{u}}} \, J^{\mathsf{T}} = t_{f} \int _{0}^{1} \Big( P_{\mathbf{u}} + \mathbf{p}^{\mathsf{T}} \mathbf{f}_{\mathbf{u}} \Big) \mathbf{C}\, \mathrm{d}\tau , \qquad \nabla _{\bar{\mathbf{u}}} \, \boldsymbol{\phi}^{\mathsf{T}} = t_{f} \int _{0}^{1} \mathbf{R}^{ \mathsf{T}} \mathbf{f}_{\mathbf{u}} \mathbf{C}\, \mathrm{d}\tau . $$

  (48)

• 6. Use these analytical gradients for solving the constrained optimization problem by a direct method, e.g., as shown in Section 2.1 by an SQP approach. Repeat steps (2)–(5) until the KKT conditions are satisfied and hence until an optimal solution $\mathbf{z}^{*^{\mathsf{T}}} = \big(t_{f}^{*},~\bar{\mathbf{u}}^{*^{\mathsf{T}}}\big)$ is found.

• 7. The states $\mathbf{x}^{*}$ according to the optimal control grid nodes $\bar{\mathbf{u}}^{*}$ have to be computed for evaluation of the Hamiltonian in Eq. (30). Moreover, the corresponding $\boldsymbol{\lambda}^{*}$ is obtained based on Eq. (31).

• 8. Finally, the optimality conditions in Eqs. (36)–(39) can be evaluated in terms of the Hamiltonian function.

4 Numerical examples

To show the use of the adjoint gradient approach in a direct optimization method and to evaluate the optimality conditions in a typical time-optimal control problem, we present two examples of a Selective Compliance Assembly Robot Arm (SCARA) in a rest-to-rest motion. The serial robot consists of two bodies connected with revolute joints and an additional mass is attached to the tool center point (TCP). Firstly, we only consider structural components that are modeled as rigid bodies. Secondly, the rigid bodies are replaced with flexible components. For both examples, the goal is to identify controls $u_{1}^{*}$ and $u_{2}^{*}$ ($m=2$) with a continuity requirement up to $\mathcal{C}^{2}$ such that the TCP moves from a prescribed initial state to a final state in minimal time. Minimizing the cost functional

$$\begin{aligned} & \underset{\mathbf{z}}{\text{min}}~J = t_{f} \int _{0}^{1} \Big[ 1 + P(u_{1},u_{2}) \Big]\mathrm{d}\tau \end{aligned}$$

(49)

$$\begin{aligned} & \text{s.t.}~\boldsymbol{\phi}(\mathbf{x}) = \mathbf{0} \end{aligned}$$

(50)

leads to the shortest operation period $t_{f}^{*}$ with respect to physical bounds of the controls, i.e., $-u_{i,\mathrm{max}} \leq u_{i} \leq u_{i,\mathrm{max}}$. The physical bounds are considered with penalty approach $P(u_{1},u_{2}) := \mu _{1} P_{1} + \mu _{2} P_{2}$, where the penalty function is given by

$$P_{i}(u_{i}):= \left \{\textstyle\begin{array}{l@{\quad}l}0 & \text{for} \quad \lvert u_{i} \rvert < u_{i,\mathrm{max}}, \\\frac{1}{2}(\lvert u_{i} \rvert - u_{i,\mathrm{max}})^{2}~~ & \text{otherwise}.\end{array}\displaystyle \right . $$

(51)

To ensure a continuity requirement up to $\mathcal{C}^{2}$ of the control $\mathbf{u}$ and to transform the original infinite optimization problem to a finite dimensional one, the interpolation scheme in Eq. (81) in the Appendix is used to parameterize the control. Hence the vector of optimization variables $\mathbf{z}$ consists of the final time $t_{f}$ and discrete grid nodes $\hat{\mathbf{u}}_{i}$, i.e., $\mathbf{z}^{\mathsf{T}} = \big(t_{f},\, \hat{\mathbf{u}}_{1}^{\mathsf{T}}, \,\hat{\mathbf{u}}_{2}^{\mathsf{T}}\big)$. The NLP problem is formulated as direct single shooting and solved by a standard SQP method implemented in the MATLAB function fmincon, in which the gradients of the Lagrange function in Eq. (28) and (29) are computed with the proposed adjoint method. In addition, the Hessian of the Lagrange function is computed by a BFGS method.

4.1 Rigid SCARA

4.1.1 Task description and optimization problem

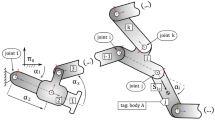
In the following example, the robot depicted in Fig. 1 is considered in the time-optimal control problem. All structural components are modeled as rigid bodies. The robot is described with a minimal set of generalized coordinates $\varphi _{1}$ and $\varphi _{2}$. The system dynamics are obtained with a coupled first-order differential equation by introducing the state variables

$$\mathbf{x}= \big(\varphi _{1},\, \varphi _{2},\, \omega _{1},\, \omega _{2}\big)^{ \mathsf{T}}, $$

(52)

where $\dot{\varphi}_{i} = \omega _{i}$. This model has been studied by several authors for time-optimal control problems, e.g., in [10]. The mass of the first body and the mass of the TCP is given by $m_{1} = m_{3} = 1~\text{kg}$, the mass of the second body is $m_{2} = 0.5~\text{kg}$, and the length of both links is $l_{1}=l_{2}=1~\text{m}$. The moment of inertia of both bodies around their centers of gravity is defined as $J_{i}=m_{i}l_{i}^{2}/12$.

Fig. 1

Planar two-arm robot with rigid bodies in a general configuration

The cost functional of the optimization problem is given in Eq. (49), and the final constraints read

$$ \boldsymbol{\phi}(\varphi _{1},\varphi _{2}, \omega _{1},\omega _{2}):=\left . \begin{pmatrix}l_{1} \cos (\varphi _{1})+l_{2}\cos (\varphi _{2}) - x_{f} \\ l_{1} \sin (\varphi _{1})+l_{2}\sin (\varphi _{2}) - y_{f} \\ \omega _{1} \\ \omega _{2}\end{pmatrix} \right |_{t=t_{f}},$$

(53)

where $x_{f}=1~\text{m}$ and $y_{f}=1~\text{m}$ denote the desired final configuration of the TCP in the workspace $\mathcal{W}$. Physical limitations of the controls are considered with the upper bounds $u_{1,\mathrm{max}}=4~\text{Nm}$ and $u_{2,\mathrm{max}}=2~\text{Nm}$. Moreover, the weights for the penalty approach are chosen as $\mu _{1}=\mu _{2}=10$. The initial conditions of the states are defined by $\mathbf{x}_{0}= (-\pi /4,\,0,\,0,\,0 )^{\mathsf{T}}$. The control $u_{i}$ is discretized with $k=50$ grid nodes and uniform intervals in the normalized time domain $\tau$, i.e., the number of optimization variables is $z = 101$. As an initial guess, the final time is taken as $t_{f}=3~\text{s}$, and the grid nodes are set to zero, $\bar{\mathbf{u}} = \mathbf{0}$.

4.1.2 Results

Figure 2 shows the time-optimal control history for both controls in the normalized time domain, where the optimized final time is given by $t_{f}^{*} = 1.8294~\text{s}$. The results are in accordance with the defined final constraints in Eq. (53), and the controls converge to bang-bang solutions with respect to the control parameterization. Note that the switching function $h_{i}$ in Eq. (43) is derived from an indirect method and evaluated in terms of the optimal SQP solution. However, the resulting switching function agrees well with the defined control in Eq. (44), and the Hamiltonian of the system is sufficiently small. The optimization result is robust with respect to initial guesses, which implies that the proposed approach converges even if the initial guess is far away from the optimal solution.

Fig. 2

Initial controls, optimal controls, and switching functions for a time-optimal rest-to-rest motion of the rigid SCARA model

Table 1 compares the number of function evaluations when numerical or adjoint gradients are used in the direct optimization method for converged solutions $\mathbf{z}^{*}$. In the table, the controls are discretized with $k=5$ and $k=50$ grid nodes each. We can see that the number of function evaluations in the case of numerical gradients is in general higher when compared to the case where analytical gradients are used. This becomes even more obvious when the number of optimization variables is increased. In addition, the computational cost is reduced for a large number of grid nodes by using adjoint gradients, since the adjoint system does not depend on the number of optimization variables. Note that the number of iterations does not depend on the way the gradients are computed, i.e., both gradients point in the same direction. To be more precise, the number of function evaluations counts the number of evaluations of the cost functional and the number of evaluations of the constraints. In the case of using finite differences, note that for each evaluation of the constraints, the state equations must be solved. Hence we observe (in general) a high computational effort. In comparison, the function evaluations for analytically derived adjoint gradients are much fewer. Here, although the calculation of the gradient is complicated, the state equations have to solved only once, and just one system of ordinary differential equations (the adjoint system) needs to be solved, which is independent of the number of grid nodes $k$. The numbers in the table are of course problem-dependent and also dependent on the solver settings, thus also on the number of iterations.

Table 1 Comparison of two different approaches to provide gradients in the SQP routine for converged solutions

4.2 Flexible SCARA

Modern robot design includes innovative lightweight techniques to reduce mass and energy consumptions in production lines. Therefore optimal control problems have to be defined for flexible multibody systems, in which the flexible components have to be able to describe large deformations during motion. Multibody systems with flexible components are often underactuated systems, and the optimal control problem becomes more complicated in comparison to fully actuated systems [32].

In this paper, we use the ANCF in the second example examining the effects due to elasticity of the SCARA. The ANCF has been developed particularly for solving large deformation problems in multibody dynamics [34]. Contrary to classical nonlinear finite element approaches used in the literature, the ANCF does not use rotational degrees of freedom and therefore does not necessarily suffer from singularities emerging from angular parameterizations. The most essential advantage of the ANCF is the fact that the mass matrix is constant with respect to the generalized coordinates. The following example is intended to show the applicability of the proposed method for solving time-optimal control problems of highly flexible multibody systems. Therefore we use a standard ANCF element, which is available and has been tested extensively in the literature; see, e.g., [1].

4.2.1 Equations of motion

Based on the proposed ANCF formulation of Berzeri and Shabana [1], a two-node element is described in the global coordinate system with the generalized coordinates

$$ \mathbf{q}^{\mathsf{T}} = \left ( {\mathbf{r}^{(1)}}^{\mathsf{T}},\, { \mathbf{r}_{\chi}^{(1)}}^{\mathsf{T}},\, {\mathbf{r}^{(2)}}^{ \mathsf{T}},\, {\mathbf{r}_{\chi}^{(2)}}^{\mathsf{T}} \right ), $$

(54)

where $\mathbf{r}^{(i)}$ denotes the nodal position vector, and $\mathbf{r}_{\chi}^{(i)}$ represents the nodal slope vector of the $i$th node. Figure 3 shows the used ANCF element in a deformed configuration including the generalized coordinates.

Fig. 3

ANCF element in a deformed configuration

An arbitrary point on the undeformed configuration is expressed as $\chi \in [0,\, l]$, where $l$ is the original length of the beam. The position vector of the beam model is defined as

$$ \mathbf{r} = \mathbf{S} \mathbf{q},$$

(55)

where the shape function matrix $\mathbf{S}$ maps the generalized coordinates into the global position vector in the reference frame of the workspace $\mathcal{W}$.

The governing equations of a single beam element require the mass matrix and generalized forces. The mass matrix of an element is defined by using the kinetic energy

$$ T=\frac{1}{2} m \int _{0}^{1} \dot{\mathbf{r}}^{\mathsf{T}} \dot{\mathbf{r}}\, \mathrm{d}\xi = \frac{1}{2} \dot{\mathbf{q}}^{ \mathsf{T}} m \int _{0}^{1} \mathbf{S}^{\mathsf{T}} \mathbf{S} \, \mathrm{d}\xi \, \dot{\mathbf{q}} = \frac{1}{2} \dot{\mathbf{q}}^{ \mathsf{T}} \mathbf{M} \dot{\mathbf{q}} $$

(56)

and the normalized beam length in the undeformed configuration $\xi = \chi /l \in [0,\, 1]$. Note that the ANCF mass matrix is constant, which leads to numerical advantages. Additionally, the elastic forces vector $\mathbf{Q}_{k}$, external applied torques $\mathbf{Q}_{u}$, and damping forces $\mathbf{Q}_{d}$ have to be defined. The elastic forces vector is defined as

$$\mathbf{Q}_{k} = \left (\frac{\partial U }{\partial \mathbf{q}} \right )^{\mathsf{T}}, $$

(57)

where the strain energy due to longitudinal and bending deformations

$$U=\frac{1}{2} l \int _{0}^{1} E\,A \varepsilon ^{2}\, \mathrm{d}\xi + \frac{1}{2} l \int _{0}^{1} E\,I \kappa ^{2}\, \mathrm{d}\xi $$

(58)

is used. Here $E$ represents the Young modulus, $A$ is the cross-sectional area, and $I$ is the second moment of area. The curvature $\kappa$ is defined with the Serret–Frenet formulas [13]

$$\kappa = \frac{| \mathbf{r}' \times \mathbf{r}'' |}{| \mathbf{r}' |^{3}}, $$

(59)

and the longitudinal strain $\varepsilon$ is formulated with the nonlinear Green–Lagrange strain measure

$$\varepsilon = \frac{1}{2} \left( \mathbf{r}^{\prime \,\mathsf{T}} \mathbf{r}' -1 \right), $$

(60)

where

$$\mathbf{r}' = \frac{\mathrm{d} \mathbf{r}}{\mathrm{d} \chi} = \frac{\mathrm{d} \mathbf{r}}{\mathrm{d} \xi} \frac{\mathrm{d} \xi}{\mathrm{d} \chi} = \frac{1}{l} \frac{\mathrm{d} \mathbf{S}}{\mathrm{d} \xi} \mathbf{q}. $$

(61)

In addition to elastic forces, the principal of virtual work due to a torque $M_{i}$ acting on the angle of rotation of the cross-section $\theta$

$$\delta W_{i}=M_{i} \delta \theta =M_{i} \frac{\partial \theta}{\partial \mathbf{q}} \delta \mathbf{q}=\mathbf{Q}_{i}^{\top} \delta \mathbf{q}, $$

(62)

leads to the generalized force $\mathbf{Q}_{i}$. Hence generalized forces associated with control $u$ and damping $f_{d} =-d\dot{\theta}$ in the revolute joint are given by

$$\begin{aligned} \mathbf{Q}_{u}=u\left (\frac{\partial \theta}{\partial \mathbf{q}}\right )^{\top}, \end{aligned}$$

(63)

$$\begin{aligned} \mathbf{Q}_{d}=f_{d}\left (\frac{\partial \theta}{\partial \mathbf{q}}\right )^{\top}, \end{aligned}$$

(64)

where $d$ is the viscous damping coefficient. Finally, the equations of motion for a single beam element can be obtained as

$$ \mathbf{M} \ddot{\mathbf{q}} + \mathbf{Q}_{k} = \mathbf{Q}_{u} + \mathbf{Q}_{d}. $$

(65)

Introducing the generalized velocities $\mathbf{v} = \dot{\mathbf{q}}$ as additional variables transforms the second-order differential equation for $\mathbf{q}$ into a first-order system

$$ \begin{pmatrix} \mathbf{I} & \mathbf{0} \\ \mathbf{0} & \mathbf{M} \\\end{pmatrix} \begin{pmatrix} \dot{\mathbf{q}} \\ \dot{\mathbf{v}} \\\end{pmatrix}=\begin{pmatrix} \mathbf{v} \\ \mathbf{Q}_{u} + \mathbf{Q}_{d} - \mathbf{Q}_{k} \\\end{pmatrix}.$$

(66)

Instead of using the augmented formulation of Eq. (65) to obtain the equations of motion for $N$ connected elements, it is possible to define an independent set of generalized coordinates to obtain the equations of motion for a constrained multibody system in the form of Eq. (66). Remark that the system Jacobians are calculated with a symbolic toolbox, simplified and factorized to reduce the complex expressions for efficient use. Note that in the two-arm SCARA example, the revolute joint between the first arm and the ground and the revolute joint between the two arms reduce the number of generalized coordinates. The following set of parameters is used in the optimization procedure: the mass of beams $m_{1} = m_{2} = 2~\text{kg}$, the beam length in undeformed configuration $l_{1} = l_{2} = 1~\text{m}$, the viscous damping coefficient $d_{1} = d_{2} = 0.1~\text{Nm/rad}$, the axial stiffness $E_{1}\,A_{1} = E_{2}\,A_{2} = 300~\text{N}$, and the bending stiffness $E_{1}\,I_{1} = E_{2}\,I_{2} = 3~\text{Nm}^{2}$. Moreover, an additional mass attached to the TCP $m_{3}=0.5~\text{kg}$ is considered, which has to be taken into account in Eq. (56) for the kinetic energy of the second beam.

4.2.2 Optimization problem

Similarly to the example in Section 4.1, the cost functional is given in Eq. (49), and the final constraints for the TCP read

$$ \boldsymbol{\phi}(\mathbf{x}):=\left . \begin{pmatrix}\mathbf{r}^{(2)} - \mathbf{x}_{f} \\\dot{\mathbf{r}}^{(2)}\end{pmatrix}\right |_{t=t_{f}}, $$

(67)

where $\mathbf{x}_{f} = \left(x_{f},\,y_{f}\right)^{\mathsf{T}}$ with $x_{f}=1~\text{m}$ and $y_{f}=1~\text{m}$ denotes the desired final configuration of the TCP in the workspace $\mathcal{W}$. The state variables of the remaining nodes are not specified and therefore free. Physical limitations of the controls are considered with the upper bounds $u_{1,\mathrm{max}}=u_{2,\mathrm{max}}=1~\text{Nm}$. The weights for the penalty approach are chosen as $\mu _{1}=\mu _{2}=50$. The initial state of the flexible SCARA is defined in the undeformed configuration as in the rigid example with $\varphi _{1} = -\pi /4~\text{rad}$ and $\varphi _{2} = 0~\text{rad}$. In this example, the control $u_{i}$ is discretized with $k=10$ grid nodes and uniform intervals in the normalized time domain $\tau$, i.e., the number of optimization variables is $z = 21$. As an initial guess, the assumption for the final time is $t_{f}=5~\text{s}$, and the grid nodes are set to zero, $\bar{\mathbf{u}} = \mathbf{0}$.

4.2.3 Results

Figure 4 shows the time-optimal control history for both controls in the normalized time domain $\tau$, where the optimized final time is given by $t_{f}^{*} = 3.7289~\text{s}$. The results are in accordance with the defined final constraints in Eq. (67), and the optimality conditions in Eqs. (36)–(39) are sufficiently small. Snapshots of the time-optimal motion are illustrated in Fig. 5, where the nodal slope vector $\mathbf{r}_{\chi}^{(i)}$ is scaled for improved representation of the structural flexibility.

Fig. 4

Initial and optimal controls for a time-optimal rest-to-rest motion of a flexible SCARA model

Fig. 5

Time-optimal control of a flexible two-arm robot for a rest-to-rest maneuver

5 Conclusion and outlook

In this paper, we presented a gradient-based technique to show a new perspective on the optimality conditions in time-optimal control problems of dynamical systems considering final constraints. Conventional solutions based on a nonlinear programming approach/SQP approach utilize the adjoint variables to assess the optimality conditions regarding the Hamiltonian function. The use of adjoint gradients for a discrete control parameterization is presented in two examples. The gradients are used to replace numerical gradients in a direct optimization method and to evaluate the optimality conditions in terms of a Hamiltonian. The present work illustrates the computational advantage especially by application of the adjoint gradients for discrete control parameterizations in time-optimal control problems of flexible multibody systems including a high number of degrees of freedom. Moreover, the comparison of function evaluations of numerical and adjoint gradients can provide a future perspective for significantly reducing the computational burden when applied to highly dimensional complex multibody system applications.

In a future work, the proposed approach can be extended to formulate the multibody system by a set of redundant coordinates similarly to [23]. Considering differential-algebraic equations requires consistent boundary conditions for the adjoint variables. A similar approach as proposed by Gear, Gupta, and Leimkuhler [11] can be used to overcome this issue.

Appendix: Formulation of cubic spline parameterization

The original infinite-dimensional optimization problem in Eqs. (1)–(3) has to be transformed into a finite-dimensional one to carry out a direct optimization method. This procedure is usually denoted as a direct transcription method [3]. In general, the literature provides various formulations that can be pursued to perform such a transformation. All methods result in a vector $\mathbf{z}$ to describe the control history. One common method is to carry out a time discretization of the control and an interpolation between the resulting subintervals; e.g., Steiner and Reichl [36] used a linear dependency between the subintervals to minimize a cost functional. A higher-order interpolation scheme is obtained using cubic splines, e.g., in [33]. In the present work, we use a cubic interpolation scheme of the control history $u(t)$:

$$\begin{aligned} &u(t) := s_{i}(t) = \hat{u}_{i} + b_{i}(t-t_{i}) + c_{i}(t-t_{i})^{2} + d_{i}(t-t_{i})^{3} \\&\text{for}~~~t\in [t_{i},\,t_{i+1}]~~~\text{with}~~~i=0,\,1,\,\dots , \,s-1, \end{aligned}$$

(68)

where $s_{i}$ is the $i$th cubic spline segment for $t\in [t_{i},\,t_{i+1}]$, and $s \in \mathbb{N}$ represents the number of piecewise defined spline functions. A given grid node is expressed with $\hat{u}_{i}$, and $\{b_{i},\,c_{i},\,d_{i}\}$ are constant spline parameters associated with the $i$th segment $s_{i}$. To determine a spline with $\mathcal{C}^{2}$ continuity, we require that

$$\begin{aligned}s_{i}(t_{i+1}) &= \hat{u}_{i+1} \\\dot{s}_{i}(t_{i+1}) &= \dot{s}_{i+1}(t_{i+1}) \\\ddot{s}_{i}(t_{i+1}) &= \ddot{s}_{i+1}(t_{i+1})\end{aligned}~~~\begin{aligned}&\text{with}~~~i=0,\,1,\,\dots ,\,s-1, \\&\text{with}~~~i=0,\,1,\,\dots ,\,s-2, \\&\text{with}~~~i=0,\,1,\,\dots ,\,s-2. \end{aligned} $$

(69)

This set of equations leads to a linear system with $h_{i} := t_{i+1}-t_{i}$:

$$\begin{aligned}\hat{u}_{i} + b_{i}h_{i} + c_{i}h_{i}^{2} + d_{i}h_{i}^{3} &= \hat{u}_{i+1} \\b_{i} + 2c_{i}h_{i} + 3d_{i}h_{i}^{2} &= b_{i+1} \\2c_{i} + 6d_{i}h_{i} &= 2c_{i+1}\end{aligned}~~~\begin{aligned}&\text{with}~~~i=0,\,1,\,\dots ,\,s-1, \\&\text{with}~~~i=0,\,1,\,\dots ,\,s-2, \\&\text{with}~~~i=0,\,1,\,\dots ,\,s-2,\end{aligned} $$

(70)

for the unknown spline parameters collected in

$$\mathbf{p}_{\mathrm{b,c,d}} = \big(b_{0},\,\dots ,b_{s-1},\,c_{0},\,\dots ,c_{s-1}, \,d_{0},\,\dots ,d_{s-1} \big)^{\mathsf{T}} \in \mathbb{R}^{3s}. $$

(71)

Since the number of linear equations $x=3s-2$ in Eq. (70) is lower than the number of unknowns $y=3s$, the linear system is underdetermined. The first and second time derivatives of the splines $s_{0}(t_{0})$ and $s_{s-1}(t_{s})$ are still undefined and can be used to determine a unique solution of the spline parameters $\mathbf{p}_{\mathrm{b,c,d}}$. One option is to prescribe the velocity of the first and last spline segment $s_{0}(t_{0})=s_{s-1}(t_{s})=0$:

$$\begin{aligned} b_{0}&=0, \end{aligned}$$

(72)

$$\begin{aligned} b_{s-1}&=-2c_{s-1}h_{s-1} -3d_{s-1}h_{s-1}^{2}. \end{aligned}$$

(73)

Now the number of linear equations is equal to the number of unknowns, and Eqs. (70)–(73) can be written in the compact form

$$ \mathbf{K}\hat{\mathbf{u}} + \mathbf{A}\mathbf{p}_{\mathrm{b,c,d}}=0, $$

(74)

where the vector $\hat{\mathbf{u}} = \left(\hat{u}_{0},\, \hat{u}_{1}, \,\dots ,\, \hat{u}_{s} \right)^{\mathsf{T}} \in \mathbb{R}^{k}$ collects all grid nodes with $k=s+1$. The coefficient matrices $\mathbf{K} \in \mathbb{R}^{3s \times k}$ and $\mathbf{A} \in \mathbb{R}^{3s \times 3s}$ can be simply determined with the underlying Eqs. (70)–(73). However, it is also possible to transform the control history in Eq. (68) into

$$u(t)=\bar{\tau}\,\mathbf{P}\mathbf{p}_{\mathrm{b,c,d}} + \bar{\delta}\hat{\mathbf{u}}, $$

(75)

where we use the abbreviations

$$\begin{aligned}\bar{\tau} = \Big( t-t_{i},\, (t-t_{i})^{2},\, (t-t_{i})^{3} \Big) \in \mathbb{R}^{3}\end{aligned} ,~~~\begin{aligned}~~~\mathbf{P} = \begin{pmatrix}\delta & \mathbf{0} & \mathbf{0} \\\mathbf{0} & \delta & \mathbf{0} \\\mathbf{0} & \mathbf{0} & \delta \end{pmatrix} \in \mathbb{R}^{3 \times 3s},\end{aligned} $$

(76)

and

$$\bar{\delta} = (\delta,\, 0 )\in \mathbb{R}^{k}. $$

(77)

The Boolean vector $\delta \in \mathbb{R}^{s}$ picks a certain quantity corresponding to the time interval $t\in [t_{i},\,t_{i+1}]$, and the components are defined by

$$\delta _{i} := \left \{\textstyle\begin{array}{l@{\quad}l}1 &\text{for}~~~t\in [t_{i},\,t_{i+1}]~~~\text{with}~~~i=0,\,1,\, \dots ,\,s-1, \\0 &\text{otherwise,}\end{array}\displaystyle \right . $$

(78)

using the Kronecker delta, e.g., $\delta = ( 0,\, 1,\, 0,\, 0 )$ for $s=4$ spline segments in the second time interval. In this sense, the Boolean matrix $\mathbf{P}$ maps all $3s$ spline parameters into those active in the $i$th time interval $t\in [t_{i},\,t_{i+1}]$. Now using Eq. (74), the control history can be expressed as a simple vector multiplication

$$ u(t) = \mathbf{c}\,\hat{\mathbf{u}} \in \mathbb{R} $$

(79)

with the time-dependent vector

$$\mathbf{c}(t) := -\bar{\tau}\mathbf{P}\mathbf{A}^{-1} \mathbf{K} + \bar{\delta} \in \mathbb{R}^{k}. $$

(80)

Note that all the information of all spline segments is given in $\mathbf{c}$. Instead of using a single control $u$, generalizations of Eq. (79) for $m$ controls are readily given by

$$ \mathbf{u}(t) = \mathbf{C}\,\bar{\mathbf{u}} \in \mathbb{R}^{m}, $$

(81)

where $\bar{\mathbf{u}}^{\mathsf{T}} = \left(\hat{\mathbf{u}}_{1}^{\mathsf{T}}, \,\dots ,\,\hat{\mathbf{u}}_{m}^{\mathsf{T}} \right) \in \mathbb{R}^{m \cdot k}$ collects all grid nodes $k$ of the $m$ control inputs, and the sparse block diagonal matrix $\mathbf{C}$ reads

$$ \mathbf{C}(t) := \begin{pmatrix}\mathbf{c} & \mathbf{0} & \cdots & \mathbf{0} \\\mathbf{0} & \mathbf{c} & \cdots & \mathbf{0} \\\vdots & \vdots & \ddots & \vdots \\\mathbf{0} & \mathbf{0} & \cdots & \mathbf{c}\end{pmatrix} \in \mathbb{R}^{m \times m \cdot k}.$$

(82)

The interpolation scheme in Eq. (81) is used in Section 2.2.2 to describe a continuous control history. The variation of grid nodes leads to

$$ \delta \mathbf{u}(t) = \mathbf{C}\,\delta \bar{\mathbf{u}}, $$

(83)

i.e., an update of the grid nodes $\delta \bar{\mathbf{u}}$ in the optimization procedure leads to an update of the control function $u(t)$, shown in Fig. 6 for a single control. It must be emphasized that all $m$ controls have to be discretized with the same number of grid nodes $k$ and time intervals $[t_{i},\,t_{i+1}]$. The discrete control parameterization can be applied for optimal control problems in direct optimization methods, but also in the same manner in indirect optimization methods.

Fig. 6

Effect of updating grid nodes $\hat{u}_{i}$ and $\hat{u}_{i+1}$ on the continuous control function $u(t)$