A review of flexible multibody dynamics for gradient-based design optimization

Abstract

Design optimization of flexible multibody dynamics is critical to reducing weight and therefore increasing efficiency and lowering costs of mechanical systems. Simulation of flexible multibody systems, though, typically requires high computational effort which limits the usage of design optimization, especially when gradient-free methods are used and thousands of system evaluations are required. Efficient design optimization of flexible multibody dynamics is enabled by gradient-based optimization methods in concert with analytical sensitivity analysis. The present study summarizes different formulations of the equations of motion of flexible multibody dynamics. Design optimization techniques are introduced, and applications to flexible multibody dynamics are categorized. Efficient sensitivity analysis is the centerpiece of gradient-based design optimization, and sensitivity methods are introduced. The increased implementation effort of analytical sensitivity analysis is rewarded with high computational efficiency. An exemplary solution strategy for system and sensitivity evaluations is shown with the analytical direct differentiation method. Extensive literature sources are shown related to recent research activities.

1 Introduction

Design optimization finds the best possible engineering design by minimizing or maximizing an objective function, while physical and mathematical design constraints are fulfilled by means of mathematical algorithms. A first study of numerical structural optimization was published in [120] where the combination of finite-element analysis with numerical optimization led to an optimal design of the now classical three-bar truss example. Significant improvements e.g. shown in [144] were achieved by the late 1990s leading to the establishing of structural and multidisciplinary design optimization as a mainstay in aerospace and mechanical engineering. This is also evident with the publication of important reference books for design optimization [9, 45, 65, 66, 68, 121, 143], which are still relevant today. While design optimization in the linear-elastic domain is well established as an industry tool, less attention has been paid to the design optimization including transient dynamics and systems with multiple bodies and their interaction. Multibody dynamics is the study and simulation of mechanisms with components that experience large rigid-body motion based on the theory of Newton, Euler, D’Alembert, and Lagrange. First applications of design optimization to multibody system analysis go back at least to [17, 18, 67, 68]. The present systematic review aims to summarize and map further developments in the field of design optimization with flexible multibody systems.

Design optimization of flexible multibody systems can be categorized into two main approaches. With the first approach, the design problem formulation is based on time-domain responses coming directly from the multibody system analysis. The second approach is based on approximation models for the optimization values such as equivalent static loading [30]. Mixed formulation in which only the sensitivities are approximated is also possible.

This review introduces the main topics for design optimization of flexible multibody dynamics and reviews concepts and studies in this field. The flexible multibody system formulations are introduced in Sect. 2. An introduction to design optimizations and an overview of optimization algorithms, optimization types, optimization formulations, and response models are given in Sect. 3. Available methods for sensitivity analysis are introduced in Sect. 4, and Sect. 5 concludes the study with a summary.

2 Flexible multibody formulations

Several formulations have been developed for the equations of motion and kinematic constraint equations of multibody systems. Before the introduction of flexible multibody dynamics, rigid multibody systems were studied. A review on rigid multibody dynamics is given in [155], and more detailed reviews on history and methods are given in [98, 119]. Flexibility is introduced to the analysis in order to consider deformations, strains, stresses, and vibrations in mechanical systems. Flexible multibody systems are generally composed of flexible—possibly in addition to rigid—bodies connected by kinematic constraints and force elements such as springs and dampers. Different formulations for flexible multibody systems are available and reviews are found in [42, 43, 57, 113, 125, 150].

We will use the following general formulation of the equation of motion for flexible multibody dynamics:

$$ \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {k}}\,\underline {q}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }=\underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}}, $$

(1)

where $\underline {q}$, $\underline {\dot {q}}$, and $\underline {\ddot {q}}$ are the generalized position, velocity, and acceleration coordinates, $\underline {\lambda }$ is the vector of Lagrange multipliers for the kinematic constraints, $\underline {\underline {m}}$ is the mass matrix, $\underline {\underline {d}}$ is the damping matrix, $\underline {\underline {k}}$ is the stiffness matrix, $J_{\underline {q}}\underline {\Phi }$ is the Jacobian matrix of the kinematic constraints vector $\underline{\Phi }$, $\underline {Q}_{\text{ext}}$ is the generalized external force vector, and $\underline {Q}_{\text{nl}}$ is a generalized force vector that contains additional nonlinear terms.

Throughout the document, the number of underlines indicates the dimension of the parameter. Symbols without underline are scalars, symbols with single underline are vectors, symbols with double underline are two-dimensional matrices, etc. Time derivatives are denoted by overdots where one overdot denotes the first time derivative and two overdots denote the second time derivative. An overline indicates that the parameter is expressed in local coordinates. Partial derivatives are denoted by $\partial$ with respect to the parameter specified in the subscript. Derivatives related to coordinates are denoted by $J$ with respect to the coordinate parameter specified in the subscript. Symbols related to optimization parameters are denoted by sans-serif symbols. Total derivatives with respect to the design variables are denoted by $\nabla _{\underline {\mathsf {x}}}$.

In a multibody system, the generalized coordinates are related by kinematic constraints, which are not to be confused with design constraints of the optimization formulation. Kinematic constraints can be categorized in holonomic and nonholonomic kinematic constraints. Holonomic kinematic constraints restrict position, velocity, and acceleration coordinates, where the velocity and acceleration constraint equations are time derivatives of the position constraint equations. Holonomic kinematic constraints reduce the number of degrees of freedom of a mechanism, and typical examples are spherical, revolute, and prismatic joints. Nonholonomic kinematic constraints restrict velocities or accelerations and cannot be integrated in time, wherefore the degrees of freedom remain unchanged. A typical example of a nonholonomic constraint is a rolling wheel. The kinematic constraints can then be further categorized by their time dependency and are referred to as scleronomous for time independence and rheonomous for time dependence.

The combination of the equations of motion and position constraint equations with the kinematic constraint vector $\underline {\Phi }$ leads to the index-3 differential–algebraic equation formulation of flexible multibody systems,

$$\begin{aligned} \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {k}}\,\underline {q}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }& =\underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}}, \\ \underline{\Phi } & =\underline{0}. \end{aligned}$$

(2)

The solution of such a system of equations is connected to numerical problems, which can be avoided by index reduction. The differentiation of the position constraint equation with respect to time leads to the velocity constraint equation and to the index-2 differential–algebraic equation formulation of flexible multibody systems given by

$$\begin{aligned} \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {k}}\,\underline {q}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }& =\underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}}, \\ J_{\underline {q}}\underline {\Phi }\,\underline {\dot {q}}+\partial _{t}\underline{\Phi } & =\underline{0}. \end{aligned}$$

(3)

The combination of the equations of motion and acceleration constraint equations leads to an index-1 differential–algebraic equation formulation of multibody systems used in many studies and textbooks such as [70, 126]. The index-1 differential–algebraic equation of flexible multibody systems is given by the following expression:

$$\begin{aligned} \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {k}}\,\underline {q}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }& =\underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}}, \\ J_{\underline {q}}\underline {\Phi }\,\underline {\ddot {q}}& =\underline {Q}_{\text{c}}, \end{aligned}$$

(4)

where $\underline {Q}_{\text{c}}$ is the right-hand side of acceleration constraints. The index-1 differential–algebraic equation of flexible multibody systems can be rewritten in matrix form,

$$ \left [ \textstyle\begin{array}{c@{\quad}c} \underline {\underline {m}}& J_{\underline {q}}\underline {\Phi }^{T}\\ J_{\underline {q}}\underline {\Phi }& \underline{\underline{0}} \end{array}\displaystyle \right ]\left [\textstyle\begin{array}{c} \underline {\ddot {q}}\\ \underline {\lambda }\end{array}\displaystyle \right ]=\left [\textstyle\begin{array}{c} \underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}}-\underline {\underline {d}}\,\underline {\dot {q}}-\underline {\underline {k}}\,\underline {q}\\ \underline {Q}_{\text{c}}\end{array}\displaystyle \right ]. $$

(5)

A significant drawback of index reduction is the associated numerical constraint drift, where small violations of the constraints at acceleration or velocity levels (or both) lead to growing errors at velocity or position level with ongoing simulation time. To combat this drift it is possible to employ stabilization techniques e.g. Baumgarte stabilization [12] which adds restoring and damping forces in $\underline {Q}_{\text{c}}$ in case of constraint violation, proportional to $\underline{\Phi }$ and $\dot{\underline{\Phi }}$. It shall be also noted that index reduction is not always necessary, since implicit integration schemes such as the Newmark-$\upbeta$ method [51, 107] and the Hilber–Hughes–Taylor method [77] (see also Sect. 2.5) can solve the index-3 or index-2 differential–algebraic equation system directly.

Another possibility for describing multibody systems is with ordinary differential equation (ODE) formulations. The equivalent rigid link system (ERLS) [146–148] is an example of such a formulation for flexible multibody systems where the equations of motion are formulated on a system level without explicit kinematic constraints. With this approach, the overall motion of a mechanism is decomposed into the rigid body motion superimposed with elastic deformation. The basis of this is an equivalent system of rigid links described with the Denavit–Hartenberg notation [37] and elastic flexibility. On the one hand, ODE formulations use a reduced number of coordinates and facilitates computations. On the other hand, ODE formulations cause loss of generality, wherefore they are not shown here.

The concentration here will be on the following three formulations of flexible multibody dynamics based on differential–algebraic equations:

• floating frame of reference formulation (FFRF),

• absolute nodal coordinate formulation (ANCF),

• absolute coordinate formulation (ACF).

Other formulations of flexible multibody dynamics used with design optimization include the nonlinear finite-element based formulation introduced by [11, 52], the flexible natural coordinates formulation introduced by [145], and the dyad method introduced by [112]. Figure 1 shows the generalized coordinates used with FFRF, ANCF, and ACF. The formulation-specific definitions will be shown in relation to the general equations of motion of flexible multibody systems shown in Eq. (1). To simplify the notation, the index of each body is omitted in the following.

Fig. 1

Generalized coordinates of flexible multibody system formulations

2.1 Floating frame of reference formulation

One of the most popular formulations is the floating frame of reference formulation (FFRF) [34, 122, 125, 127, 165, 166]. The floating frame of reference formulation can be seen as the natural extension of rigid multibody dynamics to flexibility and is mainly used to model small deformations. Though extensions of this formulation to consider large deformation are introduced in [104]. With the floating frame of reference formulation, the degrees of freedom of flexible bodies are the position and orientation coordinates of the underlying rigid bodies and superimposed flexible deformation coordinates. Flexibility is often considered as a linear problem and is solved with the finite-element method. This formulation enables model-order reduction techniques, which is often done by modal representation of deformations [167].

With FFRF, the generalized coordinates of a point on a flexible body are given by

$$ \underline {q}=\left [\textstyle\begin{array}{c@{\quad}c@{\quad}c} \underline {r}^{T} & \underline {\beta }^{T} & \overline{\underline {q}}_{f}^{T}\end{array}\displaystyle \right ]^{T}, $$

(6)

where $\underline {r}$ is the global position vector of the body reference frame, $\underline {\beta }$ is the vector of orientation coordinates of the body reference frame, and $\overline{\underline {q}}_{f}$ is the vector of elastic generalized coordinates. The position of a generic point $P$ on the body is given by

$$ \underline {r}_{P}=\underline {r}+\underline {\underline {A}}\,\overline {\underline {u}}_{P}=\underline {r}+\underline {\underline {A}}\,\left (\overline {\underline {u}}_{P,o}+\overline{\underline {\underline {S}}}\,\overline{\underline {q}}_{f}\right ), $$

(7)

where $\underline {\underline {A}}$ is the transformation matrix, $\overline {\underline {u}}_{P}$ is the local position vector, $\overline {\underline {u}}_{P,o}$ is the local position vector in the undeformed state, and $\overline{\underline {\underline {S}}}$ is the local matrix of shape functions.

The equations of motion of a system body using FFRF are given by

$$ \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {k}}\,\underline {q}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }=\underline {Q}_{\text{ext}}+\underline {Q}_{v}, $$

(8)

where $\underline {\underline {m}}$ is the mass matrix, $\underline {\underline {d}}$ is the damping matrix, $\underline {\underline {k}}$ is the stiffness matrix, $J_{\underline {q}}\underline {\Phi }^{T}$ is the Jacobian matrix of the kinematic constraints, $\underline {\lambda }$ is the vector of Lagrange multipliers, $\underline {Q}_{\text{ext}}$ is the external force vector, and $\underline {Q}_{v}$ is the quadratic velocity vector. The mass matrix in terms of the floating frame of reference is given by

$$\begin{aligned} \underline {\underline {m}}& =\left [\textstyle\begin{array}{c@{\quad}c@{\quad}c} \underline {\underline {m}}_{tt} & \underline {\underline {m}}_{tr} & \underline {\underline {m}}_{tf}\\ & \underline {\underline {m}}_{rr} & \underline {\underline {m}}_{rf}\\ \text{sym.} & & \underline {\underline {m}}_{ff} \end{array}\displaystyle \right ],\\ & =\int _{V}\rho \left [\textstyle\begin{array}{c@{\quad}c@{\quad}c} \underline {\underline {e}}& \underline {\underline {B}}& \underline {\underline {A}}\,\overline{\underline {\underline {S}}}\\ & \underline {\underline {B}}^{T}\underline {\underline {B}}& \underline {\underline {B}}^{T}\underline {\underline {A}}\,\overline{\underline {\underline {S}}}\\ \text{sym.} & & \overline{\underline {\underline {S}}}^{T}\overline{\underline {\underline {S}}} \end{array}\displaystyle \right ]\mathrm {d}V, \end{aligned}$$

(9)

where $\underline {\underline {m}}_{ff}$ is the finite-element mass matrix from linear elastodynamics, $V$ is the volume, $\rho$ is the density, $\underline {\underline {e}}$ is a unit matrix, and $\underline {\underline {B}}$ is defined by

$$ \underline {\underline {B}}=-\underline {\underline {A}}\,\tilde{\underline{\overline {\underline {u}}}}_{P}\,\overline{\underline {\underline {G}}}, $$

(10)

where $\tilde{\underline{\overline {\underline {u}}}}_{P}$ is the skew-symmetric matrix of local coordinates and $\overline{\underline {\underline {G}}}$ is a matrix that relates the local angular velocity vector and the velocity terms of the orientation parameters by

$$ \overline{\underline {\omega }}=\overline{\underline {\underline {G}}}\,\dot{\underline {\beta }}. $$

(11)

With FFRF, nonlinear terms including centrifugal and Coriolis terms are contained in the quadratic velocity vector, given by

$$\begin{aligned} \underline {Q}_{v}& =\left [\textstyle\begin{array}{c} {\underline {Q}_{v}}_{,t}\\ {\underline {Q}_{v}}_{,r}\\ {\underline {Q}_{v}}_{,f} \end{array}\displaystyle \right ],\\ & =\int _{V}\rho \left [\textstyle\begin{array}{c} -\underline {\underline {A}}\left (\tilde{\underline{\overline{\underline {\omega }}}}^{2}\,\overline {\underline {u}}_{P}+2\:\tilde{\underline{\overline{\underline {\omega }}}}\,\overline{\underline {\underline {S}}}\,\dot{\overline{\underline {q}}}_{f}-\tilde{\underline{\overline {\underline {u}}}}_{P}\,\dot{\overline{\underline {\underline {G}}}}\,\dot{\underline {\beta }}\right )\\ \overline{\underline {\underline {G}}}^{T}\tilde{\underline{\overline {\underline {u}}}}_{P}^{T}\left (\tilde{\underline{\overline{\underline {\omega }}}}^{2}\,\overline {\underline {u}}_{P}+2\:\tilde{\underline{\overline{\underline {\omega }}}}\,\overline{\underline {\underline {S}}}\,\dot{\overline{\underline {q}}}_{f}-\tilde{\underline{\overline {\underline {u}}}}_{P}\,\dot{\overline{\underline {\underline {G}}}}\,\dot{\underline {\beta }}\right )\\ -\overline{\underline {\underline {S}}}^{T}\left (\tilde{\underline{\overline{\underline {\omega }}}}^{2}\,\overline {\underline {u}}_{P}+2\:\tilde{\underline{\overline{\underline {\omega }}}}\,\overline{\underline {\underline {S}}}\,\dot{\overline{\underline {q}}}_{f}-\tilde{\underline{\overline {\underline {u}}}}_{P}\,\dot{\overline{\underline {\underline {G}}}}\,\dot{\underline {\beta }}\right ) \end{array}\displaystyle \right ]\mathrm {d}V. \end{aligned}$$

(12)

The stiffness matrix of a body in terms of FFRF is given by

$$ \underline {\underline {k}}=\left [\textstyle\begin{array}{c@{\quad}c@{\quad}c} \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\ \underline{\underline{0}} & \underline{\underline{0}} & \underline{\underline{0}}\\ \underline{\underline{0}} & \underline{\underline{0}} & \underline {\underline {k}}_{ff} \end{array}\displaystyle \right ], $$

(13)

where $\underline {\underline {k}}_{ff}$ is the finite-element stiffness matrix known from linear elastodynamics. The generalized external force vector on a body in terms of FFRF is given by

$$ \underline {Q}_{\text{ext}}=\left [\textstyle\begin{array}{c} \underline {\underline {e}}\\ {\underline {\underline {B}}}^{T}\\ {\overline{\underline {\underline {S}}}}^{T}{\underline {\underline {A}}}^{T} \end{array}\displaystyle \right ]\underline{F}_{\text{ext}}. $$

(14)

2.2 Absolute nodal coordinate formulation

Another popular formulation for flexible multibody dynamics is the absolute nodal coordinate formulation (ANCF) [57, 58, 124]. As shown in Fig. 1b, the degrees of freedom are given by the absolute nodal position coordinates and the absolute nodal slopes to model the body motion and the deformations. The absolute nodal coordinate formulation is suitable for large deformations and for structural elements such as beams and shells.

With ANCF, the global position vector is defined by

$$ \underline {r}=\underline {\underline {S}}_{g}\,\underline {q}, $$

(15)

where $\underline {\underline {S}}_{g}$ is the global shape function matrix and $\underline {q}$ is the vector of element nodal coordinates which are defined in terms of the global reference frame,

$$ \underline {q}=\left [\textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} \ldots & \underline {r}_{A}^{T} & J_{\overline{\underline {r}}}\underline {r}_{A}^{T} & \underline {r}_{B}^{T} & J_{\overline{\underline {r}}}\underline {r}_{B}^{T} & \ldots \end{array}\displaystyle \right ]^{T}, $$

(16)

where $A$ and $B$ are node indices on a flexible body (see Fig. 1b) and the nodal slopes include different cross-section directions $\overline{\underline {r}}=\left [\begin{array}{ccc} \overline{x} & \overline{y} & \overline{z}\end{array}\right ]$.

The general equation of motion for ANCF of a system body is given by

$$ \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {Q}_{\text{int}}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }=\underline {Q}_{\text{ext}}, $$

(17)

with a constant mass matrix $\underline {\underline {m}}$, the nonlinear internal force vector $\underline {Q}_{\text{int}}$, the constraint Jacobian matrix $J_{\underline {q}}\underline {\Phi }^{T}$, and the vector of generalized nodal forces $\underline {Q}_{\text{ext}}$, while centrifugal and Coriolis terms are equal to zero.

ANCF has a constant and symmetric mass matrix $\underline {\underline {m}}$ given by

$$ \underline {\underline {m}}=\int _{V}\rho \,\underline {\underline {S}}_{g}^{T}\,\underline {\underline {S}}_{g}\,\mathrm {d}V, $$

(18)

and is similar to the term $\underline {\underline {m}}_{ff}$ in FFRF, but where different shape functions are used.

When using ANCF, the internal force vector $\underline {Q}_{\text{int}}$ contains highly nonlinear stiffness terms even when a linear elastic material model is used and may include also damping terms. As shown in [57], different elastic force models have been developed. These include simplified elastic force models where transverse shear deformation is not considered [16, 54] and models with the consideration of shear and cross section deformation [108, 160].

The generalized external force vector in terms of ANCF is given by

$$ \underline {Q}_{\text{ext}}=\underline {\underline {S}}_{g}^{T}\underline{F}_{\text{ext}}. $$

(19)

2.3 Absolute coordinate formulation

The absolute coordinate formulation (ACF) defines the generalized coordinates $\underline {q}$ by the global nodal displacements composed of the sum of translational, rotational, and flexible terms,

$$ \underline {q}=\underline {q}_{t}+\underline {q}_{r}+\underline {q}_{f}=\underline {r}^{\left (n\right )}-\underline {r}_{o}^{\left (n\right )}, $$

(20)

where $\underline {r}^{\left (n\right )}$ and $\underline {r}_{o}^{\left (n\right )}$ are vectors that contain the global positions of all nodes on the body in deformed and undeformed state. The equation of motion in terms of ACF is given by [53, 55, 163]

$$ \underline {\underline {m}}_{ff}\,\underline {\ddot {q}}+\underline {\underline {A}}_{\text{bd}}\,\underline {\underline {k}}_{ff}\,\underline {\underline {A}}_{\text{bd}}^{T}\,\underline {q}_{f}+\underline {q}_{f}^{T}\,J_{\underline {q}}\underline {\underline {A}}_{\text{bd}}\,\underline {\underline {k}}_{ff}\,\underline {\underline {A}}_{\text{bd}}^{T}\,\underline {q}_{f}+J_{\underline {q}}\underline {\Phi }^{T}\,\underline {\lambda }=\underline{F}_{\text{ext}}^{\left (n\right )}, $$

(21)

where the substitution of $\underline {q}_{f}=\underline {q}-\underline {q}_{t}-\underline {q}_{r}$ and $\underline {\underline {A}}_{\text{bd}}\,\underline {\underline {k}}_{ff}\,\underline {\underline {A}}_{\text{bd}}^{T}\,\underline {q}_{t}=\underline{0}$ leads to

$$ \underline {\underline {m}}_{ff}\,\underline {\ddot {q}}+\underline {\underline {A}}_{\text{bd}}\,\underline {\underline {k}}_{ff}\,\underline {\underline {A}}_{\text{bd}}^{T}\,\underline {q}+\underline {q}_{f}^{T}\,J_{\underline {q}}\underline {\underline {A}}_{\text{bd}}\,\underline {\underline {k}}_{ff}\,\underline {\underline {A}}_{\text{bd}}^{T}\,\underline {q}_{f}-\underline {\underline {A}}_{\text{bd}}\,\underline {\underline {k}}_{ff}\,\underline {\underline {A}}_{\text{bd}}^{T}\,\underline {q}_{r}+J_{\underline {q}}\underline {\Phi }^{T}\,\underline {\lambda }=\underline{F}_{\text{ext}}^{\left (n\right )}, $$

(22)

where $\underline {q}$ is the vector of global nodal displacements, $\underline {q}_{f}$ is the vector of flexible nodal displacements, which represent the deformation of the flexible body, $\underline {\underline {A}}_{bd}$ is a block-diagonal matrix with the rotation matrices on the diagonal, $\underline {\underline {m}}_{ff}$ is the constant finite-element mass matrix, $\underline {\underline {k}}_{ff}$ is the constant finite-element small-strain stiffness matrix of the body in the reference configuration, $J_{\underline {q}}\underline {\Phi }^{T}$ is the Jacobian matrix of the kinematic constraints, and $\underline{F}_{\text{ext}}^{\left (n\right )}$ is the finite-element external force vector.

It can be noted that with ACF the rigid body motion of the flexible bodies is not described by dedicated coordinates. Therefore, the rigid body translations and rotations are calculated from the global and total displacement field. Different methods are available for these calculations and some are named in [55].

2.4 Summary of formulations

The different formulations of flexible multibody systems have different advantages and disadvantages. Table 1 shortly summarizes the main characteristics of each formulation.

Table 1 Flexible multibody formulations

Table 2 shows the system parameters of the introduced formulations. Not included into this comparison is the damping matrix and other potential nonlinear damping terms. The modeling of damping is difficult, and approximations are used often.

Table 2 Comparison of system parameters of FMBS formulations: extension and simplification of comparison shown in [163]

2.5 Time integration

System equations of multibody dynamics are solved in time with numerical time integration. Explicit and implicit time integration methods are available. Implicit methods enable larger time steps without stability issues and therefore are widely used in multibody dynamics. Time integration methods include the backward difference formula [33, 75], the Runge–Kutta methods [20, 21, 84, 85], and the generalized-$\upalpha$ method [5, 32], which is a generalization of multiple methods including the Newmark-$\upbeta$ method [51, 107] and the Hilber–Hughes–Taylor method [77]. The application to multibody dynamics of many of the time integration methods above including the adjoint variable method for sensitivity computations is shown in [20]. Other options for time integration are variational integrator and energy decaying [22, 26]. The use of time integration methods in combination with design optimization of flexible multibody dynamics is shown in Table 3. Time integration is especially important within design optimization as the sensitivities must also be integrated with respect to time (see Sect. 4).

Table 3 Time integration methods in design optimization of flexible multibody systems

Here the predictor–corrector implementation of time integration is shown with the classical Newmark-$\upbeta$ method where the accelerations are taken as primary variables. At each time step, the positions and velocities are predicted by

$$\begin{aligned} \underline{q}{}_{\text{pred}} & =\underline{q}_{n}+\Delta t\underline{\dot{q}}_{n}+\left (\frac{1}{2}-\beta \right )\Delta t^{2}\underline{\ddot{q}}_{n}, \end{aligned}$$

(23)

$$\begin{aligned} \underline{\dot{q}}{}_{\text{pred}} & =\underline{\dot{q}}_{n}+\left (1-\gamma \right )\Delta t\underline{\ddot{q}}_{n}. \end{aligned}$$

(24)

These predictors are used to update the system vectors, and matrices $\underline {\underline {m}}$, $\underline {\underline {d}}$, $\underline {\underline {k}}$, $\underline {Q}_{\text{ext}}$, $\underline {Q}_{\text{nl}}$, $J_{\underline {q}}\underline {\Phi }$ and $\underline {Q}_{\text{c}}$ before Eq. (5) is solved for accelerations. The accelerations are then used to update the predicted positions and velocities,

$$\begin{aligned} \underline{q}_{n+1} & =\underline{q}_{\text{pred}}+\beta \Delta t^{2}\underline{\ddot{q}}_{n+1}, \end{aligned}$$

(25)

$$\begin{aligned} \underline{\dot{q}}_{n+1} & =\underline{\dot{q}}_{\text{pred}}+\gamma \Delta t\underline{\ddot{q}}_{n+1}. \end{aligned}$$

(26)

2.6 Nonlinear solver

Since the system vectors and matrices ($\underline {\underline {m}}$, $\underline {\underline {d}}$, $\underline {\underline {k}}$, $\underline {Q}_{\text{ext}}$, $\underline {Q}_{\text{nl}}$, $J_{\underline {q}}\underline {\Phi }$ and $\underline {Q}_{\text{c}}$) depend on the state variables $\underline {q}$, $\underline {\dot {q}}$, a nonlinear solver is needed when an implicit integration method is employed, since in this case $\underline {q}$ and $\underline {\dot {q}}$ are functions of the acceleration $\underline {\ddot {q}}$ of the unknown time step, see Eqs. (25) and (26). Though the methodology is general, here the Newton–Raphson method is used to solve for the residual vector given by

$$ \underline {R}=\left [\textstyle\begin{array}{cc} \underline {\underline {m}}& J_{\underline {q}}\underline {\Phi }^{T}\\ J_{\underline {q}}\underline {\Phi }& \underline{\underline{0}} \end{array}\displaystyle \right ]\left [\textstyle\begin{array}{c} \underline {\ddot {q}}\\ \underline {\lambda }\end{array}\displaystyle \right ]-\left [\textstyle\begin{array}{c} \underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}}-\underline {\underline {d}}\,\underline {\dot {q}}-\underline {\underline {k}}\,\underline {q}\\ \underline {Q}_{\text{c}}\end{array}\displaystyle \right ]=\underline{0}. $$

(27)

The application of the Newton–Raphson method leads to

$$ \left [\textstyle\begin{array}{cc} J_{\underline {\ddot {q}}}\underline {R}& J_{\underline {\lambda }}\underline {R}\end{array}\displaystyle \right ]\left [\textstyle\begin{array}{c} \Delta \underline {\ddot {q}}\\ \Delta \underline {\lambda }\end{array}\displaystyle \right ]+\underline {R}=\underline{0}, $$

(28)

which is solved for the incremental updates of the acceleration $\Delta \underline {\ddot {q}}$ and Lagrangian multipliers of the kinematic constraints $\Delta \underline {\lambda }$.

The linear Eq. (28) may be solved with direct or iterative solvers, see [136] for a detailed discussion of solution methods for linear systems. Although iterative schemes may be more efficient for large systems, their convergence depends on the properties of the iteration matrix, in this case the tangent matrix of Newton’s method, in combination with iterative solvers referred to as inexact Newton method [36]. The properties and therefore the convergence may be improved significantly with preconditioning [136].

3 Design optimization of flexible multibody systems

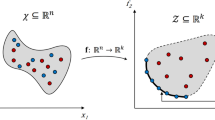
Design optimization is the application of mathematical algorithms where a set of design variables is modified to find a minimum value of an objective function while mathematical or physical design constraints are fulfilled [10, 65]. A general optimization formulation is given by the following equations:

$$\begin{aligned} \underset{\underline {\mathsf {x}}\epsilon \chi }{\text{minimize}}\quad & \mathsf {f}\left (\underline {\mathsf {x}}\right ), \end{aligned}$$

(29)

$$\text{subject to}{\mathsf{g}}_j\left(\underset{\_}{\mathsf{x}}\right)\le 0,j=1,\dots ,n_{\mathsf{g}}$$

(30)

$$\text{and}{\mathsf{h}}_k\left(\underset{\_}{\mathsf{x}}\right)=0,k=1,\dots ,n_{\mathsf{h}}$$

(31)

$$\text{with}\chi =\{{\mathsf{x}}_iϵ{\mathbb{R}}^{n_{\mathsf{x}}}:{\mathsf{x}}_i^L\le {\mathsf{x}}_i\le {\mathsf{x}}_i^U\},i=1,\dots ,n_{\mathsf{x}}$$

(32)

where $\underline {\mathsf {x}}$ is the vector of design variables, $\chi$ is the design domain defined by the upper bounds $\mathsf {x}^{U}$ and lower bounds $\mathsf {x}^{L}$ of the design variables, $\mathsf {f}$ is the objective function, $\mathsf {g}_{j}$ is an inequality design constraint function, and $\mathsf {h}_{k}$ is an equality design constraint function. Especially when solving with gradient-based optimization algorithms (Sect. 3.1), we speak of the primal analysis to calculate the system responses (see Sect. 3.4) and the sensitivity analysis to calculate the gradients (or design sensitivities, see Sect. 4). Figure 2 shows the flow chart of design optimization with multibody systems. Design updates and system evaluations are repeated until an optimal design is reached.

Fig. 2

Flow chart of design optimization with multibody systems

3.1 Optimization algorithms

Different optimization algorithms are available and are classified into gradient-based and zeroth-order algorithms (i.e. nongradient-based algorithms). With zeroth-order algorithms, no gradient information is required. Zeroth-order algorithms use either deterministic heuristic approaches or random-based approaches. The latter include biology-inspired heuristic algorithms such as genetic algorithms, evolutionary strategies, particle swarm, bee hive, and ant hill [158]. Typically, many system evaluations are required to reach an optimum, and due to the stochastic nature, repeated optimization runs may lead to different results [158]. An optimum may never be reached, and there is no check to verify if an optimum has been reached. Algorithms of this family can typically handle multimodal space and some algorithms can handle multiobjective problems e.g. [35], though gradient-based methods can also be successfully employed with multiple objectives e.g. [118].

Gradient-based algorithms are further divided into first-order algorithms and second-order algorithms and require the derivatives of objective and design constraint functions with respect to the design variables. With first-order algorithms, the first derivatives are utilized, and with second-order algorithms, the Hessian matrix is used additionally. In the latter, the Hessian can also be calculated from first derivatives via efficient algorithms e.g. Bryoden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [23, 49, 61, 128]. Gradient-based algorithms use the Karush–Kuhn–Tucker (KKT) optimality criteria to mathematically verify if an optimum has been reached [82, 89]. In the case of a nonconvex design domain, gradient-based algorithms may lead to a local optimum. In such cases, multiple optimization runs can be performed with different initial designs to increase the probability of reaching the global optimum. The required number of evaluations with gradient-based algorithms is drastically lower compared to nongradient-based algorithms [65], especially when providing analytical sensitivities. This is the case even when repeating optimization runs with different initial design.

Figure 3 shows an overview of the classification of optimization algorithms. Table 4 lists publications of design optimizations with flexible multibody dynamics where zeroth-order algorithms and gradient-based algorithms are used.

Fig. 3

Optimization algorithms

Table 4 Optimization algorithms used with flexible multibody dynamics

3.2 Types of design optimization

Design optimization is categorized by the type of design variables, especially with respect to the underlying model. As flexible multibody systems are based on finite-element modeling, we will retain the categorization from structural design optimization and expand upon this:

• parameter: parameters that describe the model, including friction, force as well as mass, damping, and stiffness (e.g. lumped parameter models);

• sizing: cross-sectional areas of bars and beams, thickness of plates and shells, also composite parameters for fiber-reinforced materials;

• shape: nodal positions of bars, beams, plates, shells, and solid elements;

• topology: material present or not, typically carried out by density of elements via the Solid Isotropic Material Parametrization (SIMP) method;

• material: material selection of structural components.

It is also possible to have mixed types of design optimization.

In flexible multibody dynamics, design optimization has seen limited usage. Table 5 lists the publications where the different types of design optimizations have been used. Parameter optimization was handled rarely. Studies including sizing optimization are found in more publications. Shape optimization is further categorized in node-based and morphing, of which the former has design variables that control each nodal position and morphing has variables that control a shape function, which in turn controls the nodal position. Morphing typically needs fewer design variables, while node-based shape optimization requires filter methods to avoid nonphysical designs. Shape optimization in concert with flexible multibody dynamics is found in a few publications. Topology optimization finds the optimal placement of material within a design space. The most common approach for topology optimization continualizes the space between void and full material via solid isotropic material with penalization (SIMP) developed by [13, 14] and thoroughly explained in [15]. The level set approach is a further method for topology optimization. Topology optimization with flexible multibody systems was studied in many publications, and also combined approaches are found.

Table 5 Types of design optimization used with flexible multibody dynamics

Table 5 shows the formulation of flexible multibody dynamics used in combination with the different types of design optimization. The consequences of the formulation of flexible multibody dynamics for the type of design optimization have not been thoroughly explained, and future research is needed. The formulation of flexible multibody dynamics and the corresponding element type limit the type of design optimization that can be employed, cf. Table 1. FFRF is used in combination with all types of design optimization. ANCF is primarily used with parameter optimization and sizing, which does not imply that it cannot be used with other types of design optimization, as the recent applications to topology optimization show. ACF was recently introduced and has therefore seen limited usage in combination with design optimization. Other formulations of flexible multibody dynamics include the nonlinear finite-element based formulation [22, 24, 26, 137–139, 141, 149], the flexible natural coordinate formulation [6, 7], and the dyad method [1, 87].

3.3 Design optimization formulations for flexible multibody systems

Dealing with flexible multibody systems, two general problem formulation families are identified: optimal control of mechanisms and structural optimization of components [140]. Using the formulation of optimal control of mechanisms, the driving forces and moments are changed to fulfill an optimality criterion on the motion of the mechanism such as trajectory optimizations [8]. With structural optimization, structural parameters of mechanism components are modified to fulfill design requirements. A typical structural optimization formulation is the minimization of the mass by modifying structural parameters and not exceeding maximum stress requirements. This work focuses on structural optimization. The design optimization of flexible multibody systems is a complex topic since the system evaluations are influenced by many effects like body motion, flexible deformation, inertia, vibration, loading, and time integration. Formulations of the optimization problem may fail or lead to nonrobust optimizations and problems with convergence [138]. Research is needed for the capabilities and consequences of the choice of flexible multibody formulations in concert with different design optimization formulations. Physical parameters used to define objective and design constraint functions in design optimizations for flexible multibody systems are given in the following [138]:

• stiffness or compliance,

• mass,

• stress or strain,

• time needed for specified task or behavior,

• energy consumption,

• comparison to ideal behavior (e.g. trajectory).

It is possible to formulate the design problem generally as an optimization problem in which the objective and optimization constraint functions are functions of the dynamical behavior. These performance measures are formulated as the sum of the behavior at the initial state $\mathcal {F}_{0}$, the final state $\mathcal {F}_{f}$, and an integral of a performance function ℱ in a defined time interval $\left [t_{0},\,t_{f}\right ]$ [6, 18, 19, 24],

$$ \Psi \left (\underline {\mathsf {x}}\right )=\mathcal {F}_{0}\left (\underline {\mathsf {x}},\underline {q}_{0},\underline {\dot {q}}_{0},\underline {\ddot {q}}_{0},t_{0}\right )+\int _{t_{0}}^{t_{f}}\mathcal {F}\left (\underline {\mathsf {x}},\underline {q},\underline {\dot {q}},\underline {\ddot {q}},t\right )dt+\mathcal {F}_{f}\left (\underline {\mathsf {x}},\underline {q}_{f},\underline {\dot {q}}_{f},\underline {\ddot {q}}_{f},t_{f}\right ). $$

(33)

This rather general formulation of objective and optimization constraint functions enables a great variety of optimization formulations. In the following, typical optimization formulations and their design variables, objective functions, and optimization constraint functions are shown in a more specific manner. It is possible to mix these formulations and combine them with other design optimization formulations.

A possible design optimization formulation of flexible multibody systems is the lightweight formulation. The minimization of the mass in general improves the behavior and the performance of a mechanism since reduced weight reduces costs, loads on kinematic joints, energy consumption and positively affects vibrations. Strain and stress are often used as constraints and material limits (including safety factors) cannot be exceeded to avoid failure of components. With the lightweight formulation, geometric parameters like cross sections of beams or thickness of shell elements are used as design variables.

Another possible design optimization formulation of flexible multibody systems is a compliance formulation. The maximization of stiffness or the minimization of compliance reduces deflections and in most cases positively affects vibrations. Topology optimization is based on the finite element method, and the material distribution inside the components is used as design parameters. Examples of design constraints of topology optimization are the maximum amount of mass which can be distributed or the maximum stress which is allowed inside the components.

Other optimization formulations are possible in regard of the control of the mechanism where the actuator forces and moments are used typically as design variables. Possible objective functions include the minimization of time or the minimization of energy consumption to perform a defined task. If an ideal behavior of the mechanism is known, a comparison between the actual design and the ideal behavior can be performed. This enables for example to consider deflections and vibrations of flexible multibody systems in the comparison of the actual and the ideal trajectory of a manipulator. Therefore, the error $\epsilon$ between the actual design and the ideal behavior can be computed for each time step. The minimization of the time integration of this error $\epsilon$ can be used as an objective function. Another possibility is to define a design constraint function where the maximum value of the error $\epsilon$ must not exceed a defined limit. A comparison of the main design optimization formulations with flexible multibody dynamics, showing their design objectives, design variables, and design constraints is given in Table 6. The application of flexible multibody dynamics enables mixed optimization formulations where e.g. optimal control and lightweight-design are combined.

Table 6 Main design optimization formulations of flexible multibody systems

The formulation and aggregation of design constraints plays a large role in optimization with flexible multibody systems. Function aggregation includes p-norm and the Kreisselmeier–Steinhauser function [88] to approximate the maximum value with a differentiable function. These methods are reviewed in [83, 86, 90]. Dynamic responses represent special challenges for the design optimization and are reviewed and used in [114, 154].

3.4 Response models in design optimization

Flexible multibody dynamics can exhibit high computational effort and as such the necessary time can limit the application of design optimization. Therefore beyond using the full multibody simulation in optimization process for the primal and sensitivity analyses, there are approximation-based methodologies. Both these methodologies can be carried out with or without updating during the optimization process. Figure 4 shows a summary of response models used for the design optimization formulation in flexible multibody dynamics.

Fig. 4

Response models used as basis for design optimization of flexible multibody systems

Mathematical approximations or surrogate modeling utilize only statistical data and no mechanical or physics-based model, though the statistical data may be generated with such a model. This is performed using a design of experiments e.g. Latin hypercube to sample the design domain, and the results are then modeled using a mathematical function. Examples of mathematical functions include linear and quadratic polynomial regression, Kriging, radial basis functions, neural networks (i.e. deep learning), amongst others. An overview of mathematical approximations can be found in [50]. Update schemes for mathematical approximations that improve the quality of the approximation during the optimization process can be found in [50, 156, 157].

Beyond the mathematical approximations there are physical approximations where a reduced physics-based model with less computational effort is used. These methods include model-order reduction and equivalent static loading (ESL). ESL, originally devised by [30, 31, 80], has found usage in crash optimization [153] as well as for flexible multibody optimization [6, 59, 60, 72, 81, 93, 100, 101, 123, 131, 132, 134]. Table 7 shows the categorization of response models.

Table 7 Categorization of response models

4 Design sensitivity analysis of flexible multibody systems

After a general introduction, sensitivity analysis applied to multibody dynamics will be addressed following the breakdown in the three parts of the multibody solving routine proposed by [152]: governing equations, time integration, and nonlinear solver. Figure 5 shows the solver routine for multibody dynamics including the sensitivity analysis with the direct differentiation method and the equations will be shown in the following. The scope is limited to the discrete sensitivity analysis, also known as discretize-then-differentiate [21, 26, 44, 91, 142]. By contrast, the continuous sensitivity analysis first differentiates the continuum system, then discretizes (i.e. differentiate-then-discretize). Flexible multibody dynamics includes both spatial as well as temporal discretization. Although continuous sensitivity analysis typically results in a simpler system, it requires proper formulation of the original continuous system, including boundary conditions, which may not exist [110].

Fig. 5

Solve routine including sensitivity analysis of a multibody system

4.1 General sensitivity analysis

Gradient-based optimization utilizes the gradients to calculate the design of the next iteration. Gradients are the derivative of the optimization functions i.e. objective and design constraint functions with respect to the design variables and are therefore also referred to as design sensitivities. They are defined by the nabla $\nabla$ operator,

$$ \nabla _{\underline {\mathsf {x}}}\mathcal {F}=\left .\frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\underline {\mathsf {x}}}\right |_{\underline {\mathsf {x}}^{\left (k\right )}}, $$

(34)

where ℱ is a generic optimization function and $\underline {\mathsf {x}}$ is the design variable vector, which is evaluated at the design variables at the $k$th iteration $\underline {\mathsf {x}}^{\left (k\right )}$. The process of calculating these is referred to as sensitivity analysis, when remaining general, or design sensitivity analysis, when specifically referring to gradients with respect to the design variables of design optimization. Accurate and efficient sensitivity analysis is crucial for gradient-based design optimization and their computational effort. Overviews on sensitivity analysis are found in [99, 135, 142]. Although second-order sensitivities (Hessian) can be derived and provided to second-order optimization algorithms, sensitivity analysis is typically limited to first-order sensitivities and as such, this is the case in this study.

The main categories of sensitivity analysis are numerical, analytical, complex step, and automatic differentiation. Further there is the numerical–analytical method, mixing both types, that is referred to as semi-analytical. The analytical family is especially important and is further categorized in the direct differentiation method and the adjoint variable method. We categorize the different methods for sensitivity analysis in the hierarchical organization found in Fig. 6.

Fig. 6

Categorization for types of design sensitivity analysis

In terms of implementation, the simplest form of sensitivity computations is the numerical method with finite differences, via forward, backward, or central differencing,

$$\begin{aligned} \left .\frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\mathsf {x}_{i}}\right |_{\underline{x}^{\left (k\right )}} & \approx \frac{\mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}+\underline{e}_{i}\Delta \mathsf {x}_{i}\right )-\mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}\right )}{\Delta \mathsf {x}_{i}}, \end{aligned}$$

(35)

$$\begin{aligned} \left .\frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\mathsf {x}_{i}}\right |_{\underline{x}^{\left (k\right )}} & \approx \frac{\mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}\right )-\mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}-\underline{e}_{i}\Delta \mathsf {x}_{i}\right )}{\Delta \mathsf {x}_{i}}, \end{aligned}$$

(36)

$$\begin{aligned} \left .\frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\mathsf {x}_{i}}\right |_{\underline{x}^{\left (k\right )}} & \approx \frac{\mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}+\underline{e}_{i}\Delta \mathsf {x}_{i}\right )-\mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}-\underline{e}_{i}\Delta \mathsf {x}_{i}\right )}{2\Delta \mathsf {x}_{i}}, \end{aligned}$$

(37)

respectively. Although the implementation of numerical sensitivities is simple, an additional system evaluation must be performed for each design variable, which drastically increases the computational effort. Due to the introduction of a discrete difference of the perturbation of $\Delta \mathsf {x}$, this method is inherently less accurate. In general, the smaller the perturbation, the more accurate the sensitivities. This is true until the machine epsilon is reached where the unit roundoff distorts the results and therefore a compromise must be found for the choice of the perturbation size. The appropriate range of the perturbation size may differ for different design variables and optimization functions, see e.g. [152], making the choice of the perturbation size even more challenging. Numerical sensitivities have been utilized in [38, 46, 47, 138] for the design optimization of flexible multibody systems.

More efficient for sensitivity computations are analytical methods, namely the direct differentiation method and the adjoint variable method. Direct sensitivity analysis is based on the direct derivation of the system equations $\mathcal {F}\left (\underline {\mathsf {x}},\underline{\mathsf{y}}\left (\underline {\mathsf {x}}\right )\right )$, which depends on design variables $\underline {\mathsf {x}}$ and on additional parameters $\underline{\mathsf{y}}$ that in turn are dependent on $\underline {\mathsf {x}}$, making use of the chain rule

$$ \frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\underline {\mathsf {x}}}=\frac{\partial \mathcal {F}}{\partial \underline {\mathsf {x}}}+\frac{\partial \mathcal {F}}{\partial \underline{\mathsf{y}}}\frac{\mathsf{d}\underline{\mathsf{y}}}{\mathsf{d}\underline {\mathsf {x}}}. $$

(38)

In the solution of multibody dynamics this is carried out with the residual equation,

$$ \frac{\mathsf{d}\underline{R}}{\mathsf{d}\underline {\mathsf {x}}}=\frac{\partial \underline{R}}{\partial \underline {\mathsf {x}}}+\frac{\partial \underline{R}}{\partial \underline{\mathsf{y}}}\frac{\mathsf{d}\underline{\mathsf{y}}}{\mathsf{d}\underline {\mathsf {x}}}=\underline{0}, $$

(39)

in which the function of interest is calculated in the balance equation (or derived from a function calculated here).

Adjoint sensitivity is based on the sensitivity of the residual of the system of equations, which we rearrange

$$ \frac{\mathsf{d}\underline{\mathsf{y}}}{\mathsf{d}\underline {\mathsf {x}}}=-\left (\frac{\partial \underline{R}}{\partial \underline{\mathsf{y}}}\right )^{-1}\frac{\partial \underline{R}}{\partial \underline {\mathsf {x}}} $$

(40)

and substitute in the original function

$$ \frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\underline {\mathsf {x}}}=\frac{\partial \mathcal {F}}{\partial \underline {\mathsf {x}}}\overset{\underline{\Lambda}}{\overbrace{-\frac{\partial \mathcal {F}}{\partial \underline{\mathsf{y}}}\left (\frac{\partial \underline{R}}{\partial \mathsf{\underline{y}}}\right )^{-1}}}\frac{\partial \underline{R}}{\partial \underline {\mathsf {x}}}, $$

(41)

where $\underline{\Lambda}$ is the vector of Lagrangian multipliers which is solved by the adjoint equation

$$ \underline{\Lambda}\frac{\partial \underline{R}}{\partial \underline{\mathsf{y}}}=-\frac{\partial \mathcal {F}}{\partial \underline{\mathsf{y}}}. $$

(42)

This adjoint system is integrated backwards in time and relies on the primal values calculated forward in time. For this reason the adjoint variable method is also referred to as reverse sensitivity analysis (and direct differential as forward sensitivity analysis in contrast). The solving of the adjoint equations therefore constitutes a terminal-value problem [142]. This presents issues in regards to the use of adaptive time integration methods [3], stability [19, 94, 116, 117], and information must be stored during the forward integration of the equations of motion, which is then required by the backward integration of the adjoint equations [18, 29]. For further information, the reader is referred to the following papers: [20, 27, 40, 74, 102, 105].

Although both direct and adjoint methods have a higher implementation effort, this is rewarded by decreased computation effort (time). If the number of system responses including objective function and design constraints is higher than the number of design variables, the direct differentiation method should be used. If instead the number of design variables is higher than the number of system responses, the adjoint variable method is more efficient.

Semi-analytical sensitivities are a mixed form in which the governing equations are differentiated analytically while the individual system parameters (i.e. system matrices) are differentiated numerically. This saves the implementation of analytical sensitivities for all possible cases or the use of automatic differentiation. The semi-analytical method comes though with the cost of numerical sensitivities of these terms, albeit significantly reducing the computational effort with respect to a numerical sensitivity analysis in concert with perturbation through the full solve routine. Here, part of the chain rule is calculated via finite differencing e.g. for the direct method:

$$ \frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\underline {\mathsf {x}}}\approx \frac{\partial \mathcal {F}}{\partial \underline {\mathsf {x}}}+\frac{\partial \mathcal {F}}{\partial \underline{\mathsf{y}}}\frac{\Delta \underline{\mathsf{y}}}{\Delta \underline {\mathsf {x}}}. $$

(43)

The complex-step method of sensitivity analysis in which the perturbation is carried out with the imaginary value $j\Delta \mathsf {x}_{i}$ originates in [95, 96, 130],

$$ \left .\frac{\mathsf{d}\mathcal {F}}{\mathsf{d}\mathsf {x}_{i}}\right |_{\underline {\mathsf {x}}^{\left (k\right )}}\approx \frac{\Im \left \{ \mathcal {F}\left (\underline {\mathsf {x}}^{\left (k\right )}+\underline{e}_{i}j\Delta \mathsf {x}_{i}\right )\right \} }{\Delta \mathsf {x}_{i}}. $$

(44)

The programming language and implementation though must permit calculations in complex arithmetic. This method was found only to be scantily used for the sensitivity analysis of flexible multibody systems e.g. by [26].

Automatic differentiation (also known as algorithmic differentiation and computational differentiation) differentiates the operations of computer code via the chain rule. This method has found limited application to the differentiation of the primal equations of flexible multibody systems e.g. [4, 25, 63]. However, automatic differentiation can be used to compute partial terms of the system parameters in the sensitivity equations [4], see Sect. 4.2.

There are also other methods, such as symbolic differentiation, that will not be discussed here. See the literature for more details [99, 135, 142].

Many studies on the application of sensitivity analysis to multibody dynamics have been performed. First uses of sensitivity analysis in rigid multibody dynamics are found in [67, 69, 129], shown also in [161]. Sensitivity analysis in combination with design optimization of flexible multibody systems is shortly reviewed in [140], and Table 8 shows the use of sensitivity methods in related publications. The most frequently used sensitivity methods are the adjoint variable method and the direct differentiation method. Numerical differentiation, the complex step method, and automatic differentiation are rarely used but serve often to check the correctness of used methods.

Table 8 Sensitivity analysis

4.2 Sensitivity analysis for governing equations

In order to illustrate the general introduction of sensitivity analysis above, the direct differentiation method is introduced. The equations of motion are differentiated with direct differentiation, avoiding the issues related to the terminal-value problem when using the adjoint variable method, see Sect. 4.1.

The sensitivity analysis is based on the general formulation of the equation of motion for flexible multibody dynamics,

$$\begin{aligned} \underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {k}}\,\underline {q}+J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }& =\underline {Q}_{\text{ext}}+\underline {Q}_{\text{nl}},\\ J_{\underline {q}}\underline {\Phi }\,\underline {\ddot {q}}& =\underline {Q}_{\text{c}}, \end{aligned}$$

from which we take the total derivative with respect to the design variables

$$\begin{aligned} \nabla _{\underline {\mathsf {x}}}\underline {\underline {m}}\,\underline {\ddot {q}}+\underline {\underline {m}}\,\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}+\nabla _{\underline {\mathsf {x}}}\underline {\underline {d}}\,\underline {\dot {q}}+\underline {\underline {d}}\,\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}+\nabla _{\underline {\mathsf {x}}}\underline {\underline {k}}\,\underline {q}+\underline {\underline {k}}\,\nabla _{\underline {\mathsf {x}}}\underline {q}+\qquad \\ \nabla _{\underline {\mathsf {x}}}J_{\underline {q}}\underline {\Phi }^{T}\underline {\lambda }+J_{\underline {q}}\underline {\Phi }^{T}\nabla _{\underline {\mathsf {x}}}\underline {\lambda }& =\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{ext}}+\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{nl}} \end{aligned}$$

(45)

$$\begin{aligned} \nabla _{\underline {\mathsf {x}}}J_{\underline {q}}\underline {\Phi }\,\underline {\ddot {q}}+J_{\underline {q}}\underline {\Phi }\,\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}& =\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{c}}, \end{aligned}$$

(46)

and rewrite these equations to matrix form where the system matrices sensitivities are moved to the right-hand side to define the pseudo load case

$$\begin{array}{c}\left[\begin{array}{cc}\underset{\_}{\underset{\_}{m}}& J_{\underset{\_}{q}}{\underset{\_}{\mathrm{\Phi }}}^T\\ J_{\underset{\_}{q}}\underset{\_}{\mathrm{\Phi }}& \underset{\_}{\underset{\_}{0}}\end{array}\right]\left[\begin{array}{c}{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{\ddot{q}}\\ {\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{\lambda }\end{array}\right]=\hfill \\ \hfill \underset{{\underset{\_}{\underset{\_}{Q}}}_{\mathrm{pseudo}}}{\underbrace{\left[\begin{array}{c}{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}{\underset{\_}{Q}}_{\text{ext}}+{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}{\underset{\_}{Q}}_{\text{nl}}-{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{\underset{\_}{m}}\underset{\_}{\ddot{q}}-{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{\underset{\_}{d}}\underset{\_}{\dot{q}}-\underset{\_}{\underset{\_}{d}}{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{\dot{q}}-{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{\underset{\_}{k}}\underset{\_}{q}-\underset{\_}{\underset{\_}{k}}{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}\underset{\_}{q}-{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}{J}_{\underset{\_}{q}}{\underset{\_}{\mathrm{\Phi }}}^T\underset{\_}{\lambda }\\ {\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}{\underset{\_}{Q}}_{\text{c}}-{\mathrm{\nabla }}_{\underset{\_}{\mathsf{x}}}{J}_{\underset{\_}{q}}\underset{\_}{\mathrm{\Phi }}\underset{\_}{\ddot{q}}\end{array}\right]}},\end{array}$$

(47)

to reveal the following equation, which will be used throughout:

$$ \left [\textstyle\begin{array}{c@{\quad}c} \underline {\underline {m}}& J_{\underline {q}}\underline {\Phi }^{T}\\ J_{\underline {q}}\underline {\Phi }& \underline{\underline{0}} \end{array}\displaystyle \right ]\left [\textstyle\begin{array}{c} \nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}\\ \nabla _{\underline {\mathsf {x}}}\underline {\lambda }\end{array}\displaystyle \right ]=\underline{\underline{Q}}{}_{\mathrm{pseudo}}. $$

(48)

As this equation is of the same form as the governing equation in the primal analysis, the same calculation routine is used. The initial conditions for the primal analysis and the sensitivity analysis must be provided at the start of the time integration. The initial sensitivities and their time derivatives can be derived with automatic differentiation or with numerical differentiation [4].

Sensitivity analysis necessitates the determination of the sensitivities of the system parameters

$$ \nabla _{\underline {\mathsf {x}}}\underline {\underline {m}},\;\nabla _{\underline {\mathsf {x}}}\underline {\underline {d}},\;\nabla _{\underline {\mathsf {x}}}\underline {\underline {k}},\;\nabla _{\underline {\mathsf {x}}}J_{\underline {q}}\underline {\Phi },\;\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{ext}},\;\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{nl}},\;\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{c}}. $$

(49)

The dependencies of the system parameters may change with different formulations of the equations of motion. This must be considered when applying the chain rule to the differentiation of the system parameters.

For example, assuming the mass matrix depends on the design variables and on positions $\underline {\underline {m}}\left (\underline {\mathsf {x}},\underline {q}\right )$, the sensitivities of the mass matrix are given by

$$\nabla _{\underline {\mathsf {x}}}\underline {\underline {m}}=J_{\underline {q}}\underline {\underline {m}}\,\nabla _{\underline {\mathsf {x}}}\underline {q}+\partial _{\underline {\mathsf {x}}}\underline {\underline {m}}. $$

A second example is shown for the external force vector which is assumed to depend on the design variables, on positions, and on velocities $\underline {Q}_{\text{ext}}\left (\underline {\mathsf {x}},\underline {q},\underline {\dot {q}}\right )$, leading to the sensitivities of the external force vector given by

$$\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{ext}}=J_{\underline {q}}\underline {Q}_{\text{ext}}\,\nabla _{\underline {\mathsf {x}}}\underline {q}+J_{\underline {\dot {q}}}\underline {Q}_{\text{ext}}\,\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}+\partial _{\underline {\mathsf {x}}}\underline {Q}_{\text{ext}}. $$

The analytical differentiation of the partial derivatives of the system parameters (e.g. $J_{\underline {q}}\underline {\underline {m}}$, $\partial _{\underline {\mathsf {x}}}\underline {\underline {m}}$, $J_{\underline {q}}\underline {Q}_{\text{ext}}$, $J_{\underline {\dot {q}}}\underline {Q}_{\text{ext}}$, $\partial _{\underline {\mathsf {x}}}\underline {Q}_{\text{ext}}$) is difficult for the general case [4] i.e. for all possible design variables. The analytical derivatives can be provided easily for some specific system parameters (e.g. $J_{\underline {q}}\underline {\underline {m}}$). In other cases, cumbersome and error-prone coding effort involved in analytic differentiation can be avoided by using other methods including automatic differentiation [4] and numerical differentiation. Examples of the semi-analytical approach for the computation of the partial derivatives with a numerical differentiation method in order to limit the implementation effort are given in [64, 152, 159]. This combines the advantage of high computational efficiency due to the analytical direct differentiation of the equation of motion including the application of the chain rule to system parameter sensitivities and the advantage of limited implementation effort due to the numerical differentiation of partial derivatives of the system parameters, leading to a semi-analytic approach.

4.3 Sensitivity analysis for time integration

The sensitivity analysis within the time integration is carried out completely analogously to the primal analysis, though using matrix-valued terms for the sensitivities instead of vectors of the system responses, shown here for Newmark-$\beta$ family of time integrators. For the prediction this becomes

$$\begin{aligned} ^{i}\nabla _{\underline {\mathsf {x}}}\underline {q}_{\text{pred}} & =\,{}^{i-1}\nabla _{\underline {\mathsf {x}}}\underline {q}+\Delta t\,{}^{i-1}\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}+\left (\frac{1}{2}-\beta \right )\Delta t^{2}\,{}^{i-1}\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}, \end{aligned}$$

(50)

$$\begin{aligned} ^{i}\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}_{\text{pred}} & =\,{}^{i-1}\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}+\left (1-\gamma \right )\Delta t\,{}^{i-1}\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}. \end{aligned}$$

(51)

These predictors are used to update the sensitivities of the system vectors and matrices $\nabla _{\underline {\mathsf {x}}}\underline {\underline {m}}$, $\nabla _{\underline {\mathsf {x}}}\underline {\underline {d}}$, $\nabla _{\underline {\mathsf {x}}}\underline {\underline {k}}$, $\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{ext}}$, $\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{nl}}$, $\nabla _{\underline {\mathsf {x}}}J_{\underline {q}}\underline {\Phi }$ and $\nabla _{\underline {\mathsf {x}}}\underline {Q}_{\text{c}}$ before Eq. (48) is solved for the acceleration sensitivities. The acceleration sensitivities are then used to update the predicted sensitivities positions and velocities

$$\begin{aligned} ^{i}\nabla _{\underline {\mathsf {x}}}\underline {q}& =^{i}\nabla _{\underline {\mathsf {x}}}\underline {q}_{\text{pred}}+\beta \Delta t^{2}\,{}^{i}\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}, \end{aligned}$$

(52)

$$\begin{aligned} ^{i}\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}& =^{i}\nabla _{\underline {\mathsf {x}}}\underline {\dot {q}}_{\text{pred}}+\gamma \Delta t\,{}^{i}\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}. \end{aligned}$$

(53)

4.4 Sensitivity analysis for the nonlinear solver

When dealing with differential–algebraic equations as shown here for flexible multibody systems, the solution of the sensitivity analysis depends on the primal system. A traditional approach for the solution of the primal analysis combined with the sensitivity analysis is the staggered direct scheme, where a linear system of the sensitivity corrector is solved directly after the convergence of the nonlinear corrector of the primal analysis [28]. A more efficient solution strategy is the simultaneous corrector method, where the primal analysis and the sensitivity analysis are solved simultaneously in a corrector iteration loop of a combined nonlinear system [97]. Further efficiency improvements can be achieved by the staggered direct method, where at each time step a corrector iteration loop for the primal analysis is followed by a second corrector iteration loop for the sensitivity analysis [48]. The lattermost method is shown here, where the Newton–Raphson step is

$$ \left [\textstyle\begin{array}{c@{\quad}c} J_{\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}}\nabla _{\underline {\mathsf {x}}}\underline {R}& J_{\nabla _{\underline {\mathsf {x}}}\underline {\lambda }}\nabla _{\underline {\mathsf {x}}}\underline {R}\end{array}\displaystyle \right ]\left [\textstyle\begin{array}{c} \Delta \nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}\\ \Delta \nabla _{\underline {\mathsf {x}}}\underline {\lambda }\end{array}\displaystyle \right ]+\nabla _{\underline {\mathsf {x}}}\underline {R}=\underline{\underline{0}}, $$

(54)

where the sensitivity Jacobians reduce simply to

$$\begin{aligned} J_{\nabla _{\underline {\mathsf {x}}}\underline {\ddot {q}}}\nabla _{\underline {\mathsf {x}}}\underline {R}& =J_{\underline {\ddot {q}}}\underline {R}\,\underline{\underline{\underline{\underline{e}}}}, \end{aligned}$$

(55)

$$\begin{aligned} J_{\nabla _{\underline {\mathsf {x}}}\underline {\lambda }}\nabla _{\underline {\mathsf {x}}}\underline {R}& =J_{\underline {\lambda }}\underline {R}\,\underline{\underline{\underline{\underline{e}}}}, \end{aligned}$$

(56)

and the Jacobians are used in the Newton–Raphson step. With this, the same solving routine can be used, by which the dimensionality has been reduced from four to two, and the necessary Jacobians have already been calculated in the primal step.

Available software and methods for the solution of differential–algebraic equations with sensitivity capabilities are given in [92]. An example of the more recent implementation is the suite of nonlinear and differential–algebraic equation solvers (SUNDIALS) [78].

5 Conclusion

Design optimization of flexible multibody dynamics is an important tool for increasing the efficiency and effectiveness of machines and mechanisms. Even with the increasing computing capacity, the authors are of the opinion that genetic algorithms can only play a limited role and that gradient-based optimization is the preferred method for optimizing flexible multibody systems due to their high efficiency. As such, the main topics of gradient-based design optimization for flexible multibody systems are introduced, and recent research activities are reviewed.

Specifically, the present work includes differential–algebraic formulations of flexible multibody systems. Advantages and disadvantages of flexible multibody system formulations, namely the floating frame of reference formulation, the absolute nodal coordinate formulation, and the absolute coordinate formulation, are shown.

Main concepts of design optimization and available algorithms in the scope of flexible multibody dynamics are introduced. Different types of design optimizations are identified and categorized into parameter optimization, sizing, shape optimization, topology optimization, and material optimization. Design optimization formulations are categorized into lightweight formulations, stiffness formulations, and optimal control formulations. For these formulations, the parameters which are used to formulate the design objectives and design constraints are shown. Three main approaches for the formulation of the design optimization problem with flexible multibody systems are found in literature and are categorized here regarding the optimization responses. Firstly, the full multibody simulation can be used in the design optimization. Secondly, mathematical approximation based methods can be used to decrease the computational effort of simulations. Thirdly, physical approximations can be used to formulate the design optimization on a reduced physical-based model.

Sensitivity analysis is the basis for gradient-based design optimizations, and available methods are introduced. The analytical methods including direct differentiation and the adjoint variable method are most used in literature and best suitable for their application to flexible multibody dynamics. The increased implementation effort connected to analytical methods is rewarded by the increased computational efficiency.

This review provides a summary of efficient gradient-based design optimization with flexible multibody dynamics. The authors hope to provide the reader a starting point in the pursuit of lighter, faster, better, and maybe even optimal mechanical systems.