Introduction

High temperature capillarity is an important scientific and technological field of research. The degree by which a liquid wets a solid is an important technological parameter for processes such as joining [1–6], solidification [7–9], and composite processing [10–14]. While wetting is a measure of the “energy” of interfaces between bulk phases, and thus a parameter associated with equilibrium thermodynamics, the rate by which a liquid spreads in contact area with a solid is equally important for technological processes [15–17]. Fundamentally, wetting depends on the chemical content and atomistic structure of the bulk phases and the interface itself. This review first attempts to identify phenomena related to wetting between phases, and then proceeds to describe how these phenomena may be modified by the presence of adsorption (segregation). This includes the role of anisotropy of crystalline materials in wetting, and the heterogeneity and roughness of surfaces, and we clearly separate between equilibrium (wetting) and kinetics (spreading).

While solid–liquid interfaces are often important for materials processing, it is the solid–solid interface which frequently determines the mechanical and functional properties of the final material system. It is the solid–solid interfacial energy which defines the nominal energy required to fracture a solid at a join, ignoring irreversible processes and deformation [18–20], and thus measuring and decreasing solid–solid interface energy offers an engineering approach for the optimization of mechanical properties via fundamental interface science [21, 22]. As such we have explicitly reviewed the concept of solid–solid wetting, how solid–solid interfacial energy and the thermodynamic work of adhesion can be experimentally measured, and how the anisotropy of crystalline materials must be taken into account.

Finally, we have reviewed the fundamentals of adsorption at the thermodynamic, or macroscopic, scale, and why adsorption must be considered in the analysis of both wetting and wetting transitions. Adsorption has also been considered at the level of the local atomistic structure, first with regard to excess distribution and then by using the concept of interface complexions. It is our hope that this review will demonstrate to the reader that fully understanding wetting phenomena requires the concept of complexions, and that including complexions offers the possibility to merge continuum and atomistic approaches to interface science.

Interfaces and their energies

In what follows, the term interface is used in a generic sense to indicate any region of a material that separates two distinguishable bulk phases. Typically, the interface can be treated as a thin slab in which the features which distinguish the two bulk phases vary from one bulk material to another, or it can be replaced by a mathematical plane. This general definition of the term interface naturally includes the surface of a solid in contact with a gas phase, and the boundary between two grains of the same phase, but with differing orientations (a grain boundary). The term ‘surface’ is reserved for the subset of interfaces between condensed phases and their equilibrium vapor. As is now well-known, if at least one of the two phases separated by an interface is crystalline, then the energyFootnote 1 of that interface, γ, may be anisotropic, i.e., it may depend on the crystallographic orientation of the interface with respect to the crystalline phase(s), and the misorientation of the abutting phases if they are both crystalline. To simplify the presentation, we will treat wetting from the simplest case and progress to more complex systems.

Macroscopic wetting of a liquid on a rigid solid substrate

Wetting phenomena involve interactions among three separated volumes, which abut three interfaces and meet at a triple line. The Young contact angle, θ Y, of a wetting phase on a rigid substrate (or wetted phase) is related to the interfacial energies by the Young equation, written here for a liquid wetting phase (L) on a solid substrate (S) in a vapor phase (V):

$$ \cos \theta_{\text{Y}} = \frac{{\gamma_{\text{SV}} - \gamma_{\text{SL}} }}{{\gamma_{\text{LV}} }} $$
(1)

where γ ij are the energies of the three interfaces ij, and i and j are the phases that coexist at equilibrium. As such, at equilibrium θ Y reflects the relative interfacial energies of the system.

This equation corresponds to the vector equilibrium obtained by representing the energies of the three interfaces at the triple line as interfacial tensions projected onto the solid plane (see Fig. 1)Footnote 2 [23]. It can also be derived from the values of the interfacial energy densities. Young’s equation will apply only if these interfacial energies are isotropic.

Fig. 1
figure 1

Young, or equilibrium, or intrinsic contact angle and interfacial energies

Full size image

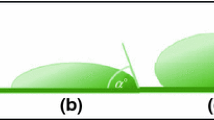
At the macroscopic scale, a liquid on a flat horizontal solid surface (or substrate) adopts a shape generally referred to as a sessile drop (see Fig. 2a). The Young contact angle, θ Y, at the solid–liquid–vapor triple line, must be measured in a plane perpendicular to both the substrate and the triple line.

Fig. 2
figure 2

Examples of a sessile drops and b capillary rise of water and depression of mercury on a same glass surface. The contact angle for a given three-phase system does not change with the macroscopic shape of the solid

Full size image

Under the influence of gravity, the shape of the drop changes as the result of an equilibrium between competing forces due to capillary pressure (under which the drop would adopt the shape of a spherical cap) and hydrostatic pressure (under which the drop would spread and flatten), but the equilibrium contact angle θ Y does not change due to the influence of gravity. The capillary length, L c, is a characteristic length scale for a liquid surface subject to both pressures:

$$ L_{\text{c}} = \sqrt {\frac{{\gamma_{\text{LV}} }}{{{{\Updelta}}\rho g}}} $$
(2)

where Δρ is the difference in density between the two fluids coexisting at the surface, and g is the acceleration due to gravity. Drops smaller than L c will remain spherical, whereas larger drops will flatten.

For a given solid–liquid–vapor system, the Young contact angle does not depend on the macroscopic shape of the solid if the solid is smoothly curved. For example, when the solid is in the shape of a small vertical tube, the contact angles inside and outside the tube are identical to that of a sessile drop of the same liquid on a planar substrate of the same solid. If the contact angle is less than 90° (greater than 90°), then the liquid on the interior of the tube will rise (be depressed) as shown in Fig. 2b; this is the phenomenon of capillary rise or depression. The length of the rise is set by the contact angle on the interior of the cylinder, by L c, and by the difference in liquid curvature between the inside and outside liquid surfaces (the curvature difference supports the hydrostatic pressure created by the capillary rise: see Fig. 2b). Cases for a surface which is not smooth will be dealt with in subsequent sections. Again, the height of the liquid in the tube results from a balance between the capillary and hydrostatic pressures.

In addition to the contact angle, the thermodynamic work of adhesion (W ad) is often used to compare the relative interfacial and surface energies of a particular system. W ad is the work per unit area necessary to separate an interface of interfacial energy γ SL into two equilibrated (i.e., including any adjustments of surface energy due to adsorption or reconstruction) surfaces of energies γ LV and γ SV:

$$ W_{\text{ad}} = \left( {\gamma_{\text{LV}} + \gamma_{\text{SV}} } \right) - \gamma_{\text{SL}} $$
(3)

It is important to differentiate between the thermodynamic work of adhesion and the work of separation. The work of separation is often used in fracture analysis, or in atomistic simulations, to define the difference in energy between an equilibrated interface and the two surfaces created immediately after the interface has been separated (i.e., before the newly created surfaces have reached equilibrium). Since the surface energy is a minimum at equilibrium, the work of separation is larger than the work of adhesion. If all the interfaces are isotropic, then by combining Eq. (3) with Young’s equation (1), W ad can be expressed as a function of the contact angle (the Young–Dupré equation):

$$ W_{\text{ad}} = \gamma_{\text{LV}} \left( {1 + \cos \theta } \right) $$
(4)

This is a very useful relationship since it expresses W ad in terms of two experimentally measurable quantities in solid–liquid–vapor systems: γ LV and θ Y.

In principle, contact angles can have any value between 0° and 180°. Materials scientists working with inorganic materials at high temperature tend to distinguish between two types of systems, “good wetting” systems where θ Y < 90°, and “bad wetting” systems, θ Y > 90°. This nomenclature is related to the ability of a liquid to spontaneously rise within an ideal vertical capillary tube when θ Y < 90°. For an isotropic system consisting of a droplet trapped between two flat coplanar plates, the capillary force between the plates is only negative (pulling the plates towards each other) when θ Y <= 90°. When θ Y > 90°, the capillary force can have either sign and the plates have an equilibrium separation at zero force (see Cannon and Carter [24, 25] for a derivation of this phenomenon as well as a variational formulation of the equilibrium shapes, and the boundary conditions to Euler’s equation which must be satisfied by the Young–Dupré equation). We prefer the use of the nomenclature: “Partial wetting” for any contact angle between 0° and 180° (see Fig. 1).

Instead of partial wetting, scientists who deal with organic systems use the terms “wetting” and “non-wetting” to describe systems which display contact angles that are zero or positive, respectively. To avoid confusion, we will use the terminology “complete” or “perfect” wetting when the contact angle is zero, and “non-wetting” when the contact angle is 180°; thus the limiting conditions of partial wetting are complete (or perfect) wetting and non-wetting.

The observation of a continuous layer at an interface does not necessarily imply perfect wetting. Such observed layers may not correspond to an equilibrium phase, but rather to an interfacial layer which minimizes the total free energy by local adjustment of structure, density, and/or chemical composition. The name “complexions” has recently been assigned to such layers. This is an important issue which will be addressed in detail in sections “Microscopic scale and adsorption” and “Complexions”. Complete wetting requires that the interfacial layer be an equilibrium bulk phase that coexists with its abutting phases (or phase). Thus, in a given system, it is essential to verify that a wetting phase conforms to the coexistence conditions of the corresponding phase diagram. In addition, the relevant phase diagram must include any species that are present in the interfacial regions, including those present in the vapor phase, because even at very low partial pressures, certain species may be adsorbed at the surfaces and interfaces (such as oxygen at metallic and oxide surfaces/interfaces). See “Panel 1”.

When the contact angle is 180°, wetting is “null”. In this case, it is the vapor phase that completely wets the solid at coexistence with the liquid. Apparent contact angles close to 180° can be obtained when the morphology of the solid surface is specifically designed to reduce the actual contact between the liquid phase and the entire area of the solid surface. This “super-hygrophobic”Footnote 3 phenomenon [26], originally referred to as “composite wetting” [27] and recently renamed the “lotus effect”, will be described in greater detail in the next section.

Contact angles near triple lines: interaction between interfaces

In the vicinity of the triple line, the distance between interfaces becomes very small, which can lead to interactions between them. These interactions occur because of the finite thickness of interfaces (as described in later sections), and can in turn produce local distortions of the liquid surface, which may be displaced either towards or away from the solid/liquid or the solid/vapor interfaces, as depicted in Fig. 5. These distortions can produce excess energies of the order of 10−9 J/m if assigned to the triple line (see for example [39, 40]). As a result of these distortions, a contact angle defined by the equilibrium of the macroscopic interfacial energies should never be measured too close to the triple line. As mentioned before, the best approach for measuring a macroscopic contact angle is to fit the shape of the liquid surface with a relevant function and truncate that shape by the substrate plane.

Fig. 5
figure 7

Sketch of the deviation of the liquid surface at the triple line of a sessile drop under the influence of attractive interactions between two surfaces on the apparent (θ Att) contact angle, versus the influence of repulsive surface interactions leading to an apparent contact angle (θ Rep) approaching 90°

Full size image

Wetting on unconstrained isotropic substrates

Wetting on a deformable substrate such as a liquid, shown schematically in Fig. 6 is characterized by a dihedral angle, ϕ, within the lenticular cap of the partially wetting phase. In the case of a three-phase, liquid 1 (L1)–liquid 2 (L2)–vapor (V) system in which all surface energies are isotropic, the dihedral angle is related to the interfacial energies by the Neumann relationship:

Fig. 6
figure 8

Wetting on a deformable surface and the resulting lenticular-shaped drop with dihedral angle ϕ

Full size image
$$ \frac{{\gamma_{{{\text{L}}1{\text{V}}}} }}{\sin \beta } = \frac{{\gamma_{{{\text{L}}1{\text{L}}2}} }}{\sin \alpha } = \frac{{\gamma_{{{\text{L}}2{\text{V}}}} }}{\sin \phi } $$
(7)

The equilibrium shape of the confined phase corresponds to the minimum of the total interfacial energy which is the sum of the energy of each interface multiplied by its area. In order for the total interfacial energy to be minimized, the interfaces between L1 and L2 and the L1 surface, which confine the L1 drop, adopt the shape of spherical caps. The schematic in Fig. 6 is valid in the absence of buoyancy, and for isotropic interfaces; with buoyancy the L2V interface will be curved. When the L2V interface is flat, the values of surface and interface energy-weighted curvatures on the two sides of the L1 lens must be equal: γ L1V/R L1V = γ L1L2/R L1L2 For the case illustrated in Fig. 6, it should be emphasized that the “apparent contact angle” above the level of the flat surface of the substrate is not related to the interfacial energies by Young’s equation (1).

An isotropic particle embedded in an internal interface will also adopt a lenticular shape, and the wetting may be characterized by the dihedral angle, ϕ, of the particle at the triple junction. A dihedral angle may also be used to describe the equilibrium angle at the groove that forms at the intersection of a grain boundary (or two-phase boundary) with another interface (see Fig. 7). The dihedral angle shown in Fig. 7a relates the energies of the interfaces on each side of the groove, γ 1 and γ 2, to the boundary energy, γ 12, as expressed by the Neumann equation (Eq. 7). This condition may also be expressed as a vector equilibrium resolved in the horizontal and vertical directions:

Fig. 7
figure 9

Wetting and grooves at internal interfaces: a general case, b and c classical sketches for a symmetrical grain boundary groove equilibrated under two different mechanisms of solid diffusion [41, 79]

Full size image
$$ \begin{aligned} & \gamma_{1} \cos \phi_{1} + \gamma_{2} \cos \phi_{2} = \gamma_{12} \\ & \gamma_{1} \sin \phi_{1} = \gamma_{2} \sin \phi_{2} \\ & \phi_{1} + \phi_{2} = \phi \\ \end{aligned} $$
(8)

It is more usual to find the dihedral angle at a grain boundary defined by Eq. (9), with the restriction of a symmetrically shaped groove (where γ i1 = γ i2 = γ i ) (see Fig. 7b, c).

$$ \cos \frac{\phi }{2} = \frac{{\gamma_{12} }}{{2\gamma_{i} }} $$
(9)

Note that the shapes of the surfaces around the groove are kinetic shapes [41] but the angle at the groove is an equilibrium angle.

Wetting and anisotropic interfaces

The assumption of interfacial energy isotropy is only valid for the interfaces of fluids and amorphous solids, whereas interfaces that involve crystalline solids (or liquid crystals) are anisotropic. Interface anisotropy issues are addressed in two subsections. The first one will describe the wetting of a crystal on a flat substrate, and the second one, the wetting of an unconstrained anisotropic substrate.

Equilibrium crystal shape

First, it is useful to introduce the concept of the ECS, or Wulff shape, of a crystal equilibrated in a vapor phase (see Fig. 8). The ECS can be obtained from a polar plot of the orientation dependence of surface energy (\( \gamma /\hat{n} \)), the so-called γ-plot, by means of the Wulff construction [42] (where \( \hat{n} \) is a unit vector normal to the surface). The ECS is convex and conveniently centered on a point referred to as the Wulff point. It may display facets (atomically flat surfaces of given orientations) and curved surfaces (atomically rough orientations). Facets occur at orientations that correspond to cusps on the γ-plot. The deeper the cusp, the lower the surface energy of this orientation, and the larger the corresponding facet on the ECS. All the orientations which exist on the ECS are stable. All orientations will be stable for the case of an ECS with facets, when facets and curved parts connect tangentially (see Fig. 8b). If a discontinuous (sharp) connection appears on the ECS, some orientations will be missing and thus unstable (see Fig. 8c) [43]. For example, for a face-centered cubic (fcc) crystal with an ECS in the shape of a cubo-octahedron, consisting of the {111} and {100} facets, these will be the only two stable orientations. The unstable orientations have a virtual energy, which cannot be measured experimentally. Such orientations decompose into micro-facets of the adjacent stable orientations present on the ECS (Fig. 8c). Their effective energy can be extracted from the ECS as suggested by Herring [44]:

$$ \gamma = \frac{1}{{a_{0} }}\sum\limits_{i} {\gamma_{i} } a_{i} $$
(10)

where a 0 is the area of the unstable plane, i represents the stable facet types, and a i and γ i are the ith facet area and surface energy, respectively (see Fig. 8d).

Fig. 8
figure 10

Equilibrium shapes and faceting: a 2D γ-plot and equilibrium shape of a crystal; b two 2D equilibrium shapes, the left one with all the orientations and the right one with missing orientations where the shape has singularities; c 3D equilibrium shape of an fcc crystal with only three types of stable orientations ({111}, {100}, and {110}); d break-up of an unstable facet into two facets with energy γ 1 and γ 2. On the right of c, two AFM micrographs show microfacetting of unstable orientations between two stable facets or three stable facets

Full size image

Solid-state wetting

Until this point we have dealt primarily with the concepts involved for wetting of a liquid in contact with a solid. These issues are important for a fundamental understanding of solid–liquid interfaces, and critical for engineering methods which depend on solid–liquid interfaces, such as solidification, soldering, and brazing. However, solid–solid interfaces are equally important for numerous technological applications as well as for fundamental studies. One fundamental goal of solid-state wetting analysis is to extract the interfacial energy between two solids. This important fundamental parameter can be used in the Young–Dupré equation (Eq. 4) to obtain the thermodynamic work of adhesion for solid–solid interfaces, which defines the lower limit of the fracture energy of an interface (ignoring dissipative processes) [45].

Why contact angles of solid crystals on a substrate should not be used?

Given the approach of Young described previously, the natural tendency of the experimentalist is to simply measure the apparent contact angle of an equilibrated crystal on a flat solid substrate, as is done in the sessile drop experiment. Unfortunately this approach is overly simplistic, and ignores the influence of the anisotropic crystal shape on the apparent contact angle. This problem is demonstrated via the simple schematic in Fig. 9a, which shows a crystal equilibrated in contact with a flat and rigid substrate, and the apparent contact angle θ. As will be discussed later in section “Microscopic scale and adsorption”, adsorption at interfaces can modify the interfacial energy. Let us suppose a hypothetical case where an additional component is added to the system of Fig. 9a, such that it adsorbs only to the interface between the substrate and the crystal (i.e., not to the free surface of the particle or the substrate) and decreases its energy. As a result, the total surface/interface areas are optimized in order to minimize the total surface/interfacial energies, and the relative interface area in Fig. 9b is increased versus Fig. 9a, for a crystal of the same volume. However, due to the equilibrium shape of the crystal, the facets have not changed and neither has the apparent contact angle. Thus a measure of solid-state wetting via apparent contact angles is obviously an erroneous approach.

Fig. 9
figure 11

Schematic drawing of a single crystal equilibrated in contact with a flat solid substrate. The apparent contact angle θ in a remains the same in b where the interface energy has been reduced due to segregation (indicated by the red line at the interface) (Color figure online)

Full size image

Winterbottom analysis

An approach to deal with experimental measurement of solid–solid interfacial energies was developed by Winterbottom [46]. This approach is based on a geometrical analysis of the Wulff shape of a crystal equilibrated on a flat solid substrate of a dissimilar material, under conditions of constant temperature, volume and chemical potentials. The Winterbottom construction is described in detail in “Panel 2”.

Dewetting and spreading

While the term ‘wetting’ has been used throughout this text as the description of a thermodynamic state (e.g., reflected by a contact angle), ‘wetting’ is sometimes incorrectly used to describe the kinetics of spreading of a liquid across a solid. The kinetics of spreading, which is driven by the minimization of surface and interface energy (defined by wetting), is obviously an important technological topic. In order to prevent confusion, we adopt ‘spreading’ to describe the kinetic changes of surface and interface area, and ‘wetting’ to describe thermodynamics (equilibrium). The term “dewetting” has also gained general use to describe the break-up (agglomeration) of a thin film in the liquid (or solid state) into drops (or particles), driven by the minimization of surface and interfacial energy in a system where the three coexisting phases are at equilibrium. While the kinetics of dewetting can be studied to reach important conclusions regarding surface transport, the equilibrium state reached by the kinetic process of dewetting offers an alternative approach to study the equilibrium state of solid–liquid and solid–solid interfaces. A recent review by Thompson [81] has been dedicated to this phenomenon. In the following we report on the main points of dewetting relevant to this paper.

Spinoidal dewetting versus nucleation of holes

There are two main proposed mechanisms for dewetting of thin films on solid surfaces: spinodal dewetting (which mostly refers to the Raleigh instability) and nucleation of voids [82]. The mechanism for the Raleigh instability in liquid-state dewetting is a wave fluctuation which grows exponentially with thermal activation, resulting in two opposite surface curvatures and the tendency to minimize surface area by breaking the film up into droplets to reach equilibrium [79]. For solid-state dewetting, spinodal dewetting occurs mostly for thin films, where the amplitude of the fluctuations is large enough to form hills and depressions via surface diffusion. When the depressions reach the substrate, agglomerated particles are formed, or break-up of the film occurs [83]. Recently, faceted film-edges were observed without depressions [84, 85] (due to surface energy anisotropy) and confirmed by a model developed by Klinger et al. [86].

In polycrystalline films, solid-state dewetting takes place either by extension of grain boundary and triple junction grooves [87, 88] from the free surface to the interface, or via nucleation of voids at the interface (see Fig. 14). Following Srolovitz and Safran [82] and using the criteria of grain boundary grooves extending from the free surface to the interface, a polycrystalline film of thickness, a, will rupture if:

$$ \frac{R}{a} \ge \frac{{3\sin ^{3} \beta }}{{2 - 3\cos \beta + \cos ^{3} \beta }} $$
(14)

where R is the grain size, and β is defined in terms the grain boundary (γ GB) and surface (γ SV) energies as \( \beta = \sin^{ - 1} \left( {{{\gamma_{\text{GB}} } \mathord{\left/ {\vphantom {{\gamma_{\text{GB}} } {\gamma_{\text{SV}} }}} \right. \kern-0pt} {\gamma_{\text{SV}} }}} \right) \) [82, 83, 89, 90]. This model ignores the influence of the film–substrate interfacial energy, and if the interfacial energy is relatively high and a mechanism exists for nucleation of voids at the interface, then voids will first form at the interface, and grow towards the surface [91, 92]. The details of the mechanism for void nucleation at the interface are not clear, although void nucleation is more likely to occur at intersections of grain boundaries with the substrate, and any perturbations or defects at the film–substrate interface. This is a field which requires further study, since the data available in the literature is sparse.

Fig. 14
figure 19

Schematic drawing of solid-state dewetting of a thin film on a substrate, where a–d grain boundary grooves from the free surface slowly increase until they contact the substrate, and e–h voids at triple junctions nucleate and grow towards the free surface

Full size image

Regardless of whether solid-state dewetting is via grain boundary grooves or void growth from the interface, the final equilibrated state is that of a single crystalline particle on a substrate. If the initial film is thin enough, equilibrated particles will form within reasonable periods of time, and can be used to study the ECS of the film material [61, 93], and the interfacial energy between the film and the substrate [56, 58, 94]. The kinetics of the dewetting process have also been used to extract surface diffusion parameters [95–97].

While fundamental studies of dewetting kinetics, and the final equilibrium configuration are important, dewetting has also been used as a method to pattern a surface with small particles for applications [81, 98–100]. Examples include catalysis [101–103], porous electrodes [104, 105], and more recently charge storage for memory applications [106–108].

Thin film stability

The discussion above leads to the necessary, albeit sometimes worrisome conclusion, that thin solid films are not stable. While this conclusion is trivial, it has important technological implications given the current dependence on thin film technology for the microelectronics industry. The minimization of total surface and interfacial energy is the driving force for dewetting, but the kinetics of the process depend on interface and surface transport mechanisms, and nucleation of the process may strongly depend on the nature and distribution of defects at the free surface, and at the interface between thin films and substrates. Given the advantages of particles with a length scale which influences their functional properties (i.e., “nano”), the last 10 years have seen a multitude of experiments designed to utilize dewetting for this purpose. However, time–temperature experiments to probe the dewetting of continuous thin film devices, which depends on the defect microstructure, are lacking.

Precursor wetting foot and kinetics of spreading

A great deal of work has been done on the influence of the triple line during spreading of a liquid on a solid, or retraction of a liquid drop (liquid-state dewetting), and the associated hygrodynamics [30, 109]. The fluid dynamics involved are beyond the scope of the present work, but we would like to clarify the context of wetting versus spreading.

It is important to clarify the concept of a precursor foot, which is an undefined amount of the component of the liquid drop which extends upon the substrate ahead the main mass of the spreading drop [110] (see Fig. 15). A precursor foot can be either a bulk liquid phase identical to the drop phase, or an adsorption layer [111–114]. The expansion of the former is driven by macroscopic phenomena related to fluid mechanics and corresponds to the achievement of complete wetting, while the latter is driven by atomistic mechanisms and is related to the equilibration of the chemistry and the structure of the bare substrate at coexistence with the phase of the drop, and it has nothing to do with the wetting of a phase [112, 113]. As we will see in subsequent sections of this review, an adsorption layer is an intrinsic part of a surface (or an interface) which is not a bulk phase. It is a region of finite thickness at a surface (or an interface) which contains all the gradients of composition and/or structure perpendicular to the surface which are necessary to minimize the surface (or interfacial) energy. To form the adsorption layer, the constituent atoms from the drop either diffuse across the solid surface or evaporate and then adsorb onto the surface. In the thermodynamic regime, the contact angle reflects the modified (lowered) solid–vapor surface energy, while in the kinetic regime the driving force for spreading reflects the instantaneous surface energy of the substrate.

Fig. 15
figure 20

Schematic drawing of a spreading drop with a a bulk precursor foot of liquid which precedes the main body, and b an adsorbate of atoms on the surface of the substrate which either diffused over the surface from the bulk drop, or evaporated from the bulk and then adsorbed to the surface from the gas phase

Full size image

Due to the combined technological and fundamental importance of spreading rates, a great deal of fundamental and phenomenological research has been invested in this topic. For ‘high’ temperature materials science, two main regimes of spreading kinetics have been identified, for reactive and non-reactive systems.

The classical “low-temperature” spreading kinetics usually employs the hydrodynamic theory, where the spreading kinetics depends on the dynamic contact angle θ D, and the capillary number C a  = νη/γ LV (γ LV is the surface energy of the liquid, ν is the velocity of the triple junction and η is the liquid viscosity) [115]. The rate of spreading is thus reflected by the capillary number which contains the velocity of the triple line:

$$ C_{a} = \frac{{\left( {\theta_{\text{D}}^{3} - \theta^{3} } \right)}}{{9\ln \frac{{L_{\text{c}} }}{{L_{\text{S}} }}}}\quad \left( {\theta_{\text{D}} \le 135^{^\circ } } \right) $$
(15)
$$ C_{a} = \frac{{\left[ {\frac{9\pi }{4} \ln \left( {\frac{{1 - \cos \theta_{\text{D}} }}{{1 + \cos \theta_{\text{D}} }}} \right)\left( {\pi - \theta_{\text{D}} } \right)^{3} - \theta^{3} } \right]}}{{9\ln \frac{{L_{\text{c}} }}{{L_{\text{S}} }}}}\quad \left( {\theta_{\text{D}} \le 135^{^\circ } } \right) $$
(16)

where θ is the equilibrium contact angle, L c is a characteristic capillary length (Eq. 2), and L S corresponds to a thickness of the meniscus immediately adjacent to the solid wall over which the ‘no-slip’ boundary condition of classical hydrodynamics is relaxed to avoid a singularity at the triple junction.

The molecular kinetic theory (MKT) of spreading was developed by Blake [116]. It assumes that the atoms of the spreading fluid replace adsorbed atoms on the surface, and yields:

$$ C_{a} = \frac{2\eta \lambda kT}{{h\gamma_{\text{LV}} }}\left[ {\sinh \left( {\frac{{\lambda^{2} \gamma_{\text{LV}} }}{2kT}\left( {\cos \theta - \cos \theta_{\text{D}} } \right)} \right)} \right]\exp \left( {\frac{{\Updelta G_{\text{w}} }}{NkT}} \right) $$
(17)

where λ is the average spacing between adsorption sites, k is Boltzmann’s constant, h is Planck’s constant, ΔG w is the activation free energy for wetting that derives mainly from solid–fluid interactions, N is Avogadro’s number, and T is temperature.

Both approaches were developed for non-reactive spreading, and the last 10 years have seen numerous experiments designed to probe which approach best describes high temperature spreading of liquid metals (for a review of the subject see [117]). From meticulous experiments [115, 118] and molecular dynamics simulations [119–121], it appears that the rate limiting mechanism for non-reactive and dissolutive spreading kinetics is friction at the triple junction, where order in the liquid at the solid–liquid interface plays a key role in defining this parameter. Order in the liquid at solid–liquid interfaces has been theoretically analyzed [122–129] and experimentally observed [130–135], and will be discussed below in terms of adsorption.

Microscopic scale and adsorption

Thus far we have discussed wetting under conditions where the compositions of the wetting and substrate phases have not been addressed explicitly. The compositions of the two condensed phases (and the vapor phase), and those of the interfacial regions in particular, are important, as we shall see, because changes in interfacial chemical compositions may cause changes in the interfacial energies that determine wetting equilibrium (see the Young, Neumann, and Herring wetting equilibrium equations described in sections “Macroscopic wetting of a liquid on a rigid solid substrate”, “Wetting on unconstrained isotropic substrates”, and “Effects of interfacial torques on wetting equilibrium”).

This section introduces some basic concepts on the thermodynamics of interfaces that are useful for treating the chemistry of interfaces, and then proceeds to couple this formalism with a more atomistic approach. The more general concept of complexions, which includes order parameters in addition to composition, will be addressed at the end of this paper.

In this section of the paper, we follow the approach developed by Gibbs [136]. In a later section, we also introduce another formalism, due to Cahn, which is equivalent to Gibbs’ treatment, but which is more transparent when dealing with multi-component, multi-phase systems that simultaneously contain several different interfaces. Gibbs is not easy to read, and so it is convenient to draw on other sources which have “translated” Gibbs’ work into a more modern thermodynamic language, such as the papers by Hirth [137, 138] and by Mullins [41], and the book by Rowlinson and Widom [139]. Parts of what is covered in this paper on the topic of interfacial thermodynamics has been excerpted from a recent review of interfacial adsorption (or segregation) [140].

We begin by reviewing the thermodynamics of interfaces, using the liquid–vapor surface as an example, i.e., we consider a system composed of a liquid in equilibrium with a vapor phase, separated by an interface. The energy associated with the interface, i.e., the surface or interfacial energy, denoted by γ (units of [energy/(unit area)], typically mJ/m2), is defined as the reversible work needed to create unit area of surface, at constant temperature (T), volume (V) (or pressure (P)), and chemical potentials of the components i of the system (μ i ).

Gibbs dividing surface

The interface is not perfectly sharp and has a finite thickness, i.e., there is a transition region separating the two phases where the local density changes from that of the liquid (referred to as phase ′) to that of the vapor (referred to as phase ″), as shown schematically in Fig. 16. The diffuseness illustrated here for a liquid/vapor interface is also present at other types of interfaces, such as grain boundaries, solid–liquid, or solid–solid interphase boundaries. Note that the gradient in composition, and in other kinds of density parameters, can vary in shape and width (see section “Complexions”). In order to avoid having to define the diffuseness of the interface, Gibbs defined a mathematical plane, known as the dividing surface, with area A, onto which he projected all the extensive thermodynamic variables pertaining to the interface. To do this, he took the value of the variable in the system containing the interface, and subtracted the value of the variable obtained from a hypothetical reference system consisting of the two bulk phases, assumed to extend uniformly all the way to this mathematical plane. An extensive variable obtained by this subtraction process is referred to as an interfacial excess quantity, and is identified by the superscript S. As an example, the interfacial excess internal energy of the system, E S, may be written as:

$$ E^{\text{S}} = E - E^{\prime } - E^{\prime \prime } $$
(18)

where E is the internal energy of the system (containing the interface), E′ is the internal energy of phase ′, and E″ is the internal energy of phase ″. This shows how the interfacial excess quantity is just the quantity in the total system, less the quantity in the bulk phases (hypothetically extended to the dividing surface). It is important to note that the position of the dividing surface is arbitrary. It can be placed at any convenient location within the bounds of the physically diffuse region. Some consequences of this arbitrariness are addressed below.

Fig. 16
figure 21

Schematic of the density variation across a liquid–vapor interface. The vertical dashed line represents the Gibbs’ dividing surface. The solid line represents the density variation in the system containing the interface. Horizontal dashed lines illustrate the definition of the hypothetical reference system

Full size image

Every extensive thermodynamic variable of the system can be written in the same manner as in Eq. 18; e.g., the number of moles of component i in the real system is expressed as: n i  = \( n_{i}^{\prime } \) + \( n_{i}^{\prime \prime } \) + \( n_{i}^{\text{s}} \). The only exception is the volume of the system, which is written:

$$ V^{\text{S}} = V^{\prime } - V^{\prime \prime } $$
(19)

i.e., Gibbs assigned no excess volume to the interface.

Complexions

What are complexions and complexion transitions?

The discussion in the previous sections clearly shows that a first (or higher) order transition can occur in the state of an interface, surface, or grain boundary, with regards to chemical excess (adsorbate). Recently, these transitions have been shown to have a significant influence on the properties of grain boundaries with regards to mobility during grain growth [159]. Scanning TEM of similar grain boundaries in the same samples suggested that the changes in grain boundary mobility are dependent upon the state of the grain boundaries with regards to transitions in adsorption, which were classified by Dillon et al. [160] as specific states according to their structural width (rather than chemical content). A structural width is a useful characterization; see comments in Eq. (59).

The concept of structural (rather than chemical) changes at a grain boundary is not new, but the recent models by Tang et al. proposed that structural transitions could be seen as first-order transitions, in a manner analogous to the adsorption transitions discussed in section “Microscopic scale and adsorption” [161–163]. Unfortunately these transitions were described by some as phase transitions, or grain boundary phase transitions, while the transitions in adsorption or structure were clearly confined to the 2D state of the interface. As a result, Cannon and Carter suggested calling this general phenomenon “complexion” transitions, where a complexion is an equilibrium 2D state of an interface [161]. It is important to differentiate between bulk phases and complexions, since complexions can only exist at the surface of a bulk phase or at the interface between two bulk condensed phases, and complexion transitions can occur without a transition in any of the adjacent bulk phases.

Interestingly, structural transitions at an interface, without any nominal change in chemistry (chemical excess) have recently been studied during wetting experiments of liquid Al in contact with sapphire [132, 164]. The ordered region in the liquid adjacent to the solid is, in effect, a complexion, where the change in order as a function of, e.g., temperature or terminating solid facet plane, are different complexions [165]. That this phenomenon is a complexion is inferred from the experimental data, but cannot be directly proven. However, recently the energy of Au–sapphire interfaces with and without a Ca–Si-based complexion were measured, and a significant difference in energy was experimentally associated with the change in the interface complexion and an increase of the chemical potentials of Si and Ca [166, 167].

An interface will have an equilibrium complexion at given values of system potentials such as pressure, temperature, and the chemical potentials of the various chemical species. For crystalline surfaces, the equilibrium complexion will depend on the surface orientation; for example, in one-component systems, the surface can undergo reconstruction, disorder, roughening or melting [168]. In binary alloys, several surface complexions have been observed, which differ in structure and composition depending on the chemical potentials [169–172]. Symmetry reconstructions at the surfaces of oxides have been studied by Rappe and co-workers [173] who plotted the equilibrium surface structures as a function of the potentials (e.g., the partial pressure of oxygen). From this discussion it is clear that surface reconstruction is necessarily a complexion transition.

At grain boundaries, complexions manifest themselves as highly localized structural changes, or as abrupt changes in the adsorption content, which display a width set by thermodynamic equilibrium, and whose presence can lead to changes in properties such as electrical conductivity, adhesion, and grain boundary mobility [63, 174–179]. In all cases, these phenomena can be treated with an identical and rigorous classical thermodynamic foundation [163]. These formulations are not new. Gibbs recognized that soap film transitions can be treated in the same manner as the equilibrium of heterogeneous materials [180]; Smith [181] provided a heuristic argument for the onset of a premelting film of finite thickness; Cahn [154] extended this idea to compositional changes in his diffuse interface treatment in critical wetting theory; Schick [156] extended this further by a careful thermodynamic treatment of the interface environment. Abrupt surface symmetry changes, and surface relaxation are also well known. Several phenomena were described in Cahn’s [154] critical wetting paper, including the abrupt transition of surface adsorption, Γ, at the exterior surface of a single phase. The term “critical wetting” has been used to describe these abrupt changes in adsorption, and this is unfortunate because these interfacial structures and compositions are not “wetting” and should not be directly associated with a wetting angle.

There is a tendency to call complexion transitions “phase transitions” and the finite films that constitute the complexions have been called “phases.” This is also unfortunate. Complexions are not phases as defined by Gibbs (p. 96 in Collected Works [180]) “…the thermodynamic state of any such body without regard to its quantity or form. …Phases (are in equilibrium) when (they) can exist together, the dividing surfaces being plane, in an equilibrium that does not depend on passive resistance”. Complexions cannot exist as a bulk phase. Their compositions and structures do not necessarily appear on an equilibrium phase diagram, and consideration of these structures as phases could lead to mistaken additional degrees of freedom, and thus misinterpretations of the Gibbs phase rule. Thus, these collective phenomena have been called “complexions” with the objective of associating them with interfaces exclusively, and remove direct association to phases.

Complexion transitions can manifest themselves in conjunction with discontinuous changes in material behavior. Dillon et al. [160] have identified six different grain boundary structures in alumina that correlate directly with grain boundary mobility. Given the number of degrees of freedom of the various grain boundaries in a polycrystalline alumina, it is unlikely that the number of complexions is limited to six. However, it may be that, at high temperatures, a relatively small number of grain boundary structures emerge and dominate behavior. Luo and co-workers [182] have associated activated sintering with complexions, and it would be expected that creep behavior, etc., will also depend on complexions. Crystals with many atoms per unit cell such as oxides, especially those which have tightly bound sub-unit cell structural units, such as silica tetrahedral, are likely candidates for disordered complexions.

Methods of treating interfaces with C components and Φ phases and its connection to complexions

Cahn [23] provides a useful and rigorous method of treating the excess quantities associated with an interface in a multi-phase multi-component system. This section provides a trivial extension of Cahn’s method to multiple interfaces. Recently Frolov and Mishin [183] have used this method to include the effect of mechanical stresses on the interfacial region.

The thermodynamic system consists of reservoirs of each of the C independent chemical species; these reservoirs maintain constant chemical potentials, but their values may be varied (e.g., dμ i) by an experimenter. An additional reservoir of an inert species allows the total pressure (i.e., the sum of partial pressures) to be controlled independently. The entire system has a thermally conductive barrier in contact with a thermal reservoir which maintains a constant temperature. The experimenter has C + 2 knobs that can be adjusted independently. The pressures within each phase must be uniform, but can take on different values within isolated bodies according to the value of γκ for isotropic surfaces (where \( \kappa \) is the curvature of the interface) or weighted mean curvature κ γ [50] for anisotropic surfaces; equilibrium requires that these quantities be uniform and have the same value on all surfaces which bound an isolated body. The system is treated as a restricted equilibrium wherein mass exchange across the interfaces is slow compared to all other processes (i.e., grain growth is slow), and this is artificial because redistribution of the species transported from the chemical reservoirs is permitted. There are other systems which might be considered. For example, if the system is closed so that the number of each species is fixed, then the Gibbs free energy would be used. Here, the grand canonical potential, Ω, is used in what follows. The Gibbs free energy function would be appropriate for nanocrystalline systems in which behavior is determined by redistribution of the adsorbate species between the bulk and interfacial regions.

Each phase has equilibrium densities associated with it, each of which depends on the various fixed and uniform potentials, the values of each phase’s densities change according to a Gibbs–Duhem equation for each phase. The discussion is simplified by gravimetric densities (i.e., the number of species in a phase per unit mass, the phase volume per unit mass, and the phase entropy per unit mass). Volumetric densities would require the introduction of a reference volume.

Values of each phase’s densities change according to a Gibbs–Duhem equation for each of the Φ phases, yielding Φ equations with C + 2 unknowns.

$$ \begin{array}{*{20}c} {\text{vap}} {\text{-}} {\text{phase}} \hfill & {0 = - s^{\text{vap}} {\text{d}}T + v^{\text{vap}} {\text{d}}P - \sum {n_{i}^{\text{vap}} {\text{d}}\mu_{i} } } \hfill & {\left( {51} \right)} \hfill \\ {\text{liq}} {\text{-}} {\text{phase}} \hfill & {0 = - s^{\text{liq}} {\text{d}}T + v^{\text{liq}} {\text{d}}P - \sum {n_{i}^{\text{liq}} {\text{d}}\mu_{i} } } \hfill & {\left( {52} \right)} \hfill \\ {\alpha {\text{-}} {\text{phase}}} \hfill & {0 = - s^{\alpha } {\text{d}}T + v^{\alpha } {\text{d}}P - \sum {n_{i}^{\alpha } {\text{d}}\mu_{i} } } \hfill & {\left( {53} \right)} \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill \\ {\pi {\text{-}} {\text{phase}}} \hfill & {0 = - s^{\pi } {\text{d}}T + v^{\pi } {\text{d}}P - \sum {n_{i}^{\pi } {\text{d}}\mu_{i} } } \hfill & {\left( {54} \right)} \hfill \\ \end{array} $$

These Φ equations with C + 2 unknowns result in DoF degrees of freedom (i.e., the maximum possible number of coexistent phases: DoF = C + 2 − Φ) in the Gibbs phase rule.

Each of the interfaces has a relationship between the change in interfacial energy and its interfacial densities (i.e., [S], [V], [N i ] where [] indicates division by a fixed reference area).

Interface Relations: Q equations and Q additional unknowns

$$ \begin{array}{lcl}{{\text{Liquid|Vapor:}}} & {{\text{d}}{\gamma ^{{\text{l|v}}}} = - {{\left[ S \right]}^{{\text{l|v}}}}{\text{d}}T + {{\left[ V \right]}^{{\text{l|v}}}}{\text{d}}P - \sum {{{\left[ {{N_i}} \right]}^{{\text{l|v}}}}{\text{d}}{\mu _i}} } & {(55)} \\ {{\text{Liquid|}}\alpha {:}} & {{{\hat{n}}^\alpha } \cdot {\text{d}}\vec \xi = - {{\left[ S \right]}^{{\text{l|}}\alpha }}{\text{d}}T + {{\left[ V \right]}^{{\text{l}}|\alpha }}{\text{d}}P - \sum {{{\left[ {{N_i}} \right]}^{{\text{l}}|\alpha }}{\text{d}}{\mu _i}} } & {(56)} \\ {\alpha \left( {0_x^\alpha } \right)|\alpha \left( {0_y^\alpha } \right)} & {{{{\hat{n}}}^{0_x^\alpha |0_y^\alpha }} \cdot {\text{d}}\vec \xi = - {{\left[ S \right]}^{0_x^\alpha |0_y^\alpha }}{\text{d}}T + {{\left[ V \right]}^{0_x^\alpha |0_y^\alpha }}{\text{d}}P - \sum {{{\left[ {{N_i}} \right]}^{0_x^\alpha |0_y^\alpha }}{\text{d}}{\mu _i}} } & {(57)} \\ \vdots & \vdots & {} \\ {\beta \left( {0_x^\beta } \right)|\alpha \left( {0_y^\beta } \right)} & {{{\hat n}^{0_x^\alpha |0_y^\beta }} \cdot {\text{d}}\vec \xi = - {{\left[ S \right]}^{0_x^\alpha |0_y^\beta }}{\text{d}}T + {{\left[ V \right]}^{0_x^\alpha |0_y^\beta }}{\text{d}}P - \sum {{{\left[ {{N_i}} \right]}^{0_x^\alpha |0_y^\beta }}{\text{d}}{\mu _i}} } & {(58)} \\ \end{array} $$

The system gains no additional degrees of freedom: DoF of the unknowns (dμ i , dT, dP, dγ, etc.) can be solved in terms of the remaining C + 2 − Φ unknowns. The extra Q unknowns differ in that they are internal variables: the experimenter has no means to adjust these quantities individually, but only indirectly through P, T, and μ i .

The above notation is cumbersome but necessary: \( \hat{n}^{\alpha } \) is the orientation of the crystalline α-interface with respect to a reference frame. \( \vec{\xi } \) is the Cahn–Hoffman anisotropic capillarity vector (which reduces to \( \hat{n}^{\alpha } \gamma \) in the isotropic case). The Cahn–Hoffman \( \vec{\xi } \) is discussed elsewhere [49], for the present purposes it suffices to recognize that \( \hat{n}^{\alpha } \cdot {\text{d}}\vec{\xi } \) represents the change in the interfacial energy for a crystalline orientation \( \hat{n}^{\alpha } \). \( 0_{x}^{\beta } |0_{y}^{\alpha } \) represents the interface between a β-phase (with a crystallographic orientation x with a normal \( \hat{n}^{\beta } \)) and an α-phase (with crystallographic orientation y with a normal \( \hat{n}^{\alpha } \)). Using an outward normal convention, \( \hat{n}^{\alpha } = - \hat{n}^{\beta } \), because both normals share the same reference frame.

Each interface must be in equilibrium with its abutting phases and examples are given above. However, because there may be extant equilibrium phases that do not abut a particular interface, the Gibbs–Duhem equation for that non-abutting phase must also appear as one of the equations used for elimination. Therefore, the behavior of an α–α grain boundary at a range of compositions where only the α phase is in equilibrium will differ from an α–α grain boundary when a β-phase is also at equilibrium. In the first case, the adsorption of a species (e.g., B) will change continuously until a complexion transition occurs, at which point the adsorption changes discontinuously at constant interfacial energy; upon further addition of B to the system, a wetting transition occurs when another phase (e.g., β) appears. In the latter case, partial or complete wetting of the grain boundary by the β-phase is always possible.

In addition to the Gibbs–Duhem equations for multicomponent and multiphase systems, one may choose to use an interface equation for each interface in Fig. 26. In this case, an adsorption isotherm equation will appear for each interface, but each will depend on the potentials that the experimentalist chooses to vary independently. In other words, changing the potentials in Fig. 26 will cause simultaneous changes on all the interfaces in a manner that is calculated above. These interfaces are not available to be controlled independently.

Fig. 26
figure 31

A thermodynamic system with a fixed pressure, temperature, and chemical potentials of C independent components. The experimentalist has the possibility of controlling any of these potentials, but the number of potentials that can be varied independently and maintain phase coexistence is determined by the Gibbs phase rule. The figure illustrates the variety of interfaces that can be considered: vapor/liquid, liquid/crystalline, vapor/crystalline, two-phase crystalline/crystalline, single-phase crystalline/crystalline, amorphous/crystalline, etc. This image is used to illustrate the development of the Gibbs adsorption isotherms for the general case of many interface types in multi-component, multiple alloy systems.

Full size image

The coupling of the interface equations at junctions, such as triple lines, has not been included in the equations above. If they were to be included, then they would give geometric boundary conditions (i.e., the contact angles) for the intersections and this discussion appears in Gibbs (Figs. 11–13 in p. 287 of [184]). Any additional energies such as triple line energies have not been included, but as Gibbs states (footnote on p. 288 of Collected Works [184]) the triple junctions can be treated analogously to interfaces, but with a line replacing a cylinder of localized inhomogeneity instead of a dividing surface replacing a localized slab of inhomogeneous material.

Connection to complexions and wetting transitions

A complexion is associated with particular values of \( \left[ S \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \), \( \left[ V \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \), and \( \left[ {N_{i} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \). (Note that \( \left[ V \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \) has units of a characteristic width of the interface, which can be used to characterize a complexion transition.) A first-order complexion transition would be associated with finite changes of \( \left[ S \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \), \( \left[ V \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \), and \( \left[ {N_{i} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \). At particular values of T, P, and μ i which define the edge of the miscibility gap, an additional phase is in equilibrium with α and β, and then DoF (i.e., DoF = C + 2 − Φ) will decrease by 1.

Each particular interface must be in equilibrium with its abutting phases, or phase in the case of a grain boundary. It is useful to consider several different cases that illustrate the differences in the computation of the adsorption or excess quantities; below we consider examples of grain boundaries in single-phase alloys, and interphase boundaries in multi-component alloys.

Isotropic grain boundary (α/α), unary phase (A)

There is one equation of the Gibbs–Duhem type and one interface equation. Eliminating dP:

$$ {\text{d}}\gamma^{\text{gb}} = \frac{{n_{\text{A}}^{\alpha } \left[ V \right]^{\text{gb}} - \left[ {N_{\text{A}} } \right]^{\text{gb}} v_{\text{A}}^{\alpha } }}{{v_{\text{A}}^{\alpha } }}{\text{d}}\mu_{\text{A}} + \frac{{s^{\alpha } \left[ V \right]^{\text{gb}} - \left[ S \right]^{\text{gb}} v_{\text{A}}^{\alpha } }}{{v_{\text{A}}^{\alpha } }}{\text{d}}T $$
(59)

If the method of the Gibbs’ dividing surface is applied to the case of a grain boundary, then the position of the dividing surface is arbitrary. If that position is chosen so that [V]gb = 0, then for the isothermal case, \( {\text{d}}\gamma^{\text{gb}} = - [N_{\text{A}} ]^{\text{gb}} {\text{d}}\mu_{\text{A}} \equiv - \varGamma_{\text{A}}^{\text{gb}} {\text{d}}\mu_{\text{A}} \); this choice ([V]gb = 0) used by Gibbs is natural if the interface is taken to be a mathematical surface, however, [V]gb is perhaps the most useful characteristic of complexion transitions and a non-zero choice is important in their characterization. [N A]gb is the excess number of atoms associated with the grain boundary, this quantity is generally negative (which means there is a depletion of atoms per unit area of grain boundary), but can be of either sign.

Note that the elimination of the variable dP produces an expression which specifies the necessary variation of P, in other words changes of P are not independent of \( {\text{d}}\mu_{\text{A}} \)and dT. This will be the case for all eliminated variables below.

Anisotropic grain boundary (α/α), binary alloy (A–B)

There is one equation of the Gibbs–Duhem type and one anisotropic interface equation: the \( {\text{d}}\gamma^{\text{gb}} \) is replaced with \( \hat{n}^{{0_{x}^{\alpha } |0_{y}^{\alpha } }} \cdot {\text{d}}\vec{\xi } \). This equation has additional degrees of freedom because the adsorption or the excess entropy will depend on the orientation of the grain boundary with respect to the crystal.

Eliminating dP using the single Gibbs–Duhem equation

$$ \hat{n}^{{0_{x}^{\alpha } |0_{y}^{\alpha } }} \cdot {\text{d}}\vec{\xi } = \frac{{n_{\text{A}}^{\alpha } \left[ V \right]^{\text{gb}} - \left[ {N_{\text{A}} } \right]^{\text{gb}} v_{\text{A}}^{\alpha } }}{{v_{\text{A}}^{\alpha } }}d\mu_{\text{A}} + \frac{{n_{\text{B}}^{\alpha } \left[ V \right]^{\text{gb}} - \left[ {N_{\text{B}} } \right]^{\text{gb}} v_{\text{B}}^{\alpha } }}{{v_{\text{A}}^{\alpha } }}{\text{d}}\mu_{\text{B}} + \frac{{s^{\alpha } \left[ V \right]^{\text{gb}} - \left[ S \right]^{\text{gb}} v_{\text{A}}^{\alpha } }}{{v_{\text{A}}^{\alpha } }}{\text{d}}T $$
(60)

In this case, there are two different Gibbs adsorption isotherm terms: one for the excess of the A-species and one for the B-species. In the example of a two-phase binary alloy given below, the loss of one degree of freedom will result in an equation with only one adsorption isotherm for the species B.

The \( \vec{\xi }\left( {\hat{n}} \right) \) are directly related with the “grain boundary Wulff shape”: for each \( \hat{n} \), the \( \vec{\xi }\left( {\hat{n}} \right) \) is the vector which coincides with a point on the Wulff shape having that \( \hat{n} \). Thus, any point that lies on the grain boundary Wulff shape consists of the set of \( \vec{\xi }\left( {\hat{n}} \right) \) such that \( \hat{n} \) is a stable orientation on the Wulff shape. In the trivial case that the Wulff shape is a circle: \( \vec{\xi }\left( {\hat{n}} \right) = \gamma^{\text{gb}} \hat{n} \).

Liquid–vapor (l|v), binary alloy (A–B)

There are two equations of the Gibbs–Duhem type with C = 2 (one for each phase), and one of the interface type. These two equations are used to solve for the changes in potentials that maintain equilibrium: Eliminating dP and dμ A from the two Gibbs–Duhem relations, and inserting these into the expression for \( {\text{d}}\gamma^{{{\text{l}}|{\text{v}}}} \):

$$ \begin{aligned} {\text{d}}\gamma^{{{\text{l}}|{\text{v}}}} & = \frac{{\left[ {N_{\text{B}} } \right]^{{{\text{l}}|{\text{v}}}} \left( {n_{\text{A}}^{\text{vap}} v^{\text{liq}} - n_{\text{A}}^{\text{liq}} v^{\text{vap}} } \right) - \left[ {N_{\text{A}} } \right]^{{{\text{l}}|{\text{v}}}} \left( {n_{\text{B}}^{\text{vap}} v^{\text{liq}} - n_{\text{B}}^{\text{liq}} v^{\text{vap}} } \right) + \left[ V \right]^{{{\text{l}}|{\text{v}}}} \left( {n_{\text{B}}^{\text{vap}} n_{\text{A}}^{\text{liq}} - n_{\text{A}}^{\text{vap}} n_{\text{B}}^{\text{liq}} } \right)}}{{n_{\text{A}}^{\text{vap}} v^{\text{liq}} - n_{\text{A}}^{\text{liq}} v^{\text{vap}} }}{\text{d}}\mu_{\text{B}} \\ & \quad - \frac{{\left[ S \right]^{{{\text{l}}|{\text{v}}}} \left( {n_{\text{A}}^{\text{vap}} v^{\text{liq}} - n_{\text{A}}^{\text{liq}} v^{\text{vap}} } \right) - \left[ {N_{\text{A}} } \right]^{{{\text{l}}|{\text{v}}}} \left( {s^{\text{vap}} v^{\text{liq}} - v^{\text{vap}} s^{\text{liq}} } \right) + \left[ V \right]^{{{\text{l}}|{\text{v}}}} \left( {s^{\text{vap}} n_{\text{A}}^{\text{liq}} - n_{\text{A}}^{\text{vap}} s^{\text{liq}} } \right)}}{{n_{\text{A}}^{\text{vap}} v^{\text{liq}} - n_{\text{A}}^{\text{liq}} v^{\text{vap}} }}{\text{d}}T \\ & = \frac{{{\text{Det}}\left( {\begin{array}{*{20}c} {\left[ {N_{\text{B}} } \right]^{{{\text{l}}|{\text{v}}}} } & {\left[ {N_{\text{A}} } \right]^{{{\text{l}}|{\text{v}}}} } & {\left[ V \right]^{{{\text{l}}|{\text{v}}}} } \\ {n_{\text{B}}^{\text{vap}} } & {n_{\text{A}}^{\text{vap}} } & {v^{\text{vap}} } \\ {n_{\text{B}}^{\text{liq}} } & {n_{\text{A}}^{\text{liq}} } & {v^{\text{liq}} } \\ \end{array} } \right)}}{{{\text{Det}}\left( {\begin{array}{*{20}c} {n_{\text{A}}^{\text{vap}} } & {v^{\text{vap}} } \\ {n_{\text{A}}^{\text{liq}} } & {v^{\text{liq}} } \\ \end{array} } \right)}}{\text{d}}\mu_{\text{B}} - \frac{{{\text{Det}}\left( {\begin{array}{*{20}c} {\left[ S \right]^{{{\text{l}}|{\text{v}}}} } & {\left[ {N_{A} } \right]^{{{\text{l}}|{\text{v}}}} } & {\left[ V \right]^{{{\text{l}}|{\text{v}}}} } \\ {s^{\text{vap}} } & {n_{\text{A}}^{\text{vap}} } & {v^{\text{vap}} } \\ {s^{\text{liq}} } & {n_{\text{A}}^{\text{liq}} } & {v^{\text{liq}} } \\ \end{array} } \right)}}{{{\text{Det}}\left( {\begin{array}{*{20}c} {n_{\text{A}}^{\text{vap}} } & {v^{\text{vap}} } \\ {n_{\text{A}}^{\text{liq}} } & {v^{\text{liq}} } \\ \end{array} } \right)}}{\text{d}}T \\ \end{aligned} $$
(61)

The term multiplying dμ B is the right-hand side of the traditional form of the Gibbs’ adsorption isotherm. In the notation defined in Eq. (39), and in Equation 514 of Gibbs’ “Equilibrium of Heterogeneous Substances” [184], this becomes \( {\text{d}}\gamma^{{{\text{l}}|{\text{v}}}} = - \varGamma_{{{\text{B}}({\text{A}})}} {\text{d}}\mu_{\text{B}} \) in the case that dT = 0 (the adsorption isotherm); in this form, the equations are derived by locating the dividing surface such that [N A]l|v = [V A]l|v = 0. The equations derived above by elimination of variables do not depend on this particular choice of location, but it can be seen that this reduces to the \( - \varGamma_{{{\text{B}}({\text{A}})}} \) form when \( \left[ {N_{\text{A}} } \right]^{{{\text{l}}|{\text{v}}}} \) and \( \left[ V \right]^{{{\text{l}}|{\text{v}}}} \) are set to zero:

$$ \varGamma_{{{\text{B}}({\text{A}})}} = \frac{{\left[ {N_{\text{B}} } \right]^{{{\text{l}}|{\text{v}}}} \left( {n_{\text{A}}^{\text{liq}} v^{\text{vap}} - n_{\text{A}}^{\text{vap}} v^{\text{liq}} } \right)}}{{n_{\text{A}}^{\text{liq}} v^{\text{vap}} - n_{\text{A}}^{\text{vap}} v^{\text{liq}} }} = \left[ {N_{\text{B}} } \right]^{{{\text{l}}|{\text{v}}}} $$
(62)

α-Crystal/β-crystal, ternary alloy (A–B–C)

There are two Gibbs–Duhem equations (one for each of the α and β phase)—each of which have three components—and an anisotropic interface equation with orientation and misorientation dependence.

Above, we have eliminated dP and dμ A in each case. The choice of eliminated variables is arbitrary and the results will be identical for any choice. However, it is convenient to eliminate variables such that the ones that remain are those which the experimentalist may wish to change. For example, suppose that we change dμ A, dP, and dT independently and allow the dμ B and dμ C to change so as to maintain equilibrium between the two phases. In this case, we would eliminate dμ B and dμ C from the Gibbs–Duhem equations and obtain:

$$ \begin{aligned} \hat{n}^{{0_{x}^{\alpha } |0_{y}^{\beta } }} \cdot {\text{d}}\vec{\xi } & = \frac{{{\text{Det}}\left( {\begin{array}{*{20}c} {\left[ {N_{\text{A}} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } & {\left[ {N_{\text{B}} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } & {\left[ {N_{\text{C}} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } \\ {n_{\text{A}}^{\alpha } } & {n_{\text{B}}^{\alpha } } & {n_{\text{B}}^{\beta } } \\ {n_{\text{A}}^{\beta } } & {n_{\text{C}}^{\alpha } } & {n_{\text{C}}^{\beta } } \\ \end{array} } \right)}}{{{\text{Det}}\left( {\begin{array}{*{20}c} {n_{\text{B}}^{\alpha } } & {n_{\text{B}}^{\beta } } \\ {n_{\text{C}}^{\alpha } } & {n_{\text{C}}^{\beta } } \\ \end{array} } \right)}}{\text{d}}\mu_{\text{A}} \\ & \quad - \frac{{{\text{Det}}\left( {\begin{array}{*{20}c} {\left[ S \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } & {\left[ {N_{\text{B}} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } & {\left[ {N_{\text{C}} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } \\ {s^{\alpha } } & {n_{\text{B}}^{\alpha } } & {n_{\text{B}}^{\beta } } \\ {s^{\beta } } & {n_{\text{C}}^{\alpha } } & {n_{\text{C}}^{\beta } } \\ \end{array} } \right)}}{{{\text{Det}}\left( {\begin{array}{*{20}c} {n_{\text{B}}^{\alpha } } & {n_{\text{B}}^{\beta } } \\ {n_{\text{C}}^{\alpha } } & {n_{\text{C}}^{\beta } } \\ \end{array} } \right)}}{\text{d}}T + \frac{{{\text{Det}}\left( {\begin{array}{*{20}c} {\left[ V \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } & {\left[ {N_{\text{B}} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } & {\left[ {N_{C} } \right]^{{0_{x}^{\alpha } |0_{y}^{\beta } }} } \\ {v^{\alpha } } & {n_{\text{B}}^{\alpha } } & {n_{B}^{\beta } } \\ {v^{\beta } } & {n_{\text{C}}^{\alpha } } & {n_{C}^{\beta } } \\ \end{array} } \right)}}{{{\text{Det}}\left( {\begin{array}{*{20}c} {n_{B}^{\alpha } } & {n_{B}^{\beta } } \\ {n_{C}^{\alpha } } & {n_{C}^{\beta } } \\ \end{array} } \right)}}{\text{d}}P \\ \end{aligned} $$
(63)

General case: Cahn’s determinants

In the sequence of examples given above, the coefficients which multiply the differential quantities become more lengthy as the system becomes more general. However, the form of the last example where the coefficients are written as a ratio of determinants indicates the possibility of a generalization to any case. The ratios are the determinants derived by Cahn using Cramer's rule.

Summary

High temperature capillarity is an important scientific and technological field of research, which covers both thermodynamics (wetting) and kinetics (spreading). In writing this review, we have first attempted to identify phenomena related to wetting, and then proceeded to describe how these phenomena may be modified by the presence of adsorption. We have also emphasized that the simple measure of a contact (or dihedral) angle is not sufficient to understand wetting, and that the anisotropy of crystalline materials can play an important role in the minimization of interface and surface energy. Furthermore, we have summarized the strong influence that chemical heterogeneity and roughness of surfaces can have on both wetting and spreading, since they impact the motion of the triple line.

We have also reviewed wetting between two solid phases, since while solid–liquid interfaces are often important for materials processing, it is the solid–solid interface which most often determines the properties of the final material system. Solid–solid interfacial energy can be experimentally measured, and allows determination of the important value of the thermodynamic work of adhesion; but once again the anisotropy of crystalline materials must be taken into account.

Finally, we have reviewed the fundamentals of adsorption at the thermodynamic, or macroscopic, scale, and how adsorption may play a decisive role in both wetting and wetting transitions. Adsorption has also been considered at the level of the local atomic structure, first with regard to excess distribution and then by using the concept of interface complexions. It is our hope that this review will convince the reader that wetting phenomena cannot be addressed without considering complexions and/or complexion transitions, and this important concept provides a bridge to future work aimed at merging continuum and atomistic approaches to interface science.