Spatial and Spectral Representations of the Geoid-to-Quasigeoid Correction

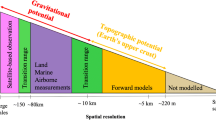
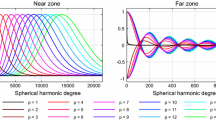
Abstract

In geodesy, the geoid and the quasigeoid are used as a reference surface for heights. Despite some similarities between these two concepts, the differences between the geoid and the quasigeoid (i.e. the geoid-to-quasigeoid correction) have to be taken into consideration in some specific applications which require a high accuracy. Over the world’s oceans and marginal seas, the quasigeoid and the geoid are identical. Over the continents, however, the geoid-to-quasigeoid correction could reach up to several metres especially in the mountainous, polar and geologically complex regions. Various methods have been developed and applied to compute this correction regionally in the spatial domain using detailed gravity, terrain and crustal density data. These methods utilize the gravimetric forward modelling of the topographic density structure and the direct/inverse solutions to the boundary-value problems in physical geodesy. In this article, we provide a brief summary of existing theoretical and numerical studies on the geoid-to-quasigeoid correction. We then compare these methods with the newly developed procedure and discuss some numerical and practical aspects of computing this correction. In global applications, the geoid-to-quasigeoid correction can conveniently be computed in the spectral domain. For this purpose, we derive and present also the spectral expressions for computing this correction based on applying methods for a spherical harmonic analysis and synthesis of global gravity, terrain and crustal structure models. We argue that the newly developed procedure for the regional gravity-to-potential conversion, applied for computing the geoid-to-quasigeoid correction in the spatial domain, is numerically more stable than the existing inverse models which utilize the gravity downward continuation. Moreover, compared to existing spectral expressions, our definition in the spectral domain takes not only the terrain geometry but also the mass density heterogeneities within the whole Earth into consideration. In this way, the geoid-to-quasigeoid correction and the respective geoid model could be determined more accurately.

Appendices

Appendix 1: Potential (of Reference Topographic Density) for External Convergence Domain

To find the spectral representation of the Newton volumetric integral in Eq. (17) for the external convergence domain, we define the fundamental harmonic function $\ell^{ - 1}$ by (e.g., Heiskanen and Moritz 1967, Eqs. 1–81)

$$\ell^{ - 1} \left( {r,\psi ,r^{\prime}} \right) = \frac{1}{r}\sum\limits_{n = 0}^{\infty } {\left( {\frac{{r^{\prime}}}{r}} \right)^{n} P_{n} \left( t \right)} \quad \left( {r \ge r^{\prime}} \right),$$

(54)

where ${\text{P}}_{\text{n}}$ is the Legendre polynomial of degree n, and t = cos ψ. Inserting Eq. (54) in Eq. (17), the topographic potential $V_{\text{e}}^{{{\text{T}},\bar{\rho }^{\text{T}} }}$ for the external convergence domain r ≥ r′ becomes

$$V_{\text{e}}^{{{\text{T}},\bar{\rho }^{\text{T}} }} \left( {r,\varOmega } \right) = G\bar{\rho }^{\text{T}} r\sum\limits_{n = 0}^{\infty } {{\iint\limits_{\phi }} {P_{n} \left( t \right)\int_{{r^{\prime} = R}}^{{R + H^{\prime}}} {\left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} } {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime}} .$$

(55)

The radial integral in Eq. (55) is further rearranged into the form

$$\int_{{r^{\prime} = R}}^{{R + H^{\prime}}} {\left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} } {\text{d}}r^{\prime} = \int_{{r^{\prime} = R}}^{{R + H^{\prime}}} {\left( {\frac{R}{r}} \right)^{n + 2} \left( {1 + \eta } \right)^{n + 2} } {\text{d}}r^{\prime}\quad \left( {n = 0, 1, \ldots } \right),$$

(56)

where $\eta = \left( {r^{\prime} - R} \right)/R.$ Applying a binomial theorem to (1 + η)ⁿ⁺², we get

$$\left( {1 + \eta } \right)^{n + 2} \, \cong \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \left( {\frac{{r^{\prime} - R}}{R}} \right)^{k} \quad \left( {n = 0, 1, \ldots } \right).$$

(57)

Substituting Eq. (57) in Eq. (56) yields

$$\int_{{r^{\prime} = R}}^{{R + H^{\prime}}} {\left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} } {\text{d}}r^{\prime} \cong \int_{{r^{\prime} = R}}^{{R + H^{\prime}}} {\left( {\frac{R}{r}} \right)^{n + 2} \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \left( {\frac{{r^{\prime} - R}}{R}} \right)^{k} } {\text{d}}r^{\prime}\quad \left( {n = 0, 1, \ldots } \right).$$

(58)

Solving the radial integral in Eq. (58) and inserting for the integral limits, we arrive at

$$\begin{aligned} & \int_{{r^{\prime} = R}}^{{R + H^{\prime}}} {\left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2}} {\text{d}}r^{\prime} \cong {\left( {\frac{R}{r}} \right)^{n + 2}\sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{l} {n + 2} \\ k \\ \end{array} }\right)} \frac{1}{{R^{k}}}\frac{{\left( {r^{\prime}-R} \right)^{k + 1} }}{k + 1}} |_{{r^{\prime} = R}}^{{R + H^{\prime}}} \\&\quad = R\left( {\frac{R}{r}} \right)^{n + 2}\sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{l} {n + 2} \\k \\ \end{array} } \right)} \left( {\frac{{H^{\prime}}}{R}} \right)^{k + 1} \frac{1}{k + 1}\quad \left( n = 0, 1, \ldots\right), \\\end{aligned}$$

(59)

where $H^{\prime} = r^{\prime} - R$. Substituting Eq. (59) in Eq. (55), the spectral form of $V_{\text{e}}^{{{{{\rm T},\rho }}^{\text{T}} }}$ becomes

$$\begin{aligned} V_{e}^{{{\text{T}},\bar{\rho }^{\text{T}} }} \left( {r,\varOmega } \right) & \cong G\bar{\rho }^{\text{T}} R^{2} \sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{r}} \right)^{n + 1} } \\ & \quad \times \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{l} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k + 1} }}\frac{1}{k + 1}{\iint\limits_{\phi }} {H^{{{\prime }k + 1}} P_{n} \left( t \right){\text{d}}\varOmega^{\prime}} \\ \end{aligned}$$

(60)

Since the expansion of $V_{\text{e}}^{{{\text{T}},\bar{\rho }^{\text{T}} }}$ into a series of spherical functions converges uniformly for the external convergence domain $r \ge R$, the interchange of summation and integration in Eq. (60) was permitted (cf. Moritz 1990). We note here that the same spectral form of Newton’s integral for the external convergence domain as derived in Eq. (61) can be found by changing the order of applying the radial integration and binomial theorem (cf. Årgen 2004; Vermeer 2008).

The Laplace harmonics $H_{n}$ of the topographic heights in Eq. (61) are defined by the following integral convolution

$$H\left( \varOmega \right) = \sum\limits_{n = 0}^{\infty } {H_{n} \left( \varOmega \right)} ,H_{n} \left( \varOmega \right) = \frac{2n + 1}{4\pi }{\iint\limits_{\phi} } {H^{\prime}P_{n} \left( t \right){\text{d}}}\varOmega^{\prime} = \sum\limits_{m = - n}^{n} {H_{n,m} Y_{n,m} \left( \varOmega \right)} ,$$

(61)

where $H_{n,m}$ are the topographic height coefficients. The corresponding higher-order harmonics $\{ H_{n}^{\left( k \right)} :k = 2,3, \ldots \}$ read

$$\begin{aligned} & H_{n}^{\left( k \right)} \left( \varOmega \right) = \frac{2n + 1}{4\pi }{\iint\limits_{\phi }} {H^{{{\prime }k}} P_{n} \left( t \right){\text{d}}}\varOmega^{\prime} \\ & \quad = \sum\limits_{m = - n}^{n} {H_{n,m}^{\left( k \right)} Y_{n,m} \left( \varOmega \right)} . \\ \end{aligned}$$

(62)

Substituting Eqs. (61) and (62) in Eq. (60), the topographic potential $V_{\text{e}}^{{{\text{T}},\bar{\rho }^{\text{T}} }}$ is obtained in the following spectral form

$$\begin{aligned} & V_{e}^{{T,\bar{\rho }^{\rm T} }} \left( {r,\varOmega } \right) = 4\pi G\bar{\rho }^{\rm T} R^{2} \sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{r}} \right)^{n + 1} \frac{1}{2n + 1}} \\ & \quad \times \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k + 1} }}\frac{1}{k + 1}\sum\limits_{m = - n}^{n} {H_{n,m}^{{\left( {k + 1} \right)}} Y_{n,m} \left( \varOmega \right)} . \\ \end{aligned}$$

(63)

Appendix 2: Potential (of Anomalous Mass Density Contrast Layer) for External Convergence Domain

To find the spectral expression of the gravitational potential $V_{\text{e}}^{\delta \rho }$ (of anomalous mass density contrast layer) for the external convergence domain, we first substitute the density contrast model from Eq. (46) to Newton’s integral in Eq. (18). After limiting the integration domain to the volumetric mass layer, the gravitational potential V ^δρ becomes

$$\begin{aligned} V^{\delta \rho } \left( {r,\varOmega } \right) & \cong G{\iint\limits_{\phi }} {\delta \rho \left( {H^{\prime}_{U} ,\varOmega^{\prime}} \right)\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\ell^{ - 1} \left( {r,\psi ,r^{\prime}} \right)} r^{{{\prime }2}} {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime} \\ & \quad + G{\iint\limits_{\phi }} {\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\beta \left( {\varOmega^{\prime}} \right)\sum\limits_{i = 1}^{I} {\alpha_{i} \left( {\varOmega^{\prime}} \right)\left( {r^{\prime} - R} \right)^{i} } \ell^{ - 1} \left( {r,\psi ,r^{\prime}} \right)} r^{{{\prime }2}} {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime}. \\ \end{aligned}$$

(64)

We note that the parameters H _U , H _L and ρ(H _U , Ω) become $H_{U}^{\prime } ,H_{L}^{\prime }$ and $\rho \left( {H_{U}^{\prime } ,\varOmega^{\prime } } \right)$ when used for volumetric integration on the right-hand side of Eq. (64), because the position of integration point is described by the coordinates (r′, Ω′).

We further define the spectral form of $V_{\text{e}}^{\delta \rho }$ in Eq. (64) for the external convergence domain. Inserting from Eq. (54) to Eq. (64), we get

$$\begin{aligned} V_{e}^{\delta \rho } \left( {r,\varOmega } \right) & \cong Gr\sum\limits_{n = 0}^{\infty } {\iint\limits_{\phi } {\delta \rho \left( {H^{\prime}_{U} ,\varOmega^{\prime}} \right)P_{n} \left( t \right)\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} } {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime}} \\ & \quad + Gr\sum\limits_{n = 0}^{\infty } {\iint\limits_{\phi } {\beta \left( {\varOmega^{\prime}} \right)\sum\limits_{i = 1}^{I} {\alpha_{i} \left( {\varOmega^{\prime}} \right)} P_{n} \left( t \right)\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {r^{\prime} - R} \right)^{i} } \left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime}} . \\ \end{aligned}$$

(65)

The solution of the radial integral in the first constituent on the right-hand side of Eq. (65) yields

$$\begin{aligned} & \int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} } {\text{d}}r^{\prime} = \left( {\frac{R}{r}} \right)^{n + 2} \int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\left( {1 + \frac{{r^{\prime} - R}}{R}} \right)^{n + 2} } {\text{d}}r^{\prime} \\ & \quad \cong \left( {\frac{R}{r}} \right)^{n + 2} \int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \left( {\frac{{r^{\prime} - R}}{R}} \right)^{k} } {\text{d}}r^{\prime} \\ & \quad = \left. {\left( {\frac{R}{r}} \right)^{n + 2} \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k} }}\frac{{\left( {r^{\prime} - R} \right)^{k + 1} }}{k + 1}} \right|_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H_{U}^{{\prime }} }} \\ & \quad = \left( {\frac{R}{r}} \right)^{n + 2} \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k} }}\frac{{H_{U}^{{{\prime }k + 1}} - H_{L}^{{{\prime }k + 1}} }}{k + 1}\quad \left( {n = 0, 1, \ldots } \right). \\ \end{aligned}$$

(66)

Similarly, the solution of the radial integral in the second constituent on the right-hand side of Eq. (65) is found to be

$$\begin{aligned} & \int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\left( {r^{\prime} - R} \right)^{i} } \left( {\frac{{r^{\prime}}}{r}} \right)^{n + 2} {\text{d}}r^{\prime} = \left( {\frac{R}{r}} \right)^{n + 2} \int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\left( {r^{\prime} - R} \right)^{i} } \left( {1 + \frac{{r^{\prime} - R}}{R}} \right)^{n + 2} {\text{d}}r^{\prime} \\ & \quad \cong \left( {\frac{R}{r}} \right)^{n + 2} \int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{{\left( {r^{\prime} - R} \right)^{k + i} }}{{R^{k} }}} {\text{d}}r^{\prime} \\ & \quad = \left( {\frac{R}{r}} \right)^{n + 2} \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k} }}\frac{{H_{U}^{{{\prime }k + i + 1}} - H_{L}^{{{\prime }k + i + 1}} }}{k + 1 + i}\quad \left( {n = 0, 1, \ldots ; i = 1, 2, \ldots , I} \right). \\ \end{aligned}$$

(67)

Inserting from Eqs. (66) and (67) to Eq. (65), we get

$$\begin{aligned} V_{e}^{\delta \rho } \left( {r,\varOmega } \right) & \cong GR\sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{r}} \right)^{n + 1} \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k} }}\frac{1}{k + 1}} \\ & \quad \times {\iint\limits_{\phi }} {\delta \rho \left( {H^{\prime}_{U} ,\dot{\varOmega }^{\prime}} \right)\left( {H_{U}^{{{\prime }k + i + 1}} - H_{L}^{{{\prime }k + i + 1}} } \right)P_{n} \left( t \right){\text{d}}}\varOmega^{\prime} \\ & \quad + GR\sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{r}} \right)^{n + 1} } \sum\limits_{i = 1}^{I} {\sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} } \frac{1}{{R^{k} }}\frac{1}{k + 1 + i} \\ & \quad \times {\iint\limits_{\phi}} {\beta \left( {\varOmega^{\prime}} \right)\alpha_{i} \left( {\varOmega^{\prime}} \right)\left( {H_{U}^{{{\prime }k + i + 1}} - H_{L}^{{{\prime }k + i + 1}} } \right)P_{n} \left( t \right){\text{d}}}\varOmega^{\prime}. \\ \end{aligned}$$

(68)

Tenzer et al. (2012a, b) defined the spherical lower-bound and upper-bound functions ${{L}}_{{n}}$ and ${{U}}_{{n}}$ of a volumetric mass density contrast layer and their higher-order terms in the following form

$$L_{n}^{{\left( {k + 1 + i} \right)}} \left( \varOmega \right) = \left\{ {\begin{array}{l}\begin{aligned} & {\frac{2n + 1}{4\pi }{\iint\limits_{\phi } }{\delta \rho \left( {H^{\prime}_{U} ,\dot{\varOmega }^{\prime}} \right)H_{L}^{k + 1} \left( {\varOmega^{\prime}} \right)P_{n} \left( t \right)d\varOmega^{\prime}}} \\ & = \sum\limits_{m = - n}^{n} {L_{n,m}^{{\left( {k + 1} \right)}} Y_{n,m} \left( \varOmega \right)}\quad i = 0 \\ & \frac{2n + 1}{4\pi }{\iint\limits_{\phi }} {\beta \left( {\varOmega^{\prime}} \right)\alpha_{i} \left( {\varOmega^{\prime}} \right)H_{L}^{k + 1 + i} \left( {\varOmega^{\prime}} \right)P_{n} \left( t \right)d\varOmega^{\prime}} \\ &= \sum\limits_{m = - n}^{n} {L_{n,m}^{{\left( {k + 1 + i} \right)}} Y_{n,m} \left( \varOmega \right)\quad i = 1,2, \ldots ,I} \hfill \\ \end{aligned} \\ \end{array} } \right.$$

(69)

and

$$U_{n}^{{\left( {k + 1 + i} \right)}} \left( \varOmega \right) = \left\{ {\begin{array}{l}\begin{aligned} & {\frac{2n + 1}{4\pi }{\iint\limits_{\phi } }{\delta \rho \left( {H^{\prime}_{U} ,\varOmega^{\prime}} \right)H_{U}^{k + 1} \left( {\varOmega^{\prime}} \right)P_{n} \left( t \right){\text{d}}\varOmega^{\prime}}} \\ &= \sum\limits_{m = - n}^{n} {U_{n,m}^{{\left( {k + 1} \right)}} Y_{n,m} \left( \varOmega \right)\quad i = 0} \\& \frac{2n + 1}{4\pi }{\iint\limits_{\phi }} {\beta \left( {\varOmega^{\prime}} \right)\alpha_{i} \left( {\varOmega^{\prime}} \right)H_{U}^{k + 1 + i} \left( {\varOmega^{\prime}} \right)P_{n} \left( t \right){\text{d}}\varOmega^{\prime}} \\ & = \sum\limits_{m = - n}^{n} {U_{n,m}^{{\left( {k + 1 + i} \right)}} Y_{n,m} \left( \varOmega \right)\quad i = 1,2, \ldots ,I} \end{aligned} \end{array} } \right.$$

(70)

Substituting Eqs. (69) and (70) in Eq. (68) and considering the series expansion up to the maximum degree of $\bar{n}$, we arrive at

$$V_{e}^{\delta \rho } \left( {r,\varOmega } \right) = \frac{\text{GM}}{R}\sum\limits_{n = 0}^{{\bar{n}}} {\left( {\frac{R}{r}} \right)^{n + 1} \sum\limits_{m = - n}^{n} {{e}V_{n,m}^{\delta \rho } Y_{n,m} \left( \varOmega \right)} } ,$$

(71)

where the potential coefficients ${\text{e}}V_{n,m}^{\delta \rho }$ read

$${e}V_{n,m}^{\delta \rho } = \frac{3}{2n + 1}\frac{1}{{\bar{\rho }^{\text{Earth}} }}\sum\limits_{i = 0}^{I} {({}_{e}Fu_{n,m}^{(i)} - {}_{e}Fl_{n,m}^{(i)} )} .$$

(72)

The numerical coefficients { ${}_{\text{e}}{\text{Fl}}_{n,m}^{(i)} ,{}_{\text{e}}{\text{Fu}}_{n,m}^{(i)} :i = 0,1, \ldots ,I$ } in Eq. (65) are given by

$${}_{\text{e}}{\text{Fl}}_{n,m}^{(i)} = \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{k + 1 + i}\frac{{L_{n,m}^{{\left( {k + 1 + i} \right)}} }}{{R^{k + 1} }}\quad \left( {i = 0, 1, \ldots , I} \right),$$

(73)

and

$${}_{\text{e}}{\text{Fu}}_{n,m}^{(i)} = \sum\limits_{k = 0}^{n + 2} {\left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array} } \right)} \frac{1}{k + 1 + i}\frac{{U_{n,m}^{{\left( {k + 1 + i} \right)}} }}{{R^{k + 1} }}\quad \left( {i = 0, 1, \ldots , I} \right).$$

(74)

Appendix 3: Potential (of Anomalous Mass Density Contrast Layer) for Internal Convergence Domain

We apply a similar procedure as used in “Appendix 2” to derive the spectral expression of the potential $V_{i}^{\delta \rho }$ (of anomalous mass density contrast layer) for the internal convergence domain. For this purpose, we define the fundamental harmonic function $\ell^{ - 1}$ in Eq. (54) for the internal convergence domain r < r′ as follows

$$\ell^{ - 1} \left( {r,\psi ,r^{\prime}} \right) = \frac{1}{{r^{\prime}}}\sum\limits_{n = 0}^{\infty } {\left( {\frac{r}{{r^{\prime}}}} \right)^{n} P_{n} \left( t \right)} \quad \left( {r < r^{\prime}} \right).$$

(75)

The substitution from Eq. (75) to Eq. (64) yields

$$\begin{aligned} & \mathop {\lim }\limits_{{r \to R^{ - } }} V_{i}^{\delta \rho } \left( {r,\varOmega } \right) = GR\sum\limits_{n = 0}^{\infty } {\iint\limits_{\phi } {\delta \rho \left( {H^{\prime}_{U} ,\varOmega^{\prime}} \right)P_{n} \left( t \right)\int_{{r^{\prime} = R + H_{L}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} } {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime}} \\ & \quad + GR\sum\limits_{n = 0}^{\infty } {\iint\limits_{\phi } {\beta \left( {\varOmega^{\prime}} \right)\sum\limits_{i = 1}^{I} {\alpha_{i} \left( {\varOmega^{\prime}} \right)} P_{n} \left( t \right)\int_{{r^{\prime} = R + H_{U}^{{\prime }} }}^{{R + H_{U}^{{\prime }} }} {\left( {r^{\prime} - R} \right)^{i} } \left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} {\text{d}}r^{\prime}{\text{d}}}\varOmega^{\prime}} . \\ \end{aligned}$$

(76)

We further rearrange the radial integral in the first constituent on the right-hand side of Eq. (76) into the following form

$$\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} } {\text{d}}r^{\prime} = \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{{r^{\prime}}}{R}} \right)^{1 - n} } {\text{d}}r^{\prime} = \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {1 + \eta } \right)^{1 - n} } {\text{d}}r^{\prime}\quad \left( {n = 0, 1, \ldots } \right),$$

(77)

and apply a binomial theorem to (1 + η)¹⁻ⁿ. Hence

$$\left( {1 + \eta } \right)^{1 - n} \cong \sum\limits_{k = 0}^{\infty } {\left( {\begin{array}{*{20}c} {1 - n} \\ k \\ \end{array} } \right)} \left( {\frac{{r^{\prime} - R}}{R}} \right)^{k} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \left( {\frac{{r^{\prime} - R}}{R}} \right)^{k} \quad \left( {n = 0, 1, \ldots } \right).$$

(78)

Inserting from Eq. (78) to Eq. (77), we get

$$\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} } {\text{d}}r^{\prime} \cong \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{{r^{\prime} - R}}{R}} \right)^{k} } {\text{d}}r^{\prime}\quad \left( {n = 0, 1, \ldots } \right).$$

(79)

The solution of the radial integral in Eq. (79) reads

$$\begin{aligned} & \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} } {\text{d}}r^{\prime} \cong \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \left. {\frac{1}{{R^{k} }}\frac{{\left( {r^{\prime} - R} \right)^{k + 1} }}{k + 1}} \right|_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} \\ & \quad = R\sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \left( {\frac{{H^{\prime}_{U} - H^{\prime}_{L} }}{R}} \right)^{k + 1} \frac{1}{k + 1}\quad \left( {n = 0, 1, \ldots } \right). \\ \end{aligned}$$

(80)

By analogy with Eq. (79), we rewrite the radial integral in the second term on the right-hand side of Eq. (76) as follows

$$\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {r^{\prime} - R} \right)^{i} } \left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} {\text{d}}r^{\prime} = \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {r^{\prime} - R} \right)^{i} \left( {1 + \eta } \right)^{1 - n} } {\text{d}}r^{\prime}\quad \left( {n = 0, 1, \ldots ; \;i = 1, 2, \ldots , I} \right).$$

(81)

The substitution for (1 + η)¹⁻ⁿ from Eq. (78) to Eq. (81) yields

$$\int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {r^{\prime} - R} \right)^{i} } \left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} {\text{d}}r^{\prime} \cong R^{i} \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {\frac{{r^{\prime} - R}}{R}} \right)^{k + i} } {\text{d}}r^{\prime}\quad \left( {n = 0,1, \ldots ;\;i = 1,2, \ldots ,I} \right).$$

(82)

The solution of the radial integral in Eq. (82) is then found to be

$$\begin{aligned} & \int_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} {\left( {r^{\prime} - R} \right)^{i} \left( {\frac{R}{{r^{\prime}}}} \right)^{n - 1} } {\text{d}}r^{\prime} \cong \left. {\sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \frac{1}{{R^{k} }}\frac{{\left( {r^{\prime} - R} \right)^{k + i + 1} }}{k + 1 + i}} \right|_{{r^{\prime} = R + H^{\prime}_{L} }}^{{R + H^{\prime}_{U} }} \\ & \quad = R^{i + 1} \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \left( {\frac{{H^{\prime}_{U} - H^{\prime}_{L} }}{R}} \right)^{k + i + 1} \frac{1}{k + 1 + i} \\ & \quad \left( {n = 0, 1, \ldots ;\; i = 1, 2, \ldots , I} \right). \\ \end{aligned}$$

(83)

Substituting from Eqs. (80) and (83) to Eq. (76) and limiting the series expansion up to the maximum degree $\bar{n}$, we arrive at

$$\mathop {\lim }\limits_{{r \to R^{ - } }} V_{i}^{\delta \rho } \left( {r,\varOmega } \right) = \frac{\text{GM}}{R}\sum\limits_{n = 0}^{{\bar{n}}} {\sum\limits_{m = - n}^{n} {{}_{i}V_{n,m}^{\delta \rho } Y_{n,m} \left( \varOmega \right)} } ,$$

(84)

where the potential coefficients ${}_{\text{i}}V_{n,m}^{\delta \rho }$ are given by

$${}_{\text{i}}V_{n,m}^{\delta \rho } = \frac{3}{2n + 1}\frac{1}{{\bar{\rho }^{\text{Earth}} }}\sum\limits_{i = 0}^{I} {\left( {{}_{i}Fu_{n,m}^{(i)} - {}_{i}Fl_{n,m}^{(i)} } \right)} .$$

(85)

The numerical coefficients { ${}_{\text{i}}{\text{Fl}}_{n,m}^{(i)} ,{}_{i}Fu_{n,m}^{(i)} :i = 0,1, \ldots ,I$ } in Eq. (86) read

$${}_{\text{i}}Fl_{n,m}^{(i)} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \frac{1}{k + 1 + i}\frac{{L_{n,m}^{{\left( {k + 1 + i} \right)}} }}{{R^{k + 1} }}\left( {i = 0, 1, \ldots , I} \right),$$

(86)

and

$${}_{i}{\text{Fu}}_{n,m}^{(i)} = \sum\limits_{k = 0}^{\infty } {\left( { - 1} \right)^{k} \left( {\begin{array}{*{20}c} {n + k - 2} \\ k \\ \end{array} } \right)} \frac{1}{k + 1 + i}\frac{{U_{n,m}^{{\left( {k + 1 + i} \right)}} }}{{R^{k + 1} }}\quad \left( {i = 0, 1, \ldots , I} \right).$$

(87)