Modeling Fluorescence Recovery After Photobleaching in Loaded Bone: Potential Applications in Measuring Fluid and Solute Transport in the Osteocytic Lacunar-Canalicular System

Abstract

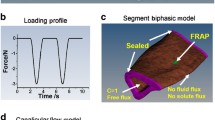
Solute transport through the bone lacunar-canalicular system is essential for osteocyte viability and function, and it can be measured using fluorescence recovery after photobleaching (FRAP). The mathematical model developed here aims to analyze solute transport during FRAP in mechanically loaded bone. Combining both whole bone-level poroelasticity and cellular-level solute transport, we found that load-induced solute transport during FRAP is characterized by an exponential recovery rate, which is determined by the dimensionless Strouhal (St) number that characterizes the oscillation effects over the mean flows, and that significant transport occurs only for St values below a threshold, when the solute stroke displacement exceeds the distance between the source and sink (the canalicular length). This threshold mechanism explains the general flow behaviors such as increasing transport with increasing magnitude and decreasing frequency. Mechanical loading is predicted to enhance transport of all tracers relative to diffusion, with the greatest enhancement for medium-sized tracers and less enhancement for small and large tracers. This study provides guidelines for future FRAP experiments, based on which the model can be used to quantify bone permeability, solute–matrix interaction, and flow velocities. These studies should provide insights into bone adaptation and metabolism, and help to treat various bone diseases and conditions.

Appendices

Appendix A: Estimation of the LCS Permeability and the Characteristic Fluid Relaxation Time

The hydraulic permeability of a single canaliculus k _p has been estimated using a model of rectangular lattice of transverse fibers in the fluid field.65

$$ k_{\rm p} = 0.0572a_0^2 \left( {\Delta /{a_0 }} \right)^{2.377}, $$

( A1)

where a ₀ is the radius of the pericellular fibers (assumed to that of proteoglycan GAG side chain, 0.6 nm), and ${\Updelta}$ is the effective spacing of the fibers of the pericellular matrix (7 nm).

The tissue level permeability k is estimated from the anatomical features of the LCS, assuming a regular array of osteocytes and homogenous canalicular distribution as in Weinbaum et al.65:

$$ k=\frac{2\pi Na^{4}q^{3}}{6\gamma ^{3}d^{2}}\left\{ {A_1 \left[ {I_1 \left( {\gamma /q} \right)-qI_1 \left( \gamma \right)} \right]+B_1 \left[ {qK_1 \left( \gamma \right)-K_1 \left( {\gamma /q} \right)} \right]+\frac{\gamma \left( {q^{2}-1} \right)}{2q}} \right\}, $$

( A2)

where a is the radius of the osteocyte process, q is the ratio of the radius of the canaliculus (b) to the radius of the osteocytic process (a), d is the average spacing between two lacunae, N is the total number of canaliculi emanating from one lacuna, γ is a dimensionless length ratio between the canalicular radius and its associated boundary layer thickness, which is approximated to be the square root of the permeability of a single canaliculus $\left(\gamma =b/{\sqrt{k_{\rm p}}}\right).$ A ₁ and B ₁ are defined as

$$ A_1 =\frac{K_0 \left( \gamma \right)-K_0 \left( {\gamma /q} \right)}{I_0 \left( {\gamma /q} \right)K_0 \left( \gamma \right)-I_0 \left( \gamma \right)K_0 \left( {\gamma /q} \right)} $$

( A3)

$$ B_1 =\frac{I_0 \left( {\gamma /q} \right)-I_0 \left( \gamma \right)}{I_0 \left( {\gamma /q} \right)K_0 \left( \gamma \right)-I_0 \left( \gamma \right)K_0 \left( {\gamma /q} \right)} $$

( A4)

where I ₀, K ₀, I ₁ and K ₁ are modified Bessel functions of the first and second kind.

The characteristic fluid relaxation time is defined as:

$$ \tau _r =\frac{\mu r_{\rm o}^2 }{k\left({13.5\,\hbox{GPa}}\right)}.$$

( A5)

where μ is the viscosity of bone fluid and assumed to be that of sea water (μ = 1.06 × 10⁻³ kg/ms); r ₀ is the radius of the periosteum. The value of τ _r is found to be 6.76 s for the mid-shaft tibia of B6 mouse (r ₀ = 0.57 mm) when the reported values of the LCS ultra- and micro-structures are used (i.e., a = 52 nm; b = 130 nm; N = 70; d = 30 μm).64,69 The sensitivity of τ _r on fiber spacing, size of cell process and canalicular wall was performed previously, and τ _r was found to be more sensitive to the fiber spacing.67

Appendix B: Fluid Pore Pressure, Pressure Gradient, and Canalicular Fluid Velocity

The intermittent dynamic force f(t) (see Fig. 1 and Eq. 1 in the text) can be expanded into a Fourier series:

$$ f(t)=F\left({A_0 +\sum_{n=1}^\infty {A_n \cos \frac{t}{t_1 +t_2 }} n\pi } \right), $$

( B1)

where F is the peak-to-peak force and 2t ₁ is the resting time and 2t ₂ is the loading period and the coefficient for each term is defined as:

$$ A_0 =-\frac{t_2 }{2\left({t_1+t_2 } \right)}, \quad A_n =\left({-1} \right)^{n}\frac{\left({t_1 +t_2} \right)^{2}}{n\pi \left[{n^{2}t_2^2 -\left({t_1 +t_2 } \right)^{2}} \right]}\sin \left({\frac{n\pi t_2}{t_1 +t_2 }} \right). $$

( B2)

Using a set of parameters [R = r/r _o; τ = t/τ _r ; T = ωτ _r ; ω = π/(t ₁ + t ₂); and P = 3 pA/(BTF)] and substituting the Fourier series of loading f(t), the poroelastic equation of the fluid pore pressure (Eq. 3 in the text) is rendered dimensionless:

$$ \frac{\partial ^{2}P}{\partial R^{2}}+\frac{1}{R}\frac{\partial P}{\partial R}+\frac{1}{R^{2}}\frac{\partial ^{2}P}{\partial \theta ^{2}}-\frac{\partial P}{\partial \tau }=-\left[ {1+\frac{Lr_{\rm o} A}{I}R\sin \theta } \right]\sum_{n=1}^\infty {nA_n \sin \left({nT\tau } \right)} $$

( B3)

where R, τ, T, and P are dimensionless radial position, time, frequency, and pressure respectively; ω is the principle angular loading frequency; F is the peak force of the dynamic loading; A is the cross-sectional area of the tibial mid-shaft, B is the Skempton parameter indicating the relative compressibility between the fluid and solid phases in bone (B = 0.53)9,10; r ₀ is the exterior radius of the tibial mid-shaft, L is the offset of the loading force to the center of the bone, I is the moment of inertia of the bone cross-section along the medial-lateral axis, and A _n are the coefficients in the Fourier expansion (Eq. B2).

The boundary conditions are zero pressure at the inner endosteal surface and a leaky outer periosteal surface (Eq. B4), as in previous models60,65,70:

$$ P=0\hbox{ at }R=\lambda ={r_i }/{r_{\rm o}}; \frac{\partial P}{\partial R}+\eta P=0\hbox{ at }R=1 $$

( B4)

where η is the coefficient with η = 0 corresponding to no leakage condition and η→∞ corresponding to free flow condition.

The analytical solution of dimensionless pressure is derived using complex function and separate variables as follows:

$$ \begin{aligned} P\left( {R,\theta ,\tau } \right)&= \sum_{n=1}^\infty {\hbox{Im}\left\{ {\left[ {\frac{A_n }{iT} \left( {1+\frac{Lr_{\rm o} A}{I}R\sin \theta } \right)+C_{0n} I_0 \left( {\sqrt{inT}R} \right)+D_{0n} K_0 \left( {\sqrt{inT}R} \right)} \right.} \right.} \\ &\left. {\left. {+\left( {C_{1n} I_1 \left( {\sqrt{inT}R} \right)+D_{1n} K_1 \left( {\sqrt{inT}R} \right)} \right)\sin \theta } \right]e^{inT\tau }} \right\} \\ \end{aligned} $$

( B5)

where

$$ C_{0n} =\frac{A_n}{iT}\frac{\sqrt{inT}K_1 \left({\sqrt{inT}} \right)-\eta \left[ {K_0 \left({\sqrt{inT}} \right)-K_0 \left({\lambda \sqrt{inT}} \right)} \right]}{I_0 \left({\lambda \sqrt{inT}} \right)\left[{\sqrt{inT}K_1 \left({\sqrt{inT}} \right)-\eta K_0 \left({\sqrt{inT}} \right)} \right]+K_0 \left({\lambda \sqrt{inT}} \right)\left[{\sqrt{inT}I_1 \left({\sqrt{inT}} \right)+\eta I_0 \left({\sqrt{inT}} \right)} \right]} $$

( B6)

$$ D_{0n} =\frac{A_n }{iT}\frac{\sqrt{inT}I_1 \left( {\sqrt{inT}} \right)+\eta \left[ {I_0 \left( {\sqrt{inT}} \right)-I_0 \left( {\lambda \sqrt{inT}} \right)} \right]}{I_0 \left( {\lambda \sqrt{inT}} \right)\left[ {\sqrt{inT}K_1 \left( {\sqrt{inT}} \right)-\eta K_0 \left( {\sqrt{inT}} \right)} \right]+K_0 \left( {\lambda \sqrt{inT}} \right)\left[ {\sqrt{inT}I_1 \left( {\sqrt{inT}} \right)+\eta I_0 \left( {\sqrt{inT}} \right)} \right]} $$

( B7)

$$ C_{1n} =-\frac{A_n Lr_{\rm o} A}{iIT}\frac{\lambda \left[ {\sqrt{inT}K_0 \left( {\sqrt{inT}} \right)+\left( {1-\eta } \right)K_1 \left( {\sqrt{inT}} \right)} \right]+\left( {1+\eta } \right)K_1 \left( {\lambda \sqrt{inT}} \right)}{I_1 \left( {\lambda \sqrt{inT}} \right)\left[ {\sqrt{inT}K_0 \left( {\sqrt{inT}} \right)+\left( {1-\eta } \right)K_1 \left( {\sqrt{inT}} \right)} \right]+\left[ {\sqrt{inT}I_0 \left( {\sqrt{inT}} \right)-\left( {1-\eta } \right)I_1 \left( {\sqrt{inT}} \right)} \right]K_1 \left( {\lambda \sqrt{inT}} \right)} $$

( B8)

$$ D_{1n} =-\frac{A_n Lr_{\rm o}A}{iIT}\frac{\lambda \left[ {\sqrt{inT}I_0 \left( {\sqrt{inT}} \right)-\left( {1-\eta } \right)I_1 \left( {\sqrt{inT}} \right)} \right]-\left( {1+\eta } \right)I_1 \left( {\lambda \sqrt{inT}} \right)}{I_1 \left( {\lambda \sqrt{inT}} \right)\left[ {\sqrt{inT}K_0 \left( {\sqrt{inT}} \right)+\left( {1-\eta } \right)K_1 \left( {\sqrt{inT}} \right)} \right]+\left[ {\sqrt{inT}I_0 \left( {\sqrt{inT}} \right)-\left( {1-\eta } \right)I_1 \left( {\sqrt{inT}} \right)} \right]K_1 \left( {\lambda \sqrt{inT}} \right)} $$

( B9)

The gradients of the dimensionless pressure in the radial and circumferential directions are obtained from Eq. (B5):

$$ \begin{aligned} \frac{\partial P}{\partial R}&=\sum_{n=1}^\infty {\hbox{Im}\left\{ {\left[ {\frac{A_n Lr_{\rm o}A}{iIT}\sin \theta +C_{0n} \sqrt{inT}I_1 \left( {\sqrt{inT}R} \right)-D_{0n} \sqrt{inT}K_1 \left( {\sqrt{inT}R} \right)} \right.} \right.}\\ &\left. {\left. {+\left( {C_{1n} \sqrt{inT}I_0 \left( {\sqrt{inT}R} \right)+\frac{C_{1n} }{R}I_1 \left( {\sqrt{inT}R} \right)-D_{1n} \sqrt{inT}K_0 \left( {\sqrt{inT}R} \right)-\frac{D_{1n} }{R}K_1 \left( {\sqrt{inT}R} \right)} \right)\sin \theta } \right]e^{inT\tau }}\right\}\\ \end{aligned} $$

(B10)

$$ \frac{\partial P}{\partial \theta }=\sum_{n=1}^\infty {\hbox{Im}\left\{ {\left[{\frac{A_n}{iT}\frac{Lr_{\rm o}A}{I}R\cos \theta +\left({C_{1n} I_1 \left({\sqrt{inT}R} \right)+D_{1n} K_1 \left( {\sqrt{inT}R} \right)} \right)\cos \theta } \right]e^{inT\tau }} \right\}} $$

(B11)

The corresponding canalicular fluid velocities in the radial and circumferential directions are derived using Darcy’s law:

$$ u_r =-\frac{k_{\rm {p}}}{\mu }\frac{\partial p}{\partial r}=-\frac{k_{\rm {p}} {BTF}}{3\mu {r}_{\rm {o}} A}\frac{\partial P}{\partial R} $$

(B12)

$$ u_\theta =-\frac{k_{\rm {p}}}{\mu r}\frac{\partial p}{\partial \theta }=-\frac{k_{\rm {p}} {BTF}}{3\mu rA}\frac{\partial P}{\partial \theta} $$

(B13)

where p is the fluid pressure, P is the dimensionless pressure, and k _p is the permeability of a single canaliculus (defined in Eq. A1 in Appendix A).

Appendix C: Unified Transport Equation for the Bone LCS

For the three-compartment transport model (shown in Fig. 3 in the text), oscillating fluid and solute flows occur in the idealized one-dimensional LCS pathway with varying cross-sectional area. A unified, compact form of the transport equation for all segments is derived here. A liner x coordinate is defined and originated from the central lacuna (Fig. 3).

In canaliculi (d _e + d _s ≤ |x | ≤ d + d _e + d _s)

The solute transport satisfies the modified diffusion-convection equation through a porous media

$$ \frac{\partial C}{\partial t}+\left( {1-\sigma_{\rm f}} \right)u\frac{\partial C}{\partial x}=D\frac{\partial ^{2}C}{\partial x^{2}}, $$

( C1)

where C is the tracer concentration, u is the bulk flow velocity (−u _θ in this case), and D is the diffusion coefficient of the tracer. The boundary conditions are

$$ C\left({\pm \left({d+d_{\rm e}+d_{\rm s}} \right),t} \right)=C_0, $$

( C2)

where C ₀ is the tracer concentration that remains constant in the two source reservoirs. Initially, a linear distribution is assumed in the canaliculi connecting the reservoir and the photobleached lacuna, assuming a relative slow photobleaching process.64

$$ C\left({x,0} \right)=C_0 +\left({C_{b}-C_0 } \right)\frac{d_{\rm s} +d_{\rm e}+d-\left| x \right|}{d}, $$

( C3)

where C _b is the concentration inside the photobleached lacuna immediately after photobleaching.

Tapered Entrance (d _s ≤ |x | ≤ d _e + d _s)

The connection between the canalicular channels and the photobleached lacuna is modeled as a tapered tube with expanding cross-sectional area. The cross-sectional area is a function of position x as:

$$ A=\left({1+\beta \frac{d_{\rm s}+d_{\rm e}-\left| x \right|}{d}} \right)^{2}A_{\rm c}, $$

( C4)

where A _c is the summation of the cross-sectional area of the connecting canaliculi. The expansion factor β describes the cross-section radius increment on unit axial distance. Since the tapered entrance connects with the lacuna at the other end, (A = A _f, extracellular fluid space in the lacuna, when |x| = d _s), β can be determined by

$$ \beta =\frac{d}{d_{\rm e}}\left( {\sqrt{{A_{\rm f}}/{A_{\rm c}}}-1} \right) $$

( C5)

The flow velocity in this section decreases with the increasing cross-sectional area:

$$ u_{\exp} =\frac{u}{\left({1+\beta \frac{d_{\rm s} +d_{\rm e}-\left| x \right|}{d}} \right)^{2}}. $$

( C6)

The solute conservation equation is

$$ A\frac{\partial C}{\partial t}+\left( {1-\sigma_{\rm {f}}} \right)u_{\exp } A\frac{\partial C}{\partial x}=D\frac{\partial }{\partial x}\left( {A\frac{\partial C}{\partial x}} \right). $$

( C7)

After substituting Eqs. (C6) and (C4) into Eq. (C7), we derive the following equation for tapered section:

$$ \frac{\partial C}{\partial t}+\left\{{\frac{\left( {1-\sigma_{\rm f}} \right)u}{\left[ {1+{\beta \left( {d_{\rm s} +d_{\rm e} -\left| x \right|} \right)}/d} \right]^{2}}+\frac{2\hbox{sgn}\left(x \right)D\beta /d}{1+{\beta \left({d_{\rm s} +d_{\rm e}-\left| x \right|} \right)}/d}} \right\}\frac{\partial C}{\partial x}=D\frac{\partial ^{2}C}{\partial x^{2}}. $$

( C8)

The initial condition for this section is that it is photobleached as the overall lacuna, i.e.,

$$ C\left( {x,0} \right)=C_{b}. $$

( C9)

Photobleached Lacuna (|x | ≤ d _s)

Assuming the cross-sectional area of the extracellular fluid space in the lacuna (A _f) remains constant along its long axis, A _f can be obtained from Eq. (C5) as

$$ A_{\rm f} =\left({1+\beta \frac{d_{\rm e}}{d}} \right)^{2}A_{\rm c} =\left({1+\beta \lambda_2} \right)^{2}A_{\rm c}, $$

( C10)

where $\lambda _2 =\frac{d_{\rm e}}{d}.$ Therefore, the fluid velocity in this region will decrease and the convection-diffusion equation becomes

$$ \frac{\partial C}{\partial t}+\frac{\left({1-\sigma_{\rm f}} \right)u}{\left({1+\beta \lambda_2 } \right)^{2}}\frac{\partial C}{\partial x}=D\frac{\partial ^{2}C}{\partial x^{2}}. $$

( C11)

The initial condition is that the entire of the lacuna will be uniformly photobleached as follows:

$$ C\left( {x,\;0} \right)=C_{b}. $$

( C12)

Unified Dimensionless Equation

The above equations can be rendered dimensionless using the following dimensionless parameters (Eq. C13).

$$ x^{\ast}=\frac{x}{d}, \quad \tau =\frac{d^{2}}{D}, \quad t^{\ast}=\frac{t}{\tau}, \quad C^{\ast}=\frac{C-C_0 }{C_0 }, \quad \hbox{Pe}=\left( {1-\sigma_{\rm f}} \right)\frac{u_0 d}{D}, \quad u^{\ast}=\frac{u}{u_0},\quad \lambda _1 =\frac{d_{\rm s}}{d}, \quad \lambda_2 =\frac{d_{\rm e}}{d} $$

( C13)

To obtain a compact form of the transport equations, we define two functions g and h that vary with spatial locations and reflect the influences of the cross-sectional area variation on convective velocity and mass flow rate:

$$ g=\left\{\begin{array}{ll} {1,} & {\lambda _1 +\lambda _2 \le \left| {x^{\ast}} \right|\le 1+\lambda _1 +\lambda _2 \left( \hbox{canaliculi} \right)} \\ {\left[ {1+\beta \left( {\lambda _1 +\lambda _2 -\left| {x^{\ast}} \right|} \right)} \right]^{-2},} & {\lambda _1 \le \left| {x^{\ast}} \right|\le \lambda _1 +\lambda _2 \left( {\hbox{tapered} \hbox{sections}} \right)} \\ {\left( {1+\beta \lambda _2 } \right)^{-2},\;} & {\left| {x^{\ast}} \right|\le \lambda _1 \left( {\hbox{photobleached} \hbox{lacuna}} \right)} \\ \end{array}\right. $$

( C14)

$$ h=\left\{ {{\begin{array}{ll} {\frac{2\hbox{sgn}\left({x^{\ast}} \right)\beta }{1+\beta \left({\lambda_1 +\lambda_2 -\left| {x^{\ast}} \right|} \right)},} & {\lambda_1 \le \left| {x^{\ast}} \right|\le \lambda _1 +\lambda _2 \left({\hbox{tapered}\,\, \hbox{sections}} \right)} \\ {0, } & {\hbox{else}} \\ \end{array} } } \right. $$

( C15)

The compact form of the transport equation is given as:

$$ \frac{\partial C^{\ast}}{\partial t^{\ast}}+\left({\hbox{Pe}\cdot u^{\ast}\cdot g+h} \right)\frac{\partial C^{\ast}}{\partial x^{\ast}}=\frac{\partial ^{2}C^{\ast}}{\partial x^{\ast2}}. $$

( C16)

The initial and boundary conditions are

$$ C^{\ast}\left({\pm\left( {1+\lambda _1 +\lambda _2 } \right),t} \right)=0, $$

( C17)

$$ C^{\ast}\left( {x,0} \right)=\left\{ {{\begin{array}{ll} {\left( {1+\lambda _1 +\lambda _2 -\left| {x^{\ast}} \right|} \right)C_{b}^\ast ,} & {\lambda _1 +\lambda _2 \le \left| {x^{\ast}} \right|\le 1+\lambda _1 +\lambda _2 \left({\hbox{canaliculi}} \right)} \\ {C_{b}^\ast ,} & {\left| {x^{\ast}} \right|\le \lambda _1 +\lambda _2 \left( {\hbox{else}} \right)} \\ \end{array} }} \right. $$

( C18)