Introduction

Predicting the evolution of existing landslides and first-failure phenomena is faced through many models that essentially belong to two broad categories, namely geotechnical models and phenomenological approaches. The former pursue several goals including the analysis of the temporal evolution of landslides and their instability (Duncan 1996; Alonso et al. 2010; Ferrari et al. 2011; Secondi et al. 2013; Crosta et al. 2014; Cotecchia et al. 2016; Soga et al. 2016; Bru et al. 2018), but the results obtained for a specific landslide are valid for that one and can hardly be extended to other, albeit similar, phenomena. Hence, for forecasting purposes, quite often the technicians make use of phenomenological approaches. These are essentially data-based models relating input and output variables through black-box procedures.

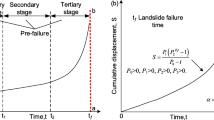
The first practical method, which pioneered phenomenological approaches to predict the time of slope failure, was proposed by Saito (1965) on the basis of the tertiary creep theory. Later, observations of large-scale slope failure tests led Fukuzono (1985) to deduce a semi-empirical relationship between velocity and acceleration in the landslide accelerating stage and develop the so-called inverse velocity method, the best-known phenomenological approach for rocks. The method uses the displacement data to estimate the collapse time by assessing, through a linear regression tool, when the inverse of the slope velocity goes to 0. It was further generalized by Voight (1988, 1989), to account for different materials, and by Rose and Hungr (2007), to cover open pit instability. Being the original method and its generalizations based on accelerating creep theory, they are suitable for short-term prediction during accelerating stages (Chen and Jiang 2020).

Recently, data-based models relying on artificial intelligence approaches, as machine learning models (Huang et al. 2017), have been applied to predict slope deformations on a limited number of displacement measures. These methods, based on statistical analysis of historical data, seek to minimize the error between the simulated and measured values in order to determine the optimal parameters for predicting deformations. They show potential applicability to mid-/long-term prediction, especially for slope deformation with a periodic variation (Chen and Jiang 2020). However, caution is advised in selecting the most suitable artificial intelligence model for the case to be studied (Lian et al. 2015).

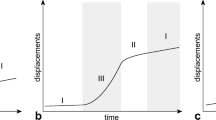
This paper proposes a new approach based on previous works that highlighted common kinematic characteristics for landslides sliding along a slip surface as firstly identified on a heuristic basis by  Leroueil et al. (1996). In particular, Grimaldi (2008) and Cascini et al. (2014) introduced, on a quantitative basis, three different trends: movements related to a stationary condition, as those in dry periods (Trend I); movements due to a recurrent perturbation as the seasonal increase in pore water pressure during the wet season (Trend II); and movements triggered by a significant perturbation, for instance an earthquake or a newly formed local slip surface connected with the main existing slip surface (Trend III). This approach has been enriched by Cascini et al. (2019) and Scoppettuolo et al. (2020), recognizing that the occasionally reactivated stages, formerly called Trend III, correspond to two different stages, i.e., what we call as true Trend III, which is typical of accelerative but not catastrophic stages, and Trend IV, which can potentially end in failure. Further and final extension by Cascini et al. (2020) and Babilio et al. (2021) to five different stages is based on mechanical and stability arguments.

As a relevant result of these contributions, it is possible to calculate piecewise smooth approximations of landslide displacement data, minimizing an appropriately defined error, whenever the record has been previously divided into monotonic stages (Babilio et al. 2021). Due to this feature, the main purpose of the approach was not prediction, but the search for the best fit of the data in a given class of functions.

The present work extends the approach to prediction of landslide evolution by exploiting the same approximation strategy. To this end, an automatic process is implemented to split the data by updating the approximation to the current data record. Therefore, the update frequency of the landslide displacement prediction corresponds to the sampling frequency.

The displacement approximation passes through the evaluation of a dimensionless quantity, the displacement exponent, related to the signs and growth properties of the displacement itself, and its first three derivatives. Since the displacement (Chen et al. 2021), velocity (Chen and Jiang 2020), and acceleration (Xu et al. 2011) are recognized as useful indicators for characterizing slope failure, we argue that the displacement exponent could be profitably exploited in the prediction of the landslide evolution.

The validity and effectiveness of the method have been tested through the application to the landslides in the dataset collected by Scoppettuolo et al. (2020) and are here exemplified with the aid of four case studies, which are representative of all the activity stages introduced by Leroueil et al. (1996) and are among the best-known case studies in the world.

The paper is organized as follows: “Materials” describes the materials underlying the method, explained in detail in “The proposed method”, while “Explanatory examples of the displacement forecasting method” provides explanatory examples that give an idea of its applicability, discussed in “Applicability of the method”. Some remarks in “Concluding remarks” close the contribution.

Materials

The international literature provides interesting insight on slope movements but does not systematically analyze or compare the landslide displacements with the aim of finding common trends where present. In view of this gap, the implementation of an appropriate dataset was the first step taken from the early stages of the research. To this end, a thorough bibliographic research began on the most documented case studies in the scientific literature, selecting papers providing the most of the following information: the adopted classification system; the size of the main landslide body, in terms of both the areal extension and depth, as well as its geological, geomorphological, and hydrogeological features; the triggering factors and the boundary conditions; the properties of soils involved in the sliding; the pore water pressure regime; significant displacement measurements and the experimental system used to acquire the experimental data; the interpretation of the landslide evolution provided by the those who acquired and interpreted the experimental data. The dataset currently collects eighteen landslides (Scoppettuolo et al. 2020), including cases of collapse of existing landslides as well as phenomena of first failure, such as those frequently occurring in open-pit mines, and thus allows for the analysis of all the stages defined by Leroueil et al. (1996).

The case studies selected are highly heterogeneous in terms of geological and hydrological contexts and triggering factors, which, depending on the case, are represented by the following: the variation of groundwater levels; climatic factors (rainfall and/or snow melt); the fluctuation of the level of the reservoir located at the foot of the landslide; excavation as in the case of open-cast mines, and so on. In most cases, landslides are translational and/or rotational phenomena involving clay, silt, limestone, debris, or rock. Sliding bodies have dimensions, i.e., length (L),  width (W), and thickness (H),  that vary over a wide range from landslide to landslide (L from 340 up to 2000 m and H from 9.6 m to 250 m, respectively), and often contain smaller phenomena within them (see Fig. 1). Displacement data records are acquired using various monitoring devices, such as inclinometers, extensometers, distometers, surface markers, and total station optical targets. Details about location, monitoring stations, length, depth and volume, composing material and movement type of the landslide included in the dataset as well as references used as the source of data are reported in (Scoppettuolo et al. 2020), where the case studies are also grouped in terms of the most relevant triggering factors.

Fig. 1
figure 1

Typical geometry of the landslides in the dataset: plan (top panel) and longitudinal cross section (bottom panel). L,  W, and H stand for the length in the direction of motion, width, and thickness of the main sliding body, respectively. Dot-dashed line and A-markers indicate the section plane and the section normal. Often, the selected papers analyze a smaller secondary landslide body of dimensions l,  w,  and h

Full size image

An overview of the recorded displacement data is provided in Fig. 2, which highlights a variety of displacement trends that are not comparable to each other. Some details become apparent (see Figs. 3, 4, and 5) by grouping together, according to the proposal of Leroueil et al. (1996), the phenomena and by using a scale suitable for the order of magnitude of the displacement of a given landslide.

Fig. 2
figure 2

Displacement data for the eighteen landslides included in the collected dataset

Full size image
Fig. 3
figure 3

Active landslides in the dataset

Full size image
Fig. 4
figure 4

Landslides characterized by occasional reactivations

Full size image
Fig. 5
figure 5

Landslides affected by failure events

Full size image

Looking at these diagrams, we observe that similar displacement patterns can be individuated for apparently different landslides; any single record can be subdivided in a sequence of stages; there are typical deformation values, which change from active landslides to failure phenomena (Scoppettuolo et al. 2020). We also observe that activity stages triggered by recurring factors, as seasonal rainfall, evolve through an alternation of linear or concave curves (Fig. 3), while occasional reactivations (Fig. 4) and failure events (Fig. 5) are characterized by convex curves.

The proposed method

The identification of common characteristics in the landslide displacements and the knowledge subsequently acquired on this topic lead us to propose the flowchart shown in Fig. 6, which indicates the steps of a consistent procedure aimed at forecasting the evolution of landslides.

Fig. 6
figure 6

A framework to forecast the landslide evolution

Full size image

The first step is to look for common kinematic patterns for each stage of the landslide. Once identified, the second step should be devoted to testing whether or not a well-defined dynamic equilibrium condition can be associated with each of the recognized kinematic trends. In case of a positive answer to the previous steps, the common kinematic and dynamic characteristics of the displacement trends should be used to predict the landslide evolution, as the third step. The flowchart, the formalization of each step, and their use to predict landslide evolution are described in the remainder of this section.

Finding common kinematic features of landslides

In the authors’ opinion, several procedures can be followed to develop each step in the flowchart. During the research that led to the proposal of Fig. 6, after collecting well-documented case studies, each single activity stage of the landslides in the dataset has been selected through the analysis of the factors that influenced their kinematic evolution. Then, an attempt was made to find a procedure to go from an apparently very large number of trends (Fig. 2) to a very small one.

Grimaldi (2008) has achieved this goal by selecting each activity stage of the available landslides and normalizing both time and displacement as

$$\begin{aligned}&T_{i,j}=\frac{t_{i,j}-t_{0,j}}{t_{n,j}-t_{0,j}}\,,\end{aligned}$$
(1)
$$\begin{aligned}&D_{i,j}=\frac{d_{i,j}-d_{0,j}}{d_{n,j}-d_{0,j}}\,, \end{aligned}$$
(2)

where \(t_{0,j}\,,\) \(t_{n,j}\,,\) \(t_{i,j}\,\) \(d_{0,j}\,,\) \(d_{n,j}\,,\) and \(d_{i,j}\) are the initial, final, and current time and displacement of the jth stage (Fig. 7a). Equations (1) and (2) made it possible to identify three different dimensionless displacement-vs-time diagrams, each of which having a physical meaning (Grimaldi 2008; Cascini et al. 2014). Later, making use of the same procedure, Scoppettuolo et al. (2020) identified 102 activity stages for the curves in Fig. 2 that, in the dimensionless displacement diagram, originate only 4 displacement classes (Fig. 7b). These typical dimensionless trends (TDTs) include landslides that move with constant velocity (Trend I); those mobilized by recurring triggering factors (Trend II); occasional reactivations (Trend III); and failure events (Trend IV). However, Scoppettuolo et al. (2020) noted that, among those recognized as Trend IV stages, and thus expected to be failure events, the only exceptions were the first two stages of the Vajont landslide, both originating from reservoir filling, which veered towards Trend II after a subsequent reservoir lowering.

Fig. 7
figure 7

Kinematic characterization of the landslides through the dimensionless representation of cumulative displacements: (a) data partition and selection of the single stage period and (b) definition of the nature of the system response. Lower graph in panel (a) and graph in panel (b) were first published in Mathematics and Mechanics of Complex Systems (Babilio et al. 2021), by Mathematical Sciences Publishers

Full size image

From the landslide displacement to the stability chart

Evaluation of the dynamic characteristics of the TDTs in Fig. 7b is the objective of the second phase of the proposed framework, which, at least in principle, can be pursued through geotechnical methods or reduced-order models. Unfortunately, neither category could be used. In fact, the methods of the former require the availability of large and accurate input data, which is not the case for all the landslides in the dataset, even if they are well monitored and studied in the literature, while those of the latter are based on complicated nonlinear equations, which are difficult to deal with for all case studies.

Instead, by paying attention to the displacement trends and their derivatives up to the third order, it was possible to analyze all the stages of activity shown in Fig. 7b. In fact, the displacement and its derivative of the first order (velocity) represent kinematic features of the landslide motion, while the derivative of the second order (acceleration) is proportional to the inertial forces acting on a moving body and, as such, can describe the dynamics of the system. In turn, the derivative of the third order (jerk) describes the variation of inertial forces over time (Chase et al. 2003; He et al. 2015; Noda et al. 2013) and can help in the dynamic analysis, even if this physical quantity is not commonly used in geology and geotechnics. The analysis is based on approximating the dimensionless trends in Fig. 7b with the power law \(D=T^x,\) suitable for interpreting all the experimental data (D,  T,  x stand for the dimensionless displacement, time, and characteristic exponent of the stage), and the subsequent calculation of the dimensionless derivatives (Cascini et al. 2020; Babilio et al. 2021).

Stable trends are characterized by an acceleration that is \(0\) (Trend I), negative (Trend II), or positive but decreasing to \(0\) (Trend III). In contrast, acceleration takes on a positive and increasing value for unstable ones (Trend IVa,b), which can be distinguished on the basis of jerk. In fact, Trend IVa is characterized by a decreasing jerk, which indicates the possibility that the landslide may decelerate as a result of specific changes in boundary conditions, while Trend IVb has an increasing jerk indicating the attainment of a condition that definitely leads to failure, as summarized in Table 1, where vanishing, positive, and negative functions are marked by “\(0\),” “\(+\),” and “−,” respectively.

Table 1 Trend classification of the D(T) function and its derivatives up to the third order. Adapted from the table first published in Mathematics and Mechanics of Complex Systems (Babilio et al. 2021), by Mathematical Sciences Publishers
Full size table

Growth properties are indicated by arrows: two-headed horizontal arrow \((\leftrightarrow )\) represents a steady state, upward arrow \((\nearrow )\) represents growth, downward arrow \((\searrow )\) stands for decrease. The last column reports the landslide signature, a compact indicator introduced by Babilio et al. (2021) built as a compound of three symbols, associated with velocity, acceleration, and jerk, in that order. Similarly to signs of functions discussed before, each symbol can assume one of the following values: “\(0\)” for a function that is either zero or constant; “−” for a positive and decreasing function, or a negative and increasing function; “\(+\)” for a positive and increasing function. Based on these concepts, the stability chart shown in Fig. 8, which allows the quantitative assessment of the dynamic equilibrium of the landslides and is the end point of the step 2 (Fig. 6), can be drawn (Babilio et al. 2021). In this chart, the stable trends are represented by \(x=1\) (Trend I), \(0<x<1\) (Trend II) and \(1<x<2\) (Trend III). For unstable trends Trend IVa and Trend IVb, the exponent value is in the range \(2\le x<3\) or is equal to or greater than 3,  respectively.

Fig. 8
figure 8

Stability chart obtained by approximating dimensionless data from landslides in Fig. 2 through the power-law function \(D=T^x.\) The colored curves represent the thresholds between fields with different stability, characterized by the exponents of the power law: \(x=1\) corresponds to Trend I, \(x\in (0,1)\) to Trend II, \(x\in (1,2)\) to Trend III, \(x\in [2,3)\) to Trend IVa, and \(x \ge 3\) to Trend IVb. Adapted from the graph first published in Mathematics and Mechanics of Complex Systems (Babilio et al. 2021), by Mathematical Sciences Publishers

Full size image

We emphasize that the procedure illustrated so far, applied to all the 102 stages in the dataset collected by Scoppettuolo et al. (2020), led to satisfactory results, in terms of approximation of displacement, velocity, acceleration, and jerk (Babilio et al. 2021). However, if the duration of a stage is not known in advance, which is the case of real-world applications, the perspective must change. Indeed, the prediction of the evolution of a landslide requires that both the trend type and the displacement have to be estimated on the basis of a limited number of displacement measures provided by a monitoring system, as shown in the following.

Forecasting the slope evolution through the displacement trends

The first block of tasks in step 3 in Fig. 6 involves the following: (i) recording, at a given time-step, displacement data of the landslide whose evolution must be predicted, (ii) nondimensionalization of data and assessing its kinematic and dynamic characteristics, and (iii) processing data to reconstruct landslide displacements. The next block uses the processed information to forecast the temporal evolution of a landslide during a single activity stage, which is an objective generally pursued by means of empirical approaches. For this purpose, two slightly different methods, one by Cascini et al. (2014), the other by Babilio et al. (2021), hereafter referred to as Approaches I and II, respectively, can be implemented as the block 2 in step 3.

According to Cascini et al. (2014), the displacement may be approximated in the Approach I trough a function written as

$$\begin{aligned} d(t)=d_{\mathrm {ref}}+\Delta t_{\mathrm {ref}} M\left( \frac{{t-t_{\mathrm {ref}}}}{{\Delta t_{\mathrm {ref}} }}\right) ^{\frac{v_{\max }}{M}}, \end{aligned}$$
(3)

with \(d_{\mathrm {ref}},\) \(t_{\mathrm {ref}},\) and \(\Delta t_{\mathrm {ref}}\) the reference displacement, time, and time interval, respectively, and M and \(v_{\max }\) a velocity coefficient and the peak velocity, both updated at the current data entry. The iterative procedure for computing the displacement from Eq. (3) has been tested on a specific case of Trend II movements, showing that reliable predictions of displacements can be obtained already from the early data records of the trend, provided few accurate measurements are available.

In Approach II, once both \(t_0\) and \(d_0\) of the activity stage are individuated, monitored displacement and time are nondimensionalized through Eqs. (1) and (2), inserted into the chart of Fig. 8 to infer the stability of the stage and the displacement is approximated by using a power-law function, of exponent x. Once x is calculated, coherently with Eqs. (1) and (2), the dimensional displacement is computed as

$$\begin{aligned} d(t)=d_{0}+\left( \frac{{t-t_{0}}}{{t_{n}-t_{0}}}\right) ^x\left( d_{n}-d_{0}\right) \,, \end{aligned}$$
(4)

where \(d_{n}\) stands for the current displacement read at time \(t_{n}.\) Both x and \(d_{n}\) are updated as \(t_{n}\) changes, that is the procedure is repeated as any new monitoring data record is acquired. Therefore, the estimated curve of the corresponding dimensional displacements gets closer and closer to monitored data and its extrapolation progressively provides an increasingly accurate estimate of the landslide temporal evolution. Furthermore, considering that, in the stability chart, the exponent x assumes well-defined values passing from one sub-domain to another, the landslide stability is automatically assessed.

The validity and effectiveness of the method, both implemented as Approach I or II, were tested by applying it to the landslides of the dataset. Noteworthy the considered records are historical data. However, by loading data entries into the procedure one by one, in order to simulate an actual forecasting application, the behavior of the tool as a blind predictor has been assessed. The obtained results allow arguing that both capture the actual shape of single-activity-stage displacement and can be exploited to draw sequences of stages as those reported in Fig. 9. Four explanatory examples will be described in detail below, in “Explanatory examples of the displacement forecasting method”.

Fig. 9
figure 9

Typical sequences of kinematic stages described in terms of (from top to bottom) displacement, velocity, acceleration, and jerk

Full size image

It must be noted that if the procedure here proposed is adopted as a framework, but Eq. (3) or (4) are substituted by any possible other function approximating experimental data, it is appropriate to recommend caution in choosing target function. Finally, with appropriate redefinition of the velocities \(v_{\max }\) and M and choice of the set of constants, Eq. (3) converges to Eq. (4), leading to the conclusion that the two approaches can be made equivalent.

Explanatory examples of the displacement forecasting method

The method has been applied to all case studies in the dataset. In addition to the approximations of displacements and evaluations of corresponding velocity, acceleration, and jerk, also the stability of each of the 102 stages has been assessed and error estimates have been considered. We refer the reader to (Babilio et al. 2021) and in particular to the Appendix therein where all test results are documented.

Here, for the sake of brevity, we detail about only four renowned landslides, namely Vallcebre, La Clapière, Vajont, and La Saxe. These case studies were selected as they (i) exhibit all the stability trends in Figs. 7b, 8, and 9, (ii) have a different size in terms of areal extension and volume, (iii) involve different geological contexts and soils, and (iv) are triggered by different external and internal factors. Indeed, the variety of types of motion (translational and rotational slides, toppling), volume sizes (from 8 up to 270 million m\(^3\)), involved materials (clays, marls, limestone, rock) of such examples, and the underlying nature of the analysis based on dimensionless quantities prove that the approach is not dependent on the type or scale of the landslide analyzed.

The monitoring data of Vallcebre, La Clapière, and Vajont landslides are retrieved from scientific papers, whereas La Saxe landslide data was kindly provided by the Geological Survey of Valle d’Aosta Region.

The obtained results can be easily replicated and compared with those arising from different procedures; moreover, the method can be tested in the field and analyzed in the light of a debate that, as for the Vajont landslide, is still alive today.

Vallcebre case study

The Vallcebre landslide is in Northeastern Pyrenees, 140 km from Barcelona (Spain), and it develops in stiff clays with shale and gypsum layers over a limestone bedrock. The experimental data of this well-monitored landslide come from wire extensometers and electronic piezometers that show a close correlation between displacements and groundwater level, in turn associated with rainfall (Corominas et al. 2005).

This originates over the years a sequence of Trends I and II (Fig. 9a) which during the observation period represents a stable condition since both acceleration and jerk vanish (Trends I) or acceleration is negative and jerk decreases (Trends II).

The landslide temporal evolution in terms of measured displacement and velocity (Fig. 10a and b, respectively), with reference to a single activity stage, has been analyzed by employing Approach I. The feasibility of the method (Cascini et al. 2014) is testified by Fig. 10, where power-law functions calibrated on the first 3,  5,  7, and 86 available data are compared with the monitored data. As is evident, the calibration with the first 7 data, that is 80 days in advance with respect to the total duration of the considered activity stage, provides a very satisfactory result. Moreover, it must be observed that the results obtained by Cascini et al. (2014) agree well with findings by Ferrari et al. (2011), who analyzed the Vallcebre landslide through the solution of equilibrium equations considering proper boundary conditions.

Fig. 10
figure 10

Forecasting the evolution of the Vallcebre landslide (Corominas et al. 2005) calibrated with increasing number of recorded data. Time in days (abscissas); displacements in mm, panel a, velocity in mm/day, panel b (ordinates). The top panels show the data recorded over the whole stage (86 observations in total). From the second to the last row of panels, from top to bottom, the predicted displacement (column a) and velocity (column b), calculated considering 3,  5,  7, and 86 records, are shown. Reproduced from (Cascini et al. 2014), with permission

Full size image

By adopting the Approach II, the stages of the landslide are suitably approximated by power laws having exponent lower than or equal to 1, both in the dimensionless and in the dimensional representation, so confirming the stability of the landslide motion.

La Clapière case study

La Clapière landslide is a large rockslide in the southern French Alps, which mobilizes a volume of approximately 55 million m\(^3\) in a gneissic rock slope covered by a forest. According to Helmstetter et al. (2004), the landslide probably started to move before the beginning of the twentieth century, although the first changes in slope geometry were estimated only in the period 1950–1980,  through an aerial photogrammetric survey. A displacement monitoring of the slope started in 1982 with the aid of topographic measurements that highlighted a complex sequence of Trend I and II and an accelerating stage, represented by a Trend III, in the period 1986–1987 (Scoppettuolo et al. 2020). The slope displacements appear related to river flow fluctuations, snow melting, and rainfalls, while Follacci et al. (1988) relate the previously mentioned occasional reactivation with the failure of the gneissic bedrock in the northwestern block.

Focusing on this stage, Fig. 11 shows the results obtained by applying the Approach II to data from a surface marker considered representative of the landslide motion.

Fig. 11
figure 11

Forecasting displacements with an increasing number of observations. The approximation of the stage record (red points) improves as any new displacement is acquired (a) through the estimates of exponent x updated at any new data entry (b). Graphs refer to the 4th activity stage, from 1 July 1986 to 25 September 1987 of La Clapière landslide. Smaller insets report the whole data record (a) and the exponent time evolution (b), from 17 January 1983 to 31 August 1994

Full size image

It can be noted that the limited number of experimental measures, taken with a time step of 3 months, leaves uncertainty in the individuation of the onset of the occasional reactivation, although the displacement trend is still correctly estimated.

In fact, the displacement exponent is \(1<x<2\) during the entire time period, testifying the occurrence of a Trend III that corresponds to a weakly stable condition for the landslide (Babilio et al. 2021).

Vajont case study

The Vajont landslide is one of the most studied slope instability in the literature (Nonveiller 1987; Semenza 2001; Kilburn and Petley 2003). Available data from monitoring stations cover the period 1960–1963. In 1960 and 1962, two fillings of the dam reservoir were responsible for two accelerating stages of the existing landslide along Monte Toc. Both those stages were followed by a deceleration stage just after the lowering of the water level in the reservoir. In 1963,  a third filling, with the water table in the reservoir at its maximum level, was followed by a catastrophic reactivation of the landslide, which mobilized 270 million m\(^3\) of rocks. These huge masses entered into the reservoir generating a 220-m-high wave that overtopped the dam and caused the death of 1917 people in the valley below, as well as huge damages.

Figure 12 shows the estimated exponent versus time referring to a time window of 1126 days, from 8 September 1960 to 9 October 1963.

Fig. 12
figure 12

The variation of the exponent x of the power law function approximating the dimensionless data for the last 1126 days before the Vajont landslide collapse

Full size image

Among the six individuated stages, those corresponding to the filling phases are the first, the fourth, and the sixth ones. The latter one, from 8 April to the day of the collapse, is associated with a Trend IVb. In that stage, the exponent increased with time, passing the threshold between Trend III and Trend IVa on 24 August (46 days before the collapse), and that between Trend IVa and Trend IVb on 20 September (19 days before the collapse), finally taking the value of 5.347.

Considering that Trend IVb is strongly unstable and implies that it is impossible to prevent landslide collapse, we argue that the use of Approach II would have allowed critical information to be obtained early enough to apply an emergency plan to protect the people at risk.

La Saxe case study

La Saxe rockslide (Fig. 13a) is located on the left-hand side of Ferret Valley, Valle d’Aosta Region (Northern Italy), where a deep-seated gravitational slope deformation can be recognized. It extends between 1870 m and 1400 m above sea level (a.s.l.) over an area of 150,000 m\(^2\), involves a total volume of about 8 million m\(^3\) and is characterized by an average slope angle of \(37^\circ\), a maximum length of 550 m, and a maximum width of 420 m (Crosta et al. 2014).

Fig. 13
figure 13

Front view of the La Saxe rockslide, from the location of the robotic total station (a), and Leica TCA robotic total station (b). Photographs taken on 3 October 2019 by M.R. Scoppettuolo. Texts and landslide sector boundaries in panel (a) by E. Babilio

Full size image

The landslide threatens the Entreves and La Palud villages, in the Courmayeur municipality, and part of the route E25 near the access to Mont Blanc Tunnel that represents a fundamental connection between Italy and France. Indeed, social and economic potential damage is very high, due to the losses in case of closure of the tunnel and for the touristic activities in Courmayeur area. For such a reason, after a local collapse of the slope, in 2014 the Italian Civil Protection classified the landslide as a national emergency.

As discussed by Alberti (2019), the monitoring system of the slope collects many and detailed information on displacements through inclinometers, wire-extensometers, Differential Monitoring System columns (by CSG s.r.l.), GPS network devices, a GB-InSAR LiSALab\(\mathrm {TM}\) system (by Ellegi s.r.l.), a high-frames camera, and a Leica TCA robotic total station (Fig. 13b), surveying 31 optical targets, and other devices. Groundwater level, snow melting, and other physical quantities affecting the slope motion, including temperature and frost level, are also systematically monitored.

Data records are regularly updated and uploaded in a website designed by Valle d’Aosta Region that is available for the sake of early warning, emergency procedures, and communication strategy (Giordan et al. 2015).

Based on the experimental data, the landslide body can be divided into five sectors: we call “1” the active sector, “2” the sector dragged by the active sector, “3” the upper sector, “4” the lower sector, and “5” the external side sector (Fig. 13a). The movement of one or more of these sectors is mainly associated to snow melting that occurs during the spring season, causing water infiltration and fluctuations in groundwater level. Figure 14 reports cumulative displacements for the period in between October 2010 and January 2019 from five targets, one for each mentioned sector (for completeness, the positions are approximately shown in Fig. 13a).

Fig. 14
figure 14

Cumulative displacement over time for optical targets (a) with a close-up of T3, A2, C1, and E1 targets (b). The large displacement recorded by target B4 corresponds to the collapse of April 2014. Positions of targets and sector boundaries are approximately shown in Fig. 13a

Full size image

From the displacement plots, we observe the common shape of diagrams, even if a significant difference, in terms of magnitude, characterizes the cumulated displacements (Fig. 14a). Among the most significant events, we observe the following: two accelerations of the sector 2 (see displacement from T3 in Fig. 14b) caused by the snow melting, dating back to March–May 2012 and April 2013; and two collapses involving limited portions of the main landslide body in the sector 1 (see displacement from B4 in Fig. 14a) that took place on 17 and 21 April 2014 (Manconi and Giordan 2015). After this last event, accelerations were characterized by smaller values also thanks to the stabilization works (drainage systems) carried out along the slope.

To test the reliability of the proposed method, by referring to B4 optical target in Fig. 13a, Approach II was applied to back-analyze the evolution of sector 1 during the springs of 2012, 2013, and 2014. Figure 15 shows as the exponent of the approximating function changes in between 1 March to 10 May 2012 and 3 April to 1 May 2013. With reference to the collapse mentioned above, Fig. 16 shows that the collapse recorded on 17 April 2014 could have been considered very probable 10 days in advance, the exponent \(x=2\) having been reached on 7 April (lower bound of Trend IVa), and inevitable 5 days in advance of 17 April, \(x=3\) (lower bound of Trend IVb) having been reached on 12 April and having a greater value thereafter.

Fig. 15
figure 15

Back-analyzed time evolution of the exponent of the approximating function in between 1 March–10 May 2012 (a) and 3 April–1 May 2013 (b)

Full size image
Fig. 16
figure 16

Forecasting the collapse in the sector 1 of the La Saxe landslide (time window lasting 32 days, from 16 March to 17 April 2014). Panel (a): the displacement data record, adaptation of approximation curves for increasing size of the data record (gray-shaded curves) and final estimate (solid black curve). Panel (b): the time evolution of the estimated exponent

Full size image

Applicability of the method

The success of a method depends on several factors, including the coherence of rationale behind it, the reliability of the predictions, and its performance in comparison with other available methods in the literature. The first two issues are discussed in the previous sections. As it concerns the third one, we observe that methods to compare must be carefully individuated by excluding those apparently similar, but actually designed to pursue different purposes.

Indeed, being both Approaches I and II tailored to predict landslide evolution over a single stage of activity, the comparison of their results with those coming from tools aimed at forecasting the landslides evolution over many stages becomes meaningless. This is, for example, the case of the Ruinon landslide that Crosta and Agliardi (2003) analyzed to verify the possibility of its collapse after a certain number of single landslide evolution stages. However, looking at the theoretical framework of the proposed method, we argue that in the future it could also be implemented to provide an insight on the evolution of landslides in the medium–long term.

Limiting ourselves to the forecasting of a single stage of activity at a time, a comparison is here proposed with the INV method (Fukuzono 1985, 1990; Voight 1988, 1989) for two cases of failure in an open pit mine, namely no. 3 and no. 4 among those reported by Carlà et al. (2017) (Fig. 17).

Fig. 17
figure 17

Time histories of failures no. 3 (a) and no. 4 (b) in a mine of classified place for the owner’s convenience. Data retrieved from (Carlà et al. 2017)

Full size image

A comparison of the results for failure no. 3 is provided in Fig. 18 that highlights a good performance for both INV (a) and present method (b) although the latter allows defining an alert threshold (at \(x>2\)) 1 h in advance respect to the former. For failure no. 4 (Fig. 19), the Fukuzono-Voight method fails the prediction while the proposed method provides an alert threshold \((x>2)\) about 2 h in advance with respect to the collapse of the slope.

Fig. 18
figure 18

Collapse time of failure no. 3 estimated through the INV method (a) and the proposed method (b)

Full size image
Fig. 19
figure 19

Collapse time of failure no. 4 estimated through the INV method (a) and the proposed method (b)

Full size image

It can be observed that processing the inverse of the velocity indirectly means to analyze Trends III and IV without discriminating between them. The relevance of acceleration is indirectly discussed by Segalini et al. (2018), who analyze several slope failures through the normalized velocity vs time observing that the collapse is recorded for trends that are similar to those here classified as IVa and IVb. This topic is also discussed by Federico et al. (2012), who relate velocity and acceleration to failures of a significant number of slopes and the corresponding diagram they obtain appears strictly related to Trends IVa and IVb.

A further observation concerns the estimate of the time evolution of the exponent through displacement records which, being discrete in time, require a sequence of approximations of the available experimental data. In the early phase of any landslide evolution stage, due to several factors, a small number of data may give rise to possible noise amplification, as observed in Fig. 15a. However, in all the case studies analyzed, this noise phenomenon is reduced as the size of the dataset increases.

Finally, we note that two of the explanatory examples we considered, namely Vallcebre and Vajont, have been analyzed in the past through reduced-order models by Ferrari et al. (2011) and Alonso et al. (2010), respectively. In our opinion, this represents an interesting starting point for a future and comprehensive understanding of the factors underlying the different dynamic equilibria of the displacement trends we have considered in the present work.

Concluding remarks

In this paper, a method to forecast the landslide evolution is proposed. The basic theoretical principles come from previously published works devoted to analyze common features emerging from landslides that are different in terms of size, mechanical properties of materials involved in the landslide, groundwater regime, and so on.

The developed strategy allows properly approximating displacement records and assessing the stability properties of a limited number of landslide stages, which are able to represent the large variety of actual landslides. The approach is based on a preliminary and technically informed partitioning of the data into different landslide stages.

Since in real-time analysis of a landslide, the duration of a given stage is not known in advance, the present contribution proposes an automatic strategy for data partitioning, based on updating the approximation to the current record. This implies generating a new approximation as soon as a new data is acquired, from which a new prediction of the landslide displacement is extrapolated.

The procedure has been tested as a blind predictor by using historical data in a one-by-one uploading process. Data, available in the scientific literature, come from well-known landslides and the results of the simulations trace what actually happened.

We close with the hope and idea for future work to consider other well-documented case studies and an experimental campaign on simplified scale models that would further confirm the validity of a method whose results to date already seem to point to it as an excellent candidate for predicting landslide evolution.