Two-phase SPH modelling of a real debris avalanche and analysis of its impact on bottom drainage screens

Abstract

Rapid flow-like landslides, particularly debris flows and debris avalanches, cause significant economic damage and many victims worldwide every year. They are usually extremely fast with the capability of travelling long distances in short times, sweeping away everything in their path. The principal objective of this paper is to test the ability of the ‘GeoFlow-SPH’ two-phase model developed by the authors, to reproduce the complex behaviour of natural debris avalanches where pore-water pressure evolution plays a key role. To reach this goal, the model is applied to reproduce the complex dynamic behaviour observed in Johnsons Landing debris avalanche including the observed bifurcation caused by the flowing out of part of the moving mass from the mid-channel. Initial thickness deposit trim-line, distribution of deposit volume, and the average velocities were provided for this real case, making it an appropriate case to validate the developed model. The paper also contributes to evaluate the SPH-FD model’s potentialities to simulate the structural countermeasure, like bottom drainage screens, used to reduce the impact of debris flows. The analysis of the results shows the adequacy of the proposed model to solve this complicated geophysical problem.

Introduction

Landslides are a major natural hazard and can be defined as a continuous movement of materials triggered from the unstable hill slope due to natural processes or anthropic actions. The most catastrophic landslides, particularly debris flows, are usually extremely rapid with the capability of traveling long distances in very short times sweeping away everything in their path, even in areas that had been considered safe, causing a large number of casualties and economic damage throughout the world every year.

In recent years, these catastrophic events have attracted significant attention due to the growing population in areas with a high risk of natural disasters and climate changes, which increase the frequency and intensity of these catastrophic landslides. Engineers and geologists attempt to understand better their mechanisms, involved in both triggering and propagation stages, to reduce the coming risk consequences of such hazards. As a result, the prediction of these phenomena’ evolution with the use of advanced simulation tools is becoming more and more important.

Debris flows are geological phenomena and usually occur after heavy rain events in mountainous regions. Therefore, they usually propagate with a large quantity of water and high pore-water pressure, which causes the materials to flow as fluidly as water. Debris avalanches are defined as extremely rapid debris flows on a steep slope. However, unlike debris flows, they do not confine in an established channel Nicol et al. (2013).

So far, many different continuum-based approaches have been attempted to model debris flows and debris avalanches and may have been experiencing difficulties in considering several dominant physical aspects of debris flows, such as the pore-water pressure evolution and the interaction between solid and fluid phases. A key idea to model debris flows is to represent adequately this coupled hydro-mechanical behaviour. This ingredient is provided, among others, by the work of Zienkiewicz and Mróz (1984) and Biot (1955, 1941), who proposed a general formulation that could be applied to debris flows.

There is a wide variety of landslides that depend largely on the processes in which the flowing mass moves down a slope. In this study, a debris avalanche’s behaviour is analysed with a two-phase model, where both solid and fluid phases and their mutual interaction are taken into account.

Some types of fast landslides, e.g. debris avalanches, present the complex coupled behaviour of pore pressure dissipation while propagating. This aspect is crucial to represent the landslide dynamics adequately and should be considered in the computational model.

In this paper, the ‘GeoFlow-SPH’ model Pastor et al. (2021) is applied to the case study of Johnsons Landing debris avalanche. The model uses the meshless numerical technique of SPH based on the theoretical one-phase framework of Pastor et al. (2004, 2009). In 2015, this one-phase model was enriched by adding a 1D finite-difference grid to each SPH node to improve the predictions’ quality in particular cases with a high permeable terrain Pastor et al. (2015). Then, Pastor et al. (2018) modified the model to include the two-phase fluid-solid description of the flowing mass. Lately, the two-phase SPH model has been generalized to overcome some limitations identified in previous models, for instance, taking into account the pore pressure evolution by considering the soil permeability Pastor et al. (2021). The authors validated the generalized model by back-analysing the Yu Tung debris flow Tayyebi et al. (2021) and Acheron rock avalanche Tayebi et al. (2021) and reproducing a small-scale laboratory test performed in Trondheim Tayyebi et al. (2021).

The paper aims to perform and validate a generalized two-phase model that can be applied to reproduce the complex behaviour of debris avalanches where the coupling between the solid skeleton and the interstitial fluid plays a determining role and taking into account the excess pore pressure is very important. This study also contributes to the analysis of a flow breaker in order to have a better understanding of its mechanisms.

The first section is dedicated to the generalized two-phase mathematical model consisting of the balance equations of mass and linear momentum, completed by a suitable consolidation equation and the Voellmy rheological equation. In the second section, the basic concepts of the smoothed particle hydrodynamics (SPH) method are presented. Besides, we present the SPH discretization of the developed mathematical equations. If we deal with a high permeability terrain, the Finite Difference Method (DFM) is applied to discretize the consolidation equation. In the fourth section, a review of the basic aspects related to Johnsons Landing debris avalanche is given. Besides, the restrictions in the computational modelling of particular debris avalanches in previous attempts are described. Then, the validation of the developed depth-integrated two-phase SPH is presented through back-analysing of a real case, aiming to test the ability of the model to reproduce the complex behaviour of a natural debris avalanche. In addition to this, the two-phase SPH-FD numerical analysis was carried out to understand how these bottom drainage screens are capable of changing the dynamics of debris avalanches.

Mathematical model

For the sake of completeness, in this section, the mathematical model is considered to represent a realistic behaviour of debris flows describing the main physical aspects, including pore-water pressure evolution and interaction between the solid skeleton and the pore fluids.

Regarding mathematical models applied to debris flows, it is worth mentioning the work of Zienkiewicz and Mróz (1984), who proposed a general formulation referred to as $v-{{p}_{w}}-\omega$ model, and the model of $v-{{p}_{w}}$ described by Zienkiewicz et al. (1999), which is based on the assumption that the velocity of the fluid phase relative to the solid phase is small.

One-phase models usually have many limitations in reproducing the debris flow’s behaviour, especially for those consisting of soil with medium to high permeability, as both solid and water particles can have different velocities. Consequently, the two-phase model has appeared to be an efficient alternative in these particular cases. We can mention the two-phase models proposed by Pitman and Le (2005), Pudasaini (2012) and Pastor et al. (2018), where the mixture of two interacting phases has been considered.

In this paper, the model recently developed by Pastor et al. (2021) is considered. This model is a more general approach for two-phase modelling and can consider the essential physical phenomena of pore-water pressure evolution capable of reproducing the dynamic behaviour of debris flows by taking into account their soil properties, including permeability and volume stiffness.

The new two-phase model has been developed to overcome some limitations identified in previous models. Firstly, the balance of momentum equation framework has been improved by implementing additional terms such as excess pore-water pressure. Secondly, the propagation-consolidation model has been used to evaluate the excess pore-water pressure along the depth of the propagating mass. As a result, the modifications and improvements of the two-phase modelling allowed us to consider several dominant physical aspects of debris flow, such as the generation of excess pore-water pressure, which increases the flow’s mobility and reduces the basal shear stress.

In many fast catastrophic landslides, it is possible to apply some interesting simplifications by transforming the three-dimensional mathematical problem into a two-dimensional form. Since these landslides usually have a small average depth compared to their length or width, the 3D governing equations can be integrated along the depth of flowing mass. As a result, the 2D depth-integrated model provides an excellent combination of accuracy and computational time. The major advantages of using this technique are (i) to reduce the number of unknowns - getting rid of the vertical variables- and (ii) to eliminate the use of special techniques such as the level set to track the free surface.

Depth integrated models introduced by Barre de Saint-Venant (1871) for solving the problems related to the fields of coastal and hydraulics engineering. A century later, Savage and Hutter (1989, 1991) proposed a depth-integrated 1D Lagrangian model to study landslide propagation. This model has been extended in order to apply to more general conditions including 2D and complex terrains (Hutter and Koch (1991); Hutter et al. (1993); Gray et al. (2001)). The interested reader will find in Hutter et al. (2005) a detailed discussion about the limitations of the depth-integrated model proposed by Savage-Hutter.

Depth-integrated models have been frequently applied to simulate flow-like landslides, being worth mentioning the works of Laigle and Coussot (1997), McDougall and Hungr (2004), Quecedo et al. (2004), and Pastor et al. (2002, 2009) with considering a depth-integrated consolidation equation. This technique has been successfully applied to debris flows by Pastor et al. (2014) and Cascini et al. (2014, 2016) and debris avalanches by Cuomo (2014); Cuomo et al. (2016).

Balance equations of mass and linear momentum

The two-phase model proposed by Pastor et al. (2021) consists of balance equations of mass and linear momentum expressed in quasi-Lagrangian form as follow:

• (i) Balance of mass:

  $$\begin{aligned} \frac{\bar{d} {{h}_{\alpha }}}{d t}+\frac{\bar{d} }{d {{x}_{\alpha i}}}\left( {{h}_{\alpha }}{{{\bar{v}}}_{\alpha i}} \right) ={{\bar{n}}_{\alpha }}{{e}_{R}} \end{aligned}$$

  (1)

• (ii) Balance of Linear momentum:

  $$\begin{aligned}{{\rho }_{\alpha }}{{h}_{\alpha }}\frac{{{{\bar{d}}}^{\left( \alpha \right) }}{{{\bar{v}}}_{\alpha }}}{dt}=& \ {{\rho }_{\alpha }}\text {grad}{{\bar{P}}_{\alpha }}-\left( \frac{1}{2}{{\rho }_{w}}{{b}_{3}}{{h}^{2}}-\Delta {{{\bar{p}}}_{w}}h \right) \text {grad}{{\bar{n}}_{\alpha }} \\ &+\tau _{B}^{\left( \alpha \right) }+{{\rho }_{\alpha }}b{{h}_{\alpha }}+\bar{R}h-{{\rho }_{\alpha }}{{\bar{v}}_{\alpha }}{{\bar{n}}_{\alpha }}{{e}_{R}} \end{aligned}$$

  (2)

where $\rho$ is the density and sub-indexe $\alpha$ denotes the solid (s) or fluid (w) phase, ${{\bar{n}}_{\alpha }}$ being the porosities of solid and fluid phases (${{\bar{n}}_{s}}=1-\bar{n}$ and ${{\bar{n}}_{w}}=\bar{n}$), ${{e}_{R}}$ erosion rate, and ${{h}_{\alpha }}=h{{\bar{n}}_{\alpha }}$. ${{b}_{3}}\left( =-\text {g} \right)$ is gravity force and its axis is vertical and points upwards. $\bar{R}={{n}^{2}}k_{w}^{-1}\left( {{{\bar{v}}}_{w}}-{{{\bar{v}}}_{s}} \right)$ is the interaction force and ${{k}_{w}}$ is the permeability which will be described in the next section. In the diffusion term of Eq. 2, the averaged pressures $\left( {{{\bar{P}}}_{\alpha }} \right)$ acting on solid or fluid phases are defined as:

$$\begin{aligned} \bar{P}_{s}=\frac{1}{2}{b}_{3}h{h}_{s}+\frac{\Delta {\bar{p}_{w}}h\bar{n}}{\rho _{s}} \ \text {For Solid} \end{aligned}$$

(3)

$$\begin{aligned} \bar{P}_{w}=\frac{1}{2}{b}_{3}h{h}_{w}-\frac{\Delta \bar{p}_{w}h\bar{n}}{\rho _w} \ \text {For Fluid} \end{aligned}$$

(4)

This indicated that, in our particular case of interest, total pore-water pressure $\left( {{p}_{w}} \right)$ is composed of a hydrostatic part $\left( {{p}_{hyd}} \right)$, which varies linearly from zero at the surface to $\rho \text {g}h$ at the bottom, and an excess pore-water pressure $\left( \Delta {{p}_{w}} \right)$ which should be computed at each time and space.

Next, the mathematical equations are given in Eqs. 1 and 2 are completed using a rheological law to compute the basal shear stress $\left( {{\tau }_{B}} \right)$. There exist various types of the rheological model, such as the Newtonian fluid which is a simple model characterized by one single constitutive parameter, and the Bingham fluid which is able to exhibit yield stress in the case of cohesive fluid. In this study, the numerical analysis was performed through Voellmy’s rheological law which has the same features as the frictional rheological model where the cohesion and viscous terms are disregarded. Besides, it is capable of considering the evolution of pore-water pressure at the basal surface. In the case of a pure frictional mass, the basal shear stress is given by:

$$\begin{aligned} {\tau }_{B}=\left( \rho _{d}^\prime\text {g}h-\Delta p_{w}^{b} \right) \frac{\bar{v}_{i}}{\left| {\bar{v}} \right| }\tan {\phi _{B}}+\rho \text {g}\frac{\left| {\bar{v}} \right| }{\xi }{{\bar{v}}_{i}} \end{aligned}$$

(5)

where $\rho _{d}^{\prime } =\left( 1-n \right) \left( {{\rho }_{s}}-{{\rho }_{w}} \right)$ is the effective density, h the propagation height, ${{\phi }_{B}}$ the basal friction angle, $\bar{v}$ the depth-averaged flow velocity, $\xi$ the turbulence coefficient and $\Delta p_{w}^{b}$ the excess pore-water pressure at the basal surface, which is computed by using a consolidation equation that will be given in the next section. It can be seen in the above equation that the basal shear stress ${{\tau }_{B}}$ will depend on the basal excess pore pressure and it is modified in accordance with pore-water pressure evolution at each node and time step. Take into account that the higher pore-water pressure, the lower is the shear stress at the basal surface.

Consolidation equation

Consolidation is an important aspect of debris flows where the gradual processing of pore pressure dissipation takes place and affects flowing materials’ behaviour. Numerical modelling of debris flows still faces challenges when it comes to adequate simulating timespace evolution of the interstitial pore water pressures in each time step. Particularly in depth-integrated models, the vertical structure of the magnitudes is lost as the only available information is their depth-integrated values. Therefore, it is necessary to implement additional equations describing how pore pressure evolves along time and depth. The first approximation extending the vertical consolidation mechanism has been modelled by Hutchinson (1986), who proposed a simple sliding-consolidation mechanism for a block to consider the coupling of pore water and air with the solid grains. Pastor et al. (2002) extended Hutchinson’s model by assuming that the pore pressure dissipations are only caused by vertical consolidation. Concerning the fast landslides, Pastor et al. (2004) proposed the propagation-consolidation model in which the pore pressure field was assumed to be a sum of the hydrostatic pressure and the excess pore-water pressure.

Pastor et al. (2015) extended this approach to fully approximate the pore pressures inside the landslide. In this technique, a finite-difference mesh, incorporating at each SPH node (SPH-FD model), is used to discretize the excess pore-water pressure along the vertical axis. Here, we recall the consolidation equation describing the evolution of pore pressure along the vertical axis, as follows:

$$\begin{aligned} \frac{{{d}^{\left( s \right) }}\Delta {{p}_{w}}}{dt}=-\rho _{d}^{'}{{b}_{3}}\frac{dh}{dt}+{{c}_{v}}\frac{{{\partial }^{2}}\Delta {{p}_{w0}}}{\partial {{x}_{3}}^{2}}-{{E}_{m}}\frac{1}{\left( 1-n \right) }\frac{{{d}^{\left( s \right) }}n}{dt} \end{aligned}$$

(6)

where ${{c}_{v}}$ is the consolidation coefficient and ${{E}_{m}}$ the oedometric modulus. Based on the above equation, the pore water pressures are also influenced by the propagation height and velocity, and the porosity variations. The consolidation parameter of ${{c}_{v}}$ plays a significant role as a high value of the coefficient allows the rapid dissipation of excess pore-water pressure through the consolidation process. It can be obtained as follows:

$$\begin{aligned} {{c}_{v}}={{k}_{v}}{{k}_{w}} \end{aligned}$$

(7)

where ${{k}_{v}}$ is the stiffness of the mixture and ${{k}_{w}}$ the permeability. In order to compute the geotechnical parameter of ${{k}_{w}}$, the following laws have been implemented in the GeoFlow-SPH program:

• (i) Darcy’s law: It is a simple law in which ${{k}_{w}}$ is given by:

  $$\begin{aligned} {{k}_{w}}=\frac{{{{\bar{k}}}_{w}}}{{{\rho }_{w}}\text {g}} \end{aligned}$$

  (8)

  where ${{\bar{k}}_{w}}$ is the hydraulic conductivity.

• (ii) Anderson and Jackson law (1967): The second alternative law has been used by Pitman and Le (2005). It is recommended to apply it when the relative velocity is more extensive. It is given by:

  $$\begin{aligned} {{k}_{w}}=\left( \frac{{{V}_{T}}}{\left( {{\rho }_{s}}-{{\rho }_{w}} \right) \text {g}} \right) \left( \frac{{{n}^{m}}}{1-n}\right) \end{aligned}$$

  (9)

  where ${{V}_{T}}$ is the terminal velocity and m a constant.

• (iii) Kozeny-Carman law Kozeny (1927): The third alternative law can be used to calculate the drag force of fluid-like flow, passing through densely packed grains. It is given by:

  $$\begin{aligned} {{k}_{w}}=\left( \frac{{{{\bar{k}}}_{w0}}}{{{\rho }_{w}}\text {g}}\right) \left( \frac{{{n}^{3}}}{1-{{n}^{2}}}\right) \end{aligned}$$

  (10)

  where ${{\bar{k}}_{w0}}$ is the initial hydraulic conductivity.

Numerical methods

In this section, the Lagrangian meshless numerical method of smoothed particle hydrodynamics (SPH) used to discretize the depth-integrated equations is described. In the SPH method, the continuum body, in our case a flowing mass, is discretised with a set of material points or particles having individual properties. It is based on approximating functions and differential operators, such as gradient or divergence, by integral approximations defined in terms of a smoothing kernel function.

The technique was developed in the late 70’s by Lucy (1977) and Gingold and Monaghan (1977) to model very complex astrophysical problems. Subsequently, it has gained popularity due to its capability to deal with large deformations avoiding expensive remeshing operations. Today, SPH is applied in many areas, among which it is worth mentioning the problems found in Solid Mechanics, including modelling of flowing material McDougall and Hungr (2004); McDougall (2006); Rodriguez-Paz and Bonet (2005) and soil–water interaction Bui et al. (2007, 2008); Blanc and Pastor (2012, 2013). Good reviews can be found in the texts of Li and Liu (2004); Liu and Liu (2003).

In the case of depth-integrated models, the different types of numerical methods has been used to simulate landslide propagation. It is worth mentioning the work of Pudasaini Pudasaini (2012), Pastor et al. Pastor et al. (2002) for eulerian type (finite volumes or elements), and Pastor et al. Pastor et al. (2009), McDougall and Hungr (2004) and Rodriguez-Paz and Bonet (2005) for Lagrangian type (SPH).

SPH particles interact through a kernel function that determines the pattern to interpolate for a function approximation and defines the support domain’s dimension, as depicted in Fig. 1a.

Fig. 1

(a) Numerical integration in the particle support, and (b) The cubic spline kernel and its first derivative

The performance of the SPH model is closely linked to the type of weighting functions and their properties. In this study, the required properties of each point are determined using the cubic spline kernel. Figure 1b. depicts the kernel and its first derivative. The SPH procedure is started by approximating a given function $f\left( {{x}_{i}} \right)$ at a position vector ${{x}_{i}}$ in space. It is expressed as follows:

$$\begin{aligned} f\left( {x}_{i} \right) =\int f\left( {{x}_{j}} \right) W\left( {{x}_{i}}-{{x}_{j}},{{h}_{sm}} \right) d{x}_{j} \end{aligned}$$

(11)

Once the information is stored into nodes or particles, the integral interpolation of SPH kernel approximation is replaced with a discretized form of summation over all the particles within the region of compact support of kernel function. It is expressed as follows:

$$\begin{aligned} f{{\left( {{x}_{i}} \right) }_{h}}\tilde{=}\underset{j=1}{\overset{N}{\mathop \sum }}\,f\left( {{x}_{j}} \right) W\left( {{x}_{i}}-{{x}_{j}},{{h}_{sm}} \right) {{\omega }_{j}} \end{aligned}$$

(12)

where the infinitesimal volume $\left( d{{x}_{j}} \right)$ of the continuous integral representations is replaced by the volume of a neighbouring particle $\left( {{\omega }_{j}} \right)$.

Numerical solution of the balance equations

In order to generalize the model, the mathematical equations are discretized by using the two-phase SPH technique to deal with two phases of flow involving solid and water. Therefore, two sets of nodes are introduced, one to represent the solid particles’ movement and another to represent the fluid particles’ movement, as depicted in Fig. 2.

Fig. 2

SPH interactions for two-phase: 1) soil–soil (I-J) and 2) soil-water (I-K)

Next, the depth-integrated balance equations of mass and linear momentum expressed in quasi-Lagrangian form (Eqs. 1 and 2) are discretized using the SPH technique. Depending on the symmetrized form chosen to discretize the gradient of the pressure and porosity, the following discretized forms of the balance equations of mass and linear momentum are obtained:

$$\begin{aligned} \frac{\bar{d}{{h}_{i}}}{dt}+{{h}_{i}}{{\rho }_{i}}\underset{j=1}{\overset{Nh}{\mathop \sum }}\,{{m}_{j}}\left( \frac{{{{\bar{v}}}_{j}}}{{{\rho }_{j}}^{2}}-\frac{{{{\bar{v}}}_{i}}}{{{\rho }_{i}}^{2}} \right) \text { }\!\!~\!\!\text { grad}{{W}_{ij}}={{\bar{n}}_{i}}{{e}_{R}} \end{aligned}$$

(13)

$$\begin{aligned} \begin{aligned}\frac{\bar{d}\bar{v}_{i}}{dt}=&-\underset{j=1}{\overset{Nh}{\mathop \sum }}\,{{m}_{j}}\left( \frac{\bar{P}_{i}}{h_{i}^{2}}+\frac{\bar{P}_{j}}{h_{j}^{2}} \right) \text { grad}{{W}_{ij}}\\ {}&-\left( \frac{1}{2}\frac{{\rho }_{w}}{{\rho }_{\alpha }}{{b}_{3}}h_{i}^{2}-\frac{\Delta {\bar{p}_{w}}{{h}_{i}}}{{{\rho }_{\alpha }}} \right) \underset{j=1}{\overset{N}{\mathop \sum }}\,{{m}_{j}}\left( \frac{\bar{n}_{i}}{h_{i}^{2}}+\frac{\bar{n}_{j}}{h_{j}^{2}} \right) \text { grad}{{W}_{ij}}\\ {}&+\frac{1}{{{\rho }_{\alpha }}{{h}_{i}}}{{\tau }_{B}}+{{b}_{i}}+\frac{1}{{{\rho }_{\alpha }}}{{\bar{R}}_{\alpha }}-\frac{1}{{{h}_{i}}}{{\bar{v}}_{i}}{{\bar{n}}_{i}}{{e}_{R}}\end{aligned} \end{aligned}$$

(14)

where ${{m}_{J}}$ is a fictitious volume with dimensions ${{L}^{3}}$. The interested reader will find in the article by Pastor et al. (2021) a detailed explanation about the governing equations.

Numerical solutions of the consolidation equation

In this section, the equations are built by using the notation given in Fig. 3. To compute basal pore-water pressure, it is possible to assume that the following Fourier series can approximate the second term of the Eq. 6:

$$\begin{aligned} \Delta {{p}_{w}}\left( {{x}_{1}},{{x}_{2}},{{x}_{3}},t\right) =\underset{k=1}{\overset{{{N}_{k}}}{\mathop \sum }}\,\Delta {{p}_{wk}}\left( {{x}_{1}},{{x}_{2}},t \right) {{N}_{k}}\left( {{x}_{3}} \right) \end{aligned}$$

(15)

where ${{N}_{k}}\left( {{x}_{3}} \right)$ are shape functions that are used to approximate the excess pore pressure variations along ${{x}_{3}}$.

Fig. 3

(a) Notation and reference system. (b) Initial and deformed configuration of a column of the landslide mass Pastor et al. (2015)

Among different alternatives, harmonic functions have been chosen because it satisfies the boundary conditions. Assuming the hypothesis that the pore pressure is zero on the free surface and the basal surface is impermeable, the harmonic function is:

$$\begin{aligned} {{N}_{k}}\left( {{x}_{3}} \right) =\cos \left\{ \frac{2k-1}{2h}\pi \left( {{x}_{3}}+z \right) \right\} \end{aligned}$$

(16)

where $k=1\ldots \text { }\!\!~\!\!\text { }{{N}_{k}}$. For $k=1$, the above equation transforms into:

$$\begin{aligned} {{N}_{1}}\left( {{x}_{3}} \right) =\cos \left\{ \frac{\pi }{2}\frac{\left( {{x}_{3}}+z \right) }{h} \right\} \end{aligned}$$

(17)

If the analysis is limited to only one of the Fourier components, the expression of the excess pore pressure becomes:

$$\begin{aligned} \Delta {{p}_{w}}\left( {{x}_{1}},{{x}_{2}},{{x}_{3}},t \right) =\Delta {{p}_{w1}}\left( {{x}_{1}},{{x}_{2}},t \right) \cos \left\{ \frac{\pi }{2}\frac{\left( {{x}_{3}}+z \right) }{h} \right\} \end{aligned}$$

(18)

At basal ${{x}_{3}}=0$, we arrive at:

$$\begin{aligned} \Delta {{p}_{w}}=\Delta p_{w}^{b}\cos \left\{ \frac{\pi }{2}\frac{z}{h} \right\} \end{aligned}$$

(19)

where $\Delta p_{w}^{b}$ is the excess pore-water pressure at the basal surface. The above equation can be written as:

$$\begin{aligned} \frac{\partial \Delta {{p}_{w}}}{\partial t}=\frac{\partial \Delta p_{w}^{b}}{\partial t}\cos \left( \frac{\pi }{2}\frac{z}{h} \right) \end{aligned}$$

(20)

At basal, we also have the following classical consolidation equation:

$$\begin{aligned} \frac{\partial \Delta {{p}_{w}}}{\partial t}={{c}_{v}}\frac{{{\partial }^{2}}\Delta {{p}_{w0}}}{\partial {{z}^{2}}} \end{aligned}$$

(21)

Considering the Fourier series given in Eq. 15, the term on the RHS of the above equation is written as:

$$\begin{aligned} {{c}_{v}}\frac{{{\partial }^{2}}\Delta {{p}_{w0}}}{\partial {{z}^{2}}}=-\frac{{{c}_{v}}{{\pi }^{2}}}{4{{h}^{2}}}\cos \left( \frac{\pi }{2}\frac{z}{h} \right) \Delta p_{w0}^{b} \end{aligned}$$

(22)

Combining the last three equations, the second term of Eq. 6 can be written as:

$$\begin{aligned} \frac{\partial \Delta p_{w}^{b}}{\partial t}=-\frac{{{c}_{v}}{{\pi }^{2}}}{4{{h}^{2}}}\Delta p_{w0}^{b} \end{aligned}$$

(23)

Considering that (i) at basal ${{x}_{3}}=0$, (ii) the quarter cosines shape function is used to solve the second term, and (iii) there exists no porosity in basal -the third term of Eq. 6 is eliminated-, the time-evolution of excess pore-water pressure is given by:

$$\begin{aligned} \frac{{{d}^{\left( s \right) }}\Delta {{p}_{w}}}{dt}=-\rho _{d}^{{b}_{3}}\frac{dh}{dt}-\beta \Delta p_{w0}^{b} \end{aligned}$$

(24)

where for simplification, we introduce $\beta ={{c}_{v}}{{\pi }^{2}}/4{{h}^{2}}$.

The above equation is a first-order linear differential equation from which the following solution of the ordinary differential equation can be obtained:

$$\begin{aligned} {{p}_{w}}={{p}_{w0}}\text {exp}\left( -\beta t \right) +\frac{1}{\beta }\frac{dh}{dt}\left( 1-\text {exp}\left( -\beta t \right) \right) \end{aligned}$$

(25)

The second alternative numerical model was proposed by Pastor et al. (2015), who combined a Finite Difference Method (FDM) for the 1D equation of vertical consolidation and depth-integrated one-phase SPH model for the propagation analysis (SPH-FD model). Pastor et al. (2021) extended the model to a two-phase model in order to fully approximate the pore pressures inside a landslide. In this technique, a finite-difference mesh, incorporated at each SPH node that represents solid particles, is used to discretize pore-water pressures along the vertical axis, as depicted in Fig. 4.

Fig. 4

A 1D finite-difference mesh at each SPH node that represents solid particles

In this framework, the spatial discretization of the excess pore pressure evolution will be simply made by a set of 1D finite-difference meshes, while the time discretization will be carried out with an updated Lagrangian approach where the reference configuration will be at time t as depicted in Fig. 3. To solve this equation, we will consider the landslide mass decomposed into differential elements of volume having, at a given time (t), a height (h), and a cross-section.

Considering the differential volume element sketched in Fig. 3b, the consolidation equation given in Eq. 6 can be rewritten as:

$$\begin{aligned} \frac{{{d}^{\left( s \right) }}\Delta {{p}_{w}}}{dt}=-\rho _{d}^{'}{{b}_{3}}\frac{dh}{dt}\left( 1-\frac{{{x}_{3}}}{h} \right) +{{c}_{v}}\frac{{{\partial }^{2}}\Delta {{p}_{w0}}}{\partial {{x}_{3}}^{2}}-{{E}_{m}}\frac{1}{\left( 1-n \right) }\frac{{{d}^{\left( s \right) }}n}{dt} \end{aligned}$$

(26)

where the consolidation equation is discretized by making two changes: (i) height variation and (ii) porosity variation.

Now, a set of ordinary differential equations is produced in a discretized form with respect to time. The balance equations of mass and momentum have been discretized with SPH, while the consolidation equation has been discretized using a set of finite difference meshes. One of the advantages of incorporating a set of finite difference meshes and SPH node is its ability to simulate cases where basal pore pressures go to zero as a consequence of the landslide crossing a terrain with very high permeability.

The resulting equations are discretized in time with a suitable algorithm such as the 4th order Runge Kutta method in the SPH and FTCS in the FDM, which are explicit because of their simplicity and rapid computation speed. It is important to note that two timescales exist in the governing equations, (i) a propagation time related to the variation rate of h and (ii) a consolidation time. The solution depends on the ratio between both timescales.

The time step is an essential factor for calculating new physical quantities of each particle which moves according to the updated values at each time step. Therefore, a certain quantity of time steps is needed to assure the method’s stability and get reasonable results. This study will perform adaptive time-stepping, which is calculated under the Courant Friendrichs-Levy (CFL) condition.

Case study: Johnsons Landing debris avalanche

Description

The Johnsons Landing landslide is an appropriate real case exercise to benchmark the capabilities of the developed computational model. It was selected based on reliable information, including topography, the initial thickness of the landslide, distribution of deposit volume, final run-out, and estimated velocities, provided by Nicol et al. (2013), who conducted an in-depth investigation on the day of the debris avalanche. The geotechnical parameters were estimated by taking into account these field evidences.

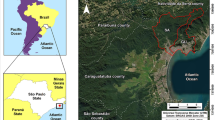
It occurred approximately two km northeast of the small community of Johnsons Landing, located on Kootenay Lake, on the morning of July 12th, 2012. Figure 5 provides a general view of the avalanche and its location.

Fig. 5

Aerial view of the Johnsons Landing debris avalanche. (Coordinates: $~50^\circ 05'00\prime \prime N~116{}^\circ 53'00\prime \prime W$)

As shown in Fig. 5, the debris avalanche was triggered in the upper channel where the unstable materials, include soil and rock, flowed into the mid-channel. Then, a small portion of the material flow avulsed from the mid-channel at a sharp 70° bend and travel along the drainage line until it reached the mouth of the gully (labelled as “Gar Creek Fan”). Much of the debris avalanche flowed out of the channel, ran down to the Johnsons Landing bench and spread out over the terrace surface (The location of the bench is shown in Fig. 5), causing the loss of four fatalities and the damage of several homes and a public road.

It is estimated that about 320,000 ${{m}^{3}}$ of unstable material travelled down the channel, at the flow velocities of between 25-35 m/s based on super-elevation data. It was estimated that $140,400~{{m}^{3}}$ of material deposited in the upper channel, $55,100~{{m}^{3}}$ deposited in the mid-channel, $169,000~{{m}^{3}}$ deposited on the bench, and $17,300~{{m}^{3}}$ deposited on the lower channel. Therefore, the deposit volume increased to about 381,800 ${{m}^{3}}$ Nicol et al. (2013).

In order to model a debris avalanche, there exist different computer-based models to back-analyse the dynamics of the event, and estimate its potential run-out distance and deposit volume. In this paper, the simulation modelling of the debris avalanche is performed through the GeoFlow-SPH code, which has been developed at Madrid by an expert research team for more than a decade. The Johnsons Landing debris avalanche is an appropriate benchmark case to examine the performance of the numerical code. As shown in Fig. 5, the debris avalanche bifurcated into two branches at the mid-channel. In such cases, the back-analysed amount of deposited debris volumes were usually varied from on-site estimated volumes due to the complexity of their dynamics behaviours.

The first challenge here is to reproduce the small portion of the material flow that ran down to the lower channel to form a channelized debris flow. Such branches with a small amount of flowing materials are not usually considered in simulation models due to the significant amount of volume that is usually predicted to deposit in these branches, which does not agree with the observed results. To reproduce the on-site estimated volumes, the researchers consider two alternatives:

• (i) Applying a two-rheology model to consider a low basal resistance to flow in the propagation path and high flow resistance in the branches, or

• (ii) assuming that a channel obstruction is present, for instance due to an accumulation of timber, and it is located upstream of the branch to avoid extension of the debris in these areas Aaron (2017); Pirulli et al. (2018).

The second challenge of the Johnsons Landing debris avalanche is to reproduce the process of the flowing material along the channel until it reached the mid-channel, where the debris avalanche flowed out and ran down to the Johnsons Landing bench (see Fig. 5).

In this study, the debris avalanche is simulated using a depth-integrated two-phase SPH model with a frictional rheological law capable of considering the effect of basal pore pressure evolution.

Numerical results

The numerical analysis of Johnsons Landing debris avalanche is performed through the GeoFlow-SPH model, a depth-integrated two-phase model proposed by Pastor et al. (2021). The Johnsons Landing debris avalanche was simulated based on the provided initial thickness and topography, a regular 999x555 grid with a 3-meter step.

Regarding consolidation modelling, a quarter cosines shape function has been applied to approximate the vertical distribution of excess pore-water pressure (see Sect. 3.2). In order to obtain consolidation coefficient $\left( {{c}_{v}}={{k}_{w}}{{k}_{v}} \right)$, we applied Anderson law (see Eq. 9) using back-calculated parameters including terminal velocity $\left( {{V}_{T}} \right)$ of $7\times {{10}^{-6}}m/\text {s}$, and stiffness of the mixture $\left( {{k}_{v}} \right)$ of $8\times {{10}^{8}}N/{{m}^{2}}$, assuming that the debris avalanche consists of a low-medium permeable soil.

According to the RDCK report Nicol et al. (2013), the debris avalanche largely consists of a saturated loose granular material. To consider a relatively high fluid content, we have taken the densities of solid particles and fluid ${{\rho }_{s}}=2400~\text {kg}/{{m}^{3}}$ and ${{\rho }_{w}}=1000~\text {kg}/{{m}^{3}}$ respectively, and an initial porosity of 0.28, for which the mixture density is $\rho =2050~\text {kg}/{{m}^{3}}$.

In Fig. 6, we provide the distribution of pore-water pressure at two different time steps. At the start, the relative pore-water pressure ($p_{w}^{rel})$ was taken as 1, indicating that the flowing material was completely liquefied (See Fig. 6a). Then, the pore-water pressure is dissipating during the propagation stage, as shown in Fig. 6b, until the debris-flow reaches the deposition area.

Fig. 6

The distribution of relative pore-water pressure at (a) 4s and (b) 40s of the propagation time

The Johnson’s Landing debris avalanche has been studied through voellmy rheological model. Concerning the two rheological parameters, the turbulence coefficient $\left( \xi \right)$ is taken as $500~m/{{s}^{2}}$ and the basal friction angle is found to be as high as $75{}^\circ$ due to taking into account the evolution of pore-water pressures at the basal surface. No changes in the rheological model have been applied in this numerical simulation, and entrainment was not considered in the modelling.

The frictional rheological equation implemented in the numerical simulation is capable of considering the effect of the pore pressure evolutions. Therefore, unlike the previous attempts to simulate the debris avalanche, it is not needed to adopt two different basal friction angles, a low value for the upper channel and a considerably higher value to simulate the high flow resistance in the bench area. As can be seen in Eq. 5, the generation of pore-water pressure is similar to reducing the friction angle and the dissipation of pore-water pressure is equivalent to increasing the friction angle.

Figure 7a shows the observed deposit based on the provided information Nicol et al. (2013). Figure 7b shows the deposit shape and velocity results obtained from the simulation model at the propagation time of 80s. As can be seen, a large volume of the debris avalanche flows out of the channel and deposits over the Johnsons Landing bench, while the rest of the materials that have a lower speed are running down through the sharp bend. The comparison of deposit shapes obtained from simulation and observed results shows that the developed model is capable of reasonably predict the deposit shape of the debris avalanche in all the zones.

Fig. 7

(a) Johnsons Landing debris avalanche’s deposit trimline and the distribution based on the provided information. (b) The well-matched deposit shape and the velocity results obtained from the simulation model

We provide in Fig. 8a topographical map showing the landslide path and the numerical results of final deposit thickness at the propagation time of 200s produced by the GeoFlow-SPH model. The results demonstrated that the proposed simulation models were successfully reproduced the overtopping of the landslide debris at the $70^\circ$ bend and the deposition of the debris on the Johnsons Landing bench. Following the previous simulation results, a considerable amount of material travels all the way down the lower channel to the fan.

Fig. 8

Final deposit thickness computed using two-phase SPH model

The estimated and computed volumes (Geoflow-SPH model) have been reported at four deposition areas in Table 1. The computed and estimated deposition volumes Nicol et al. (2013) are found to be relatively close. However, more material was deposited on the lower channel in the simulation. These differences are due to limitations in depth-integrated models and might be solved using 3D models, which are very expensive in terms of consuming time.

Table 1 Comparison between estimated and computed volumes deposited along the runout path

It is evident that a high flow velocity along the upper channel is required to reproduce the overtopping of the debris at the sharp bend. In order to reach this threshold value of flow velocity, a flow of debris with high water content and high pore pressure should be considered in the simulation.

The average velocity was obtained based on super-elevation data Nicol et al. (2013) and estimated to be between $25-35~m/s$ as the flow travelled down to the bench. The numerical results of the front and average velocities are depicted in Fig. 9. The GeoFlow-SPH code is able to calculate the average velocity of all the particles with a non-zero velocity at each time step. To obtain front velocities, first, we select one of the leading solid SPH nodes that reached the front of the deposition area. Then, we monitor the evolution of the node during the propagation stage.

Fig. 9

The computed front and average velocities of debris avalanche for Johnsons Landing

It has also been reported that the minimum flow velocity required for the landslide debris to overtop the $70{}^\circ$ bend was around 27 m/s. In the simulation, the resulting flow replicates the similar front velocity at the propagation time of 40s where the moving mass reached the mid-channel.

So far, the Johnsons Landing debris avalanche has been modeled using a depth-integrated two-phase SPH model. Compared to previous analyses, the use of the Voellmy rheological model with considering the evolution of basal pore pressure gives reasonable results without requiring to apply a two-rheology model or assuming a channel obstruction.

Reducing the impact of the debris avalanche

Following the removal of over $320,000~{{m}^{3}}$ of material, the debris avalanche ran down the hillside and caused the damage of several homes and a public road and the loss of four fatalities. To mitigate the potential destructiveness of these flow-like landslides, structural countermeasures are often used to reduce flow mobility or even retain the flow. There exist many different debris-resisting structures to cope with the threat related to debris avalanches and debris flows including artificial barriers Wendeler et al. (2007), sabo dams Mizuyama (2008), check dams Popescu and Sasahara (2009), baffles Ng et al. (2015), Geosynthetics-reinforced barriers Cuomo et al. (2020), bottom drainage screen Yifru et al. (2018).

In this paper, a numerical simulation is conducted to investigate the structural countermeasure of bottom drainage screens using to decline the propagating mass’s velocity. This energy drainage structure is designed to dissipate basal pore-water pressure and separate some amount of water from the sediment through the grid. It is important to note that the pore-water pressures play a paramount role in the behaviour of channelized flows compared to other flows that develop along open slope. Thus, bottom drainage screens are used as effective control work against these channelized flows. It also has a simple engineering structure and design and can be easily installed, repaired, and maintained. The bottom drainage screens are also used upstream of sabo dams and artificial barriers to make the structural countermeasures more effective in controlling sediment discharge and converting flows to a less-harmful level.

The idea of installing bottom drainage screens along the propagation path of debris flows to reduce their impact was proposed by Hashimoto in Japan in the 1950s Kiyono et al. (1986); Gonda (2009). Due to the effectiveness of this energy dissipating structure, several small-scale physical models have been conducted to have a better understanding of debris-flow screens and their mechanism including (i) the effects of different opening widths of permeable screens on the debris-flow run-out distance Gonda (2009), (ii) the effects of different bed sediments with different blocking and opening widths Kim (2013) and (iii) the effects of different location of debris flow screens, in the middle or at the end of propagation path, on the behaviour of debris flows Yifru et al. (2018).

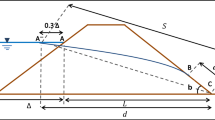
Figure 10a shows a bottom drainage screen (2.4 m long and $19^\circ$ steep) conducted by Gonda Gonda (2009) and constructed in the Kamikami-Horisawa Valley (Japan). Figure 10b shows that a large portion of boulders trapped over the permeable screen and the debris flow run-out effectively reduced. Screens can consist of parallel grids, steel rods or wooden logs, with specified opening widths.

Fig. 10

Bottom drainage screens in the Kamikami-Horisawa Valley, (a) before and (b) after the occurrence of a debris flow

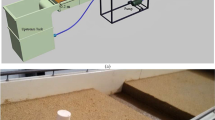
The interaction of moving mass and a permeable screen, accompanied by pore-water pressure dissipation and increasing the shearing resistance of soil particles, is a complex process. Developing a numerical simulation to deal with such soil-structure interaction is a great challenge. To this aim, Pastor et al. (2015) proposed the one-phase SPH-FD model, which combines a depth-integrated SPH model for the propagation analysis and a 1D Finite Difference mesh for the consolidation analysis along the vertical axis of the flowing mass. To overcome one-phase modelling limitations, Pastor et al. (2018) extended it to a two-phase numerical model described in Sect. 3, adding some new features such as porosity variations. The authors have validated the developed two-phase SPH-FD method by simulating numerically a small scale flume test, equipped with a permeable screen, performed at the Trondheim university Tayyebi et al. (2021). After comparing the numerical and experimental results, we concluded that the proposed model is capable of reproducing the propagation of the debris flows properly, and more importantly to correctly performs the timespace evolution of pore-water pressures over an impermeable and permeable bottom boundary.

In Fig. 11, we have plotted the vertical profiles of total pore-water pressure on impermeable and permeable basal surface. The distribution of pore-water pressure is simulated based on the following assumptions: (i) The total pore-water pressure is composed of hydrostatic pressure (${{p}_{hyd}}$) and excess pore-water pressure ($\Delta {{p}_{w}}$). (ii) Once the solid SPH nodes are propagating over the permeable screen, the total pore-water pressure dissipates at the basal surface. As a result, the hydrostatic pressure $\left( p_{hyd}^{b} \right)$ instantly becomes equal, but opposite in sign, to the excess pore-water pressure $\left( \Delta p_{w}^{b} \right)$. (iii) During propagation over the permeable screen, the pore-water pressure remains in the body of flowing mass.

Fig. 11

The total pore-water pressure distribution of debris-flow on an impermeable terrain (run-out channel) and a permeable grid

Consequently, the pore-water pressure will dissipate from the shearing zone. In return, the soil particles regain their contact friction, and thereby the shearing resistance of the moving debris increases. The developed model is capable of considering this physical aspect by applying the frictional rheological equation given in Eq. 5.

As shown in Fig. 12, we modified the geometric data by assuming that two debris flow screens are positioned along the propagation path. To have the highest efficiency, the first screen was located at the toe of the upper channel for the advantage of having a relatively gentler slope and a narrower width. It is designed to reduce the velocity and prevent overtopping of the flowing mass and, consequently, secure homes and a public road on the bench area. The second breaker was located at the lower channel’s crown to stop the mobilized volume of the debris avalanche from accelerating and travelling down. The first screen is located at an elevation of 756m with an area of $30m\times 30m$ and the second screen at an elevation of 729m with an area of $45m\times 25m$. This complex debris avalanche scenario has been modelled here by using the depth-integrated two-phase SPH-FD model. Forward analyses have been conducted using the same rheological and consolidation parameters used for the back analyses.

Fig. 12

The locations of debris-flow screen

As described in Sect. 3.2, two alternative methods can be applied to describe excess pore pressure evolution. First, the vertical distribution of pore-water pressure is approximated using a quarter cosines shape function. Second, the consolidation equation is discretized by using the finite difference method.

In the previous simulated model, the moving mass was able to flow freely over the natural terrain without any obstacle. For such cases, it is not needed to consider basal surface permeability and is recommended to use the less computationally expensive method of quarter cosines shape function. In this method, as described in detail in Sect. 3.2, boundary conditions fulfil with a zero value at the surface and zero gradients at the basal surface, by assuming the hypothesis that the pore pressure is zero on the free surface and the bottom is impermeable, to approximate the vertical distribution of pore water pressure. However, applying a simple shape function to describe pore-water pressure evolution presents some limitations in modeling the cases with a permeable terrain. In such cases, once the basal pore pressure is set to dissipate at the permeable screen, the whole pressure along the vertical axis dissipates, while pore pressure should exist in the flowing mass body.

The evolution of pore-water pressure in the current simulated model can’t be described using a simple shape function due to the limitation of the ability to model the cases with a permeable terrain. Therefore, the second alternative has been applied to the current case equipped with a bottom drainage screen to compute run-out distance and deposition heights on the screen and the deposition areas of the debris avalanche. In this method, a set of finite difference meshes and solid SPH nodes incorporate to simulate this particular case in which basal pore pressures dissipate rapidly due to the flowing mass propagating over terrain with high permeability. In Fig. 13, we present a results sequence of the total pore-water pressure at the basal surface at the initial time and time 150s.

Fig. 13

Results sequence of total pore pressure at (a) 0s and (b) 150s

During the run-out, the total pore-water pressure is a sum of the hydrostatic part and the excess pore-water pressure. Except when the moving mass is crossing a permeable screen, which in this case, the total pore-water pressure at the basal surface becomes zero. As we have assumed that the flowing material was fully liquefied at the triggering stage, the maximum total pore-pressure at starting conditions is equal to ${{p}_{w}}=\left( \bar{\rho }'+{{\rho }_{w}} \right) gh,$ where the submerged density $\bar{\rho }'$ is given by $\bar{\rho }'=\left( {{\rho }_{s}}-{{\rho }_{w}} \right) \left( 1-n \right)$ which the result is $415.5~kPa~\left( {{p}_{w}}=2{{\rho }_{w}}\text {g}h \right)$, where the maximum height $\left( h \right)$ is 212 cm.

In Fig. 14, the numerical results of final deposition thickness at the propagation time of 150s are shown. As can be seen, a large volume of the flowing mass is deposited between two permeable screens at the mid-channel with a maximum height of 14m. When the debris avalanche crosses the screen, the moving flow’s speed declines rapidly, and it breaks. Consequently, the moving mass does not reach the threshold value of flow velocity required for the debris avalanche to overtop the $70^\circ$ bend.

Fig. 14

The final deposition thickness of debris flow with screens

The numerical results show that the bottom drainage screen is capable of dissipating a significant amount of energy, or pore-water pressure, and effectively reduces the run-out distance of the debris avalanche. The results demonstrated that the proposed model is capable of considering the effect of terrain with high permeability and take into account the behaviour of a debris flow propagating over a permeable screen.

Conclusion

This paper presented two computational simulations using a depth-integrated two-phase SPH model capable of considering pore-water pressure evolution in debris flows. The pore-water pressures are influenced by the consolidation coefficient and the variations of height and porosity. Two alternative methods are applied to describe the evolution of pore-water pressure. First, the vertical distribution of pore-water pressure is approximated using a quarter cosines shape function. Second, the consolidation equation is discretized using the finite difference method for the particular flows crossing over terrain with high permeability.

The model is later used to simulate the Johnsons Landing debris avalanche that occurred in Canada in 2012. This real case was selected based on reliable information and an accurate dataset, including topography, initial thickness, distribution of deposit volume, and estimated velocities. An important physical aspect of the debris avalanche is its large velocity caused by high pore pressures in their lower part of the upper channel. This was the key challenge in the numerical simulation as it caused a large volume of material overtopped debris at the 70° bend and deposited on the bench area.

The model performance was illustrated by comparing the numerical result with the field in-depth investigation. The numerical results show the high capability of the developed two-phase model and illustrate the significant importance of the pore pressure evolution to properly reproduce the dynamics behaviour of debris flows.

The paper also analysed the effects of the bottom drainage screen on the evolution of debris avalanches. Comparing the numerical results, it is possible to evaluate how the installation of the bottom drainage screens can dissipate a significant amount of energy and reduce the debris avalanche’s run-out distance. Besides, the SPH-FD model’s potentialities have been evaluated to satisfactorily simulate a large-scale event and capture the mechanism of this debris flow breaker structure.