1 Introduction

Embankment dams are widely constructed across rivers and valleys as an economical type of dams that utilizes the available materials in surrounding environment to retain water for several purposes such as water storage, water diversion and protection from floods [1,2,3,4,5]. Embankment dams can be homogeneous, in which one type of soil is used, or zoned constructed with different types of soil, rock, sand or clay compositions [6,7,8]. Although the benefits of embankment dams, they may cause some environmental changes and consequences due to the storing and leakage of water [9, 10]. There are two processes in which embankment dams lose water from their reservoirs, namely evaporation and seepage [11,12,13,14]. Evaporation process cannot be controlled, while water losses due to seepage can be minimized by using some construction techniques [15,16,17]. Moreover, seepage flow causes internal erosion of embankment dam soil, which can result in dam failure [18]. Seepage line and discharge depend on various factors acting on water including the soil medium the dams’ geometric conditions [16, 17, 19,20,21,22]. In order to avoid seepage-related problems on embankment dams, adequate seepage control in all construction stages and during dam operation must be insured [15, 23,24,25,26].

The large number of embankments failure that recorded in the last two centuries motivated the scientific studies on the matter [27, 28]. The emergence of a scientific approach to seepage control began in the eighteenth and nineteenth centuries, when advances in mathematics, physics and engineering provided new tools for understanding the behavior of water in the ground. Scientific researches started when Henri Darcy published his study regarding fluid flow through a porous media in 1856 [29]. He has developed his formula, which is well known today as Darcy’s law, and it is widely used theoretical framework for seepage analysis. It can be defined as:

$$v_{{\text{d}}} = \, k \, i \, = \, Q/A$$
(1)
$$Q = k \, i \, A$$
(2)

where Q is seepage rate (m3/s), vd is velocity of discharge (m/s), i is hydraulic gradient (m/m), k is permeability coefficient (m/s) and A is cross-sectional area which is normal to the flow direction (m2).

Following Darcy, Forchheimer found that Laplace differential equation can be considered as the governing equation to seepage flow, and then he introduced a robust graphical technique for approximating solutions to Laplace’s equation [28]. Following its adoption [29], this method gained widespread popularity in the analysis of seepage for embankment dams, eventually evolving into the established procedure for such analyses [25]. Several improvements have followed the previous theories by Dupuit, Schaffernak–VanIterson and Casagrande [30,31,32]. Casagrande developed his formula to calculate the rate of seepage as:

$$q \, = \, k \, a{\text{ sin}}^{2} \beta$$
(3)

where q represents the Darcy flux or flow rate (m2/s), k stands for hydraulic conductivity or permeability (m/s), a denotes the seepage surface length (m), and \(\beta\) represents the downstream slope angle (See Fig. 1).

Fig. 1
figure 1

The solution proposed by Casagrande for the flow through an embankment dam [33]

Full size image

The calculation of the seepage surface length “a” with the use of the upstream head “h” is expressed as follows:

$$a = S - \sqrt {S^{2} - \frac{{h^{2} }}{{{\text{sin}}^{2} \beta }}}$$
(4)

where S signifies the length of the ĀBC curve (in meters), and h represents the upstream head (in meters).

However, S can be approximated with about a 4–5% error, as a length of the ĀC straight line, then:

$$S = \sqrt {d^{2} + h^{2} }$$
(5)
$$d \, = \, L \, + \, 0.3\Delta$$
(6)

The graphical method has a disadvantage of time-consuming due requiring long seepage line plotting procedure and it is subjected to personal skills [25]. To deal with this problem, analytical solutions were introduced by [30] to draw profile of phreatic line through an earth dam. Moreover [25] used analytical solutions for seepage analysis and determining the length of the drainage blanket and downstream slope cover of earth dams.

On the other hand, calculating the seepage rate and drawing the seepage line experimentally were performed by constructing scaled physical models [22, 26, 34,35,36,37,38,39,40,41], as they help to understand seepage behavior through embankment dams [16, 42, 43]. Nevertheless, due to the various limitations and constraints associated with physical modeling, numerical modeling has emerged as an alternative method widely employed by numerous researchers (e.g., [43,44,45,46]) to address highly intricate engineering problems, including seepage studies. As the numerical models are purely mathematical approach, their results may significantly differ from physical models [19, 44, 45].

Researchers usually validate numerical models by comparing to the field testing results [46, 47]. Reviewing literatures indicated that there is no sufficient studies on comparing results that may obtained from using the different methods (experimental, mathematical, graphical or numerical) as researchers usually use only one method in a study to estimate seepage rate and draw seepage line. Hence, although numerical modeling, nowadays, has widely employed by researchers, there is still no clear agreement on the conditions that affect suitability and accuracy of using such type of modeling.

In this research, an examination of the seepage line within embankment dams was conducted, and the seepage rate was assessed using three distinct methods: physical models, numerical models and mathematical calculations. Subsequently, comparison results have been conducted. The significance of the research can be summarized as an assessment for the ability and accuracy of numerical modeling based on SEEP/W software in predicting seepage line and seepage rate through homogenous embankment dams. The assessment involved three homogeneous embankment dam models with different downstream drainage filters (toe drain, minimum and maximum horizontal drain length). Hence, it gives a clear picture about conditions that make the SEEP/W model suitable or inappropriate to compute the seepage flow rates through embankment dams.

2 Materials and Methods

Comparison analysis of seepage through homogenous embankment dams was conducted using physical, numerical and mathematical models. For the comparison, conditions of experimental tests were considered for mathematical calculation and numerical analysis. Figure 2 illustrates the study flowchart.

Fig. 2
figure 2

Flowchart of the study

Full size image

2.1 Design of Embankment Dam Models

The study was conducted on a theoretical homogeneous embankment dam with a height of 0.36 m, crest width of 0.2 m, upstream slope (H:V) of 2.5:1 and downstream slope (H:V) of 2:1. Embankment dam dimensions were chosen based on the availability of space in the laboratory. Three homogeneous embankment dam models with different downstream drainage filters were considered. The three models are (a) model with toe drain; (b) model with minimum horizontal drain length; (c) model with maximum horizontal drain length. The minimum and maximum lengths of horizontal drain were computed utilizing Chahar equation [48] which can be defined as:

$$\begin{aligned} & L_{{{\text{min}}}} = \frac{{(1 + n^{2} )}}{{2n^{2} }}\\ &\quad \left[ {0.3m + n + F_{{\text{b}}} (m + n) + T - \sqrt {(0.3m + n + F_{{\text{b}}} (m + n) + T)^{2} - n^{2} } } \right] \end{aligned}$$
(7)
$$L_{{{\text{max}}}} = F_{{\text{b}}} (m + n) + T + h\frac{{(1 + n^{2} )}}{{2n^{2} }}\left[ {0.3m + n - \sqrt {(0.3m + n)^{2} - n^{2} } } \right]$$
(8)

where Lmax represents the horizontal drain length (in meters), Fb stands for free board (in meters), m denotes upstream slope (in meters), n represents downstream slope (in meters), T signifies width of crest (in meters) and h represents head of upstream (in meters) Fig. 3.

Fig. 3
figure 3

Embankment dam model inside the rectangular tank a embankment cross section b downstream drainage

Full size image

2.2 Materials and Experimental Setup

The body of the embankment dam models is made from soil, while the drainage filters, which are toe and horizontal drains, are made from gravel. We conducted laboratory tests to search the characteristics of the soil and gravel. The models were situated within a rectangular tank constructed from transparent Perspex acrylic sheets. The dimensions of the rectangular tank are length = 2.4 m, width = 0.5 m and height = 0.5 m (Fig. 4).

Fig. 4
figure 4

The cross sections of the three physical homogeneous embankment dam models a model with toe drain; b model with minimum drain length; c model with maximum drain length

Full size image

2.3 Experimental Tests

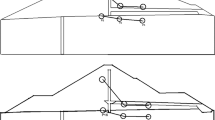
The experiments were conducted with a fully saturated soil and a constant value of upstream water level of 0.3 m. (Assuming that the freeboard of the dam is 0.06 m, hence the maximum water level is 0.3 m.) Four holes were drilled into the downstream slope of the dam at distances of 0.87, 1.04, 1.28 and 1.46 m from the upstream heel. These holes were used to monitor the seepage line by measuring the water height within them. Seepage rates were determined using the volumetric method, which involved measuring the volume of water that flowed out from the downstream outlet of the model per hour [49].

2.4 Mathematical Calculations

The mathematical method proposed by Casagrande (as shown in Fig. 1) was applied to depict the seepage line in all three embankment dam models. The calculations were conducted at the same four points that considered in the experimental tests. The seepage rate was mathematically determined by (3–6).

2.5 Numerical Modeling

SEEP/W software, which is a powerful widely used finite element-based geotechnical software, was used to model water flowing through soil of embankment dams [50]. SEEP/W software uses several mathematical equations of fluid such as Darcy’s law, partial differential water flow equations, finite element water flow equations, etc. SEEP/W software was applied to illustrate the seepage lines for the three models of embankment dam and to compute the associated seepage rates.

3 Results

3.1 Preexperimental Tests

Prior to experimental tests, laboratory tests for soil and gravel were conducted. Soil sample was found to be silty sand, and the hydraulic conductivities for soil and gravel was 3.493 * 10−6 m/s and 0.016 m/s, respectively. The minimum and maximum length of horizontal drain, which calculated using Eqs. (7) and (8), is 0.435 m and 0.63 m, respectively. Figure 4 presents the cross sections of the three models used in this study.

3.2 Experimental Tests

Experiments have been conducted using three embankments models. The values of water level of the seepage line at the four holes for three models are presented in Table 1.

Table 1 Water level of the seepage line at the four holes
Full size table

Observations for the first model (Model a) showed that there was an intersection between seepage line and downstream slope and a portion of the seepage exited the embankment through the downstream face, flowing out between distances ranging from 1.41 to 1.48 m from the embankment’s heel (as illustrated in Fig. 5).

Fig. 5
figure 5

Seepage line intersection with the downstream slope of the model with toe drain

Full size image

The intersection between seepage line and the downstream slope poses a potential threat to the embankment dam stability due to the risk of piping. The use of volumetric method revealed that the discharge of seepage is q = 1.77E−06 m3/s/m.

The seepage line remains within the body of the embankment dam for the rest two models, i.e., models with minimum and maximum drain length (Fig. 6). The difference between the two models is the length of downstream cover. Thus, observations acknowledged that the use of horizontal drain prevents seepage from exiting the embankment model. The values of discharge of seepage are q = 3.98E−07 and q = 6.11E−07 m3/s/m for the models with minimum and maximum drain length, respectively.

Fig. 6
figure 6

Seepage line within the body of embankment models

Full size image

3.3 Mathematical Calculations

The mathematical calculations (Casagrande equation) for seepage loss and seepage line are presented in Table 2. From Table 2, the seepage loss through the embankment dam for the model with toe drainage q = 1.2924E−07 m3/s/m, while for the models with minimum and maximum drain length are q = 1.78E−07 and q = 2.253E−07 m3/s/m, respectively.

Table 2 Mathematical calculations of water level of the seepage line
Full size table

3.4 Numerical Modeling

Figure 7 shows the seepage line using SEEP/W model for the three models. From Fig. 7a, it is clear that there is an intersection between seepage line and the downstream face of the embankment model. The intersection was at the distances of 1.46–1.7 m from the embankment toe. According to the SEEP/W model, the seepage flow rates are q = 1.62E−07 m3/s/m, q = 2.88E−07 m3/s/m and q = 4.373E−07 m3/s/m for the models a–c, respectively.

Fig. 7
figure 7

Seepage line using SEEP/W software, a model with toe drain; b model with minimum drain length; c model with maximum drain length

Full size image

4 Discussion

Figure 8 presents the comparison of seepage lines through the three models (physical, mathematical and numerical). From the figure, it can be seen that both Casagrande equations and SEEP/W model have generated seepage lines that closely align with the observed seepage line, as the location of the seepage line was approximately consistent across all three techniques. (The maximum difference at any distance is less than 0.02 m.) However, while the water level of the seepage line for model b at the 1.28 m distance from the upstream heel is 0.155 as obtained from Casagrande equations and SEEP/W model (See Table 2 and Fig. 7), the water level of the seepage line measured from the physical model b at the same distance is 0.17 m (Table 1), which indicated that the actual seepage line through embankment dams follows the basic parabola approximately and not exactly. Furthermore, it can be noted from Fig. 8 that there is no significant change at 1.04 m distance from the upstream heel for these three models.

Fig. 8
figure 8

The seepage line using the three models a model with toe drain; b model with minimum drain length; c model with maximum drain length

Full size image

The above findings also indicated by [30, 51] from their comparison of the upper flow lines in a homogeneous and isotropic embankment, obtained using different methods. Comparisons that conducted by [30] acknowledged that the use of dimensional analysis to draw profile of phreatic line through homogeneous and nonhomogeneous earthen dams prove to be an easy and sufficiently accurate method when compared with conventional methods (such as Kozeny, A. Casagrande, & Stello) and also by centrifuge model test results conducted by [52]. Additionally, [30] found a fluctuation on the actual seepage line that measured through several homogeneous embankment dams. On the other hand, the comparisons that conducted by [51] acknowledged that analyzing free surface problems using numerical solution of finite difference equations provided similar results to those obtained with the popular numerical methods, such as the finite element method.

The results of seepage flow rate using three models are represented in Table 3. From Table 3, seepage flow rate calculated from SEEP/W through model (a) is close to that computed by Casagrande equations, while there is a big difference in the results of seepage rate comparing to that observed from the physical model. This observation suggests that when the seepage line intersects with the downstream slope, the likelihood of piping occurring within the embankment dam model increases, ultimately leading to a higher total seepage rate. In the case of models equipped with horizontal drains (models (b) and (c)), the seepage rate observed in the physical models is slightly greater than that obtained from SEEP/W software, and it surpasses the values calculated using Casagrande’s solution. The implementation of horizontal drains proves to be of paramount importance in controlling the seepage line’s position, which, in turn, enhances the stability of earth dams. Furthermore, an increase in the length of horizontal drains results in a larger cover for the seepage line but concurrently leads to a higher seepage rate. These findings also indicated by [53] who conducted a comparison for seepage performance for different drainage systems. Moreover, the minimum and maximum lengths of horizontal drain that insure the dam safety were studied by [48]. Hence, an optimum length of horizontal drains should be conserved by designer engineers to obtain the best factors of dam safety. More studies on this matter using different type of soil, different physical model dimensions and different software are recommended.

Table 3 Seepage flow rate obtained through the three models
Full size table

5 Conclusions

To avoid seepage-related problems on embankment dams, adequate seepage control must be insured in all construction and operation stages. In this study, three different modeling approaches—experimental, mathematical and numerical were employed to examine the seepage flow within three homogeneous embankment dam models. The seepage lines and seepage flow rates obtained through these methods were compared with those derived from Casagrande’s equations and the SEEP/W software. The comparisons acknowledged that the seepage lines are approximately at the same location for the three methods. (The maximum difference at any distance is less than 0.02 m.) However, results obtained from physical models showed that the actual seepage lines through embankment dams were fluctuated and they approximately follow the basic parabola and not exactly. On the other hand, the results showed that there is a gap between results from physical and numerical modeling for the first model, and hence the SEEP/W model was inappropriate to calculate the volume of water flow when the seepage line intersected with the downstream slope due to the risk of piping occurrence. For the rest of models, SEEP/W obtained good matching results with physical and mathematical methods. Therefore, the use of numerical modeling is recommended for seepage analysis through homogenous embankment dams when sufficient downstream cover is available. The findings also underscore the significance of applying horizontal drains to control the seepage line position within an embankment dam. An adequate design of horizontal drains of embankment dam should be insured because while increasing the length of horizontal drains increases the cover of seepage line, it increases the seepage rate and water loss as well. Finally, numerical model users should keep in their mind that the results of seepage line and seepage rate obtain from the software are approximation results and not exact. Further studies and researches using different type of soil, different physical model dimensions and different software are recommended.