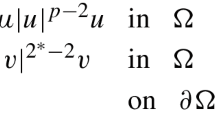On elliptic systems with Sobolev critical growth

Abstract

In this paper, we study the following Dirichlet problem with Sobolev critical exponent

$$\begin{aligned} \left\{ \begin{array}{ll}\displaystyle -\Delta u=|u|^{2^*-2}u+\displaystyle \frac{\alpha }{2^*}|u|^{\alpha -2}|v|^{\beta }u,&{}\quad x\in \Omega , \\ -\Delta v=|v|^{2^*-2}v+\displaystyle \frac{\beta }{2^*}|u|^{\alpha }|v|^{\beta -2}v,&{}\quad x\in \Omega , \end{array} \right. \end{aligned}$$

where $\alpha , \beta >1,$ $\alpha +\beta =2^*:=\frac{2N}{N-2}(N\ge 3)$ and $\Omega ={\mathbb {R}}^N$ or $\Omega$ is a smooth bounded domain in ${\mathbb {R}}^N$. When $\Omega ={\mathbb {R}}^N$, we obtain a uniqueness result on the least energy solutions and show that a manifold of the synchronized type of positive solutions is non-degenerate for the above system for some ranges of the parameters $\alpha , \beta , N$. Our analysis also yields non-uniqueness of positive vector solutions for other parameters. Moreover, we establish a global compactness result and we extend a classical result of Coron on the existence of positive solutions of scalar equations with critical exponent on domains with nontrivial topology to the above elliptic system.

Appendix: Some technical calculations

Proof of (ii)–(iv) of Lemma 2.2

By simple calculation, we have

$$\begin{aligned} f'(\tau )=\frac{2\tau (2^*+\alpha \tau ^\beta -\beta \tau ^{\beta -2}-2^*\tau ^{2^*-2})}{2^*(1+\tau ^\beta +\tau ^{2^*})^{\frac{2}{2^*}+1}}=\frac{2\tau }{2^*(1+\tau ^\beta +\tau ^{2^*})^{\frac{2}{2^*}+1}}g(\tau ). \end{aligned}$$

and

$$\begin{aligned} g'(\tau )=\tau ^{\beta -3}h(\tau ), \end{aligned}$$

where

$$\begin{aligned} h(\tau ):=\alpha \beta \tau ^2-2^*(2^*-2)\tau ^\alpha -\beta (\beta -2). \end{aligned}$$

If $1<\beta<2, 1<\alpha <2$, then $N>4$. Without loss of generality, we assume $\alpha \ge \beta$. Directly calculation says that $h(\tau )$ attains its minimum at $\tau _1=\Bigr (\frac{2^*(2^*-2)}{2\beta }\Bigr )^{\frac{1}{2-\alpha }}$ and

$$\begin{aligned} h(\tau _1)=\beta (2-\beta )-\frac{2^*(2^*-2)(2-\alpha )}{2}\Bigr (\frac{2^*(2^*-2)}{2\beta }\Bigr )^{\frac{\alpha }{2-\alpha }}. \end{aligned}$$

So if $\beta (2-\beta )\ge \frac{2^*(2^*-2)(2-\alpha )}{2}\Big (\frac{2^*(2^*-2)}{2\beta }\Big )^{\frac{\alpha }{2-\alpha }}$, then $g'(\tau )\ge 0.$ Thus $\tau _{min}$ is unique and $f(\tau _{min})<1$.

If $N\ge 8$, then $2^*=2+\frac{4}{N-2}\le \frac{8}{3}$ and $1<\alpha<\frac{5}{3}, 1<\beta \le \frac{4}{3}$. Thus

$$\begin{aligned} \frac{2^*(2^*-2)(2-\alpha )}{2}\Big (\frac{2^*(2^*-2)}{2\beta }\Big )^{\frac{\alpha }{2-\alpha }} \le \frac{8(2-\alpha )}{9}\Big (\frac{8}{9\beta }\Big )^{\frac{\alpha }{2-\alpha }}<\Big (\frac{8}{9}\Big )^2 \end{aligned}$$

and

$$\begin{aligned} \beta (2-\beta )\ge \frac{4}{3}\Big (2-\frac{4}{3}\Big )=\frac{8}{9}. \end{aligned}$$

So there exists a unique $\tau >0$ satisfying (2.1) and $\tau =\tau _{min},f(\tau _{min})<1$.

If $N=7$, then $2^*=\frac{14}{5}$ and $h(\tau )$ attains its minimum at $\tau _1=\big (\frac{28}{25\beta }\big )^{\frac{1}{2-\alpha }}$. Now, we discuss in the following case:

Case (i) $1<\beta <\frac{28}{25}$.

In this case, $\frac{42}{25}<\alpha <\frac{9}{5}$. Now, we claim that if $\tau >\tau _1$, then $g(\tau )>0.$

Indeed,

$$\begin{aligned} \displaystyle g(\tau )= & {} 2^*-\beta \tau ^{\beta -2}+(\alpha \tau ^\beta -2^*\tau ^{2^*-2})\\\ge & {} \displaystyle 2^*-\beta \tau ^{\beta -2}+\min _{\tau>0}(\alpha \tau ^\beta -2^*\tau ^{2^*-2})\\= & {} \displaystyle 2^*-\beta \tau ^{\beta -2}-\frac{\alpha (2-\alpha )}{2^*-2}\left( \frac{2^*(2^*-2)}{\alpha \beta }\right) ^{\frac{\beta }{2-\alpha }}\\>&2^*-\beta \tau _1^{\beta -2}-\frac{\alpha (2-\alpha )}{2^*-2}\left( \frac{2^*(2^*-2)}{\alpha \beta }\right) ^{\frac{\beta }{2-\alpha }}\\= & {} \frac{14}{5}-\beta \left( \frac{25}{28}\beta \right) ^{\frac{2-\beta }{2-\alpha }}-\frac{5}{4} \alpha (2-\alpha )\left( \frac{56}{25\alpha \beta }\right) ^{\frac{\beta }{2-\alpha }}\\\ge & {} \frac{14}{5}-\beta -\frac{5}{4} \alpha (2-\alpha )\left( \frac{56}{25\alpha \beta }\right) ^{\frac{\beta }{2-\alpha }}\\> & {} \frac{42}{25}-\frac{5}{4}\alpha (2-\alpha )\left( \frac{56}{25\alpha \beta }\right) ^5, \end{aligned}$$

where we have used the fact

$$\begin{aligned} \frac{2-\beta }{2-\alpha }>1,\quad \frac{\beta }{2-\alpha }<5. \end{aligned}$$

Consider $M(\alpha ):=\displaystyle \alpha (2-\alpha )\left( \frac{1}{\alpha \beta }\right) ^5$ in $\left( \frac{42}{25},\frac{9}{5}\right)$. We find

$$\begin{aligned} \displaystyle M'(\alpha )= & {} -\alpha ^{-4}\beta ^{-5}-4(2-\alpha )\alpha ^{-5}\beta ^{-5}+5(2-\alpha )\alpha ^{-4}\beta ^{-6}\\= & {} \displaystyle \alpha ^{-5}\beta ^{-6}[-\alpha \beta -4(2-\alpha )\beta +5\alpha (2-\alpha )]\\= & {} \displaystyle \alpha ^{-5}\beta ^{-6}\left( -8\alpha ^2+\frac{132}{5}\alpha -\frac{112}{5}\right) \\\le & {} \displaystyle \left( \frac{42}{25}\right) ^{-5}\left( \frac{28}{25}\right) ^{-6}\left[ -8\left( \frac{42}{25}\right) ^2+\frac{132}{5}\left( \frac{42}{25}\right) -\frac{112}{5}\right] \\< & {} 0, \end{aligned}$$

which means that $M(\alpha )$ is decreasing in $\left( \frac{42}{25},\frac{9}{5}\right)$.

Hence,

$$\begin{aligned} \displaystyle g(\tau ) \ge \frac{42}{25}-\frac{5}{4}\left( \frac{56}{25}\right) ^5M\left( \frac{42}{25}\right) =\frac{42}{25}-\frac{84}{125}\left( \frac{25}{21}\right) ^5>0, \quad \forall \quad \tau >\tau _1. \end{aligned}$$

Since $h(\tau _1)<0$ and $g(0)=-\infty$, we conclude that there exists a unique $\tau >0$ satisfying (2.1) and $\tau =\tau _{min}$, $f(\tau _{min})<1.$

Case (ii) $\frac{28}{25}\le \beta \le \frac{7}{5}.$

In this case, $\frac{7}{5}\le \alpha \le \frac{42}{25}.$ Now, we claim that

$$\begin{aligned} \beta (2-\beta )\ge \frac{2^*(2^*-2)(2-\alpha )}{2}\left( \frac{2^*(2^*-2)}{2\beta }\right) ^{\frac{\alpha }{2-\alpha }}. \end{aligned}$$

In fact,

$$\begin{aligned} \beta (2-\beta )\ge \frac{7}{5}\left( 2-\frac{7}{5}\right) =\frac{21}{25}. \end{aligned}$$

Moreover,

$$\begin{aligned}&\displaystyle \frac{2^*(2^*-2)(2-\alpha )}{2}\left( \frac{2^*(2^*-2)}{2\beta }\right) ^{\frac{\alpha }{2-\alpha }}\\= & {} \displaystyle \frac{28}{25}(2-\alpha )\left( \frac{28}{25\beta }\right) ^{\frac{\alpha }{2-\alpha }} \le \displaystyle \frac{28}{25}(2-\alpha )\\\le & {} \frac{28}{25}\left( 2-\frac{7}{5}\right) =\frac{84}{125}.\\ \end{aligned}$$

Then $h(\tau _1)>0$ and $g'(\tau )>0$. Hence there exists a unique $\tau >0$ satisfying (2.1) and $\tau =\tau _{min}$, $f(\tau _{min})<1.$

If $1<\beta <2,\alpha >2$, then $N=3,4,5$. If $1<\beta <2,\alpha =2$, then $N=5$.

In these cases, $h(\tau )$ has a unique zero point $\tau _0>0$, such that $h(\tau )>0,\,\forall \,\tau \in (0,\tau _0)$, $h(\tau )<0,\,\forall \, \tau \in (\tau _0,+\infty )$. Notice that $f(0)=1$ and $f(\tau )\rightarrow 1$ as $\tau \rightarrow +\infty$, we see that the graphs of $h(\tau ),g(\tau ),f(\tau )$ are as follows.

From the above graphs, we conclude that there are exactly $0<\tau _1<\tau _2<+\infty$ satisfying (2.1) and attaining the minimum and the maximum of $f(\tau )$ respectively, $f(\tau _1)<1,f(\tau _2)>1.$

If $\beta =2$, then $N=3,4,5$. By the proof of part (i) of Lemma 2.2, we can easily obtain (iii).

If $\beta >2$, then $N=3,4,5$. When $\beta >2,N=4,5$ or $4<\beta <5,N=3$, we have $1<\alpha <2$. This case can be reduced to the case $1<\beta <2,\,\alpha >2$ by the symmetry of the system.

Now we consider the case $2\le \alpha < 4,$ and $2<\beta \le 4$. In this case, $N=3$.

If $2\sqrt{10}-4\le \beta <4,N=3$. By simple calculation, we can obtain that $h(\tau )$ has a unique maximum point $\tau _2=(\frac{\beta }{12})^{\frac{1}{\alpha -2}}$ and

$$\begin{aligned} h(\tau _2)= & {} \beta (4-\beta )\left( \frac{\beta }{12}\right) ^{\frac{2}{\alpha -2}}-\beta (\beta -2)\\< & {} \beta (4-\beta )\frac{\beta }{12}-\beta (\beta -2)\\= & {} \displaystyle \frac{\beta }{12}[-(\beta +4)^2+40]\\\le & {} 0. \end{aligned}$$

So there exists a unique $\tau >0$ satisfying (2.1) and attains the maximum of $f(\tau )$, $f(\tau )>1$.

If $2<\beta <2\sqrt{10}-4,N=3$, then $\beta<3<\alpha <4$ and $h(\tau _2)>0$. If $\tau<\tau _2=(\frac{\beta }{12})^{\frac{1}{\alpha -2}}<1$, then

$$\begin{aligned} g(\tau )= & {} 6+\tau ^{\beta -2}(\alpha \tau ^2-\beta )-6\tau ^4\\>&6-\beta \tau ^{\beta -2}-6\tau ^4\\>&6-\beta \left( \frac{\beta }{12}\right) ^{\frac{\beta -2}{\alpha -2}}-6\left( \frac{\beta }{12}\right) ^{\frac{4}{\alpha -2}}\\>&3-6\left( \frac{\beta }{12}\right) ^{\frac{4}{\alpha -2}}>3-6\left( \frac{\beta }{12}\right) ^2\\> & {} 0. \end{aligned}$$

Thus there exists a unique $\tau >0$ satisfying (2.1) and attaining the maximum of $f(\tau )$, $f(\tau )>1$.

If $\beta =4$ and $N=3$, then $\alpha =2$ and $h(\tau )=-16\tau ^2-8<0$. So $g'(\tau )<0$. By the graph of $f(\tau )$, then there exists a unique $\tau >0$ satisfying (2.1) and attaining the maximum $f(\tau )>1$.$\square$

Lemma 4.1

Suppose $\tau >0$ satisfies

$$\begin{aligned} g(\tau ):=2^*+\alpha \tau ^\beta -\beta \tau ^{\beta -2}-2^*\tau ^{2^*-2}=0. \end{aligned}$$

then

$$\begin{aligned} g_1(\tau ):=\frac{2^*(\beta +\alpha \tau ^{2^*-2})}{2^*+\alpha \tau ^\beta }-1\ne 1. \end{aligned}$$

Proof

Arguing by contradiction, we assume that $g_1(\tau )=1$. Then we have

$$\begin{aligned} \displaystyle 2^*\tau ^{2^*-2}-2\tau ^\beta =\frac{2^*(2-\beta )}{\alpha }. \end{aligned}$$

(4.1)

Meanwhile, $\tau$ satisfies

$$\begin{aligned} \displaystyle 2^*+\alpha \tau ^\beta -\beta \tau ^{\beta -2}-2^*\tau ^{2^*-2}=0. \end{aligned}$$

(4.2)

By (4.1), we know that if $\beta \ne 2$, then $\tau \ne 0$ i.e. $\tau >0$.

We will proceed in the following 5 cases.

Case 1 $\beta >2,\alpha \ge 2$.

In this case, $N=3,2^*=6$. If $\alpha =2$, then $\beta =4$. By direct calculation, (4.1) cannot hold. Thus $g_1(\tau )\ne 1$. If $\alpha>2, \beta >2$, by (4.1), we have $2^*\tau ^{2^*-2}<2\tau ^\beta$, thus $\tau<(\frac{2}{2^*})^{\frac{1}{\alpha -2}}<1.$ Then

$$\begin{aligned}&\displaystyle 2^*+\alpha \tau ^\beta -\beta \tau ^{\beta -2}-2^*\tau ^{2^*-2}\\&\quad>\displaystyle 2^*+\alpha \tau ^\beta -\beta \tau ^{\beta -2}-2\tau ^\beta \\&\quad =\displaystyle 2^*+(\alpha -2) \tau ^\beta -\beta \tau ^{\beta -2}\\&\quad> 2^*-\beta \tau ^{\beta -2}>2^*-\beta =\alpha >0. \end{aligned}$$

This is a contradiction with (4.2). Thus we have $g_1(\tau )\ne 1.$

Case 2 $\beta >2,1<\alpha <2$.

In this case, $2^*>3$ and $N=3,4,5.$ Since $\beta >2$, by (4.1), we have $2^*\tau ^{2^*-2}<2\tau ^\beta$. Then $\tau>(\frac{2}{2^*})^{\frac{1}{\alpha -2}}>1.$

Set $m(\tau ):=2^*+\alpha \tau ^\beta -\beta \tau ^{\beta -2}-2^*\tau ^{2^*-2}$. By (4.1), we have

$$\begin{aligned} m(\tau )=\frac{2^*(2^*-2)}{\alpha }-(2-\alpha )\tau ^\beta -\beta \tau ^{\beta -2}. \end{aligned}$$

Since $m(\tau )$ is a decreasing function of $\tau$, $m(\tau )<m\left( \left( \frac{2}{2^*}\right) ^{\frac{1}{\alpha -2}}\right) .$ Set

$$\begin{aligned} H(\alpha ,\beta ):=m\left( \left( \frac{2}{2^*}\right) ^{\frac{1}{\alpha -2}}\right) =\frac{2^*(2^*-2)}{\alpha }- (2-\alpha )\left( \frac{2^*}{2}\right) ^{\frac{\beta }{2-\alpha }}-\beta \left( \frac{2^*}{2}\right) ^{\frac{\beta -2}{2-\alpha }}. \end{aligned}$$

Next, we prove that $H<0.$

In fact, if $N=3$, then $2^*=6$ and $1<\alpha<2,4<\beta <5.$ Since $\displaystyle \frac{\beta -2}{2-\alpha }>2$,

$$\begin{aligned} H(\alpha ,\beta )= & {} \frac{24}{\alpha }-(2-\alpha )3^{\frac{\beta }{2-\alpha }}-\beta 3^{\frac{\beta -2}{2-\alpha }}\\<&\displaystyle 24-9\beta<-12<0. \end{aligned}$$

If $N=4$, then $2^*=4$ and $1<\alpha<2,2<\beta <3.$ Since $\displaystyle \frac{\beta -2}{2-\alpha }=1$ and $\displaystyle \frac{\beta }{2-\alpha }>3$,

$$\begin{aligned} H(\alpha ,\beta )= & {} \frac{8}{\alpha }-(2-\alpha )2^{\frac{\beta }{2-\alpha }}-\beta 2^{\frac{\beta -2}{2-\alpha }}\\<&\displaystyle \frac{8}{\alpha }-8(2-\alpha )-2\beta =\frac{8}{\alpha }+10\alpha -24\\< & {} 4+10\times 2-24=0, \end{aligned}$$

where we have used the fact that $M(\alpha ):=\displaystyle \frac{8}{\alpha }+10\alpha$ is increasing in (1, 2).

If $N=5$, then $2^*=\frac{10}{3}$ and $1<\alpha<\frac{4}{3},2<\beta <\frac{7}{3}.$ Since $2<\alpha \beta <\frac{28}{9}$ and $\frac{\beta }{2-\alpha }>2$,

$$\begin{aligned} H(\alpha ,\beta )= & {} \frac{40}{9\alpha }-(2-\alpha )\left( \frac{5}{3}\right) ^{\frac{\beta }{2-\alpha }}-\beta \left( \frac{5}{3}\right) ^{\frac{\beta -2}{2-\alpha }}\\<&\displaystyle \frac{40}{9\alpha }-(2-\alpha )\left( \frac{5}{3}\right) ^2-\beta =\frac{40-9\alpha \beta }{9\alpha }+\frac{25}{9}\alpha -\frac{50}{9}\\<&\displaystyle \frac{22}{9\alpha }+\frac{25}{9}\alpha -\frac{50}{9}<\displaystyle \frac{22}{9\times \frac{4}{3}}+\frac{25}{9}\times \frac{4}{3}-\frac{50}{9}\\<&\frac{11}{6}-\frac{50}{27}<0, \end{aligned}$$

where we have used the fact that $M_1(\alpha ):=\frac{22}{9\alpha }+\frac{25}{9}\alpha$ is increasing in $(1,\frac{4}{3})$. Since $H<0$, $m(\tau )<0$. This is a contradiction with (4.2). Thus $g_1(\tau )\ne 1$.

Case 3 $\alpha \ge 2, 1<\beta <2$.

In this case, $2^*>3$, then $N=3,4,5$.

If $\alpha =2,1<\beta <2$, then by direct calculation, we have that if $g_1(\tau )=1$, then $\tau =\left( \frac{2^*(2-\beta )}{2\beta }\right) ^{\frac{1}{\beta }}$.

On the other hand, if $m(\tau )=0$, then $\tau ^{\beta -2}=\frac{2^*}{2}$. So

$$\begin{aligned} \left( \frac{2^*}{2}\right) ^{\frac{\beta }{2-\beta }}<\left( \frac{2^*}{2}\right) ^{\frac{2}{2-\beta }}=\frac{\beta }{2-\beta }, \end{aligned}$$

which is impossible and hence $g_1(\tau )\ne 1$.

The case $\alpha >2, 1<\beta <2$ can reduced to the case $\beta >2, 1<\alpha <2$ by the symmetry of the system.

Case 4 $1<\alpha <2$, $1<\beta <2$.

Without loss of generality, we assume that $1<\beta \le \alpha <2$. Since $1<\alpha <2$ and $1<\beta <2$, $N>4$. By the graph of $m(\tau )$, we have that $m(\tau )$ attains its maximum at $\tau _{max}=\left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{1}{2}}$ and $m(\tau _{max})=\frac{2^*(2^*-2)}{\alpha }-2\left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{\beta }{2}-1}$. So when $\left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{2-\beta }{2}}<\frac{2\alpha }{2^*(2^*-2)}$, we have $m(\tau )<0$.

Now, we claim that if $N\ge 9$, then

$$\begin{aligned} \left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{2-\beta }{2}}<\frac{2\alpha }{2^*(2^*-2)}. \end{aligned}$$

(4.3)

Indeed, by $2>\alpha \ge \beta >1$, then $2^*\le 2\alpha <2(2^*-1)$. When $N\ge 9$, we have $2^*\le \frac{18}{7}$. Thus

$$\begin{aligned} \left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{2-\beta }{2}}\le \left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{1}{2}}<\left( \frac{1}{3-2^*}\right) ^{\frac{1}{2}} <\left( \frac{7}{3}\right) ^{\frac{1}{2}}. \end{aligned}$$

and

$$\begin{aligned} \frac{2\alpha }{2^*(2^*-2)}\ge \frac{1}{2^*-2}\ge \frac{7}{4}>\left( \frac{7}{3}\right) ^{\frac{1}{2}}. \end{aligned}$$

So we have (4.3). Then $m(\tau )<0$. This is a contradiction with (4.2). So we have $g_1(\tau )\ne 1$.

When $N=8$, we have $2^*=\frac{8}{3}$ and $\frac{4}{3}\le \alpha<\frac{5}{3}, 1<\beta \le \frac{4}{3}$. Now, we discuss in the following case:

Case (i) $\frac{4}{3}\le \alpha <\frac{62}{39}$.

In this case, we have that

$$\begin{aligned} \left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{2-\beta }{2}}\le \left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{1}{2}}=\left( \frac{4-2^*}{2-\alpha }-1\right) ^{\frac{1}{2}}<\frac{3}{2}. \end{aligned}$$

and

$$\begin{aligned} \frac{2\alpha }{2^*(2^*-2)}=\frac{9\alpha }{8}\ge \frac{3}{2}. \end{aligned}$$

Thus (4.3) holds. Then $m(\tau )<0$. This is a contradiction with (4.2). So we have $g_1(\tau )\ne 1$.

Case (ii) $\frac{62}{39}\le \alpha <\frac{5}{3}$.

In this case $1<\beta \le \frac{14}{13}$. Now, we claim that for any $\tau >0$,

$$\begin{aligned} G(\tau ):=2^*\tau ^{2^*-2}-2\tau ^\beta -\frac{2^*(2-\beta )}{\alpha }<0. \end{aligned}$$

In fact, by directly calculation, we know that $G(\tau )$ attains its maximum at $\tau _{max}=\left( \frac{8}{9\beta }\right) ^{\frac{1}{2-\alpha }}<1.$

$$\begin{aligned} G(\tau _{max})= & {} \displaystyle 2^*\tau _{max}^{2^*-2}-2\tau _{max}^\beta -\frac{2^*(2-\beta )}{\alpha }\\= & {} \displaystyle \left( \frac{8}{9\beta }\right) ^{\frac{\beta }{2-\alpha }}(3\beta -2)-\frac{8}{3}\frac{2-\beta }{\alpha }\\<&3\beta -2-\frac{8}{3}\frac{2-\beta }{\alpha }=3\beta -2-\frac{8}{3}\left( 1-\frac{2}{3\alpha }\right) \\= & {} \displaystyle \frac{10}{3}+\frac{16}{9\alpha }-3\alpha \\\le & {} \frac{10}{3}-\frac{62}{13}+\frac{104}{93}<0. \end{aligned}$$

Thus (4.1) cannot hold. Combining the above discussion, we obtain $g_1(\tau )\ne 1$ if $N=8$.

When $N=7$, we have $2^*=\frac{14}{5}$ and $\frac{7}{5}\le \alpha<\frac{9}{5}, 1<\beta \le \frac{7}{5}$. Now, we discuss in the following case:

Case (i) $\frac{7}{5}\le \alpha <\frac{314}{205}$.

In this case, $\frac{52}{41}< \beta \le \frac{7}{5}$ and

$$\begin{aligned} \left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{2-\beta }{2}}<\left( \frac{2-\beta }{2-\alpha }\right) ^{\frac{1}{2}}=\left( \frac{\frac{6}{5}}{2-\alpha }-1\right) ^{\frac{1}{2}}\le \frac{5}{4}. \end{aligned}$$

and

$$\begin{aligned} \frac{2\alpha }{2^*(2^*-2)}=\frac{25\alpha }{28}\ge \frac{5}{4}. \end{aligned}$$

Thus (4.3) holds. Then $m(\tau )<0$. This is a contradiction with (4.2). So we have $g_1(\tau )\ne 1$.

Case (ii) $\frac{314}{205}\le \alpha <\frac{9}{5}$.

In this case, $1< \beta \le \frac{52}{41}$. If $\frac{28}{25}\le \beta <\frac{52}{41}$, by simple calculation, we have $G(\tau )$ attains its maximum at $\tau _{max}=\big (\frac{28}{25\beta }\big )^{\frac{1}{2-\alpha }}\le 1$ and

$$\begin{aligned} T(\beta ):=G(\tau _{max}) =\left( \frac{5}{2}\beta -2\right) \left( \frac{28}{25\beta }\right) ^{\frac{\beta }{2-\alpha }}+\frac{56}{25\alpha }-\frac{14}{5}. \end{aligned}$$

Then

$$\begin{aligned} T'(\beta )=-\displaystyle \frac{10}{5\beta -4}\left( \frac{28}{25\beta }\right) ^{\frac{5\beta }{5\beta -4}}\ln \left( \frac{28}{25\beta }\right) +\frac{56\times 25}{(70-25\beta )^2}. \end{aligned}$$

Therefore if $\frac{28}{25}\le \beta <\frac{52}{41}$, then $T'(\beta )>0$ and so

$$\begin{aligned} T(\beta )\le T\left( \frac{52}{41}\right) <0. \end{aligned}$$

Thus (4.1) cannot hold. Then $g_1(\tau )\ne 1$. When $1<\beta <\frac{28}{25}$. By the proof of Lemma 2.2 (ii) for $N=7$, we have that there has a unique $\tau _0$ such that $g(\tau )=0$ i.e. (4.1) holds and $0<\tau _0<1$ by the graph of $g(\tau )$. But, when $0<\tau <1$, $G(\tau )\le G(1)<0$. Thus (4.1) and (4.2) cannot hold simultaneously. Combining the above discussion, if $N=7$, then $g_1(\tau )\ne 1$.

Case 5 $\beta =2.$

If $\beta =2$ and $N=3$, by the proof of Lemma 2.2 (iii), we have a unique $\tau >0$ such that $g(\tau )=0$, that is $4(1+\tau ^2)=6\tau ^4$. Then it is easy to verify that (4.1) cannot holds. Thus $g_1(\tau )\ne 1$.

If $\beta =2$ and $N=4$, by the proof of Lemma 2.2 (iii), we have a unique $\tau =1$ such that $g(\tau )=0$. Then (4.1) cannot holds. Thus $g_1(\tau )\ne 1$.

If $\beta =2$ and $N=5$, by Lemma 2.2 (iii), we have $\tau >0$. Then by a similar argument as Case 2, we have $g_1(\tau )\ne 1$.$\square$