A Novel Notion of Local and Nonlocal Deformation-Gamuts to Model Elastoplastic Deformation

Abstract

Localization and nonlocalization are characterized as a measure of degrees of separation between two material points in material’s discrete framework and as a measure of unshared and shared information, respectively, manifested as physical quantities between them, in the material’s continuous domain. A novel equation of motion to model the deformation dynamics of material is proposed. The shared information between two localizations is quantified as nonlocalization via a novel multiscale notion of Local and Nonlocal Deformation-Gamuts or DG Localization and Nonlocalization. Its applicability in continuum mechanics to model elastoplastic deformation is demonstrated. It is shown that the stress–strain curves obtained using local and nonlocal deformation-gamuts are found to be in good agreement with the Ramberg–Osgood equation for the material considered. It is also demonstrated that the cyclic strain hardening exponent and cyclic stress–strain coefficient computed using local and nonlocal deformation-gamuts are comparable with the experimental results as well as the theoretical estimations published in the open literature.

1 Introduction

Every entity is a notion in itself subjected to the influence of its surroundings. Locality is defined as the influence on any entity by its immediate surroundings. Nonlocality is the influence on the entity by its far surroundings. The idea of near and far surroundings, however, is very subjective.

1.1 Brief Overview of Localization

The concept of localization was conceived from the field theories in classical physics as an alternative to the concept of action at a distance. Since then, it has been investigated extensively in many areas of pure and applied mathematical and physical sciences at multiple scales. For example, in classical physics the nonlocal laws of attraction such as Newton’s universal law of gravitation [1] or Coulomb’s inverse square law [2, 3], are purely based on the distance between two localized masses or charges. However, the local laws of resistance, for instance Newton’s laws of motion [4], disregard the distance between a localized mass and the entity exerting force on it, and in electromagnetism the localized electromagnetic field is determined using Maxwell’s equations [5] that completely disregard the distance between the sources of this field as well. In relativistic dynamics the notion of localization is contingent upon the invariant physical state of the entity. While general relativity addresses the nonlocal interaction between two invariant entities localized in space-time continuum, special relativity utilizes the concept of invariant parameter evolution to determine the relationship between space and time. For example, Einstein’s famous equation about mass energy equivalence addresses the relationship between the intrinsic localized energy of any mass at rest and the speed of light.

1.2 Nonlocality and Locality in Continuum Mechanics

Nonlocality is a widely used notion in continuum mechanics to model natural development of discontinuities in deforming materials. By natural development it is presumed that there are no pre-existing discontinuities.

Some local fracture-mechanics-based numerical models, such as the cohesive-crack model, extended finite element method, or the cracking particles method, attempt to model natural cracking effectively. However, it is required to have a pre-existing crack to model its natural propagation via these methods. Cohesive-zone models introduced by Barenblatt [6] and Dugdale [7], and later investigated by Xu and Needleman [8], de Borst [9], Hirmand and Papoulia [10] and many other researchers in open literature, for example, take into account the stress–displacement relationship around the tip of an existing crack in the finite element framework. In the extended finite element method, developed by Mo$\ddot{\text {e}}$s, Belytschko and collaborators [11, 12], the existing discontinuity is categorized as a strong or a weak discontinuity in the form of the solution variable of a problem or the derivative of the solution variable, respectively. The solution space is extended using discontinuous functions. In cracked-particle method, proposed by Rabczuk and Belytschko and further studied by other authors [13, 14], the displacement field is decomposed into the usual continuous part and the enriched discontinuous part. While the discretization of the continuous displacement field is usually done using moving least squares shape functions of linear completeness, the enriched displacement field is obtained as a product of the shape function with enrichment functions, identical to the Heaviside step function, attributing the jump.

To address the natural development of discontinuities, Eringen et al. proposed the idea of nonlocal continuum field theory [15,16,17,18,19] that independently addresses the state of a material point of the body, relative to the state of all the material points of the body influencing the behavior of that material point. The constitutive equations defining the state as a relationship between response objects and functions of independent objects use integral functionals instead of partial spatial derivatives. The volume encompassed by the material points influencing the material point in consideration is defined as its neighborhood. Additionally, Silling considered relative change in the states between two material points as well. Silling, thus, modified Eringen’s mathematical framework, resulting in the so-called peridynamics [20,21,22,23,24,25,26,27,28,29]. In order to address non-uniform neighborhood sizes across the material domain, the concept of dual-horizon peridynamics was proposed by Ren et al. [30]. It was also demonstrated that this concept is able to address the “ghost force” issue and thus eliminates the need of surface correction. Based on the hypothesis that the nature of locality is inversely dependent on the size of the neighborhood, Madenci et al. [31] proposed peridynamic differential operator to convert the local form of differential equations to their nonlocal form. Local to nonlocal conversion in the peridynamic differential operator is carried out by considering a different infinitesimally small incremental neighborhood volume for each material point. A nonlocal operator method was proposed by Ren et al. [32] considering “locality” as a special case of “nonlocality”. In this method the local differential operators are replaced by several nonlocal differential operators to solve partial differential equations.

1.3 Brief Overview of This Study

The frameworks proposed by Eringen et al. and Silling, and the subsequent nonlocal frameworks, consider nonlocality based on the Euclidean distance between the two material points. In these frameworks all the interactions are treated as direct and nonlocal. These frameworks do not take into account the degrees of separation of any two interacting material points.

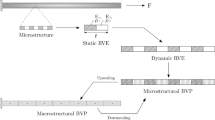
Our study builds on the research conducted thus far in the area of nonlocal continuum mechanics. In view of the subjective nature of the idea of near and far surroundings, in this study we define localization and nonlocalization as a measure of degrees of separation between two material points in material’s discrete framework, and as a measure of unshared and shared information, respectively, between them in material’s continuous domain. Based on these definitions, we introduce a new, independent, multiscale notion of Local and Nonlocal Deformation-Gamuts or DG Localization and Nonlocalization, and quantify the localized and nonlocalized information by means of DG Functional that we developed for continuous and discrete domains. In this paper we demonstrate its applicability to model elastoplastic deformation in the most natural manner.

This paper is organized as follows. In Sect. 2, we briefly provide preliminary background of the underlying computational framework for our study. In Sect. 3, based on our novel notion of Local and Nonlocal Deformation-Gamuts, we propose a governing equation of motion to model the deformation dynamics of a material. We discuss our notion in detail in the subsections of Sect. 3. Based on the discussion in Sect. 3, we re-express our proposed equation of motion in Sect. 4. In the subsections, we propose methodologies to determine the parameters used in our notion. In Sect. 5, we simulate specimens of two materials: AL 7075 T651 (Extruded) and AMS 4911 (BT20) Titanium Alloy, subjected to monotonic and cyclic loadings. We compare our results with the theoretical and published experimental results. In the final section, we provide concluding remarks.

2 Preliminary Background: Computational Framework

In the following subsections we provide the underlying computational framework for our study.

2.1 Local and Nonlocal Bonds/Interactions¹

Consider a system of masses interacting with one another as shown in Fig. 1.

Fig. 1

A Dynamical System of Masses Interacting with One Another

In the context of Fig. 1, for $p, q \in \{1,2,3,4\}$, $m_{p}$ is a mass illustrated by its respective dark circle. It is subjected to an external force $F_{p}$. Two masses $m_{p}$ and $m_{q}$ interact with each other via bond illustrated by a linear massless spring between them. The bond constant between these masses is $C_{p,q}$. We identify the bond constant $C_{p,q}$ and the interaction between the corresponding masses as local if $|p-q| = 1$. The bond constant $C_{p,q}$ and the interaction between the corresponding masses are nonlocal if $|p-q| \ne 1$.

In general, in computational framework we recognize the interaction between two masses as local if the degree of separation, or the “social distance”, between them is one; and nonlocal if the degrees of separation between them are two or more.

We indicate the subscript q as $q_{_{L}}$ if its corresponding mass is locally interacting with $m_{p}$, and as $q_{_{NL}}$ if its corresponding mass is nonlocally interacting with $m_{p}$.

2.2 Local and Nonlocal Elasticity Matrices

The equation of motion for the dynamical system in Fig. 1 is,

$$\begin{aligned} \mathbf{M} \ddot{\mathbf{U }} + \mathbf{K} _{_{NL}} \mathbf{U} = \mathbf{F} , \end{aligned}$$

(1)

where $\mathbf{M} = \begin{bmatrix} m_{1}&{} 0 &{} 0 &{} 0 \\ 0 &{} m_{2} &{} 0 &{} 0 \\ 0 &{} 0 &{} m_{3} &{} 0 \\ 0&{} 0 &{} 0 &{} m_{4} \end{bmatrix}$ is the mass matrix, $\ddot{\mathbf{U }}=\left( \begin{array}{c} \ddot{u}_1 \\ \ddot{u}_2 \\ \ddot{u}_3 \\ \ddot{u}_4 \end{array} \right)$ is the vector valued displacement of masses, $\mathbf{U} =\left( \begin{array}{c} u_1 \\ u_2 \\ u_3 \\ u_4 \end{array} \right)$ is the displacement vector of masses, and $\mathbf{F} =\left( \begin{array}{c} F_1 \\ F_2 \\ F_3 \\ F_4 \end{array} \right)$ is the external force vector. We identify,

$$\begin{aligned} \mathbf{K} _{_{NL}} = \begin{bmatrix} \sum _{q=1}^{4} C_{1,q} &{} - C_{1,2} &{} - C_{1,3} &{} - C_{1,4}\\ - C_{2,1} &{} \sum _{q=1}^{4}C_{2,q} &{} - C_{2,3} &{} - C_{2,4} \\ - C_{3,1} &{} - C_{3,2} &{} \sum _{q=1}^{4} C_{3,q} &{} - C_{3,4} \\ - C_{4,1} &{} - C_{4,2} &{} - C_{4,3} &{} \sum _{q=1}^{4} C_{4,q} \end{bmatrix} \end{aligned}$$

(2)

as Nonlocal Elasticity Matrix.

Assuming that the masses in the system in Fig. 1 interact only locally and that the nonlocal bonds do not exist, we express local elasticity matrix, $\mathbf{K} _{_L}$, in the Eq. (3) as,

$$\begin{aligned} \mathbf{K} _{_{L}} = \begin{bmatrix} C_{1,2} &{} - C_{1,2} &{} 0 &{} 0\\ - C_{2,1} &{} C_{2,1} + C_{2,3} &{} - C_{2,3} &{} 0 \\ 0 &{} - C_{3,2} &{} C_{3,2} + C_{3,4} &{} - C_{3,4} \\ 0 &{} 0 &{} - C_{4,3} &{} C_{4,3} \end{bmatrix}. \end{aligned}$$

(3)

We, thus, distinguish Nonlocal Elasticity Matrix with elements for only local bond constants as Local Elasticity Matrix. A subtle way to look at it is that the local elasticity matrix is a special case of nonlocal elasticity matrix in which nonlocal bonds do not have any material properties. Thus, for the system in Fig. 1, the local elasticity matrix is a tridiagonal nonlocal elasticity matrix with bandwidth 1.

An Indicative Remark:

Consider a material domain made up of n material points locally and nonlocally interacting with one another. Since the degree of separation between material points in local elasticity matrix is one, it is unable to model inelasticity and retrieves a brittle material in modeling.

To model inelasticity and to ensure that the dynamics of the material is the same for any number of degrees of separation considered, we effectively and strategically distribute the material properties associated with the local elements of the local elasticity matrix over the local and nonlocal elements of the nonlocal elasticity matrix.

2.3 Nonlocal Force-Field

We distribute material properties by means of the nonlocal force-field generated from the total potential (strain) energy of the material. A force-field is a mathematical expression describing the dependence of the energy of a system on the coordinates of its particles. It is a widely used notion in Molecular Dynamics (MD). In molecular dynamics, it consists of an analytical form of the interatomic potential energy, and a set of parameters entering into this form [33]. It is a simplified model, with sufficient details to reproduce the properties of interest, of the true potential of particles being held by simple harmonic forces. The Nonlocal Force-Field is a special case of energy functions or potentials between material points at continuum scale. It represents a set of parameters in a functional form used to calculate the potential energy of a system of material points. Nonlocal Force-Field ensures the conservation of total potential energy of the material domain. This allows us to strategically distribute the material properties over the local and nonlocal elements of Nonlocal Elasticity Matrix.

For a material domain made up of n material points locally and nonlocally interacting with one another, the total potential energy while the material is deforming is given as,

$$\begin{aligned} \mathbb {U} = \frac{1}{4}\sum _{p=1}^{n}\sum _{\begin{array}{c} q=1\\ q \ne p \end{array}}^{n}(\mathbf{u} _p - \mathbf{u} _q)^T\mathbf{C} _{_{p,q}}(\mathbf{u} _p - \mathbf{u} _q). \end{aligned}$$

(4)

In Eq. (4), $\mathbf{C} _{p,q}$ is the nonlocal elasticity matrix between material points p and q, and $\mathbf{u} _p$ and $\mathbf{u} _q$ are their displacements due to the deformation.

In MD, the total energy of the system of n particles (material points / particles) with interaction described by an empirical potential is expanded in many-body expansion [34, 35] as,

$$\begin{aligned} \mathbb {U}(\mathbf{x}_1, \mathbf{x}_2, \dots , \mathbf{x}_n) = \sum \limits _{p=1}^{n}{\mathbb {U}}^{(1)}(\mathbf{x}_p) + \sum \limits \limits _{p=1}^{n}\sum \limits _{\begin{array}{c} q = 1 \\ q \ne p \end{array}}^{n}{\mathbb {U}}^{(2)}(\mathbf{x}_p,\mathbf{x}_q) + \sum \limits _{p=1}^{n}\sum \limits _{\begin{array}{c} q = 1 \\ q \ne p,r \end{array}}^{n}\sum \limits _{\begin{array}{c} r = 1 \\ r \ne q,p \end{array}}^{n}{\mathbb {U}}^{(3)}(\mathbf{x}_p,\mathbf{x}_q,\mathbf{x}_r). \end{aligned}$$

(5)

In Eq. (5), the superscripted bracketed integers (1), (2) and (3) represent one, two and three-body potentials, respectively. Thus, ${\mathbb {U}^{(1)}}$ is a one-body term due to an external field or boundary conditions. These potentials represent rigid-body motion and add to 0. ${\mathbb {U}^{(2)}}$ is a two-body term or pair potential. In MD, this pair potential is usually expressed using any empirical functional with a well-defined potential well-depth as a measure of how strongly two particles attract each other, with the right side of the well-depth as the attractive side and the left side as the repulsive side. ${\mathbb {U}^{(3)}}$ is a three-body term that arises when the direct interaction of a pair of atoms or material points is modified by the presence of a third atom or material point. This modification in the interaction between a pair of atoms or material points happens when some of the interactive potential between them is shared as an indirect interaction with the third atom or material point.

Thus, considering parallelism with MD, from Eqs. (4) and (5) we have,

$$\begin{aligned} \mathbb {U} = {\mathbb {U}}(\mathbf{x} _1,\mathbf{x} _2, \dots , \mathbf{x} _n) = \sum _{p=1}^{n}\sum _{\begin{array}{c} q = 1 \\ q \ne p \end{array}}^{n}{\mathbb {U}}^{(2)}(\mathbf{x} _p, \mathbf{x} _q). \end{aligned}$$

(6)

The total internal force that material point p is subjected to, contributing to its nonlocal force-field, is given as the vector sum of the forces from all the pair-potentials involving p,

$$\begin{aligned} {\overrightarrow{f}}_{{\textit{ff}}_{p}} = -\sum _{\begin{array}{c} q = 1 \\ q \ne p \end{array}}^{n} \nabla _\mathbf{x _{p}}{\mathbb {U}_{_p}^{(2)}}(\mathbf{x} _p, \mathbf{x} _q), \end{aligned}$$

(7)

where the gradient $\nabla _\mathbf{x _{p}}$ operates on the position $\mathbf{x} _p$ of the material point p. Any change in the total potential energy that results from a displacement of material point p contributes to the force acting on the material point p in the direction of displacement. The left-hand side in Eq. (7) is the localized force associated with the localized potential at material point p, and its right-hand side is the force-field generated by the internal forces in the local and nonlocal bonds of p.

In order to obtain a desired distribution of localized potentials of the material points over their nonlocal bonds, we introduce a novel notion of local and nonlocal deformation-gamuts in Sect. 3.

3 Governing Equation of Motion for Deformation Dynamics based on Local and Nonlocal Deformation-Gamuts

Based on the variation in energy states across material’s spatial domain, we express the governing equation of motion of a material point $\mathbf{x}$, influencing its local and nonlocal domains, as shown in Eq. (8),

$$\begin{aligned} {\rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t) + \displaystyle \int \limits _{V_{_L}(\mathbf{x} )}(1-\mathcal {R}_\mathbf{x , \mathbf{x} '})\nabla _{_\mathbf{x }}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dV_{_L}(\mathbf{x} ') + \int \limits _{V_{_{NL}}(\mathbf{x} )}\nabla _{_\mathbf{x }}\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ',t)dV_{_{NL}}(\mathbf{x} ') = \mathbf{F} _{d}(\mathbf{x} ,t).} \end{aligned}$$

(8)

The expression in Eq. (8) is motivated by the phenomenon of modification in the direct interaction between two material points due to the presence of some third material point. This phenomenon is discussed in Subsect. 2.3. In Eq. (8), $\rho _{_{L@\mathbf{x} }}$ is the material’s mass-density associated with the local volume around material point $\mathbf{x}$, the subscript $L@\mathbf{x}$ is read as “localized at $\mathbf{x}$”, $\ddot{\mathbf{u }}$ is the acceleration of the material point $\mathbf{x}$ in the reference configuration, $\mathbf{F} _{d}(\mathbf{x} ,t)$ is the external force-density that the local volume around material point $\mathbf{x}$ is subjected to, $V_{_{L}}(\mathbf{x} )$ as well as $V_{_{NL}}(\mathbf{x} )$ are local and nonlocal volumes, respectively, around material point $\mathbf{x}$, $\mathbf{x} '$ in $V_{_{L}}(\mathbf{x} )$ directly interacts with $\mathbf{x}$ and $\mathbf{x} '$ in $V_{_{NL}}(\mathbf{x} )$ indirectly interacts with $\mathbf{x}$. $\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)$ and $\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ', t)$ are local and nonlocal potentials associated with material point $\mathbf{x}$. The parameter $\mathcal {R}_\mathbf{x , \mathbf{x} '}$ modifies the direct interaction between two material points $\mathbf{x}$ and $\mathbf{x} '$ and thus quantifies the indirect interaction between $\mathbf{x}$ and some $\mathbf{x} '$. All these notions are discussed in detail in Subsect. 3.1.

For a discretized domain, $\rho _{_{L@\mathbf{x} }}$, $\ddot{\mathbf{u }}(\mathbf{x} ,t)$ and $\mathbf{F} _{d}(\mathbf{x} ,t)$ assume the form of mass matrix, vector valued displacement of masses and external force vector, respectively, similar to the one expressed in Eq. (1). The discretized versions of the remaining parameters in Eq. (8) are discussed in Subsect. 3.2.

3.1 DG Functional for Continuous Domain

For a continuous domain, at any instant²t, the functional at material particle $\mathbf{x}$ is expressed as,

$$\begin{aligned} DG_{_{_L}}(\mathbf{x} ) = \int \limits _{V_{_L}(\mathbf{x} )}\mathcal {R}_\mathbf{x , \mathbf{x} '}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ')dV_{_L}(\mathbf{x} ') \end{aligned}$$

(9)

and

$$\begin{aligned} DG_{_{_{NL}}}(\mathbf{x} ) = \int \limits _{V_{_{NL}}(\mathbf{x} )}\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ')dV_{_{NL}}(\mathbf{x} '). \end{aligned}$$

(10)

Equation (9) represents Local Deformation-Gamut or DG Localization. It corresponds to the local elasticity matrix $\mathbf{K} _{_{L}}$ in discretized domain. Equation (10) represents Nonlocal Deformation-Gamut or DG Nonlocalization. It corresponds to the nonlocal elasticity matrix $\mathbf{K} _{_{NL}}$ in discretized domain. The term $\mathbb {U}_{_L}$ is the potential energy between the material particles $\mathbf{x}$ and $\mathbf{x} '$ in the local domain. It is the energy associated with the local interactions in $\mathbf{K} _{_{L}}$. The term $\mathbb {U}_{_{NL}}$ is the potential energy between the material particles $\mathbf{x}$ and $\mathbf{x} '$ in the nonlocal domain. It is the energy associated with the nonlocal interactions in $\mathbf{K} _{_{NL}}$.

In order to ensure that the total energy remains conserved, at any instant t, it is required that,

$$\begin{aligned} DG_{_{_L}}(\mathbf{x} ) = DG_{_{_{NL}}}(\mathbf{x} ). \end{aligned}$$

(11)

In the above equations, material point $\mathbf{x} '$ locally and/or nonlocally interacts with $\mathbf{x}$. The subscripts L and NL refer to Local and Nonlocal domains, respectively, and $\mathcal {R}$ is a parameter that quantifies the amount of potential associated with local interactions to be shared with nonlocal interactions. It is defined as,

$$\begin{aligned} \mathcal {R}_\mathbf{x , \mathbf{x} '} \left\{ \begin{array}{lcl} \in (0,1) &{} : &{} V_{_{L}}(\mathbf{x} ) \text { defined on } \mathbf{K} _{_L},\\ = 1 &{} : &{} V_{_{NL}}(\mathbf{x} ) \text { defined on } \mathbf{K} _{_{NL}}. \end{array} \right. \end{aligned}$$

The terms $V_{_L}$ and $V_{_{NL}}$ are local and nonlocal volumes around the material particle $\mathbf{x}$. In a discretized domain, these volumes can be distinctly identified with reference to the degrees of separation. According to the definitions of local and nonlocal interactions, the volume encompassed by local interactions in any matrix, $\mathbf{K} _{_L}$ or $\mathbf{K} _{_{NL}}$, is local volume in that matrix for the corresponding material point. The region made up by the nonlocal interactions in both matrices is the nonlocal volume for that matrix.

However, in continuous domain the notion of local or nonlocal volume is very subjective. We define the local volume as a three-dimensional region within the material where the energy-density is more than other regions. The nonlocal volume is the three-dimensional region that binds two or more local volumes. The energy-density in this region is relatively less than that of the local volumes that it is binding together.

Thus, for a continuous domain characterized over nonlocal elasticity matrix $\mathbf{K} _{_{NL}}$, nonlocal volume is the region shared by local volumes from the domain’s corresponding local elasticity matrix $\mathbf{K} _{_L}$. This argument, thus, identifies a subtle difference between the local elasticity matrix $\mathbf{K} _{_L}$ and the nonlocal elasticity matrix $\mathbf{K} _{_{NL}}$ that, the local elasticity matrix represents an undiscretized specimen in which local domains are not bounded. The binding of the local domains introduces nonlocality, which is manifested in the nonlocal elasticity matrix $\mathbf{K} _{_{NL}}$. The parameter, $\mathcal {R}$, thus quantifies the potency of this binding region.

At any given scale, external energy supplied to the material-domain via some external force vector, will propagate through the nonlocal regions to cause the material to release corresponding bond potentials, and thus causing degradation in material properties. Since there are no binding regions in the domain represented by $\mathbf{K} _{_L}$, it retrieves brittle material. The binding phenomenon engineers material properties, and the measure of the bind quantifies nonlocality.

3.2 DG Functional for Discretized Domain

For a local interaction and the nonlocal interactions influenced by it, the discretized version of the functional is given as,

$$\begin{aligned} DG_{_{_L}}(p) = \mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}}) \end{aligned}$$

(12)

and

$$\begin{aligned} DG_{_{_{NL}}}(p) = \sum _{q_{_{NL}}}\mathbb {U}_{_{NL}}(p,q_{_{NL}}), \end{aligned}$$

(13)

where $q_{_L}$ and $q_{_{NL}}$ are the material points interacting with p locally and nonlocally, respectively.

In Eqs. (12) and (13) it is assumed that the material point p interacts with all the material points in its nonlocal domain with equal intensity. With respect to the parallelism with MD, it means that the potential well-depth is the same for all nonlocal interactions that the material point p is connected to. If we identify the relative difference between these well-depths, a more precise version of the functional can be derived as under:

For a particular local interaction, Eq. (12) can be written as,

$$\begin{aligned} \mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}})= & {} \sum _{q_{_{NL}}}\mathbb {U}_{_{NL}}(p,q_{_{NL}}) \\ \nonumber= & {} \mathbb {U}_{_{NL}}(p,p+2) + \mathbb {U}_{_{NL}}(p,p+3) + \dots + \mathbb {U}_{_{NL}}(p,p+n^{l}_{_{NL}}) \\ \nonumber= & {} w_{p,p+2}\mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}}) + w_{p,p+3}\mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}}) + \\ \nonumber&\dots + w_{p,p+n^{l}_{_{NL}}}\mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}}) \\ \nonumber= & {} \sum _{q_{_{NL}}}w_{p,q_{_{NL}}}\mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}}) \\ \nonumber= & {} \sum _{q_{_{NL}}}\sum _{q_{_{NL}}}w_{p,q_{_{NL}}}\mathbb {U}_{_{NL}}(p,q_{_{NL}}). \end{aligned}$$

(14)

In Eq. (14), $n^{l}_{_{NL}}$ is the last nonlocal material point interacting with the material point under consideration, and weighting factor $w_{p,q_{_{NL}}}$ is a fraction associated with nonlocal interaction $pq_{_{NL}}$. $w_{p,q_{_{NL}}}$ quantifies the percentage of the local potential being distributed that the corresponding nonlocal bond bears. It is thus clear that $\sum \limits _{q_{_{{NL}}}}w_{p,q_{_{NL}}} = 1$. These weights establish a direct relationship with the potential well-depth between the two material points. Equation (12) indicates that the well-depth for all the points in nonlocal domain are equal. It physically implies that material point p attracts all the material points in its nonlocal domain with equal strength. Equation (14) identifies relative differences between the strengths, such that each potential well-depth is specific to a particular material point in the nonlocal domain.

Thus, for a particular local interaction, the functional for discretized domain can be briefly written as,

$$\begin{aligned} DG_{_{_L}}(p) = \mathcal {R}_{p,q_{_L}}\mathbb {U}_{_{L}}(p,{q_{_L}})\end{aligned}$$

(15)

$$\begin{aligned} DG_{_{_{NL}}}(p) = \sum _{q_{_{{NL}}}}\sum _{q_{_{{NL}}}}w_{p,q_{_{NL}}}\mathbb {U}_{_{NL}}(p,q_{_{NL}}), \end{aligned}$$

(16)

where $\sum \limits _{q_{_{{NL}}}}w_{p,q_{_{NL}}} = 1$, $q_{_L}$ and $q_{_{NL}}$ are the local and nonlocal material points, respectively, interacting with p.

In a continuous domain the weighted $DG_{_{_{NL}}}(\mathbf{x} )$, for the fraction of local interactions between material points $\mathbf{x}$ and $\mathbf{x} '$ quantified as $\int \limits _{V_{_L}(\mathbf{x} )} \mathcal {R}_\mathbf{x , \mathbf{x} '}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ')dV_{_L}(\mathbf{x} ')$, is given as,

$$\begin{aligned} DG_{_{_{NL}}}(\mathbf{x} ) = \int \limits _{V_{_{NL}}(\mathbf{x} )}\int \limits _{V_{_{NL}}(\mathbf{x} )}w_\mathbf{x ,\mathbf{x} '}\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ')dV_{_{NL}}(\mathbf{x} ')dV_{_{NL}}(\mathbf{x} '), \end{aligned}$$

(17)

where $\int \limits _{V_{_{NL}}(\mathbf{x} )}w_\mathbf{x ,\mathbf{x} '}dV_{_{NL}}(\mathbf{x} ') = 1$.

DG Functional is capable of modeling material degradation as required. By selecting appropriate values of $\mathcal {R}$ and w one can produce the inelastic curve as desired. It simulates the specimen in the most natural manner. Inelasticity occurs as the potential energy is released when the bond breaks, and as the material loses the corresponding amount of elastic modulus. No explicit model for plastic strain is required.

3.3 $\mathcal {R}$ as a Function of Material Properties and Ramberg–Osgood Parameters

In this section, we express $\mathcal {R}$ as a function of Material Properties and Ramberg–Osgood Parameters.

Fig. 2

Ramberg–Osgood Stress–Strain Curve / Weight-Fractions

The Ramberg–Osgood equation for stress–strain curve [38] is given as,

$$\begin{aligned} \epsilon = \frac{\sigma }{E} + K_{ro}\left( \frac{\sigma }{\sigma _y}\right) ^{n_{ro}}. \end{aligned}$$

(18)

It is illustrated by red curve in Fig. 2. Here, $\sigma$ is stress, $\epsilon$ is strain, E is the Young’s modulus of the material, $K_{ro}$ and $n_{ro}$ are Ramberg–Osgood parameters describing the hardening behavior of the material. They are material constants. Typically, $n_{ro} \ge 5$ and the yield offset $K_{ro} = 0.002$. In Fig. 2, $\sigma _y$ is the yield-stress, $\epsilon _y$ is the yield-strain, $\sigma _f$ is the failure-stress, $\epsilon _f$ is the failure-strain, $\sigma _E = E\epsilon _f$ is the failure-stress of the material had it been brittle, $U_T$ is the modulus of toughness of the material, and $U_S$ is the modulus of softness as defined in the Subsect. 3.3.

Modulus of Softness: We define Modulus of Softness, $U_S$, as the total inability of the material (or a bond) to absorb elastic energy up to the point of failure. It is the area between the black dashed curve and the red stress–strain curve.

Expression for $\mathcal R(E, \sigma _y, \epsilon _y, \sigma _f, \epsilon _f, K_{ro}, n_{ro})$: Based on our definition of the Modulus of Softness, we express $\mathcal R(E, \sigma _y, \epsilon _y, \sigma _f, \epsilon _f, K_{ro}, n_{ro})$ as,

$$\begin{aligned} \mathcal {R}(E, \sigma _y, \epsilon _y, \sigma _f, \epsilon _f, K_{ro}, n_{ro}) = \frac{U_S}{U_S + U_T}. \end{aligned}$$

(19)

In Eq. (19), we determine $U_T$ as,

$$\begin{aligned} U_T&= \sigma _f\epsilon _f - \int _{0}^{\sigma _f}\left( \frac{\sigma }{E} + K_{ro}\left( \frac{\sigma }{\sigma _y}\right) ^{n_{ro}}\right) d\sigma \\ \nonumber&= \sigma _f\epsilon _f - \frac{\sigma _f^2}{2E} - \frac{K_{ro}\sigma _y}{n_{ro} + 1}\left( \frac{\sigma _f}{\sigma _y}\right) ^{n_{ro} + 1}, \end{aligned}$$

(20)

and $U_S$ as,

$$\begin{aligned} U_S&= \frac{1}{2}\sigma _E\epsilon _f - U_T \\ \nonumber&= \frac{1}{2} E\epsilon _f^2 - \sigma _f\epsilon _f + \frac{\sigma _f^2}{2E} + \frac{K_{ro}\sigma _y}{n_{ro} + 1}\left( \frac{\sigma _f}{\sigma _y}\right) ^{n_{ro} + 1}. \end{aligned}$$

(21)

This gives,

$$\begin{aligned} \mathcal {R}(E, \sigma _y, \epsilon _y, \sigma _f, \epsilon _f, K_{ro}, n_{ro}) = \frac{\frac{1}{2}E\epsilon _f^2 - \sigma _f\epsilon _f + \frac{\sigma _f^2}{2E} + \frac{K_{ro}\sigma _y}{n_{ro} + 1}\left( \frac{\sigma _f}{\sigma _y}\right) ^{n_{ro} + 1}}{\frac{1}{2}E\epsilon _f^2}. \end{aligned}$$

(22)

Thus, for elastoplastic materials, $0< \mathcal {R} < 1$; and for brittle materials, $\mathcal {R} \approx 0$.

Each material point in the material domain undergoes deformation identical to the stress–strain behavior of its corresponding material. Thus, for isotropic materials, all material points follow the same stress–strain behavior. However, $\mathcal {R}$ at each material point, expressed as $\mathcal {R}_\mathbf{x }$, depends entirely on the modulus of softness localized at $\mathbf{x}$. Each $\mathcal {R}_\mathbf{x }$ can be further decomposed into $\mathcal {R}_\mathbf{x , \mathbf{x} '}$ as needed. The variation of $\mathcal {R}$ across the material domain is discussed in detail in the Subsect. 4.1.

3.4 Calibration of Weights

We further decompose the modulus of softness, $U_S$, over any material point p’s nonlocal domain using the weight-fractions indicated in Eq. (14).

As shown in Fig. 2, the Modulus of Softness of the material, i.e., the area between the black dashed curve and the red stress–strain curve, is discretized into number of trapezoids equal to an integral multiple of the number of nonlocal material points in the nonlocal domain of p. For the sake of simplicity, let the number of trapezoids is equal to the number of nonlocal material points interacting with p. Based on the fact that interactions between p and its nearer nonlocal material points release more energy upon deformation, as compared to the interactions between the farther nonlocal material points, we associate the trapezoid with the largest area to the nearest nonlocal material point. We, then, compute the uncalibrated weight $w_{p,q_{_{NL-UC}}}$ as,

$$\begin{aligned} w_{p,q_{_{NL-UC}}} = \frac{A_{q_{_{NL}}}}{U_S}, \end{aligned}$$

(23)

where $A_{q_{_{NL}}}$ is the area of the trapezoid associated with the nonlocal material point $q_{_{NL}}$.

Fig. 3

Typical Uncalibrated and Calibrated Weights for any Material Point

A typical Uncalibrated Weights vs Distance of the Nonlocal Material Points from p curve is shown in Fig. 3. It is noticeable that these uncalibrated weights represent uncalibrated modulus of softness. Assuming a normal distribution of weights over the nonlocal domain of p, and using curve for uncalibrated weights (the red curve in Fig. 3) as reference, we determine the correct standard deviation, $\sigma _{{stdev@p}}$, at each material point p. The process of calibrating weights is essentially the process of “redistributing probabilities” for optimal dynamics. It is important to preserve areas under both the curves to ensure the conservation of $U_S$. The calibrated weights, as indicated in Eq. (14), are obtained as,

$$\begin{aligned} w_{p,q_{_{NL}}} = \frac{y_{q_{_{NL}}}}{\sum _{q_{_{NL}}}{y_{q_{_{NL}}}}}, \end{aligned}$$

(24)

where

$$\begin{aligned} y_{q_{_{NL}}} =\frac{e^{-\frac{l^2_{p,q_{_{NL}}}}{2\sigma ^2_{{stdev@p}}}}}{\sqrt{2\pi \sigma ^2_{{stdev@p}}}}. \end{aligned}$$

(25)

In Eq. (25), l is the Euclidean distance between the material points p and $q_{_{NL}}$ in the reference configuration. A typical Calibrated Weights vs Distance of the Nonlocal Material Points from p curve is shown in Fig. 3. These calibrated weights quantify the correct amount of energy released when the interaction ceases and thus quantify the correct gain in the inability of the material to absorb elastic energy. The calibrated standard deviation, $\sigma _{{stdev@p}}$, physically quantifies the length of effective interaction of material point p.

For a continuous nonlocal domain the calibrated weights in Eqs. (24) and (25) are expressed as,

$$\begin{aligned} w_\mathbf{x , \mathbf{x} '} = w(\mathbf{x} , \mathbf{x} ') = \frac{y(\mathbf{x} , \mathbf{x} ')}{\displaystyle \int \limits _{V_{_{NL}}(\mathbf{x} )}{y(\mathbf{x} , \mathbf{x} ')d \mathbf{x} '}}, \end{aligned}$$

(26)

where

$$\begin{aligned} y(\mathbf{x} , \mathbf{x} ') =\frac{e^{-\frac{l^2(\mathbf{x} , \mathbf{x} ')}{2\sigma ^2{_{{{stdev@\mathbf{x} }}}}}}}{\sqrt{2\pi \sigma ^2{_{{{stdev@\mathbf{x} }}}}}}. \end{aligned}$$

(27)

In Eq. (27), l is the Euclidean distance between the material points $\mathbf{x}$ and $\mathbf{x} '$. It is a function of their positions in the reference configuration. $\sigma {_{{{stdev@\mathbf{x} }}}}$ is the standard deviation of the distribution of weight fractions over the nonlocal domain of $\mathbf{x}$.

The methodology to determine $\sigma {_{{{stdev@\mathbf{x} }}}}$ is discussed in the Subsect. 4.2.

4 Modified Governing Equation of Motion for Deformation Dynamics based on Local and Nonlocal Deformation-Gamuts

In the context of the discussion in Subsects. 3.1−3.4, Eq. (8) is re-expressed as,

$$\begin{aligned} {\rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t) + \displaystyle \int \limits _{V_{_L}(\mathbf{x} )}(1-\mathcal {R}_\mathbf{x , \mathbf{x} '})\nabla _{_\mathbf{x }}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dV_{_L}(\mathbf{x} ') + \int \limits _{V_{_{NL}}(\mathbf{x} )}\int \limits _{V_{_{NL}}(\mathbf{x} )}w_\mathbf{x ,\mathbf{x} '}\nabla _{_\mathbf{x }}\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ',t)dV_{_{NL}}(\mathbf{x} ')dV_{_{NL}}(\mathbf{x} ') = \mathbf{F} _{d}(\mathbf{x} ,t).} \end{aligned}$$

(28)

Conceptual visual representations of the local and nonlocal deformation-gamuts in Eq. (28) for some continuous domain are provided in Figs. 4 and 5, respectively.

Fig. 4

Local Deformation-Gamuts

In the figures, a continuous material domain discretized using optimal number of material points is illustrated. Each material point is identified as, either $\mathbf{x}$ as a material point in consideration, or as $\mathbf{x} '$ as a material point locally and/or nonlocally interacting with $\mathbf{x}$. For the discretized framework, they are indexed using p, and $q_{_L}$ or $q_{_{NL}}$, respectively. Local deformation-gamuts are shown in Fig. 4 using different gray shades and the direct interactions therein with darker dotted lines. Nonlocal deformation-gamuts are illustrated in Fig. 5 using a different blue shades and the indirect interactions therein using lighter dotted lines. In both the figures, different shades indicate variation in energy states across the material domain.

In view of the subjective nature of the local and nonlocal volumes in a continuous domain, the boundary of each local and nonlocal domain is chosen arbitrarily. This indicates that there is no limit to the number of material points belonging to the local or nonlocal domain of any particular $\mathbf{x}$, and that any domain is not restricted by any specific physical boundary measured using Euclidean distance between $\mathbf{x}$ and $\mathbf{x} '$.

Fig. 5

Nonlocal Deformation-Gamuts

As identified earlier in this section, two material points $\mathbf{x}$ and $\mathbf{x} '$ may interact locally or nonlocally, or, locally and nonlocally. Thus, the nonlocal domain can be imagined as an “energy-cloud above the local domain that binds local domains together. This is depicted in Figs. 6 and 7. In a perfectly isotropic pristine material, if each material point is assumed to be interacting with all other material points, then the nonlocal domain may simply be visualized as an “energy-cloud” above the local domain.

In Fig. 6, a particular material point $\mathbf{x}$ is shown to be interacting locally and nonlocally with many material points $\mathbf{x} '$s. The gray shade represents direct interactions, and the blue shade represents indirect interactions forming the so-called energy-cloud above the local domain. A finer visual of this phenomenon is presented in Fig. 7 using three material points. In Fig. 7, material points $\mathbf{x} '_1$ and $\mathbf{x} '_2$ are interacting with the material point $\mathbf{x}$ locally (directly) and nonlocally (indirectly). $\mathbf{x} '_1$ is local to $\mathbf{x}$ for the direct interaction between them, and nonlocal for the indirect interaction between them. This indirect interaction between $\mathbf{x}$ and $\mathbf{x} '_1$ happens when a fraction of direct interaction between $\mathbf{x}$ and $\mathbf{x} '_2$ is shared with $\mathbf{x}$ and $\mathbf{x} '_1$, and which $\mathbf{x} '_2$ is relatively inertial to. This causes some modification in the interaction between $\mathbf{x}$ and $\mathbf{x} '_2$. The same applies to the direct interaction between $\mathbf{x}$ and $\mathbf{x} '_2$, for which $\mathbf{x} '_2$ is local to $\mathbf{x}$. $\mathbf{x} '_2$ is nonlocal to $\mathbf{x}$ for the indirect interaction between them.

Fig. 6

“Energy–Cloud”

Fig. 7

Local/nonlocal interactions

It is noticeable that if the indirect interactions in the nonlocal domains are considered as direct, then the interactions in the local domains are indirect. Thus, local and nonlocal deformation-gamuts maintain a duality.

In the following subsections, we provide methodologies to quantify nonlocal deformation gamuts from local deformation-gamuts and to determine the effective distance of interaction of a material point.

4.1 Quantification of Nonlocal Deformation-Gamuts

As discussed in the Subsect. 3.1, the parameter $\mathcal {R}$ quantifies the amount of potential associated with the local interactions to be shared with nonlocal interactions. It thus quantifies nonlocal deformation-gamuts across the material domain.

In order to determine $\mathcal {R}$ at each material point, expressed as $\mathcal {R}_\mathbf{x }$, we consider material’s localized static displacement field under any external load.

For a given static displacement field of the material, the fraction of total potential energy localized at a material point is expressed as,

$$\begin{aligned} \mathbb {U}^{*}_{_{L@\mathbf{x }}}= \frac{\int \limits _{V_{_L}(\mathbf{x} )}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ')dV_{_L}(\mathbf{x} ')}{\mathbb {U}}. \end{aligned}$$

(29)

In Eq. (29), the superscript $*$ represents a dimensionless quantity, $\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ')$ is the potential energy between the material points $\mathbf{x}$ and $\mathbf{x} '$ as discussed in the Subsect. 3.1, and $\mathbb {U}$ is the total potential energy of the material obtained from its given static displacement field.

As indicated in the Subsect. 3.3, each material point in the material domain undergoes deformation identical to the stress–strain behavior of its corresponding material. Thus, the scaled potential energy, associated with the elastic deformation, localized at $\mathbf{x}$ when the material fails, is expressed as,

$$\begin{aligned} \mathbb {U}_{_L}(\mathbf{x} )= \frac{\int \limits _{V_{_L}(\mathbf{x} )}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ')dV_{_L}(\mathbf{x} ')}{\mathbb {U}} \times \frac{1}{2} E \epsilon _{f}^2. \end{aligned}$$

(30)

The strain at $\mathbf{x}$, when the material fails, is estimated from Eq. (30) as,

$$\begin{aligned} \epsilon _{f@\mathbf{x }} = \sqrt{\frac{2\mathbb {U}_{_L}(\mathbf{x} )}{E}} = \left( \sqrt{\mathbb {U}^{*}_{_{L@\mathbf{x }}}}\right) \epsilon _{f}. \end{aligned}$$

(31)

We estimate $\sigma _{f@\mathbf{x }}$, the stress at $\mathbf{x}$ when the material fails, by means of the Ramberg–Osgood equation as under.

Considering the fact that the notion of $\mathcal {R}$ is almost ineffective before the material starts yielding, using the Ramberg–Osgood equation, Eq. (18), we determine the preliminary estimation of $\sigma _{f@\mathbf{x }}$ as,

$$\begin{aligned} \sigma _{f@\mathbf{x }} = {\left\{ \begin{array}{ll} \sigma _y\left( \frac{1}{K_{ro}}\left( \epsilon _{f@\mathbf{x }} - \frac{\sigma _y}{E}\right) \right) ^{\frac{1}{n_{ro}}}, &{} \text {if}\ \epsilon _{f@\mathbf{x }} > \epsilon _y \text {, and} \\ E\epsilon _{f@\mathbf{x }}, &{} \text {if} \ \epsilon _{f@\mathbf{x }} \le \epsilon _y. \end{array}\right. } \end{aligned}$$

(32)

Next, using $\sigma _{f@\mathbf{x }}$ obtained in Eq. (32), we compute the residual strain at $\mathbf{x}$, $\epsilon _{f@\mathbf{x }}^{(r)}$, as,

$$\begin{aligned} \epsilon _{f@\mathbf{x }}^{(r)} = \epsilon _{f@\mathbf{x }} - \left( \frac{\sigma _{f@\mathbf{x }}}{E} + K_{ro}\left( \frac{\sigma _{f@\mathbf{x }}}{\sigma _y}\right) ^{n_{ro}}\right) . \end{aligned}$$

(33)

Using the residual strain at $\mathbf{x}$ obtained in Eq. (33), we obtain the residual stress at $\mathbf{x}$ as,

$$\begin{aligned} \sigma _{f@\mathbf{x }}^{(r)} = \frac{\epsilon _{f@\mathbf{x }}^{(r)}}{\frac{1}{E} + \frac{n_{ro}K_{ro}}{\sigma _y^{n_{ro}}} \sigma _{f@\mathbf{x }} ^{n_{ro}-1}}. \end{aligned}$$

(34)

The corrected stress at $\mathbf{x}$ when the material fails, is then obtained as,

$$\begin{aligned} \sigma _{f@\mathbf{x }}^{(c)} = \sigma _{f@\mathbf{x }} - \sigma _{f@\mathbf{x }}^{(r)}. \end{aligned}$$

(35)

Considering $\sigma _{f@\mathbf{x }}^{(c)}$ as the new $\sigma _{f@\mathbf{x }}$, this procedure is repeated until $\epsilon _{f@\mathbf{x }}^{(r)}$ drops below the desired tolerance.

Using Eq. (19), $\mathcal {R}_\mathbf{x }$ is, then, obtained as,

$$\begin{aligned} \mathcal {R}_\mathbf{x } = \frac{\frac{1}{2}E\epsilon _{f@\mathbf{x }} ^2 - \sigma _{f@\mathbf{x }}\epsilon _{f@\mathbf{x }} + \frac{\sigma _{f@\mathbf{x }}^2}{2E} + \frac{K_{ro}\sigma _y}{n_{ro} + 1}\left( \frac{\sigma _{f@\mathbf{x }}}{\sigma _y}\right) ^{n_{ro} + 1}}{\frac{1}{2}E\epsilon _{f@\mathbf{x }} ^2}. \end{aligned}$$

(36)

It should be noted here that, $\mathcal {R}_\mathbf{x }$ is positive if material points $\mathbf{x}$ are influencing material points $\mathbf{x} '$, and negative otherwise.

At the continuum scale of isotropic materials, $\mathcal {R}_\mathbf{x} , \mathbf{x} ' = \mathcal {R}_\mathbf{x }$ is constant for all the local interactions of $\mathbf{x}$ unless any local interaction is already assigned a different value of $\mathcal {R}_\mathbf{x , \mathbf{x} '}$ for the conservation of localized potential energy. However, a problem-specific calibration of $\mathcal {R}_\mathbf{x , \mathbf{x} '}$ can be carried out to establish a precise bridge between different scales ranging from macro-micro-molecular, to map nonlocal force-fields at different scales including MD force-fields for the multiscale modeling of different types of materials.

4.2 Effective Nonlocal Deformation-Gamut of a Material Point

As discussed in the Subsect. 3.4, $\sigma {_{{{stdev@\mathbf{x} }}}}$ physically quantifies the length of effective interaction of material point $\mathbf{x}$.

In order to estimate $\sigma {_{{{stdev@\mathbf{x} }}}}$ from the given static displacement field of the material, based on the discussion in Sects. 3.2 and 3.4, we express,

$$\begin{aligned} \mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ') = w_\mathbf{x ,\mathbf{x} '} \mathcal {R}_\mathbf{x , \mathbf{x} '} \mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} '). \end{aligned}$$

(37)

It should be noted that in Eq. (37), $\mathbf{x} '$ in $\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ')$ and $w_\mathbf{x ,\mathbf{x} '}$ belongs to the nonlocal deformation-gamut of $\mathbf{x}$; and $\mathbf{x} '$ in $\mathbb {U}_{_{L}}(\mathbf{x} ,\mathbf{x} ')$ and $\mathcal {R}_\mathbf{x ,\mathbf{x} '}$ belongs to the local deformation-gamut of $\mathbf{x}$.

From Eqs. (26), (27) and (37), we get,

$$\begin{aligned} \frac{\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ')}{\mathcal {R}_\mathbf{x , \mathbf{x} '} \mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ')} = \frac{\frac{e^{-\frac{l^2(\mathbf{x} , \mathbf{x} ')}{2\sigma ^2{_{{{stdev@\mathbf{x} }}}}}}}{\sqrt{2\pi \sigma ^2{_{{{stdev@\mathbf{x} }}}}}}}{\displaystyle \int \limits _{V_{_{NL}}(\mathbf{x} )}{\frac{e^{-\frac{l^2(\mathbf{x} , \mathbf{x} ')}{2\sigma ^2{_{{{stdev@\mathbf{x} }}}}}}}{\sqrt{2\pi \sigma ^2{_{{{stdev@\mathbf{x} }}}}}}d \mathbf{x} '}}. \end{aligned}$$

(38)

We assume that the nonlocal deformation-gamut of any material point $\mathbf{x}$ extends over the entire material domain, and consider that the influence of $\mathbf{x}$ on the material points $\mathbf{x} '$ that are far beyond the effective distance of interaction, is negligible. Thus, for any two material points $\mathbf{x} '_{q_{NL=i}}$ and $\mathbf{x} '_{q_{NL=j}}$, we can deduce from Eq. (38) that,

$$\begin{aligned} \frac{\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} '_{q_{NL=i}})}{\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} '_{q_{NL=j}})} = \frac{e^{-\frac{l^2(\mathbf{x} , \mathbf{x} '_{q_{NL=i}})}{2\sigma ^2{_{{{stdev@\mathbf{x} }}}}}}}{ e^{-\frac{l^2(\mathbf{x} , \mathbf{x} '_{q_{NL=j}})}{2\sigma ^2{_{{{stdev@\mathbf{x} }}}}}}} = e^{\frac{l^2(\mathbf{x} , \mathbf{x} '_{q_{NL=j}})-l^2(\mathbf{x} , \mathbf{x} '_{q_{NL=i}})}{2\sigma ^2{_{{{stdev@\mathbf{x} }}}}}}. \end{aligned}$$

(39)

This gives,

$$\begin{aligned} \sigma {_{{{stdev@\mathbf{x} }}}} = \sqrt{\frac{l^2(\mathbf{x} , \mathbf{x} '_{q_{NL=j}})-l^2(\mathbf{x} , \mathbf{x} '_{q_{NL=i}})}{2\ln \left( \frac{\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} '_{q_{NL=i}})}{\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} '_{q_{NL=j}})}\right) }}. \end{aligned}$$

(40)

In the computational framework for Eq. (40), the two nonlocal potentials that we choose are the maximum and minimum potentials from the ensemble of uncalibrated nonlocal potentials. This is discussed in Sect. 5.

5 Numerical Examples

Consider a one-dimensional prismatic specimen as shown in Fig. 8 with length L, cross sectional area A, mass density $\rho$, Young’s Modulus E, and Poisson’s Ratio $\nu$, is subjected to an external tensile force F on its both ends. Let the specimen be discretized in n material points, each indexed by p and q. We allow material points q to interact with material points p locally and nonlocally.

Fig. 8

1-D Discretized Elastic Specimen

We considered specimens for two materials: Al 7075 T651 (Extruded) [39] and AMS 4911 (BT20) Titanium Alloy [40], of length = 0.1 m, breadth = 0.01 m, and thickness = 0.01 m.

For both materials, the specimens were discretized with 200, 400, 500, 600, 800 and 1000 local bonds of equal lengths. The simulation was carried out for monotonic as well as cyclic loadings. For monotonic loading, an initial external tensile force of 0.01 N was applied on both ends of the prismatic specimen, and it was increased by $1\%$ after every static displacement. For cyclic loading, the tensile force was unloaded in the similar fashion as the external stress on the specimens became larger than the corresponding yield stress.

The simulation procedure for both the materials is given in Sect. 5.1, and the results are shown in Sects. 5.2, 5.3 and 5.4. The stress–strain data, to determine Ramberg–Osgood parameters, was obtained from web-based engineering toolkits and MechaniCalc, Inc. [41]. Unless given, the Ramberg–Osgood parameters for the stress–strain curves were determined using methodology provided in MMPDS handbook (Chapter 9 in [42]).

5.1 Simulation Procedure

A computer program in MATLAB was written from scratch. The procedures to develop local and nonlocal elasticity matrices, used in our simulation, are demonstrated in Appendix A.

A general recipe for the simulation is provided underneath along with the equations used for our computational framework:

• 1. The static displacement field of the material was determined using the local elasticity matrix. $\mathcal {R}_{p}$ was estimated for each material point from the static displacement field using the discretized version of Eq. (36) as,

  $$\begin{aligned} \mathcal {R}_{{p}} = \frac{\frac{1}{2}E\epsilon _{f@\text {{p}}} ^2 - \sigma _{f@\text {{p}}}\epsilon _{f@\text {{p}}} + \frac{\sigma _{f@\text {{p}}}^2}{2E} + \frac{K_{ro}\sigma _y}{n_{ro} + 1}\left( \frac{\sigma _{f@\text {{p}}}}{\sigma _y}\right) ^{n_{ro} + 1}}{\frac{1}{2}E\epsilon _{f@\text {{p}}} ^2}. \end{aligned}$$

  (41)

  $\mathcal {R}_{p,q_{_L}}$ was set as $\mathcal {R}_{p}$ unless assigned any other value in any prior step or iteration.

• 2. Nonlocal Elasticity Matrix was developed for the computed values of $\mathcal {R}_{p}$ based on the procedure given in Appendix A.

• 3. From the uncalibrated ensemble of nonlocal potentials and weights obtained from the nonlocal elasticity matrix computed in step 2, $\sigma {_{{{stdev@{p}}}}}$ for each material point and the corresponding calibrated weights, $w_{p,q_{_{NL}}}$, were estimated.

  • $\sigma {_{{{stdev@{p}}}}}$ was estimated as under. For the discretized domain, Eq. (39) takes the form,

    $$\begin{aligned} \frac{\mathbb {U}_{{p,q_{_{NL=i}}}}}{\mathbb {U}_{{p,q_{_{NL=j}}}}} = e^{\frac{l^2_{{p,q_{_{NL=j}}}}-l^2_{{p,q_{_{NL=i}}}}}{2\sigma ^2{_{{{stdev@{p}}}}}}}. \end{aligned}$$

    (42)

    Summation of the natural logarithms on both sides of Eq. (42) for the entire gamut of nonlocal potentials, gives,

    $$\begin{aligned} \ln \left( \frac{\text {max}\left( \mathbb {U}_{{p,q_{_{NL}}}}\right) }{\text {min}\left( \mathbb {U}_{{p,q_{_{NL}}}}\right) }\right) = \frac{l^2_{{p,q_{_{NL=farthest}}}}-l^2_{{p,q_{_{NL=nearest}}}}}{2\sigma ^2{_{{{stdev@{p}}}}}}. \end{aligned}$$

    (43)

    The underlying assumption behind Eq. (43) is that interactions between p and its nearer nonlocal material points release more energy upon deformation, as compared to the interactions between the farther nonlocal material points. This is discussed in the Subsect. 3.4. Equation (43) gives,

    $$\begin{aligned} \sigma {_{{{stdev@{p}}}}} = \sqrt{\frac{l^2_{{p,q_{_{NL=farthest}}}}-l^2_{{p,q_{_{NL=nearest}}}}}{2\ln \left( \frac{\text {max}\left( \mathbb {U}_{{p,q_{_{NL}}}}\right) }{\text {min}\left( \mathbb {U}_{{p,q_{_{NL}}}}\right) }\right) }}. \end{aligned}$$

    (44)

    In Eq. (44), $q_{_{NL=farthest}}$ and $q_{_{NL=nearest}}$ are, respectively, the farthest and nearest nonlocal material points from p. The maximum and minimum values of the nonlocal potentials are chosen from the ensemble of the nonlocal potentials associated with p obtained from the nonlocal elasticity matrix determined in step 2.

  • The calibrated weights were estimated using Eqs. (24) and (25). The denominator in Eq. (24) is approximately equal to 1. However, since the development of nonlocal elasticity matrix for our framework ensures the orientation of lengths in the same direction, the weights were estimated as,

    $$\begin{aligned} w_{p,q_{_{NL}}} = 2\frac{e^{-\frac{l^2_{p,q_{_{NL}}}}{2\sigma ^2_{{stdev@p}}}}}{\sqrt{2\pi \sigma ^2_{{stdev@p}}}}. \end{aligned}$$

    (45)

• 4. To determine the desired Nonlocal Elasticity Matrix, nonlocal potential for each nonlocal interaction was calibrated using the calibrated weights as,

  $$\begin{aligned} \mathbb {U}_{{p,q_{_{NL}}}} = w_{p,q_{_{NL}}} \mathcal {R}_{p,q_{_{L}}}\mathbb {U}_{p,q_{_{L}}} = \frac{1}{2} w_{p,q_{_{NL}}} \left( \mathcal {R}_{p,q_{_{L}}}\Vert {\overrightarrow{f}}_{{\textit{ff}}_{p,q_{_{L}}}}\Vert \right) l_{p,q_{_{NL}}}\epsilon _{p,q_{_{NL}}}. \end{aligned}$$

  (46)

The discretized form of the equation of motion, Eq. (8), is given by Eq. (1). It was simulated using implicit Modal Analysis. In order to determine the critical time step, $\Delta t_{cri}$, we followed the stability analysis described by Bathe (section 9.4.2 in [43]).

$$\begin{aligned} \Delta t \le \Delta t_{cri} = \frac{2}{\omega _{max}}. \end{aligned}$$

(47)

Instead of $\omega _{max}$, we used the natural frequency of the Nonlocal Elasticity Matrix that is nearest to the natural frequency $\left( \frac{1}{2\pi }\sqrt{\frac{E}{\rho L^2}}\right)$ of the specimen to determine the critical time step. For the simulations, we considered $\Delta t = \Delta t_{cri}$.

In Eq. (46), $\Vert {\overrightarrow{f}}_{{\textit{ff}}_{p,q_{_{L}}}}\Vert$ is the magnitude of the localized internal force between material points p and $q_{_L}$, as discussed in Sect. 2.3. $\epsilon _{p,q_{_{NL}}}$ is the strain that bond $p,q_{_{NL}}$ experiences during deformation. Equation (46) quantifies the amount of elastic energy that the bond $p,q_{_{NL}}$ will absorb before its failure. As discussed before, the calibrated weights quantify the correct gain in the inability of the material to absorb elastic energy as the material degrades. This inability in terms of elastic energy, associated with an individual bond, is a measure of its rate as expressed in Eq. (48),

$$\begin{aligned} \frac{d\mathbb {U}_{{p,q_{_{NL}}}}}{dt} \rightarrow 0. \end{aligned}$$

(48)

From Fig. 2 and Eq. (24), it is clear that any calibrated weight $w_{p,q_{_{NL}}}$ represents the family of all the bonds that will collectively gain the inability to absorb elastic energy (area of the corresponding calibrated trapezoid) when the specimen experiences the strain corresponding to its calibrated weight. Equation (48) serves as a general failure criterion for a nonlocal interaction quantified by Eq. (46). It, thus, initiates dynamic material degradation in the nonlocal domain. In the numerical examples considered in this study, material degradation is introduced by breaking all the bonds corresponding to their weight, when the specimen experiences the corresponding strain. From MD perspective, it can be interpreted from Eq. (46) that the weight $w_{p,q_{_{NL}}}$ splits the homogenized well-depth into specific well depths, each of which corresponds to a particular nonlocal bond connected with p. Conclusively, this method inherently determines the “critical stretch” for each bond, beyond which the material points cease to interact.

In the following subsections, we present the results for the deformation-gamuts parameters, and monotonic as well as cyclic loadings. The material properties are,

For Material: Al 7075 T651 (Extruded) we have, Young’s Modulus $E = 71.6$ GPa, $\sigma _f = 665.8$ MPa, $\epsilon _f = 0.115$, $\sigma _y = 538.6$ MPa, $\epsilon _y = 0.009522$, $n_{ro} = 17.8702$, and $K_{ro} = 0.002$, Mass Density $\rho = 2810$ $kg/m^3$, Poisson’s Ratio $\nu = 0.33$.

For Material: AMS 4911 (BT20) Titanium Alloy we have, Young’s Modulus $E = 115.7$ GPa, $\sigma _f = 933$ MPa, $\epsilon _f = 0.516$, $\sigma _y = 867$ MPa, $\epsilon _y = 0.009494$, $n_{ro} = 47.61$, and $K_{ro} = 0.002$, Mass Density $\rho = 4430$ $kg/m^3$, Poisson’s Ratio $\nu = 0.31$.

5.2 Deformation-Gamuts Parameters

Deformation-Gamuts parameters are illustrated in this section.

Fig. 9

$\mathcal {R}$ Mechanism for Al 7075 T651

Fig. 10

$\mathcal {R}$ Mechanism for AMS 4911 (BT20) Titanium Alloy

The variations of $\mathcal {R}_\mathbf{x }$ across the length of the specimens of both materials, Al 7075 T651 and AMS 4911 (BT20) Titanium Alloy, are shown in Figs. 9 and 10, respectively. The variation of $\mathcal {R}_\mathbf{x }$ across the Titanium alloy specimen is relatively denser than across the Aluminum alloy specimen. This is expected because Titanium is tougher than Aluminum. It shares higher percentage of the localized potentials with its nonlocal domain as compared to the Aluminum alloy.

Fig. 11

$\sigma {_{{{stdev@\mathbf{x} }}}}$ for AL 7075 T651

Fig. 12

$\sigma {_{{{stdev@\mathbf{x} }}}}$ for AMS 4911 (BT20) Titanium Alloy

The effective length of interaction of each material point for both specimens is shown in Figs. 11 and 12.

Fig. 13

Typical Calibrated Weights for material points @ $l = 0$ and $l = \frac{l}{8}$ for Al 7075 T651

Fig. 14

Typical Calibrated Weights for material points @ $l = 0$ and $l = \frac{l}{8}$ for AMS 4911 (BT20) Titanium Alloy

Figures 13 and 14 show the typical calibrated weights for material points located at the distances $l = 0$ and $l = \frac{l}{8}$ of the specimens of both materials. The gap between the two curves at $l = \frac{l}{8}$ is the local domain of that material point.

5.3 Monotonic Loading

The results for monotonic loading are provided in this section.

Fig. 15

Static Displacement Field for Al 7075 T651

Fig. 16

Static Displacement Field for AMS 4911 (BT20) Titanium Alloy

Static displacement of each material point, obtained using the Local Elasticity Matrices of both materials, is illustrated in Figs. 15 and 16. An external tensile force of 0.01 N was applied on both ends of the prismatic specimen to compute the static displacement at each time step. The third static displacements of both specimens were considered to compute the Nonlocal Elasticity Matrices for both materials.

The simulated numerical values of the total static displacement and the change in the total potential energy are provided in Table 1.

Table 1 Simulated values of $\Delta L$ and $\Delta \mathbb {U}$

The analytical results obtained using equations $\Delta L = \frac{F\times \text {length}}{\text {breadth}\times \text {depth}\times E}$ and $\Delta \mathbb {U} = \frac{1}{2}\frac{\text {breadth}\times \text {depth}\times E}{L}\Delta L^2$ are,

Al 7075 T651 (Extruded): $\Delta L$ = $2.79340\times 10^{-5}$ m, $\Delta \mathbb {U}$ = $2.79340\times 10^{-7}$ J,

AMS 4911 (BT20) Titanium Alloy: $\Delta L$ = $1.72863\times 10^{-5}$ m, $\Delta \mathbb {U}$ = $1.72864\times 10^{-7}$ J.

Fig. 17

Engineering Stress vs. Strain Curve for Al 7075 T651

Fig. 18

Engineering Stress vs. Strain Curve for AMS 4911 (BT20) Titanium Alloy

The stress–strain curves for both materials, simulated using the Nonlocal Elasticity Matrices, are illustrated in Figs. 17 and 18. They are found to be in good agreement with the stress–strain curve obtained using Ramberg–Osgood equation of the respective material.

5.4 Cyclic Loading

We provide the results for cyclic loading in this section.

Fig. 19

Steady-State Cyclic Stress–Strain behavior for one of the cycles of Al 7075 T651

Fig. 20

Steady-State Cyclic Stress–Strain behavior for one of the cycles of AMS 4911 (BT20) Titanium Alloy

Fig. 21

Steady-State Cyclic Stress–Strain behavior of Al 7075 T651 for Several Cycles

Fig. 22

Steady-State Cyclic Stress–Strain behavior of AMS 4911 (BT20) Titanium Alloy for Several Cycles

The response of both the materials subjected to cyclic inelastic loading can be observed in the form of stable hysteresis loops in Figs. 19, 20, 21, and 22.

Fig. 23

Log-log fit for Stress vs. Plastic-Strain amplitudes of Al 7075 T651

Fig. 24

Log-log fit for Stress vs. Plastic-Strain amplitudes of AMS 4911 (BT20) Titanium Alloy

The log-log plots³ of the stress amplitudes vs. plastic-strain amplitudes obtained from the hysteresis loops of both the materials are provided in Figs. 23 and 24. The slopes and the y-intercepts of the linear fits were obtained using the “poly1” fit function available in MATLAB.

The simulated results for Al 7075 T651 (Extruded) are: Cyclic Strain Hardening Exponent $= 0.06244$, Cyclic Stress–Strain Coefficient $= 791.6$ MPa.

The experimental results obtained by Brammer [39] are: Cyclic Strain Hardening Exponent $= 0.0662$, Cyclic Stress–Strain Coefficient $= 792.8$ MPa.

The simulated results for AMS 4911 (BT20) Titanium Alloy are: Cyclic Strain Hardening Exponent $= 0.04762$, Cyclic Stress–Strain Coefficient $= 1105.4$ MPa. The theoretical estimations published by Zhang et al. [40] are: Cyclic Strain Hardening Exponent $= 0.0484$ (section 3.2 in [40]), Cyclic Stress–Strain Coefficient $= 1340.5 - 1537.6$ MPa (section 4 in [40]).

6 Discussion and Concluding Remarks

In this study, we defined localization and nonlocalization as a measure of social distance between two entities in a discrete framework, and as a measure of unshared and shared information, respectively, between them in a continuous domain. Based on these definitions we introduced a novel, independent, multiscale notion of DG Localization and Nonlocalization. We demonstrated its applicability in continuum mechanics. Based on the distribution of energy-density and energy states over the spatial domain of any material, we strategically distributed material properties over the material’s nonlocal domain by means of an effective nonlocal force-field. We, then, used our notion to carry out simulation in the most natural manner and demonstrated its ability to model elastoplastic deformation even if only material’s stress–strain data (engineering or true) is available from experiment.

Nonlocal information is that fraction of local information which is indirectly shared with another nonlocal entity. With reference to Nonlocal Elasticity Matrix $\mathbf{K} _{_{NL}}$, it is that fraction of information between p and $q_{_L}$ that is shared with $q_{_{NL}}$, and which $q_{_{L}}$ is relatively inertial to. This implies that, in order to ensure the conservation of energy and to maintain stability of the system, nonlocality is actually manifested in the higher order terms, ${\mathbb {U}^{(3)}}$, of Eq. (5). As discussed earlier, this term arises when the interaction of a pair of atoms or material points is modified by the presence of a third atom or material point. These higher order terms are “not taken into account” in theories in which nonlocality is characterized as a measure of Euclidean distance between two entities. In our work this modification is inherently manifested.

Based on the assumption that every material point interacts with all other material points locally and nonlocally, it is evident that material degradation is dynamically initiated when two material points stop interacting in one of the domains. However, a crack is manifested only when two material points cease to interact completely. This means that if a material point $\mathbf{x} '$ is interacting with $\mathbf{x}$ in its local and nonlocal domains, a crack is dynamically initiated at the instant when $\mathbf{x} '$ ceases to interact with $\mathbf{x}$ in its both domains. For scenarios in which $\mathbf{x} '$ is interacting with $\mathbf{x}$ in only one of the domains, the dynamic initiation of crack typically happens when $\mathbf{x} '$ ceases to interact with $\mathbf{x}$ in the domain of interaction. The dynamic crack initiation is also governed by the Eq. (48). For the dynamic material degradation or crack initiation in local domains, $\mathbb U_{_L}$ is to be considered in the equation instead of $\mathbb U_{_{NL}}$. This addresses one of the challenges in dynamic fracture about crack initiation related to the material degradation listed by Cox et al. [44].

DG Functional is a multiscale notion. However, the expression itself is scale independent. This means that the expression of the functional as a whole remains the same at any scale. However, the expression of the energy, $\mathbb {U}$, may vary while transiting from any continuum scale to molecular scale, as demonstrated in the Appendix A. DG Functional, thus, establishes a bridge between continuum mechanics and molecular dynamics. In the continuum mechanics framework of our work, the “critical stretch” is inherently determined between two material points $\mathbf{x}$ and $\mathbf{x} '$ by means of the calibrated weight ${w}_\mathbf{x , \mathbf{x} '}$ between them. For Lennard-Jones potential used in the Appendix A, the typical cut-off distance between two particles is usually $2.5 \text { to } 5.5 \times \text {van der Waals radius}$ [34,35,36,37]. The bridge between continuum mechanics and molecular dynamics, thus, offers a reconciliation between the atomic-level descriptions of dynamic crack initiation with criteria used for initiation in the continuum regime [44]. Conclusively, it can also be inferred that a scale-dependent relationship can be developed expressing the transition of classical parameters to molecular parameters.

$\mathcal {R}_\mathbf{x }$ provides a measure of the contribution, in terms of the localized modulus of softness, of a particular material point in the overall deformation dynamics of the material. It, thus, governs the micro-mechanism of the shared potential. We observe a substantial difference in the variation of $\mathcal {R}_\mathbf{x }$ across the material domains of soft and tough materials. The distribution of $\mathcal {R}_\mathbf{x }$ is relatively denser across the material domain of a tough material than that of a soft material. As identified in Sect. 3.1, the supplied external energy interacts with the shared potentials to cause material degradation or cracks. One of the conditions for crack arrest is expressed using energy balance so that the available energy for crack propagation is less than the energy absorbed by the material during crack propagation [45, 46]. It can be thus deduced that $\mathcal {R}_\mathbf{x }$, to a degree, quantifies the so-called postulated material property: “crack arrest toughness” [44], as a difference between the localized external energy and the localized modulus of softness.

It is noticeable that as $\mathcal {R}_\mathbf{x , \mathbf{x} '} \rightarrow 0$, the red curve in Fig. 3 moves closer to the vertical axis. The equation of motion proposed for conventional peridynamics [20,21,22,23,24,25,26,27,28,29] can, thus, be retrieved from the equation of motion, Eq. (8). However, the subtle difference between our work and peridynamics is that, in conventional peridynamics nonlocality is construed based on the Euclidean distance between two material points. In conventional peridynamic framework, even a direct interaction between two material points with one degree of separation is considered nonlocal and bond constants are determined by comparing classical strain energy within a horizon with peridynamic strain energy. In our work we distinctly identify the near force as a local interaction, by means of the degree of separation or the social distance between two material points regardless of the Euclidean distance between them. Additionally, we use the actual total strain energy of the deforming material to determine bond constants. The pair-wise functionals developed for conventional bond-based or state-based peridynamics attempt to retain locality by using coefficients that decay rapidly, and by allowing their effect to be felt only up to the horizon limit (for bond-based peridynamics [23]) or twice the size of the horizon (for state-based peridynamics [27]). However, from the discussion in Sects. 3.4 and 4.2, as well as the results obtained in Sects. 5.2, 5.3 and 5.4, we realize that the effective distance of interaction of a material point $\mathbf{x}$ is approximately equal to $3\times \sigma {_{{{stdev@\mathbf{x} }}}}$ regardless of the size of the horizon, bond-length, grid-size and the grid-type (uniform or non-uniform). Effective distance of interaction is the distance beyond which the two material points cease to interact. It can be physically interpreted as the distance between two material points at which the change in the potential between them is negligible. From Eq. (40), it is also noticeable that in our work every material point determines its own effective distance of interaction. It can be noticed from Figs. 11 and 12 that every material point is under the influence of many distances of interaction of many material points across the domain. Thus, our work, in general, encompasses the idea of dual horizon peridynamics as well.

We showed that explicit knowledge of critical stretch, as well as plastic strain or its rate is not needed. In our work plasticity is introduced via potentials associated with the nonlocal bonds. These potentials are determined using the calibrated weights that quantify the correct gain in the inability of the bond to absorb elastic energy. In this study, we have used the same lattice structure for the discretization of local and nonlocal domains. However, in order to understand the precise role of nonlocal domain in slip and twinning mechanisms, it can be defined for all fourteen Bravais lattice structures to correctly quantify the inner friction and dislocation glide due to the breaking of nonlocal bonds.

In Appendix B we have shown that Eq. (8) is consistent to the classical theory of elasticity. In this study we have considered only 1D prismatic specimen subjected to monotonic and cyclic loadings. In order to extend this theory to 2D/3D cases in which complex structural systems are subjected to various loads like, bending, torsion, buckling, thermal, etc., one needs to take into account the coupling of the degrees of freedom as well. Additionally, the challenge lies in identifying when two degrees of freedom of different kinds become uncoupled. Speculatively, matrices, similar to the global stiffness matrices used in the finite element analysis, can be developed as local elasticity matrices and the corresponding nonlocal elasticity matrices can be generated with distributed material properties. We wish to explore this further in our follow-up research.

At continuum scale DG Functional is based on the variation in energy-density or energy states across the material domain. Since the variation in energy-density and its states could be either linear or stochastic, DG Functional is, conclusively, applicable to domains with stochastically varying material properties as well.

Appendices

Appendices

1.1 A Methodology to determine Nonlocal Elasticity Matrix by distributing Material Properties

For the specimen shown in Fig. 8, let: Length, L = 0.1 m, Breadth = 0.01 m, Depth = 0.01 m, Mass Density, $\rho$ = 7850 $kg/m^3$ $= 76982.20272482401$ $N/m^3$, Young’s Modulus of Elasticity, E = 200 GPa, Poisson’s Ratio, $\nu$ = 0.27, discretized using five local bonds of equal lengths, and six material points of equal mass densities, is subjected to a tensile force of 1000 N on both the ends. Let every material point is interacting with other material points locally and nonlocally. The initial conditions (at $t^{s}_{0}$) are, $\mathbf{U} = [\mathbf{0} ]$ and $\dot{\mathbf{U }} = [\mathbf{0} ]$. (Conversion: 1 kg $=$ 9.80665002864 N.)

The mass matrix $\mathbf{M}$ (in N) is a $6 \times 6$ diagonal matrix with each diagonal element $m_{p,p} = 0.128303 N$.

The external force vector $\mathbf{F} =\left( \begin{array}{c} -1000 \text { } 0 \text { } 0 \text { } 0 \text { } 0 \text { } 1000 \end{array} \right) ^T N$, and the initial positions of the material points, at $t^{s}_{0}$, are $\mathbf{X} =\left( \begin{array}{c} 0.0 \text { } 0.02 \text { } 0.04 \text { } 0.06 \text { } 0.08 \text { } 0.10 \end{array} \right) ^T m$.

The elements of local elasticity matrix are computed as $C_{p,q_{_L}} = \frac{A_{p,q_{_L}} E_{p,q_{_L}}}{l_{p,q_{_L}}}$, where $p,q_{_L}$ is the local bond, $A_{p,q_{_L}}$ is the cross sectional area of the local element. In this case, it is the same for all local elements. $E_{p,q_{_L}} = E = 200$ GPa, and $l_{p,q_{_L}}$ is the local bond length.

Let the instant for $n^{th}$ static displacement be given by $t^s_n$. Under the external force vector $\mathbf{F}$, we obtain the static positions of material points using local elasticity matrix as, $\mathbf{X} =\left( \begin{array}{c} -0.000004939\text { } 0.0199969 \text { } 0.0399991 \text { } 0.0600009 \text { } 0.0800031 \text { } 0.100004939 \end{array} \right) ^T$ m at $t^{s}_{1}$, $\mathbf{X} =\left( \begin{array}{c} -0.000009881 \text { } 0.0199938 \text { } 0.0399981 \text { } 0.0600018 \text { } 0.0800061 \text { } 0.100009881 \end{array} \right) ^T$ m at $t^{s}_{2}$, $\mathbf{X} =\left( \begin{array}{c} -0.000014827 \text { } 0.0199907 \text { } 0.0399971 \text { } 0.0600028 \text { } 0.0800092 \text { } 0.100014827 \end{array} \right) ^T$ m at $t^{s}_{3}$.

At $t^{s}_{3}$, the geometry of the specimen is: Length = 0.10002965 m, Breadth = 0.009992 m, Depth = 0.009992 m, the local and nonlocal bond lengths are:

$\text {Bond Lengths:}$

$$\begin{aligned} \begin{bmatrix} 0&{} 0.0200056&{} 0.0400120&{} 0.0600176&{} 0.0800240&{} 0.1000296\\ 0.0200056&{} 0&{} 0.0200064&{} 0.0400120&{} 0.0600184&{} 0.0800240\\ 0.0400120&{} 0.02000642&{} 0&{} 0.0200056&{} 0.0400120&{} 0.0600176\\ 0.0600176&{} 0.04001203&{} 0.02000561&{} 0&{} 0.0200064&{} 0.0400120\\ 0.0800240&{} 0.06001846&{} 0.04001203&{} 0.0200064&{} 0&{} 0.0200056\\ 0.1000296&{} 0.08002405&{} 0.06001763&{} 0.0400120&{} 0.0200056&{} 0 \end{bmatrix} m, \end{aligned}$$

(49)

and local elasticity matrix is:

$\mathbf{K} _{_{L}} = 10^9 \times$

$$\begin{aligned} \begin{bmatrix} 0.9981201 &{} -0.9981201 &{} 0 &{} 0 &{} 0 &{} 0\\ -0.9981201 &{} 1.9961986 &{} -0.9980785 &{} 0 &{}0 &{} 0\\ 0 &{} -0.9980785 &{} 1.9961978 &{} -0.9981192 &{} 0 &{} 0\\ 0 &{} 0 &{} -0.9981192 &{} 1.9961978 &{} -0.9980785 &{} 0\\ 0 &{} 0 &{} 0 &{} -0.9980785 &{} 1.9961986 &{} -0.9981201\\ 0 &{} 0 &{} 0 &{} 0 &{} -0.9981201 &{} 0.9981201 \end{bmatrix} N/m. \end{aligned}$$

(50)

The potential energies associated with local bonds due to displacements of the material points between $t^{s}_{2}$ and $t^{s}_{3}$ are obtained as,

$\pmb {\mathbb {U}}_{{{L}}} =$

$$\begin{aligned} \begin{bmatrix} 0.0017376&{} 0.0017376&{} 0&{} 0&{} 0&{} 0\\ 0.0017376&{} 0.0040313&{} 0.0022936&{} 0&{} 0&{} 0\\ 0&{} 0.0022936&{} 0.0040413&{} 0.0017477&{} 0&{} 0\\ 0&{} 0&{} 0.0017477&{} 0.0040413&{} 0.0022936&{} 0\\ 0&{} 0&{} 0&{} 0.0022936&{} 0.0040313&{} 0.0017376\\ 0&{} 0&{} 0&{} 0&{} 0.0017376&{} 0.0017376 \end{bmatrix} J. \end{aligned}$$

(51)

The magnitudes of the local internal forces due to displacements of the material points between $t^{s}_{2}$ and $t^{s}_{3}$ are obtained as,

${\textit{f}}_{{\textit{ff}_{L}}} = 10^3 \times$

$$\begin{aligned} \begin{bmatrix} 1.8624765&{} 1.8624765&{} 0&{} 0&{} 0&{} 0\\ 1.8624765&{} 4.0022114&{} 2.1397348&{} 0&{} 0&{} 0\\ 0&{} 2.1397348&{} 4.0076064&{} 1.8678715&{} 0&{} 0\\ 0&{} 0&{} 1.8678715&{} 4.0076064&{} 2.1397348&{} 0\\ 0&{} 0&{} 0&{} 2.1397348&{} 4.0022114&{} 1.8624765\\ 0&{} 0&{} 0&{} 0&{} 1.8624765&{} 1.8624765 \end{bmatrix} N. \end{aligned}$$

(52)

In Eq. (51), the off-diagonal elements are the potential energies associated with the local bonds, and the diagonal elements are the summation of the potential energies from the local bonds that the material point is connected with. Similarly, in Eq. (52) the off-diagonal elements are the magnitudes of the internal forces in the corresponding bonds, and the diagonal elements are the summation of the magnitudes of the forces that the material points are subjected to. These diagonal elements also represent the localized physical quantities associated with the local volumes in discretized domain. In order to obtain the desired material properties, we intend to distribute these potentials and internal forces over the nonlocal bonds. We follow the procedure as underneath.

As discussed in Sect. 2.3, our framework is parallel to molecular dynamics computations. In MD, a bond is required to have a well-defined potential well-depth as a measure of how strongly the two particles attract each other. As a direct analogy to a spring-mass balance, the length of a spring at rest and without any mass attached to it, corresponds to the van der Waals radius between two particles. A stretched spring balanced by some mass represents the well-depth, the strength with which two particles attract each other. The right side of the well-depth is the attractive side, and the left is the repulsive side. When the particles are separated, they stop interacting when the change in the potential energy between them asymptotically approaches to zero. Thus, any functional that is capable of modeling these properties can be used to quantify the bond constant. Developing such new functionals is a vast research topic in itself.

In this study, we use Lennard-Jones potential [36, 37], Fig. 25, to compute Nonlocal Force-field for the dynamics between times $t^{s}_{3}$ and $t^{s}_{4}$.

Fig. 25

Lennard-Jones Potential

Hence from Eq. (6), we have,

$$\begin{aligned} {\mathbb {U}_{_{LJ}}(l_{_{p,q}})} = {\mathbb {U}^{(2)}_{_{LJ}}(l_{_{p,q}})} = 4\epsilon _{_{LJ}}\left[ \left( \frac{\sigma _{_{LJ}}}{l_{p,q}}\right) ^{12} - \left( \frac{\sigma _{_{LJ}}}{l_{p,q}}\right) ^6\right] , \end{aligned}$$

(53)

where ${\mathbb {U}}_{_{LJ}}$ is the interparticle potential between the two particles, $\epsilon _{_{LJ}}$ is the well-depth and a measure of how strongly the two particles attract each other, $\sigma _{_{LJ}}$ is the distance at which the interparticle potential between the two particles is zero. It gives a measurement of how close two nonbonding particles can get and is thus referred to as the van der Waals radius. It is equal to one-half of the internuclear distance between nonbonding particles. Thus, for any given external load, if $t^{s}_{n}$ is the instant at which static displacements of the particles and thus the static deflection of the structure or the specimen occurs, it is clear that the distance at which the intermolecular potential between the two particles is zero must be computed from the positions of the particles at the time step $t^{s}_{n-2}$. It should be noted here that after every static displacement, the specimen will have a new geometry. $l_{_{p,q}}$ is the distance of separation between atoms p and q. The term $\frac{1}{l_{_{p,q}}^{12}}$ signifies the repulsion between atoms when they are brought close to each other; and the term $\frac{1}{l_{_{p,q}}^{6}}$, dominating at large distance, constitute the attractive part and describes the cohesion to the system.

We start with the material point $p = 1$. From $\mathbf{X}$ at $t^{s}_{2}$, we have,

${\sigma _{{_{LJ}}_{1,2}}}_{_{t^{s}_{3}}} = 0.020003728448820$ m, ${\sigma _{{_{LJ}}_{1,3}}}_{_{t^{s}_{3}}} = 0.040008012037143$ m, ${\sigma _{{_{LJ}}_{1,4}}}_{_{t^{s}_{3}}} = 0.060011751322506$ m, ${\sigma _{{_{LJ}}_{1,5}}}_{_{t^{s}_{3}}} = 0.080016034910829$ m, ${\sigma _{{_{LJ}}_{1,6}}}_{_{t^{s}_{3}}} = 0.100019763359649$ m.

In order to distribute a fraction of localized potential energies ${\mathbb {U}}_{{{L}}}$ and localized force-fields ${f}_{{\text {ff}_{L}}}$, quantified by $\mathcal {R}$, over their nonlocal domains, we use nonlocal ${\sigma _{{_{LJ}}_{p,q}}}_{_{t^{s}_{3}}}$ to compute the homogenized ${\epsilon _{_{LJ}}}_{p}$ for nonlocal domain.

From Eqs. (7) and (53) we obtain the expressions for potential energy and force-field for nonlocal domains as,

$$\begin{aligned} \mathcal {R}_{p} \mathbb {U}_{{p}}= {\epsilon _{_{LJ}}}_{p} \sum _{q_{_{NL}}} \frac{12 {\sigma ^6_{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}^8}\left[ 1 - 2\left( \frac{{\sigma _{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}}\right) ^6\right] \; (u_p - u_{q_{_{NL}}})^2,\end{aligned}$$

(54)

$$\begin{aligned} \mathcal {R}_{p} f_{{\textit{ff}}_{p}}= {\epsilon _{_{LJ}}}_{p} \sum _{q_{_{NL}}} \frac{24 {\sigma ^6_{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}^8}\left[ 1 - 2\left( \frac{{\sigma _{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}}\right) ^6\right] \;(u_p - u_{q_{_{NL}}}). \end{aligned}$$

(55)

In Eqs. (54) and (55), $p,q_{_{NL}}$’s are nonlocal bonds, $l_{_{p,q_{_{NL}}}}$ are the bond lengths obtained from Eq. (49), and $u_p - u_{q_{_{NL}}}$ is the relative displacement between material points p and $q_{_{NL}}$ from $t^{s}_{2}$ to $t^{s}_{3}$. Thus, for $\mathcal {R}_{p} = 0.0001$, $p \in \{1,2,3,4,5,6\}$, we obtain ${\epsilon _{_{LJ}}}_{p=1} = 1.218713424263186$ J.

The nonlocal quantities are then computed as,

$$\begin{aligned} \mathbb {U}_{{p,q_{_{NL}}}} = \frac{12 {\epsilon _{_{LJ}}}_{p} {\sigma ^6_{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}^8}\left[ 1 - 2\left( \frac{{\sigma _{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}}\right) ^6\right] \;(u_p - u_{q_{_{NL}}})^2,\end{aligned}$$

(56)

$$\begin{aligned} f_{{\textit{ff}}_{p,q_{_{NL}}}}= \frac{24 {\epsilon _{_{LJ}}}_{p} {\sigma ^6_{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}^8}\left[ 1 - 2\left( \frac{{\sigma _{_{LJ}}}_{p,q_{_{NL}}}}{l_{_{p,q_{_{NL}}}}}\right) ^6\right] \;(u_p - u_{q_{_{NL}}}). \end{aligned}$$

(57)

In both Eqs. (56) and (57), $p,q_{_{NL}}$’s are nonlocal bonds. After distributing the quantified fraction of the physical quantities over the nonlocal domain of $p = 1$, we get,

${\pmb {\mathbb {U}}_{{{NL}}}}_{{{_{t^s_3}}}} =$

$$\begin{aligned} \begin{bmatrix} 0&{} 0.0017375023&{} 0.0000000682&{} 0.0000000444&{} 0.0000000341&{} 0.0000000269\\ 0.0017375023&{} 0&{} 0&{} 0&{} 0&{} 0.0000000341\\ 0.0000000682&{} 0&{} 0&{} 0&{} 0&{} 0.0000000444\\ 0.0000000444&{} 0&{} 0&{} 0&{} 0&{} 0.0000000682\\ 0.0000000341&{} 0&{} 0&{} 0&{} 0&{} 0.0017375023\\ 0.0000000269&{}0.0000000341&{} 0.0000000444&{} 0.0000000682&{} 0.0017375023&{} 0 \end{bmatrix} J, \end{aligned}$$

(58)

${{\textit{f}}_{{\textit{ff}}_{{NL}}}}_{{{_{t^s_3}}}} = 10^3 \times$

$$\begin{aligned} \begin{bmatrix} 0&{} 1.8622903&{} 0.0000731&{} 0.0000476&{} 0.0000365&{} 0.0000288\\ 1.8622903&{} 0&{} 0&{} 0&{} 0&{} 0.0000365\\ 0.0000731&{} 0&{} 0&{} 0&{} 0&{} 0.0000476\\ 0.0000476&{} 0&{} 0&{} 0&{} 0&{} 0.0000731\\ 0.0000365&{} 0&{} 0&{} 0&{} 0&{} 1.8622903\\ 0.0000288&{} 0.0000365&{} 0.0000476&{} 0.0000731&{} 1.8622903&{} 0 \end{bmatrix} N. \end{aligned}$$

(59)

Since the system in the example is semi-definite, and symmetric from both ends, nonlocal domains of $p = 1$ and $p = n$ have the same distribution in Eqs. (58) and (59).

We follow the same procedure to quantify the nonlocal domains of the remaining material points. After summing up the off-diagonal elements of each row for its diagonal element, we obtain the energy distribution and nonlocal force-field as,

${\pmb {\mathbb {U}}_{{{NL}}}}_{{{_{t^s_3}}}} =$

$$\begin{aligned} \begin{bmatrix} 0.0017376761&{} 0.0017375023&{} 0.0000000682&{} 0.0000000444&{} 0.0000000341&{} 0.0000000269\\ 0.0017375023&{} 0.0040313142&{} 0.0022934104&{} 0.0000002183&{} 0.0000001488&{} 0.0000000341\\ 0.0000000682&{} 0.0022934104&{} 0.0040413746&{} 0.0017476331&{} 0.0000002183&{} 0.0000000444\\ 0.0000000444&{} 0.0000002183&{} 0.0017476331&{} 0.0040413746&{} 0.0022934104&{} 0.0000000682\\ 0.0000000341&{} 0.0000001488&{} 0.0000002183&{} 0.0022934104&{} 0.0040313142&{} 0.0017375023\\ 0.0000000269&{} 0.0000000341&{} 0.0000000444&{} 0.0000000682&{} 0.0017375023&{} 0.0017376761 \end{bmatrix} J, \end{aligned}$$

(60)

${{\textit{f}}_{{\textit{ff}}_{{NL}}}}_{{{_{t^s_3}}}} = 10^3 \times$

$$\begin{aligned} \begin{bmatrix} 1.8624765&{} 1.8622903&{} 0.0000731&{} 0.0000476&{} 0.0000365&{} 0.0000288\\ 1.8622903&{} 4.0022114&{} 2.1395209&{} 0.0002162&{} 0.0001474&{} 0.0000365\\ 0.0000731&{} 2.1395209&{} 4.0076064&{} 1.8677485&{} 0.0002162&{} 0.0000476\\ 0.0000476&{} 0.0002162&{} 1.8677485&{} 4.0076064&{} 2.1395209&{} 0.0000731\\ 0.0000365&{} 0.0001474&{} 0.0002162&{} 2.1395209&{} 4.0022114&{} 1.8622903\\ 0.0000288&{} 0.0000365&{} 0.0000476&{} 0.0000731&{} 1.8622903&{} 1.8624765 \end{bmatrix} N. \end{aligned}$$

(61)

We then compute the elements of nonlocal elasticity matrix as the ratio of the internal bond forces to the equivalent relative displacement of the material point p i.e., $\frac{{\mathbf {f}{_{{\textit{ff}}_{{p,q}_{_{NL}}}}}_{_{t^s_3}}}}{\mathbf {\eta }^{eq}{_{_{p_{_{t^s_3}}}}}}$. In order to keep the internal forces, and the total potential energy of the bonds conserved, it is necessary to consider the equivalent relative displacement of the material point p. It is given as,

$$\begin{aligned} {\mathbf {\eta }^{eq}{_{_{p_{_{t^s_3}}}}}} = \frac{\sum \limits _{q}{\mathbf {f}{_{{\textit{ff}}_{{p,q}_{_L}}}}_{_{{t^s_3}}}} - \sum \limits _{q}{\mathbf {f}^d{_{{\textit{ff}}_{{p,q}_{_{NL}}}}}_{_{{t^s_3}}}}}{\sum \limits _{q}{C_{{p,q}_{_L}}}_{_{{t^s_3}}} - \sum \limits _{q}{C^d_{{p,q}_{_{NL}}}}_{_{{t^s_3}}}}, \end{aligned}$$

(62)

where $\mathbf {f}{_{\textit{ff}}}$’s are as defined earlier, ${C_{{p,q}_{_L}}}_{_{{t^s_3}}}$ is the local bond constant for the bond $p,q_{_L}$ at the time step $t^s_3$, as found in the Local Elasticity Matrix $\mathbf{K} _{_{L}}$; and ${C^d_{{p,q}_{_{NL}}}}_{_{{t^s_3}}}$’s are the bond constants of the bonds $p,q_{_{NL}}$’s at the time step $t^s_3$ that have been computed in the Nonlocal Elasticity Matrix $\mathbf{K} _{_{NL}}$ already.

For $\mathcal {R}_{p} = 0.0001$, $p \in \{1,2,3,4,5,6\}$, we obtain the Nonlocal Elasticity Matrix $\mathbf{K} _{_{NL}}$ as,

$\mathbf{K} _{_{NL}} = 10^9 \times$

$$\begin{aligned} \begin{bmatrix} 0.9981201 &{} -0.9980202 &{} -0.0000391 &{} -0.0000255 &{} -0.0000196 &{} -0.0000154\\ -0.9980202 &{} 1.9961986 &{} -0.9979787 &{} -0.0001070 &{} -0.0000729 &{} -0.0000196\\ -0.0000391 &{} -0.9979787 &{} 1.9961978 &{} -0.9980473 &{} -0.0001070 &{} -0.0000255\\ -0.0000255 &{} -0.0001070 &{} -0.9980473 &{} 1.9961978 &{} -0.9979787 &{} -0.0000391\\ -0.0000196 &{} -0.0000729 &{} -0.0001070 &{} -0.9979787 &{} 1.9961986 &{} -0.9980202\\ -0.0000154 &{} -0.0000196 &{} -0.0000255 &{} -0.0000391 &{} -0.9980202 &{} 0.9981201 \end{bmatrix} N/m. \end{aligned}$$

(63)

Young’s modulus of Elasticity can then be distributed as $E_{p,q} = \frac{C_{p,q}{l_{p,q}}_{_{t^s_3}}}{{A_{p,q}}_{_{t^s_3}}}$, where $C_{p,q}$’s are the elements of $\mathbf{K} _{_{NL}}$ as given in Eq. (63).

As a quantity of interest, ${\epsilon _{_{LJ}}}_{p}$ for the local domain may be computed as,

$$\begin{aligned} {\epsilon _{_{LJ}}}_{p} = \frac{\mathbb {U}_{{p,q_{_{L}}}}}{\frac{12{\sigma ^6_{_{LJ}}}_{p,q_{_{L}}}}{l_{_{p,q_{_{L}}}}^8}\left[ 1 - 2\left( \frac{{\sigma _{_{LJ}}}_{p,q_{_{L}}}}{l_{_{p,q_{_{L}}}}}\right) ^6\right] (u_p - u_{q_{_{L}}})^2}, \end{aligned}$$

(64)

where, $\mathbb {U}_{{p,q_{_{L}}}}$ is obtained from Eq. (60), $l_{_{p,q_{_{L}}}}$ is obtained from Eq. (49), and ${\sigma _{_{LJ}}}_{p,q_{_L}}$ as well as the relative displacements are obtained as discussed earlier in this appendix.

1.2 B Consistency with the Classical Theory of Elasticity

The underlying ideology behind distributing material properties over the local and nonlocal domains is to ensure that the dynamics of the material is the same for any number of degrees of separation considered regardless of the Euclidean distance between the two material points. To ensure that the elastic deformation is consistent with the one obtained with classical theory of elasticity, we rewrite Eq. (8) as,

$$\begin{aligned} \mathbf{F} _{d}(\mathbf{x} ,t) - \rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t) = \displaystyle \int \limits _{V_{_L}(\mathbf{x} )}\nabla _{_\mathbf{x }}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dV_{_L}(\mathbf{x} ') - \displaystyle \int \limits _{V_{_L}(\mathbf{x} )} \mathcal {R}_\mathbf{x , \mathbf{x} '}\nabla _{_\mathbf{x }}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dV_{_L}(\mathbf{x} ') + \int \limits _{V_{_{NL}}(\mathbf{x} )}\nabla _{_\mathbf{x }}\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ',t)dV_{_{NL}}(\mathbf{x} '). \end{aligned}$$

(65)

Upon integrating Eq. (65) over all the local domains we obtain,

$$\begin{aligned} \displaystyle \int \limits _{{L}} \left( \mathbf{F} _{d}(\mathbf{x} ,t) - \rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t)\right) dL = \displaystyle \int \limits _{{L}} \displaystyle \int \limits _{V_{_L}(\mathbf{x} )}\nabla _{_\mathbf{x }}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dV_{_L}(\mathbf{x} ')dL- \displaystyle \int \limits _{{L}} \displaystyle \int \limits _{V_{_L}(\mathbf{x} )} \mathcal {R}_\mathbf{x , \mathbf{x} '}\nabla _{_\mathbf{x }}\mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dV_{_L}(\mathbf{x} ')dL+ \displaystyle \int \limits _{{L}} \int \limits _{V_{_{NL}}(\mathbf{x} )}\nabla _{_\mathbf{x }}\mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ',t)dV_{_{NL}}(\mathbf{x} ')dL. \end{aligned}$$

(66)

This gives,

$$\begin{aligned} \displaystyle \int \limits _{{L}} \left( \mathbf{F} _{d}(\mathbf{x} ,t) - \rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t)\right) dL = \displaystyle \int \limits _{{L}} \mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dL- \displaystyle \int \limits _{{L}} \mathcal {R}_\mathbf{x , \mathbf{x} '} \mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dL+ \displaystyle \int \limits _{{L}} \mathbb {U}_{_{NL}}(\mathbf{x} ,\mathbf{x} ',t)dL. \end{aligned}$$

(67)

The underlying fact behind integrating over all the local domains is that this integration covers the entire material body, and thus, all material points interact with one another either locally or nonlocally. Thus, the second and third terms on the right hand side of Eq. (67) balance out each other. Hence,

$$\begin{aligned} \displaystyle \int \limits _{{L}} \left( \mathbf{F} _{d}(\mathbf{x} ,t) - \rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t)\right) dL = \displaystyle \int \limits _{{L}} \mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dL. \end{aligned}$$

(68)

This gives,

$$\begin{aligned} \displaystyle \int \limits _{{L}} \mathbf{F} _{d}(\mathbf{x} ,t)dL = \displaystyle \int \limits _{{L}} \rho _{_{L@\mathbf{x} }} \ddot{\mathbf{u }}(\mathbf{x} ,t)dL + \displaystyle \int \limits _{{L}} \mathbb {U}_{_L}(\mathbf{x} ,\mathbf{x} ', t)dL. \end{aligned}$$

(69)

Equation (69) indicates that the external energy supplied to the entire body is either converted to the kinetic energy or potential energy without any loss. This shows that Eq. (8) is consistent with the classical theory of elasticity. It is also noticeable from Eq. (69) that when the kinetic energy is zero, all of the external energy is converted to the potential (strain) energy and is distributed over the local bonds as per the governing physics. Thus, discretization done using only local bonds will give correct static displacements of the material points and thus the correct static deformation of the material overall.