Abstract
We are interested in studying the stationary solutions and phase transitions of aggregation equations with degenerate diffusion of porous medium-type, with exponent \(1< m < \infty \). We first prove the existence of possibly infinitely many bifurcations from the spatially homogeneous steady state. We then focus our attention on the associated free energy, proving existence of minimisers and even uniqueness for sufficiently weak interactions. In the absence of uniqueness, we show that the system exhibits phase transitions: we classify values of m and interaction potentials W for which these phase transitions are continuous or discontinuous. Finally, we comment on the limit \(m \rightarrow \infty \) and the influence that the presence of a phase transition has on this limit.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this work, we deal with the properties of the set of stationary states and long-time asymptotics for a general class of nonlinear aggregation-diffusion equations of the form
where \(1< m <\infty \) is the nonlinear diffusivity exponent of porous medium type [V07], \(\beta >0\) measures the relative strength between repulsion (by nonlinear diffusion) and attraction-repulsion (by the nonlocal aggregation terms), and \(W \in C^2(\Omega )\) is the attractive-repulsive interaction potential. Here \(\Omega \) denotes the d-dimensional torus \({\mathbb {T}}^d\) having side length \(L>0\), with \({\mathcal {P}}(\Omega )\) being the set of Borel probability measures on \(\Omega \), and \({L}^m(\Omega )\) the set of m-power integrable functions on \(\Omega \). Notice that for \(m=1\) we recover the linear diffusion case which is related to certain nonlocal Fokker–Planck equations, also referred to as McKean–Vlasov equations in the probability community. These equations also share the feature of being gradient flows of free energy functionals of the form
for \(\rho \in {L}^m(\Omega ) \cap {\mathcal {P}}(\Omega )\), as discussed extensively in the literature [JKO98, Ott01, Vil03, CMV03, AGS08]. We refer to [CCY19] for a recent survey of this active field of research. Note that although we have included the free energy for \(m=1\) in (1.2), we will mostly be dealing with case \(m>1\) in this article. We will only discuss the case \(m=1\) as a limiting case of the energies \({\mathcal {F}}_\beta ^m\) as \(m \rightarrow 1\). The case \(m=1\) is treated in more detail in [CGPS20].
Aggregation-diffusion equations such as (1.1) naturally appear in mathematical biology [BCM07, VS15, CMS+19, BDZ17, BCD+18] and mathematical physical contexts [Oel90, Phi07, FP08, BV13] as the typical mean-field limits of interacting particle systems of the form
where \(W^N=\frac{1}{\beta _1} \varphi ^N + W\) and \( \varphi ^N (x) = N^{\xi } \varphi (N^{\xi /d}x), \text{ for } \text{ all } x\in {\mathbb {R}}^d . \) Here, \(\varphi \) is a the typical localized repulsive potential, for instance a Gaussian, and \(0<\xi <1\). Notice that due to the choice of \(\xi \), the shape of the potential gets squeezed to a Dirac Delta at 0 slower than the typical relative particle distance \(N^{-1/d}\). Also, \(\beta _2^{-1} \ge 0\) is the strength of the independent Brownian motions driving each particle. We refer to [Oel90, Phi07, BV13] for the case of quadratic diffusion \(m=2\) with \(\beta _1=\beta \), \(\nu =0\), and to [FP08] for related particle approximations for different exponents m. The McKean–Vlasov equation \(m=1\) is obtained for the particular case \(\beta _1=+\infty \) and \(\beta _2=\beta \), being the inverse temperature of the system for the linear case, and its derivation is classical for regular interaction potentials W, see for instance [Szn91].
Analysing the set of stationary states of the aggregation-diffusion equation (1.1) and their properties depending on \(\beta \), the relative strength of repulsion by local nonlinear diffusion and attraction-repulsion by nonlocal interactions, is a very challenging problem. As with the linear case, the flat state
is always a stationary solution of the system. The problem lies in constructing nontrivial stationary solutions and minimisers. In the linear diffusion case \(m=1\), we refer to [CP10, CGPS20] where quite a complete picture of the appearance of bifurcations and of continuous and discontinuous phase transitions is present, under suitable assumptions on the interaction potential W. Bifurcations of stationary solutions depending on a parameter are usually referred in the physics literature as phase transitions [Daw83]. In this work we make a distinction between the two: referring to the existence of nontrivial stationary solutions as bifurcations and the existence of nontrivial minimisers of \({\mathcal {F}}_\beta ^m\) as phase transtions. Particular instances of phase transitions related to aggregation-diffusion equations with linear diffusion have been recently studied for the case of the Vicsek–Fokker–Planck equation on the sphere [DFL15, FL12] and the approximated homogeneous Cucker–Smale approximations in the whole space [Tug14, BCnCD16, ASBCD19]. We also refer to [Sch85] where the problem was studied on a bounded domain for the Newtonian interaction, and to [Tam84] where the problem was studied on the whole space with a confining potential.
However, there are no general results in the literature for the nonlinear diffusion case (1.1), \(m>1\), except for the particular case of \(m=2\), \(d=1\), with W given by the fundamental solution of the Laplacian with no flux boundary conditions (the Newtonian interaction) recently studied in [CCW+20]. Despite the simplicity of the setting in [CCW+20], this example revealed how complicated phase transitions for nonlinear diffusion cases could be. The authors showed that infinitely many discontinuous phase transitions occur for that particular problem. Let us mention that the closer result in the periodic setting is [CKY13], where the authors showed that no phase transitions occur for small values of \(\beta \), when the flat state is asymptotically stable, for \(m \in (1,2]\).
Our main goal is thus to develop a theory for the stationary solutions and phase transitions of (1.1) for general interactions \(W \in C^2(\Omega )\) and nonlinear diffusion in the periodic setting, something that has not been previously studied in the literature. This paper can be thought of as an extension of the results in [CGPS20] to the setting of nonlinear diffusion. Considering this, we need to define appropriately the notion of phase transition for the case \(m \in (1, \infty )\), as done in [CP10] for the linear case \(m=1\).
Note that, unlike in the linear setting, the \({L}^1(\Omega )\) topology is not the natural topology to define phase transitions. It seems that for \(m>1\) the correct topology to work in is \({L}^\infty (\Omega )\) (cf. Definition 5.10 and Remark 5.17 below). For our results we will often require compactness of minimisers in this topology. One possible way of obtaining this compactness is via control of the Hölder norms of the stationary solutions of (1.1). In Sect. 3 we briefly comment on the existence of solutions to (1.1) before proceeding to the proof of Hölder regularity. Since this is a key element of the subsequent results and the proof of Hölder regularity for such equations is not in the literature we include the proof in full detail in Sect. 3. It relies on the so-called method of intrinsic scaling introduced by DiBenedetto for the porous medium equation (cf. [DiB79]), which is a version of the De Giorgi–Nash–Moser iteration adapted to the setting of degenerate parabolic equations. We make modifications to the method to deal with the presence of the nonlocal drift term \(\nabla \cdot (\rho \nabla W \star \rho )\). We remark here that the proof of this result is completely independent of the rest of the paper. In a first reading, readers more interested in the properties of stationary solutions and phase transitions might choose to skip the proof and continue to Sect. 4. As a consequence of the proof of Hölder regularity, we also obtain uniform-in-time equicontinuity of the solutions away from the initial datum in Corollary 3.4.
After the proof of the Hölder regularity we proceed to Sect. 4, where we discuss the local bifurcations of stationary solutions from the flat state \(\rho _\infty \). In Theorem 4.4, we provide conditions on the interaction potential W and on the parameter \(\beta =\beta _*\), such that \((\rho _\infty ,\beta _*)\) is a bifurcation point using the Crandall–Rabinowitz theorem (cf. Theorem B.1). In fact for certain choices of W one can show that there exist infinitely many such bifurcation points. We then move on to Sect. 5, where we prove the existence and regularity of minimisers \({\mathcal {F}}_\beta ^m\). We also show that, for \(\beta \) small enough, the flat state is the unique minimiser of the energy for \(m \in (1,\infty ]\), thus extending the result of [CKY13]. In Theorem 5.8, we use the uniform equicontinuity in time obtained in Corollary 3.4 to prove that solutions of (1.1) converge to \(\rho _\infty \) in \({L}^\infty (\Omega )\) whenever it is the unique stationary solution. We show that, as in the linear case, the notion of H-stability (cf. Definition 2.1), provides a sharp criterion for the existence or non-existence of phase transitions. We then proceed, in Lemmas 5.15 and 5.16 Proposition 5.18, to provide sufficient conditions for the existence of continuous or discontinuous phase transitions, where the proofs rely critically on the Hölder regularity obtained in Sect. 3. We also provide general conditions on W for the existence of discontinuous phase transitions. We conclude the section by showing that \(m \in [2,3]\) all non-H-stable potentials W are associated with discontinuous phase transitions of \({\mathcal {F}}_\beta ^m\), while for \(m=4\) we can construct a large class of W that lead to continuous phase transitions of \({\mathcal {F}}_\beta ^m\). We summarise our results below:
-
(1)
The proof of Hölder regularity of the weak solutions of (1.1) can be found in Theorem 3.3 and the preceding lemmas of Sect. 3.
-
(2)
The result on the existence of local bifurcations of the stationary solutions is contained in Theorem 4.4.
-
(3)
The results on phase transitions are spread out throughout Sect. 5. The result on the long-time behaviour of solutions before or in the absence of a phase transition can be found in Theorem 5.8. The main result on the existence of discontinuous transition points is Theorem 5.19 while the explicit conditions for a continuous transition point can be found in Theorem 5.24.
-
(4)
In Sect. 6, we treat the mesa limit \(m \rightarrow \infty \). The \(\Gamma \)-convergence of the sequence of energies \({\mathcal {F}}_\beta ^m\) to some limiting free energy \({\mathcal {F}}^\infty \) as \(m \rightarrow \infty \) can be found in Theorem 6.1. We then provide a characterisation of the minimisers of the limiting variational problem in terms of the size of the domain and the potential W in Theorem 6.2.
In Sect. 7, we display the results of some numerical experiments which we hope will shed further light on the theoretical results, while also providing us with some conjectures about the behaviour of the system in settings not covered by the theory.
2 Preliminaries and Notation
As mentioned earlier, we denote by \({\mathcal {P}}(\Omega )\) the space of all Borel probability measures on \(\Omega \) with \(\rho \) the generic element which we will often associate with its density \(\rho (x) \in {L}^1(\Omega )\), if it exists. We use the standard notation of \({L}^p(\Omega )\) and \( {H}^s(\Omega )\) for the Lebesgue and periodic \({L}^2\)-Sobolev spaces, respectively. We denote by the \(C^k(\Omega ),C^\infty (\Omega )\) the space of k-times (\(k \in {\mathbb {N}}\)) continuously differentiable and smooth functions, respectively.
Given any function in \(f \in {L}^2(\Omega )\) we define its Fourier transform as
where
and \(N_k\) is defined as
Using this we have the following representation of the convolution of two functions \(W, f \in {L}^2(\Omega )\) where W is even along every coordinate
where \(\mathrm {Sym}_k(\Lambda )=\mathrm {Sym}(\Lambda )/H_k\). \(\mathrm {Sym}(\lambda )\) represents the symmetric group of the product of two-point spaces, \(\Lambda =\{1,-1\}^d\), which acts on \({\mathbb {Z}}^d\) by pointwise multiplication, i.e. \((\sigma (k))_i=\sigma _i k_i, k \in {\mathbb {Z}}^d, \sigma \in \mathrm {Sym}(\Lambda )\). \(H_k\) is a normal subgroup of \(\mathrm {Sym}(\Lambda )\) defined as follows
We need to quotient out \(H_k\) as there might be some repetition of terms in the sum \(\sum _{\sigma \in \mathrm {Sym}(\Lambda )}\) if \(k \in {\mathbb {N}}^d\) is such that \(k_i=0\) for some \(i \in \{1, \dots ,d\}\). Another expression that we will use extensively in the sequel is the Fourier expansion of the following bilinear form
The following notion will play an important role in the subsequent analysis.
Definition 2.1
A potential \(W \in {L}^2(\Omega )\) is said to be H-stable denoted by \(W \in {\mathbf {H}}_s\) if
If this does not hold, we denote this by \(W \in {\mathbf {H}}_s^c\). The above condition is equivalent to the following inequality holding true for all \(\eta \in {L}^2(\Omega )\) :
Furthermore, if \(\eta ,W \not \equiv 0\), we have that
3 Existence and Regularity of Solutions
We are interested in solutions of the following nonlinear-nonlocal PDE
where \(1< m <\infty \), \(\beta >0\), and \(W \in C^2(\Omega )\) is even along every co-ordinate and has mean zero. It is not immediately clear what the correct notion of solution for the above PDE is, as it need not possess classical solutions. We introduce the appropriate notion of solution in the following definition.
Definition 3.1
A weak solution of (3.1) is a bounded, measurable function
with
such that
for all \(\phi \in {H}^1([0,T];{L}^2(\Omega )) \cap {L}^2([0,T]; {H}^1_0(\Omega ))\) and \(\rho (\cdot ,0)=\rho _0\).
Theorem 3.2
Given \(\rho _0 \in {L}^2(\Omega ) \cap {L}^m(\Omega ) \cap {\mathcal {P}}(\Omega )\), there exists a unique weak solution of (3.1). Furthermore \(\rho (\cdot ,t) \in {\mathcal {P}}(\Omega )\) for all \(t \ge 0\).
The proof of this result is classical and we will not include it. It relies on regularisation techniques which remove the degeneracy in the problem. The meat of the matter is proving estimates uniform in the regularisation parameter. We refer to [BCL09, BS10] for proofs of this result with \(W \in C^2(\Omega )\).
We turn our attention to the regularity of solutions of (3.1). The proof is based on the method of intrinsic scaling introduced by DiBenedetto for the porous medium equation [DiB79, Urb08]. It is also similar in spirit to the proof in [KZ18] where regularity was proved for a degenerate diffusion equation posed on \({\mathbb {R}}^d\) with a potentially singular drift term. We also direct the readers to [HZ19] where Hölder regularity was proven for drift-diffusion equations with sharp conditions on the drift term using a different strategy of proof. Since we will mainly be concerned with stationary solutions we assume for the time being that there exists some universal constant \(M>0\) such that \(\Vert \rho \Vert _{{L}^\infty (\Omega _T)} \le M\), where \(\Omega _T\) is the parabolic domain \(\Omega _T:=\Omega \times [0,T]\) and \(\Omega _\infty :=\Omega \times [0,\infty )\). We first state the result regarding Hölder regularity.
Theorem 3.3
Let \(\rho \) be a weak solution of (3.1). with initial datum \(\rho _0 \in {L}^\infty (\Omega ) \cap {\mathcal {P}}(\Omega )\), such that \(\Vert \rho \Vert _{{L}^\infty (\Omega _T)} \le M< \infty \). Then \(\rho \) is Hölder continuous with exponent \(a \in (0,1)\) dependent on the data, m, d, W, and \(\beta \). Moreover, the Hölder exponent a depends continuously on \(\beta \) for \(\beta >0\).
We also have the following consequence of the above result:
Corollary 3.4
Let \(\rho \) be a weak solution of (3.1) with initial datum \(\rho _0 \in {L}^\infty (\Omega ) \cap {\mathcal {P}}(\Omega )\), such that \(\Vert \rho \Vert _{{L}^\infty (\Omega _\infty )} \le M< \infty \). Then, for some \(C>0\), it holds that
for all \(x,y \in {\mathbb {T}}^d\) and \(0<C<t_1<t_2<\infty \). Note that the constants \(C_h\) and a are independent of x, y and \(t_1,t_2\).
We remind the reader that the above results are used to obtain the desired regularity and compactness of minimisers in Lemma 5.4 and the equicontinuity in time of solutions for the long-time behaviour result in Theorem 5.8, although they are of independent interest by themselves. The proof of Theorem 3.3 and Corollary 3.4 can be found in Sect. 8.
4 Characterisation of Stationary Solutions and Bifurcations
Now that we have characterised the notion of solution for (3.1) we study the associated stationary problem which is given by
with the notion of solution identical to the one defined in Theorem 3.1. One can immediately see that \(\rho _\infty \) (cf. (1.3)) is a solution to (4.1) for all \(\beta >0\). As mentioned earlier, (3.1) and (4.1) are intimately associated to the free energy functional \({\mathcal {F}}_\beta ^m : {\mathcal {P}}(\Omega ) \rightarrow (-\infty ,+\infty ]\) which is defined as
whenever the above quantities are finite and as \(+\infty \) otherwise. We will often use the shorthand notation \(S_\beta ^m(\rho ):=\frac{\beta ^{-1}}{m-1} \int _{\Omega } \rho ^m(x) \mathop {}\!\mathrm{d} x- \frac{\beta ^{-1}}{m-1}\) and \(S_\beta :=\beta ^{-1} \int _{\Omega } (\rho \log \rho )(x) \mathop {}\!\mathrm{d} x\) for the entropies and \({\mathcal {E}}(\rho ):=\frac{1}{2}\iint _{\Omega \times \Omega } W(x-y) \rho (x) \rho (y) \mathop {}\!\mathrm{d} x \mathop {}\!\mathrm{d} y\) for the interaction energy. We will also drop the superscript m and just use \({\mathcal {F}}_\beta (\rho )\) whenever \(m=1\).
Another object that will play an important role in the analysis below is the following self-consistency equation
for some constant \(C>0\). We discuss how the above equation, solutions of (4.1), and \({\mathcal {F}}_\beta ^m(\rho )\) are related to each other for the case \(m>1\) in the following proposition (the case \(m=1\) is discussed in [CGPS20] and the proofs are essentially identical).
Proposition 4.1
Let \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^m(\Omega )\) and fix \(\beta>0,m>1\). Then the following statements are equivalent
-
(1)
\(\rho \) is a weak solution of (4.1)
-
(2)
\(\rho \) is a critical point of \({\mathcal {F}}_\beta ^m\), i.e. the metric slope \(|\partial {\mathcal {F}}_\beta ^m |(\rho )\) is 0.
-
(3)
For every connected component A of its support \(\rho \) satisfies the self-consistency equation, i.e.
$$\begin{aligned} \beta ^{-1}\frac{m}{m-1}\rho ^{m-1} + W \star \rho =C(A, \rho ) \end{aligned}$$(4.2)with \(C(A,\rho )\) given by
$$\begin{aligned} C(A,\rho )= \beta ^{-1}\frac{m}{|A|(m-1)}\Vert \rho \Vert _{L^{m-1}(A)}^{m-1} + \frac{1}{|A|}\int _{A} W \star \rho (x) \mathop {}\!\mathrm{d} x . \end{aligned}$$
Remark 4.2
We have used the notation
for \(1< m < \infty \), even though this is not a norm for \(1< m <2\).
Remark 4.3
Note that if a stationary solution \(\rho \) is fully supported then the constant \(C(A,\rho )=C(\Omega ,\rho )\) reduces to
where we have used the fact that W has mean zero. We can now formally pass to the limit \(m \rightarrow 1\) to obtain
The solutions of the above equation are studied in detail in [CGPS20].
Now that we have various equivalent characterisations of stationary solutions of (3.1), we proceed to state and prove the main result of this section regarding the existence of bifurcations from the uniform state \(\rho _\infty \) (cf. (1.3)). Before doing this however we need to introduce some relevant notions. We denote by \({H}^n_0(\Omega )\) the homogeneous \({H}^n(\Omega )\) space and by \({H}^n_{0,s}(\Omega )\) the closed subspace of \({H}^n_0(\Omega )\) consisting of functions which are even along every coordinate (pointwise a.e.). Note that the \(\{e_k\}_{k \in {\mathbb {N}}^d, k \ne 0}\) form an orthogonal basis for \({H}^n_{0,s}(\Omega )\). We then introduce the following map \(F : {H}^n_{0,s}(\Omega ) \times {\mathbb {R}}_+ \rightarrow {H}^n_{0,s}(\Omega )\) for \(n>d/2\) which is given by
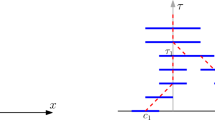
Note that if \(F(\eta ,\beta )=0\) then the pair \((\rho _\infty + \eta ,\beta )\) satisfies (4.2) on all of \(\Omega \). If one can show that \((\rho _\infty + \eta )(x) \ge 0, \forall x \in \Omega \) then we have found a bonafide stationary solution of (3.1) by the equivalency established in Proposition 4.1. Thus, we would like to study the bifurcations of the map F from its trivial branch \((0,\beta )\) . To this order we compute its Fréchet derivatives around 0 as follows:
for some \(e_1,e_2,e_3 \in {H}^n_{0,s}(\Omega )\). We then have the following result:
Theorem 4.4
(Existence of bifurcations). Consider the map \(F : {H}^n_{0,s}(\Omega ) \times {\mathbb {R}}_+ \rightarrow {H}^n_{0,s}(\Omega )\) for \(n>d/2\) as defined in (4.3) with its trivial branch \((0,\beta )\). Assume there exists \(k^* \in {\mathbb {N}}^d, k^* \not \equiv 0\) such that the following two conditions are satisfied
-
(1)
\({\hat{W}}(k^*) <0\)
-
(2)
\({\text {card}}\{k \in {\mathbb {N}}^d, k \not \equiv 0: \frac{{\hat{W}}(k)}{\Theta (k)} = \frac{{\hat{W}}(k^*)}{\Theta (k^*)}\}=1\) .
Then, \((0,\beta _*)\) is a bifurcation point of \((0,\beta )\) with
i.e. there exists a neigbourhood N of \((0,\beta _*)\) and a curve \((\eta (s),\beta (s)) \in N, s \in (-\delta ,\delta ), \delta >0\) such that \(F(\eta (s),s)=0\). The branch \(\eta (s)\) has the form
where \(\Vert r\Vert _{{H}^n_{0,s}(\Omega )}=o(s)\) as \(s \rightarrow 0\). Additionally, we have that \(\beta '(0)=0\) and
Proof
The proof of this theorem relies on the Crandall–Rabinowitz theorem (cf. Theorem B.1). Note that \(F \in C^2({H}^n_{0,s}(\Omega ) \times {\mathbb {R}}_+; {H}^n_{0,s}(\Omega ))\). Thus, we need to show that: (a) \(D_{\eta }F(0,\beta _*): {H}^n_{0,s}(\Omega ) \rightarrow {H}^n_{0,s}(\Omega )\) is Fredholm with index zero and has a one-dimensional kernel and (b) for any \(e \in \ker (D_{\eta }F(0,\beta _*)), e \ne 0\) it holds that \(D^2_{\eta \beta }F(0,\beta _*)(e) \notin {\mathrm{Im}}\,(D_{\eta }F(0,\beta _*))\).
For (a) we first note that \(D_{\eta }F(0,\beta _*)\) is a compact perturbation of the identity as the operator \(W \star e\) is compact on \({H}^n_{0,s}\). It follows then that it is a Fredholm operator. Note that the functions \(\{e_k\}_{k \in {\mathbb {N}}^d, k \ne 0}\) diagonalise the operator \(D_{\eta }F(0,\beta _*)\). Indeed, we have
Note that if the conditions (1) and (2) in the statement of the theorem are satisfied it follows, using the expression for \(\beta _*\), that \(D_{\eta }F(0,\beta _*)(e_k)=0\) if and only if \(k = k^*\). Thus, we have that \(\ker (D_{\eta }F(0,\beta _*))= \text {span}(e_{k^*})\). This completes the verification of the condition (1) in Theorem B.1.
For condition (2) in Theorem B.1, we note again by the diagonalisation of \(D_{\eta }F(0,\beta _*)\) that \({\mathrm{Im}}\,(D_{\eta }F(0,\beta _*))= \{\text {span}(e_{k^*})\}^{\perp }\). Thus, we have that
We can now compute the derivatives of the branch. Using the identity [Kie12, I.6.3], it follows that \(\beta '(0)=0\) if \(D^2_{\eta \eta }F(0,\beta _*)(e_{k^*},e_{k^*}) \in {{\,\mathrm{Im}\,}}(D_\eta F(0,\beta _*) )\). Thus, it is sufficient to check that
where the last inequality follows by using the expression for \(e_{k^*}^2\) from Proposition 5.23 and orthogonality of the basis \(\{e_k\}_{k \in {\mathbb {N}}^d}\). Here \(\langle \cdot ,\cdot \rangle \) denotes the dual pairing in \({H}^n_{0,s}\). Thus, we have that \(\beta '(0)=0\). Finally we can compute \(\beta ''(0)\) by using [Kie12, I.6.11] to obtain
This completes the proof of the theorem. \(\quad \square \)
Remark 4.5
Since \({H}^n_{0,s}(\Omega )\) is continuously embedded in \(C^0(\Omega )\) it follows that for the branch of solutions \(\rho _\infty + \eta (s)\) found in Theorem 4.4 are in fact strictly positive for s sufficiently small and are thus stationary solutions by the result of Proposition 4.1. Any interaction potential W(x) such that infinitely many k satisfy the conditions of Theorem 4.4 will have infinitely many bifurcation points \((0,\beta _k)\) from the trivial branch. A typical example would a be a potential for which the map \(k \mapsto {\hat{W}}(k)\) is strictly negative and injective.
Remark 4.6
Note that \(\beta ''(0)>0\) for all \(m \in (1,2) \cup (3,\infty )\). This means that the branch turns to the right, i.e. it is supercritical. On the other hand if \(m \in (2,3)\), then \(\beta ''(0)<0\). This means that the branch turns to the left, i.e. it is subcritical. If \(m \in \{2,3\}\) we have that \(\beta ''(0)=0\). The relation of this phenomenon to the minimisers of the free energy will be discussed in Proposition 5.22.
5 Minimisers of the Free Energy and Phase Transitions
The nontrivial stationary solutions found as a result of the bifurcation analysis in the previous section need not correspond to minimisers of the free energy, \({\mathcal {F}}_\beta ^m(\rho )\). Indeed, we do not know yet if minimisers even exist. We start first by proving the existence of minimisers of \({\mathcal {F}}_\beta ^m\). We then show that for \(\beta \) sufficiently small \({\mathcal {F}}_\beta ^m\) has a unique minimiser, namely \(\rho _\infty \) (cf. (1.3)).
The natural question to ask then is if this scenario changes for larger values of \(\beta \). We provide a rigorous definition by which this change can be characterised via the notion of a transition point and define two possible kinds of transition points, continuous and discontinuous. We then provide necessary and sufficient conditions on W for the existence of a transition point and sufficient conditions for the existence of continuous and discontinuous transition points.
We start with a technical lemma that provides us with some useful a priori bounds on the minimisers of \({\mathcal {F}}_\beta ^m\).
Lemma 5.1
(\({L}^{\infty }(\Omega )\)-bounds). Assume \(\beta>0,m>1\). Then there exists some \(B_{\beta ,m}>0\), such that if \(\rho \in {\mathcal {P}}(\Omega )\) with \(\Vert \rho \Vert _{{L}^\infty (\Omega )}>B_{\beta ,m}\), then there exists \({\bar{\rho }} \in {\mathcal {P}}(\Omega )\) with \(\Vert {\bar{\rho }}\Vert _{{L}^\infty (\Omega )}\le B_{\beta ,m}\) with
Proof
We start by noting that the following bounds hold
We divide our analysis into two cases. For \(B>0\) and \(\rho \in {\mathcal {P}}(\Omega )\) let
and
Case 1: \((\rho ,B)\) s.t. \(\varepsilon _B\ge \frac{1}{2}\)
We then have the following bounds on the entropy.
It follows then that we have the following bound on the free energy.
If we define a constant \(B_1\) as follows
such that for \(B>B_1\), \(1/|\Omega |\) has a lower value of the free energy than \(\rho \).
Case 2: \((\rho ,B)\) s.t. \(\varepsilon _B < \frac{1}{2}\)
We write \(\rho = \rho _B + \rho _r\), where \(\rho _B:= \rho \cdot \chi _{{\mathcal {B}}_B}\) and \(\rho _r:=\rho -\rho _B\). We then have the following bound on the entropy.
We can assume without loss of generality that \({\mathcal {F}}_\beta ^m(\rho )< {\mathcal {F}}_\beta ^m(\rho _\infty )\), otherwise the proof is complete. It follows then that
By expanding \({\mathcal {E}}(\rho )\), the following estimate can be obtained
where we have used the fact that \(\varepsilon _B <1/2\). Define \(\bar{\rho _r} := (1-\varepsilon _B)^{-1} \rho _r \in {\mathcal {P}}(\Omega )\). We have
One can control the second term in the brackets as follows
for any \(\delta < 1\). Setting \(\delta =\frac{1}{2}\), we obtain
Similarly, for the interaction energy we can compute the difference as follows
Using the fact that \(\varepsilon _B< 1/2\) we can obtain
Now, we can define a second constant as follows
such that for \(B>B_2\), \(\bar{\rho _r}\) has a lower value of the free energy than \(\rho \). We now set our constant as follows
and set \({\bar{\rho }}\) to either be \((1/|\Omega |)\) or \(\bar{\rho _r}\). The constant 2 in front of \(B_2(\beta ,m)\) follows from the fact that \(\bar{\rho _r}\) has been normalised. \(\quad \square \)
The expression for the constant \(B_{\beta ,m}\) is explicit as a result of which we can even obtain some uniform control in m.
Corollary 5.2
Let \((\beta ,m) \in (0,C)\times [1+ \varepsilon ,\infty )=:A \subset (0,\infty ) \times (1,\infty )\) for some \(C,\varepsilon >0\). Then \(B^\star :=\sup _A B_{\beta ,m} < \infty \).
We now proceed to the existence result for minimisers of \({\mathcal {F}}_\beta ^m\).
Theorem 5.3
(Existence of minimisers). Fix \(\beta >0\) and \(m>1\), then \({\mathcal {F}}_\beta ^m: {\mathcal {P}}(\Omega ) \rightarrow (-\infty ,+\infty ]\) has a minimiser \(\rho ^* \in {\mathcal {P}}(\Omega ) \cap {L}^\infty (\Omega )\). Additionally we have that
Proof
We note first that, from (5.1) and (5.2), \({\mathcal {F}}_\beta ^m\) is bounded below on \({\mathcal {P}}(\Omega )\). Let \(\{\rho _n\}_{n \in {\mathbb {N}}}\) be a minimising sequence. Note that by Lemma 5.1 we can pick this sequence such that \(\Vert \rho _n\Vert _{{L}^\infty (\Omega )} \le B_{\beta ,m}\). By the Banach–Alaoglu theorem we have a subsequence \(\{\rho _{n_k}\}_{k \in {\mathbb {N}}}\) and measure \(\rho ^* \in {L}^\infty (\Omega )\) such that
Furthermore, we can find another subsequence (which we do not relabel), such that
Note that \(\rho ^*\) is nonnegative a.e. and also has mass one. Thus, \(\rho ^* \in {\mathcal {P}}(\Omega ) \cap {L}^\infty (\Omega )\). The proof would be complete if we can show lower semicontinuity of \({\mathcal {F}}_\beta ^m\) in weak \({L}^2(\Omega )\). Note that for \(W \in C^2(\Omega )\), \({\mathcal {E}}(\rho )\) is continuous. On the other hand, \(S_\beta ^m(\rho )\) is convex and lower semicontinuous in the \({L}^2(\Omega )\) topology. It follows from fairly classical results (cf. [Bre11, Theorem 3.7]) that \({\mathcal {F}}_\beta ^m\) is also weakly lower semicontinuous. This concludes the proof of existence of minimisers. The bound simply follows from the fact that norms are lower semicontinuous under weak-\(*\) convergence. \(\quad \square \)
Lemma 5.4
(Regularity and compactness of minimisers). Let \(\rho _\beta \in {\mathcal {P}}(\Omega )\) be a minimiser of \({\mathcal {F}}_\beta ^m(\rho )\). Then \(\rho _\beta \) is Hölder continuous with exponent \(a \in (0,1)\) given by Theorem 3.3, where a depends continuously on \(\beta \). Let \(\{\rho _\beta \}_{\beta \in I}\) be a family of such minimisers, where \(I \subset {\mathbb {R}}_+\) is some bounded interval. Then the family \(\{\rho _\beta \}_{\beta \in I}\) is relatively compact in \(C^0(\Omega )\).
Proof
The proof of the first statement follows simply by applying Proposition 4.1 and Theorem 3.3 with \(M=B_{\beta ,m}\). For the second statement, let \({\bar{I}}\) be the closure of I. Then applying (8.17) for some \(x,y \in {\mathbb {T}}^d\), we have that
where \(a=a(\beta ),C_h=C_h(\beta )\). Setting \(a^\star = \max _{{\bar{I}}}a(\beta )\) and \(B^\star \) to be as in Corollary 5.2, we have that
where \(C_h^\star \) is some new constant depending on \(B^\star \), m, d, and W. Thus, the family \(\{\rho _\beta \}_{\beta \in I}\) is equicontinuous. It is clearly equibounded from Corollary 5.2. Applying the Arzelà–Ascoli theorem, the result follows. \(\quad \square \)
Now that we have shown existence and regularity of minimisers we show that for \(\beta \) small or \(W \in {\mathbf {H}}_s\) minimisers of \({\mathcal {F}}_\beta ^m\) are unique and given by \(\rho _\infty \). To show this we start with the following lemma which shows positivity of stationary solutions for \(\beta \) sufficiently small.
Lemma 5.5
There exists an \(\delta >0\) depending on m and W, such that for all \(\beta <\delta \) it holds that if \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^m(\Omega )\) is a stationary solution of (3.1), then \(\rho (x) \ge \frac{1}{2 |\Omega |}\) for all \(x \in \Omega \).
Proof
Note that if \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^m(\Omega )\) is stationary, then, by Proposition 4.1, it satisfies on each connected component A of its support
with \(C(A,\rho )\) given by
Thus, we have that \(\rho \in {L}^\infty (\Omega )\). Using a mollification argument and (4.2), one can then obtain the following bound
By Theorem 3.3, it follows that \(\rho \) is a-Hölder continuous. Note further that we have that
Thus, we can choose \(\beta \) to be small enough, dependent on m and W, and apply the bound to argue that
Thus, the result follows. \(\quad \square \)
We can now use the positivity estimate of Lemma 5.5 to prove that for \(\beta \) sufficiently small stationary solutions of (3.1) (and thus minimisers of \({\mathcal {F}}_\beta ^m\)) are unique. This improves the result of [CKY13], in which uniqueness is proved only for \(1 < m \le 2\).
Lemma 5.6
For \(\beta \ll 1\) and \(m \in (1,\infty )\), \(\rho _\infty \) is the unique stationary solution of (3.1) and minimiser of the free energy, \({\mathcal {F}}_\beta ^m\).
Proof
Assume \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^m(\Omega )\) is a stationary solution of (3.1). Then, we can apply the same argument as in the proof of Lemma 5.5 to obtain
It follows that
Let us now assume that \(\beta <\delta \), where \(\delta \) is the constant from the statement of Lemma 5.5. Furthermore, if \(1<m<2\) the constant \(C(\Omega ,\rho )\) in Proposition 4.1 can be controlled as follows
where in the last step we have applied Jensen’s inequality. Thus, we have
for all \(x \in \Omega \). Thus, for \(1< m< 2\), we can apply the above bound to (5.3) to obtain
If \(\beta \) is sufficiently small, we have that \(\Vert \nabla \rho \Vert _{{L}^\infty (\Omega )}=0\). Thus, \(\rho =\rho _\infty \) for \(\beta \) sufficiently small. Similarly for \(2 \le m < \infty \), we can apply the bound from Lemma 5.5 to obtain
Applying a similar argument as before, we have that, for \(\beta \ll 1\), \(\rho =\rho _\infty \). Thus, for \(\beta \ll 1\), \(\rho _\infty \) is the unique stationary solution of (3.1) and, by Proposition 4.1, the unique minimiser of \({\mathcal {F}}_\beta ^m\). \(\quad \square \)
We also have the following result on uniqueness of minimisers when \(W \in {\mathbf {H}}_s\).
Theorem 5.7
Let \(W \in {\mathbf {H}}_s\) and \(m \in (1,\infty )\). Then \({\mathcal {F}}_\beta ^m(\rho )\) has a unique minimiser \(\rho =\rho _\infty \).
Proof
We first consider the case in which \(W \in {\mathbf {H}}_s\). We write the linear interpolant as \(\rho _t= \rho _0 + t \eta \) where \(\eta = \rho _1-\rho _0\) where \(\rho _0,\rho _1 \in {\mathcal {P}}(\Omega )\) with \({\mathcal {F}}_\beta ^m(\rho _0),{\mathcal {F}}_\beta ^m(\rho _1)<\infty \). Differentiating with respect to t twice we obtain that
For \(W \in {\mathbf {H}}_s\) the above expression is strictly positive. Thus, \({\mathcal {F}}_\beta ^m(\rho _t)\) is a convex function, from which it follows that \({\mathcal {F}}_\beta ^m\) must have unique minimisers. We further argue that the minimiser must be \(\rho _\infty \). Indeed, we have for any \({\mathcal {P}}(\Omega ) \ni \rho \ne \rho _\infty \) that
where the first inequality follows from Jensen’s inequality and the second one from the fact that \(W \in {\mathbf {H}}_s\) and Definition 2.1. \(\quad \square \)
We know now from Lemma 5.6, that for \(\beta \ll 1\), \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_\beta ^m\) and stationary solution of (3.1). We now present the following result on the long-time behaviour of (3.1) in this regime:
Theorem 5.8
(Long-time behaviour). Let \(\rho \) be a weak solution of (3.1) with initial datum \(\rho _0 \in {L}^\infty (\Omega ) \cap {\mathcal {P}}(\Omega )\). Assume that \(\beta \) and W are such that \(\rho _\infty \) is the unique stationary solution of (3.1) (and, therefore, the unique minimiser of \({\mathcal {F}}_\beta ^m\)). Then, it holds that
Proof
We start by showing that if \(\rho _0 \in {L}^\infty (\Omega ) \cap {\mathcal {P}}(\Omega )\), then \(\Vert \rho \Vert _{{L}^\infty (\Omega _\infty )} \le M < \infty \). We choose as a test function in the weak formulation, \(\phi =p \rho ^{p-1}\), for some \(p>1\). Note that we can justify this choice by mollifying \(\phi \) and then passing to the limit. We then obtain from (3.2) the following expression
Plugging in the value of \(\phi \) on the right hand side and integrating by parts, we obtain
Applying the Lebesgue differentiation theorem, we obtain that for t a.e., it holds that
Note that we can control the second term on the right hand side of the above expression as follows
where we have used the fact that \(1<p <\frac{ (m+p-1) d}{d-2}\) and the constant \(\theta \in (0,1)\) is given by
We now apply the Sobolev inequality on the torus, to obtain
Note that the constant \(C_d\) in the above estimate depends only on dimension and is independent of \(p>1\). We set \(q_1:=(m+p-1)/(p(1-\theta ))\) and \(q_2:=q_1/(q_1-1)\). Note that from the definition of \(\theta \) we have
Thus, we have that
We can thus apply Young’s inequality with \(q_1,q_2\) to obtain
where \(C_{p,m,\beta }>0\) is given by
Multiplying through by \(\Vert \Delta W\Vert _{{L}^\infty (\Omega )}(p-1)\), we can apply the estimate in (5.5) to (5.4) to obtain
Applying Grönwall’s inequality, we obtain that
It follows that
Note now that
as \(p \rightarrow \infty \). It follows then that we can find a constant M dependent on \(\Vert \rho _0\Vert _{{L}^\infty (\Omega )}\), d, \(\beta \), and m but independent of t and p such that
for all \(t \in [0,\infty )\). Passing to the limit as \(p \rightarrow \infty \), it follows that
for all \(t \in [0,\infty )\). We can now apply Theorem 3.3 to argue that the solution \(\rho \) is Hölder continuous with some exponent \(a \in (0,1)\). Furthermore, we can apply Corollary 3.4, to argue that
for all \(x,y \in {\mathbb {T}}^d\) and \(0<C<t_1<t_2<\infty \). Consider now the solution semigroup \(S_t: Z_E \rightarrow Z_E, t \ge 0\) associated to the evolution in (3.1), where
for some \(E \in {\mathbb {R}}\). We make \(Z_E\) into a complete metric space by equipping it with the \(d_2(\cdot ,\cdot )\) Wasserstein distance. The fact that it is complete follows from the fact that \({\mathcal {F}}_\beta ^m\) is lower semicontinuous with respect to convergence in \(d_2(\cdot ,\cdot )\). Note that the family of mappings \(\{S_t\}_{t \ge 0}\) forms a metric dynamical system in the sense of [CH98, Definition 9.1.1]. This follows from the fact (cf. [AGS08, Theorem 11.2.8]) the evolution defines a gradient flow \(\rho \in C([0,\infty );Z_{E_0})\) in \({\mathcal {P}}(\Omega )\) in the sense of [AGS08, Definition 11.1.1] where \(E_0= {\mathcal {F}}_\beta ^m(\rho _0)\). We now define the \(\omega \)-limit set associated to the initial datum \(\rho _0 \in {L}^\infty (\Omega ) \cap {\mathcal {P}}(\Omega )\), as follows
Since the metric space \(Z_{E_0}\) is compact, it follows that the set \(\bigcup _{t \ge 0}S_t(\rho _0)\) is relatively compact in \(Z_{E_0}\). Applying [CH98, Theorem 9.1.8], we have that \(\omega (\rho _0) \ne \emptyset \) and
where \(\rho (\cdot ,t)\) is the unique solution of (3.1) with initial datum \(\rho _0 \in {\mathcal {P}}(\Omega ) \cap {L}^\infty (\Omega )\). We now need to show that \(\omega (\rho _0)\) is contained in the set of stationary solutions of (3.1). Assume \(\rho _* \in \omega (\rho _0)\), then there exists a time-diverging sequence \(t_n \rightarrow \infty \) such that
Since the solution \(\rho (\cdot ,t)\) is gradient flow of the free energy \({\mathcal {F}}_\beta ^m\) with respect to the \(d_2(\cdot ,\cdot )\) distance on \({\mathcal {P}}(\Omega )\), it follows that the following energy-dissipation equality holds true for all \(t \in [0,\infty )\) (cf. [AGS08, Theorem 11.1.3])
where \(|\partial {\mathcal {F}}_\beta ^m|: {\mathcal {P}}(\Omega ) \rightarrow (-\infty ,+\infty ]\) is the metric slope of \({\mathcal {F}}_{\beta }^m\) and is given by
Bounding the energy from below and then passing to the limit as \(t \rightarrow \infty \) in (5.8), we obtain
We now consider the time-diverging sequence \(t_n \rightarrow \infty \) and the sequence of curves \(\{\rho _n\}_{n \in {\mathbb {N}}} \in C([0,1];Z_{E_0})\) with \(\rho _n(\cdot ,t)=\rho (\cdot ,t_n+t)\). For each \(n \in {\mathbb {N}}\), we have that
for all \(t_1,t_2 \in [0,1]\), where in the last step we have used (5.7). We can thus apply the generalised Arzelá–Ascoli/Aubin–Lions compactness theorem (cf. [AGS08, Proposition 3.3.1]) to argue that there exists a curve \(\mu \in C([0,1];Z_{E_0})\) such that \(\rho _n(\cdot ,t)\) converges to \(\mu (\cdot ,t)\), in the sense of weak convergence of probability measures, for all \(t \in [0,1]\). Furthermore, from the lower semicontinuity of \(|\partial {\mathcal {F}}_\beta ^m|\) (cf. [AGS08, Theorem 5.4.4]) and Fatou’s lemma, we have that
where in the last step we have used (5.9). It follows that \(|\partial {\mathcal {F}}_\beta ^m|(\mu (\cdot ,t))=0\) for t a.e. Thus, since \(\mu \) is continuous, we can find a sequence of times \(m \in {\mathbb {N}}\), \(t_m \rightarrow 0\), such that \(|\partial {\mathcal {F}}_\beta ^m|(\mu (\cdot ,t_m))=0\) and \(d_2(\mu (\cdot ,t_m),\mu (\cdot ,0)) \rightarrow 0\) as \(m \rightarrow \infty \). Note further that \(\mu (\cdot ,0)= \lim _{n\rightarrow \infty } \rho (\cdot ,t_n)=\rho _*\). From the lower semicontinuity of \(|\partial {\mathcal {F}}_\beta ^m|(\cdot )\) we have that
Applying Proposition 4.1, it follows that \(\rho _* \in Z_{E_0} \subset {\mathcal {P}}(\Omega ) \cap {L}^m(\Omega )\) is necessarily a stationary solution of (3.1). Since \(\rho _\infty \) is the unique stationary solution, it follows that
However, from (5.6) and (5.7), we know that, for any time-diverging sequence \(t_n \rightarrow \infty \), \(\{\rho (\cdot ,t_n)\}_{n \in {\mathbb {N}}}\) has a convergent subsequence in \({L}^\infty (\Omega )\), whose limit must be \(\rho _\infty \) by (5.10). Since the limit is unique, it follows that
\(\square \)
Remark 5.9
We remark that the technique used in the proof of Theorem 5.8 can be adapted to study the asymptotic properties of general gradient flows in the space of probability measures. These ideas have been expanded upon in [CGW20].
From Theorem 5.7, it is also immediately clear that \(W \in {\mathbf {H}}_s^c\) is a necessary condition for the existence of a nontrivial minimiser at higher values of the parameter \(\beta \). Indeed, Theorem 5.7 tells us that if \(W \in {\mathbf {H}}_s\) then minimisers of \({\mathcal {F}}_\beta ^m\) are unique and are given by \(\rho _\infty \). Before we discuss this any further, we introduce a notion of transition point that allows us to capture a change in the set of minimisers.
Definition 5.10
(Transition point). A parameter value \(\beta _c>0\) is said to be a transition point of \({\mathcal {F}}_\beta ^m\) if the following conditions are satisfied.
-
(1)
For \(\beta <\beta _c\), \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_\beta ^m\).
-
(2)
At \( \beta =\beta _c\), \(\rho _\infty \) is a minimiser of \({\mathcal {F}}_\beta ^m\).
-
(3)
For \(\beta >\beta _c\), there exists \({\mathcal {P}}(\Omega ) \ni \rho _\beta \ne \rho _\infty \), such that \(\rho _\beta \) is a minimiser of \({\mathcal {F}}_\beta ^m\).
We further classify transition points into discontinuous and continuous transition points.
Definition 5.11
(Continuous and discontinuous transition points). A transition point \(\beta _c\) of \({\mathcal {F}}_\beta ^m\) is said to be a continuous transition point if
-
(1)
At \( \beta =\beta _c\), \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_\beta ^m\).
-
(2)
For any family of minimisers \(\{\rho _\beta \}_{\beta >\beta _c}\) it holds that
$$\begin{aligned} \limsup _{\beta \rightarrow \beta _c^+} \Vert \rho _\beta - \rho _\infty \Vert _{{L}^\infty (\Omega )} =0 . \end{aligned}$$
A transition point \(\beta _c>0\) of \({\mathcal {F}}_\beta ^m\) which is not continuous is said to be discontinuous.
It turns out that \(W \in {\mathbf {H}}_s^c\) is in fact a sufficient condition for the existence of a transition point. This result is analogous to the result in case \(m=1\) discussed in [GP70, CP10, CGPS20].
Proposition 5.12
Assume \(W \in {\mathbf {H}}_s^c\). Then there exists some parameter value \(0< \beta _c \le \beta _\sharp ^m\) with \(\beta _\sharp ^m\) defined as
such that \(\beta _c\) is a transition point of \({\mathcal {F}}_\beta ^m\). Thus, \(W \in {\mathbf {H}}_s^c\) is a necessary and sufficient condition for the existence of a transition point.
Proof
Consider the measure \(\rho ^\varepsilon =\rho _\infty + \varepsilon e_{k^\sharp } \in {\mathcal {P}}(\Omega )\) for \(0 < \varepsilon \ll 1\) where \(k^\sharp \in {\mathbb {N}}^d\) is defined as
if it is defined uniquely. If not we pick any \(k^\sharp \) that realises the minimum of the above expression. We now consider an expansion of the energy \({\mathcal {F}}_\beta ^m(\rho ^\varepsilon )\) around \(\rho ^\varepsilon \) which we will use repeatedly throughout the rest of this section. We Taylor expand around \(\rho _\infty \) to obtain
where the function \(f(x) \in (\rho _\infty , \rho ^\varepsilon (x))\). For \(\varepsilon >0\) small enough, the highest order term can be controlled as follows
For \(\beta >\beta _\sharp ^m\), the second order term in the above expression has a negative sign. Thus, for \(\varepsilon >0\) sufficiently small we have that \({\mathcal {F}}_\beta ^m(\rho ^\varepsilon )< {\mathcal {F}}_\beta ^m(\rho _\infty ) \). Since, by Theorem 5.3, minimisers of \({\mathcal {F}}_\beta ^m\) exists for all \(\beta >0\), it follows that for all \(\beta >\beta _\sharp ^m\) there exist nontrivial minimisers of the free energy. Thus, there exists some \(\beta _c\le \beta _\sharp ^m\) which is a transition point of the free energy \({\mathcal {F}}_\beta ^m(\rho )\). \(\quad \square \)
Remark 5.13
We note here that the \(\beta _\sharp ^m\) defined in the statement of Proposition 5.12 corresponds exactly to the point of critical stability of the uniform state \(\rho _\infty \), i.e. if the stationary problem is linearised about \(\rho _\infty \), then \(\beta _\sharp ^m\) corresponds to the value of the parameter at which the first eigenvalue of the linearised operator crosses the imaginary axis.
Before attempting to provide conditions for the existence of continuous and discontinuous transition points we define the function \({\mathbf {F}}^m:(0,\infty ) \rightarrow {\mathbb {R}}\)
Lemma 5.14
For all \(\beta >0\), the function \({\mathbf {F}}^m\) is continuous. Assume further that there exists \(\beta '>0\) and \({\mathcal {P}}(\Omega )\ni \rho _{\beta '} \ne \rho _\infty \) such that \({\mathcal {F}}_{\beta '}^m(\rho _{\beta '})={\mathbf {F}}^m(\beta ')\). Then for all \(\beta >\beta '\), \({\mathcal {F}}_\beta ^m(\rho _\infty )> {\mathbf {F}}^m(\beta )\).
Proof
We note that for \(0<\beta \le \beta _c\) (where \(\beta _c\) is possibly \(+\infty \)) we have that \({\mathbf {F}}^m(\beta )= {\mathcal {F}}_\beta ^m(\rho _\infty )\) which is clearly a continuous function of \(\beta \). Let \(\beta _2>\beta _1>\beta _c\) (if \(\beta _c<\infty \), else we are done) and let \(\rho _{\beta _1}\) be the minimiser of \({\mathcal {F}}_{\beta _1}^m\). Note however due to the structure of the free energy we have that
To obtain continuity of \({\mathbf {F}}^m\), note that the steps of the above equation would still hold with \(\beta _1\) and \(\beta _2\) exchanged. Using that \(\rho _{\beta _1}\) and \(\rho _{\beta _2}\) are uniformly bounded by Theorem 5.3, one has the desired continuity.
Assume now that \({\mathcal {F}}_{\beta '}^m(\rho _{\beta '})= {\mathcal {F}}_{\beta '}^m(\rho _\infty )\) and let \(\beta >\beta '\). We then have that
\(\square \)
We will now try and refine our descriptions of discontinuous and continuous transition points in analogy with the results in [CP10, CGPS20].
Lemma 5.15
If a transition point \(\beta _c>0\) is continuous, then \(\beta _c=\beta _\sharp ^m\).
Proof
We know already from Proposition 5.12 that \(\beta _c \le \beta _\sharp ^m\). Let us assume that \(\beta _c<\beta _\sharp ^m\). We know from Definition 5.11 that \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_{\beta _c}^m\). Additionally for any sequence of minimisers \(\{\rho _\beta \}_{\beta >\beta _c}\) we know that
Consider such a sequence and set \(\eta _\beta =\rho _\beta -\rho _\infty \). For \(\beta >\beta _c\), we expand the free energy about \(\rho _\infty \) as follows
where \(f(x) \in (\rho _\infty ,\rho _\beta (x))\) and can be bounded by \(\Vert \rho _\beta \Vert _{{L}^\infty (\Omega )}\le B_{\beta ,m}\le B\) from the result of Theorem 5.3 and Corollary 5.2. Additionally we can control \(\dfrac{{\hat{W}}(k)}{\Theta (k)}\) to obtain the following bound
Note that due to the fact that \(\Vert \eta _\beta \Vert _{{L}^\infty (\Omega )} \rightarrow 0\) as \(\beta \rightarrow \beta _c^+\), we have that \(\Vert \eta _\beta \Vert _{{L}^3(\Omega )}^3\) is \(o(\Vert \eta _\beta \Vert _{{L}^2(\Omega )}^2)\), i.e. \(\Vert \eta _\beta \Vert _{{L}^3(\Omega )}^3 \le \Vert \eta _\beta \Vert _{{L}^\infty (\Omega )}\Vert \eta _\beta \Vert _{{L}^2(\Omega )}^2\). This leaves us with
Since \(\beta _c<\beta _\sharp ^m\), the term in the brackets is positive close to \(\beta _c\) we obtain a contradiction as \(\rho _\beta \) is a nontrivial minimiser of \({\mathcal {F}}_\beta ^m\). Thus, we must have that \(\beta _c=\beta _\sharp ^m\).
\(\square \)
From Definition 5.11, we see that some \(\beta _c>0\) is a discontinuous transition point if it violates either (or both) of the conditions (1) and (2). In the following lemma, we will show that if (2) is violated then (1) is as well.
Lemma 5.16
Assume \(\beta _c>0\) is a discontinuous transition point of the energy \({\mathcal {F}}_{\beta }^m\) and that for some family of minimisers \(\{\rho _\beta \}_{\beta >\beta _c}\) it holds that
Then there exists \({\mathcal {P}}(\Omega )\ni \rho _{\beta _c} \ne \rho _\infty \) such that:
-
(1)
\({\mathbf {F}}^m_{\beta _c}={\mathcal {F}}_{\beta _c}^m(\rho _{\beta _c})= {\mathcal {F}}_{\beta _c}^m(\rho _\infty )\).
-
(2)
\(S_{\beta _c}^m(\rho _{\beta _c})> S_{\beta _c}^m(\rho _\infty )\) and \({\mathcal {E}}(\rho _{\beta _c})< {\mathcal {E}}(\rho _\infty )=0\).
Proof
Consider a sequence of points \(\{\beta _n\}_{n \in {\mathbb {N}}} >\beta _c\) and \(\beta _n \rightarrow \beta _c \) as \(n \rightarrow \infty \). We know that the set of minimisers \(\{\rho _{\beta _n}\}_{n \in {\mathbb {N}}} \) is compact in \(C^0(\Omega ) \cap {\mathcal {P}}(\Omega )\) from Lemma 5.4. Thus, there exists a subsequence \(\rho _{\beta _{n}} \in \{\rho _\beta \}_{\beta >\beta _c} \) (which we do not relabel) and a limit \(\rho _{\beta _c} \in {\mathcal {P}}(\Omega ) \cap C^0(\Omega )\) such that
From the statement of the lemma we know that \(\rho _{\beta _c} \ne \rho _\infty \). All that remains is to show that \(\rho _{\beta _c}\) is a minimiser of \({\mathcal {F}}_{\beta _c}^m\). We first note that \(\lim _{n \rightarrow \infty }{\mathcal {F}}_{\beta _n}(\rho _{\beta _n})= {\mathcal {F}}_{\beta _c}(\rho _{\beta _c})\). This follows from the fact that the interaction energy \({\mathcal {E}}\) is continuous on \(C^0(\Omega ) \cap {\mathcal {P}}(\Omega )\) for \(W \in C^2(\Omega )\) and the entropy \(S_{\beta }^m\) is essentially an \({L}^m\)-norm and is thus also controlled by the \(C^0(\Omega )\) topology. Finally we use the result of Lemma 5.14 to note that
which completes the proof of (1). The proof of (2) follows immediately from the fact that \(\rho _\infty \) is the unique minimiser of \(S_\beta ^m(\rho )\) on \({\mathcal {P}}(\Omega )\) (which is a consequence of Jensen’s inequality). \(\quad \square \)
Remark 5.17
The above lemma tells us that we have not lost much by defining discontinuous transition points with respect to the \({L}^\infty (\Omega )\) norm since the transition points obtained are discontinuous with respect to the \({L}^p(\Omega )\) norm as well for all \(p \in [1,\infty ]\). Indeed if we consider the sequence constructed in the proof of Lemma 5.16\(\{\rho _{\beta _n}\}_{n \in {\mathbb {N}}}\) it follows that
where \(\rho _{\beta _c}\) is the limiting object btained in the proof of Lemma 5.16. Thus, \(\limsup \limits _{\beta \rightarrow \beta _c^+} \Vert \rho _{\beta }-\rho _\infty \Vert _{{L}^p(\Omega )} \ne 0\) for all \(p \in [1,\infty ]\).
In the following proposition we outline the strategy we will use to provide sufficient conditions for the existence of continuous and discontinuous transition points.
Proposition 5.18
Assume that \(W \in {\mathbf {H}}_s^c\) so that there exists a transition point \(\beta _c>0\) of \({\mathcal {F}}_\beta ^m\). Then:
-
(a)
If \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_{\beta _\sharp ^m}^m\), then \(\beta _c=\beta _\sharp ^m\) is a continuous transition point.
-
(b)
If \(\rho _\infty \) is not a minimiser of \({\mathcal {F}}_{\beta _\sharp ^m}^m\), then \(\beta _c<\beta _\sharp ^m\) is a discontinuous transition point.
Proof
For the proof of Proposition 5.18(a) we note that \(\beta _c\) already satisfies condition (1) of Definition 5.11. All we need to show is that it satisfies condition (2). Assume \(\beta _c< \beta _\sharp ^m\), then by the very definition of a transition point we would have a contradiction since \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_\beta ^m\) at \(\beta =\beta _\sharp ^m\). It follows then that \(\beta _c=\beta _\sharp ^m\). Assume now that condition (2) of Definition 5.11 is violated, i.e. there exists a family of minimisers \(\{\rho _\beta \}_{\beta >\beta _\sharp ^m}\) such that
By Lemma 5.16 it follows that there exists \({\mathcal {P}}(\Omega )\ni \rho _{\beta _\sharp ^m} \ne \rho _\infty \) which minimises \({\mathcal {F}}_{\beta _\sharp ^m}^m\). This is a contradiction.
For Proposition 5.18(b), we note that since \(\rho _\infty \) is not a minimiser at \(\beta =\beta _\sharp ^m\) by Definition 5.10 and Proposition 5.12 it follows that \(\beta _c<\beta _\sharp \). Thus, by Lemma 5.15, \(\beta _c\) is a discontinuous transition point. \(\quad \square \)
The next theorem provides conditions on the Fourier modes of W(x) for the existence of discontinuous transition points. It can be thought of as the analogue for the case of nonlinear diffusion.
Theorem 5.19
Assume \(W \in {\mathbf {H}}_s^c\) and \(m \ne 2\). Define, for some \(\delta >0\), the set \(K^\delta \) as follows
We define \(\delta _*\) to be the smallest value, if it exists, of \(\delta \) for which the following condition is satisfied:
We remark that two of the modes in the above expression can be repeated. For example, we could have \(k^a=2, k_b=1,k_c=1\). Then if \(\delta _*\) is sufficiently small, \({\mathcal {F}}_\beta ^m\) exhibits a discontinuous transition point at some \(\beta _c<\beta _\sharp \).
Proof
We know already from Proposition 5.12 that the system possesses a transition point \(\beta _c\). We are going to use Proposition 5.18(b) and construct a competitor \(\rho \in {\mathcal {P}}(\Omega )\) which has a lower value of the free energy than \(\rho _\infty \) at \(\beta =\beta _\sharp ^m\). Define the function
and let
for some \(\varepsilon >0\), sufficiently small. We denote by \(|K^{\delta _*}|\) the cardinality of \(K^{\delta _*}\), which is necessarily finite as \(W \in {L}^2(\Omega )\). Expanding about the free energy about \(\rho _\infty \) we obtain
where the function \(f(x) \in (\rho _\infty , \rho ^\varepsilon (x))\). We use the definition of \(\beta _\sharp ^m\) and control the highest order term in the same manner as Proposition 5.12 to simplify the expansion as follows:
Setting \(\varepsilon =\delta _*^{\frac{1}{2}}\) (if \(\delta _* >0\), otherwise we stop here), we obtain
One can now check that under condition (A1), it holds that
where the constant a is independent of \(\delta _*\). Indeed, the cube of the sum of n numbers \(a_i\), \(i=1, \dots , n\) consists of only three types of terms, namely: \(a_i^3\), \(a_i^2 a_j\) and \(a_i a_j a_k\). Setting the \(a_i=w_{s(i)}\), with \(s(i) \in K^{\delta _*}\), one can check that the first type of term will always integrate to zero. The sum of the other two will take nonzero and in fact positive values if and only if condition (A1) is satisfied. This follows from the fact that
Also the term \(\gamma (m)^3m(m-2)\) is always negative. Thus, for \(\delta _*\) sufficiently small, considering the fact that \(|K^{\delta _*}| \ge 2\) and is nonincreasing as \(\delta _*\) decreases, \(\rho ^\varepsilon \) has smaller free energy and \(\rho _\infty \) is not a minimiser at \(\beta =\beta _\sharp ^m\). \(\quad \square \)
Remark 5.20
The case \(m=2\) is special, as transition points for any \(W \in {\mathbf {H}}_s^c\) are necessarily discontinuous. This case will be treated in detail in Proposition 5.22.
The following lemma shows that discontinuous transitions are stable in m.
Lemma 5.21
Assume \(W \in {\mathbf {H}}_s^c\) such that \({\mathcal {F}}^{m'}_\beta \) has a discontinuous transition point and \(\beta _c^{m'} < \beta _\sharp ^{m'}\). Then for \(m \in (m'- \varepsilon ,m'+\varepsilon )\) (or \(m \in [1,1+\varepsilon )\) for \(m'=1\)) for some \(\varepsilon >0\) small enough, \({\mathcal {F}}_\beta ^m\) has a discontinuous transition point at some \(\beta _c^m<\beta _\sharp ^m\).
Proof
We start with the case \(m'>1\). Denote by \(\rho ^* \in C^0(\Omega ) \cap {\mathcal {P}}(\Omega )\) the nontrivial minimiser of \({\mathcal {F}}_{\beta _\sharp ^{m'}}^{m'}(\rho )\). We know that
It would be sufficient for the purposes of this proof to show that such a nontrivial minimiser exists for \({\mathcal {F}}_{\beta _\sharp ^{m}}^{m}\) for m close enough to \(m'\). Choosing \(\rho ^*\) to be the competitor state, we have
Since \(\beta _\sharp ^m \rightarrow \beta _\sharp ^{m'}\) and \((m-1)^{-1}(a^m -1) \rightarrow (m'-1)^{-1}(a^{m'} -1) , a \ge 0\) as \(m \rightarrow m'\), it follows, using the fact that \(\rho * \in C^0(\Omega )\), that we can choose m close enough to \(m'\) so that the above term is strictly positive. We then have that for \(m \in (m'-\varepsilon ,m'+\varepsilon )\) for some \(\varepsilon >0\) small enough, \(\rho _\infty \) is not a minimiser of the free energy \({\mathcal {F}}_{\beta _\sharp ^m}^m(\rho )\). By Proposition 5.18(b), it follows that \({\mathcal {F}}^m_\beta \) possesses a discontinuous transition point at some \(\beta _c^m < \beta _\sharp ^{m}\). The case \(m'=1\) can be treated similarly. \(\quad \square \)
In the following proposition, we single out some special values of m at which one always finds a discontinuous transition point for \(W \in {\mathbf {H}}_s^c\).
Proposition 5.22
Assume \(W \in {\mathbf {H}}_s^c\) such that \(\beta _c\) is a transition point of \({\mathcal {F}}_\beta ^m\). Then if \(m \in [2,3]\), \(\beta _c\) is a discontinuous transition point. Specifically for the case \(m=2\) we have that
-
(1)
\(\beta _c^2=\beta _\sharp ^2\)
-
(2)
There exists a one parameter family of minimiser \(\{\rho _\alpha \}_{\alpha \in [0,|\Omega |^{-1/2}\Theta (k^\sharp )^{-1}]}\) of \({\mathcal {F}}_{\beta _\sharp ^2}^2\) with \(\rho _0=\rho _\infty \).
Proof
We will try again to show that we have a competitor at \(\beta _\sharp ^m\). We start with the case \(2<m<3\). Consider the competitor
for \(\varepsilon >0\) and small and \(k^\sharp :=\arg \min _{k \in {\mathbb {N}}^d \setminus \{0\}}{\hat{W}}(k)/\Theta (k) \) if it is uniquely defined or any one such k if it is not. Expanding the energy upto fifth order and noting that second order terms vanish we obtain
where the function \(f(x) \in (\rho _\infty , \rho ^\varepsilon (x))\). We again bound the highest order term as in Proposition 5.12 and use the fact that \(\int _{\Omega } e_k^3 \mathop {}\!\mathrm{d} x=0\) for any \(k \in {\mathbb {N}}^d \setminus \{0\}\) to obtain
Since \(m(m-2)(m-3)\) is negative for \(m \in (2,3)\), for \(\varepsilon >0\) sufficiently small, we have shown that \(\rho _\infty \) is no longer the minimiser of \({\mathcal {F}}_{\beta _\sharp ^m}^m\). The result follows by Proposition 5.18(b): we have a discontinuous transition point at some \(\beta _c<\beta _\sharp ^m\).
We now consider the case \(m=2,3\). Using the same expansion we have that
Thus, \(\rho _\infty \) is not the unique minimiser of \({\mathcal {F}}_{\beta _\sharp ^m}^m\) for \(m=2,3\). It then follows from Definition 5.10 that there must be a discontinuous transition point at \(\beta _c^m \le \beta _\sharp ^m\).
Consider now the convex interpolant \(\rho _t:= (1-t) \rho _0 + t\rho _1, t \in (0,1) \) for \(\rho _0,\rho _1 \in {\mathcal {P}}(\Omega )\) such that \({\mathcal {F}}_\beta ^2(\rho _0), {\mathcal {F}}_\beta ^2(\rho _1)< \infty \). We then have that
Note that the above expression is strictly positiove if \(\beta <\beta _\sharp ^2\). Thus, \({\mathcal {F}}_\beta ^2\) is strictly convex for \(\beta <\beta _\sharp ^2\) and has only one minimiser, namely, \(\rho _\infty \). Since the function \({\mathbf {F}}\) is continuous (cf. Lemma 5.14), it follows that \(\beta _c^2=\beta _\sharp ^2\) for all \(W \in {\mathbf {H}}_s^c\). Furthermore, \(\rho _\alpha = \rho _\infty + \alpha e_{k^\sharp }\) form a one-parameter family of minimisers of \({\mathcal {F}}_{\beta _\sharp ^2}^2\) for \(\alpha \in [0,|\Omega |^{-1/2}\Theta (k^\sharp )^{-1}]\). \(\quad \square \)
We conclude the section by discussing the existence of continuous transition points. We show that for \(m=4\) one can construct a large class of potentials for which the transition point \(\beta _c\) is continuous. We start with the following proposition.
Proposition 5.23
Let \(k \in {\mathbb {N}}^d\) be such that \(k \not \equiv 0\) and let \(k_i \in {\mathbb {N}}, i=1, \dots , d\) be such that
Then we have:
where
Similarly
with
Note that \(P_2(k) \cap P_3(k)=\emptyset \). Similarly, we have that
where the constants \(c^{\sigma _1,\sigma _2}_{j}, c^{\sigma _1,\sigma _2,\sigma _3}_{\ell }, C_0,C_{k}^\sigma \in {\mathbb {R}}\) depend only on d, k, and \(\rho _\infty \) but are independent of the coefficients \(a_{\sigma (k)} \in {\mathbb {R}}\).
Proof
The proof is simply a careful application of the trigonometric identities \(\cos ^2(a)= 2^{-1}(1+ \cos (2a))\), \(\cos ^3(a)=4^{-1}(\cos (3a)+3\cos (a))\), and \(\sin ^3(a) = 4^{-1}(3\sin (a) - \sin (3a))\). \(\quad \square \)
We now proceed to the result concerning continuous transition points for \(m=4\).
Theorem 5.24
Let \(W \in {\mathbf {H}}_s^c\), such that \(\beta _c<\infty \) is a transition point of \({\mathcal {F}}_\beta ^4\). Assume that
is uniquely defined. Furthermore, we assume that \({\hat{W}}(k) \ge 0\) for all \(k \ne k^\sharp \) and that
where the sets \(P_2,P_3\) and the constants \(c^{\sigma _1,\sigma _2}_{j}, c^{\sigma _1,\sigma _2,\sigma _3}_{\ell }\) are as defined in Proposition 5.23. Then \(\beta _c=\beta _\sharp ^4\) is a continuous transition point. Note that the constant \(\Theta (k)\) for \(k \in {\mathbb {N}}^d\) is as defined in (2.1).
Proof
We will rely on Proposition 5.18(a) for the proof of this result. We need to show that, at \(\beta =\beta _\sharp ^4\), \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}_\beta ^4\). Let \(\rho \in {\mathcal {P}}(\Omega ) \in {L}^\infty (\Omega )\) be any measure different from \(\rho _\infty \). Then it is sufficient to show that \({\mathcal {F}}_{\beta _\sharp ^4}^4(\rho ) > {\mathcal {F}}_{\beta _\sharp ^4}^4(\rho _\infty )\) (it is sufficient to check bounded densities from the result of Lemma 5.1). We now define \(\eta := \rho -\rho _\infty \) and note that \(\eta \) has the following properties
We can compute the free energy of \(\rho \) as follows
where we have used (2.2). Simplifying further, by using the definition of \(\beta _\sharp ^4\) and the fact that \(\eta \) has mean zero, we obtain
We define \(\eta _2:=\eta - f_{\eta ,k^\sharp }\) where \(f_{\eta ,k^\sharp }=\sum _{\sigma \in \mathrm {Sym}_{k^\sharp }(\Lambda )}{\hat{\eta }}(\sigma (k^\sharp ))e_{\sigma (k^\sharp )}\) and deal with the two terms \(I_1\) and \(I_2\) separately. We then have
where we have used the fact that
We now use the fact that \(\eta \) has mean zero from (5.11) and Proposition 5.23 to obtain
For the second term we obtain
Applying Proposition 5.23 again, we obtain
where we have used the fact that \(\hat{\eta _2}(\sigma (k^\sharp ))=0\) for all \(\sigma \in \mathrm {Sym}_{k^\sharp }(\Lambda )\). We now note that
Putting (5.12), (5.13), (5.14), and (5.15), together we obtain
Note now that
Thus, it follows that
where in the last step we have simply used the fact that \({\hat{W}}(k) \ge 0\) for all \(k \ne k^\sharp \). We now note that
where we have used the fact that \(|\mathrm {Sym}_k(\Lambda )| =\Theta (k)^2\). Additionally, we have that
where in the last step we applied Jensen’s inequality and used the fact that the integrand has unit \({L}^2(\Omega )\) norm. For any \(k \in {\mathbb {N}}^d\), we define the following quantity
and note that
Finally, we can rewrite the inequality in (5.16) as
where
Assume that \(|{\hat{\eta }}|_{k^\sharp } \ne 0\). Then (.A2) and (A3) along with the expression for \(\beta _\sharp ^4\), (5.17), and the fact that \(|{\hat{\eta }}(k)| \le N_{k} \), imply that the discriminants of the quadratic expressions in (5.18) are all negative, i.e. \((B_j^{\sigma _1,\sigma _2})^2-4 A_jC_j<0,(B_\ell ^{\sigma _1,\sigma _2,\sigma _3})^2-4 A_\ell C_\ell <0\). Indeed, we have that
Similarly,
Thus, it follows that \({\mathcal {F}}_{\beta _\sharp ^4}^4(\rho )>{\mathcal {F}}_{\beta _\sharp ^4}^4(\rho _\infty )\). On the other hand if \(|{\hat{\eta }}|_{k^\sharp } \ne 0\), the proof follows by noting that any contribution from the interaction energy is positive and that \(\rho _\infty \) is the unique minimiser of \(S_{\beta ,4}(\rho )\). The fact that \(\beta _c=\beta _\sharp ^4\) is a consequence of Lemma 5.15.
\(\square \)
Remark 5.25
Note that although the assumptions in Theorem 5.24 seem complicated, all they really require is that all Fourier coefficients of W, except the dominant negative mode \({\hat{W}}(k^\sharp )\) are nonnegative and that a finitely many of them “positive enough” compared to \({\hat{W}}(k^\sharp )\). Consider \(d=1\), with \(W(x)= w_1 e_1(x) + w_2 e_2(x) + w_3 e_3(x)\) with \(w_1<0\) and \(w_2,w_3>0\). If, for some explicitly computable positive constants \(c_2,c_3>0\), \(w_2 > c_2 |w_1| \) and \(w_3 > c_3 |w_1|\), the conditions of Theorem 5.24 are satisfied and the transition point \(\beta _c=\beta _\sharp ^4\) is continuous. In this setting, \(P_2(1)=\{e_2\}\) and \(P_3(1)=\{e_3\}\).
6 The Mesa Limit \(m \rightarrow \infty \)
A natural question to ask is ho w the sequence of free energies \({\mathcal {F}}_\beta ^m: {\mathcal {P}}(\Omega ) \rightarrow (-\infty ,+\infty ]\) behave in the limit as \(m \rightarrow \infty \). We conjecture the following limit free energy, \({\mathcal {F}}^\infty :{\mathcal {P}}(\Omega ) \rightarrow (-\infty ,+\infty ]\),
This is analogous to the so-called mesa limit of the porous medium equation considered by Caffarelli and Friedman [CF87]. It is also studied in [CKY18, CT20] for Newtonian interactions and [KPW19] for general drift-diffusion equations. We rederive the result in our setting.
Theorem 6.1
Consider the sequence of functionals \(\{{\mathcal {F}}_\beta ^m\}_{m \ge 1}\) defined on \({\mathcal {P}}(\Omega ) \cap {L}^\infty (\Omega )\) equipped with the weak-\(*\) topology. Then
for any fixed \(\beta >0\).
Proof
-
(1)
Recovery sequence: For each \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^\infty (\Omega )\) we choose \(\rho _m=\rho \) as the recovery sequence. The interaction energy term remains unchanged as it is independent of m, while \((m-1)^{-1}\) converges to 0 as \(m \rightarrow \infty \). Assume first that \(\Vert \rho \Vert _{{L}^\infty (\Omega )}>1\). It follows that there exists some \(\varepsilon >0\) and a set A of positive measure susch that \(\rho |_{A} > 1+ \epsilon \). Thus, we have
$$\begin{aligned} \frac{\beta ^{-1}}{m-1}\int _{\Omega } \rho ^m \mathop {}\!\mathrm{d} x \ge \frac{\beta ^{-1}}{m-1}|A|(1+\epsilon )^m {\mathop {\rightarrow }\limits ^{m \rightarrow \infty }} \infty , \end{aligned}$$and thus \({\mathcal {F}}_\beta ^m(\rho ) \rightarrow \infty \) for all \(\Vert \rho \Vert _{{L}^\infty (\Omega )}>1\). Now, let us assume that \(\Vert \rho \Vert _{{L}^\infty (\Omega )}\le 1\). This gives us
$$\begin{aligned} \frac{\beta ^{-1}}{m-1}\int _{\Omega } \rho ^m \mathop {}\!\mathrm{d} x \le \frac{\beta ^{-1}}{m-1} \Vert \rho \Vert _\infty ^{m-1} {\mathop {\rightarrow }\limits ^{m \rightarrow \infty }}0 , \end{aligned}$$and thus completes the construction of the recovery sequence.
-
(2)
\(\Gamma \text {-} \liminf \): Assume that there exists \(\{\rho _m\}_{m\ge 1}\) such that \(\rho _m \rightharpoonup \rho \) in \({L}^\infty \)-weak-\(*\). For \(W \in C^2(\Omega )\), the interaction energy is continuous and so we can disregard its behaviour. We start with the case in which \(\Vert \rho \Vert _{{L}^\infty (\Omega )} \le 1\). In this case the entropic term, \(S_\beta ^m(\rho _m)\), can be controlled from below by 0 and thus the \(\Gamma \text {-} \liminf \) holds trivially. The other case left to treat is when \(\Vert \rho \Vert _{{L}^\infty (\Omega )}>1\). This implies again that there exists some \(\varepsilon >0\) and a set of positive measure A such that \(\rho |_A >1+ \varepsilon \). It follows from the weak-\(*\) convergence that
$$\begin{aligned} \lim _{m \rightarrow \infty }\int _{A} \rho _m \mathop {}\!\mathrm{d} x = (1+ \epsilon )|A| + \delta , \end{aligned}$$for some fixed positive constant \(\delta >0\) independent of m. We define the sets \(A^+_m:= \{x \in A: \rho _m >(1+ \varepsilon )\}\) and \(A^-_m: = A\setminus A^+_m\). There also exists \(N \in {\mathbb {N}}\) such that for \(m \ge N\), \(\int _{A} \rho _m \mathop {}\!\mathrm{d} x \ge (1+ \epsilon )|A| + \delta /2\). Thus, for \(m \ge N\) we have that
$$\begin{aligned} \int _{A^+_m} \rho _m \mathop {}\!\mathrm{d} x + \int _{A^-_m} \rho _m \mathop {}\!\mathrm{d} x \ge (1+ \epsilon )|A^+_m| + (1+ \epsilon )|A^-_m| + \delta /2 \end{aligned}$$from which it follows that
$$\begin{aligned} \int _{A^+_m} \rho _m \mathop {}\!\mathrm{d} x \ge \delta /2 . \end{aligned}$$This gives us the estimate we need on the entropic term since
$$\begin{aligned} \frac{\beta ^{-1}}{m-1} \int _{\Omega } \rho _m^m \mathop {}\!\mathrm{d} x&\ge \frac{\beta ^{-1}}{m-1} \int _{A^+_m}\rho _m^m \mathop {}\!\mathrm{d} x\\&\ge \frac{\beta ^{-1}}{m-1} (1+ \epsilon )^{m-1} \int _{A^+_m} \rho _m \mathop {}\!\mathrm{d} x \\&\ge \frac{\beta ^{-1}}{m-1} (1+ \epsilon )^{m-1} \delta /2. \end{aligned}$$Passing to the limit as \(m \rightarrow \infty \), the result follows.
\(\square \)
We would now like to understand how the presence of phase transitions for finite m affects the minimisers of \({\mathcal {F}}^\infty \). This is discussed in the next result.
Theorem 6.2
(Minimisers of the mesa problem). Let \({\mathcal {F}}^\infty :{\mathcal {P}}(\Omega ) \rightarrow (-\infty ,+\infty ]\) be as defined in (6.1). Then
-
(a)
If \(|\Omega |<1\), \({\mathcal {F}}^\infty \equiv +\infty \).
-
(b)
If \(|\Omega |=1\), \({\mathcal {F}}^\infty (\rho )< +\infty \) if and only if \(\rho =\rho _\infty \). Thus, \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}^\infty \).
-
(c)
If \(|\Omega |>1\) and \(W \in {\mathbf {H}}_s\) and \(W \not \equiv 0 \), \(\rho _\infty \) is the unique minimiser of \({\mathcal {F}}^\infty \). On the other hand if \(W \in {\mathbf {H}}_s^c\) there exists \({\mathcal {P}}(\Omega ) \ni \rho \ne \rho _\infty \) such that \(\rho \) is the minimiser of \({\mathcal {F}}^\infty \) with \({\mathcal {F}}^\infty (\rho ) < {\mathcal {F}}^\infty (\rho _\infty )\). Furthermore, there exists a sequence, \(\{\rho _m\}_{m \ge 1}\) of nontrivial minimisers of \({\mathcal {F}}_\beta ^m\) such that \(\rho _m \rightharpoonup \rho \) in \({L}^\infty \)-weak-\(*\) as \(m \rightarrow \infty \).
Proof
The proof of Theorem 6.2(a) follows from the fact that if \(|\Omega |<1\), then for any \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^1(\Omega )\) there exists a set A of positive measure such that \(\rho (x) >1\) for all \(x \in A\). Indeed, if this were not the case we would have that
which would be a contradiction. Thus, we have that \(\Vert \rho \Vert _{{L}^\infty (\Omega )}>1\) for all \(\rho \in {\mathcal {P}}(\Omega ) \cap {L}^1(\Omega )\) and so \({\mathcal {F}}^\infty \equiv \infty \).
The proof of Theorem 6.2(b) is similar. If \(\rho \ne \rho _\infty \), we can again find a set of positive measure A such that \(\rho (x)>1\) for all \(x \in A\). We then repeat the same argument as in the previous case.
Assume now that \(|\Omega |>1\) and \(W \in {\mathbf {H}}_s, W \not \equiv 0\) (if W is identically zero then clearly \({\mathcal {F}}^\infty \equiv 0\)). Since W is mean-zero we have that
On the other hand if \({\mathcal {P}}(\Omega ) \cap {L}^\infty (\Omega ) \ni \rho \ne \rho _\infty \), we know from Definition 2.1, that
Finally consider the case \(W \in {\mathbf {H}}_s^c\). Let \(\beta >0\) be fixed and note that, since \(|\Omega |>1\), \(\beta _\sharp ^m \rightarrow 0\) as \(m \rightarrow \infty \). Clearly for m large enough a nontrivial minimiser \(\rho _m \in {\mathcal {P}}(\Omega )\) exists for \(\beta >0\) from the result of Proposition 5.12. Consider the measure \(\rho ^\varepsilon = \rho _\infty + \varepsilon e_{k^\sharp }\) where \(k^\sharp \) is as defined previously. We then have the following bound
where the function \(f(x) \in (\rho _\infty , \rho ^\varepsilon (x))\). Note that \(|f| \le (\rho _\infty + \varepsilon N_{k^\sharp })\). Thus, we have the bound
Additionally note that if \(\varepsilon \) is small enough and \(\rho _\infty <1\), the last term tends to 0 as \(m \rightarrow \infty \). Also since \(W \in {\mathbf {H}}_s^c\), the second term in the above expression is negative for m large enough as \(m \rho _\infty ^m \rightarrow 0\) as \(m \rightarrow \infty \). It follows from this that, for m large enough, the following estimate holds
where \(C_1,C_2>0\) are independent of m. it hus follows from Theorem 6.1, (6.2), and the definition of \(\Gamma \)-convergence that
where \(\rho \in {\mathcal {P}}(\Omega )\) is the minimiser of \({\mathcal {F}}^\infty \). Thus, \(\rho \ne \rho _\infty \) and the result follows. \(\quad \square \)
7 Numerical Experiments
The numerical experiments in this section are meant to shed light on the qualitative features of the global bifurcation diagram of the system, while also serving as a source of possible conjectures that can be studied in future work. They were performed using a modified version on the numerical scheme in [CCH15].
7.1 Discontinuous bifurcations for \(m >2\) and \(W=-\cos (2 \pi x/L)\)
Stationary solutions in the long-time limit for \(m\ge 2\) and \(W=-\cos (2 \pi x/L)\). The black dot denotes the point of linear stability \(\beta _\sharp ^m\) while the red dot denotes the value of \(\beta \) at which the support of the stationary solution is a strict subset of \({\mathbb {T}}\). Note that \(\Vert \rho _{s}\Vert _{{L}^\infty }=0.1\) corresponds to the flat state \(\rho _\infty \)
Fig. 1 shows the branches of stationary solutions obtained in the long-time limit for \(m \ge 2\) and \(W=-\cos (2 \pi x/L)\). The black dot denotes the point of linear stability \(\beta _\sharp ^m\) while the red dot denotes the value of \(\beta \) at which the support of the stationary solution is a strict subset of \({\mathbb {T}}\). Note that the diagram does not necessarily reflect the actual bifurcation diagram of the system as it is obtained from the long-time dynamics and thus will only see stable solutions. We already know that this choice of W satisfies the conditions of Theorem 4.4 and so there will a bifurcation at \(\beta _\sharp ^m\) (the black points in Fig. 1). One would expect this branch to turn to the right for \(m \in (2,3)\) (cf. Remark 4.6) and then turn back. We conjecture that the red points are all saddle-node bifurcations and correspond to discontinuous phase transitions for \(m\ge 2\) due to Lemma 5.15 and the fact that they lie ahead of the corresponding \(\beta _\sharp ^m\).
7.2 The mesa minimisers
In Fig. 2, we plot the stationary solutions observed in the long-time limit for m large and \(\beta >\beta _c\). Since the stationary solutions are potentially minimisers of \({\mathcal {F}}_\beta ^m\) and the minimisers converge to the minimisers of \({\mathcal {F}}^\infty \) as \(m \rightarrow \infty \) (cf. Theorem 6.1), the plots in Fig. 2 provide us with some information about the structure of the minimisers of the mesa problem. It seems to be that they converge to the indicator function of some fixed set. A natural next question one can ask is what happens to the continuity of phase transitions in the limit as \(m \rightarrow \infty \).
8 Proof of Hölder Regularity
We divide the proof into two parts. In Sect. 8.1, we derive some a priori estimates that will be useful in the proof of regularity. In Sect. 8.2, we perform the so-called reduction of oscillation scheme and complete the proof of Theorem 3.3. As mentioned earlier, readers interested only in bifurcations and phase transitions can skip directly to Sect. 4.
Before turning to the proof of Theorem 3.3, we introduce some notation. Since the Eq. (3.1) is invariant under translations of the co-ordinate axis, we define the parabolic cylinder
centred at (0, 0) and note that we can move it to any point by adding \((x_0,t_0)\). We also used \(K_R\) as a shorthand for \([-R,R]^d\). We denote the parabolic boundary by
We use the following shorthand notation:
Additionally, we consider the cut-off functions \(\zeta \) such that
Through the rest of this section we will also use f(x, t) to denote \(W \star \rho (x,t)\). Note that
The reader should note that proof of regularity holds for any \(f \in C^2(\Omega )\) that for which one can prove bounds of the kind shown above. We note before starting the proof that all estimates in the proof have constants that depend continuously on \(\beta >0\). Thus, the Hölder exponent a and semi-norm \(|\rho |_a\) also depend continuously on \(\beta >0\).
8.1 A priori estimates
There are two a priori estimates that play a key role in the proof of Hölder regularity: a Cacciopoli-type energy estimate and a logarithmic estimate. The proof of the energy estimate is essentially the same as [Urb08, Proposition 2.4] and we state it without proof.
Lemma 8.1
(Energy estimates). Pick \(k, \ell \in {\mathbb {R}}_+\) and some cut-off function \(\zeta \), such that \(\zeta = 0\) on \(\partial _p Q(\tau ,R)\). Then it holds for any weak solution of (3.1) that
Similarly we have,
We note that Urbano [Urb08, Proposition 2.4] proves the above energy estimate for the p-Laplace equation, \(\partial _t \rho - \Delta _p \rho =0\). The proof in our setting follows the same technique. We test the weak formulation in Theorem 8.3 (see page 33) against \(\phi = ((\rho _{\pm }^\ell )_h-k)_{\pm }\zeta ^2\), for some cut-off function \(\zeta \) supported in \(Q(\tau ,R)\) and integrate by parts. Applying similar bounds as in [Urb08, Proposition 2.4] and then passing to the limit as \(h \rightarrow 0\), we obtain the desired energy estimate. We also refer the reader to [Rod16, Proposition 2.7] where the proof of the energy estimate is carried out for the porous medium equation, \(\partial _t \rho - \Delta \rho ^m=0\), which is closer in structure to (3.1). We now move on to the logarithmic estimate. The proof of this needs to be adapted from the classical estimate in the presence of the drift term \(\nabla \cdot (\nabla f \rho )\). Before stating and proving it, we introduce the following function
where s is a bounded, measurable function on \(Q(\tau ,R)\) and
The function has certain useful properties, namely,
We also need to define the Steklov average for any \(\rho \in {L}^1(\Omega \times [0,T])\) for any \(0<h<T\) as follows
The Steklov average has certain nice properties which we state without proving.
Lemma 8.2
[Urb08, Lemma 2.2]. Let \(\rho \in {L}^q([0,T]; {L}^r(\Omega ))\) then \(\rho _h\) converges to \(\rho \) in \(\rho \in {L}^q([0,T]; {L}^r(\Omega ))\) as \(h \rightarrow 0\) for \(q,r \in (1,\infty )\). Additionally, if \(\rho \in C([0,T]; {L}^2(\Omega ))\), then \(\rho _h(\cdot ,t)\) converges to \(\rho (\cdot ,t)\) in \({L}^q(\Omega )\) for \(t \in [0,T]\).
Using this we have the following alternative notion of a weak solution of
Definition 8.3
A weak solution of (3.1) is a bounded measurable function
with
such that
for all \(\phi \in {H}^1_0(\Omega )\), \(h \in (0,T)\), \(t \in (0,T]\) and \(\rho (x,0)=\rho _0\).
Proposition 8.4
[Urb08]. The notion of weak solution introduced in Theorem 3.1 and Theorem 8.3 are equivalent.
Lemma 8.5
(Logarithmic estimates). Let \(\rho \) be a nonnegative weak solution of (3.1) and \(\zeta \) be a time-independent cut-off function, then it holds that
for any \(-\tau \le t \le 0\).
Proof
We start by testing (8.2) against \(((\psi ^\pm )^2)'(\rho _h) \zeta ^2\) and integrating by parts to obtain
Consider the first term on the LHS and integrating from \(-\tau \) to t
Passing to the limit as \(h \rightarrow 0\) we obtain that
Now consider the second term on the LHS of (8.3) (after passing to the limit as \(h \rightarrow 0\))
where the last expression follows from Youngs inequality. Finally we consider the last term on the LHS of (8.3) (after passing to the limit as \(h \rightarrow 0\))
Putting it all together we obtain
Taking into account the support of \(\zeta \), one obtains the result of the lemma. \(\quad \square \)
8.2 Proof of Theorem 3.3
We now get to the meat of the regularity argument, i.e. the reduction of oscillation. We assume again that \(\rho \) is a nonnegative weak solution of (3.1). We pick a cylinder \(Q(4R^{2- \varepsilon },2R)\) that lies inside \(\Omega _T\) (shifted to (0, 0)) for \(0<R<1\). Then we can define
along with
We then define the rescaled cylinder
which holds true if
For a fixed \(\varepsilon >0, \alpha \in (0,1)\) if the above inequality does not hold true for any R that can be made arbitrarily small, it follows that \(\omega \) is comparable to the radius of the cylinder and thus we have Hölder continuity already. The proof of this statement is by contradiction. Let \(\omega _R:= \mathop {{\mathrm{ess\,osc}}}\nolimits _{Q(4R^{2- \varepsilon },2R)} \rho \). Then for any point \((x,t) \in \Omega _T\) we set \(R:= d_{{\mathbb {T}}^d}(x,0) + |t|^{1/2}\), the parabolic distance to the origin. Thus, we have
We will specify the value of \(\alpha \) later. We thus have by this inclusion that
We will also assume throughout the remainder of this proof that \(\mu ^- <\omega /4 \), as otherwise the equation is uniformly parabolic in \(Q(4R^{2- \varepsilon }, 2R)\). Before we proceed we pick some \(\nu _0 \in (0,1)\) and divide our analysis into two cases.
Case 1
or
Case 2
or equivalently
We now treat the two cases independently.
8.2.1 Reduction of oscillation in case 1
In the first case, we start by proving the following result.
Lemma 8.6
Assume that \(\mu ^-< \omega /4\) and that (8.5). holds for some \(\nu _0\)(to be chosen), then
Proof
We start by considering the sequence
such that \(R_0=R\) and \(R_n \rightarrow R/2\) as \(n \rightarrow \infty \). We then construct a sequence of nested shrinking cylinders \(Q(\omega ^{1-m}R_n^2, R_n)\) along with cut-off functions \(\zeta _n\) satisfying
We now apply the energy estimate of Lemma 8.1 in \(Q(\omega ^{1-m}R_n^2, R_n)\) with \(\ell = \mu ^- + \omega /4\), and \(k_n=\mu ^- + \omega /4 + \omega /(2^{n+1})\) for the function \((\rho ^\ell _- -k_n )_-\). We will bound the terms on the LHS and RHS separately. Considering first the terms on the LHS we have
where we have used the fact that \(\rho ^\ell _-= \max (\rho , \mu ^- + \omega /4) \ge \mu ^- + \omega /4 \ge \omega /4\). For the RHS we first note the following facts:
-
(1)
\(0 \le \mu ^- \le \omega /4 \) which implies that \(\rho \le 5 \omega /4\), \(\ell \le \omega /2\), and \(\rho ^\ell _- \le 5 \omega /4\) .
-
(2)
\(\ell = \mu ^- + \omega /4< k_n\) which implies that \(\chi _{[\rho \le \ell ]} \le \chi _{[\rho \le k_n]}=\chi _{[(\rho - k_n)_->0]} \).
-
(3)
If \(\rho ^\ell _-= \rho \), then \(\chi _{[(\rho ^\ell _-- k_n)_->0]}=\chi _{[(\rho - k_n)_->0]} \). On the other hand if \(\rho ^\ell _-= \ell \), we have that \(\rho \le \ell < k_n\) we have that \(\chi _{[(\rho - k_n)_->0]} =0 =\chi _{[(\ell - k_n)_->0]} = \chi _{[(\rho ^\ell _- - k_n)_->0]} \).
-
(4)
\((l-k_n)_{-}=\omega /(2^{n+1}) \le \omega /2\), \((\rho ^\ell _{-}-k_n)_{-}\le \omega /2^{n+1} \le \omega /2\), \((\rho - \ell )_{-} \le \omega /4\) .
We now proceed to bound individual terms on the RHS of (8.1). For the first term we have:
For the second term:
For the third term:
For the final two terms we have:
where in the last step we have used the fact that \(R^\varepsilon \omega ^{1-m}<\alpha <1\) and that \(R <L\). Putting the bounds for the LHS and RHS of (8.1) together we obtain
Let \({\bar{t}}=\omega ^{m-1}t\) and define the following rescaled functions
In these new variables the inequality simplifies to
where
Furthermore we have
where in the last step we have used the embedding into the parabolic space \(V^2\)(cf. Lemma A.4). Thus, we have
where we have used the fact that \(\bar{\zeta _n}=1\) on \(Q(R_{n+1}^2,R_{n+1})\) and have used (8.7). Thus, we have
where we use the fact that \(|Q(R_{n}^2, R_{n})|= R_{n+1}^{d+2} \le R^{d+2}\) and \(R_n/R_{n+1} \le 2\). Setting
we have the recursive inequality
with the constant C independent of \(\omega , R,n\) and dependent only \(d,m,\beta ,f\). Setting \(\nu _0=C^{-(d+2)/2} 4^{-(d+2)^2/2}\), we see that \(X_0 \le \nu _0\) is equivalent (8.5) to being satisfied with constant \(\nu _0\), since \(k_0= \omega /2\). Thus, for this choice, \(X_n \rightarrow 0\) by the geometric convergence lemma (cf. Lemma A.2). It follows then, after changing variables, that \(\rho ^\ell _- > \mu ^- + \omega /4\) a.e. in \(Q(\omega ^{1-m}(\frac{R}{2})^2, \frac{R}{2})\). The result follows by noting that \(\rho ^\ell _- > \mu ^- + \omega /4=\ell \) implies that \(\rho ^\ell _- =\rho \). \(\quad \square \)
Corollary 8.7
(Reduction of oscillation in case 1). Assume that (8.5) holds with constant \(\nu _0\) as specified in the proof of Lemma 8.6. Then there exists a \(\sigma _1 \in (0,1)\), independent of \(\omega \), R, such that
Proof
We have by the result of the previous lemma that
Thus, we have that
Thus, the result holds with \(\sigma _1=\frac{3}{4}\). \(\quad \square \)
8.2.2 Reduction of oscillation in case 2
We now assume that (8.6) holds but with the constant \(\nu _0\) fixed from the previous argument. We argue now that if (8.6) is satisfied then there exists some \(t_0\),
such that
We prove this by contradiction. Assume this is not the case then
which contradicts (8.6). We now proceed to prove the following lemma.
Lemma 8.8
Assume that (8.6). holds. Then there exists a \(q \in {\mathbb {N}}\), depending only on the data, such that
for all \(t \in [-\frac{\nu _0}{2}\omega ^{1-m}R^2,0]\) and \(\alpha \) in (8.4) chosen to be small, depending only on \(\nu _0\), m, d, \(\beta \), W, M but independent of R and \(\omega \).
Proof
The proof of this lemma relies on the Lemma 8.5 with the function \(\psi ^+(u)\) on the cylinder \(Q(-t_0,R)\). We choose
where the constant \(n>1\) will be chosen later. It is fine to apply it to this function as we can assume that
otherwise the proof of the lemma would be complete with \(q=2\). Indeed, we would have for all \(t \in [t_0,0]\):
Before we write down the inequality, we need to further understand the properties of the function \(\psi ^+(\rho )\) defined on the cylinder \(Q(-t_0,R)\). Note first that
Furthermore in \(Q(-t_0,R)\), we have that
Therefore
Furthermore, we need to study the properties of \((\psi ^+)'(\rho )\):
Thus, we have
We now proceed to writing down the estimate
for any \(t_0 \le t \le 0\). We choose a time-independent cut-off function \(0 \le \zeta \le 1\) such that
Consider now the first term involving f on the RHS of (8.8)
where we have simply applied Young’s inequality and the constant \(\lambda \in (0,1/2) \). We derive a similar bound for the second term involving f as follows
Putting it all together we can get rid of the negative term in (8.8) and take the \({\mathrm{ess\,sup}}\) to obtain:
We proceed to bound each of the terms individually. For the first term on the RHS of (8.9) we obtain:
For the second term we use the fact that \(\rho \le 5 \omega /4\) to obtain:
For the third term we use the fact that \(5/4 \omega \ge \rho \ge \omega /2\) on the supports of \(\psi ^+(\rho )\) and \((\psi ^+)'(\rho )\) to obtain:
Similarly for the final term we obtain
For the LHS of (8.6), consider the set
It is clear that \(\zeta =1\) on \(S_t\) and, since \(-\rho +k + \omega /2^{n+1}<0\), the function
is decreasing in \(H^+_{\rho ,k}\). Thus, in \(S_t\) we have
Thus, we have
Putting all the terms back together we obtain and bounding \(\omega ^2\) by \(M^2\),
Finally, we obtain the estimate we need
where one should note that \(R \le L\) and the term \(R^\varepsilon \omega ^{1-m}\) can be controlled by \(\alpha \) through (8.4). Note that for the term in the first set of brackets we can choose \(d \delta \le 3 \nu _0^2/16\) and n large enough such that
because \((1- \nu _0/2)(1+ \nu _0) >1\). Now that n and \(\delta \) have been fixed we note that the constant \(\alpha \) in (8.4) can be made small enough (independent of \(\omega \) and R) so that terms in the other two brackets are lesser that \(3\nu _0^2/16\). This gives us
The proof follows by setting \(q=n+1\) and noting that \([t_0,0] \supset [-\frac{\nu _0}{2}\omega ^{1-m}R^2,0]\). \(\quad \square \)
We now proceed to prove that \(\rho \) is strictly lesser than its supremum in a smaller parabolic cylinder.
Lemma 8.9
Assume that (8.6). holds. Then there exists some \(s_0 \in {\mathbb {N}}\) large enough, independent of \(\omega \), such that
Proof
The proof is similar to that of Lemma 8.6 and relies on the energy estimates in Lemma 8.1. We start by considering the sequence
such that \(R_0=R\) and \(R_n \rightarrow R/2\) as \(n \rightarrow \infty \). We then construct a sequence of nested shrinking cylinders \(Q(\nu _0 2^{-1}\omega ^{1-m}R_n^2, R_n)\) along with cut-off functions \(\zeta _n\) satisfying
We now apply the energy estimate of Lemma 8.1 in \(Q(\nu _0 2^{-1}\omega ^{1-m}R_n^2, R_n)\) with \(\ell = \mu ^+ - \omega /2^{s_0}\), and \(k_n=\mu ^+ - \omega /(2^{s_0}) - \omega /(2^{n+s_0})\) for the function \((\rho ^\ell _+ -k_n )_+\). We will bound the terms on the LHS and RHS separately. Considering first the terms on the LHS we have
where we have used the fact that when \(|\nabla (\rho ^\ell _+ -k)_+ \zeta _n|\) is nonzero, \(\rho ^\ell _+ \ge k_n \ge \omega /2\). For the RHS we first note the following facts:
-
(1)
\(0 \le \mu ^- \le \omega /4 \) which implies that \(\rho \le 5 \omega /4\), and \(\rho ^\ell _+ \le 5 \omega /4\) .
-
(2)
\(\ell = \mu ^- - \omega /2^{s_0}> k_n\) which implies that \(\chi _{[\rho \ge \ell ]} \le \chi _{[\rho \ge k_n]}=\chi _{[(\rho - k_n)_+>0]} \).
-
(3)
If \(\rho ^\ell _+= \rho \), then \(\chi _{[(\rho ^\ell _+- k_n)_+>0]}=\chi _{[(\rho - k_n)_+>0]} \). On the other hand if \(\rho ^\ell _+= \ell \), we have that \(\rho \ge \ell \ge k_n\). Thus, we have that \(\chi _{[(\rho - k_n)_+>0]} =\chi _{[(\rho ^\ell _+ - k_n)_+>0]} \).
-
(4)
\((l-k_n)_{+}=\omega /(2^{n+s_0}) \le \omega /2^{s_0-1}\), \((\rho ^\ell _{+}-k_n)_{+}\le \omega /2^{n+s_0} \le \omega /2^{s_0-1}\), \((\rho - \ell )_{+} \le \omega /2^{s_0-1}\).
Applying, essentially the same bounds as Lemma 8.6, we obtain
Let \({\bar{t}}=\nu _0^{-1} 2\omega ^{m-1}t\) and define the following rescaled functions
In these new variables the inequality simplifies to
where
Since \(\nu _0 \in (0,1)\) it simplifies to,
Furthermore we have
where in the last step we have used the emebedding into the parabolic space \(V^2\) (cf. Lemma A.4). Thus, as in Lemma 8.6 we have
This can be simplified to
where
and the constant C independent of \(\omega , R,n\) and dependent only \(d,m,\beta ,f\). Thus, if
by the geometric convergence lemma (cf. Lemma A.2), \(X_n \rightarrow 0\) and the result follows as in the proof of Lemma 8.6. Thus, all that remains to be shown is (8.10) holds. Before we do this we introduce the following notation
and
In this notation (8.10) reads as
The above inequality means that the subset of \(Q (\frac{\nu _0}{2}\omega ^{1-m}R^2,R)\) where \(\rho \) is close to its supremum can be made arbitrarily small. To show this, we apply the energy estimate of Lemma 8.1 to the function \((\rho ^{\mu ^+}_+- k)_+\) with
with a cut-off function \(\zeta \) defined in \(Q (\frac{\nu _0}{2}\omega ^{1-m}R^2,2R)\) such that
We delete the first term on the LHS and bound the rest as follows:
where we have used the fact that when \(|\nabla (\rho - k)_+ \zeta |\) is nonzero then \(\rho>k > \omega /2\). For the terms on the RHS we bound them as in Lemma 8.6 (note that two of the terms are zero because \(\rho \le \ell =\mu ^+\) a.e. (x, t)). Thus, we have the bound
Since \(|Q(\nu _0 2^{-1}\omega ^{1-m}R^2, 2R)|= 2^{d+1} |Q(\nu _0 2^{-1}\omega ^{1-m}R^2, R)|\), multiplying my \(\omega ^{1-m}\) this reduces to
Note now that \(B_s \subset Q(\nu _0 2^{-1}\omega ^{1-m}R^2, R)\) and, in \(B_s\), \(|\nabla (\rho -k)_+|=|\nabla (\rho -k)|=|\nabla \rho |\). Thus, the above inequality gives us
We now apply the lemma of De Giorgi (cf. Lemma A.3) with \(k_1=\mu ^+ - \omega /2^s\) and \(k_2= \mu ^+ - \omega /2^{s+1}\), to obtain that for all \(t \in [-\nu _0 2^{-1} \omega ^{1-m}R^2,0]\)
Since \(q \le s-1\), by Lemma 8.8, it follows that \(|B_{s-1}(t)| \le |B_{q}(t)| \le (1- \nu _0^2/4)|K_R|\) for all \(t \in [-\nu _0 2^{-1} \omega ^{1-m}R^2,0]\). Thus, for all such t it follows that
Thus, (8.12) can be rewritten as
for \(t \in [-\nu _0 2^{-1} \omega ^{1-m}R^2,0]\). We integrate the above inequality over \( [-\nu _0 2^{-1} \omega ^{1-m}R^2,0]\) to obtain
where in the last step we have applied (8.11). Squaring both sides we obtain
Since \(q<s<s_0\), we sum the above inequality for \(s=q+1, \dots , s_0-2\) to obtain
Note that \(\sum _{s=q+1}^{s_0-2}|B_{s} \setminus B_{s+1}| \le |Q(\nu _0 2^{-1}\omega ^{1-m}R^2, R)|\). Additionally, \(B_{s_0-1} \subset B_s\) for all \(s=q+1, \dots , s_0-2 \). Thus, we have
For \(s_0 \in {\mathbb {N}}\) sufficiently large independent of \(\omega \), R, (8.10) is satisfied and the result follows. \(\quad \square \)
Finally we can state the reduction of oscillation result in case 2.
Corollary 8.10
(Reduction of oscillation in case 2). Assume that (8.5) holds with constant \(\nu _0\) as specified in the proof of Lemma 8.6. Then there exists a \(\sigma _2 \in (0,1)\), independent of \(\omega \), R, such that
Proof
We know from Lemma 8.9 that there exists some \(s_0 \in {\mathbb {N}}\) such that
Thus
Thus, for \(\sigma _2=(1- \frac{1}{2^{s_0}})\) the result follows. \(\quad \square \)
We combine the two cases into one:
Lemma 8.11
(Total reduction of oscillation). Fix some \(0<R<L\) such that \(Q(4R^{2-\varepsilon }, 2R) \subset \Omega _T\). Assume that \({\mathrm{ess\,osc}}_{Q(4R^{2-\varepsilon }, 2R)} \rho \le \omega \) and \(\alpha \omega ^{m-1}> R^{\varepsilon }\) and that \(\mu ^{-}> \omega /4\). Then there exists a constant \(\sigma \in (0,1)\), depending only on the data (and continuously on \(\beta >0\)), and independent of \(\omega \) and R, such that
Proof
The proof follows from the fact that \(Q(\nu _0 2^{-1}\omega ^{1-m}(\frac{R}{2})^2, \frac{R}{2}) \subset Q(\omega ^{1-m}(\frac{R}{2})^2, \frac{R}{2})\) and setting \(\sigma = \max \{\sigma _1,\sigma _2\}\). \(\quad \square \)
We can now complete the proof of Theorem 3.3:
Proof of Theorem 3.3
We now show that there exist constants \(\gamma >1\), \(a \in (0,1)\), depending only on the data (W, \(\beta \), m, d, M), such that for all \(0 \le r \le L\) we have
where \(\omega = c_1 M\) and \(c_1\) is chosen to be large enough so that \(\alpha \omega ^{m-1} >L^{\varepsilon }\). We choose as our starting point the cylinder \(Q(4(L/2)^{2-\varepsilon },L) \subset \Omega _T\). We start by defining
for \(k =0,1, \dots \) and \(\varepsilon \le (m-1)\). We already have that \(\alpha \omega ^{m-1}>R_0^\varepsilon \) for all \(0 \le r \le R\). This implies that
Additionally, we also have that
It follows that
Furthermore, we have
where we have applied Lemma 8.11. We can repeat the procedure starting at \(R_k\) with \(\omega _k= \sigma ^k \omega \) and \(\mu ^-_k:= {\mathrm{ess\,inf}}_{Q(\omega ^{1-m}R_k^2,R_k)} \rho \) assumed to be smaller than \(\omega _k/4\). If this is not the case, then the equation is uniformly parabolic in \(Q(\omega ^{1-m}R_k^2,R_k)\) and by parabolic regularity theory (cf. [LSU68]), (8.13) holds for some constants \(\gamma '>1,a' \in (0,1)\), depending only on the data. The dependence of the constants on \(\beta >0\) is continuous.
Assuming \(\mu ^-_k>\omega _k/4\) and applying the results of Lemma 8.11 to \(R_{k+1}\) we obtain
By induction it follows that
Additionally, for all \(0 \le r \le L\) we have that
for some k. Picking \(a= \log _{c_0} \sigma >0\), we derive
Thus, we have
where \(\gamma = \max \{\sigma ^{-1},\gamma '\} >1\) and \(a= \min \{\log _{c_0} \sigma ,a'\} \in (0,1)\) since \(\sigma>\sigma _1>1/2>c_0\). Note that (8.13) implies that \(\rho \) is continuous. One can see this by mollifying with some standard mollifier \(\varphi ^\varepsilon \) and applying Arzelà–Ascoli to show that the limit as \(\varepsilon \rightarrow 0\) is continuous.
Now that we have control on the oscillation of the solution we can proceed to the proof of Hölder regularity. Consider a weak solution \(\rho (x,t)\) defined on \(\Omega _T\). We would like the Hölder regularity to be uniform in space and time so we consider only those points such that \((x,t) +Q(4(L/2)^{2-\varepsilon },L) \subset \Omega _T^\circ \). The local regularity near \(\partial _p \Omega _T\) can be derived in a similar manner. Fix two points (x, t) and (y, t) for some t large enough, and consider the recursive scheme starting from \(K:=(x,t)+Q(4(L/2)^{2-\varepsilon },L) \subset \Omega _T\). Setting \(r=d_{{\mathbb {T}}^d}(x,y)\) and applying (8.13), we obtain
For the time regularity we consider two points \((x,t_1),(x,t_2) \in \Omega _T, t_1>t_2 \) assuming that \(|t_1-t_2|^{1/2} \le \omega ^{1-m}(L/2)^2\). We consider the recursive scheme starting from \(K:=(x,t_1)+Q(4(L/2)^{2-\varepsilon },L) \subset \Omega _T\). Setting \(r= \omega ^{(m-1)/2}|t_1-t_2|^{1/2}\), we obtain
For \(|t_1-t_2|^{1/2} > \omega ^{1-m}(L/2)^2\), the proof is easier since
Combining (8.14), (8.15), and (8.16) together we have the required Hölder regularity away from the boundary:
where \(a\in (0,1)\) depends continuously on \(\beta >0\) and \(C_h\) depends on M, L, m, \(\gamma \), and d. The regularity near the parabolic boundary can be derived in a similar manner. \(\quad \square \)
Remark 8.12
We note that the proof of Corollary 3.4 follows from the fact that the constant \(C_h\) is uniform in time as long as we are far enough from the initial data \(\rho _0\), i.e. if \(0<C<t_1<t_2<\infty \) for some constant \(C>0\).
References
Ambrosio, L., Gigli, N., Savaré, G.: Gradient Flows in Metric Spaces and in the Space of Probability Measures. Lectures in Mathematics ETH Zürich, Birkhäuser Verlag, Basel (2008)
Aceves-Sánchez, P., Bostan, M., Carrillo, J.-A., Degond, P.: Hydrodynamic limits for kinetic flocking models of Cucker–Smale type. Math. Biosci. Eng. 16(6), 7883–7910 (2019)
Barré, J., Carrillo, J.A., Degond, P., Peurichard, D., Zatorska, E.: Particle interactions mediated by dynamical networks: assessment of macroscopic descriptions. J. Nonlinear Sci. 28(1), 235–268 (2018)
Blanchet, A., Carrillo, J.A., Laurençot, P.: Critical mass for a Patlak–Keller–Segel model with degenerate diffusion in higher dimensions. Calc. Var. Partial Differ. Equ. 35(2), 133–168 (2009)
Burger, M., Capasso, V., Morale, D.: On an aggregation model with long and short range interactions. Nonlinear Anal. Real World Appl. 8(3), 939–958 (2007)
Barbaro, A.B.T., Cañizo, J.A., Carrillo, J.A., Degond, P.: Phase transitions in a kinetic flocking model of Cucker–Smale type. Multiscale Model. Simul. 14(3), 1063–1088 (2016)
Barré, J., Degond, P., Zatorska, E.: Kinetic theory of particle interactions mediated by dynamical networks. Multiscale Model. Simul. 15(3), 1294–1323 (2017)
Brezis, H.: Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext, Springer, New York (2011)
Bertozzi, A.L., Slepčev, D.: Existence and uniqueness of solutions to an aggregation equation with degenerate diffusion. Commun. Pure Appl. Anal. 9(6), 1617–1637 (2010)
Bodnar, M., Velázquez, J.: Friction dominated dynamics of interacting particles locally close to a crystallographic lattice. Math. Methods Appl. Sci. 36(10), 1206–1228 (2013)
Carrillo, J.A., Chertock, A., Huang, Y.: A finite-volume method for nonlinear nonlocal equations with a gradient flow structure. Commun. Comput. Phys. 17(1), 233–258 (2015)
Carrillo, J.A., Chen, X., Wang, Q., Wang, Z., Zhang, L.: Phase transitions and bump solutions of the Keller–Segel model with volume exclusion. SIAM J. Appl. Math. 80(1), 232–261 (2020)
Carrillo, J.A., Craig, K., Yao, Y.: Aggregation-diffusion equations: dynamics, asymptotics, and singular limits. In: Bellomo, N., Degond, P., Tadmor, E. (eds.) Active Particles. Modeling and Simulation in Science, Engineering and Technology, vol. 2, pp. 65–108. Birkhäuser/Springer, Cham (2019)
Caffarelli, L.A., Friedman, A.: Asymptotic behavior of solutions of \(u_t=\Delta u^m\) as \(m\rightarrow \infty \). Indiana Univ. Math. J. 36(4), 711–728 (1987)
Carrillo, J.A., Gvalani, R.S., Pavliotis, G.A., Schlichting, A.: Long-time behaviour and phase transitions for the Mckean–Vlasov equation on the torus. Arch. Ration. Mech. Anal. 235(1), 635–690 (2020)
Carrillo, J.A., Gvalani, R.S., Wu, J.: An invariance principle for gradient flows in the space of probability measures. arXiv e-prints arXiv:2010.00424 (2020)
Cazenave, T., Haraux, A.: An Introduction to Semilinear Evolution Equations. Oxford Lecture Series in Mathematics and its Applications, vol. 13. The Clarendon Press, Oxford University Press, New York (1998). Translated from the 1990 French original by Yvan Martel and revised by the authors
Chayes, L., Kim, I., Yao, Y.: An aggregation equation with degenerate diffusion: qualitative property of solutions. SIAM J. Math. Anal. 45(5), 2995–3018 (2013)
Craig, K., Kim, I., Yao, Y.: Congested aggregation via Newtonian interaction. Arch. Ration. Mech. Anal. 227(1), 1–67 (2018)
Carrillo, J.A., Murakawa, H., Sato, M., Togashi, H., Trush, O.: A population dynamics model of cell–cell adhesion incorporating population pressure and density saturation. J. Theoret. Biol. 474, 14–24 (2019)
Carrillo, J.A., McCann, R.J., Villani, C.: Kinetic equilibration rates for granular media and related equations: entropy dissipation and mass transportation estimates. Rev. Mat. Iberoam. 19(3), 971–1018 (2003)
Chayes, L., Panferov, V.: The McKean–Vlasov equation in finite volume. J. Stat. Phys. 138(1–3), 351–380 (2010)
Craig, K., Topaloglu, I.: Aggregation-diffusion to constrained interaction: minimizers & gradient flows in the slow diffusion limit. Ann. Inst. H. Poincaré Anal. Non Linéaire 37(2), 239–279 (2020)
Dawson, D.A.: Critical dynamics and fluctuations for a mean-field model of cooperative behavior. J. Stat. Phys. 31(1), 29–85 (1983)
Degond, P., Frouvelle, A., Liu, J.-G.: Phase transitions, hysteresis, and hyperbolicity for self-organized alignment dynamics. Arch. Ration. Mech. Anal. 216(1), 63–115 (2015)
De Giorgi, E.: Sulla differenziabilità e l’analiticità delle estremali degli integrali multipli regolari. Mem. Accad. Sci. Torino. Cl. Sci. Fis. Mat. Nat. 3(3), 25–43 (1957)
DiBenedetto, E.: Regularity results for the porous media equation. Ann. Mat. Pura Appl. 4(121), 249–262 (1979)
DiBenedetto, E.: Degenerate Parabolic Equations. Universitext. Springer-Verlag, New York (1993)
Frouvelle, A., Liu, J.-G.: Dynamics in a kinetic model of oriented particles with phase transition. SIAM J. Math. Anal. 44(2), 791–826 (2012)
Figalli, A., Philipowski, R.: Convergence to the viscous porous medium equation and propagation of chaos. ALEA Lat. Am. J. Probab. Math. Stat. 4, 185–203 (2008)
Gates, D.J., Penrose, O.: The van der Waals limit for classical systems. III. Deviation from the van der Waals–Maxwell theory. Commun. Math. Phys. 17(3), 194–209 (1970)
Hwang, S., Zhang, Y.P.: Continuity results for degenerate diffusion equations with \(L^{p}_t L^{q}_{x}\) drifts. arXiv e-prints arXiv:1906.04961 (2019)
Jordan, R., Kinderlehrer, D., Otto, F.: The variational formulation of the Fokker–Planck equation. SIAM J. Math. Anal. 29(1), 1–17 (1998)
Kielhöfer, H.: Bifurcation Theory: An Introduction with Applications to Partial Differential Equations. Applied Mathematical Sciences, 2nd edn. Springer, New York (2012)
Kim, I., Požár, N., Woodhouse, B.: Singular limit of the porous medium equation with a drift. Adv. Math. 349, 682–732 (2019)
Kim, I., Zhang, Y.P.: Regularity properties of degenerate diffusion equations with drifts. SIAM J. Math. Anal. 50(4), 4371–4406 (2018)
Ladyženskaja, O.A., Solonnikov, V.A., Uraltceva, N.N.: Linear and Quasilinear Equations of Parabolic Type. Translated from the Russian by S. Smith. Translations of Mathematical Monographs, Vol. 23. American Mathematical Society, Providence, RI (1968)
Nirenberg, L.: Topics in Nonlinear Functional Analysis. Courant Lecture Notes in Mathematics. vol. 6. New York University, Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI. Chapter 6 by E. Zehnder, Notes by R. A. Artino, Revised reprint of the 1974 original (2001)
Oelschläger, K.: Large systems of interacting particles and the porous medium equation. J. Differ. Equ. 88(2), 294–346 (1990)
Otto, F.: The geometry of dissipative evolution equations: the porous medium equation. Commun. Partial Differ. Equ. 26(1–2), 101–174 (2001)
Philipowski, R.: Interacting diffusions approximating the porous medium equation and propagation of chaos. Stoch. Process. Appl. 117(4), 526–538 (2007)
Rodrigues, A.M.: Regularity properties for the porous medium equation. Master’s thesis, Unviersidade de Coimbra (2016)
Schaaf, R.: Stationary solutions of chemotaxis systems. Trans. Am. Math. Soc. 292(2), 531–556 (1985)
Sznitman, A.-S.: Topics in propagation of chaos. In: Hennequin, P.L. (ed.) École d’Été de Probabilités de Saint-Flour XIX—1989. Lecture Notes in Mathematics, pp. 165–251. Springer, Berlin (1991)
Tamura, Y.: On asymptotic behaviors of the solution of a nonlinear diffusion equation. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 31(1), 195–221 (1984)
Tugaut, J.: Phase transitions of McKean–Vlasov processes in double-wells landscape. Stochastics 86(2), 257–284 (2014)
Urbano, J.M.: The Method of Intrinsic Scaling: A Systematic Approach to Regularity for Degenerate and Singular PDEs. Lecture Notes in Mathematics, vol. 1930. Springer-Verlag, Berlin (2008)
Vázquez, J.L.: The Porous Medium Equation. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, Oxford, Mathematical theory (2007)
Villani, C.: Topics in Optimal Transportation. Graduate Studies in Mathematics, vol. 58. American Mathematical Society, Providence, RI (2003)
Volkening, A., Sandstede, B.: Modelling stripe formation in zebrafish: an agent-based approach. J. R. Soc. Interface 12(112), 20150812 (2015)
Acknowledgements
The authors would like to thank Felix Otto and Yao Yao for useful discussions during the course of this work. We are also grateful to the reviewers for their careful reading of the manuscript and their useful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Mouhot.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
JAC was partially supported by EPSRC Grant number EP/P031587/1 and the Advanced Grant Nonlocal-CPD (Nonlocal PDEs for Complex Particle Dynamics: Phase Transitions, Patterns and Synchronization) of the European Research Council Executive Agency (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 883363). RSG was funded by an Imperial College President’s PhD Scholarship, partially through EPSRC Award Ref. 1676118. Part of this work was carried out at the “Junior Trimester Programme in Kinetic Theory” held at the Hausdorff Research Institute for Mathematics, Bonn. RSG is grateful to the institute for its hospitality.
Appendices
Appendix A. Some useful results
In this section we state some useful lemmas and inequalities which we will use in the proof of Theorem 3.3.
Lemma A.2
(Geometric convergence lemma). Let \(\{X_n\}_{n \in {\mathbb {N}}}\) be a sequence of nonnegative real numbers satisfying the recurrence inequality
for some \(C,b>1\) and \(a>0\). If \(X_0 \le C^{-1/a}b^{-1/a^2}\), then \(\lim \limits _{n \rightarrow \infty }X_n=0\).
Let \(\Omega \subset {\mathbb {T}}^d\) be a smooth, convex, open subdomain. Then we have the following lemma due to De Giorgi [DG57]:
Lemma A.3
Given a function \(v \in W^{1,1}(\Omega )\) and real numbers \(k_1<k_2\) we define
Then there exists a constant \(C=C(d)\) such that
where \(R= \mathrm {diam}(\Omega ).\)
Consider now the parabolic space \(V^2(\Omega _T)\), equipped with the norm
We then have the following embedding [DiB93, page 9]:
Lemma A.4
Let \(\rho \in V^2(\Omega _T)\). Then there exists a constant \(C_d\) depending only on d such that
Appendix B. Bifurcation theory
We state here the Crandall–Rabinowitz theorem (cf. [Nir01, Kie12]) for bifurcations with a one-dimensional kernel.
Theorem B.1
Consider a separable Hilbert space X with \(U \subset X\) an open neighbourhood of 0, and a nonlinear \(C^2\) map, \(F: U \times V \rightarrow X\), where V is an open subset of \({\mathbb {R}}_+\) such that \(F(0,\kappa )=0\) for all \(\kappa \in V\). Assume the following conditions are satisfied for some \(\kappa _* \in V\):
-
(1)
\(D_x(0,\kappa _*)F\) is a Fredholm operator with index zero and has a one-dimensional kernel.
-
(2)
\(D^2_{x\kappa }(0,\kappa _*)F[\hat{v_0}] \notin {{\,\mathrm{Im}\,}}(D_x(0,\kappa _*))\), where \(\hat{v_0} \in \ker (D_x(0,\kappa _*)), \Vert \hat{v_0}\Vert =1\) .
Then, there exists a nontrivial \(C^1\) curve through \((0,\kappa _*)\) such that for some \(\delta >0\),
and \(F(x(s),\kappa (s))=0\). Additionally, for some neighbourhood of \((0,\kappa _*)\), this is the only such solution (apart from the trivial solution) and it has the following form:
where \(\Psi : \ker (D_x(0,\kappa _*)) \times {\mathbb {R}}_+ \rightarrow (\ker (D_x(0,\kappa _*)) )^\perp \) is a \(C^1\) map and \(\psi :(-\delta ,\delta ) \rightarrow V\) is a \(C^1\) function such that \(\psi (0)=\kappa _*\). Furthermore if \(D_\kappa \Psi (v_0,\kappa _*)=0\), we obtain a simplified expression of the form
such that \(\lim \limits _{|s| +|\psi (s)-\kappa _*| \rightarrow 0} \frac{\Vert r_1(s\hat{v_0},\psi (s))\Vert }{|s| +|\psi (s)-\kappa _*|}=0\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Carrillo, J.A., Gvalani, R.S. Phase Transitions for Nonlinear Nonlocal Aggregation-Diffusion Equations. Commun. Math. Phys. 382, 485–545 (2021). https://doi.org/10.1007/s00220-021-03977-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-021-03977-4