A probabilistic model of weld penetration depth based on process parameters

Abstract

In welded structures using robotized metal active gas (MAG) welding, unwanted variation in penetration depth is typically observed. This is due to uncertainties in the process parameters which cannot be fully controlled. In this work, an analytical probabilistic model is developed to predict the probability of satisfying a target penetration, in the presence of these uncertainties. The proposed probabilistic model incorporates both aleatory process parameter uncertainties and epistemic measurement uncertainties. The latter is evaluated using a novel digital tool for weld penetration measurement. The applicability of the model is demonstrated on fillet welds based on an experimental investigation. The studied input process parameters are voltage, current, travel speed, and torch travel angle. The uncertainties in these parameters are modelled using adequate probability distributions and a statistical correlation based on the volt-ampere characteristic of the power source. Using the proposed probabilistic model, it is shown that a traditional deterministic approach in setting the input process parameters typically results in only a 50% probability of satisfying a target penetration level. It is also shown that, using the proposed expressions, process parameter set-ups satisfying a desired probability level can be simply identified. Furthermore, the contribution of the input uncertainties to the variation of weld penetration is quantified. This work paves the way to make effective use of the robotic welding, by targeting a specified probability of satisfying a desired weld penetration depth as well as predicting its variation.

1 Introduction

The robotic arc welding process involves complicated sensing and control techniques applied to various process parameters. These measures enhance the quality and improve repeatability of welds [1]. However, there remains limitations in making welded joints consistent and repeatability is still difficult to achieve. One of the major limitations is the inability to fully control input process parameters due to aleatory uncertainties. These stems from imperfect operating conditions such as measuring inaccuracies as well as limited capability of power sources to control and provide required dynamic and static characteristics [2]. The limited accuracy in measuring devices, repeatability in robots, and controllability in power sources results in variations in gun angle, torch travel angle, and robot trajectory [3] as well as current and voltage [4]. Reducing this process variation is crucial in reducing over-processing, saving cost, and increasing production capacity [5]. Thus, it is of utmost importance to understand the influence of welding process parameters on weld profile and produced quality, regarding both average values and variabilities.

Weld penetration depth is one of the critical weld profile parameters that have significant influence on fatigue life and structural integrity [6]. This can, for instance, be observed for load carrying welds, where the stress concentration factors (SCF) at the weld toe and weld root decrease with increasing weld penetration depth, see Fig. 1. Therefore, physical trial and error tests are widely used in industry to ensure a desired weld penetration depth. Beside these, various predictive tools have been developed, such as mathematical models based on experimental results [1], artificial neural network (ANN) models [8], and numerical simulations [9]. Furthermore, many efforts have been carried out to highlight variables that affect weld penetration depth, such as shielding gas type [10, 11], arc type [12], arc stability [13], gun angle [1], initial gap [14], welding current [15,16,17], arc voltage [15, 18], and welding speed [15]. However, the limitation of having uncertainties in those welding parameters is not addressed. Therefore, these studies cannot predict the influence of variation in welding parameters on the variation in the weld penetration depth. Moreover, to the best of the authors’ knowledge, there is no established model for the probability of satisfying welding requirements, in terms of weld penetration depth. Predicting this probability is however crucial to ensure a required reliability level in manufacturing.

Fig. 1

a Sketch of cruciform joint. b Effect of weld penetration depth on stress concentration factor and fatigue life, computed using the effective notch method [7], in load and non-load carrying welds

In this work, a probabilistic model is proposed to estimate the probability of satisfying a desired penetration depth as well as to predict its variation. The uncertain process parameters are voltage, current, travel speed, and torch travel angle which were studied based on an experimental investigation. The weld penetration depth is evaluated from macrographs using a digital tool developed in MatLab [19]. The epistemic measurement uncertainty related to this evaluation is quantified and incorporated in the probabilistic model. The paper starts with an overview on welding parameters and sources of uncertainties, followed by the presentation of the studied experimental set-up. Thereafter, the proposed probabilistic model is thoroughly presented. Finally, in the result section, the applicability of the model and its advantage over the traditional deterministic approach currently used in the manufacturing process are demonstrated.

2 Welding parameters and sources of uncertainty

In this section, the welding parameters and sources of uncertainties are described. These parameters are set-up and measured experimentally and the described uncertainties are based on industrial recommendations.

2.1 Weld penetration depth

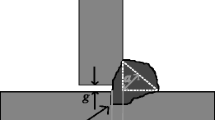
For T-type fillet welds, the penetration depth is defined as the distance the fusion line extends in the root between the web and flange plates [14]. A schematic illustration of bead geometry and weld penetration depth is shown in Fig. 2 a. When measuring penetration depth, a certain level of uncertainty in the measured values is difficult to avoid. This uncertainty is epistemic [20] and can be quantified based on repeated measurements, see Section 3.3.

Fig. 2

Illustration of output and input welding parameters: a Bead geometry. b Travel direction and torch travel angle. c Volt-ampere characteristic for constant voltage power source

2.2 Travel speed and torch travel angle

The travel speed is the linear rate with which the torch arc moves along the weld bead. A schematic illustration of the torch arc movement is shown in Fig. 2 b. Conservatively, the travel speed may vary by ± 10% of the pre-set value due to undesirable vibration or backlash. The torch travel angles, defined in Fig. 2 b, is set using a digital angle gauge. Various factors results in variation in the torch travel angle, such as limited repeatability in robots and inaccuracies of measuring devices. The assumption is that the uncertainty is ± 3 degrees of the setting value. It should be observed that this variation is assumed to be the same regardless of the pre-set value.

2.3 Voltage and current

The voltage is pre-set at the power source which has a constant voltage characteristic. However, the dynamic characteristic of the welding arc, under the influence of electric and thermal conductivity of arc and arc length [4], results in variations in both voltage and current. This variation is assumed to be within ± 20% of their average values. It should be noted, however, that this uncertainty could be larger than what is assumed in this work [21].

The power source makes simultaneous millisecond changes in both voltage and current, in order to maintain a stable arc condition. Thus, during welding, the voltage and current are correlated [22]. The typical volt-ampere characteristic for constant voltage power source can be seen in Fig. 2 c. The slope α defined as

$$ \alpha =-\frac{{\Delta} V}{{\Delta} I}, $$

(1)

is used to computed the statistical correlation between voltage and current, see Section 4.2. A value of α = 0.02 V/A is used in this work, which was verified both mathematically and experimentally [22] for similar operation conditions as in the present experimental investigation.

3 Experimental investigation

3.1 Experimental set-up

Cruciform joints were produced from SSAB Domex 650 MC steel sheets with dimensions 700 × 700 × 10 mm. The steel sheets were fixed in zero gap and tack welded with approximately 20-mm weld length at the ends on each side. A single pass weld with a weld leg length of 7 mm was produced from robotic MAG welding in PA welding position [23], where the gun angle between the plates was 45 degrees. There were four welds with selected welding process parameters on each cruciform joint, see Fig. 1 a. The steel sheets were fixed by an external fixture to prevent welding distortion. After welding the first pass, the specimen was allowed to cool down to room temperature and then rotated to weld another pass with the same welding direction. The welding equipment consists of a Motoman HP20-B00 robot equipped with a Motoman CWK- 400 welding torch, MT1-250 positioner, and EWM Phoenix 521 Progress Pulse coldArc power source to which a Phoenix Progress Drive coldArc wire feed unit was connected. An ESAB AristoRod 13.29 solid wire having 1.2-mm diameter was used as filling material and the shielding gas was Mison-18 gas (20 l/min). During welding, the current was measured using a LEM HT 500-SBD current transducer and the voltage was measured between the wire feeder and the grounding point of the positioner. After welding, the cross sections were taken at the steady state part of the welds. The macrographs were made, with grinding and polishing to 1.0-μ m diamond size followed by etching with 2% Nital.

3.2 Design of experiment

The design of experiments used is shown in the top plots of Fig. 3. There are low, medium, and high settings where welding travel speed and wire feed speed are correlated, in order to achieve the required leg length of 7 mm. For each travel speed value, a three-level full factorial design is used, where the voltage range depends on the travel speed. The torch travel angle was varied as 20, 25, and 30 degrees. The tip-to-workpiece distance is defined as the distance between the end of the contact tip and workpiece, which were selected as 20, 25, and 30 mm. In Fig. 4, the corresponding measured mean values for the studied parameters in this work are shown, i.e., current, voltage, torch travel angle, and travel speed. As can be seen, a total of 81 experimental data are filling the design space for each of the three different travel speeds. It should also be noted that the mean measured values are typically lower than the pre-set values depending on the response of the power source, and that the welding current is strongly correlated to tip-to-workpiece distance [22]. The experimental set-up in Figs. 3 and 4 are detailed in Table 1. The travel angle, contact to work distance, and measured voltage/current values are tabulated. As can be seen, the measured voltage is lower than the pre-set one (i.e., 28.1 V vs. 29.6 V).

Fig. 3

Design of experiment, pre-set values

Fig. 4

Design of experiment, measured mean values

Table 1 Design of Experiment, pre-set values and measured mean values

3.3 Penetration measurements

The penetration depth is numerically evaluated using manual input positions in digital images of macrographs. The measurement procedure consists of four steps, see Fig. 5 a: defining a length scale, line AB, locating the flange plate (interpolated line), line CD, locating the web plate (extrapolated line), line EF, and locating the fusion zone in the vicinity of the flange plate, line GH. The computed penetration depth is the distance between the green crosses, see Fig. 5 a and b.

Fig. 5

Epistemic measurement uncertainty

The uncertainty of the measured weld penetration is dependent on the uncertainty from measuring the scale, the uncertainty from estimating the intersection of the plates—i.e., from where the penetration should be measured, and the uncertainty from estimating the weld penetration maxima. A quantification of the contribution of these uncertainties is performed using Monte Carlo (MC) simulation, where the location of the defined points A–F is assumed normally distributed, see Fig. 5 b. For the points A and B, the standard deviation is set to 1.1 pixels. For the rest of the points the standard deviation is set to 1.35 pixels. These input uncertainties in the location of the points (i.e., 1.1 pixels and 1.35 pixels) are computed using ten (10) manual measurements of the penetration on one randomly selected macrograph.

As can be seen from Fig. 5 c, the resulting standard deviation of the measured penetration is 0.11 mm, or equivalently ± 0.21 mm at 95% confidence interval. Since the uncertainties in the input points (locations A–H) are independent of the calculated lengths, it is clear that the uncertainty in the penetrations depth does not depend on its mean value. From Fig. 5 d, it is noted that the largest contribution to the uncertainty is the extrapolated line, EF, which corresponds to the blue point cloud in Fig. 5 b.

4 Probabilistic model

In this section, the uncertainty in welding penetration y is quantified based on the uncertainty in process parameters x as well as the variance of the epistemic measurement uncertainty $\sigma _{\theta }^{2}$. An overview of the steps involved is shown in the flowchart in Fig. 6. A quadratic deterministic trend model with coefficients A, k, and c is first fitted to the experimental observations, see Section 4.1. The uncertainty in process parameters is thereafter modelled with probability distributions f_Xi and correlation matrix C, see Sections 4.2 and 4.3. These are used together with the deterministic model coefficients as inputs to compute of the probability density function (PDF) and cumulative distribution function (CDF), f_Y and F_Y, respectively, of the weld penetration. The three steps that constitutes the probabilistic model, i.e, normalizing transformation, computation of statistical moments and Edgeworth expansion [24, 25] are detailed in Section 4.3.

Fig. 6

Flowchart of proposed probabilistic model

4.1 Quadratic deterministic model

Denote the voltage, current, travel speed, and torch angle by x₁, x₂, x₃, and x₄, respectively. The penetration y as a function of the process parameters x = [x₁, x₂, x₃, x₄]^T is modelled using a hyper-parabolic function according to

$$ \left\{ \begin{array}{llll} & y={{\mathbf{x}}^{T}}\mathbf{Ax}+{{\mathbf{k}}^{T}}\mathbf{x}+c \\ & {{A}_{ij}}=\sqrt{ \left| {{A}_{ii}}{{A}_{jj}} \right|}, i\ne j \end{array} \right., $$

(2)

where k = [k₁, k₂, k₃, k₄]^T and A_ij is the ij:th component of the matrix A. The requirements $A_{ij} =\sqrt { \left |A_{ii} A_{jj} \right |}$ for i≠j results in a parabolic function in the x_ix_j-plane. However, since cross-terms between travel speed and voltage cannot be accurately determined using the present design of experiment, see Fig. 4, we set A₂₃ = 0. The model has a total of 9 fitting parameters, A₁₁, A₂₂, A₃₃, A₄₄, k₁, k₂, k₃, k₄, and c. These are determined by minimizing the sum of the squared residual error from the 81 experimental observations (Fig. 4).

4.2 Model of input uncertainties

The welding process parameters are uncertain and assumed to follow distributions according to Table 2, with mean value μ_xi and standard deviation σ_xi. Two cases are studied, where the choice of log-normal distribution in Case 2 ensures that voltage, current, and travel speed are positive quantities.

Table 2 Description of random variables

For the voltage and current, most of the variation is within ± 20% of the mean value, see Section 2, i.e., ± 0.2μ_xi. If normal distribution and 95% confidence is assumed, this uncertainty range is equal to ± 2σ_xi, resulting in a coefficient of variation of σ_xi/μ_xi = 0.1. The uncertainty in the travel speed is assumed to be ± 10% of its mean value, i.e., a coefficient of variation of 0.05. For the torch travel angle, the standard deviation σ_x4 = 1.5^o, corresponding to ± 3^o with 95% confidence, is assumed independent of the mean value.

The voltage and current are correlated with a correlation coefficient $\rho _{x_{1}x_{2} }$. The other variables are assumed uncorrelated. The vector x = [x₁, x₂, x₃, x₄]^T of process parameters is therefore assumed to follow a multivariate distribution with mean vector μ_x = [μ_x1, μ_x2, μ_x3, μ_x4]^T and covariance matrix K given by

$$ \mathbf{K}=\left[ \begin{array}{ccccccc} {{\sigma }_{{{x}_{1}}}}^{2} & {{\rho }_{{{x}_{1}}{{x}_{2}}}}{{\sigma }_{x1}}{{\sigma }_{x2}} & 0 & 0 \\ {} & {{\sigma }_{{{x}_{2}}}}^{2} & 0 & 0 \\ {} & \text{SYM} & {{\sigma }_{x3}}^{2} & 0 \\ {} & {} & {} & {{\sigma }_{x4}}^{2} \end{array} \right]. $$

(3)

In the following, an expression for the correlation coefficient $\rho _{x_{1}x_{2} }$ between voltage and current will be derived based on the volt-ampere characteristic for constant voltage power source with α = 0.02V/A, see Section 2.3. The covariance matrix between voltage and current can be written using eigenvalue decomposition, see Fig. 7, as

$$ {{\mathbf{K}}_{{{x}_{1}}{{x}_{2}}}}=\left[ \begin{array}{cccccc} {{\mathbf{v}}_{1}} & {{\mathbf{v}}_{2}} \end{array} \right]\text{diag}\left[ {{s}_{1}},{{s}_{2}} \right]{{\left[ \begin{array}{cccc} {{\mathbf{v}}_{1}} & {{\mathbf{v}}_{2}} \end{array} \right]}^{-1}} $$

(4)

where v₁ = [1,1/α]^T and v₂ = [1,−α]^T are eigenvectors and s₁ and s₂ are corresponding eigenvalues. The eigenvalues are found by evaluating (4) and comparing to Eq. 3, i.e., by solving $\left \{\left (\mathbf {K}_{x_{1} x_{2} } \right )_{11} =\sigma _{x_{1} } {~}^{2} ,\left (\mathbf {K}_{x_{1} x_{2} } \right )_{22} =\sigma _{x2} {~}^{2} \right \}$, which results in s₁ ≈ σ_x2 and s₂ ≈ σ_x1 for small α. Inserting the expression for the eigenvalues into (4) and using $\left (\mathbf {K}_{x_{1} x_{2} } \right )_{12} =\rho _{x_{1} x_{2} } \sigma _{x1} \sigma _{x2}$, results in

$$ {{\rho }_{x1x2}}\approx -\alpha \frac{{{\sigma }_{x2}}}{{{\sigma }_{x1}}}, $$

(5)

where it is assumed that α is small and the standard deviation of the current is substantially larger than the standard deviation of the voltage. Equation 5 is valid for $\alpha \frac {{{\sigma }_{x2}}}{{{\sigma }_{x1}}}<1$, otherwise the correlation coefficient is set to ρ_x1x2 = − 1. It should be noted that a deterministic relation between voltage and current, i.e., x₁ = αx₂ (see Section 2.3), implies that σ_x1 = ασ_x2 or $\frac {{{\sigma }_{x2}}}{{{\sigma }_{x1}}} =\frac {1}{\alpha }$. Therefore, if $\frac {{{\sigma }_{x2}}}{{{\sigma }_{x1}}} =\frac {1}{\alpha }$, the relation between voltage and current is deterministic, i.e. ${{\rho }_{x_{1}x_{2}}}=-1$, which is correctly predicted by Eq. 5.

Fig. 7

Bivariate normal distribution (Case 1) described by the covariance matrix according to Eq. 3. The correlation coefficient according to Eq. 5 depends on the volt-ampere characteristic, slope α (1), for constant voltage power source

The error 𝜃 in the measured penetration, see Table 2, is assumed to follow a normal distribution $\mathcal {N} \left (0,\sigma _{\theta } {~}^{2} \right )$, with mean value zero and standard deviation σ_𝜃 = 0.11mm estimated from repeated measurement, see Section 3.3. Therefore, two types of uncertainties are considered: the aleatory uncertainty in process parameters x and the epistemic measurement uncertainty $\theta \sim \mathcal {N} \left (0,\sigma _{\theta } {~}^{2} \right )$ in the penetration y.

4.3 Model of uncertainty in weld penetration

4.3.1 Model including aleatory uncertainties

In order to quantify the uncertainty in the weld penetration based on the input parameter uncertainty, a variable transformation is first performed. The vector x of input parameters is expressed in terms of standard normal and uncorrelated variables x_N according to [26, 27]

$$ \mathbf{x}={{\mathbf{S }}_{\text{eq}}}\mathbf{TD}{{\mathbf{x}}_{\text{N}}}+{{\boldsymbol{\mu }}_{\mathbf{x},\text{eq}}}, $$

(6)

where T is an orthogonal transformation matrix with columns consisting of the normalized eigenvectors of the correlation matrix

$$ \mathbf{C}=\left[ \begin{array}{cccccc} 1 & {{\rho }_{{{x}_{1}}{{x}_{2}}}} & 0 & 0 \\ {} & 1 & 0 & 0 \\ {} & \text{SYM} & 1 & 0 \\ {} & {} & {} & 1 \end{array} \right], $$

(7)

with $\rho _{x_{1}x_{2} }$ given in Eq. 5, D is a diagonal matrix consisting of the square root of the corresponding eigenvalues, S_eq is a diagonal matrix with equivalent standard deviations $\sigma _{x_{i} ,\text {eq}}$ according to

$$ {{\mathbf{S }}_{\text{eq}}}=\text{diag}\left[ {{\sigma }_{{{x}_{1}},\text{eq}}},{{\sigma }_{{{x}_{2}},\text{eq}}},{{\sigma }_{{{x}_{3}},\text{eq}}},{{\sigma }_{{{x}_{4}},\text{eq}}} \right], $$

(8)

and μ_x,eq = [μ_x1,eq, μ_x2,eq, μ_x3,eq, μ_x4,eq]^T is the vector of equivalent means. The equivalent mean values μ_xi,eq and standard deviations σ_xi,eq, [27, 28], are given by

$$ \left\{\begin{array}{l} {\sigma_{xi\text{,eq}} =\frac{\varphi \left( {\Phi}^{-1} \left[F_{Xi} \left( \mu_{xi} \right)\right]\right)}{f_{Xi} \left( \mu_{xi} \right)} } \\ {\mu_{xi\text{,eq}} =\mu_{xi} -{\Phi}^{-1} \left[F_{Xi} \left( \mu_{xi} \right)\right]\sigma_{xi\text{,eq}} } \end{array}\right. , $$

(9)

where the PDF and CDF of the input variable x_i, $f_{Xi} \left (x_{i} \right )$ and $F_{Xi} \left (x_{i} \right )$, respectively, are evaluated at the mean value μ_xi. From Eq. 9 it is seen that, for the special case where x_i is normally distributed, the equivalent mean and standard deviation are simply reduced to the mean and standard deviation of x_i, i.e., μ_xi,eq = μ_xi and σ_xi,eq = σ_xi. The deterministic model of the penetration according to Eq. 2 can thus be expressed in the transformed normalized space using Eq. 6, i.e.,

$$ y={{\mathbf{x}}_{\text{N}}}^{T}\mathbf{{A}^{\prime}}{{\mathbf{x}}_{\text{N}}}+{{\mathbf{{k}^{\prime}}}^{T}}{{\mathbf{x}}_{\text{N}}}+{c}^{\prime}, $$

(10)

where

$$ \left\{ \begin{array}{ccc} & \mathbf{{A}^{\prime}}=\mathbf{D}{{\mathbf{T}}^{T}}{{\mathbf{S }}_{\text{eq}}}\mathbf{A}{{\mathbf{S }}_{\text{eq}}}\mathbf{TD} \\ & \mathbf{{k}^{\prime}}={{\mathbf{k}}^{T}}{{\mathbf{S }}_{\text{eq}}}\mathbf{TD}+2{{\boldsymbol{\mu }}_{\mathbf{x},\text{eq}}}^{T}\mathbf{A}{{\mathbf{S }}_{\text{eq}}}\mathbf{TD} \\ & {c}^{\prime}=c+{{\boldsymbol{\mu }}_{\mathbf{x},\text{eq}}}^{T}\mathbf{A}{{\boldsymbol{\mu }}_{\mathbf{x},\text{eq}}}+{{\mathbf{k}}^{T}}{{\boldsymbol{\mu }}_{\mathbf{x},\text{eq}}} \end{array} \right.. $$

(11)

Based on Eq. 10, the first four statistical moments of the weld penetration can be computed, see flowchart according to Fig. 6. These are the mean value μ_y and standard deviation σ_y of the penetration, skewness λ, and kurtosis γ of its probability distribution. Denote by η_j the eigenvalues of $\mathbf {A}^{\prime }$, P the orthogonal transformation matrix with columns consisting of the corresponding normalized eigenvectors and $\overline {\mathbf {k}}^{T} =\mathbf {k}^{\prime T}\mathbf {P}$. The mean value, standard deviation, skewness, and kurtosis can be computed according to

$$ \mu_{y} =\sum\limits_{j}\eta_{j} +c^{\prime}, $$

(12)

$$ \sigma_{y} =\sqrt{\sum\limits_{j}\left( 2\eta_{j} {~}^{2} +\bar{k}_{j} {~}^{2} \right) } , $$

(13)

$$ \lambda =\frac{2\sum\limits_{j}\left( 4\eta_{j} {~}^{3} +3\eta_{j} \bar{k}_{j} {~}^{2} \right) }{\sigma_{y} {~}^{3} } $$

(14)

and

$$ \gamma =\frac{48\sum\limits_{j}\left( \eta_{j} {~}^{4} +\eta_{j} {~}^{2} \bar{k}_{j} {~}^{2} \right) }{\sigma_{y} {~}^{4} } . $$

(15)

The probability density function (PDF), $f_{Y} \left (y\right )$, of the weld penetration can be expressed given the above statistical moments based on an Edgeworth expansion [24, 25] according to

$$ \begin{array}{@{}rcl@{}} {{f}_{Y}}\left( y \right)&=&{{f}_{Y}^{\text{Norm}}}\left( y|{{\mu }_{y}},{{\sigma }_{y}} \right)\\ &&\times \left[ 1+{{H}_{3}}\left( \frac{y-{{\mu }_{y}}}{{{\sigma }_{y}}} \right)\frac{\lambda }{6}+{{H}_{6}}\left( \frac{y-{{\mu }_{y}}}{{{\sigma }_{y}}} \right)\frac{{{\lambda }^{2}}}{72}\right.\\ &&~\quad\left.+{{H}_{4}}\left( \frac{y-{{\mu }_{y}}}{{{\sigma }_{y}}} \right)\frac{\gamma }{24} \right] \end{array} $$

(16)

where $f_{Y}^{\text {Norm}} \left (y|\mu _{y} ,\sigma _{y} \right )$ is the normal PDF with mean value and standard deviation, μ_y and σ_y, respectively, and the i:th probabilists’ Hermite polynomials $H_{i} \left (\bullet \right )$ are evaluated at $\frac {y-\mu _{y} }{\sigma _{y} }$. Note that the PDF in Eq. 16 is given by the normal distribution $f_{Y}^{\text {Norm}} \left (y|\mu _{y} ,\sigma _{y} \right )$ multiplied by a correction factor which is a function of the skewness and kurtosis. The cumulative distribution function (CDF), $F_{Y} \left (y\right )$, is given by integration of the PDF yielding

$$ \begin{array}{@{}rcl@{}} {{F}_{Y}}\left( y \right)&=&{{F}_{Y}^{\text{Norm}}}\left( y|{{\mu }_{y}},{{\sigma }_{y}} \right)-{{\sigma }_{y}}{f_{Y}^{\text{Norm}}}\left( y|{{\mu }_{y}},{{\sigma }_{y}} \right)\\ &&\left[ {{H}_{2}}\left( \frac{y-{{\mu }_{y}}}{{{\sigma }_{y}}} \right)\frac{\lambda }{6}+{{H}_{5}}\left( \frac{y-{{\mu }_{y}}}{{{\sigma }_{y}}} \right)\frac{{{\lambda }^{2}}}{72}\right.\\ &&\quad\left.+{{H}_{3}}\left( \frac{y-{{\mu }_{y}}}{{{\sigma }_{y}}} \right)\frac{\gamma }{24} \right] \end{array} $$

(17)

where ${{F}_{Y}^{\text {Norm}}}$ is the normal CDF. The reliability, defined as the probability p_s of satisfying a weld penetration larger than a required value y₀, can thereafter be computed as

$$ \text{Prob}[y>y_{0}]=1-{{F}_{Y}}\left( {{y}_{0}} \right). $$

(18)

The expressions for the PDF, CDF, and the reliability Prob[y > y₀] according to Eqs. 16, 17, and 18, respectively, can be applied directly given $\mathbf {{A}^{\prime }}$, $\mathbf {{k}^{\prime }}$, and $c^{\prime }$. As can be seen from Eq. 11, these are functions of the deterministic fitting parameters (A, k, and c), the correlation between the process parameters (through T and D) as well as μ_x,eq and S_eq which in turn are functions of the distributions of the process parameters as is seen from Eq. 9.

4.3.2 Model including epistemic uncertainty

If the same experiment is repeated, different penetrations may be observed. This type of epistemic uncertainty is assumed to be independent of the considered point x. It is normally distributed with zero mean and its variance $\sigma _{\theta }^{2}$ is computed from the repeated experimental observations, see Section 3.3. The penetration model including both aleatory uncertainties and the epistemic measurement uncertainty, see Table 2, can be written by adding the epistemic uncertainty variable $\theta =\sigma _{\theta } \theta _{\text {N}}\sim \mathcal {N} \left (0,\sigma _{\theta } {~}^{2} \right )$ to Eq. 10, i.e.,

$$ y={{\mathbf{x}}_{\text{N}}}^{T}\mathbf{{A}^{\prime}}{{\mathbf{x}}_{\text{N}}}+{{\mathbf{{k}^{\prime}}}^{T}}{{\mathbf{x}}_{\text{N}}}+{c}^{\prime}+{{\sigma }_{\theta }}{{\theta }_{N}}, $$

(19)

where $\theta _{\text {N}} \sim \mathcal {N} \left (0,1\right )$. The standard deviation according to Eq. 12 is therefore modified to account for the additional random variable 𝜃 = σ_𝜃𝜃_N according to

$$ \sigma_{y} =\sqrt{\sum\limits_{j}\left( 2{\eta_{j}^{2}} +\bar{k}_{j}^{2} \right)+\sigma_{\theta } {~}^{2} } . $$

(20)

It should be noted that, by adding the measurement uncertainty, the mean μ_y of the penetration is unchanged. However, the standard deviation σ_y increases, which results in a decrease of the skewness λ and kurtosis γ of the distribution according to Eqs. 14 and 15, respectively.

5 Results

5.1 Deterministic model

Based on the measured penetration values at the 81 data points, see Fig. 4, the deterministic model according to Eq. 2 is fitted. This results in:

$$ \left\{ \begin{array}{lllll} \mathbf{A} = {{10}^{-6}}\left[ \begin{array}{cccccccc} 1.440\cdot {{10}^{-5}} & 8.771\cdot {{10}^{-3}} & 0 & 1.182\cdot {{10}^{-2}} \\ {} & -5.343 & 3.038 & 7.198 \\ {} & \text{SYM} & -1.727 & 4.093 \\ {} & {} & {} & -9.698 \end{array} \right] \\ \mathbf{k} = {{\text{10}}^{-2}}{{\left[ \begin{array}{cccccc} 1.935 & 0.6900 & -1.165 & -1.960 \end{array} \right]}^{T}} \\ & \\ c = 1.537 \end{array} \right. . $$

(21)

As an example of the applicability of the proposed model, assume that the torch travel angle needs to be determined under the specified condition x₁ = 30 V, x₂ = 300 A, and x₃ = 30 cm/min. Assume further that a weld penetration depth of 3 mm is required. A solution using the above deterministic model is found by setting y ≈ 3 mm, resulting in x₄ ≈ 25^∘. In the following, the set-up 30 V, 300 A, 30 cm/min, and 25^∘ is denoted as the deterministic set-up.

In Fig. 8, contour plots of the weld penetration computed using the above model are shown. The deterministic set-up is marked by a red point. In Fig. 9, the predicted influence of changes in process parameters on the weld penetration is shown. As is seen, the largest influence is attributed to the current.

Fig. 8

Contour plots of deterministic model of weld penetration according to Eq. 2 as a function of: a travel speed and travel angle at 30 V and 300 A, b travel angle and voltage at 30 cm/min and 300 A, c travel angle and current at 30 cm/min and 30 V, d travel speed and voltage at 25^∘ and 300 A, e travel speed and current at 25^∘ and 30 V, and g voltage and current at 25^∘ and 30 cm/min. The marked red point corresponds to a deterministic set-up which predicts a penetration of approximately 3 mm

Fig. 9

Influence on weld penetration, based on deterministic model according to Eq. 2, of: a current at different voltage levels, b current for different torch travel angles ,c current at different travel speed levels, and d voltage at different travel speed levels

5.2 Probabilistic model

In this section, the probabilistic model is presented and compared with the deterministic model with respect to the reliability of its prediction. Recall that given the specified condition x₁ = 30 V, x₂ = 300 A, x₃ = 30 cm/min, and the requirement y ≈ 3 mm, the deterministic model resulted in x₄ = 25^∘. In this section, the randomness of the process parameters is considered, see Table 2. Therefore, the above-specified condition is instead given by the mean values μ_x1 = 30 V, μ_x2 = 300 A, and μ_x3 = 30 cm/min. Furthermore, the requirement on weld penetration is expressed as $\text {Prob} \left [y>3 \text {mm}\right ]>R$, where R = 0.9 is a required reliability level. This probability of satisfying the desired penetration level can be computed from Eq. 18. For demonstration purposes, the computation of this probability for the above-specified mean values is detailed when the random variables are normally distributed according to Case 1 in Table 2. Following the steps in Section 4.3, the vector of means is given by μ_x,eq = [30,300,30,μ_x4]^T, where the mean value of torch travel angle μ_x4 that yields a reliability level $\text {Prob} \left [y>3 \text {mm}\right ]\approx 0.9$ is to be determined. The diagonal matrix of equivalent standard deviations (8) is given by $\mathbf {S}_{\text {eq}} =\text {diag}\left [3,30,1.5,1.5\right ]$, see Table 2. Note that for the special case of normally distributed variables, μ_xi,eq = μ_xi and σ_xi,eq = σ_xi, as can be seen from Eq. 9. The correlation matrix C (7) is expressed as a function of the correlation coefficient which is computed using Eq. 5 as ρ_x1x2 = − 0.2. The orthogonal transformation matrix with columns consisting of the normalized eigenvectors of the correlation matrix C and the diagonal matrix consisting of the square root of the corresponding eigenvalues are computed as

$$ \mathbf{T}=\left[ \begin{array}{cccccccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \frac{1}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}} \end{array} \right] $$

(22)

and $\mathbf {D}=\text {diag}\left [1.0945,1,1,0.8955\right ]$, respectively. Given A, k, and c according to Eq. 21, $\mathbf {A}^{\prime }$, $\mathbf {k}^{\prime }$, and $\mathbf {c}^{\prime }$ are evaluated from Eq. 11. It should be noted that these are function of the mean μ_x4. Computing the eigenvalues and eigenvectors of $\mathbf {A}^{\prime }$ results in:

$$ \left\{ \begin{array}{llll} & {{\mu }_{y}}=3.409-9.698\cdot {{10}^{-6}}{{\mu }_{x4}}^{2}-1.504\cdot {{10}^{-2}}{{\mu }_{x4}} \\ & {{\sigma }_{y}}=\sqrt{9.148\cdot {{10}^{-5}}{{\mu }_{x4}}+1.875\cdot {{10}^{-7}}{{\mu }_{x4}}^{2}+2.710\cdot {{10}^{-2}}} \\ & \lambda =\frac{-2.670\cdot {{10}^{-6}}{{\mu }_{x4}}-5.422\cdot {{10}^{-9}}{{\mu }_{x4}}^{2}-3.296\cdot {{10}^{-4}}}{{{\sigma }_{y}}^{3}} \\ & \gamma =\frac{1.033\cdot {{10}^{-7}}{{\mu }_{x4}}+2.097\cdot {{10}^{-10}}{{\mu }_{x4}}^{2}+1.274\cdot {{10}^{-5}}}{{{\sigma }_{y}}^{4}} \end{array} \right.. $$

(23)

Given the above statistical moments of the weld penetration, the PDF and CDF, Eqs. 16 and 17, respectively, can be computed as a function of the mean torch travel angle μ_x4. The PDF is plotted in Fig. 10 a based on the deterministic prediction μ_x4 = 25^∘ for the distribution according to Case 1 as well as Case 2 in Table 2. As can be seen, the probability of violating the requirement y > 3 mm is given by the integral over the red shaded region. Based on the CDF, it is computed that the reliability requirement $\text {Prob} \left [y>3 \text {mm}\right ]\approx 0.9$ is satisfied if the mean torch travel angle is decreased to μ_x4 = 12^∘, see PDF and blue shaded area in Fig. 10 a. In Fig. 10 b, the probability $\text {Prob} \left [y>y_{0} \right ]$ is plotted for both the deterministic and probabilistic set-up, μ_x4 = 25^∘ and μ_x4 = 12^∘, respectively. As can be seen, the deterministic set-up yields $\text {Prob}\left [y>3 \text {mm}\right ]\approx ~0.58$, which is far below the required reliability of 0.9. It is also seen that the results using the distributions according to Case 1 and Case 2 are similar.

Fig. 10

a Probability density function (16) of weld penetration and b probability of satisfying a weld penetration of y₀ mm (18), for both the deterministic and probabilistic set-up as well as Case 1 and Case 2 distributions of process parameters according to Table 2

In Fig. 11, the effect of changing one variable at a time around the deterministic set-up is shown. As can be seen, the 90% reliability requirement may be satisfied by any of the following changes: decreasing mean travel angle to 12^∘, decreasing mean travel speed to 10 cm/min, increasing mean voltage to 41 V, or increasing mean current to 350 A. It is also seen that the current has the highest influence on the reliability. In Fig. 12, contour plots of the probability $\text {Prob} \left [y>3 \text {mm}\right ]$ computed using the proposed probabilistic model for distributions according to Case 1 are shown. A marked red point and cross correspond to the deterministic and probabilistic set-up, respectively. The dashed vertical lines in the top contours show the boundary for the region where the model is extrapolated. As can be seen, the model is extrapolated for values of the mean torch travel angle lower than 20^∘, see design of experiment according to Fig. 3.

Fig. 11

Probability of satisfying a weld penetration of 3 mm as function of a mean travel angle, b mean travel speed, c mean voltage, and d mean current for Case 1 and Case 2 distributions (Table 2) of process parameters

Fig. 12

Contour plots of the probability of satisfying a weld penetration depth of 3 mm (18) with Case 1 distributions in Table 2 as a function of: a mean speed and angle, b mean angle and voltage, c mean angle and current, d mean speed and voltage, e mean speed and current, and g mean voltage and current. Marked red point and cross correspond to deterministic and probabilistic set-up, respectively. Dashed vertical line is the boundary to the extrapolation region of the model

In Fig. 13, the reliability of satisfying different penetration requirements as a function of means of process parameters is shown, with distribution according to Case 1 in Table 2. As can be seen from Fig. 13 a and b, changes in means of process parameters around the deterministic set-up (μ_x1 = 30V, μ_x2 = 300A, μ_x3 = 30cm/min, and μ_x4 = 25^∘) strongly influence the reliability $\text {Prob} \left [y>3 \text {mm}\right ]$. However, the reliability $\text {Prob} \left [y>2 \text {mm}\right ]\approx 1$ is very high and its sensitivity very low to changes in means of input process parameters. From Fig. 13 a, it may also be seen that the very low reliability $\text {Prob} \left [y>3.5 \text {mm}\right ]\approx 0$ cannot be increased by changes of mean travel angle and/or mean travel speed. A change in mean current and voltage is instead necessary; see Fig. 13 b.

Fig. 13

Reliability of satisfying different penetration requirements as a function of means of process parameters. The parameters are distributed according to Case 1 in Table 2

An important application of the proposed probabilistic model is the study of the variance of the weld penetration $\sigma _{y} {~}^{2}$, see Eq. 20. The sensitivity of variance of the weld penetration with respect to a 50% reduction in variance of one process parameter at a time is shown in Fig. 14. The sensitivities are both shown at the deterministic and probabilistic set-up, in Fig. 14 a and b, respectively. As can be seen, a 50% reduction in the variance $\sigma _{x2} {~}^{2}$ of the current results in a 12% (Fig. 13a) and 14% (Fig. 13b) decrease in $\sigma _{y} {~}^{2}$. The effect of a reduction of the variance of the welding speed is however negligible. It can also be seen that a reduction of the epistemic measurement uncertainty is important. This in turn motivates the development of more accurate measurement method.

Fig. 14

Sensitivity of variance of penetration with respect to decrease in variance of process parameters at a deterministic set-up and b probabilistic set-up. The parameters are distributed according to Case 1 in Table 2

6 Discussion

A deterministic hyper-parabolic model is applied to express the weld penetration as a function of process parameters. The model is simple for practicing engineers, with 2n + 1 fitting coefficients for n process parameters. For the 4 studied process parameters in this work, the model captures both the trend and non-linearity of weld penetration. Based on the computed deterministic sensitivities, it has been shown that the largest influence is attributed to the current. This is in accordance with results presented in previous work [15].

A probabilistic model based on the fitting coefficients of the quadratic deterministic model, the joint probability distribution of process parameters as well as the epistemic measurement uncertainty is proposed. The presented probability formulas for both the PDF and CDF are closed-form analytical expressions. Probabilistic sensitivities, defined as the influence of the means of process parameters on the probability of satisfying a desired penetration depth, can be efficiently computed. Although the proposed probabilistic approach has major advantages compared with traditional deterministic methods, further experimental validation of the computed probabilities is necessary. This would however necessitate a substantially larger experimental dataset than the 81 experiments used in this work, depending on the reliability level to be validated. Furthermore, in order to extend the usage of the proposed probability model, it should also cover a wide range of materials, plate thickness, welding positions, welding robots, and power sources.

It has been shown that the predicted penetration depth using the deterministic model is 3 mm for the arbitrarily chosen set-up, 30 V, 300 A, 30 cm/min, and 25^∘. However, the probability of satisfying a 3-mm penetration depth, computed for the same set-up using the proposed probability model, is only 58%. This result is not specific for the studied set-up. It can be expected that deterministic predictions generally yield reliability levels between 40 and 60% depending on the skewness of the PDF of the weld penetration.

The aleatory process parameter uncertainty is modelled using either normal or log-normal distributions. It is observed that the probability of satisfying the predicted penetration is similar in both cases. Although the formulation of the probabilistic model is simpler using normal variables, a log-normal distribution is more appropriate to describe positive quantities such as current, voltage and welding speed.

The epistemic measurement uncertainty is modelled using a normal distribution with a standard deviation 0.1 mm. However, the contribution of welding distortion of the specimen is not taken into account in the proposed estimation. Therefore, the epistemic measurement uncertainty is likely to be higher than the estimated valued, since distortion from welding is likely to increase the error of approximating the plates by a line. It should however be noted that this error is likely to be small, since the gap size is fixed to zero and the welding distortion is prevented by external fixture (see Section 3.1). It should also be noted that, an epistemic model uncertainty, i.e., uncertainties in the model itself, can be added to the proposed formulation through the law of total probability [29].

7 Conclusion

The following conclusions can be summarized:

• When a reliability level of 90% is required, the proposed probabilistic model yields process parameters set-ups that differs significantly compared with a traditional deterministic approach. This is due to the fact that deterministic approaches yield reliability levels close to 50% regardless of the input uncertainties.

• Using the proposed probabilistic model, it is concluded that the uncertainty in welding current shows the largest contribution to the variation in the weld penetration depth. Therefore, in order to limit this variation, the capability of power sources to control and provide required characteristics has to be enhanced.

• A digital image tool is developed to measure the penetration depth and quantify the epistemic measurement uncertainty. It is shown that this source of uncertainty has a substantial contribution to the overall uncertainty in penetration depth.

• The proposed probability model can be used to formulate guidelines for process parameters set-ups that satisfy a desired reliability level. The approach paves the way for optimization under uncertainty, since both probabilities and sensitivities can be efficiently computed.