Skip to main content
SpringerLink
Log in

Theory and computation of higher gradient elasticity theories based on action principles

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

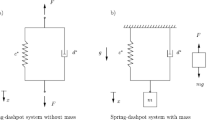
Abstract

In continuum mechanics, there exists a unique theory for elasticity, which includes the first gradient of displacement. The corresponding generalization of elasticity is referred to as strain gradient elasticity or higher gradient theories, where the second and higher gradients of displacement are involved. Unfortunately, there is a lack of consensus among scientists how to achieve the generalization. Various suggestions were made, in order to compare or even verify these, we need a generic computational tool. In this paper, we follow an unusual but quite convenient way of formulation based on action principles. First, in order to present its benefits, we start with the action principle leading to the well-known form of elasticity theory and present a variational formulation in order to obtain a weak form. Second, we generalize elasticity and point out, in which term the suggested formalism differs. By using the same approach, we obtain a weak form for strain gradient elasticity. The weak forms for elasticity and for strain gradient elasticity are solved numerically by using open-source packages—by using the finite element method in space and finite difference method in time. We present some applications from elasticity as well as strain gradient elasticity and simulate the so-called size effect.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Abali, B.E.: Computational Reality, Solving Nonlinear and Coupled Problems in Continuum Mechanics. Advanced Structured Materials. Springer Nature, Singapore (2017a)

  2. Abali, B.E.: Technical University of Berlin, Institute of Mechanics, Chair of Continuums Mechanics and Material Theory.Computational Reality. http://www.lkm.tu-berlin.de/ComputationalReality/ (2017b)

  3. Abali, B.E., Müller, W.H.: Numerical solution of generalized mechanics based on a variational formulation. In Oberwolfach Reports - Mechanics of Materials, European Mathematical Society Publishing House 17(1), pp. 9–12 (2016)

  4. Abali, B.E., Müller, W.H., Eremeyev, V.A.: Strain gradient elasticity with geometric nonlinearities and its computational evaluation. Mech. Adv. Mater. Modern Process. 1, 4 (2015)

    Article  Google Scholar 

  5. Ahrens, J., Geveci, B., Law, C.: ParaView: An End-User Tool for Large Data Visualization. In: Visualization Handbook, chapter 36. Elsevier Academic Press (2011)

  6. Alnæs, M.S., Mardal, K.-A.: On the efficiency of symbolic computations combined with code generation for finite element methods. ACM Trans. Math. Softw. (TOMS) 37(1), 6 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  7. Alnaes, M.S., Mardal, K.A.: SyFi and SFC: Symbolic Finite Elements and Form Compilation, vol. 15. Springer, Berlin (2012)

    Google Scholar 

  8. Auffray, N., dell’Isola, F., Eremeyev, V., Madeo, A., Rosi, G.: Analytical continuum mechanics à la Hamilton-Piola least action principle for second gradient continua and capillary fluids. Math. Mech. Solids 20(4), 375–417 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  9. Ayachit, U.: The paraview guide: a parallel visualization application. Technical report, Kitware (2015)

  10. Barenblatt, G.I.: Scaling, Self-similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics. Cambridge University Press, Cambridge (1996)

    Book  MATH  Google Scholar 

  11. Bilotta, A., Formica, G., Turco, E.: Performance of a high-continuity finite element in three-dimensional elasticity. Int. J. Numer. Methods Biomed. Eng. 26(9), 1155–1175 (2010)

    Article  MATH  Google Scholar 

  12. Brezny, R., Green, D.: Characterization of edge effects in cellular materials. J. Mater. Sci. 25(11), 4571–4578 (1990)

    Article  Google Scholar 

  13. Chen, C., Fleck, N.: Size effects in the constrained deformation of metallic foams. J. Mech. Phys. Solids 50(5), 955–977 (2002)

    Article  MATH  Google Scholar 

  14. dell’Isola, F., Andreaus, U., Placidi, L.: At the origins and in the vanguard of peridynamics, non-local and higher-gradient continuum mechanics: an underestimated and still topical contribution of gabrio piola. Math. Mech. Solids 20, 887–928 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  15. dell’Isola, F., Sciarra, G., Vidoli, S.: Generalized Hooke’s law for isotropic second gradient materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 465, 2177–2196 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  16. Eremeyev, V.A.: On equilibrium of a second-gradient fluid near edges and corner points. In: Advanced Methods of Continuum Mechanics for Materials and Structures, pp. 547–556. Springer (2016)

  17. Eremeyev, V.A., Altenbach, H.: Equilibrium of a second-gradient fluid and an elastic solid with surface stresses. Meccanica 49(11), 2635–2643 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Eringen, A.: Theory of micropolar elasticity. Technical report, DTIC Document (1967)

  19. Giorgio, I.: Numerical identification procedure between a micro-cauchy model and a macro-second gradient model for planar pantographic structures. Zeitschrift für angewandte Mathematik und Physik 67(4), 95 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  20. Gnu Public . Gnu general public license. http://www.gnu.org/copyleft/gpl.html (2007)

  21. Hoffman, J., Jansson, J., Johnson, C., Knepley, M., Kirby, R., Logg, A., Scott, L. R., Wells, G.N.: Fenics. (http://www.fenicsproject.org/) (2005)

  22. Javili, A., dell’Isola, F., Steinmann, P.: Geometrically nonlinear higher-gradient elasticity with energetic boundaries. J. Mech. Phys. Solids 61(12), 2381–2401 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. Jones, E., Oliphant, T., Peterson, P., et al.: SciPy: Open source scientific tools for Python. http://www.scipy.org/ (2001)

  24. Kesler, O., Gibson, L.J.: Size effects in metallic foam core sandwich beams. Mater. Sci. Eng. A 326(2), 228–234 (2002)

    Article  Google Scholar 

  25. Langanten, H.P., Logg, A.: Solving PDEs in Python, Volume 3 of Simula SpringerBriefs on Computing. Springer, Berlin (2017)

    Google Scholar 

  26. Logg, A., Mardal, K.A., Wells, G.N.: Automated Solution of Differential Equations by the Finite Element Method the FEniCS Book, Volume 84 of Lecture Notes in Computational Science and Engineering. Springer, Berlin (2011)

    Google Scholar 

  27. Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16(1), 51–78 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  28. Mindlin, R.D.: Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1(4), 417–438 (1965)

    Article  Google Scholar 

  29. Mindlin, R.D., Tiersten, H.F.: Effects of couple-stresses in linear elasticity. Arch. Ration. Mech. Anal. 11, 415–448 (1962)

  30. Morrison, J.: The yield of mild steel with particular reference to the effect of size of specimen. Proc. Inst. Mech. Eng. 142(1), 193–223 (1939)

    Article  Google Scholar 

  31. Neff, P., Ghiba, I.-D., Madeo, A., Placidi, L., Rosi, G.: A unifying perspective: the relaxed linear micromorphic continuum. Contin. Mech. Thermodyn. 26(5), 639–681 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  32. Oliphant, T.E.: Python for scientific computing. Comput. Sci. Eng. 9(3), 10–20 (2007)

    Article  Google Scholar 

  33. Pideri, C., Seppecher, P.: A homogenization result for elastic material reinforced periodically with high rigidity elastic fibres. Comptes Rendus de l’Academie des Sci. Ser. IIB Mech. Phys. Chem. Astron. 8(324), 475–481 (1997)

    MATH  Google Scholar 

  34. Placidi, L., Andreaus, U., Della Corte, A., Lekszycki, T.: Gedanken experiments for the determination of two-dimensional linear second gradient elasticity coefficients. Zeitschrift für angewandte Mathematik und Physik 66(6), 3699–3725 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  35. Polizzotto, C.: A second strain gradient elasticity theory with second velocity gradient inertia-part i: constitutive equations and quasi-static behavior. Int. J. Solids Struct. 50(24), 3749–3765 (2013a)

    Article  Google Scholar 

  36. Polizzotto, C.: A second strain gradient elasticity theory with second velocity gradient inertia-part ii: dynamic behavior. Int. J. Solids Struct. 50(24), 3766–3777 (2013b)

    Article  Google Scholar 

  37. Reiher, J.C., Giorgio, I., Bertram, A.: Finite-element analysis of polyhedra under point and line forces in second-strain gradient elasticity. J. Eng. Mech. 143, 04016112 (2016)

  38. Romano, G., Barretta, R., Barretta, A.: On maupertuis principle in dynamics. Rep. Math. Phys. 63(3), 331–346 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  39. Scerrato, D., Zhurba Eremeeva, I.A., Lekszycki, T., Rizzi, N.L.: On the effect of shear stiffness on the plane deformation of linear second gradient pantographic sheets. ZAMM J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik 96(11), 1268–1279 (2016)

    Article  MathSciNet  Google Scholar 

  40. Steigmann, D.J., dell’Isola, F.: Mechanical response of fabric sheets to three-dimensional bending, twisting, and stretching. Acta Mech. Sin. 31(3), 373–382 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  41. Toupin, R.A.: Theories of elasticity with couple-stress. Arch. Ration. Mech. Anal. 17(2), 85–112 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  42. Turco, E., Golaszewski, M., Cazzani, A., Rizzi, N.L.: Large deformations induced in planar pantographic sheets by loads applied on fibers: experimental validation of a discrete lagrangian model. Mech. Res. Commun. 76, 51–56 (2016)

    Article  Google Scholar 

  43. Yang, J., Lakes, R.S.: Experimental study of micropolar and couple stress elasticity in compact bone in bending. J. Biomech. 15(2), 91–98 (1982)

    Article  Google Scholar 

Download references

Acknowledgements

This work was completed while B. E. Abali was supported by a Grant from the Max Kade Foundation to the University of California, Berkeley.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of California, Berkeley, 6124 Etcheverry Hall, Mailstop 1740, Berkeley, CA, 94720, USA

    B. Emek Abali

  2. Institute of Mechanics, Chair of Continuum Mechanics and Theory of Materials, Technische Universität Berlin, Einsteinufer 5, 10587, Berlin, Germany

    Wolfgang H. Müller

  3. Dipartimento di Ingegneria Strutturale e Geotecnica, Sapienza Universita di Roma, Via Eudossiana 18, 00184, Roma, Italia

    Francesco dell’Isola

Authors
  1. B. Emek Abali
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wolfgang H. Müller
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Francesco dell’Isola
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Emek Abali.

Appendices

Appendix A: Convergence for linear elasticity

Standard h-convergence has been conducted by decreasing the mesh size in every tetrahedron. We use the same geometry and boundary conditions and compute \(L_2\) norm of the solution (displacement vector) over the whole mesh. We restrict the analysis to the first five time steps, \(t_1\), \(t_2\), \(t_3\), \(t_4\), and \(t_5\), and expect a linear relation for every time step between (log of) degrees of freedom (dofs) and (log of) \(L_2\) norm. The results are compiled in Table 2 and shown in Fig. 5.

Table 2 Convergence analysis for linear elastic transient FEM computation
Full size table
Fig. 5
figure 5

For the linear elastic transient FEM, plot of degrees of freedom versus \(L_2\) norm over the whole mesh in a log-log scale. Colors denote different time steps

Full size image

Appendix B. Convergence for nonlinear elasticity

Standard h-convergence has been conducted with the same geometry and boundary conditions for the first five time steps, \(t_1\), \(t_2\), \(t_3\), \(t_4\), and \(t_5\). The results are compiled in Table 3 and shown in Fig. 6.

Table 3 Convergence analysis for nonlinear elastic transient FEM computation
Full size table
Fig. 6
figure 6

For the nonlinear elastic transient FEM, plot of degrees of freedom versus \(L_2\) norm over the whole mesh in a log-log scale. Colors denote different time steps

Full size image
Table 4 Convergence analysis for linear strain gradient elastic transient FEM computation
Full size table

Appendix C: Convergence for linear strain gradient elasticity

Standard h-convergence has been conducted with the same geometry and boundary conditions for the first five time steps, \(t_1\), \(t_2\), \(t_3\), \(t_4\), and \(t_5\). The results are compiled in Table 4 and shown in Fig. 7.

Fig. 7
figure 7

For the linear strain gradient elastic transient FEM, plot of degrees of freedom versus \(L_2\) norm over the whole mesh in a log-log scale. Colors denote different time steps

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abali, B.E., Müller, W.H. & dell’Isola, F. Theory and computation of higher gradient elasticity theories based on action principles. Arch Appl Mech 87, 1495–1510 (2017). https://doi.org/10.1007/s00419-017-1266-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-017-1266-5

Keywords

Search

Navigation