Abstract
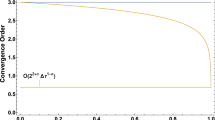
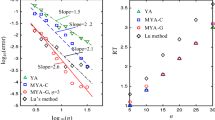
We present here a high-order numerical formula for approximating the Caputo fractional derivative of order \(\alpha\) for \(0<\alpha<\)1. This new formula is on the basis of the third degree Lagrange interpolating polynomial and may be used as a powerful tool in solving some kinds of fractional ordinary/partial differential equations. In comparison with the previous formulae, the main superiority of the new formula is its order of accuracy which is \(4-\alpha ,\) while the order of accuracy of the previous ones is less than 3. It must be pointed out that the proposed formula and other existing formulae have almost the same computational cost. The effectiveness and the applicability of the proposed formula are investigated by testing three distinct numerical examples. Moreover, an application of the new formula in solving some fractional partial differential equations is presented by constructing a finite difference scheme. A PDE-based image denoising approach is proposed to demonstrate the performance of the proposed scheme.





Similar content being viewed by others
References
Aubert, G., Kornprobst, P.: Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations, vol. 147. Springer, Berlin (2006)
Brunner, H., Han, H., Yin, D.: Artificial boundary conditions and finite difference approximations for a time-fractional diffusion-wave equation on a two-dimensional unbounded spatial domain. J. Comput. Phys. 276, 541–562 (2014)
Burden, R., Faires, J.D.: Numerical Analysis, 9th edn. Brooks/Cole, Boston (2011)
Cao, J., Li, C., Chen, Y.: High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (II). Fract. Calc. Appl. Anal. 18, 735–761 (2015)
Cao, J., Xu, C., Wang, Z.: A high order finite difference/spectral approximations to the time fractional diffusion equations. Adv. Mater. Res. 875, 781785 (2014)
Cao, W., Zeng, F., Zhang, Z., Karniadakis, G.E.: Implicit-explicit difference schemes for nonlinear fractional differential equations with nonsmooth solutions. SIAM J. Sci. Comput. 38(5), A3070–A3093 (2016)
Cui, M.: Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 228, 7792–7804 (2009)
Deng, W.H., Hesthaven, J.S.: Local discontinuous Galerkin methods for fractional diffusion equations. Math. Model. Numer. Anal. 47, 1845–1864 (2013)
Deng, W.H., Hesthaven, J.S.: Local discontinuous Galerkin methods for fractional ordinary differential equations. BIT 55(4), 967–985 (2015)
Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)
Dimitrov, Y.: Three-point approximation for Caputo fractional derivative. Commun. Appl. Math. Comput. 31(4), 413–442 (2017)
Gao, G.H., Sun, Z.Z., Zhang, H.W.: A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J. Comput. Phys. 259, 33–50 (2014)
Gonzalez, R., Woods, R.: Digital Image Processing, 2nd edn. Prentice Hall, New York (2001)
Guo, Z., Sun, J., Zhang, D., Wu, B.: Adaptive Perona-Malik model based on the variable exponent for image denoising. IEEE Trans. Image Process. 21, 958–967 (2012)
Jain, A.K.: Fundamentals of Digital Image Processing. Prentice Hall, Englewood Cliffs (1989)
Langlands, T., Henry, B.: The accuracy and stability of an implicit solution method for the fractional diffusion equation. J. Comput. Phys. 205, 719–736 (2005)
Lee, S.H., Seo, J.K.: Noise removal with Gauss curvature-driven diffusion. IEEE Trans. Image Process. 14, 904–909 (2005)
Li, C., Chen, A., Ye, J.: Numerical approaches to fractional calculus and fractional ordinary differential equation. J. Comput. Phys. 230, 3352–3368 (2011)
Lin, Y., Xu, C.: Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 225, 1533–1552 (2007)
Lv, C., Xu, C.: Error analysis of a high order method for time-fractional diffusion equations. SIAM J. Sci. Comput. 38, A2699–A2724 (2016)
Meerschaert, M., Tadjeran, C.: Finite difference approximations for fractional advection-dispersion flow equations. J. Comput. Appl. Math. 172, 65–77 (2004)
Perona, P., Malik, J.: Scale-space and edge detection using an isotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 12, 629–639 (1990)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Roop, J.P.: Computational aspect of FEM approximation of fractional advection dispersion equation on bounded domains in \(R^2\). J. Comput. Appl. Math. 193(1), 243–268 (2006)
Sun, Z.Z., Wu, X.: A fully discrete difference scheme for a diffusion-wave system. Appl. Numer. Math. 56, 193–209 (2006)
Xu, Q., Hesthaven, J.S.: Discontinuous Galerkin method for fractional convection-diffusion equations. SIAM J. Numer. Anal. 52(1), 405–423 (2014)
Yeganeh, S., Mokhtari, R., Hesthaven, J.S.: Space-dependent source determination in a time-fractional diffusion equation using a local discontinuous Galerkin method. BIT Numer. Math. 57(3), 685–707 (2017)
Zhuang, P., Gu, Y.T., Liu, F., Turner, I., Yarlagadda, P.K.D.V.: Time-dependent fractional advection-diffusion equations by an implicit MLS meshless method. Int. J. Numer. Methods Eng. 88, 1346–1362 (2011)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Mokhtari, R., Mostajeran, F. A High Order Formula to Approximate the Caputo Fractional Derivative. Commun. Appl. Math. Comput. 2, 1–29 (2020). https://doi.org/10.1007/s42967-019-00023-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42967-019-00023-y