Abstract
This study contributes to the discrete differential geometry of triangle meshes, in combination with discrete line congruences associated with such meshes. In particular we discuss when a congruence defined by linear interpolation of vertex normals deserves to be called a ‘normal’ congruence. Our main results are a discussion of various definitions of normality, a detailed study of the geometry of such congruences, and a concept of curvatures and shape operators associated with the faces of a triangle mesh. These curvatures are compatible with both normal congruences and the Steiner formula.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The system of lines orthogonal to a surface (called the normal congruence of that surface) has close relations to the surface’s curvatures and is a well studied object of classical differential geometry, see e.g. [14]. It is quite surprising that this natural correspondence has not been extensively exploited in discrete differential geometry: most notions of discrete curvature are constructed in a way not involving normals, or involving normals only implicitly. There are however applications such as support structures and shading/lighting systems in architectural geometry where line congruences, and in particular normal congruences, come into play [21]. We continue this study, elaborate on discrete normal congruences in more depth and present a novel discrete curvature theory for triangle meshes which is based on discrete line congruences.
Contributions and overview. We organize our presentation as as follows. Section 2 summarizes properties of smooth congruences and elaborates on an important example arising in the context of linear interpolation of surface normals.
Section 3 first recalls discrete congruences following the work of Wang et al. [21] and then focuses on the interesting geometry of a new version of discrete normal congruences (defined over triangle meshes). We shed new light onto the behavior of linearly interpolated surface normals and discuss the problem of choosing vertex normals.
In Sect. 4, discrete normal congruences lead to a curvature theory for triangle meshes which has many analogies to the classical smooth setting. Unlike most other concepts of discrete curvature, it assigns values of the curvatures (principal, mean, Gaussian) to the faces of a triangle mesh. We discuss internal consistency of this theory and show by examples (Sect. 5), that it is well suited for curvature estimation and other applications.
Previous work. Smooth line congruences represent a classical subject. An introduction may be found in the monograph by Pottmann and Wallner [16]. Discrete congruences have appeared both in discrete differential geometry and geometry processing. Let us first mention contributions which study congruences based on triangle meshes: A computational framework for normal congruences and for estimating focal surfaces of meshes with known or estimated normals has been presented by Yu et al. [22]. The paper by Wang et al. [21] is described in more detail below.
Congruences associated with quad meshes are discrete versions of parametrized congruences associated with parametrized surfaces. In particular, the so-called torsal parametrizations are discussed from the integrable systems perspective by Bobenko and Suris [3]. An earlier contribution in this direction is due to Doliwa et al. [6]. These special parametrizations also occur as node axes in torsion-free support structures in architectural geometry [12, 15, 17].
Curvatures of triangle meshes are a well studied subject. One may distinguish between numerical approximation schemes (such as the jet fitting approach [4] or integral invariants [18]) on the one hand, and extensive studies from the discrete differential geometry perspective on the other hand. Without going into any detail we mention that these include discrete exterior calculus [5], the geometry of offset-like sets and distance functions [13], or various ways of defining shape operators [8, 9]. Naturally, also Yu et al. [22] address this topic when studying discrete normal congruences and focal surfaces. We present here yet another definition of curvatures for triangle meshes which is based on discrete normal congruences, and which is at the same time motivated by the Steiner formula (which also plays an important role in [2, 13, 15]).
2 Smooth Line Congruences
The introduction into line congruences in this section follows the paper by Wang et al. [21]. A line congruence  is a smooth 2D manifold of lines described locally by lines L(u, v) which connect corresponding points \({\mathbf a}(u,v)\) and \({\mathbf b}(u,v)\) of two surfaces. With \({\mathbf e}(u,v)={\mathbf b}(u,v)-{\mathbf a}(u,v)\) indicating the direction of the line L(u, v) (see Fig. 1), we employ the volumetric parametrization
is a smooth 2D manifold of lines described locally by lines L(u, v) which connect corresponding points \({\mathbf a}(u,v)\) and \({\mathbf b}(u,v)\) of two surfaces. With \({\mathbf e}(u,v)={\mathbf b}(u,v)-{\mathbf a}(u,v)\) indicating the direction of the line L(u, v) (see Fig. 1), we employ the volumetric parametrization
Any 1-parameter family  of lines results in a ruled surface \({\mathbf r}(t,\lambda )= {\mathbf x}(u(t),v(t),\lambda )\) contained in the congruence. We are particularly interested in developable ruled surfaces: The developability condition reads
of lines results in a ruled surface \({\mathbf r}(t,\lambda )= {\mathbf x}(u(t),v(t),\lambda )\) contained in the congruence. We are particularly interested in developable ruled surfaces: The developability condition reads
if we use subscripts to indicate differentiation and square brackets for the determinant. Equation (1) tells us that for any (u, v) there are up to two so-called torsal directions \(u_t:v_t\) which belong to developable surfaces. This behaviour is quite analogous to the fact that for any point in a smooth surface there are two principal tangent directions which belong to principal curvature lines. By integrating the torsal directions one creates ruled surfaces which are developable, which is analogous to finding principal curvature lines by integrating principal directions.
(a) A line congruence  is described by a surface \({\mathbf a}(u,v)\), and direction vectors \({\mathbf e}(u,v)\). (b) Developables
is described by a surface \({\mathbf a}(u,v)\), and direction vectors \({\mathbf e}(u,v)\). (b) Developables  ,
,  contained in
contained in  . The set of all regression curves \(c_i\) of these developables makes up the focal sheets \(F_1\), \(F_2\) of the congruence (here only \(F_1\) is shown). The tangent planes of
. The set of all regression curves \(c_i\) of these developables makes up the focal sheets \(F_1\), \(F_2\) of the congruence (here only \(F_1\) is shown). The tangent planes of  ,
,  along the common line are the torsal planes or focal planes of that line. These images are taken from [21]
along the common line are the torsal planes or focal planes of that line. These images are taken from [21]
Normal Congruences.
The normals of a surface constitute the normal congruence of that surface. For such congruences the analogy between torsal directions and principal directions mentioned above is actually an equality: The surface normals along a curve form a developable surface if and only if that curve is a principal curvature line [14].
The reference surface \({\mathbf a}(u,v)\) might be the base surface the lines of  are orthogonal to, but this does not have to be the case. The congruence does not change if the reference surface is changed to \({\mathbf a}^*(u,v)={\mathbf a}(u,v)+\lambda (u,v) {\mathbf e}(u,v)\), so deciding whether or not
are orthogonal to, but this does not have to be the case. The congruence does not change if the reference surface is changed to \({\mathbf a}^*(u,v)={\mathbf a}(u,v)+\lambda (u,v) {\mathbf e}(u,v)\), so deciding whether or not  is a normal congruence depends on existence of an alternative reference surface \({\mathbf a}^*\) orthogonal to the lines of
is a normal congruence depends on existence of an alternative reference surface \({\mathbf a}^*\) orthogonal to the lines of  , i.e., \(\langle {\mathbf e},{\mathbf a}^*_u\rangle =\langle {\mathbf e},{\mathbf a}^*_v\rangle =0\). Assuming without loss of generality that \(\Vert {\mathbf e}(u,v)\Vert =1\) and using \(\langle {\mathbf e},{\mathbf e}_u \rangle =\langle {\mathbf e},{\mathbf e}_v \rangle =0\) the orthogonality condition reduces to \( \lambda _u = - \langle {\mathbf a}_u,{\mathbf e}\rangle \), \(\lambda _v = - \langle {\mathbf a}_v,{\mathbf e}\rangle \). This PDE for the function \(\lambda \) has a solution if and only if the integrability condition \(\lambda _{uv}=\lambda _{vu}\) holds. It is easy to see that this is equivalent to
, i.e., \(\langle {\mathbf e},{\mathbf a}^*_u\rangle =\langle {\mathbf e},{\mathbf a}^*_v\rangle =0\). Assuming without loss of generality that \(\Vert {\mathbf e}(u,v)\Vert =1\) and using \(\langle {\mathbf e},{\mathbf e}_u \rangle =\langle {\mathbf e},{\mathbf e}_v \rangle =0\) the orthogonality condition reduces to \( \lambda _u = - \langle {\mathbf a}_u,{\mathbf e}\rangle \), \(\lambda _v = - \langle {\mathbf a}_v,{\mathbf e}\rangle \). This PDE for the function \(\lambda \) has a solution if and only if the integrability condition \(\lambda _{uv}=\lambda _{vu}\) holds. It is easy to see that this is equivalent to
It is not difficult to see that (2) is equivalent to the condition that developables contained in  intersect at right angles.
intersect at right angles.
Focal surfaces and focal planes.
Loosely speaking, an intersection point of a line in  with an infinitesimally neighbouring line produces a focal point of the congruence
with an infinitesimally neighbouring line produces a focal point of the congruence  . The rigorous definition of focal point is a point \({\mathbf x}(u,v,\lambda )\) where the derivatives of \({\mathbf x}\) are not linearly independent: One gets the condition
. The rigorous definition of focal point is a point \({\mathbf x}(u,v,\lambda )\) where the derivatives of \({\mathbf x}\) are not linearly independent: One gets the condition
i.e., up to two focal points per line. It is not difficult to see that such singularities are exactly the singularities of developables contained in  , see Fig. 1b. For this reason, the tangent planes of developables contained in
, see Fig. 1b. For this reason, the tangent planes of developables contained in  are called focal planes as well as torsal planes. Such a focal plane/torsal plane is spanned by a line L(u, v) together with a torsal direction.
are called focal planes as well as torsal planes. Such a focal plane/torsal plane is spanned by a line L(u, v) together with a torsal direction.
For normal congruences, the focal points are precisely the principal centers of curvature; they exist always unless one of the principal curvatures is zero. In each point of the surface, the focal plane (i.e., torsal plane) is spanned by the surface normal and a principal tangent.
Example: Congruences defined by linear interpolation.
Congruences of the special form
play an important role, both for us and in other places: for example, the set of lines described by such a congruence is the one generated by Phong shading, when one linearly interpolates vertex normals in a triangle.
Congruences defined by a “linear” volumetric parametrization \({\mathbf x}(u,v,\lambda )\) turn out to be useful for linear interpolation of triangle meshes, but they have counter-intuitive properties. (a) Planes \(P_\lambda \) defined by \(\lambda = \mathrm{{const}}\) are visualized as triangles. Interestingly, all of these triangles contain a planar developable  with a parabola \(r_\lambda \) as curve of regression. In particular the red triangle \(P_{\lambda _1}\) represents a torsal plane for the blue line \(L(\frac{1}{3}, \frac{1}{3})\) which connects the barycenters of triangles \(P_\lambda \). The image further shows many lines \(P_{\lambda _1}\cap P_\beta \), of the planar developable
with a parabola \(r_\lambda \) as curve of regression. In particular the red triangle \(P_{\lambda _1}\) represents a torsal plane for the blue line \(L(\frac{1}{3}, \frac{1}{3})\) which connects the barycenters of triangles \(P_\lambda \). The image further shows many lines \(P_{\lambda _1}\cap P_\beta \), of the planar developable  . (b) The focal surface F of
. (b) The focal surface F of  agrees with the envelope of the family of planes \(P_{\lambda }\). It is in general the tangent surface of a cubic polynomial curve \({\mathbf r}\). We show in red and yellow the two sheets of this tangent surface F which are separated by the regression curve \({\mathbf r}\). We also indicate the point of tangency \(T_\lambda \) where \(P_\lambda \) touches \({\mathbf r}\). The hyperbolic congruence lines (those which are contained in two focal planes) are bitangents of the focal surface, i.e., they touch F in two points. The regression parabolas \(r_\lambda \) are contained in F and are obtained by intersecting F with one of its tangent planes \(P_{\lambda }\)
agrees with the envelope of the family of planes \(P_{\lambda }\). It is in general the tangent surface of a cubic polynomial curve \({\mathbf r}\). We show in red and yellow the two sheets of this tangent surface F which are separated by the regression curve \({\mathbf r}\). We also indicate the point of tangency \(T_\lambda \) where \(P_\lambda \) touches \({\mathbf r}\). The hyperbolic congruence lines (those which are contained in two focal planes) are bitangents of the focal surface, i.e., they touch F in two points. The regression parabolas \(r_\lambda \) are contained in F and are obtained by intersecting F with one of its tangent planes \(P_{\lambda }\)
We consider the planes “\(P_\alpha \)” which are defined as the set of all points \({\mathbf x}(u,v,\alpha )\), and we study the affine mappings
The lines L(u, v) of the congruence are precisely the lines which connect points \({\mathbf x}(u,v,\alpha )\in P_\alpha \) and \({\mathbf x}(u,v,\beta )\in P_\beta \). These congruences are studied e.g. in [16, Ex. 7.1.2]. Let us summarize some of their properties, which are illustrated by Fig. 2.
-
(i)
Each intersection line \(L = P_{\alpha }\cap P_{\beta }\) of two planes in the family \(P_{\lambda }\) is contained in the congruence
 . This follows from the fact that L is spanned by the points \(X=\phi _{\alpha \beta }^{-1}(L)\cap L\) and \(\phi _{\alpha \beta }(X)=L\cap \phi _{\alpha \beta }(L)\).
. This follows from the fact that L is spanned by the points \(X=\phi _{\alpha \beta }^{-1}(L)\cap L\) and \(\phi _{\alpha \beta }(X)=L\cap \phi _{\alpha \beta }(L)\). -
(ii)
The lines \(P_\alpha \cap P_\beta \) with \(\alpha \) fixed, constitute a developable surface
 which is planar and contained in \(P_\alpha \) (in general, it is the tangent surface of a parabola \(r_\alpha \)).
which is planar and contained in \(P_\alpha \) (in general, it is the tangent surface of a parabola \(r_\alpha \)). -
(iii)
For properties of the focal surface, see Fig. 2.
3 Discrete Normal Congruences
Wang et al. [21] define discrete congruences by means of correspondences between combinatorially equivalent triangle meshes A, B with vertices \(\{{\mathbf a}_i\}\) and \(\{{\mathbf b}_i\}\). Each pair of corresponding triangles \({\mathbf a}_i{\mathbf a}_j{\mathbf a}_k\) and \({\mathbf b}_i{\mathbf b}_j{\mathbf b}_k\) defines, via linear interpolation, a piece of a smooth line congruence of the kind described by Eq. (4):
If the domain is restricted to \(u\ge 0\), \(v\ge 0\), \(u+v\le 1\), then the correspondence \({\mathbf x}(u,v,0)\longmapsto {\mathbf x}(u,v,1)\) is precisely the affine mapping of triangle \({\mathbf a}_i{\mathbf a}_j{\mathbf a}_k\) to triangle \({\mathbf b}_i{\mathbf b}_j{\mathbf b}_k\). Equations (1) and (3) serve to compute torsal directions and focal points of this congruence, and also to trace the developables contained in this congruence (see Fig. 3).
A piecewise-linear correspondence between meshes A and B defines a piecewise-smooth congruence  . (a) Integrating torsal directions yields corresponding polylines in meshes A and B. (b) Connecting corresponding points of those two polylines yields a piecewise-flat developable
. (a) Integrating torsal directions yields corresponding polylines in meshes A and B. (b) Connecting corresponding points of those two polylines yields a piecewise-flat developable  . These images are taken from [21]
. These images are taken from [21]
Discrete normal congruences—Version 1.
It is not straightforward to define which correspondence between triangle meshes defines a normal congruence. Firstly this is because congruences of the form (4) are never normal except for degenerate cases. Secondly such a normal congruence would automatically lead to a good definition of constant-distance offset mesh of a triangle mesh which is lacking so far.
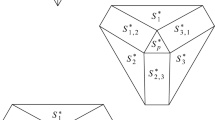
We discuss two suitable definitions of “normal congruence” and start with a version already published. Wang et al. [21] require normality to hold only in the barycenters of faces (i.e., they require that Eq. (2) holds for barycenters of faces), see Fig. 4. Figure 5 shows an example demonstrating the efficiency of this definition. Proposition 3.1 below gives an equivalent analytic condition.
Congruences defined by the piecewise-affine correspondence of meshes A, B can be called discrete-normal, if the normality condition is fulfilled for barycenters of faces. This figure also illustrates the auxiliary projection used by Eq. (7). This normality condition is called ‘version 1 normality’ here (image taken from [21])
We demonstrate that Eq. (7) is a working definition of normality: Given a triangle mesh \(\{{\mathbf a}_i\}\) (white), we find unit vectors \({\mathbf e}_i\) by optimizing for shading effects according to Wang et al. [21] under the normality constraint (7). Subsequently we check if a triangle mesh \(\{{\mathbf a}_i^*\}\) orthogonal to the congruence can be found. We let \({\mathbf a}_i^*={\mathbf a}_i + \lambda _i {\mathbf e}_i\) and solve for \(\lambda _i\) such that the faces of the new mesh are orthogonal to the congruence in their barycenters. The result of this computation yields a mesh \(\{{\mathbf a}_i^*\}\) (yellow) where face normals and congruence lines (in face barycenters) differ by an angle \(\beta \), which assumes a maximum of \(4.1^\circ \), a mean of \(0.9^\circ \), and a median of \(0.8^\circ \). Instead of the mesh computed here, any constant-distance offset would have been a solution as well. We chose one which lies at a small distance from the original mesh
Proposition 3.1
Consider two combinatorially equivalent triangle meshes and the line congruence  defined by the piecewise-linear correspondence of faces. For each pair \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\), \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\) of corresponding faces perform orthogonal projection in direction of the line which connects their respective barycenters, yielding triangles \(\bar{\mathbf a}_1\bar{\mathbf a}_2\bar{\mathbf a}_3\), \(\bar{\mathbf b}_1\bar{\mathbf b}_2\bar{\mathbf b}_3\). Then
defined by the piecewise-linear correspondence of faces. For each pair \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\), \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\) of corresponding faces perform orthogonal projection in direction of the line which connects their respective barycenters, yielding triangles \(\bar{\mathbf a}_1\bar{\mathbf a}_2\bar{\mathbf a}_3\), \(\bar{\mathbf b}_1\bar{\mathbf b}_2\bar{\mathbf b}_3\). Then  is normal in the barycenters of the two faces if and only if the following analogue of (2) holds:
is normal in the barycenters of the two faces if and only if the following analogue of (2) holds:
It is sufficient that these conditions hold for at least one choice of indices \(i,j,k\in \{1,2,3\}\), \(i\ne j\ne k\).
Discrete normal congruences—Version 2.
There is an obvious analogy between conditions (2) and (7): they express normality in the smooth and discrete cases respectively. However Eq. (7) is not entirely satisfying as a definition since it involves a projection operator. It is therefore natural to define discrete-normality by the following two equations which replace Eqs. (6), (7):
We will show that theses conditions are suitable to define normality of discrete congruences defined by a correspondence of triangle meshes. Besides numerical experiments (see later), we show geometric properties of congruences which fulfill these conditions. The first property is a discrete version of the following two facts (i) A normal congruence  has a 1-parameter family of surfaces orthogonal to it, and (ii) for any point in such a surface there are 3 mutually orthogonal planes spanned by the normal and the two principal directions. We show that in the discrete-normal case, there are analogous principal trihedra:
has a 1-parameter family of surfaces orthogonal to it, and (ii) for any point in such a surface there are 3 mutually orthogonal planes spanned by the normal and the two principal directions. We show that in the discrete-normal case, there are analogous principal trihedra:
Proposition 3.2
Consider two combinatorially equivalent triangle meshes and the line congruence  defined by the piecewise-affine correspondence of faces, and consider in particular one such pair \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\), \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\) of corresponding faces. In the generic case, the normality condition (6*) implies the following property:
defined by the piecewise-affine correspondence of faces, and consider in particular one such pair \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\), \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\) of corresponding faces. In the generic case, the normality condition (6*) implies the following property:
For each plane \(P_{\lambda }\) spanned by the vertices \((1-\lambda ){\mathbf a}_i + \lambda {\mathbf b}_i\) there is a congruence line \(N_\lambda = L(u_\lambda ,v_\lambda )\) such that the two focal planes of that line together with \(P_\lambda \) form a trihedron of mutually orthogonal planes.
The meaning of “generic” is discussed in the proof.
Proof
Generically, vectors \({\mathbf e}_i={\mathbf b}_i-{\mathbf a}_i\) are linearly independent, so we can express a normal vector \({\mathbf n}\) of the triangle \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) (which spans \(P_0\)) as a linear combination \({\mathbf n}=\sum _{i=1}^3\alpha _i{\mathbf e}_i\). Generically, \(\sum \alpha _i\ne 0\), so by multiplying \({\mathbf n}\) with a factor we can achieve \(\sum \alpha _i=1\) and by relabeling the coefficients \(\alpha _i\) we get \({\mathbf n}= (1-u-v){\mathbf e}_1 + u{\mathbf e}_2 + v{\mathbf e}_3\). Then Equation (5) shows that the line L(u, v) is orthogonal to \(P_0\).
Consider the affine correspondence of triangles \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) and \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\) followed by orthogonal projection onto \(P_0\). A vertex \({\mathbf a}_i\) is mapped to \(\bar{\mathbf b}_i={\mathbf b}_i+\lambda _i{\mathbf n}\). There is a linear mapping \(\alpha \) with \(\alpha ({\mathbf a}_i-{\mathbf a}_j)=\bar{\mathbf b}_i-\bar{\mathbf b}_j\). It is clear from Fig. 3 that the eigenvectors of \(\alpha \) indicate the directions of torsal planes through the line L(u, v). Conditions (6*), (7*) imply
i.e., symmetry of \(\alpha \) and orthogonality of eigenvectors of \(\alpha \). This shows orthogonality of torsal planes and verifies the statement for the case \(\lambda =0\). The case \(\lambda =1\) is analogous, since condition (6*) is invariant if we replace \({\mathbf a}_i\) by \({\mathbf b}_i\) and vice versa. For all other values \(\lambda \ne 1\) we note that replacing vertices \({\mathbf b}_i\) by vertices \({\mathbf a}_i+\lambda {\mathbf e}_i\) inflicts the change \({\mathbf e}_i\rightarrow \lambda {\mathbf e}_i\) without changing \({\mathbf a}_i\), which does not affect the normality condition (7*).
The “principal” trihedra mentioned in Proposition 3.2, when moved to the origin, lie tangent to a so-called Monge cone. Since these planes rotate about an entire cone as the interpolation parameter \(\lambda \) varies, one cannot without restrictions interpret these principal trihedra as tangent planes plus principal planes of an offset family of surfaces. Such an interpretation is valid only for small \(\lambda \)
As illustrated by Fig. 2, congruences defined by the affine correspondence of triangles have counter-intuitive properties: The planes \(P_\lambda \) generated by linear interpolation of the defining triangles at the same time are the focal planes of  (and vice versa) since any \(P_\lambda \) carries the developable surface generated by the lines \(\{P_\lambda \cap P_\alpha \}_{\alpha \in \mathbb R}\). The torsal planes \(P_\lambda \) are tangent to the focal surface F of
(and vice versa) since any \(P_\lambda \) carries the developable surface generated by the lines \(\{P_\lambda \cap P_\alpha \}_{\alpha \in \mathbb R}\). The torsal planes \(P_\lambda \) are tangent to the focal surface F of  . It is known that F is the tangent surface of a cubic polynomial curve, cf. [16, Ex. 7.1.2]. Proposition 3.2 now tells us that this curve has infinitely many triples of mutually orthogonal tangent planes. Translating these planes (the principal trihedra) through the origin, they become tangent planes of the directing cone of F, which is a quadratic cone. This cone is quadratic and must likewise have infinitely many orthogonal circumscribed trihedra. It is therefore a so-called Monge cone, see Fig. 6.
. It is known that F is the tangent surface of a cubic polynomial curve, cf. [16, Ex. 7.1.2]. Proposition 3.2 now tells us that this curve has infinitely many triples of mutually orthogonal tangent planes. Translating these planes (the principal trihedra) through the origin, they become tangent planes of the directing cone of F, which is a quadratic cone. This cone is quadratic and must likewise have infinitely many orthogonal circumscribed trihedra. It is therefore a so-called Monge cone, see Fig. 6.
There is a phenomenon in geometry, called porism, cf. [7]. It refers to situations where existence of one object of a certain kind implies existence of an entire 1-parameter family of such objects. Monge cones are an instance of a porism: If a quadratic cone has one circumscribed orthogonal trihedron, then one can move this trihedron around the cone while it remains tangential. This fact is classical knowledge in projective geometry, see e.e. [1, pp. 33–34].
The same porism is hidden in the proof of Proposition 3.2: The normality condition (6*) was equivalent to existence of the principal trihedron associated with \(P_0\), but it also implied existence of the trihedron for all \(P_\lambda \).
Details on principal trihedra in discrete-normal congruences.
We wish to interpret the three mutually orthogonal planes referred to by Proposition 3.2 as the tangent plane and principal planes of a surface. In particular the normal vector \({\mathbf n}_\lambda \) of \(P_\lambda \) shall be the normal vector, and the line \(N_\lambda \) shall be the surface normal, while the torsal planes should represent the principal directions. In order to understand better the behaviour of the objects involved, we study the volumetric parametrization according to Eq. (4) in an adapted coordinate system: the plane \(P_0\) is the xy plane, and the two torsal planes associated with it shall be the xz and zy planes. Since the affine correspondence between planes \(P_0,P_1\) may be defined by any pair of corresponding triangles, we choose \({\mathbf a}_1={\mathbf o}\), \({\mathbf a}_2=(1,0,0)\), \({\mathbf a}_3=(0,1,0)\). We may still change the plane \(P_1\) without changing the congruence, so we choose \({\mathbf b}_1=(0,0,1)\). The vertices \({\mathbf b}_2,{\mathbf b}_3\) must lie in the xy and xz planes because of our assumption on the torsal planes. Thus we get
We will later interpret \(\kappa _1,\kappa _2\) as principal curvatures and vectors (1, 0, 0) and (0, 1, 0) as principal directions. Obviously, they are eigenvectors of the linear map \(\alpha \) which occurs in the proof of Proposition 3.2. The plane \(P_\lambda \) is given as
This is a cubic family of planes. Translating them through the origin yields the planes \(n_{1,\lambda } x_1 + n_{2,\lambda } x_2 + n_{3,\lambda } x_3 = 0\), which are tangent planes of the tangent cone illustrated in Fig. 6. Since the plane coefficients satisfy the quadratic equation \( (\kappa _1-\kappa _2)n_1n_2-an_2n_3+bn_1n_3=0\), it is indeed a quadratic cone.Footnote 1
We now look for a line \(L(u_\lambda ,v_\lambda )\) orthogonal to \(P_\lambda \). The direction of L(u, v) can be read off (8), so the condition \(L(u_\lambda ,v_\lambda )\parallel {\mathbf n}_\lambda \) reads
In particular we see that the curve \({\mathbf x}(u_\lambda ,v_\lambda ,0)\), consisting of all points \(N_\lambda \cap P_0\), is a conic. In fact, for every \(\alpha \), the curve \(\{N_\lambda \cap P_\alpha \}_{\lambda \in \mathbb R}\) is a conic it corresponds to the curve \(N_\lambda \cap P_0\) under the affine mapping \(\phi _{0\alpha }:{\mathbf x}(u,v,0)\mapsto (u,v,\alpha )\), see Fig. 7a. The surface of all \(N_\lambda \)’s is then algebraic of 4\(^{\circ }\).
Behaviour of the principal trihedron and the normal \(N_\lambda \) of planes \(P_\lambda \) in a congruence defined by the affine correspondence between two triangles. (a) The normals \(N_\lambda \) (green) intersect the plane \(P_0\) in the points \({\mathbf c}(u_\lambda ,v_\lambda ,0)\) of a conic (red). (b) As \(\lambda \) changes, the apex \({\mathbf c}_\lambda ={\mathbf x}(u_\lambda ,v_\lambda ,\lambda )\) of the principal trihedron (yellow) moves along a straight straight line (blue). The ruled surfaces traced out by the edges of the trihedron are shown; their union forms one algebraic ruled surface of degree four
Let us now compute the “apex” \({\mathbf c}_\lambda =N_\lambda \cap P_\lambda ={\mathbf x}(u_\lambda ,v_\lambda ,\lambda )\) of the principal trihedron: From
we see that \({\mathbf c}_\lambda \) moves on a straight line, but the parametrization of this line is cubic. Since the planes \(P_\lambda \) and the torsal planes stem from the same 1-parameter family of planes, any torsal plane will play the role of \(P_{\lambda '}\) for another value \(\lambda '\); in total each orthogonal trihedron will occur three times, and each of the three edges of the trihedron will play the role of \(N_\lambda \) three times (see Fig. 7b). We summarize:
Proposition 3.3
If a congruence is defined by the affine correspondence between two triangles \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) and \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\) and satisfies the normality condition (6*), then its focal surface has a 1-parameter family of circumscribed ‘principal’ orthogonal trihedra whose apex moves on a straight line and whose edges form an algebraic surface of degree 4 which contains that line as a triple line.
The complicated geometry of these congruences reflects the difficulties in defining offset pairs of triangle meshes.
Discrete normal congruences — Version 3.
An elementary computation shows that either of the two conditions (6*), (7*) is implied by the stronger condition
when imposed on all three edges of a triangle. This third version of normality is a more direct expression of the orthogonality between triangle mesh and congruence: the edges \({\mathbf a}_i{\mathbf a}_j\) of the mesh are required to be orthogonal to the arithmetic mean of normal vectors \({\mathbf e}_i,{\mathbf e}_j\) at either endpoint of the edge.
Optimization of normal congruences. For a given mesh with vertices \({\mathbf a}_i\), a discrete-normal congruence, defined by unit vectors \({\mathbf e}_i\), has been found by global optimization such that one of the normality conditions considered here is fulfilled. Each of these conditions is linear, so optimization was done by least squares. It turns out that there is no substantial difference between Eqs. (6*) and (11). Faces are colored according to the angle \(\beta \) enclosed between the congruence line at the barycenter and the face’s normal there. We also give statistics on \(\beta \) for each figure
Comparison of definitions.
The various definitions of discrete normal congruences have different advantages. When one wants to design a normal congruence (as in Wang et al. [21]), version 1 may be better because it ensures orthogonality of focal planes in the part of the line congruence which is actually realized. Using version 2, orthogonal focal planes may occur outside the realized part. On the other hand, when using the normal congruence of a given surface, version 2 has the advantage that one plane of a principal frame contains the base mesh triangle; moreover discrete principal directions are orthogonal and lie in the plane of the triangle. Version 3 normality is not used here except for Fig. 8 where we show that imposing version 3 normality leads to results comparable to version 2. Since the weaker condition of version 2 is sufficient to achieve the same results, it is not necessary to impose version 3 normality.
4 Curvatures of Faces of Triangle Meshes
Recall that a smooth normal congruence  possesses a surface A orthogonal to the lines of
possesses a surface A orthogonal to the lines of  . Then automatically all offsets \(A^t\) also lie orthogonal to
. Then automatically all offsets \(A^t\) also lie orthogonal to  . We assume labeling of offsets such that surfaces \(A^t\), \(A^s\) are at constant distance \(|t-s|\) from each other. Then corresponding infinitesimal surface area elements “\(\mathord {{ {dA}}}^t(u,v)\)” obey Steiner’s formula
. We assume labeling of offsets such that surfaces \(A^t\), \(A^s\) are at constant distance \(|t-s|\) from each other. Then corresponding infinitesimal surface area elements “\(\mathord {{ {dA}}}^t(u,v)\)” obey Steiner’s formula
where H and K denote mean and Gaussian curvature of the surface \(A^0\), respectively. The sign of H depends on the unit normal vector field; in our case the unit normal vector field points from \(A^0\) to the surfaces \(A^t\) with \(t>0\).
We now return to a discrete congruence  defined by the piecewise-linear correspondence between triangle meshes A, B. Assuming A, B approximate an offset pair of surfaces at distance 1, we consider corresponding faces \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) and \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\). We write \({\mathbf b}_i = {\mathbf a}_i + {\mathbf e}_i\), where the vectors \({\mathbf e}_i\) approximate unit normal vectors of the mesh A. An offset mesh at distance approximately t then has vertices and faces
defined by the piecewise-linear correspondence between triangle meshes A, B. Assuming A, B approximate an offset pair of surfaces at distance 1, we consider corresponding faces \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) and \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\). We write \({\mathbf b}_i = {\mathbf a}_i + {\mathbf e}_i\), where the vectors \({\mathbf e}_i\) approximate unit normal vectors of the mesh A. An offset mesh at distance approximately t then has vertices and faces
We further assume that the congruence  is a normal congruence (which we have defined in two different ways).
is a normal congruence (which we have defined in two different ways).
-
If
 is normal in the sense of Eqs. (6) and (7), then we apply the projection mentioned in Proposition 3.1, resulting in vertices \(\bar{\mathbf a}_1\bar{\mathbf a}_2\bar{\mathbf a}_3\), \(\bar{\mathbf b}_1\bar{\mathbf b}_2\bar{\mathbf b}_3\). The projection is in the direction of a certain unit vector \({\mathbf n}\).
is normal in the sense of Eqs. (6) and (7), then we apply the projection mentioned in Proposition 3.1, resulting in vertices \(\bar{\mathbf a}_1\bar{\mathbf a}_2\bar{\mathbf a}_3\), \(\bar{\mathbf b}_1\bar{\mathbf b}_2\bar{\mathbf b}_3\). The projection is in the direction of a certain unit vector \({\mathbf n}\). -
As an alternative, the congruence may be normal in the sense of Eqs. (6*), (7*). Here we consider orthogonal projection onto the plane \(P_0\) which contains \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\). This projection results in vertices \(\bar{\mathbf a}_i={\mathbf a}_i\) and \(\bar{\mathbf b}_i\). The projection is in direction of the unit normal vector \({\mathbf n}={\mathbf n}_0\) of the plane \(P_0\).
We now study the behaviour of the area of the face \(\varDelta ^t\) as t changes. We do not measure the actual area, but apply the projection just mentioned. The area of projected triangles is measured via a determinant in the plane:
With the notation \(\bar{\mathbf a}_{ij} = \bar{\mathbf a}_i-\bar{\mathbf a}_j\), \(\bar{\mathbf b}_{ij} = \bar{\mathbf b}_i-\bar{\mathbf b}_j\), \(\bar{\mathbf e}_{ij} = \bar{\mathbf b}_{ij}-\bar{\mathbf a}_{ij}\) we get
Discrete curvatures and shape operator.
The obvious similarity of this relation with (12) immediately leads to a definition of the mean curvature H and the Gauss curvature K of the face \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) under consideration:
Principal curvatures \(\kappa _1,\kappa _2\) are defined by the relations
Completing the analogy with the smooth case, we define a shape operator \(\varLambda \) as the linear mapping which maps
Recall that the bar indicates projection (which in turn depends on which version of “normality” we employ). In analogy to the smooth case, principal directions are given by the focal planes of the congruence  . All these notions fit together:
. All these notions fit together:
Proposition 4.1
The eigenvalues of the shape operator \(\varLambda \) are the principal curvatures \(\kappa _1,\kappa _2\), and its trace and determinant are given by 2H and K, respectively. Eigenvectors of \(\varLambda \) indicate the principal directions.
Proof
We first show the statement for ‘version 2’ normality. Recall the linear mapping \(\alpha \) in the proof of Proposition 3.2 which maps \(\bar{\mathbf a}_i-\bar{\mathbf a}_j\mathop {\longmapsto }\limits ^{\alpha }(\bar{\mathbf a}_i+\bar{\mathbf e}_i) - (\bar{\mathbf a}_j+\bar{\mathbf e}_j)\). Since by construction, \(\varLambda =\mathord {\mathrm{{id}}}-\alpha \), \(\varLambda \) has the same eigenvectors as \(\alpha \), i.e., the torsal directions. The statement about \(\mathop {\mathrm{{tr}}}\varLambda \) and \(\det \varLambda \) follows from the relations \( \det \varLambda = \frac{\det (\varLambda ({\mathbf x}),\varLambda ({\mathbf y}))}{\det ({\mathbf x},{\mathbf y})}\) and \(\mathop {\mathrm{{tr}}}\varLambda =\frac{\det (\varLambda ({\mathbf x}),{\mathbf y})+\det ({\mathbf x},\varLambda ({\mathbf y}))}{\det ({\mathbf x},{\mathbf y})}\) which generally hold for linear mappings of \(\mathbb R^2\). The statement about eigenvalues follows immediately.
For version 1 normality the proof is the same, only the bars have a different meaning. The mapping \(\alpha \) is also referred to in the proof of Proposition 3.1 in [21].
Since we have defined principal curvatures \(\kappa _1,\kappa _2\) implicitly via mean curvature H and Gauss curvature K, their relation to focal geometry is still unclear. In the smooth case, points at distance \(1/\kappa _i\) from the surface are focal points of the normal congruence. This property holds in the discrete case too, if we use version 2 normality:
Proposition 4.2
Consider a congruence with parametric representation \({\mathbf x}(u,v,\lambda )\) which is defined by the correspondence of two triangles \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) and \({\mathbf b}_1{\mathbf b}_2{\mathbf b}_3\). Assume that it is normal in the sense of Eq. (6*), and consider (in the notation of Proposition 3.2) the plane \(P_0\) which contains \({\mathbf a}_1{\mathbf a}_2{\mathbf a}_3\) and the corresponding normal \(L(u_0,v_0)\). Then the focal points of that line lie at distance \(1/\kappa _1\), \(1/\kappa _2\) from the plane \(P_0\), with \(\kappa _i\) as the principal curvatures, i.e., the focal points are precisely the points \({\mathbf x}(u_0,v_0,1/\kappa _i)\).
Proof
We consider the parametrization (8) which is with respect to an adapted coordinate system, so that \(u_0=0\) and \(v_0=0\). It is easy to see that the values \(\kappa _1,\kappa _2\) occurring there are indeed the principal curvatures. A simple computation shows that for the special case \(u=v=0\), the determinant of partial derivatives of \({\mathbf x}(u,v,\lambda )\) specializes to \( \mathopen [{\mathbf x}_u,{\mathbf x}_v,{\mathbf x}_\lambda \mathclose ] = (1-\lambda \kappa _1)(1-\lambda \kappa _2). \) Thus we have a singularity if \(\lambda =1/\kappa _i\).
Special cases.
An umbilic point is characterized by equality of principal curvatures, i.e., \(\kappa _1=\kappa _2=\kappa \). In this case some of the geometric objects discussed above simplify. E.g. the above-mentioned cubic family of planes becomes the set of tangent planes of a quadratic cone with vertex \((0,0,1/\kappa )\). Such an umbilic occurs every time two corresponding triangles \( {\mathbf a}_1 {\mathbf a}_2 {\mathbf a}_3\) and \({\mathbf b}_1 {\mathbf b}_2 {\mathbf b}_3\) are in homothetic position, but the converse is not true.
A parabolic point is characterized by one principal curvature, say \(\kappa _1\), being zero. In this case, Eq. (8) immediately shows that the congruence vectors \({\mathbf e}_1, {\mathbf e}_2, {\mathbf e}_3\) associated with vertices \({\mathbf a}_1, {\mathbf a}_2, {\mathbf a}_3\) are not linearly independent, so Proposition 3.2 does not apply. Along the x axis, the lines of the congruence are parallel to each other, which is in accordance with the fact that the focal point \((0,0,1/\kappa _1)\) has moved to infinity. The above-mentioned cubic family of planes is quadratic (in fact, it is the family of tangent planes of a parabolic cylinder).
Remark 4.3
We should mention that the approach to curvatures presented here carries over to relative differential geometry where the image of the Gauss map is not a sphere but a general convex body [19]. Another straightforward extension is to curvatures at vertices, which however does not lead to a shape operator in such a natural manner.
5 Results and Discussion
Numerical examples. Vertex normals of a mesh can be estimated (e.g. as area-weighted averages of face normals). Any such collection of sensible normals is not far away from being a “normal” congruence in our sense. By applying optimization, we can make it as normal as possible, meaning that (6) is fulfilled in the least-squares sense. Numerical experiments show that this improves the quality of the normal field (even if there are not enough d.o.f. to satisfy (6) fully if the vertices of the mesh are kept fixed). Since curvatures and the distribution of normals are inseparable, it makes sense to study curvatures not only as quantities derived from a mesh, but as quantities which arise naturally from the the result of the optimization procedure just mentioned. In this way the natural sensitivity of curvatures with respect to noise is moderated.
The basic task is, of course, the computation of a normal congruence for a given mesh. This is done via a standard optimization procedure, which is initialized from estimated vertex normals. We express the validity of the normality condition in terms of least squares, and minimize subject to the constraints that (in the terminology of previous sections), vectors \({\mathbf e}_i\) are of unit length. Figure 8 shows an example. In particular one can see that normality according to Eq. (6) (“version 1”) behaves differently from normality according to Eq. (6*) (“version 2”), while there is hardly any difference between conditions (6*) and (11).
Degrees of freedom and topology. When optimizing a normal congruence of a mesh with v vertices, e edges and f faces, we count 3v variables for the normals and \(f+v\) constraints. If a number b of boundary vertices is present, we fix the normals at the boundary, resulting in \(3(v-b)\) variables and \(f+(v-b)\) constraints, i.e., \(2v-f-2b\) d.o.f. Elementary manipulations show that
with \(\chi =f+v-e\) as the Euler characteristic. We see for meshes of sphere topology we can expect a unique solution, but topological features diminish the available degrees of freedom. If boundary normals are kept fixed, long boundaries diminish this freedom even more. By allowing vertices to move during optimization, we can achieve zero residual again, but of course a compromise has to be found between the quality of the normal congruence and the deviation of the mesh from its previous shape. Table 1 shows some numerical experiments.
Computing mean curvature H and Gaussian curvature K by means of normal congruences: “version 1” and “version 2” refer to normality defined by Eqs. (6) and (6*), respectively. Estimated normals are optimized so as to become a normal congruence which allows us to compute curvatures in faces. For comparison, curvatures computed by a 3rd order jet fit have been used, cf. [4]. The color scale is the same for each kind of curvature and each model, throughout the 3 methods of computation. One can hardly see any difference. For each mesh, normal congruences have been computed in the way employed for Fig. 8
We compute asymptotic lines and principal curvature lines of meshs by various means. For the figures of the first column, we have used the 3rd order jet fit method of [4]. For the second column, we used the method of normal cycles (see e.g. [20]). The 3rd and 4th column are computed using our the shape operators, where version 1 and version 2 refer to normality w.r.t. Eqs. (6), (6*), respectively. In both cases the normal congruence needed for defining the shape operator was obtained in the same way as for Fig. 8
Computing Curvatures. Once a normal congruence is available, we can compute curvatures (see Fig. 9) and we can integrate the field of principal curvature directions as well as the field of asymptotic directions (see Fig. 10 for an example). It must be said, however, that we do not want to compete with the many other methods for computing curvatures, and we do not regard the ability to compute curvatures a main result of this study.
Robustness by using normals. Fig. 11 demonstrates that considering a mesh and its normal congruence together allows us to handle optimization/smoothing in a stable way. After a mesh and its normals have been perturbed (Fig. 11b), an optimization procedure attempts to restore both. We use a target functional composed of a sum of least squares expressing condition (6*) and also the property of vectors \({\mathbf e}_i\) having length 1 (weight 1), proximity to the input data (weight 1/4), Laplacian fairing for the mesh (weight \(10^{-6}\)), Laplacian fairing for the normal vectors (weight \(10^{-4}\)) and compatibility between normal and mesh by penalizing deviation from orthogonality between congruence lines in mesh barycenters and face (weight \(10^{-4}\)). Figure 11c shows the repaired mesh.
Computing normals and principal curvature lines for noisy data. Subfigure a shows a triangulated cylinder and some of its principal curvature lines. In b the jet fit method has been used to obtain principal curves for data where noise has been added to both vertex coordinates and normals. Subfigure c shows the result of optimization applied to (b), which results in a smooth mesh equipped with a normal congruence. For c we again show the principal curvature lines computed by our method
Relevance for discrete differential geometry.
The idea of employing the Steiner formula for defining curvatures has proved very helpful in bringing together various different notions of curvature, and indeed, various different notions of discrete surfaces (like discrete minimal surfaces and discrete cmc surfaces) which were defined in a way not involving curvature directly but by other means like Christoffel duality. We refer to [2, 3] for more details. The theory presented in [2] is restricted to offset-like pairs of polyhedral surfaces where corresponding edges and faces are parallel. There are ongoing efforts to extend this theory to more general situations (we point to recent work on quad meshes [10] and on isothermic triangle meshes of constant mean curvature [11]). It is therefore remarkable that at least for the situation described here, triangle meshes allow an approach to curvatures and even a shape operator which is likewise guided by the Steiner formula, but without the rather restrictive property of parallelity (which for triangle meshes would be even more restrictive).
Future Research.
As to discrete differential geometry, it is still unclear how known constructions of special discrete surfaces relate to the curvatures defined here: For instance, it seems difficult to gain nice geometric properties from the condition vanishing mean curvature. Nevertheless one of the known constructions of discrete minimal surfaces might be equipped with a canonical normal congruence such that, when our theory is applied, mean curvature vanishes.
Further applications of line congruences have been discussed by Wang et al. [21], but there might be other examples of geometry processing tasks where the notion of line congruence, or even normal congruence, becomes relevant.
Notes
- 1.
The vector of coefficients \((n_1,n_2,n_3)\) of the equation of a plane is a normal vector of that plane. This shows that the orthogonal polar cone of the Monge cone fulfills the equation \((\kappa _1-\kappa _2)x_1x_2-ax_2x_3+bx_1x_3=0\). Since the Monge cone had many circumscribed orthogonal trihedra, its polar cone has many inscribed orthogonal frames. These frames are generated by translating the frames seen in Fig. 7b through the origin.
References
Baker, H.F.: Principles of Geometry, vol. II, 2nd edn. Cambridge University Press (1930)
Bobenko, A., Pottmann, H., Wallner, J.: A curvature theory for discrete surfaces based on mesh parallelity. Math. Annalen 348, 1–24 (2010)
Bobenko, A., Suris, Yu.: Discrete Differential Geometry: Integrable Structure. American Mathematical Society (2009)
Cazals, F., Pouget, M.: Estimating differential quantities using polynomial fitting of osculating jets. In: Kobbelt, L., Schröder, P., Hoppe, H. (eds.) Proceedings of Symposium on Geometry Processing, pp. 177–187. Eurographics Association (2003)
Desbrun, M., Meyer, M., Schröder, P., Barr, A.: Discrete differential-geometry operators for triangulated 2-manifolds. In: Visualization & Mathematics, vol. 3, pp. 35–57. Springer (2003)
Doliwa, A., Santini, P., Mañas, M.: Transformations of quadrilateral lattices. J. Math. Phys. 41, 944–990 (2000)
Dragović, V., Radnović, M.: Poncelet porisms and beyond. Birkhäuser, Basel (2011)
Grinspun, E., Gingold, Y., Reisman, J., Zorin, D.: Computing discrete shape operators on general meshes. Comput. Graph. Forum 25(3), 547–556 (2006). Proc. Eurographics
Hildebrandt, K., Polthier, K.: Generalized shape operators on polyhedral surfaces. Comput. Aided Geom. Des. 28, 321–343 (2011)
Hoffmann, T., Sageman-Furnas, A., Wardetzky, M.: A discrete parametrized surface theory in \(\mathbb{R}^3\). Int. Math. Res. Not. (2016), to appear
Lam, W.Y., Pinkall, U.: Isothermic triangulated surfaces. Math. Annalen (2016), to appear
Liu, Y., Pottmann, H., Wallner, J., Yang, Y.L., Wang, W.: Geometric modeling with conical meshes and developable surfaces. ACM Trans. Graphics 25(3), 681–689 (2006). Proc. SIGGRAPH
Morvan, J.M.: Generalized Curvatures. Springer (2008)
Porteous, I.R.: Geometric Differentiation for the Intelligence of Curves and Surfaces. Cambridge University Press (1994)
Pottmann, H., Liu, Y., Wallner, J., Bobenko, A., Wang, W.: Geometry of multi-layer freeform structures for architecture. ACM Trans. Graphics 26(3), # 65,1–11 (2007). Proc. SIGGRAPH
Pottmann, H., Wallner, J.: Computational Line Geometry. Springer (2001)
Pottmann, H., Wallner, J.: The focal geometry of circular and conical meshes. Adv. Comp. Math 29, 249–268 (2008)
Pottmann, H., Wallner, J., Huang, Q., Yang, Y.L.: Integral invariants for robust geometry processing. Comput. Aided Geom. Des. 26, 37–60 (2009)
Simon, U., Schwenck-Schellschmidt, A., Viesel, H.: Introduction to the affine differential geometry of hypersurfaces. TU Berlin & Science Univ, Tokyo (1992)
Sun, X., Morvan, J.M.: Curvature measures, normal cycles and asymptotic cones. Actes des recontres du C.I.R.M. 3(1), 3–10 (2013). Proc. “Courbure discrète: théorie et applications”
Wang, J., Jiang, C., Bompas, P., Wallner, J., Pottmann, H.: Discrete line congruences for shading and lighting. Comput. Graph. Forum 32(5), 53–62. Proc. Symp, Geometry Processing (2013)
Yu, J., Yin, X., Gu, X., McMillan, L., Gortler, S.: Focal surfaces of discrete geometry. In: Belyaev, A., Garland, M. (eds.) Proceedings of Symposium on Geometry Processing, pp. 23–32. Eurographics Association (2007)
Acknowledgments
The authors are grateful to Alexander Bobenko for fruitful discussions and to the anonymous reviewers for their suggestions. This research was supported by the DFG Collaborative Research Center, TRR 109, “Discretization in Geometry and Dynamics” through grants I705 and I706 of the Austrian Science Fund (FWF).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution-Noncommercial 2.5 License (http://creativecommons.org/licenses/by-nc/2.5/) which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.
Copyright information
© 2016 The Author(s)
About this chapter
Cite this chapter
Sun, X., Jiang, C., Wallner, J., Pottmann, H. (2016). Vertex Normals and Face Curvatures of Triangle Meshes. In: Bobenko, A. (eds) Advances in Discrete Differential Geometry. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-50447-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-662-50447-5_8
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-50446-8
Online ISBN: 978-3-662-50447-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)






 . This follows from the fact that L is spanned by the points
. This follows from the fact that L is spanned by the points  which is planar and contained in
which is planar and contained in 





 is normal in the sense of Eqs. (
is normal in the sense of Eqs. (

