Modelling of Landslide-Structure Interaction (LSI) Through Material Point Method (MPM)

Abstract

A novel numerical approach, namely Material Point Method (MPM), is applied to analyze the build-up of pore water pressure inside the landslide body during the impact against different types of structures. To this aim, the landslide soil is schematized as a two-phase elasto-plastic material, while the structural materials are assumed as one-phase elasto-plastic bodies. The complex Landslide-Structure Interaction (LSI) is simulated for different landslide scenarios, including the formation of “dead-zones” behind the structures and/or the run-up mechanisms, even including in some cases unacceptable displacements or the complete disruption of the impacted structure. Independent on site-specific conditions, it is shown that landslide pore water pressures undergo significant tempo-spatial evolution during a dynamic impact, meaning that a hydro-mechanical coupled approach is fully needed for an adequate LSI analysis.

1 Introduction

The impact of debris flows against rigid walls, obstacles, barriers, and similar types of protection structures, has been attracting the interest of practitioners and scientists since decades. There is in fact the practical challenge to adequately design such structures. In doing that, the inner complexity of flow-like landslides must be considered.

It is indeed a multi-scale and multi-phase problem.

• i) Multiscale problem: It is well known that shallow landslides may occur at several locations during a rainstorm. Thus, the so-called territorial (also named regional, or large-area) approaches are needed to assess the observed landslide source areas (back-analysis) or to forecast the potential landslide failure zones (forward-analysis). Regarding that, it is worth mentioning some pioneering works (Dietrich et al. 1998; SHALSTAB model), paving the way to enhanced approaches including unsaturated soil (Baum et al. 2008; Cuomo and Iervolino 2016; TRIGRS model), failure probability (Tofani et al. 2017; Cuomo et al. 2021a; HIRESSS model), soil liquefaction (Lizárraga et al. 2017). The propagation (even along large distances) of the flows is another demanding issue to be analyzed basically, because detailed and large Digital Terrain Model (DTM) must be used as input data to achieve realistic simulations of the field behavior. In addition (and related) to that, it is a significant computational effort needed, which has favored the fluorescence of many different (continuum-, discrete-, or combined) approaches. The interested readers can find details about Smooth Particle Hydrodynamics (Pastor et al. 2009; Cuomo et al. 2015), Discrete Element Method (Chen and Song 2021), Material Point Method (Yerro 2015; Cuomo et al. 2021b), and other methods in the scientific literature. For instance, Cuomo (2020) reviewed the engineering analysis methods applicable to detect the potential landslide source areas and the following propagation zones.

• ii) Multi-phase problem: Especially the propagation of flow-like landslides is affected by excess pore water pressures. Despite this feature, empirical propagation methods based on slope morphology, or more elaborated (still simplified) approaches have been used for years. The concept of apparent friction angle is useful in case of granular/debris landslide materials, allowing to analyze the landslide motion and the governing equations in terms of total stresses. It is a way to by-pass the computation of pore water pressure, if moderate changes happen during the process. A significant novelty was introduced by the so-called landslide propagation-consolidation model proposed by Hutchnison (1986), later enriched by Pastor and co-workers in the early 2000s. Nowadays, several hydro-mechanical coupled approaches exist for both landslide initiation and propagation modelling (Cuomo 2020).

2 Approaches for LSI Modelling

The landslide impact, more in general, the Landslide-Structure Interaction (LSI) is governed by the multi-scale and multi-phase features discussed before.

However, while practitioners have preferred (i) empirical approaches and they are looking forward to having available (ii) analytical approaches, researchers have also developed (iii) physical models and (iv) numerical approaches.

• i) Empirical approach: These approaches provide an estimation of the maximum impact pressure (or force). Some (hydro-static) methods require only the flow unit weight and thickness (Scotton and Deganutti 1997; Scheidl et al. 2013); other (hydro-dynamic) methods use as input the flow density and the square velocity of the flow (Bugnion et al. 2012; Canelli et al. 2012); other (mixed) methods consider both the static and the dynamic components of the flow (Arattano and Franzi 2003; Cui et al. 2015). None of them allow assessing the evolution of the impact force over the time. Recent research tried to overcome these limitations. Di Perna et al. (2022) proposed an enhanced empirical method, firstly calibrated via numerical analyses, then validated referring to a large dataset of real debris flows from China (Hong et al. 2015). This method allows estimating the impact duration (not only the peak impact pressure), which regulates the deformation of the protection barrier.

• ii) Analytical approach: Yong et al. (2019) proposed an analytical solution for estimating the sliding of a barrier under the impact of a boulder, both assumed as rigid, with the impact studied through the elastic collision principles. Li et al. (2021) proposed an analytical model to estimate the peak impact pressure that a debris flow exerts on a rigid barrier. Song et al. (2021) obtained an analytical model for evaluating the deflection of a flexible barrier (a net fixed to the ground) through the validation against experimental results of centrifuge tests. Ng et al. (2021a) proposed an analytical impact equation for the design of multiple rigid barriers, stressing that the height of the first barrier governs the impact dynamics of debris flow on the next barrier in a channel. Cuomo et al. (2022) casted an analytical method to simulate the inelastic collision of the impacting landslide and the protection barrier. From there, the landslide energy release and the deformation plus the eventual displacement of the barrier is determined.

• iii) Physical model: Flume experiments are a powerful, although expensive, tool to observe into details complex soil-structure behaviors. Bugnion et al. (2012), in their 41 m long experiments of hillslope debris flows, stated that pressures depend primarily on the flow speed, which in turn appears to depend on the grain-size and water content. Experiences from Hong Kong highlighted that a large flume model is needed to study the impact mechanisms of two-phase flows, as observed in a 28 m long flume (Ng et al. 2019, 2021b).

  Reduced-scale laboratory tests have been used to derive and validate the most common empirical formulations (Hübl et al. 2009; Scheidl et al. 2013).

• iv) Numerical approach: LSI has been studied through Eulerian methods (e.g., Moriguchi et al. 2009), Smoothed-Particle Hydrodynamics (SPH) (Bui and Fukagawa 2013) or Discrete Element Method (DEM) (Leonardi et al. 2016; Calvetti et al. 2017; Shen et al. 2018). Cuomo et al. (2021c, 2022) applied an advanced numerical code based on Material Point Method (MPM), i.e., the Anura 3D code (with recent enhancements developed by Deltares), to entirely reproduce the LSI including the mutual actions between the landslide and the barrier as well as the landslide propagation during the LSI, i.e., the eventual barrier overtopping of some part of the landslide volume.

For those structures behaving as “rigid” during the LSI, any of those approaches is useful. Whereas, if the impacted structure may undergo significant damage, numerical models are preferable, but they need careful calibration.

3 Damage and Protection

Within a framework of landslide risk mitigation, we may assume that an impacted structure can undergo: i) limited damage to non-structural elements, ii) damage to the structure (with eventual partial destruction), iii) collapse.

Examples of the cases (i) and (ii) are respectively provided in Figs. 1 and 2. The features of the flow-like landslides have been reviewed before.

Fig. 1

Example of damage to non-structural elements caused by the impact of flow-like landslides in the Sarno area, Campania, southern Italy, 1998 (from Mavrouli et al. 2014)

Fig. 2

Example of a building partially destroyed by a flow-like landslide occurred in the Cervinara area, Campania, southern Italy, 1999 (from Cascini et al. 2011)

Here it is worth point out that the structures impacted are typically constituted by bricks or concrete elements eventually reinforced with steel bars. It entails that complex 3D structural configurations should be analyzed, where linear and planar structural elements interact to develop proper resisting mechanisms. Nevertheless, the analysis of combined materials such bricks and mortar, or concrete and steel, requires a sound structural scheme to be defined, where the geometrical items (e.g., pillars, beams) and connections (hinges, joints) are modelled.

The occurrence of any damage scenario and its severity is the outcome of different factors combined. The type of urbanization (dense or sparse), the construction features (type, materials, age, etc.), the exposure (direct or limited) to the impact, the type of impact (frontal or lateral), and other site- or case-specific features. Thus, the assessment of potential damage to a structure requires analyses and zoning at detailed scale.

Reinforcing the structures against flow-like landslides impact is difficult to be pursued. The main limitation is that structures are conceived to bring their self-weight and the external loads, which are predominantly vertically oriented. Thus, providing additional resisting mechanisms against horizontal (or quasi-) actions is doable in practice only for special cases or for limited size/extension of the structure.

More often, the endangered structures are protected by means of concrete walls, blocks, or combinations of rigid-like vertical elements like baffles.

Reinforced Concrete (RC) walls are commonly used as protection measures in hilly areas to contain falling boulders and landslide debris, and the sliding displacement of these barriers is a key design issue when space is limited. RC walls are usually made as slab concrete dams, that can be reinforced with counterfort. For such slender constructions, the flow impact dynamics must be carefully evaluated, as the wall must retain the flowing material without tilting or without showing excessive displacements. For these reasons, the foundations of these structures are particularly large. In bedrock, the foundations are usually made by steel tension anchors (ribbed bars), while in loose deposits, the ground must sustain the weight of the concrete construction together with the loads generating from the impact (Barbolini et al. 2009). An example is provided in Fig. 3.

Fig. 3

Example of Reinforced Concrete (RC) wall used as diverting dam against snow avalanches at Odda, Norway (Barbolini et al. 2009)

An alternative can be a Mechanically Stabilized Earth (MSE) wall. In the context of landslide protection, they are also called Deformable Geosynthetics-Reinforced Barrier (DGRB), as they are composed of granular soil and geosynthetics reinforcement elements, such as high tenacity polyester (PET) geogrids (Cuomo et al. 2020a). These geostructures have been formerly investigated (Gioffrè et al. 2017; Cuomo et al. 2019) to reduce the runout (and the potential damage) of flow-like landslides, while they are typically used as deformable barriers against snow avalanches or rockfalls (Fig. 4).

Fig. 4

Example of MSE walls used as protection structures (Barbolini et al. 2009)

The stability of a DGRB is derived by the interaction of coarse material with the reinforcements, involving friction and tension resistances. The facing is relatively thin, with the primary function of preventing erosion of the structural backfill. The result is a massive structure that is flexible and can withstand various loads combinations. DGRB is an appropriate protection structure when a medium to very high kinetic energy event is expected, i.e., from a few hundred kilojoules to tens of megajoules (Descoeudres 1997). The other advantages are the low maintenance costs and the reduced visual impact since DGBR are greened (Brunet et al. 2009). Nevertheless, they are not appropriate on steeper slopes and their construction generally requires extensive space and accessibility for heavy vehicles.

The optimal location of the barriers (RC or MSE walls) is an issue. In fact, to minimize the height and length of the barrier (hence the cost), they must be located at the distal part of the propagation path so that flow velocity has reduced before; however, the barrier should be not so close to the structures to be protected.

What is really challenging is to find a mathematical framework to properly describe the so different materials and behavior of both (i) the flow-like landslide and (ii) the impacted structure.

One relatively new method, namely Material Point Method (MPM), allows simulating large deformations and displacements (with no restriction), that are typical features of both a flow-like landslide and a building structure under severe external loads such an impulsive impact.

4 Remarks on Material Point Method (MPM)

4.1 Framework

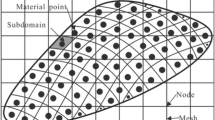
MPM can be considered a modification of the well-known FEM, and it is particularly suited for large deformations (Sulsky et al. 1995). The continuum body is schematized by a set of Lagrangian points, called material points (MPs). Large deformations are modelled by a set of MPs moving through a background mesh, which also covers the domain where the material is expected to move. The MPs carry all the physical properties of the continuum such as stress, strain, density, momentum, material parameters, and other state parameters, whereas the background mesh is used to solve the governing equations without storing any permanent information.

The interaction between phases (solid and liquid in a saturated soil) can be tracked through the “two-phase single-point” formulation (Jassim et al. 2013; Ceccato et al. 2018), where the liquid and the solid acceleration fields are the primary unknowns (Fern et al. 2019).

On the other hand, the so-called “one-phase single-point” formulation can be opportunely adopted for dry soils or for saturated soil in the simplified hypothesis that the ratio of pore water pressure divided by total stress is constant inside the deforming body and throughout the whole deformation process.

The contact between different bodies (flow-base, flow-barrier) is handled with a frictional contact algorithm. An improved contact algorithm, proposed by Martinelli and Galavi (2022), was used, being the velocity of the liquid phase corrected to prevent both inflow and outflow.

Moreover, the computational scheme proposed by Martinelli and Galavi (2022) is adopted to compute accurate reaction forces along contact surfaces, especially between non-porous structures and soils with high liquid pressures. The contact algorithm cannot be applied along the impacted sides of the barrier, therefore the interface flow-barrier is perfectly rough and permeable.

4.2 One-Phase Formulation

The conservation of mass is reported in Eq. (1) and is automatically satisfied as the solid mass remains constant in each MP during deformation.

$$ \frac{d\rho}{d t}+\rho \nabla \bullet \mathbf{v}=\mathbf{0} $$

(1)

The conservation of momentum includes the conservation of both linear and angular momentum. The former is represented by the equation of motion, even known as Newton’s second law (Eq. 2), while the conservation of angular momentum refers to the symmetry condition of the stress matrix (σ = σ^T).

$$ \rho \frac{d\mathbf{v}}{dt}=\nabla {\boldsymbol{\upsigma}}^T+\rho \boldsymbol{g} $$

(2)

Finally, the constitutive equation needs to be expressed to include the stress-strain dependency (Eq. 3). The term D is the stiffness matrix; $\dot{\boldsymbol{\sigma}^{\prime }}$and $\dot{\varepsilon}$ are the stress and strain rate tensors of the solid phase, respectively. Ω is the spin tensor and ${\dot{\varepsilon}}_{vol}$ is the volumetric strain increment. To simulate large deformations (Eq. 3 is derived) the Jaumann’s stress rate of Kirchhoff stress can be considered; on the other hand, the Cauchy one which is limited to small strain rate (Martinelli and Galavi 2022).

$$ \dot{\boldsymbol{\sigma}^{\prime }}=\mathbf{D}\dot{\varepsilon }+\Omega {\boldsymbol{\sigma}}^{\prime }-{\boldsymbol{\sigma}}^{\prime}\Omega -{\dot{\varepsilon}}_{vol}{\boldsymbol{\sigma}}^{\prime } $$

(3)

In undrained conditions, the stress state can be described in terms of effective stresses. The excess pore pressures can be computed by means of the so-called Effective Stress Analysis (Eq. 4), which assumes strain compatibility between the solid skeleton and the interstitial liquid.

$$ \Delta {p}_L={\mathrm{K}}_L\Delta {\varepsilon}_{vol} $$

(4)

The time integration scheme considered in MPM is explicit, since most of the dynamic problems, including wave or shock propagation, cannot be treated properly by an implicit integration which tends to smooth the solution (Fern et al. 2019).

Let’s consider the critical time step Δt_cr as the time increment during which a wave with speed c crosses the smallest element length d (Eq. 5).

$$ \Delta {t}_{cr}=\frac{d}{c}=\frac{d}{\sqrt{E/\rho }} $$

(5)

The critical time step defines the biggest time increment which can be used for a stable calculation, but often it can’t be estimated in case of non-linear problems. For this reason, the critical time step is multiplied by an additional factor C_NB (namely Courant number) to reach stability. The Courant number has values between 0 and 1. Generally, the smaller the Courant number and the smaller the time step, improving the accuracy of the numerical results.

4.3 Two-Phase Formulation

A saturated porous medium is schematized as a solid phase which represents the solid skeleton, whereas the liquid phase fills the voids among the grains. Each MP represents a volume of the mixture V, given by the sum of the solid V_S and liquid V_L phases volumes. The behaviour of a saturated porous medium is here described using only one set of MPs, in which the information about both the solid and liquid constituents is stored.

The velocity field of solid and liquid phases are both used, but the material points move throughout the mesh with the kinematics of the solid skeleton. The equations to be solved concern the balance of dynamic momentum of solid and liquid phases, the mass balances, and the constitutive relationships of solid and liquid phases. The accelerations of the two phases are the primary unknowns: the solid acceleration a_S, which is calculated from the dynamic momentum balance of the solid phase (Eq. 6), and the liquid acceleration a_L, which is obtained by solving the dynamic momentum balance of the liquid phase (Eq. 7). The interaction force between solid and liquid phases is governed by Darcy’s law (Eq. 8). Numerically, these equations are solved at grid nodes considering the Galerkin method (Luo et al. 2008) with standard nodal shape functions and their solutions are used to update the MPs velocities and momentum of each phase. The strain rate $\dot{\boldsymbol{\varepsilon}}$ of MPs is computed from the nodal velocities obtained from the nodal momentum.

$$ {n}_S{\rho}_S{\mathbf{a}}_S=\nabla \bullet \left(\sigma -{n p}_L\mathbf{I}\right)+\left({\rho}_m-{n\rho}_L\right)\mathbf{b}+{\mathbf{f}}_d $$

(6)

$$ {\rho}_L{\mathbf{a}}_L=\nabla {p}_L-{\mathbf{f}}_d $$

(7)

$$ {\mathbf{f}}_d=\frac{n{\mu}_L}{k}\left({\mathbf{v}}_L-{\mathbf{v}}_S\right) $$

(8)

The resolution of solid and liquid constitutive laws (Eqs. 9 and 10) allows calculating the increment of effective stress dσ^′ and excess pore pressure dp_L, respectively. The mass balance equation of the solid skeleton is then used to update the porosity of each MP (Eq. 11), while the total mass balance serves to compute the volumetric strain rate of the liquid phase (Eq. 12) since fluxes due to spatial variations of liquid mass are neglected (∇nρ_L = 0).

$$ \mathrm{d}{\boldsymbol{\sigma}}^{\prime }=\mathbf{D}\bullet \mathrm{d}\boldsymbol{\varepsilon } $$

(9)

$$ {\mathrm{d}p}_L={\mathbf{K}}_L\bullet \mathrm{d}{\varepsilon}_{\boldsymbol{vol}} $$

(10)

$$ \frac{Dn}{Dt}={n}_S\nabla \bullet {\mathbf{v}}_{\boldsymbol{S}}=\mathbf{0} $$

(11)

$$ \frac{D{\varepsilon}_{vol}}{Dt}=\frac{n_S}{n}\nabla \bullet {\mathbf{v}}_{\boldsymbol{S}}+\nabla \bullet {\mathbf{v}}_{\boldsymbol{L}} $$

(12)

In the two-phase single-point formulation the liquid mass, and consequently the mass of the mixture, is not constant in each material point but can vary depending on porosity changes. Fluxes due to spatial variations of liquid mass are neglected and Darcy’s law is used to model solid-liquid interaction forces. For this reason, this formulation is generally used in problems with small gradients of porosity, and laminar and stationary flow in slow velocity regime. However, this formulation proves to be suitable for studying flow-structured-interaction (Cuomo et al. 2021c). The water is assumed linearly compressible via the bulk modulus of the fluid K_L and shear stresses in the liquid phase are neglected.

The current MPM code uses three-node elements which suffer kinematic locking, which consists in the build-up of fictitious stiffness due to the inability to reproduce the correct deformation field (Mast et al. 2012). A technique used to mitigate volumetric locking is the strain smoothening technique, which consists of smoothing the volumetric strains over neighbouring cells. The reader can refer to Al-Kafaji (2013) for a detailed description.

Regarding the critical time step, the influence of permeability and liquid bulk modulus must be considered as well (Mieremet et al. 2016). In particular, the time step required for numerical stability is smaller in soil with lower permeability (Eq. 13).

$$ \Delta {t}_{cr}=\mathit{\min}\left(\frac{d}{\sqrt{\left(E+{\mathbf{K}}_L/n\right)/{\rho}_m}};\frac{2\left({\rho}_m+\left(1/n-2\right){\rho}_L\right){k}_{sat}}{\rho_L\boldsymbol{g}}\right) $$

(13)

The sliding modelling of the flowing mass on the rigid material is handled by a frictional Mohr-Coulomb strength criterion. The contact formulation was used to ensure that no interpenetration occurs, and the tangential forces are compatible with the shear strength along the contact. The reaction force acting on the structure at node j was calculated as in Eq. (14).

$$ {F}_j(t)={m}_{j,S}\varDelta {a}_{S, contact}+{m}_{j,L}\varDelta {a}_{L, contact} $$

(14)

The terms Δa_{S, contact} and Δa_{L, contact} are the change in acceleration induced by the contact formulation, for both solid and liquid phase, and m_{i, S} and m_{i, L} are the corresponding nodal masses. The total reaction force is the integral of the nodal reaction forces along the barrier.

5 Modelling the Damage of an Infill Wall

5.1 Input Scheme

To analyse the complex mechanisms of a flow-like landslide impact against a RC framed building with URM infill walls, the numerical modelling of a single URM wall is firstly conducted.

Here, the experimental tests of Vaculik (2012) on URM wall are modelled. The wall is made of two components: standard Australian clay bricks with nominal dimensions 230 mm × 110 mm × 76 mm, perforated with two rows of five holes and mortar joints with standard thickness of 10 mm using a composition of 1:2:9 (portland cement, lime and sand). The dimensions of the wall are h = 2494 mm and B = 4080 mm, with the lateral boundary confined in embedded return wall, each 480 mm long (Fig. 5).

Fig. 5

Cracks of the interior face of the wall resulting from the experiment of Vaculik (2012)

Some mechanical properties taken from literature for both bricks and mortar-joint are reported in Table 1. The MPM computational domain has been set both in 3D and 2D for different purposes. The 3D scheme (Fig. 6a) is used to reproduce the mechanical response of the wall under OOP pressure. In such model all the boundary conditions can be considered, either as the fixities or as mortar joints. Conversely, a 2D simplified model (Fig. 6b) must be validated for later extensive applications to design-oriented analyses.

Table 1 Some material properties from literature

Fig. 6

Computational domain used to simulate the experiments of Vaculik (2012): (a) 3D model; (b) 2D model (barycentric vertical cross-section of the wall)

The URM wall is schematized as an equivalent uniform continuous frictional-cohesive material, with the mechanical parameters (Table 2), selected as follows. The density (ρ = 1936 kg/m³) and the Poisson ratio (ν = 0.2) are those measured for the wall by Vaculik (2012). The Young’s modulus (E) is taken from the experimental evidence reported by Vaculik (2012) for combo p2 (E = 2240 kPa) or assumed as equal to that of the mortar for combo p1 (E = 442 kPa). The cohesion of the wall material is varied to get numerical results similar to the experimental ones. The internal friction angle (φ') is set equal to the average value reported by Vaculik (2012) and Graziotti et al. (2019) for the mortar bed-joints. The K0 value is determined as 1-senφ' using the friction angle of the brick since it is plausible that the horizontal and vertical stress distribution is like that of a brick column. The tensile strength (f_t) of the wall is simply obtained as the ratio between cohesion (c’) and friction angle (tanφ'), assuming that the friction angle is the same in both compressive and tensile stress (Table 2).

Table 2 Sets of material properties used for modelling the URM wall

5.2 Numerical Results

The 3D computational mesh is 1.00 m × 4.08 m × 3.00 m large and made of 116,325 tetrahedral (four-noded) elements with average size of about 0.1 m inside and outside the wall (Fig. 8a). In 2D conditions, the domain is 3.50 m × 3.00 m and made of 2605 three-noded triangular elements, ranging from 0.08 m (inside the wall) to 0.50 m (Fig. 8b). The wall is fixed at top and bottom sides. Several simulations were performed assessing the combos p1 and p2 of Table 2 as the best-fitting set of parameters for simulating the experiments of Vaculik (2012) in 3D and 2D conditions, respectively.

A selection of results is reported in Fig. 9, with reference to the deviatoric strain defined as ${\varepsilon}_d=\frac{2}{3}\sqrt{{\left({\varepsilon}_x-{\varepsilon}_y\right)}^2+{\left({\varepsilon}_y-{\varepsilon}_z\right)}^2+{\left({\varepsilon}_z-{\varepsilon}_x\right)}^2}$.

The load capacity of unreinforced masonry wall depends on: dimensions and support conditions, amount of compressive and tensile strength of the masonry. Particularly, the crack patterns and the load-displacement curve depend on different kinds of wall supports.

For numerical modelling, all the boundaries of the wall are fixed, thus yielding deformations occur as follows: (i) first at the top of the wall, (ii) then at the bottom of the wall, (iii) at the side boundaries of the wall. From now on, yielding zones enlarged along the boundaries where they appeared but (iv) a plastic hinge forms at the mid-height of the wall, and (v) yielding also appears along the diagonal directions (Fig. 7a). This is in accordance with the experiment of Vaculik (2012), as reported in Fig. 5, showing that 3D simulations allow a better understanding of how plastic deformations develop during the OOP loading.

Fig. 7

Deviatoric strain computed for different external force: (a) 3D modelling; (b) 2D modelling (barycentric vertical cross-section)

Figure 7b reports the development of plastic deformations in the 2D barycentric vertical cross-section of the wall. Firstly, two plastic hinges appear along the extremities of the wall (F = 30.5 kN), then for F = 34.5 kN the mid-height of the wall starts to yield due to excessive bending, and finally the plastic deformations increase and spread over the central zone of wall for F = 40.3 kN (Fig. 7b). Such results are consistent with 3D simulation results, demonstrating that also a 2D simplified model scheme could be used in real applications.

A quantitative comparison between numerical and experimental outcomes in terms of horizontal displacements of the wall is provided in Fig. 8, showing that both 3D and 2D modelling clearly well reproduce the failure mechanism of the wall. Moreover, it is possible to derive the load-displacement curve from both 2D and 3D simulations and compare it with that obtained from the experimental test (Cuomo et al. 2020b). The experimental curve shows a different trend after reaching a horizontal displacement of about 18 mm due to the decreasing of the external load, with a maximum displacement of 30 mm and a final recovery of about 15 mm. This recovery path is neglected for the numerical modelling. However, the F-Δ plot in the loading phase is well captured by 3D and 2D simulations (i.e., for Δ = 0–18 mm).

Fig. 8

Horizontal displacements computed through 3D and 2D MPM modelling compared to those measured at the ultimate strength of the wall (Fu = 30.5 kN) by Vaculik (2012)

6 Modelling Landslides Impacting a Two-Storey Building

6.1 Input Scheme

The 2D modelling of the URM wall proved sufficient compared to 3D, with remarkably reduced computational time. A 2D modelling is here used to simulate the interaction between a flow landslide and a two-storey RC framed building.

For the modelling of the building, the bearing frame is assumed rigid and fixed in space, while the non-structural external and internal URM walls can be deformed and eventually destroyed following the impact of the landslide. Such modelling aims to highlight that even the collapse of non-structural elements can pose serious risks to people.

The geometric schematization of the building is reported in Fig. 9. The external walls are 0.3 m thick, with two panels 0.1 m thick separated by a 0.1 m internal cavity. The height of the walls excluding the thickness of the exposed beam (0.60 m) is equal to 2.5 m. The computational mesh and material points distribution for both the building and the landslide are reported in Fig. 10a, b, respectively. The overall computational domain (Fig. 11) is characterized by 12,279 triangular elements with average size of 0.1 m for the smaller structural elements and of 0.5 m elsewhere.

Fig. 9

Geometric schematization of the RC framed building with URM infill walls

Fig. 10

Computational mesh of building (a) and landslide (b)

Fig. 11

Overall computational domain for the 2D modelling of the landslide and the two-storey building

Figure 11 even highlights the considerable size of the landslide compared to that of the building.

The flow and the wall are modelled through the single-point MPM formulation, respectively with two-phase and one-phase.

All the walls are modelled with the same constitutive law of the previous section and the mechanical properties are those of the combo p2 (Table 2), which proved to be the best-fitting set in the 2D modelling of the URM wall. Regarding the constraints: the extremity of each wall is fixed in x-direction, so the wall can be considered pinned-pinned.

Another issue is the modelling of the landslide. The height of the impacting mass has been assumed equal to the first-floor height, as deducted from in-situ investigations (Faella and Nigro 2003), that is equal to 3 m in this example, while the length is set to 21 m (i.e., seven times the height).

It is worth noting that the Landslide-Structure Interaction is referred to the site scale. Due to high computational time of the simulations, it is difficult to reproduce the entire landslide dynamics also including the triggering and propagation stages of the landslide. Hence, the attention is focused on the moment before the impact, considering a simplified initial configuration of the landslide with a 45°-inclined front and a prolonged tail. Moreover, two landslides with different initial velocity (5 and 10 m/s) are considered.

The landslide material is assumed as a saturated mixture with linear distribution of initial pore-water pressure and an elasto-plastic behaviour at failure. The contact along the base is assumed to be smooth to avoid reduction in velocity due to friction. The initial stress distribution is set through gravity loading. Based on literature values and other related researches (Cuomo et al. 2020a), the mechanical properties are selected as follows: density of the mixture (ρ_m) equal to 1800 kg/m³, Poisson ratio (ν) of 0.25, Young’s modulus (E) equal to 2000 kPa, nil cohesion (c’), internal friction angle (φ') is 20°, nil dilatancy angle, hydraulic conductivity (k) equal to 10⁻³ m/s, liquid viscosity (μ_L) of 10⁻³ Pa·s, liquid bulk modulus (K_L) of 30 MPa. Moreover, two initial landslide velocity (5 and 10 m/s) are considered.

6.2 Numerical Results

The impact of the landslide with initial velocity of 5 m/s against the RC building is firstly investigated with reference to some snapshots reported in Fig. 12. Specifically, the distribution of landslide pore-water pressure and deviatoric strain inside the infill walls is shown.

Fig. 12

Pore-water pressure (landslide) and deviatoric strain (infill walls) distribution during impact (v₀ = 5 m/s)

At the impact stage, the front of the landslide is compressed against the external wall (t = 0.50 s), showing the increase in pore-water pressure (up to 226 kPa) and consequent increment of total earth pressure on the wall, which of course fails with no chance to withstand to such large external action. In the following moments, the flow continues to propagate dragging all the walls of the ground floor, without showing signs of stopping and therefore also the pore-water pressure is not reduced.

Worse is the case of a landslide with higher initial velocity (v₀ = 10 m/s), reported in Fig. 13. Interestingly, the pore-water pressure at impact (t = 0.50 s) is much higher and the deformations inside the walls are larger than the previous case of Fig. 15. After the impact, the landslide material runs up along the structure, causing the damage and the final collapse of the first-floor wall (t > 1.50 s). This means that people behind that wall would be seriously injured. In the meantime, large part of the flow continues to propagate and destroy the URM walls at the ground. This type of impact mechanism is named “run-up” mechanism, which consists in the formation of a vertical jet with high speed that overruns the structure. Such behaviour of the flow mostly depends on flow velocity (or related quantities), soil mechanical behaviour and geometry of the impacted structure.

Fig. 13

Pore-water pressure (landslide) and deviatoric strain (infill walls) distribution during impact (v₀ = 10 m/s)

Nevertheless, the structural elements (especially RC columns) of the ground floor are almost certainly overloaded laterally from the flow. Therefore, a 3D modelling of the entire structure would be advisable even if a proper schematization of the mechanical behaviour of the bearing frame would be mandatory.

However, it is worth remarking that the topic here is referred to landslides still catastrophic but not able to destroy the whole building. Hence, the present model may help for a preventive assessment inside the zones of the urban areas where building collapses are not expected while damage to non-structural elements may happen.

In such scenario, the type and the amount of damage must be properly evaluated to direct the actions for the emergency phase and to design the correct mitigation options for reinforcement and protection of the buildings.

7 Modelling Landslides Impacting a RC Wall

7.1 Input Scheme

This section investigates the failure mechanisms of a RC protection wall under the impact of a flow-like landslide (Fig. 14). The geometric configuration, the mechanical properties, smooth contact at the base, initial velocity and pore-water pressure of the landslide are the same proposed in the previous section.

Fig. 14

Geometric schematization for the LSI numerical simulations with RC walls

The RC wall is schematized as a homogeneous material, with frictional contact at base and elasto-plastic behaviour. The wall is 6 m high with a foundation platform of 11 m (see Table 3 and Fig. 14 for dimensions details). The material properties used in the study were determined by Ardiaca (2009) from design regulations, considering the type of concrete with a characteristic compressive strength of 25 MPa. The base-concrete interface is handled with a frictional contact, imposing a coefficient equal to 0.67 (Ilori et al. 2017). The mechanical properties of the RC wall are: barrier density (ρ_b) equal to 2500 kg/m³; effective friction angle (φ') of 35°; cohesion (c') as 510 kPa; Young’s modulus (E) = 30,000 MPa; Poisson’s ratio (ν) equal to 0.25; tensile strength (f_t) of 750 kPa and frictional coefficient (tanδ_b) equal to 0.24.

Table 3 Geometric features of the RC wall

The computational unstructured mesh (Fig. 15) is made of 17,267 triangular elements with dimensions ranging from 0.10 (in the proximity of the wall and the impact area) to 0.50 m (elsewhere). The flow and the RC wall are modelled through the two-phase and one-phase single-point MPM formulation, respectively. Also here, the build-up of excess pore-pressure during the impact is considered as well as the hydromechanical coupling and the elasto-plastic failure criterion of the flow.

Fig. 15

Computational domain for the 2D MPM modelling of the landslide and the RC wall

7.2 Numerical Results

Selected results are shown as the spatial distribution of pore-water pressure within the flow mass and the appearance of deviatoric deformations inside the structure. Firstly, the flow with initial velocity equal to 5 m/s is considered (Fig. 16).

Fig. 16

Pore-water pressure (landslide) and deviatoric strain (RC wall) distribution during impact (v₀ = 5 m/s)

At impact (t = 1.00 s) the pore-water pressure increases up to 288 kPa, then diminishes (t = 1.50 s) due to the beginning of wall mobilization and increases again (t = 2.00 s) due to the rising of the flow along the vertical column. After that, the liquid pressure is mostly decreasing, indicating that the landslide is losing kinetic energy. The internal shear deformations of the wall are practically nil; thus, the wall is subjected to a rigid translation with a final displacement equal to 0.90 m.

In the case of a faster flow (Fig. 17), the pore-water pressure at impact (t = 0.50–1.00 s) reaches higher values than before (up to 515 kPa), but in the following time lapse the values diminish drastically. Also here, there is a rigid translation of the wall exhibiting an excessive final displacement (12 m). However, deformations are relevant, causing a slight bensing of the column. A correct design of the barrier requires the coexistence of two mechanisms (shifting and bending) in a way that the barrier does not move too far, and the vertical wall does not bend too much. However, the structure seems to completely stop the entire propagating mass, since the amount of flow material that exceed the barrier is very few, therefore the effectiveness of preventing the overtopping of the barrier is very high.

Fig. 17

Pore-water pressure (landslide) and deviatoric strain (RC wall) distribution during impact (v₀ = 10 m/s)

8 Modelling Landslides Impacting a Deformable Barrier

8.1 Input Scheme

The interaction between the landslide and a Deformable Geosynthetics-Reinforced Barrier (DGRB) is analysed (Fig. 18), with the same mechanical and geometric features of the flow used before.

Fig. 18

Geometric schematization for the LSI numerical simulations with deformable barrier

A full numerical analysis of the geosynthetics-reinforced soil structure is quite complex since modelling each component and their interactions is challenging. Thus, an equivalent approach is here employed to analyse the DGRB. A composite reinforced soil properties is considered and with less input parameters needed. However, localized failures cannot be reproduced, as the individual material properties are not considered and the interaction between the soil and the reinforcement cannot be studied independently.

The assessment of the elasto-plastic parameters to set for the equivalent approach is carried out considering the internal friction angle (φ'), Young’s modulus (E) and Poisson’s ratio (ν) of the equivalent material equal to those typically employed for the backfill soil for practical applications. In addition, a tensile strength equal to the ultimate shear resistance of the geosynthetics reinforcement is imposed for this equivalent material. What is the most difficult to determine is the cohesion value. In such equivalent approach, the cohesion in the reinforced zone is increased using pseudo cohesion or anisotropic cohesion approach which states that the additional strength of the reinforced soil can be imparted by an apparent anisotropic cohesion (Nguyen et al. 2021; Maji et al. 2016). In this study, the value of cohesion was found by making sure that the Factor of Safety (FS) under gravity load obtained for the composite structure is the same than in the equivalent model.

The barrier is 6 m high, 11 m wide and the inclination of the impacted side is 70° (Table 4). The failure behaviour is non-associative (zero dilatancy) elasto-plastic criterion.

Table 4 Geometric features of the barrier

The mechanical properties chosen for the barrier are: the barrier density (ρ_b) equal to 2000 kg/m³; effective friction angle (φ’) of 38°; cohesion (c’) as 58 kPa; Young’s modulus (E) equal to 15 MPa; Poisson’s ratio (ν) equal to 0.25; tensile strength (f_t) of 100 kPa and frictional coefficient (tanδ_b) equal to 0.29. The frictional resistance along the base is set equal to the 80% of the strength properties of the base material (Cuomo et al. 2019).

The homogeneous barrier with the achieved cohesion equal to 58 kPa represents a composite structure with FS = 3.73 under gravity load. The factor of safety is calculated through LEM analysis, with Morgenstern-Price method.

The flow and barrier are modelled through the single-point MPM formulation, respectively with two-phase and one-phase. The computational unstructured mesh is made of 16,356 triangular elements with dimensions ranging from 0.10 (to refine the impact zone) to 0.50 m (Fig. 19).

Fig. 19

Computational domain for the 2D MPM modelling of the landslide and the deformable barrier

Also in this case, the landslide is assumed as approaching the barrier with a fixed geometric configuration and constant velocity (5 and 10 m/s), until LSI begins.

8.2 Numerical Results

The results of pore-water pressure (landslide) and deviatoric strain (barrier) are reported first for the flow with low initial velocity (Fig. 20). In particular, the liquid pressure reaches the maximum value of 153 kPa after some instants from impact (t = 1.00 s). This is probably related to the increase of the impacted area. Simultaneously, the shear deformations along the impacted side are growing.

Fig. 20

Pore-water pressure (landslide) and deviatoric strain (barrier) distribution during impact (v₀ = 5 m/s)

For t > 1.50 s, the kinetic energy of the flow decreases and this is well understandable from the lower values of p_L,max and from the unchanging deformations inside the barrier. Moreover, the barrier does not show any horizontal displacement and all the flow is completely block by the barrier.

In the case of a faster flow (Fig. 21) the results are quite different, since the maximum value of p_L,max is higher than before (386 kPa) and it is reached at t = 0.50 s. The deviatoric strains inside the impacted zone are larger than Fig. 20.

Fig. 21

Pore-water pressure (landslide) and deviatoric strain (barrier) distribution during impact (v₀ = 10 m/s)

At t = 1.00 s, the barrier begins to move and thus the pore-water pressure drastically decreases. Then the run-up of the landslide along the barrier side generates some compression and therefore the liquid pressure increases again (t = 1.50 s). At the same time, the deviatoric plastic deformations begin widespread in the upper zone of the barrier due to the impact of the downward flow. After that, the landslide dissipates more and more kinetic energy and therefore pore-water pressure diminishes and the deviatoric strains inside the structure remain unchanged.

The deformable barrier with these geometric characteristics can withstand the potential of the flow, showing a plausible displacement of 1.90 m and retaining a large amount of flow volume. However, the acceptability threshold of the barrier final displacement must be evaluated from site to site.

9 Concluding Remarks

The paper proposed a comparative numerical modelling, based on Material Point Method (MPM), relative to the impact of flow-like landslides against different types of structures like a two-strorey building, a Reinforced Concrete (RC) protection wall, and a Deformable Geosynthetics-Reinforced Barrier (DGRB).

The numerical MPM-based modelling of LSI for those different types of structures outlined that landslide pore water pressure largely increase in the early stages of the impact (t < 1 s), while reducing later dependent on landslide deformation plus propagation (Table 5) and related also to the displacement plus deformation of the protection structure.

Table 5 Maximum pore water pressure (liquid pressure, p_L,max) inside the landslide body at different time lapses, and maximum horizontal displacement (Dx) of the structure during the Landslide-Structure Interaction (LSI)

The excess pore water pressure generated during the Landslide-Structure Interaction (LSI) is modelled, and it is proved as an important mechanism contributing to landslide run-up, overtopping and structure displacement or disruption until failure or unserviceability condition.