Introduction

A number of civil engineering structures are constructed of concrete (plain and reinforced). The interaction of the concrete structure with the surrounding soil often influence some capacity parameters related to the limiting loads, or stress for the structure in question. One of the basic assumption of Terzaghi’s in deriving the bearing capacity equation is “the base of the footing is rough”, to what degree? Other areas of importance are skin friction component of a concrete pile capacity, both driven and bored. For concrete driven pile, the effect of concrete–soil interface properties on estimation of skin frication capacity is reliably well predicted by relevant equations for example Nordlund [1], However, for bored in-situ concrete pile both qualitative and quantitative assumptions are made on the influence of interface friction. The most common one for a C-∅ soil is the tangent of two-third of internal angle of friction of the soil as the angle of wall friction value for the soil concrete interface. A similar value is assumed in the stability analysis of a retaining wall.

A number of works have been carried out on the friction characteristics of granular soil–concrete interface with both static and dynamic load conditions for example [2], Who proposed a modified Ramberg–Osgood model was for the modeling of soil–concrete interface behavior [3], demonstrated the presence of a shear band whose thickness, is 5D 50. Zhang and Zhang [4], developed equipment for conducting static and cyclic shear test. In a series of experiments on the behavior of interface between gravel and rough steel plate under static and cyclic loading, they proposed five laws governing the behavior of interface of structure and granular material. These laws briefly are;

  • Strength law the shear stress of the interface has a linear relationship with the normal stress.

  • Shear law the relationship between shear stress and shear strain at the interface is not a softening type.

  • Shear deformation law which is in two parts, (a) the shear stress-relative displacement relations are not exactly the same when the loading direction reverses, which is due to anisotropy of the interface after initial strong confinement effect. (b) The shear displacement can be decomposed into shear deformation of the soil and sliding at the interface.

  • Compressive law the vertical deformation at the interface in the shear process can be decomposed into permanent part and reversible part.

  • Evolution law the meso-scale change in the shear zone is a process of partible breakage and shearing compression.

These laws were possible to be proposed using highly specialized equipment which are not available to the present authors.

Zhu et al. [5], studied shear test on the interface between coarse-grained soil and concrete as further work carried out by Peng et al. [6], and concluded that simple shear test represents a low stress situation as is obtainable in concrete pile soil interface and is more suitable for studying the shear displacement and deformation properties of interface in low stress state, while torsional shear tests simulates is more suitable for testing the strength of the interface.

The present study is a direct shear test of a C-∅ soil on in situ concrete. A soil–concrete bond type specimen interface is investigated and the validity of the notion of using the tangent of two-third of angle of internal friction as friction value.

Study objectives

The study using direct shear equipment aims to;

  1. 1.

    To estimate shear strength properties of a common foundation soil, a C-∅.

  2. 2.

    Investigate the shear strength properties of Bond type specimen for soil–concrete interface.

  3. 3.

    Examine using both results from 1 and 2 to what extent the tangent of two-third of internal angle of friction principle is valid;

Materials and methods

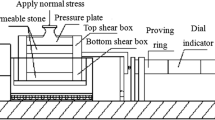
The soil utilized in the study is a predominantly cohesion less soil. The soil samples used were obtained in an undisturbed state from a block sample of 200 mm × 200 mm × 200 mm size from trial pit at location dug behind the health center on the University of Uyo, permanent site. Basic indices which includes; plastic limit, liquid limit, for the soil were determined for classification purposes. Among other test carried out were moisture content and sieve analysis. These tests were carried out in accordance with relevant ASTM standards. A direct shear test in accordance with ASTM D3080/D3080M-11 [7]. Standard was carried on the soil sample alone. It was also carried out on soil–concrete specimens.

For the soil–concrete test, bond type specimens (as against precast) were used in the experiment. They were prepared as follows. Concrete sample set with characteristic strength of 25 N/mm2 were prepared in a mold which has the same size as the shear box square ring with a dimension of 60 mm × 60 mm × 20 mm in height. Light grease was applied inside of the mold. Concrete paste was prepared and scooped into the mold. This was vibrated until the mixture fills half of the mold. There is a mark indicating half the height of the mold. Soil cutter was used to cut soil from the trial pit soil block sample and placed to fill the remainder half of the mould.

The mold was removed after some hours and concrete side of the unit place in a water dish for curing of the concrete. The concrete was cured for 28 days. Cement used was ordinary Portland cement with specified strength of 32.5 N/mm2 at 28 days. Six bond type soil–concrete specimen were prepared, with three each designated sets 1 and 2 respectively. A set of specimen for each externally applied normal load, such that two specimens are utilized for each normal load.

The whole assemblage was now put in a digital shear machine ring device. Direct shear digital machine used was model 30-WF6016 T2 (Wykeham Farrance) attached to data logger which records all parameters automatically during a testing operation. Strain controlled test was the type that was carried out with the sample sets. The machine applied strain at the rate of 0.5 mm/min. The direct shear test machine is equipped with strain gauges transducers to measure both horizontal and vertical deformations from the start to the end of the test. It has facility to determine both the peak and residual shear strength of soil, but the latter was not determined for the specimens in this study. Normal load applied were 50, 100, and 150 kg. Porous plate was placed on top of the soil to allow drainage from soil simulating drained condition.

Results and discussions

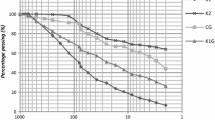
The soil indices are presented in Table 1. The grain size analysis for the soil is presented in Fig. 1. Coefficient of uniformity (Cu) and curvature (Cc) of the soil are 4.44 and 0.625. The soil is classified as silty sand (SM) using Unified Soil Classification System (USCS).

Table 1 Soil index properties and classification
Full size table
Fig. 1
figure 1

Grain size analysis result for soil used in the experiment

Full size image

Shear test results on soil to soil interface

The shear–horizontal displacement curves for the different normal loads applied on the two sets of specimen utilized in the experiment on soil to soil interface are presented in Figs. 2 and 3.

Fig. 2
figure 2

Shear stress versus horizontal displacement curve for soil to soil test for specimens set 1

Full size image
Fig. 3
figure 3

Shear stress versus horizontal displacement curve for soil to soil test for specimens set 2

Full size image

The two soil to soil test specimens developed peak shear stress of 21.41 and 27.94 kPa at horizontal displacement values of 5.3 and 5.4 mm for the average normal stress of 138 kPa, 53.71 and 53.48 kPa at horizontal displacement of 9.6 and 9.6 mm, at the average normal stress of 277 kPa, and 144.76, and 133.48 kPa at displacement values of 8.8, and 8.7 mm for 417 kPa normal stress. These values are presented in Fig. 2 for sample set 1 and Fig. 3 for sample set 2. The closeness of the horizontal deformation values for the respective load for the tests is an indication of the similar consistency of the undisturbed soil samples utilized in the experiment, hence reliable values are expected. Though the relative densities were not quantitatively determined the similarities in the plot of shear stress versus horizontal deformation for both samples at the same average normally applied load also indicate similar relative soil consistencies. For both samples, at the applied normal stress of 138 and 277 kPa, the shape of the curve from previous works [8, 9], indicates ‘loose’ relative densities, while at 417 kPa, the shape indicates a dense soil consistency.

Two approaches were used in computing the angle of internal friction of the soil from shear box data. The conventional one is to plot the shear stress values against horizontal displacement, for each normal load applied, determine the peak values, and plot same with the normal load applied. The arc tan of the slope of the resulting graph gives angle of internal friction of the soil. The other approach is to use the peak shear stress values and the corresponding normal stresses computed, and plot same for the three load sequence applied. The former with a slightly higher but not significant coefficient of correlation than the latter gives a lager value for the angle of frictional resistance. The results for the two approaches are presented in Table 2, while Figs. 4 and 5 presents a typical plot of shear stress versus normal stress for each approach method respectively.

Table 2 Angle of internal friction computation results
Full size table
Fig. 4
figure 4

Shear stress versus normal stress plot, soil to soil using conventional approach for sample 2

Full size image
Fig. 5
figure 5

Shear stress versus normal stress plot, soil to soil using peak normal stress method for sample 1

Full size image

Shear test results on soil to concrete interface

In interfacial studies between soil and other objects, two types of classification are made depending on the position of the material being investigated. If in the shear box set up the materials is on top of the soil this is call Type ‘A’ apparatus set up, that is the normal load is applied to the set up through the material. Whereas if the soil is on top of the other materials it is called Type B apparatus set up. The apparatus set up in this study is Type ‘B’.

The apparatus type is thought to influence the results of the shear tests differently: Robinson [10]. He further reports that the following factors affect interfacial friction between a surface and a sandy soil. These factors are;

  • Surface roughness.

  • Density of sand.

  • Normal stress.

  • Rate of deformation.

  • Size of apparatus.

  • Grain size and shape.

  • Type of apparatus.

The above listings are based on a number of works which includes Potyondy [11], Rowe [12], Heerema [13], Jewell and Wroth [14], Kishida and Uesugi [15]. Some of these factors are closely related.

Surface roughness, rate of deformation, and density of sand

Surface texture (surface topography, and the degree of surface roughness) [16, 17], and surface hardness are known to influence interface properties and strength. Without the facility to profile the surface of the concrete surface using equipment like Taylor-Hobson Talysurf stylus profilometer; recourse is made to the horizontal displacement values and pattern. Tables 3 and 4 presents computational details for Normal stress load of 138 kPa for both sample sets 1 and 2.

Table 3 Typical computation for test at 138 kPa normal stress for soil–concrete interface for specimen 1 in set 1
Full size table
Table 4 Typical computation for test at 138 kPa normal stress for soil–concrete interface for specimen 1 in set 2
Full size table

For the 138 kPa normal loads, the horizontal displacement is 6.399 mm at a peak shear stress of 213.38 kPa for sample set 1 and 4.89 mm at a peak shear stress of 219.94 kPa for sample set 2. For the 277 kPa normal load, sample set 1 has a horizontal displacement of 4.633 mm at a maximum shear stress of 239.46 kPa, and for sample set 2, 4.89 mm at shear stress of 219.74 kPa. For 477 kPa normal stress, 13.129 mm horizontal displacement, at maximum shear stress of 384.50 kPa for sample set 1, and 6.21 mm at maximum shear stress of 367.45 kPa for set 2. Figures 6 and 7 presents these results for sample sets 1 and 2 respectively, while Figs. 8 and 9 presents the shear versus normal stress plot using the conventional and the peak normal stress approaches respectively. The non-uniform values of horizontal displacement indicated by the different sample sets at the same normal stress is a measure of the non-consistent surface or surface roughness of the soil concrete interface in the two sample sets. A smaller horizontal displacement over a given similar duration between two tests is an indication of lesser rough surface. Reference the above, sample set 1 is rougher than sample set 2. Furthermore, the relative roughness is also indicated by ratio of shear force to the normal force (\(\tau /N\)) called the friction ratio. This ratio obtained for each externally applied normal load is a measure of the coefficient of static friction (degree of roughness) between the soil and concrete. For the peak shear stress they are 1.40, 0.80, and 0.72 for sample set 1 and, 1.31, 0.73, 0.79 for sample set 2 for the 138, 277, and 477 kPa normal loads respectively. Average values for each of the sample set are 0.97, and 0.94 respectively, indicating that sample set 1 are rougher than sample set 2.

Fig. 6
figure 6

Shear stress versus horizontal displacement curve for soil to concrete for specimen sample set 1

Full size image
Fig. 7
figure 7

Shear stress versus horizontal displacement curve for soil to concrete for specimen sample set 2

Full size image
Fig. 8
figure 8

Shear versus normal stress plot using conventional approach for soil concrete interface for sample 1

Full size image
Fig. 9
figure 9

Shear versus normal stress plot using peak normal stress approach for soil concrete interface for sample 1

Full size image

In an experimental study of interface behavior between composite piles and two sands (density sand and model sand), by the US Federal Highway Administration [18] the surface of concrete piles used were profiled with Taylor-Hobson Talysurf stylus profilometer, and roughness parameters were obtained which includes, maximum peak-to-valley height (Rt), average mean line spacing(Sm), and arithmetic average roughness (Ra). Relative roughness were calculated using each of these parameters by dividing them with diameter at 50% finer (D50). Values obtained were 0.67 irrespective of the peak shear stress associated with the direct shear tests used, indicating the same level of roughness for the samples surface. Using the values of the ratios of computed shear stress to computed normal stress (\(\tau /N\)) obtained at the peak shear stress as relative roughness values in the current study, and D50 as 0.3 mm for the soil used which is essentially sandy; Rt obtained were 0.419, 0.239, and 0.216 mm (average is 0.291 mm) for sample set 1, and 0.394, 0.218, and 0.237 mm (average is 0.283 mm) for sample set 2. This still shows that sample set 1 is rougher, affirming deductions made with respect to horizontal displacements and roughness above.

The angle of internal friction computed for the soil–concrete interface are 24.93° and 27.94°. These values were computed based on the normal stress associated with maximum or peak shear stress developed by the specimens for each externally applied normal load during testing. Whereas, 30.62° and 32.13° were the angles obtained using the normal stress from externally applied normal load increments. These values are larger than those computed with the normal stress associated with the peak shear stress occurring during the test.

The fact that the second set of specimen though less rough than the first but with a friction angle greater than the first could be an indication of the Evolution law proposed by Zhang and Zhang [4]. This affirms that there could be particle breakage or strain hardening at high normal stress value, in the shear zone which could lead to increase in frictional resistance between the soil and concrete which is manifested by larger friction angle than that given by the rougher set 1 concrete specimen.

While the rate of deformation was used to establish the degree of roughness of the concrete specimens, it does not have any influence on the magnitude of friction angle. This is consonance with findings by Heerema [13] and Lemos [19], who reported deformation rates of 0.7 to 600 mm/s and 6.3 × 10−5 to 2.22 mm/s. The deformation rate for the sample specimens in the study is about 0.0075 mm/s, which falls in the range of those reported by Lemos [19].

Stress level and friction values

Two approaches can be used to interpret the tangent of two-third angle principle.

The first, the use of the internal friction angles obtained for the soil–concrete interface which is often not known unless a laboratory test carried out that simulates the expected field condition. The tangent of two-third of the smaller angles of internal friction are 0.298, and 0.34 (average 0.32); while for the larger angles 0.372 and 0.392 (average 0.382). Referencing these values to the \(\tau /N\) values in the experiments, the vertical or normal stress values that can develop these roughness values is between 141 kPa (Tables 3, 4) to about 430 kPa (Table 5). These ranges of values are typical of pad footing on soil, and retaining wall base slabs on soil in which the friction coefficient is crucial for stability analysis against sliding. Hence for different stress load on the same type of soil the range of safe friction factor is the same. This value is conservative for the range of these stresses. However the resulting shape of shear stress versus horizontal displacement graph for the 417 kPa normal load shows an indication of a loose soil consistency in both samples. The two curves for this situation presented in Figs. 6 and 7 only indicate a slight peak just before failure. For the 417 kPa applied normal load in both samples; the normal stress associated with the shear stress of about 300 kPa, which represents the peak of the near-linear part of the curve in Figs. 6 and 7. This will set a safe limit for the normal stress for this state. The associated normal stress will be about 440 kPa from Table 5, with coefficient of friction at around 0.74, this represent a safe upper bound load for the situation beyond which there will be significant displacement.

Table 5 Typical computation for test at 477 kPa normal stress for soil–concrete interface for specimen 3 set 2
Full size table

Based on the above, a lower and upper stress level should be specified for a given friction value. Below the lower bound stress, the friction factors based on the two-third angle of internal friction become exaggerated. Since the friction is proportional to the applied normal stress, lower normal stress value below the lower bound leads to lower friction factor. Hence unreliable friction factor value is given by using the two-third principle for this case.

The second approach is to use the internal friction angle for the virgin soil. From Table 2 the friction values for the two angles by the two methods are between 0.16 and 0.19. These values gives a normal stress value range of 75.81–139 kPa based on Tables 3, 4, and 5. While this meet the lower bound stress situation of the first approach, it does not meet the upper stress level of this second approach. It can results in too conservative value that can lead excessive and unnecessary design that will increase the weight of the structure (for example in case of retaining wall) to achieve stability against friction. The first approach of using the values obtain from direct shear box test is therefore more favourable.

For Type ‘B’ apparatus similar to the one used in this study; the friction factor is found to be higher in samples that developed dense relative densities than those that developed loose one. Tables 3 and 4 which represent the former situation have peak friction values of 1.4 and 1.3 respectively, while Table 5 which represents the latter condition (loose density) as represented in Fig. 7; has a lower peak friction value of 0.79. This indicates that friction values increase with density. The above is consistent the results obtained by Potyondy [11] and Acar et al. [20].

For the two samples the shape of the resulting curves (Figs. 6, 7) for each of the normal stress are very similar, although the roughness for the two samples are different. This indicates that the densities developed during the interfacial interaction are independent of the relative roughness of the concrete surface.

Conclusions

The normal stress associated with the peak shear stresses should be used in estimating friction factor because it gives lower values and thus a more conservative estimate and hence safer values.

To reliably use an angle of internal friction to estimate friction factor, a direct shear test on model specimen of the soil and concrete should be carried out using a range of normal stress that includes the normal stress expected in the field. This will allow better judgement on the value of the tangent of the two-third of the internal angle of friction adopted as friction factor. Furthermore a range of stress level should also be specified for any friction value listed.

There is possible increase in the angle of internal friction as load is increased. This is due to the breakages that may occur during the loading, a manifestation of the Evolution law according to Zhang and Zhang [4].

In the absence of a profilometer to determine relative roughness of a surface, the ratio of shear stress to normal stress can serve as a valid alternative.