Abstract
An (n, m, t)-homomorphic secret sharing (HSS) scheme allows n clients to share their inputs across m servers, such that the inputs are hidden from any t colluding servers, and moreover the servers can evaluate functions over the inputs locally by mapping their input shares to compact output shares. Such compactness makes HSS a useful building block for communication-efficient secure multi-party computation (MPC).
In this work, we propose a simple compiler for HSS evaluating multivariate polynomials based on two building blocks: (1) homomorphic encryption for linear functions or low-degree polynomials, and (2) information-theoretic HSS for low-degree polynomials. Our compiler leverages the power of the first building block towards improving the parameters of the second.
We use our compiler to generalize and improve on the HSS scheme of Lai, Malavolta, and Schröder [ASIACRYPT’18], which is only efficient when the number of servers is at most logarithmic in the security parameter. In contrast, we obtain efficient schemes for polynomials of higher degrees and an arbitrary number of servers. This application of our general compiler extends techniques that were developed in the context of information-theoretic private information retrieval (Woodruff and Yekhanin [CCC’05]), which use partial derivatives and Hermite interpolation to support the computation of polynomials of higher degrees.
In addition to the above, we propose a new application of HSS to MPC with preprocessing. By pushing the computation of some HSS servers to a preprocessing phase, we obtain communication-efficient MPC protocols for low-degree polynomials that use fewer parties than previous protocols based on the same assumptions. The online communication of these protocols is linear in the input size, independently of the description size of the polynomial.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In lightweight secure multi-party computation (MPC) protocols, communication is usually the bottleneck for efficiency. For example, typical protocols based on oblivious-transfer (OT) have a communication complexity linear in the circuit size of the function being computed. A promising approach to bypass this barrier is homomorphic secret sharing (HSS) for multivariate polynomials, which enables low communication MPC protocols, while retaining practical efficiency. In this work, we study this problem and present a set of new lightweight techniques to maximize the degree of polynomials supported by HSS without increasing the communication cost.
1.1 Homomorphic Secret Sharing
An (n, m, t)-HSS scheme allows n input clients to share their secret inputs \((x_1,\ldots ,x_n)\) to m non-communicating servers, such that the latter can homomorphically evaluate any admissible public function f over the shares, and produce the output shares \((y_1,\ldots ,y_m)\). Using these, an output client can recover \(f(x_1,\ldots ,x_n)\). Shares of HSS should be much shorter, or ideally of size independent of the size of the description of the function f being computed. This non-trivial feature distinguishes HSS from OT-based MPC. As for ordinary threshold secret sharing schemes, security requires that the servers cannot learn anything about the inputs assuming at most t of them are corrupt.
HSS was conceived [10] as a lightweight alternative to fully-homomorphic encryption (FHE) [23] and it leverages the non-collusion of the servers to achieve better efficiency. Indeed, any homomorphic encryption for a function class \(\mathcal {F} \) can be seen as an (n, 1, 1)-HSS for the same class. Due to the distributed setting, homomorphic secret sharing can be constructed from assumptions that do not imply a fully homomorphic encryption scheme, such as the intractability of the Diffie-Hellman (DDH) problem [20], or even information-theoretically.
Boyle et al. [10] proposed a DDH-based (n, 2, 1)-HSS scheme for branching programs, where the reconstruction function is simply the addition of output shares. This enables many important applications, such as low-communication 2-party computation, efficient round-optimal multiparty computation protocols, and 2-server private-information retrieval. See [12] for a comprehensive discussion on the matter. One drawback of the scheme is that its correctness holds only for an inverse polynomial probability. Amplifications through parallel repetition results in a loss of concrete efficiency.
Boyle, Kohl, and Scholl [13] proposed a counterpart of [10] based on the learning with errors (LWE) assumption with negligible error. Similar to FHE, their scheme is only concretely efficient in an amortized sense and only for SIMDFootnote 1-style computations. Boyle et al. [9] proposed an (n, 2, 1)-HSS scheme for constant-degree polynomials based on the learning parity with noise (LPN) assumption. The scheme does not apply to the multi-input setting, i.e., the entire input must come from a single party, and the share size  (as opposed to the trivial \(O(n^d)\)) grows exponentially with the degree d.
(as opposed to the trivial \(O(n^d)\)) grows exponentially with the degree d.
In a different line of work originated by Catalano and Fiore [15], Lai, Malavolta, and Schröder (LMS) [31] considered a variant of the HSS model, where the reconstruction function is not necessarily linear. While this notion is strictly weaker than that considered by Boyle et al. [10], it is still useful in some context to “amplify” the homomorphic capability of some encryption schemes, leveraging the existence of multiple non-colluding servers. They proposed a construction of (n, m, 1)-HSS for degree \(d < (k+1)m\) polynomials using only a homomorphic encryption scheme for degree k polynomials (k-HE), for any \(k \ge 1\). The LMS construction [31] focused on the case \(t=1\). Their discussion of how the construction can be extended to \(t > 1\) was non-constructive. A constructive version for general \(t \ge 1\) was proposed in [35]. The main shortcoming of LMS [31, 35] is that it is only efficient for a small number of servers, i.e., \(m = O(\log \lambda )\), where  is the security parameter. This is due to the difficulty of the combinatorial problem of assigning monomials of the expanded form of \(\prod _{\ell \in [d]} (\sum _{i \in [n]} X_i)\) to m servers so that each monomial is computed by exactly one server.
is the security parameter. This is due to the difficulty of the combinatorial problem of assigning monomials of the expanded form of \(\prod _{\ell \in [d]} (\sum _{i \in [n]} X_i)\) to m servers so that each monomial is computed by exactly one server.
1.2 Power of Low-Degree Polynomials
The homomorphic computation of low-degree polynomials enables several interesting applications, that we discuss below.
-
1.
Private Information Retrieval: An m-server private information retrieval (PIR) protocol allows a client to retrieve the entry of a certain database (stored by all servers) without revealing which entry he is interested in. HSS offers a natural implementation of PIR by allowing the client to secret share the index across all servers, who can homomorphically evaluate the index selection function and return the corresponding entry of the database to the client. It is a well-known fact that the index selection function can be expressed as a low-degree polynomial (logarithmic in the size of the database).
-
2.
Private Queries: In the context of private queries, even a few extra degrees of computation turn out to be useful. Instead of the simple index selection, the servers can answer more complex queries, such as conjunctive statements [6]. As a concrete example, a client can query how many database entries contain a 1 at positions (i, j), without revealing the indices (i, j), by just adding a single degree to the polynomial homomorphically evaluated by the servers. See [3] for an elaborate discussion on the matter. Other examples of useful queries computable with low-degree polynomials include pattern matching over unsorted databases [1, 2].
-
3.
Machine Learning: HSS for low-degree polynomials can be used to securely compute repeated linear operations, such as matrix multiplication (for small amounts of matrices). These operations are recurrent for many interesting tasks, such as the secure computation of the training phase (e.g., [26]) and classification phase of (e.g., [8]) of machine learning.
-
4.
Biometrics: In applications of biometrics it is often required to compare or compute the distance of two data points. These tasks, such as the comparison of two integers [33], Hamming distance [38], and edit distance [16], can be represented as the computation of low-degree polynomials.
-
5.
Statistical Analysis: Low-degree polynomials allow one to compute statistics over private data, such as low-order moments, correlations, and linear regressions. See, e.g. [15] and references therein.
1.3 Our Results
The starting point of this work is the observation that the LMS construction can be viewed more abstractly as compiling an information-theoretic (IT) HSS scheme into its computational counterpart using k-HE. In their case, the IT HSS scheme consisted of the so called CNF secret sharing scheme [29], consequently, the inefficiency of their scheme for  servers is essentially due to the difficulty of evaluating CNF shares, which in turn is related to the #P-hard problem of computing the permanent of matrices [27]. With this view, it is natural to ask if the CNF scheme can be replaced with another IT HSS scheme, so that its (k-HE-compiled) computational variant is efficient for
servers is essentially due to the difficulty of evaluating CNF shares, which in turn is related to the #P-hard problem of computing the permanent of matrices [27]. With this view, it is natural to ask if the CNF scheme can be replaced with another IT HSS scheme, so that its (k-HE-compiled) computational variant is efficient for  servers.
servers.
Generic Compiler from IT HSS to HSS Using HE. In this work, we answer the above question positively. Specifically, we propose a generic compiler based on homomorphic encryption that compiles a certain class of IT HSS for degree-d polynomials into their computational counterpart with less client computation (and hence shorter output shares). In other words, for a fixed client computation cost, the computational variant supports higher degrees.
Theorem 1
(Informal). Let \(k, \ell \in \mathbb {N}\) be constants with \(k \le \ell \), and \(d < \frac{(\ell +1)m}{t}\). Suppose there exists an IT (n, m, t)-HSS for degree-d polynomials satisfying certain structural properties, and a CPA-secure k-HE scheme. Further suppose that the IT HSS scheme has recovery information size \(\rho \), input share size \(\alpha \), output share size \(\beta \), server computation \(\sigma \), and client computation \(\gamma \). Then there exists an (n, m, t)-HSS for degree-d polynomials with the following efficiency measures:
-
Recovery information size \(\rho ' = \rho \)
-
Input share size \(\alpha ' = \rho + \alpha \)
-
Output share size \(\beta ' = \rho ^{\ell - k}\)
-
Server computation \(\sigma ' = \sigma + \beta \rho ^\ell \)
-
Client computation \(\gamma ' = m \rho ^{\ell - k}\)
All  factors contributed by the ciphertext size and \(\log |\mathbb {F}|\) are omitted.
factors contributed by the ciphertext size and \(\log |\mathbb {F}|\) are omitted.
For \(k = \ell \), when the base IT HSS scheme is instantiated with the CNF schemeFootnote 2, we recover the LMS schemes [31, 35].
Theorem 1 might seem confusing at first glance – Our compiler turns a degree-d IT HSS into another degree-d computational HSS. What is the gain? We highlight that the output share size of the resulting HSS is independent of that of the base HSS, which could be much larger. From another perspective, for a fixed communication cost, the compiled (computational) HSS supports a higher degree than the base (IT) HSS.
More concretely, as we will see later in Corollary 1 (setting \(\ell = k+1\)), with  communication, the compiled HSS supports degree \(<(k+2)m/t\) with m servers, instead of \(<2m/t\) by the base HSS. Note that the supported degree is proportional to km, i.e., the expressiveness of k-HE is amplified multiplicatively by the number of servers m.
communication, the compiled HSS supports degree \(<(k+2)m/t\) with m servers, instead of \(<2m/t\) by the base HSS. Note that the supported degree is proportional to km, i.e., the expressiveness of k-HE is amplified multiplicatively by the number of servers m.
Generalizations of Existing Compatible IT HSS. In search of a substitute of the CNF scheme, we observe that implicit in the work of Woodruff and Yekhanin [37] lies an IT HSS, which was implicitly used to construct information-theoretic secure multi-party computation protocols [3]. This scheme, which we denote by \(\mathsf {WY}_1\) (first-order Woodruff-Yekhanin HSS), can be seen as a generalization of the well-known Shamir secret sharing scheme [36], which we denote by \(\mathsf {WY}_0\).
To recall, in the Shamir secret sharing scheme, a secret \(\mathbf {x} \in \mathbb {F}^n\) is shared into \((\mathbf {s}_1, \ldots , \mathbf {s}_m) = (\varphi (1), \ldots , \varphi (m))\) for some degree-t polynomial \(\varphi \) with \(\varphi (0) = \mathbf {x}\). To evaluate a degree-d polynomial f, where \(d < \frac{m}{t}\), server j sends \(f(\mathbf {s}_j) = (f \circ \varphi )(j)\) to the output client. Since \(f \circ \varphi \) is a polynomial of degree at most \(dt < m\), the output client can recover \(f(\mathbf {x}) = (f \circ \varphi )(0)\) by Lagrange interpolation. Notice that the Shamir secret sharing scheme is compact in the sense that, while an input share is of length n, an output share is of constant length. The latter is in some sense “wasteful”, since increasing the output share length to n (which we refer to as balanced), does not increase the overall asymptotic communication complexity. To utilize this “wasted” space, the idea of Woodruff and Yekhanin is to let the servers further compute the n first-order derivatives of f evaluated at \(\mathbf {s}_j\). Since m additional data points are available, the degree of f can now be as high as \(d < \frac{2m}{t}\), and \(f(\mathbf {x}) = (f \circ \varphi )(0)\) can be recovered by Hermite interpolation.
Our idea to further increase the degree of the supported polynomials is to let the servers compute even higher-order derivatives.Footnote 3 With some routine calculation one can show that the output share size is \(O(n^\ell )\) if derivatives of up to the \(\ell \)-th order are evaluated and sent to the output client. While this does not necessarily help in a standalone use of the HSS scheme, since it increases the overall communication complexity (and also client computation), it turns out that the increased communication can be brought back down again using the k-HE-based compiler, so that the resulting scheme is balanced or even compact.
Theorem 2
(Informal). For any constant \(\ell \in \mathbb {N}\) and \(d < \frac{(\ell +1)m}{t}\), there exists an IT (n, m, t)-HSS scheme \(\mathsf {WY}_\ell \) for degree-d polynomials with the following efficiency measures:
-
Recovery information size \(\rho = n\)
-
Input share size \(\alpha = n\)
-
Output share size \(\beta = n^\ell \)
-
Server computation \(\sigma = |f| n^{\ell -1}\)
-
Client computation \(\gamma = mn^\ell \)
Furthermore, \(\mathsf {WY}_\ell \) satisfies the structural requirements of the k-HE-based compiler. All  factors are omitted.
factors are omitted.
Implications. When \(\mathsf {WY}_\ell \) is compiled with the k-HE based compiler, we obtain the following result.
Corollary 1
(Informal). Let \(k, \ell \in \mathbb {N}\) be constants with \(k \le \ell \), and \(d < \frac{(\ell +1)m}{t}\). Suppose there exists a CPA-secure k-HE scheme. Then there exists an (n, m, t)-HSS for degree-d polynomials with the following efficiency measures:
-
Recovery information size \(\rho ' = n\)
-
Input share size \(\alpha ' = n\)
-
Output share size \(\beta ' = n^{\ell - k}\)
-
Server computation \(\sigma ' = |f| n^{\ell -1} + n^{2\ell }\)
-
Client computation \(\gamma ' = m n^{\ell - k}\)
All  factors contributed by the ciphertext size and \(\log |\mathbb {F}|\) are omitted.
factors contributed by the ciphertext size and \(\log |\mathbb {F}|\) are omitted.
 contributed by \(\log |\mathbb {F}|\) and k-HE ciphertext size are omitted.
contributed by \(\log |\mathbb {F}|\) and k-HE ciphertext size are omitted.As shown in Table 1, if we treat \(\ell \) as a constant, the k-HE-compiled \(\mathsf {WY}_\ell \) scheme strictly outperforms the k-HE-compiled \(\mathsf {CNF}_\ell \) scheme (\(\ell = 1\) in LMS [31, 35]) in all parameters. We are mostly interested in the setting where the communication is balanced, in the sense that the input share size is comparable to the output share size. From Corollary 1, this can be achieved by setting \(\ell = k+1\).
In Table 2, we highlight some practically interesting parameters for the k-HE-compiled \(\mathsf {WY}_\ell \) scheme. For a fixed communication cost  , we state the relation between k, \(\ell = k+1\) (so that the HSS is balanced), the corruption threshold t, the number of servers m, and the degree d of supported polynomials. The degree d reported for each setting of (t, m) is generally higher than that supported by LMS [31] (\(t=1\)) and [35] (\(t \ge 1\)) by an additive factor of m/t, since they did not consider balanced HSS schemes. We focus on small \(k = O(1)\) since for such values of k it is not known how a k-HE can be bootstrapped [23] into an FHE. For
, we state the relation between k, \(\ell = k+1\) (so that the HSS is balanced), the corruption threshold t, the number of servers m, and the degree d of supported polynomials. The degree d reported for each setting of (t, m) is generally higher than that supported by LMS [31] (\(t=1\)) and [35] (\(t \ge 1\)) by an additive factor of m/t, since they did not consider balanced HSS schemes. We focus on small \(k = O(1)\) since for such values of k it is not known how a k-HE can be bootstrapped [23] into an FHE. For  , k-HE can be realized based on assumptions that are not known to imply FHE: For polynomials whose outputs are contained in a polynomial-size space, the ElGamal encryption [21] is a 1-HE based on the decisional Diffie Hellman (DDH) assumption, and the BGN encryption [7] is a 2-HE based on the subgroup decision assumption. For large outputs, the Paillier encryption [34] and Damgård–Jurik encryption [19] are 1-HE based on the decisional composite residuosity assumption. The additive variant of ElGamal [14] is a 1-HE based on DDH in groups with a discrete-logarithm-easy subgroup. For general \(k = O(1)\), k-HE can be construction from the learning with errors assumption with smaller parameters than those which imply FHE, and therefore are concretely efficient.
, k-HE can be realized based on assumptions that are not known to imply FHE: For polynomials whose outputs are contained in a polynomial-size space, the ElGamal encryption [21] is a 1-HE based on the decisional Diffie Hellman (DDH) assumption, and the BGN encryption [7] is a 2-HE based on the subgroup decision assumption. For large outputs, the Paillier encryption [34] and Damgård–Jurik encryption [19] are 1-HE based on the decisional composite residuosity assumption. The additive variant of ElGamal [14] is a 1-HE based on DDH in groups with a discrete-logarithm-easy subgroup. For general \(k = O(1)\), k-HE can be construction from the learning with errors assumption with smaller parameters than those which imply FHE, and therefore are concretely efficient.
Application to MPC with Preprocessing. In typical (n, m, t)-HSS schemes, including ones constructed in this work, there exists \(p < m\) such that any p input shares are distributed uniformly over an efficiently sampleable space. In other words, the input shares of any, say the first, p parties contain no information about the input \((x_1,\ldots ,x_n)\), and can be generated in a preprocessing phase even before the inputs \((x_1,\ldots ,x_n)\) are known. We formalize this as the p-preprocessing property, and show that the \(\mathsf {WY}_\ell \) scheme its k-HE-compiled counterpart support  -preprocessing.
-preprocessing.
We then show that, given a general purpose MPC protocol (whose communication cost might be linear in the function description size), an HSS for polynomials with p-preprocessing can be compiled into a communication-efficient MPC for polynomials with preprocessing. Our technique generalizes the approach taken in [5] for obtaining 2-party MPC with preprocessing from 3-server PIR.
Recall that an MPC protocol with preprocessing is split into two phases – a preprocessing phase and an online phase. In the preprocessing phase, a trusted party performs an input-independent preprocessing on the function f, and distributes shares of the preprocessing result to the m participants. Alternatively, the trusted party can be emulated by an MPC among the m parties. Then, in the online phase, the m parties collectively receive their online inputs \((x_1,\ldots ,x_n)\), where each party either possesses a share or a disjoint subset of entries of \((x_1,\ldots ,x_n)\), and interact in an online MPC protocol to compute \(f(x_1, \ldots , x_n)\). The hope is that, by exploiting the offline preprocessing, the online communication cost can be reduced such that it is independent of the description size of f.
Our idea is to push the work of the first p servers in an HSS scheme with p-preprocessing to the preprocessing phase of the MPC protocol, and thereby reduce the minimal necessary number of parties required to run the protocol. The MPC preprocessing first generates the inputs shares of the first p HSS servers, which can be done independently of the input. It then homomorphically evaluates f on the p input shares to produce p output shares. The input and output shares of the first p HSS servers are then secret shared among the m MPC participants.
In the online phase, the m MPC participants receive their respective inputs \((x_1,\ldots ,x_n)\) and engage in an MPC protocol to generate the remaining input shares. Naturally, the j-th participant gets the \((p+j)\)-th HSS input share. Each participant can then proceed to homomorphically evaluate f on their input shares, and then engage in another MPC to recover the computation result from all output shares.
Note that the two MPC sub-protocols run in the online phase are computing functions whose circuit size is comparable to the input size, independently of |f|. For degree d polynomials, |f| can be of size \(O(n^d)\). Our MPC protocol therefore potentially achieves an exponential improvement over general-purpose MPC, without using heavy tools such as FHE.
In the case where t is a multiple of \(\ell +1\), when instantiated with the k-HE-compiled \(\mathsf {WY}_\ell \) scheme and, say, an OT-based MPC, we obtain an m party MPC protocol with preprocessing for degree-d polynomials, where \(d < \frac{(\ell +1)m}{t} + 1\), i.e., the degree grows by 1 compared to a direct use of HSS without increasing the number of participants. The online communication is  . As long as \(|f| = \omega (mn^{\ell -k})\), which holds for the vast majority of n-variate polynomials of degree \(d<\frac{(\ell +1)m}{t} + 1\), our preprocessing MPC achieves a communication complexity sublinear in |f|. Due to the requirement that t is a multiple of \(\ell +1\), the preprocessing technique seems to be more suited to the setting where t is large (close to m). In Table 3, we highlight some practically interesting parameters for the MPC protocols with preprocessing obtained via our transformation.
. As long as \(|f| = \omega (mn^{\ell -k})\), which holds for the vast majority of n-variate polynomials of degree \(d<\frac{(\ell +1)m}{t} + 1\), our preprocessing MPC achieves a communication complexity sublinear in |f|. Due to the requirement that t is a multiple of \(\ell +1\), the preprocessing technique seems to be more suited to the setting where t is large (close to m). In Table 3, we highlight some practically interesting parameters for the MPC protocols with preprocessing obtained via our transformation.
 communication, based on HE for linear or quadratic functions.
communication, based on HE for linear or quadratic functions.Beyond the computation of degree-d polynomials, our preprocessing MPC can be used as a building block in MPC for structured circuits whose “gates” compute degree-d mappings, similar to the ideas of [10, 11, 17] for evaluating layered circuits and circuits over low-degree gates. Some examples for useful circuits of this kind were given in [17]. These include circuits for Fast Fourier Transform (FFT), symmetric-key cryptography, and dynamic programming.
1.4 Related Work
In addition to the aforementioned related works, we point out that the task of evaluating degree-d n-variate polynomials privately was also considered in the context of maliciously-secure MPC, where the adversary is allowed to corrupt all but one parties, i.e., \(t = m-1\), whereas we only consider HSS and MPC schemes in the semi-honest setting. Below we discuss the semi-honest protocols implicitly described in two maliciously-secure MPC, both of which are indirectly based on the idea of compiling an IT HSS using a k-HE (for \(k=1\)), which is made explicit in this work. These schemes inherently require that the polynomial to be evaluated is represented in expanded form, and consequently has only polynomially-many monomials. In contrast, our \(\mathsf {WY}\)-based schemes support polynomials represented by polynomial-sized arithmetic circuits.
The semi-honest part of the 2-party protocol of Franklin and Mohassel [22] is precisely the HSS obtained by compiling \(\mathsf {CNF}_1\) with a 1-HE in the setting where \((t,m) = (1,2)\). They also proposed an m-party (maliciously-secure) protocol for degree-d polynomials which achieves computation and communication complexity  , which is comparable to the 1-HE compiled \(\mathsf {WY}_{\ell }\) scheme which has communication complexity \(m(\ell n)^{\ell - 1}\) and supports polynomials of degree at least \(\ell + 1\) (c.f., Table 1).
, which is comparable to the 1-HE compiled \(\mathsf {WY}_{\ell }\) scheme which has communication complexity \(m(\ell n)^{\ell - 1}\) and supports polynomials of degree at least \(\ell + 1\) (c.f., Table 1).
Underneath the protocol of Dachman-Soled et al. [18] lies the following protocol for evaluating a (publicly known) monomial \(\mu (x_1,\ldots ,x_n)\) where \((x_1,\ldots ,x_n)\) are jointly contributed by m parties. First, the monomial is split into \(\mu = \mu _1 \cdot \ldots \cdot \mu _m\), where \(\mu _i(x_1,\ldots ,x_n)\) is a monomial which depends only on the inputs of the i-th party. Party 1 encrypts the evaluation of \(\mu _1\) using a 1-HE and sends the ciphertext \(c_1\) to Party 2. Then, for  , Party i homomorphically multiplies \(\mu _i\) to the ciphertext \(c_{i-1}\) encrypting \(\mu _1 \cdot \ldots \cdot \mu _{i-1}\) received from Party \(i-1\) to obtain a new ciphertext \(c_i\). Finally, Party i sends \(c_i\) to Party \(i+1\) if \(i \ne m\), or to everyone if \(i = m\). Based on the above incremental evaluation protocol, the (maliciously-secure) protocol of Dachman-Soled et al. [18] requires (roughly) \(O(n^2 \log ^2 d)\) communication and \(O(n \log d)\) computation, where the logarithmic dependency on d is achieved by having each party precompute the powers-of-2 of their inputsFootnote 4. Due to the logarithmic dependency on d and the limit of the number of monomials, their scheme seems best suited for evaluating sparse polynomials of a high degree
, Party i homomorphically multiplies \(\mu _i\) to the ciphertext \(c_{i-1}\) encrypting \(\mu _1 \cdot \ldots \cdot \mu _{i-1}\) received from Party \(i-1\) to obtain a new ciphertext \(c_i\). Finally, Party i sends \(c_i\) to Party \(i+1\) if \(i \ne m\), or to everyone if \(i = m\). Based on the above incremental evaluation protocol, the (maliciously-secure) protocol of Dachman-Soled et al. [18] requires (roughly) \(O(n^2 \log ^2 d)\) communication and \(O(n \log d)\) computation, where the logarithmic dependency on d is achieved by having each party precompute the powers-of-2 of their inputsFootnote 4. Due to the logarithmic dependency on d and the limit of the number of monomials, their scheme seems best suited for evaluating sparse polynomials of a high degree  .
.
2 Preliminaries
Let  denote the security parameter. The set of all polynomials and negligible functions in
denote the security parameter. The set of all polynomials and negligible functions in  are denoted by
are denoted by  and
and  respectively. An algorithm with input length n is
respectively. An algorithm with input length n is  if it can be computed by a probabilistic Turing machine whose running time is bounded by some function
if it can be computed by a probabilistic Turing machine whose running time is bounded by some function  . We use [n] to denote the set \(\{1,\ldots ,n\}\), and \(\mathbb {N}_0\) to denote the set of all non-negative integers. Given a finite set S, we denote by \(x \leftarrow S\) the sampling of an element uniformly at random in S.
. We use [n] to denote the set \(\{1,\ldots ,n\}\), and \(\mathbb {N}_0\) to denote the set of all non-negative integers. Given a finite set S, we denote by \(x \leftarrow S\) the sampling of an element uniformly at random in S.
For simplicity, throughout this work we fix a field \(\mathbb {F}\) which is sufficiently large, such that for any polynomial \(f \in \mathbb {F}[X_1,\ldots ,X_n]\) we will be considering, we have  . An \(\mathbb {F}\) element can therefore be represented by
. An \(\mathbb {F}\) element can therefore be represented by  bits. Let \(\mathbf {e} = (e_1, \ldots , e_n) \in \mathbb {N}_0^n\) and \(\mathbf {x} = (x_1, \ldots , x_n) \in \mathbb {F}^n\). We define the weight function \(\mathsf {wt}(\mathbf {e}) := e_1 + \ldots + e_n\). We use \(\mathbf {x}^\mathbf {e}\) to denote the expression \(\mathbf {x}^\mathbf {e} := x_1^{e_1} \ldots x_n^{e_n}\).
bits. Let \(\mathbf {e} = (e_1, \ldots , e_n) \in \mathbb {N}_0^n\) and \(\mathbf {x} = (x_1, \ldots , x_n) \in \mathbb {F}^n\). We define the weight function \(\mathsf {wt}(\mathbf {e}) := e_1 + \ldots + e_n\). We use \(\mathbf {x}^\mathbf {e}\) to denote the expression \(\mathbf {x}^\mathbf {e} := x_1^{e_1} \ldots x_n^{e_n}\).
2.1 Homomorphic Encryption for Degree-k Polynomials (k-HE)
We recall the notion of homomorphic encryption for degree-k polynomials over \(\mathbb {F}\).
Definition 1
(Homomorphic Encryption). A homomorphic encryption scheme  for degree-k polynomials over \(\mathbb {F}\), k-HE for short, consists of the following
for degree-k polynomials over \(\mathbb {F}\), k-HE for short, consists of the following  algorithms:
algorithms:
-
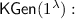 The key generation algorithm takes as input the security parameter
The key generation algorithm takes as input the security parameter  and outputs the public key
and outputs the public key 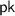 and the secret key
and the secret key 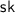 .
. -
 The encryption algorithm takes as input the public key
The encryption algorithm takes as input the public key  and a message \(\mathbf {x} \in \mathbb {F}^n\) for some
and a message \(\mathbf {x} \in \mathbb {F}^n\) for some 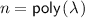 ; it returns a ciphertext \(\mathbf {c} \in \mathcal {C}^n\) in some ciphertext space \(\mathcal {C}\).
; it returns a ciphertext \(\mathbf {c} \in \mathcal {C}^n\) in some ciphertext space \(\mathcal {C}\). -
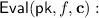 The evaluation algorithm takes as input the public key
The evaluation algorithm takes as input the public key  , (the description of) a polynomial \(f \in \mathbb {F}[X_1,\ldots ,X_n]\), and a ciphertext \(\mathbf {c} \in \mathcal {C}^n\) for some
, (the description of) a polynomial \(f \in \mathbb {F}[X_1,\ldots ,X_n]\), and a ciphertext \(\mathbf {c} \in \mathcal {C}^n\) for some  ; it returns a ciphertext \(c' \in \mathcal {C}\).
; it returns a ciphertext \(c' \in \mathcal {C}\). -
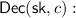 The decryption algorithm takes as input the private key
The decryption algorithm takes as input the private key 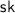 and a ciphertext \(\mathbf {c} \in \mathcal {C}^n\) for some
and a ciphertext \(\mathbf {c} \in \mathcal {C}^n\) for some  ; it returns a plaintext \(\mathbf {x} \in \mathbb {F}^n\).
; it returns a plaintext \(\mathbf {x} \in \mathbb {F}^n\).
We focus only on compact HE schemes [23], where the size of the ciphertext space  is independent of the size of the supported polynomials.
is independent of the size of the supported polynomials.
Definition 2
(Correctness). A k-HE scheme is said to be correct if for any  , any
, any  , any positive integer
, any positive integer  , any polynomial \(f \in \mathbb {F}[X_1,\ldots ,X_n]\) of degree at most k, and message \(x \in \mathbb {F}^n\), we have
, any polynomial \(f \in \mathbb {F}[X_1,\ldots ,X_n]\) of degree at most k, and message \(x \in \mathbb {F}^n\), we have

where the probability is taken over the random coins of  and
and  . The scheme is perfectly correct if the above probabilities are exactly 1.
. The scheme is perfectly correct if the above probabilities are exactly 1.
Definition 3
(CPA-Security). A homomorphic encryption scheme \(\mathsf {HE} \) is IND-CPA-secure (has indistinguishable ciphertexts under chosen plaintext attack) if for any  adversary
adversary 

where the experiment  is defined in Fig. 1.
is defined in Fig. 1.
3 Definition of Homomorphic Secret Sharing
We recall the notion of homomorphic secret sharing [12]. The definitions presented here are for the variant in the public-key setup model [31]. For the definitions in the plain model, we refer to [12, 31].
Definition 4
(Homomorphic Secret Sharing (HSS)). An n-input m-server homomorphic secret sharing scheme  for degree-d polynomials over \(\mathbb {F}\) consists of the following
for degree-d polynomials over \(\mathbb {F}\) consists of the following  algorithms:
algorithms:
-
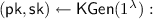 On input the security parameter
On input the security parameter 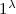 , the key generation algorithm outputs a public key
, the key generation algorithm outputs a public key 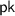 and a secret key
and a secret key 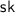 .
. -
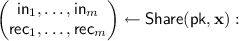 Given a public key
Given a public key 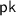 , and an input \(\mathbf {x} \in \mathbb {F}^n\), the sharing algorithm outputs a a set of input shares \((\mathsf {in} _1, \ldots , \mathsf {in} _m)\) where
, and an input \(\mathbf {x} \in \mathbb {F}^n\), the sharing algorithm outputs a a set of input shares \((\mathsf {in} _1, \ldots , \mathsf {in} _m)\) where 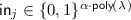 and their corresponding recovery information \((\mathsf {rec} _1, \ldots , \mathsf {rec} _m)\) where
and their corresponding recovery information \((\mathsf {rec} _1, \ldots , \mathsf {rec} _m)\) where 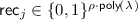 .
. -
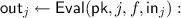 The evaluation algorithm is executed by a server
The evaluation algorithm is executed by a server  on inputs the public key
on inputs the public key  , an index j, (the description of) a degree-d polynomial f, and a share \(\mathsf {in} _j\). Upon termination, the server
, an index j, (the description of) a degree-d polynomial f, and a share \(\mathsf {in} _j\). Upon termination, the server 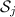 outputs the corresponding output share
outputs the corresponding output share 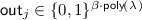 .
. -
 On input a secret key
On input a secret key 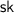 , a tuple of output shares \((\mathsf {out} _1, \ldots , \mathsf {out} _m)\), and a tuple of recovery information \((\mathsf {rec} _1, \ldots , \mathsf {rec} _m)\), the decoding algorithm outputs the result y of the evaluation.
, a tuple of output shares \((\mathsf {out} _1, \ldots , \mathsf {out} _m)\), and a tuple of recovery information \((\mathsf {rec} _1, \ldots , \mathsf {rec} _m)\), the decoding algorithm outputs the result y of the evaluation.
The efficiency measures \(\rho = \rho (n)\), \(\alpha = \alpha (n)\) and \(\beta = \beta (n)\) are the lengths of the recovery information, input shares, and output shares respectively (omitting  factors). An HSS scheme is said to be compact if
factors). An HSS scheme is said to be compact if  (independent of n), and balanced if \(\beta = O(\alpha )\).
(independent of n), and balanced if \(\beta = O(\alpha )\).
Remark 1
In the syntax, we decide to split the recovery information into m chunks \((\mathsf {rec} _1,\ldots ,\mathsf {rec} _m)\), so that it is more convenient to describe the compiler in Sect. 5, and so that we can omit a factor of m from the measure \(\rho \) to reduce clutter. In general, the recovery information can be grouped into a single object \(\mathsf {rec} \) and the definition \(\rho \) can be changed accordingly.
Remark 2
In the literature, an HSS scheme is usually defined without the recovery information \((\mathsf {rec} _1,\ldots ,\mathsf {rec} _m)\), i.e., \(\rho = 0\). We remark that given an HSS scheme with efficiency measures \((\rho ,\alpha ,\beta )\), we can construct another scheme (with the same security under the same assumptions) with efficiency measures \((0,\alpha +m \rho ,\beta +m \rho )\), by having the input client secret-share r to the servers and the servers relaying those shares to the output client. We use the present definition for convenience.
Remark 3
Our syntax describes a setting where a single party provides all n inputs to the \(\mathsf {Share} \) algorithm for simplicity. In the case where the input \(x_i\) is provided by party i, we can consider an alternative syntax of \(\mathsf {Share} \) which inputs  and outputs \((\mathsf {in} _{i,j}, \mathsf {rec} _{i,j})\). The \(\mathsf {Share} \) algorithm of all HSS schemes considered in this work can be “split” to suit the multi-input syntax.
and outputs \((\mathsf {in} _{i,j}, \mathsf {rec} _{i,j})\). The \(\mathsf {Share} \) algorithm of all HSS schemes considered in this work can be “split” to suit the multi-input syntax.
Definition 5
(Correctness). An n-input m-server HSS scheme for degree-d polynomials is correct if for any  , any
, any  , any \(f \in \mathbb {F}[X_1,\ldots ,X_n]\) with \(\deg (f) \le d\), any n-tuple of inputs \(\mathbf {x} = (x_1, \dots , x_n) \in \mathbb {F}^n\), it holds that
, any \(f \in \mathbb {F}[X_1,\ldots ,X_n]\) with \(\deg (f) \le d\), any n-tuple of inputs \(\mathbf {x} = (x_1, \dots , x_n) \in \mathbb {F}^n\), it holds that

where the probability is taken over the random coins of \(\mathsf {Share} \) and  . The scheme is perfectly correct if the above probability is exactly 1.
. The scheme is perfectly correct if the above probability is exactly 1.
The security of an HSS scheme is analogous to the CPA-security of HE, and guarantees that no information about the message is disclosed to any t servers.
Definition 6
(Security). An n-input m-server HSS scheme is t-secure if for any  there exists a negligible function
there exists a negligible function  such that for any
such that for any  algorithm
algorithm  ,
,

where  is defined in Fig. 2 for \(b \in \{0,1\}^{} \).
is defined in Fig. 2 for \(b \in \{0,1\}^{} \).
We use the short hand (n, m, t)-HSS to refer to n-input, m-server, t-secure homomorphic secret sharing.
Definition 7
(p-Preprocessing). We say that an (n, m, t)-HSS scheme  supports p-preprocessing if there exists
supports p-preprocessing if there exists  algorithms \((\mathsf {PreProc}, \mathsf {ShareComp})\) such that, for any
algorithms \((\mathsf {PreProc}, \mathsf {ShareComp})\) such that, for any  , any
, any  and any \(\mathbf {x} \in \mathbb {F}^n\), the following distributions are identical:
and any \(\mathbf {x} \in \mathbb {F}^n\), the following distributions are identical:

If an HSS scheme supports p-preprocessing, it means that the shares of the first p servers are independent of the input \(\mathbf {x}\), and can thus be computed in a preprocessing phase when the input \(\mathbf {x}\) is yet unknown.
Definition 8
(Information-Theoretic HSS). We say that  is information-theoretic (IT) if
is information-theoretic (IT) if  outputs empty strings, and \(\mathsf {HSS} \) is secure against unbounded adversaries. In such case we simply write
outputs empty strings, and \(\mathsf {HSS} \) is secure against unbounded adversaries. In such case we simply write  to denote the HSS scheme and omit the public and secret key inputs to the algorithms \(\mathsf {Share} \),
to denote the HSS scheme and omit the public and secret key inputs to the algorithms \(\mathsf {Share} \),  , and
, and  . In case \(\mathsf {HSS} \) supports p-preprocessing, we also omit the public key input to \(\mathsf {PreProc}\) and \(\mathsf {ShareComp}\).
. In case \(\mathsf {HSS} \) supports p-preprocessing, we also omit the public key input to \(\mathsf {PreProc}\) and \(\mathsf {ShareComp}\).
4 Information-Theoretic Homomorphic Secret Sharing
Information-theoretic HSS exists implicitly in the literature of secret sharing and private information retrieval (PIR). The simplest examples are the additive secret sharing scheme and Shamir’s secret sharing scheme [36]. The former is an \((n,m,m-1)\)-HSS for degree-1 polynomials, i.e., linear functions, with efficiency measures while the latter is an (n, m, t)-HSS for degree- polynomials. Both schemes are compact as an output share consists of a single \(\mathbb {F}\) element.
polynomials. Both schemes are compact as an output share consists of a single \(\mathbb {F}\) element.
In the following, we extract two IT HSS schemes – the “CNF” scheme \(\mathsf {CNF}_0\) [29] and the scheme \(\mathsf {WY}_1\) from Woodruff and Yekhanin [37] – from the literature of private information retrieval (PIR) which are generalizations of the additive and Shamir secret sharing schemes respectively. We then present the “\(\ell \)-th order” generalizations of the two schemes – \(\mathsf {CNF}_\ell \) and \(\mathsf {WY}_\ell \) – which aim to support higher-degree polynomials at the cost of, among other parameters, larger recovery information size and higher degree client computation. The generalizations are done in a way compatible with the compiler to be presented in Sect. 5, so that the higher degree client computation can be delegated back to the servers in the compiled schemes. While the \(\mathsf {CNF}_\ell \) scheme is strictly inferior to the \(\mathsf {WY}_\ell \) for all \(\ell \), we include it since compiling \(\mathsf {CNF}_1\) with our compiler in Sect. 5 captures the LMS scheme [31, 35].
4.1 CNF Secret Sharing
A generalization of the additive secret sharing scheme is the so called CNF secret sharing scheme [29], where CNF stands for conjunctive normal form. The scheme was first used in the context of PIR by Ishai and Kushilevitz [28].
Original Scheme \(\mathsf {CNF}_0\). The idea of the CNF scheme is to write \(\mathbf {x} \in \mathbb {F}^n\) as a sum of random elements so that \(\mathbf {x} = \sum _\mathbf {u} \mathbf {c}_{\mathbf {u}}\), where \(\mathbf {u} = (u_1, \ldots , u_m) \in \{0,1\}^m\) runs through all possible choices of choosing t out of m objects. The j-th share is then defined as \(\mathbf {s}_j := (\mathbf {c}_\mathbf {u})_{\mathbf {u}: u_j = 0}\), i.e., all \(\mathbf {c}_\mathbf {u}\) where the j-th bit of \(\mathbf {u}\) is 0. The scheme is t-secure because, given any t-subset \(\{j_1,\ldots ,j_t\} \subseteq [m]\), there exists \(\mathbf {c}_{\mathbf {u}^*}\), where \(u^*_j = 1\) for all \(j \in \{j_1,\ldots ,j_t\}\), which is not known to this subset of servers.
The CNF scheme is clearly linearly homomorphic. Thus, for evaluating a polynomial of degree d, it suffices to show how a monomial \(\mathbf {x}^\mathbf {e}\) where \(\mathsf {wt}(\mathbf {e}) = d\) can be evaluated. Without loss of generality, we consider the monomial
To let the output client recover \(x_1 \cdots x_d\), one way is to have (at least) one server being able to compute for each \((\mathbf {u}_1,\ldots ,\mathbf {u}_d)\) the term \(\prod _{i=1}^d c_{i,\mathbf {u}_i}\). If so, we distribute the terms so that each term is computed by exactly one server. Each server can compute the partial sum of all the terms that it is assigned, and send this sum to the output client. The latter can then sum over all partial sums and recover \(x_1 \cdots x_d\).
We now examine the term \(\prod _{i=1}^d c_{i,\mathbf {u}_i}\) for any fixed \(\mathbf {u}_1,\ldots ,\mathbf {u}_d \in \{0,1\}^{m} \) with \(\mathsf {wt}(\mathbf {u}_i) = t\). Consider the string \(\mathbf {u} = \mathbf {u}_1 \vee \ldots \vee \mathbf {u}_d\) obtained by bit-wise OR operations. Note that if \(d \le \frac{m-1}{t}\), we have
Therefore there must exist \(j^* \in [m]\) such that \(\mathbf {u}_{i,j^*} = 0\) for all \(i \in [d]\). That is, server \(j^*\) possesses \(c_{1,\mathbf {u}_1}, \ldots , c_{d,\mathbf {u}_d}\) and can thus compute the term.
Although it is information theoretically possible for the parties to compute \(x_1 \cdots x_d\), there seems to be no natural way to distribute the terms among the servers. In particular, as noted in [27], when \(t = 1\), \(m = d + 1\), and the terms are distributed greedily to the servers, then the last server would need to compute the permanent of a d-by-d matrix, which is #P-hard. The difficulty of distributing the terms limits the number of servers in [31, 35] to be logarithmic in  .
.
For the case \(t = 1\), [27, Section 5.2] showed an alternative method of computing \(x_1 \cdots x_d\) efficiently. The idea is essentially to first locally convert a CNF share into a Shamir share of the same secret, and then perform homomorphic evaluation on the Shamir share. We present here a generalization of the method for any \(t < m\). Fix an arbitrary m-subset  . Define the degree-dt polynomial
. Define the degree-dt polynomial
such that \(p(0) = \prod _{i=1}^{d} \sum _{\begin{array}{c} \mathbf {u} \in \{0,1\}^{m}: \\ \mathsf {wt}(\mathbf {u}) = t \end{array}} c_{i,\mathbf {u}} = x_1 \cdots x_d\). Note that \(p(\zeta _j)\) does not depend on the values of \(c_{i,\mathbf {u}}\) where the j-th bit of \(\mathbf {u}\) is 1, and can therefore be computed by the j-th server. Since the degree of p is \(dt \le m-1\), p(0) can be recovered by interpolating \(p(\zeta _1), \ldots , p(\zeta _m)\).
In general, given an n-variate degree-d polynomial f, we can define
The value \(f(\mathbf {x})\) can be recovered by \(f(\mathbf {x}) = p_f(0)\).
Generalized Scheme \(\mathsf {CNF}_\ell \). In the above, the client is required to perform only a simple linear computation for recovery. We show that the computation of higher degree polynomials is possible, if the client is willing to perform a degree-\(\ell \) computation for \(\ell > 1\).
We first consider the naive strategy of distributing terms to servers, and discuss the interpolation-based approach later. In the former setting, it suffices to have that, for any fixed \(\mathbf {u}_1,\ldots ,\mathbf {u}_d \in \{0,1\}^{m} \) with \(\mathsf {wt}(\mathbf {u}_i) = t\), there exists a server \(j^* \in [m]\) and an index set I of size \(|I| \ge d - \ell \) such that \(u_{i,j^*} = 0\) for all \(i \in I\). Server \(j^*\) can therefore compute \(\prod _{i \in I} c_{i,\mathbf {u}_i}\), and leave the computation of \(\prod _{i \in [d] \setminus I} c_{i,\mathbf {u}_i}\) to the output client. To compute the latter, the client would need to store locally a copy of all shares – the recovery information is the same as the input shares.
We argue that if \(dt < (\ell +1) m\), then the above condition is satisfied. Suppose not, then for all \(j \in [m]\), we have \(|\{i \in [d]: u_{i,j} = 0\}| \le d - \ell - 1\). In other words, for all \(j \in [m]\), we have \(|\{i \in [d]: u_{i,j} = 1\}| \ge \ell + 1\). Summing up the weights of all \(\mathbf {u}_i\), we have \(\sum _{i=1}^d \mathsf {wt}(\mathbf {u}_i) \ge (\ell +1)m\). By the pigeonhole principle, there must exist \(i^*\) such that
which is a contradiction as \(\mathsf {wt}(\mathbf {u}_i) = t\) for all \(i \in [d]\).
The CNF scheme suffers from many drawbacks. First, each input share consists of \(\left( {\begin{array}{c}m\\ t\end{array}}\right) n\) \(\mathbb {F}\) elements. It also suffers from inefficient evaluation, unless the interpolation-based evaluation is used, which makes it equivalent to the scheme presented in Sect. 4.2, except with larger input shares. Finally, the output share size is upper bounded by the number of monomials of degree at most \(\ell \) over the variables \((c_{i,u})_{i \in [n], \mathbf {u} \in \{0,1\}^{m}: \mathsf {wt}(\mathbf {u}) = t}\), i.e., \(\left( {\begin{array}{c}\left( {\begin{array}{c}m\\ t\end{array}}\right) n+ \ell \\ \ell \end{array}}\right) = O((m^t n)^{\ell })\).
We next state the formal theorem about the \(\mathsf {CNF}_\ell \) scheme. Its proof is already written inline in the above discussion.
Theorem 3
Let \(d < \frac{(\ell +1)m}{t}\). The \(\ell \)-th order CNF secret sharing scheme \(\mathsf {CNF}_\ell \) is an IT (n, m, t)-HSS for degree-d polynomials, with efficiency measures \((\rho ,\alpha ,\beta ) = \left( m^t n, m^t n, (m^t n)^\ell \right) \).
Similar to the \(\ell = 0\) case, the above approach suffers in evaluation efficiency since there is no natural way to distribute the terms. Naturally, one would hope to use a generalization of the interpolation-based approach to achieve the same parameter ( ). Indeed, in Sect. 4.2 we recall and generalize a technique by Woodruff and Yekhanin [37] of using partial derivatives and Hermite interpolation to support higher degree polynomials, which would also be applicable in \(\mathsf {CNF}_\ell \). Since the resulting schemes, which we denote by \(\mathsf {WY}_\ell \), are superior to \(\mathsf {CNF}_\ell \) in all parameters, we do not discuss applying the technique to \(\mathsf {CNF}_\ell \) in detail.
). Indeed, in Sect. 4.2 we recall and generalize a technique by Woodruff and Yekhanin [37] of using partial derivatives and Hermite interpolation to support higher degree polynomials, which would also be applicable in \(\mathsf {CNF}_\ell \). Since the resulting schemes, which we denote by \(\mathsf {WY}_\ell \), are superior to \(\mathsf {CNF}_\ell \) in all parameters, we do not discuss applying the technique to \(\mathsf {CNF}_\ell \) in detail.
4.2 \(\ell \)-th Order Woodruff-Yekhanin HSS
In an insightful work of Woodruff and Yekhanin [37], they constructed a PIR scheme which can be viewed as an (n, m, t)-HSS for degree- polynomials, which we call the first-order Woodruff-Yekhanin HSS \(\mathsf {WY}_1\). The idea of the scheme is as follows.
polynomials, which we call the first-order Woodruff-Yekhanin HSS \(\mathsf {WY}_1\). The idea of the scheme is as follows.
First Order Scheme by Woodruff and Yekhanin. We begin with the sharing procedures of Shamir’s scheme. To secret-share \(\mathbf {x} \in \mathbb {F}^n\), the input client sample a random (vector valued) degree-t polynomial \(\varphi (Z)\) so that \(\varphi (0) = \mathbf {x}\). The j-th share is defined as \(\mathbf {s}_j := \varphi (j)\). What differs from Shamir’s scheme is that the input client also computes, as recovery information, the derivatives of \(\varphi \) evaluated at \(j \in [m]\), denoted by \(\varphi ^{(1)}(j)\), \(\varphi '(j)\), or \(\frac{d\varphi }{dZ}(j)\).
To evaluate a polynomial f of degree  over a share \(\mathbf {s}_j\), server j computes as in Shamir’s scheme \(f(\mathbf {s}_j) = f(\varphi (j))\). Additionally, it computes all partial derivatives of f evaluated at \(\mathbf {s}_j\), denoted by \(\left( \frac{\partial f}{\partial X_i}(\mathbf {s}_j)\right) _{i \in [n]}\). The j-th output share is defined as \(y_j := \left( f(\mathbf {s}_j), \frac{\partial f}{\partial X_1}(\mathbf {s}_j), \ldots , \frac{\partial f}{\partial X_n}(\mathbf {s}_j)\right) \).
over a share \(\mathbf {s}_j\), server j computes as in Shamir’s scheme \(f(\mathbf {s}_j) = f(\varphi (j))\). Additionally, it computes all partial derivatives of f evaluated at \(\mathbf {s}_j\), denoted by \(\left( \frac{\partial f}{\partial X_i}(\mathbf {s}_j)\right) _{i \in [n]}\). The j-th output share is defined as \(y_j := \left( f(\mathbf {s}_j), \frac{\partial f}{\partial X_1}(\mathbf {s}_j), \ldots , \frac{\partial f}{\partial X_n}(\mathbf {s}_j)\right) \).
Finally, to decode the output shares, the output client first recover \((f \circ \varphi )'(\mathbf {s}_j) = \frac{df \circ \varphi }{dZ}(\mathbf {s}_j)\) by using the chain rule of derivatives. Then, since \(f \circ \varphi \) is a univariate polynomial of degree at most \(2m-1\), it is possible to recover \(f(\varphi (0)) = f(x)\) from m points on \(f \circ \varphi \) and m points on \((f \circ \varphi )'\) using Hermite interpolation.
The scheme of Woodruff and Yekhanin is balanced, meaning that both input and output shares consist of O(n) \(\mathbb {F}\) elements. The result can be seen as a trade-off between \(\frac{m}{t}\) degrees and compactness, when compared to Shamir’s scheme. If we view the sharing, evaluation, and decoding procedures of an HSS as one MPC protocol, then for a fixed input share size, a balanced HSS and a compact HSS would give MPC protocols with the same asymptotic communication complexity. In this sense, the extra \(\frac{m}{t}\) degrees are gained for free.
Generalization to Higher Orders. Intuitively, a way to support polynomials of even higher degrees is to further sacrifice the output share size. The idea is to let the servers compute all partial derivatives of order at most \(\ell \), so that a polynomial of degree at most \(d < \frac{(\ell +1)m}{t}\) can be supported. In a standalone application of the HSS, this would not make sense as it is “wasteful” to have a smaller input share size than the output share size. However, with the observation that, in our compiler constructed in Sect. 5, the output share size of the resulting HSS scheme is independent of that of the base scheme, sacrificing the output share size even more for the support of more degrees might be worth it. We therefore formalize this intuition in Fig. 3 and call the resulting scheme the \(\ell \)-th order Woodruff-Yekhanin HSS, denoted by  .
.
For \(\mathbf {e} \in \mathbb {N}_0^n\), we use the notation \(f^{(\mathbf {e})}(\mathbf {x})\) to denote the high-order partial derivative \(\frac{\partial ^{\mathsf {wt}(\mathbf {e})} f}{\partial X_1^{e_1} \ldots \partial X_n^{e_n}}\) evaluated at \(\mathbf {x}\). For \(u \in [\ell ]\), we make use of a generalization of the Faa di Bruno formula [32] which expresses \((f \circ \varphi )^{(u)}(j)\) as a linear function of \((f^{(\mathbf {e})}(\mathbf {s}_j))_{\mathbf {e} \in \mathbb {N}^n_0: \mathsf {wt}(\mathbf {e}) \le u}\) with coefficients determined by degree-u polynomials of \((\varphi ^{(h)}(j))_{h \in [u]}\). We denote this formula by

Finally, we use the notation
to denote the value \(f(\varphi (0))\) recovered using Hermite interpolation.
Theorem 4
Let \(d < \frac{(\ell +1)m}{t}\). The \(\ell \)-th order Woodruff-Yekhanin HSS \(\mathsf {WY}_\ell \) is an IT (n, m, t)-HSS for degree-d polynomials with efficiency measures \((\rho ,\alpha ,\beta ) = \left( \ell n, n, n^\ell \right) \).
Proof
Input shares of \(\mathsf {WY}_\ell \) are just shares of the Shamir secret sharing scheme. Security thus follows immediately. More seriously, for any fixed t-subset of input shares  and any input \(\mathbf {x} \in \mathbb {F}^n\), there exists a unique degree-t polynomial \(\varphi \) such that \(\varphi (0) = \mathbf {x}\) and \(\varphi (j) = \mathsf {in} _j\) for all
and any input \(\mathbf {x} \in \mathbb {F}^n\), there exists a unique degree-t polynomial \(\varphi \) such that \(\varphi (0) = \mathbf {x}\) and \(\varphi (j) = \mathsf {in} _j\) for all  . The set
. The set  therefore contain no information about the true input.
therefore contain no information about the true input.
The support of degree-d polynomials follows immediately from Hermite interpolation. Specifically, we note that the output client obtains the following \((\ell +1)m\) data points:
for a univariate degree-dt polynomial \(f\circ \varphi \) and its derivatives. Since \(dt \le (\ell +1)m-1\) the client is able to recover \(f(\mathbf {x}) = f(\varphi (0))\) using Hermite interpolation.
The size of a recovery information \(\rho = \ell n\) and that of an input share \(\alpha = n\) can be easily observed. For the size of an output share, observe that an output share consists of \(\left( f(\mathbf {s}_j), f^{(\mathbf {e})}(\mathbf {s}_j)\right) _{\mathbf {e} \in \mathbb {N}^n_0: \mathsf {wt}(\mathbf {e}) \le \ell }\). The set  counts the number of n-variate monomials of degree at most \(\ell \), and thus is of size \(\left( {\begin{array}{c}n+\ell \\ \ell \end{array}}\right) = O(n^\ell )\). We thus have \(\beta = n^\ell \).
counts the number of n-variate monomials of degree at most \(\ell \), and thus is of size \(\left( {\begin{array}{c}n+\ell \\ \ell \end{array}}\right) = O(n^\ell )\). We thus have \(\beta = n^\ell \).
Note that \(\mathsf {WY}_0\) is simply the Shamir secret sharing scheme.
Computational Complexity. We remark about the computational complexity of the servers and the output client. It is well-known, e.g., by the Baur-Strassen theorem [4] or in the field of auto-differentiation, that if a multivariate polynomial f can be computed by an arithmetic circuit of size denoted by |f|, then there exists a circuit of size O(|f|) which computes f and all n first-order partial derivatives of f simultaneously. Applying this recursively to the n first-order partial derivatives suggests that the server computation is bounded by \(O(|f| n^{\ell - 1})\).
On the output client side, we note that

is a linear function with \(\left( {\begin{array}{c}n+u\\ u\end{array}}\right) \le \left( {\begin{array}{c}n+\ell \\ \ell \end{array}}\right) \) terms, where each coefficient is a degree-u polynomial with at most \(\left( {\begin{array}{c}2u\\ u\end{array}}\right) \le \left( {\begin{array}{c}2\ell \\ \ell \end{array}}\right) \) terms. The output client needs to evaluate \(\ell m\) of these. Lastly, the Hermite interpolation is a linear function with \((\ell +1)m\) terms. Therefore, the output client computation is bounded by \(O\left( \ell m \cdot \left( {\begin{array}{c}n+\ell \\ \ell \end{array}}\right) \cdot \left( {\begin{array}{c}2\ell \\ \ell \end{array}}\right) \right) = O\left( \ell m (\ell n)^\ell \right) \). For the cases of \(\ell = 1\) or \(\ell = 2\), the output client computation is O(mn) and \(O(mn^2)\) respectively.
Preprocessing. In the \(\mathsf {Share} \) algorithm of \(\mathsf {WY}_\ell \), a degree-t polynomial \(\varphi \) is sampled such that the input \(\mathbf {x}\) is encoded as \(\varphi (0) = \mathbf {x}\). Note that \(\varphi \) is not determined until \(t+1\) points on it or its derivatives are fixed. We can therefore exploit this property and push the sampling of \(p \le \frac{t}{\ell +1}\) shares and their corresponding recovery information, which in total consist of \(p (\ell +1) \le t < t+1\) points, to a preprocessing phase.
Theorem 5
Let \(p \le \frac{t}{\ell +1}\). The \(\ell \)-th order Woodruff-Yekhanin HSS \(\mathsf {WY}_\ell \) supports p-preprocessing.
Proof
We show that \(\mathsf {WY}_\ell \) supports p-preprocessing by constructing the algorithms \(\mathsf {WY}_\ell .(\mathsf {PreProc},\mathsf {ShareComp})\) in Fig. 4.
5 Compiler from IT HSS to HSS Using HE
For \(d < (k+1)m\) and  , Lai, Malavolta, and Schröder [31] proposed an (n, m, 1)-HSS scheme for degree-d polynomials based on any k-HE scheme. Generalizing their approach, we present a compiler based on homomorphic encryption from IT HSS to HSS. Our compiler makes use of the following elementary observation. Let \(f(\mathbf {X})\) be a \(\rho \)-variate degree-\(\ell \) polynomial. For any \(0 \le k \le \ell \), note that \(f(\mathbf {X})\) can be written as
, Lai, Malavolta, and Schröder [31] proposed an (n, m, 1)-HSS scheme for degree-d polynomials based on any k-HE scheme. Generalizing their approach, we present a compiler based on homomorphic encryption from IT HSS to HSS. Our compiler makes use of the following elementary observation. Let \(f(\mathbf {X})\) be a \(\rho \)-variate degree-\(\ell \) polynomial. For any \(0 \le k \le \ell \), note that \(f(\mathbf {X})\) can be written as
where \(f_\mathbf {e}(\mathbf {X})\) is a \(\rho \)-variate degree-k polynomial. Note that \(|\{\mathbf {e} \in \mathbb {N}_0^{\rho }: \mathsf {wt}(\mathbf {e}) \le \ell - k\}|\) is the number of \(\rho \)-variate monomials of degree at most \(\ell - k\), and can be computed by \(\left( {\begin{array}{c}\rho +\ell - k\\ \ell - k\end{array}}\right) = O(\rho ^{\ell -k})\).
5.1 The Compiler
Let  be a an IT (n, m, t)-HSS for degree-d polynomials with the following properties:
be a an IT (n, m, t)-HSS for degree-d polynomials with the following properties:
-
The recovery information \(\mathsf {rec} _j\) is a vector \(\mathbf {r}_j \in \mathbb {F}^{\rho }\) for all \(j \in [m]\).
-
The output share \(\mathsf {in} _j\) is a vector \(\mathbf {y}_j \in \mathbb {F}^{\beta }\) for all \(j \in [m]\).
-
The decoding algorithm
 is a linear function of \((\mathbf {y}_1, \ldots , \mathbf {y}_m)\), where the coefficient of \(\mathbf {y}_j\) is computed by a degree-\(\ell \) polynomial of \(\mathbf {r}_j\), where \(\ell \ge k\). More concretely,
is a linear function of \((\mathbf {y}_1, \ldots , \mathbf {y}_m)\), where the coefficient of \(\mathbf {y}_j\) is computed by a degree-\(\ell \) polynomial of \(\mathbf {r}_j\), where \(\ell \ge k\). More concretely, 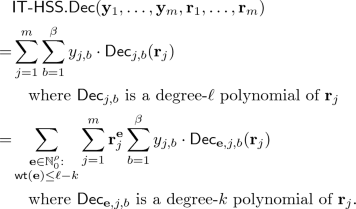
The idea of the compiler is to delegate the computation of  to server j by encrypting \(r_j\) with a homomorphic encryption scheme \(\mathsf {HE} \) which supports the evaluation of degree-k polynomials. Formally, we construct an (n, m, t)-HSS for degree-d polynomials, denoted
to server j by encrypting \(r_j\) with a homomorphic encryption scheme \(\mathsf {HE} \) which supports the evaluation of degree-k polynomials. Formally, we construct an (n, m, t)-HSS for degree-d polynomials, denoted  , in Fig. 5.
, in Fig. 5.
Note that when \(k = \ell \) the decoding function is simply

In this case the input client does not need to store a local copy of the recovery information.
Theorem 6
Let  be an (n, m, t)-HSS for degree-d polynomials satisfying the above properties, and \(\mathsf {HE} \) be a CPA-secure k-HE scheme, then \(\mathsf {HSS} \) is an (n, m, t)-HSS for degree-d polynomials. If
be an (n, m, t)-HSS for degree-d polynomials satisfying the above properties, and \(\mathsf {HE} \) be a CPA-secure k-HE scheme, then \(\mathsf {HSS} \) is an (n, m, t)-HSS for degree-d polynomials. If  and \(\mathsf {HE} \) are correct, then \(\mathsf {HSS} \) is correct. If
and \(\mathsf {HE} \) are correct, then \(\mathsf {HSS} \) is correct. If  has the efficiency measures \((\rho ,\alpha ,\beta )\), then \(\mathsf {HSS} \) has the efficiency measures \((\rho ',\alpha ',\beta ') = \left( \rho , \rho + \alpha , \rho ^{\ell - k} \right) \). If \(k = \ell \), then \(\rho ' = 0\). Note that \(\beta '\) is independent of \(\beta \).
has the efficiency measures \((\rho ,\alpha ,\beta )\), then \(\mathsf {HSS} \) has the efficiency measures \((\rho ',\alpha ',\beta ') = \left( \rho , \rho + \alpha , \rho ^{\ell - k} \right) \). If \(k = \ell \), then \(\rho ' = 0\). Note that \(\beta '\) is independent of \(\beta \).
Proof
The correctness of \(\mathsf {HSS} \) is already proven in-line in the above discussion.
For security, note that an input share \(\mathsf {in} '_j\) consists of an input share \(\mathsf {in} _j\) of the underlying IT HSS scheme and an \(\mathsf {HE} \) ciphertext \(\tilde{r}_j\). We can thus prove security by a simple hybrid argument, where we consider an intermediate hybrid security experiment where the ciphertexts \(\tilde{r}_j\) are replaced by ciphertexts encrypting zeros. Clearly, this hybrid experiment is indistinguishable from the security experiment for HSS, based on the CPA-security of \(\mathsf {HE} \). Next, we observe that the environment of the hybrid experiment can be simulated perfectly using an adversary against the security of the underlying IT HSS scheme. We can therefore conclude that the advantage of any (unbounded) adversaries in the hybrid experiment is identical to that against the security of the underlying IT HSS scheme, which is negligible.
The correctness of \(\rho '\) and \(\alpha '\) follows from simple observations. For the correctness of \(\beta '\), we observe that an output share consists of \((\tilde{d}_{\mathbf {e},j})_{\mathbf {e} \in \mathbb {N}_0^{\rho }: \mathsf {wt}(\mathbf {e}) \le \ell - k}\), where each \(\tilde{d}_{\mathbf {e},j}\) is of fixed  size since \(\mathsf {HE} \) is assumed to be compact. Note that the index set
size since \(\mathsf {HE} \) is assumed to be compact. Note that the index set  is of size \(\left( {\begin{array}{c}\rho +\ell -k\\ \ell -k\end{array}}\right) = O(\rho ^{\ell - k})\).
is of size \(\left( {\begin{array}{c}\rho +\ell -k\\ \ell -k\end{array}}\right) = O(\rho ^{\ell - k})\).
5.2 Computation Complexity
The computation complexity of the compiled scheme depends on that of the base scheme. Suppose that the base scheme has server computation \(\sigma \). We also assume that  can be computed in
can be computed in  time, and
time, and  can be computed in time
can be computed in time  . Then, the server computation of the compiled scheme is
. Then, the server computation of the compiled scheme is

and the client computation is  .
.
5.3 Preprocessing
We show that if the base scheme  supports p-preprocessing and satisfies certain additional properties, then \(\mathsf {HSS} \) p-preprocessing.
supports p-preprocessing and satisfies certain additional properties, then \(\mathsf {HSS} \) p-preprocessing.
Theorem 7
If  supports p-preprocessing, then so does \(\mathsf {HSS} \).
supports p-preprocessing, then so does \(\mathsf {HSS} \).
Proof
We construct the algorithms \(\mathsf {HSS}.(\mathsf {PreProc},\mathsf {ShareComp})\) in Fig. 6.
5.4 Instantiations
Both \(\mathsf {CNF}_\ell \) and \(\mathsf {WY}_\ell \) constructed in Sect. 4 satisfy the properties required by the compiler. The main HSS scheme in [31] can be seen as the result of applying the k-HE-based compiler on the \(\mathsf {CNF}_\ell \) scheme in the setting with \(k = \ell \). Lai, Malavolta, and Schröder [31] discussed the setting with \(t > 1\), but did not provide any concrete schemes. A constructive version for general \(t \ge 1\) was proposed in [35]. The approach of compiling \(\mathsf {CNF}_\ell \) gives concrete schemes and significantly simplifies the analysis in [31] (c.f., Sect. 4.1).
As discussed in Sect. 4, \(\mathsf {CNF}_\ell \) is almost strictly inferior to \(\mathsf {WY}_\ell \). We therefore focus on the instantiations with a linearly-homomorphic HE (\(k=1\)) and the \(\ell \)-th order Woodruff-Yekhanin IT-HSS \(\mathsf {WY}_\ell \) which has efficiency measures \((\rho ,\alpha ,\beta ) = (\ell n,n,n^\ell )\) and supports polynomials of degree \(d < \frac{(\ell +1)m}{t}\). When \(\ell = 1\), we obtain a compact HSS with efficiency measures \((\rho ',\alpha ',\beta ') = (0,n,1)\) supporting polynomials of degree \(d < \frac{2m}{t}\), where decoding is linear. When \(\ell = 2\), we obtain a balanced HSS with efficiency measures \((\rho ',\alpha ',\beta ') = (mn, n, n)\) supporting polynomials of degree \(d < \frac{3m}{t}\), where decoding is quadratic.
6 Application to MPC with Preprocessing
In the following we show an application of HSS to multi-party computation (MPC) with preprocessing. Specifically, we show how to generically construction an m-party MPC protocol for degree-d polynomials resistant against the corruption of t parties, assuming the existence of an \((n,m+p,t)\)-HSS for degree-d polynomials that supports p-preprocessing. A similar result for the restricted case of 2 parties was given (implicitly) in [5]. The salient point of our construction is that the online communication complexity of the MPC scheme is independent of the size of the polynomial being computed. For certain regimes of parameters, this leads to an exponential improvement in the communication complexity of the online phase, when compared with general-purpose MPC solutions.
6.1 Protocol Description
In the following we describe our (semi-honest) MPC protocol for degree-d polynomials assuming the existence of a \((n,m+p,t)\)-HSS scheme with perfect correctness and a general purpose (semi-honest) m-party MPC that is resilient against the corruption of up to t parties. For a definition of MPC and its notion of simulation-based semi-honest security, we refer to [24]. The scheme is detailed below.
Preprocessing: We assume that the (input-independent) preprocessing phase is run by a trusted party, which can be substituted by an execution of a general-purpose MPC protocol jointly executed by the m participants. The preprocessing phase proceeds as follows.
-
1.
Generate a key for the HSS scheme via
 .
. -
2.
Run
 to obtain \((\mathsf {in} _1, \dots , \mathsf {in} _{p}, \mathsf {rec} _1, \dots , \mathsf {rec} _{p})\).
to obtain \((\mathsf {in} _1, \dots , \mathsf {in} _{p}, \mathsf {rec} _1, \dots , \mathsf {rec} _{p})\). -
3.
Run
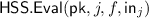 to obtain \(\mathsf {out} _j\), for all \(j \in [p]\).
to obtain \(\mathsf {out} _j\), for all \(j \in [p]\). -
4.
Let s be the concatenation of the variables
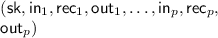 as defined above. The preprocessing algorithm computes an t-out-of-mFootnote 5 secret sharing of s and returns to each party the public key
as defined above. The preprocessing algorithm computes an t-out-of-mFootnote 5 secret sharing of s and returns to each party the public key  and the j-th share \(s_j\).
and the j-th share \(s_j\).
Online: The online phase is jointly executed by the m participants, who collectively receive the inputs \(\mathbf {x}\), i.e., either \(\mathbf {x}\) is secret shared among the m participants or each participant has knowledge of a disjoint subset of entries of \(\mathbf {x}\). The j-th party inputs the j-th output of the preprocessing phase  and its share of \(\mathbf {x}\). The parties jointly compute the following function using a general-purpose MPC protocol. For simplicity we assume that the function takes as input the variable s as defined in the preprocessing, which can be obtained by running the reconstruction procedure of the t-out-of-m secret sharing scheme.
and its share of \(\mathbf {x}\). The parties jointly compute the following function using a general-purpose MPC protocol. For simplicity we assume that the function takes as input the variable s as defined in the preprocessing, which can be obtained by running the reconstruction procedure of the t-out-of-m secret sharing scheme.
-
1.
Run \(\mathsf {HSS}.\mathsf {ShareComp}(\mathsf {in} _1, \ldots , \mathsf {in} _{p}, \mathsf {rec} _1, \ldots , \mathsf {rec} _{p}, \mathbf {x})\) to obtain the tuple \((\mathsf {in} _{p+1},\ldots , \mathsf {in} _{m+p}, \mathsf {rec} _{p+1}, \ldots , \mathsf {rec} _{m+p})\).
-
2.
The j-th participant is given \(\mathsf {in} _{p+j}\) and an t-out-of-m secret share of \(\tilde{s} = (\mathsf {rec} _{p+1}, \ldots , \mathsf {rec} _{m+p})\).
The j-th party locally computes  to obtain \(\mathsf {out} _{p+j}\). Then the m parties engage once again in a general-purpose MPC on input the secret key
to obtain \(\mathsf {out} _{p+j}\). Then the m parties engage once again in a general-purpose MPC on input the secret key  , the output shares \((\mathsf {out} _1, \dots , \mathsf {out} _{m+p})\), and the reconstruction information \((\mathsf {rec} _1, \dots , \mathsf {rec} _{m+p})\). Whenever some information is not available to any party in plain, the MPC protocol reconstructs it from the shares.
, the output shares \((\mathsf {out} _1, \dots , \mathsf {out} _{m+p})\), and the reconstruction information \((\mathsf {rec} _1, \dots , \mathsf {rec} _{m+p})\). Whenever some information is not available to any party in plain, the MPC protocol reconstructs it from the shares.
-
1.
Run
 and return the output to all parties.
and return the output to all parties.
6.2 Analysis
The security of the MPC protocol follows from a standard argument, which we sketch in the following. Observe that the view of the parties consist of the public key of the HSS scheme together with HSS shares of the input \(\mathbf {x}\) and the t-out-of-m secret sharing of the variables s and \(\tilde{s}\). By the semi-honest security of the MPC protocol, the MPC transcript does not reveal anything beyond the output of the computation. Thus the t-out-of-m security of the resulting MPC follows by a reduction against the HSS scheme (observe that the variables s and \(\tilde{s}\) are information-theoretically hidden from the eyes of any t-subset of the participants).
We analyze the communication complexity of our protocol when instantiating the general-purpose MPC with any OT-based protocol (e.g. [25]) and the HSS scheme with k-HE-compiled variant of \(\mathsf {WY}_\ell \) described in Sect. 5. To reduce cluttering, we assume that t and \(1 \le k \le \ell \) are constants, e.g., \(t = 1\), \(k=1\), and \(\ell = 1\) or 2. Recall that (compiled) \(\mathsf {WY}_\ell \) supports  -preprocessing. We therefore set
-preprocessing. We therefore set  . The communication complexity of the preprocessing phase is upper bounded by
. The communication complexity of the preprocessing phase is upper bounded by

On the other hand, the online communication is upper bounded by

In case t is a multiple of \(\ell +1\), the protocol allows the participants to jointly evaluate a degree d multivariate polynomial where \(d < \frac{(\ell +1)m}{t} + 1\), i.e., we gain 1 degree compared to using the k-HE-compiled \(\mathsf {WY}_\ell \) scheme as-is. The size of the circuit representation of such a polynomial ranges from a constant to \(O(n^d)\). Thus for large enough m, the communication complexity of the online phase is exponentially smaller than that of a naive implementation using a general-purpose MPC protocol. We stress that this result is obtained without relying on heavy machinery, such as fully-homomorphic encryption.
7 Conclusion
With the conceptual observation that the HSS scheme of [31] can be abstractly seen as compiling the \(\mathsf {CNF}\) IT HSS using a k-HE, in this work we have constructed a generic compiler which turns a class of compatible IT HSS for degree-d polynomials into a computational one with more favourable parameters.
A generic compiler has many advantages. For starters, it allows instantiation with \(\mathsf {WY}\), which, unlike \(\mathsf {CNF}\), scales well with a large number of servers. In contrast, [31] using \(\mathsf {CNF}\) becomes exponentially inefficient. Due to degree-amplification, this improvement is significant in practice as higher degrees can be supported by simply employing more servers. The preprocessing property of \(\mathsf {WY}\) also allows application to preprocessing MPC, which was not possible with [31]. Other choices of instantiating the IT-HSS and k-HE potentially yield further improvements.
Notes
- 1.
Single-Instruction-Multiple-Data.
- 2.
More rigorously, the LMS construction can be seen as compiling the “first-order CNF scheme” which we define in Sect. 4.
- 3.
The idea of generalizing the approach of Woodroof and Yekhanin to higher order derivatives was already explored in the context of locally decodable codes [30] although in very different parameter settings. To the best of our knowledge, its application in cryptography is new to this work.
- 4.
This degree reduction technique is generic and also applies to our HSS-based schemes.
- 5.
We use t-out-of-m secret sharing to refer to an m-party secret sharing scheme which is resilient against t corrupt parties.
References
Akavia, A., Feldman, D., Shaul, H.: Secure search via multi-ring fully homomorphic encryption. IACR Cryptology ePrint Archive 2018/245 (2018)
Akavia, A., Gentry, C., Halevi, S., Leibovich, M.: Setup-free secure search on encrypted data: faster and post-processing free. Proc. Privacy Enhancing Technol. 2019(3), 87–107 (2019)
Barkol, O., Ishai, Y.: Secure computation of constant-depth circuits with applications to database search problems. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 395–411. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_24
Baur, W., Strassen, V.: The complexity of partial derivatives. Theor. Comput. Sci. 22(3), 317–330 (1983). https://doi.org/10.1016/0304-3975(83)90110-X
Beimel, A., Ishai, Y., Kumaresan, R., Kushilevitz, E.: On the cryptographic complexity of the worst functions. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 317–342. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_14
Boneh, D., Gentry, C., Halevi, S., Wang, F., Wu, D.J.: Private database queries using somewhat homomorphic encryption. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 102–118. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38980-1_7
Boneh, D., Goh, E.-J., Nissim, K.: Evaluating 2-DNF formulas on ciphertexts. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 325–341. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_18
Bost, R., Popa, R.A., Tu, S., Goldwasser, S.: Machine learning classification over encrypted data. In: NDSS, vol. 4324, p. 4325 (2015)
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y., Kohl, L., Scholl, P.: Efficient pseudorandom correlation generators: silent OT extension and more. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 489–518. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_16
Boyle, E., Gilboa, N., Ishai, Y.: Breaking the circuit size barrier for secure computation under DDH. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part I. LNCS, vol. 9814, pp. 509–539. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_19
Boyle, E., Gilboa, N., Ishai, Y.: Secure computation with preprocessing via function secret sharing. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019, Part I. LNCS, vol. 11891, pp. 341–371. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_14
Boyle, E., Gilboa, N., Ishai, Y., Lin, H., Tessaro, S.: Foundations of homomorphic secret sharing. In: Karlin, A.R. (ed.) ITCS 2018, vol. 94, pp. 21:1–21:21. LIPIcs, January 2018. https://doi.org/10.4230/LIPIcs.ITCS.2018.21
Boyle, E., Kohl, L., Scholl, P.: Homomorphic secret sharing from lattices without FHE. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477, pp. 3–33. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_1
Castagnos, G., Laguillaumie, F.: Linearly homomorphic encryption from \(\sf DDH\). In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 487–505. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_26
Catalano, D., Fiore, D.: Using linearly-homomorphic encryption to evaluate degree-2 functions on encrypted data. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, pp. 1518–1529. ACM Press, October 2015. https://doi.org/10.1145/2810103.2813624
Cheon, J.H., Kim, M., Lauter, K.: Homomorphic computation of edit distance. In: Brenner, M., Christin, N., Johnson, B., Rohloff, K. (eds.) FC 2015. LNCS, vol. 8976, pp. 194–212. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48051-9_15
Couteau, G.: A note on the communication complexity of multiparty computation in the correlated randomness model. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477, pp. 473–503. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_17
Dachman-Soled, D., Malkin, T., Raykova, M., Yung, M.: Secure efficient multiparty computing of multivariate polynomials and applications. In: Lopez, J., Tsudik, G. (eds.) ACNS 2011. LNCS, vol. 6715, pp. 130–146. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21554-4_8
Damgård, I., Jurik, M.: A generalisation, a simplification and some applications of Paillier’s probabilistic public-key system. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 119–136. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_9
Diffie, W., Hellman, M.E.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 31, 469–472 (1985)
Franklin, M., Mohassel, P.: Efficient and secure evaluation of multivariate polynomials and applications. In: Zhou, J., Yung, M. (eds.) ACNS 2010. LNCS, vol. 6123, pp. 236–254. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13708-2_15
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 169–178. ACM Press, May/June 2009. https://doi.org/10.1145/1536414.1536440
Goldreich, O.: Foundations of Cryptography: vol. 2, 1st edn. Basic Applications. Cambridge University Press, New York (2009)
Goldreich, O., Micali, S., Wigderson, A.: How to prove all NP statements in zero-knowledge and a methodology of cryptographic protocol design (extended abstract). In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 171–185. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_11
Graepel, T., Lauter, K., Naehrig, M.: ML confidential: machine learning on encrypted data. In: Kwon, T., Lee, M.-K., Kwon, D. (eds.) ICISC 2012. LNCS, vol. 7839, pp. 1–21. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37682-5_1
Harsha, P., Ishai, Y., Kilian, J., Nissim, K., Venkatesh, S.: Communication vs. computation. Comput. Complex. 16(1), 1–33 (2007). https://doi.org/10.1007/s00037-007-0224-y10.1007/s00037-007-0224-y
Ishai, Y., Kushilevitz, E.: Improved upper bounds on information-theoretic private information retrieval (extended abstract). In: 31st ACM STOC, pp. 79–88. ACM Press, May 1999. https://doi.org/10.1145/301250.301275
Ito, M., Saito, A., Nishizeki, T.: Secret sharing schemes realizing general access structure. In: Proceedings of IEEE Global Telecommunication Conference (Globecom 1987), pp. 99–102 (1987)
Kopparty, S., Saraf, S., Yekhanin, S.: High-rate codes with sublinear-time decoding. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd ACM STOC, pp. 167–176. ACM Press, June 2011. https://doi.org/10.1145/1993636.1993660
Lai, R.W.F., Malavolta, G., Schröder, D.: Homomorphic secret sharing for low degree polynomials. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018, Part III. LNCS, vol. 11274, pp. 279–309. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03332-3_11
Mishkov, R.: Generalization of the formula of Faa di Bruno for a composite function with a vector argument. Int. J. Math. Math. Sci. 24, 481–491 (2000)
Naehrig, M., Lauter, K.E., Vaikuntanathan, V.: Can homomorphic encryption be practical? In: Proceedings of the 3rd ACM Cloud Computing Security Workshop, CCSW 2011, pp. 113–124. ACM (2011). https://dl.acm.org/citation.cfm?id=2046682
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Phalakarn, K., Suppakitpaisarn, V., Attrapadung, N., Matsuura, K.: Constructive t-secure homomorphic secret sharing for low degree polynomials. In: Bhargavan, K., Oswald, E., Prabhakaran, M. (eds.) INDOCRYPT 2020. LNCS, vol. 12578, pp. 763–785. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-65277-7_34
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Woodruff, D., Yekhanin, S.: A geometric approach to information-theoretic private information retrieval. In: 20th Annual IEEE Conference on Computational Complexity (CCC 2005), pp. 275–284. IEEE (2005)
Yasuda, M., Shimoyama, T., Kogure, J., Yokoyama, K., Koshiba, T.: Packed homomorphic encryption based on ideal lattices and its application to biometrics. In: Cuzzocrea, A., Kittl, C., Simos, D.E., Weippl, E., Xu, L. (eds.) CD-ARES 2013. LNCS, vol. 8128, pp. 55–74. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40588-4_5
Acknowledgment
Yuval Ishai is supported by ERC Project NTSC (742754), ISF grant 2774/20, NSF-BSF grant 2015782, and BSF grant 2018393. Russell W. F. Lai is supported by the State of Bavaria at the Nuremberg Campus of Technology (NCT) – a research cooperation between the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) and the Technische Hochschule Nürnberg Georg Simon Ohm (THN).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Ishai, Y., Lai, R.W.F., Malavolta, G. (2021). A Geometric Approach to Homomorphic Secret Sharing. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)





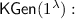 The key generation algorithm takes as input the security parameter
The key generation algorithm takes as input the security parameter  and outputs the public key
and outputs the public key  and the secret key
and the secret key  .
. The encryption algorithm takes as input the public key
The encryption algorithm takes as input the public key  and a message
and a message 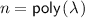 ; it returns a ciphertext
; it returns a ciphertext 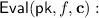 The evaluation algorithm takes as input the public key
The evaluation algorithm takes as input the public key  , (the description of) a polynomial
, (the description of) a polynomial  ; it returns a ciphertext
; it returns a ciphertext 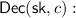 The decryption algorithm takes as input the private key
The decryption algorithm takes as input the private key 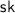 and a ciphertext
and a ciphertext  ; it returns a plaintext
; it returns a plaintext 
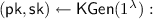 On input the security parameter
On input the security parameter 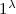 , the key generation algorithm outputs a public key
, the key generation algorithm outputs a public key  and a secret key
and a secret key  .
.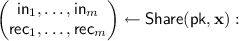 Given a public key
Given a public key 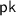 , and an input
, and an input 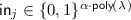 and their corresponding recovery information
and their corresponding recovery information 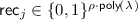 .
.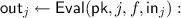 The evaluation algorithm is executed by a server
The evaluation algorithm is executed by a server  on inputs the public key
on inputs the public key  , an index j, (the description of) a degree-d polynomial f, and a share
, an index j, (the description of) a degree-d polynomial f, and a share  outputs the corresponding output share
outputs the corresponding output share  .
. On input a secret key
On input a secret key  , a tuple of output shares
, a tuple of output shares 


 -Preprocessing of the
-Preprocessing of the  is a linear function of
is a linear function of 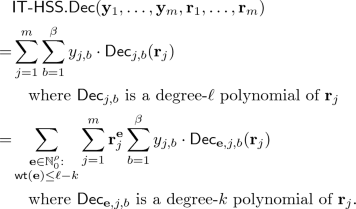

 to
to 
 to
to  .
. to obtain
to obtain 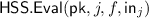 to obtain
to obtain 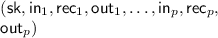 as defined above. The preprocessing algorithm computes an t-out-of-m
as defined above. The preprocessing algorithm computes an t-out-of-m and the j-th share
and the j-th share  and return the output to all parties.
and return the output to all parties.