Breaking the Circuit Size Barrier for Secure Computation Under DDH

Abstract

Under the Decisional Diffie-Hellman (DDH) assumption, we present a 2-out-of-2 secret sharing scheme that supports a compact evaluation of branching programs on the shares. More concretely, there is an evaluation algorithm $\mathsf{Eval}$ with a single bit of output, such that if an input $w\in \{0,1\}^n$ is shared into $(w^0,w^1)$, then for any deterministic branching program P of size S we have that $\mathsf{Eval}(P,w^0)\oplus \mathsf{Eval}(P,w^1)=P(w)$ except with at most $\delta$ failure probability. The running time of the sharing algorithm is polynomial in n and the security parameter $\lambda$, and that of $\mathsf{Eval}$ is polynomial in $S,\lambda$, and $1/\delta$. This applies as a special case to boolean formulas of size S or boolean circuits of depth $\log S$. We also present a public-key variant that enables homomorphic computation on inputs contributed by multiple clients.

The above result implies the following DDH-based applications:

• A secure 2-party computation protocol for evaluating any branching program or formula of size S, where the communication complexity is linear in the input size and only the running time grows with S.

• A secure 2-party computation protocol for evaluating layered boolean circuits of size S with communication complexity $O(S/\log S)$.

• A 2-party function secret sharing scheme, as defined by Boyle et al. (Eurocrypt 2015), for general branching programs (with inverse polynomial error probability).

• A 1-round 2-server private information retrieval scheme supporting general searches expressed by branching programs.

Prior to our work, similar results could only be achieved using fully homomorphic encryption. We hope that our approach will lead to more practical alternatives to known fully homomorphic encryption schemes in the context of low-communication secure computation.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In this paper we introduce a simple new technique for low-communication secure computation that can be based on the Decisional Diffie-Hellman (DDH) assumption and avoids the use of fully homomorphic encryption. We start with some relevant background.

Since the seminal feasibility results of the 1980s [3, 8, 23, 38], a major challenge in the area of secure computation has been to break the “circuit size barrier.” This barrier refers to the fact that all classical techniques for secure computation required a larger amount of communication than the size of a boolean circuit representing the function to be computed, even when the circuit is much bigger than the inputs. The circuit size barrier applied not only to general circuits, but also to useful restricted classes of circuits such as boolean formulas (namely, circuits with fan-out 1) or branching programs (a stronger computational model capturing non-uniform logarithmic-space computations). Moreover, the same barrier applied also to secure computation protocols that can rely on a trusted source of correlated randomness, provided that this correlated randomness needs to be reusable.

The first significant progress has been made in the context of private information retrieval (PIR), where it was shown that for the bit-selection function $f(x,i)=x_i$ it is possible to break the circuit size barrier either in the multi-server model [9, 11], where a client holds i and two or more servers hold x, or in the two-party model [27] under standard cryptographic assumptions. However, progress on extending this to other useful computations has been slow, with several partial results [4, 10, 17, 25, 30] that do not even cover very simple types of circuits such as general DNF or CNF formulas, let alone more expressive ones such as general formulas or branching programs.¹

All this has changed with Gentry’s breakthrough on fully homomorphic encryption (FHE) [19, 33]. FHE enables local computations on encrypted inputs, thus providing a general-purpose solution to the problem of low-communication secure computation. On the down side, even the best known implementations of FHE [24] are still quite slow. Moreover, while there has been significant progress on basing the feasibility of FHE on more standard or different assumptions [7, 21, 36], the set of cryptographic assumptions on which FHE can be based is still very narrow, and in particular it does not include any of the “traditional” assumptions that were known in the 20th century.

1.1 Our Contribution

Our new approach was inspired by the recent work on function secret sharing (FSS) [6]. A (2-party) FSS scheme for a function class $\mathcal F$ allows a client to split (a representation of) $f\in \mathcal F$ into succinctly described functions $f_0$ and $f_1$ such that for any input x we have that $f(x)=f_0(x)+f_1(x)$ (over some Abelian group), but each $f_b$ hides f.

The notion of FSS was originally motivated by applications to m-server PIR and related problems. FSS schemes for simple classes of functions such as point functions were constructed from one-way functions in [6, 22]. However, a result from [6] shows that 2-party FSS for richer circuit classes, from $\mathrm {AC}^0$ and beyond, would imply (together with a mild additional assumption) breaking the circuit size barrier for similar classes.

The idea is that by encrypting the inputs and applying FSS to the function $f'$ that first decrypts the inputs and then computes f, the parties can shift the bulk of the work required for securely evaluating f to local evaluations of $f'_0$ and $f'_1$. Thus, breaking the circuit size barrier reduces to securely distributing the generation of $f'_0$ and $f'_1$ from f and the secret decryption keys, which can be done using standard secure computation protocols and reused for an arbitrary number of future computations. This was viewed in [6] as a negative result, providing evidence against the likelihood of basing powerful forms of FSS on assumptions that are not known to imply FHE.

We turn the tables by constructing FSS schemes for branching programs under DDH, which implies low-communication secure 2-party computation protocols under DDH.

Homomorphic secret sharing. For the purpose of presenting our results, it is more convenient to consider a dual version of FSS that can also be viewed as a form of “homomorphic secret sharing,” or alternatively a variant of threshold FHE [1, 19]. Concretely, a client wants to split a secret input $w\in \{0,1\}^n$ into a pair of shares $(w^0,w^1)$, each of which is sent to a different server. Each individual share should computationally hide w. Each server, holding (a representation of) a function $f\in \mathcal F$, can apply an evaluation algorithm to compute $y_b=\mathsf{Eval}(f,w^b)$, so that $y_0+y_1=f(w)$. Note that this is precisely the original notion of FSS with the roles of the function and input reversed.²

Cast in the this language, our main technical contribution is such a homomorphic secret sharing scheme, based on DDH, with output group $\mathbb {Z}_2$ (or any other $\mathbb {Z}_p$), and the class $\mathcal F$ of functions represented by deterministic³ branching programs. The scheme only satisfies a relaxed form of the above correctness requirement: for every input w and branching program P, the probability of producing local outputs that do not add up to the correct output P(w) is upper bounded by an error parameter $\delta >0$ which affects the running time of $\mathsf{Eval}$. This probability is over the randomness of the sharing. The running time of the sharing algorithm is $n\cdot \mathsf{poly}(\lambda )$, where $\lambda$ is a security parameter. The running time of $\mathsf{Eval}$ is polynomial in $S,\lambda$, and $1/\delta$.

We would like to stress that branching programs are quite powerful and capture many useful real-life computations. In particular, a branching program of size S can simulate any boolean formula of size S or boolean circuit of depth $\log _2S$, and polynomial-size branching programs can simulate any computation in the complexity classes $\mathrm {NC}^1$ or (non-uniform) deterministic log-space.

We also present a public-key variant of the homomorphic secret sharing scheme. This variant can be viewed as a threshold homomorphic encryption scheme with secret evaluation keys and additive reconstruction. That is, there is a key generation algorithm that outputs a single public key and a pair of secret evaluation keys. Given the public key, an arbitrary number of clients can encrypt their inputs. Each server, given the public ciphertexts and its secret evaluation key, can locally compute an additive share of the output.

The above results imply the following applications, all based on the DDH assumption alone.

Succinct secure computation of branching programs. The general transformation from FSS to secure two-party computation described above can be used to obtain succinct two-party protocols for securely evaluating branching programs with reusable preprocessing. However, the public-key variant of our construction implies simpler and more efficient protocols. The high level approach is similar to that of other low-communication secure protocols from different flavors of FHE [1, 19, 29], except for requiring secret homomorphic evaluation keys and an additional error-correction sub-protocol. For a two-party functionality with a total of n input bits and $m=m(n)$ output bits, where each output can be computed by a polynomial-size branching program (alternatively, logarithmic space Turing Machine or NC$^1$ circuit), the protocol can be implemented with a constant number of rounds and $n+m\cdot \mathsf{poly}(\lambda )$ bits of communication, where $\lambda$ is a security parameter. To reduce the $n\cdot \mathsf{poly}(\lambda )$ cost of a bit-by-bit encryption of the inputs, the protocol employs a hybrid homomorphic encryption technique from [20].

Breaking the circuit size barrier for “well structured” circuits. In the case of evaluating general boolean circuits, we can make the total communication slightly sublinear in the circuit size by breaking the computation into segments of logarithmic depth and homomorphically computing additive shares of the outputs of each segment given additive shares of the inputs. For instance, we can evaluate a layered circuit of size S using $O(S/\log S)$ bits of communication (ignoring lower order additive terms; see Sect. 4 for a more precise statement). We employ error-correcting codes with encoding and decoding in NC$^1$ to ensure that errors introduced by the computation of a segment are corrected before propagating to the next segment.

Function secret sharing. Using a universal branching program we can reverse the roles of P and w in the above homomorphic secret sharing scheme, obtaining a polynomial-time 2-party FSS scheme for branching programs. Unlike the main definition of FSS from [6] here we can only satisfy a relaxed notion that allows an inverse polynomial error probability. However, the error probability can be made negligible in the context of natural applications. An m-party FSS scheme for circuits was recently obtained by Dodis et al. [15] under the Learning with Errors (LWE) assumption, by making use of multi-key FHE [12, 28, 29]. Our construction gives the first FSS scheme that applies to a rich class of functions and does not rely on FHE.

Private information retrieval. Following the application of FSS to PIR from [6] with a simple repetition-based error-correction procedure, a consequence of the above result is a 1-round 2-server (computational) PIR scheme in which a client can privately search a database consisting of N documents for existence of a document satisfying a predicate P, where P is expressed as a branching program applied to the document. For instance, any deterministic finite automaton can be succinctly expressed by such a branching program. The length of the query sent to each server is polynomial in the size of the branching program and a computational security parameter, whereas the length of the answer is a statistical security parameter times $\log N$.

1.2 Overview of Techniques

We now describe the main ideas behind our construction. It will be convenient to use the homomorphic secret sharing view: a client would like to share an input w between 2 servers so that the servers, on input P, can locally compute additive shares of P(w).

Let $\mathbb {G}$ be a DDH group of prime order q with generator g. Our construction employs three simple ideas.

The first is that a combination of a threshold version of ElGamal and linear secret sharing allows the servers to locally multiply an encrypted input x with a linearly secret-shared value y, such that the result $z=xy$ is shared multiplicatively between the servers; namely the servers end up with elements $z_i\in \mathbb {G}$ such that the product of the $z_i$ is $g^{z}$. This idea alone is already useful, as it gives an $(m-1)$-private m-server protocol for computing any degree-2 polynomial P with small integer coefficients held by the servers on a vector w of small integers held by the client, where the communication complexity in each direction is essentially optimal.

To see how this step is possible, consider a simplified version of the world, where (instead of requiring ElGamal) it held that $g^w$ is a secure encryption of w. In this world, we can secret share input w by giving both servers a copy of the encryption $g^w$. Then, given an additive secret sharing $x_0,x_1$ of another value x, the servers can generate a multiplicative sharing of wx, by each computing $(g^w)^{x_b}$. Indeed, $(g^{w x_0})\cdot (g^{w x_1}) = g^{wx}$. Extending this idea to ElGamal (as, alas, $g^w$ is not a secure encryption) can be done via comparable “linear algebra in the exponent” given additive shares of x as well as for xc, where c is the ElGamal secret key.

What seems to stop us at degree-2 polynomials is the fact that z is now shared multiplicatively rather than linearly, so the servers cannot multiply z by a new input encrypted by the client. Moreover, converting multiplicative shares to additive shares seems impossible without the help of the client, due to the intractability of computing discrete logarithms in $\mathbb {G}$. The second, and perhaps most surprising, idea is that if we allow for an inverse polynomial error probability, and assuming there are only $m=2$ servers, the servers can convert multiplicative shares of $g^z$ into linear shares of z without any interaction. For simplicity, suppose $z\in \{0,1\}$. Taking the inverse of the second server’s share, the servers now hold group elements $g_0,g_1$ such that $g_0=g_1$ if $z=0$ and $g_1=g\cdot g_0$ if $z=1$. Viewing the action of multiplication by g as a cycle over $\mathbb {Z}_q$, the elements $g_0,g_1$ are either in identical positions, or $g_1$ is one step ahead. Conversion is done by picking a pseudo-random $\delta$-sparse⁴ subset $\mathbb {G}' \subset \mathbb {G}$ and having each server $b\in \{0,1\}$ locally find the minimal integer $z_b\ge 0$ such that $g_b \cdot g^{z_b}\in \mathbb {G}'$. The first such $z_b$ is expected to be found in roughly $1/\delta$ steps and if it is not found in $(1/\delta )\log (1/\delta )$ steps, we set $z_b=0$. The key observation is that except with $O(\delta )$ probability, both searches will find the same point in $\mathbb {G}'$ and the servers end up with integers $z_1,z_2$ such that $z_1-z_2=z$, yielding the desired linear sharing of z.

Once we have a linear sharing of z, we can freely add it with other values that have a similar linear representation. We cannot hope to multiply two linearly shared values, but only to multiply them with another encrypted input. However, in order to perform another such a multiplication, we need additive shares not only of z, but also of zc for the ElGamal key c.

The third idea is that the client can assist the conversion by also providing an encryption of each input w multiplied by the secret key. This introduces two problems: the first is that semantic security may break down given a circular encryption of the secret key, which we handle either by assuming circular security of ElGamal or (with some loss of efficiency) by using the circular-secure variant of Boneh et al. [5] instead of standard ElGamal. A more basic problem is that for the conversion to produce correct results with high probability, the secrets must be small integers, whereas c (and so zc) is a large number. This is handled by providing an encryption of each input x multiplied by each bit of the secret key, and applying a linear combination whose coefficients are powers of 2 to the linear shares of the products of x and the bits of the key.

These ideas allow the servers to compute a restricted type of “straight-line programs” on the client’s input, consisting of a sequence of instructions that either: load an input into memory, add the values of two memory locations, or multiply a memory location by an input. (Note that we cannot multiply two memory locations, which would allow evaluation of arbitrary circuits.) Such programs can emulate any branching program of size S by a sequence of O(S) instructions.

It is instructive to note that the only limit on the number of instructions performed by the servers is the accumulation of error probabilities. This is analogous to the accumulation of noise in FHE schemes. However, the mechanisms for coping with errors are very different: in the context of known FHE schemes the simplest way of coping with noise is by using larger ciphertexts, whereas here we can reduce the error probability by simply increasing the running time of the servers, without affecting the ciphertext size or the complexity of encryption and decryption at all. We can also further trade running time for succinctness: the share size in our basic construction can be reduced by replacing the binary representation of the secret key with a representation over a larger basis, which leads to a higher homomorphic evaluation time.

The surprising power of local share conversions, initially studied in [14], has already been observed in the related contexts of information-theoretic PIR and locally decodable codes [2, 16, 39]. However, the type of share conversion employed here is very different in nature, as it is inherently tied to efficient computation rather than information.

Interestingly, our share conversion technique has resemblance to a cryptanalytic technique introduced by van Oorschot and Weiner for the purpose of parallel collision finding [37], where a set of “distinguished points” is used to synchronize two different processors.

1.3 Future Directions

This work gives rise to many natural open questions and future research directions. Can one bootstrap from branching programs to general circuits without relying on FHE? Can similar results be obtained for more than 2 parties? Can similar results be based on other assumptions that are not known to imply FHE? Can the dependence on the error parameter $\delta$ be eliminated or improved? To what extent can our protocols be optimized for practical use?

We hope that our approach will lead to faster solutions for some practical use-cases of FHE.

2 Preliminaries

We describe the necessary primitives and assumptions we rely on.

Function representations. We capture a function representation (such as a circuit, formula, or branching program) by an infinite collection $\mathcal {P}$ of bit strings P (called “programs”), each specifying an input length n and an output length m, together with an efficient algorithm $\mathsf{Evaluate}$, such that $y \leftarrow \mathsf{Evaluate}(P, w)$ (denoted by shorthand notation “P(w)”), for any input $w \in \{0,1\}^n$, defines the output of P on w.

Homomorphic secret sharing. A (2-party) Homomorphic Secret Sharing (HSS) for a class of programs $\mathcal P$ consists of algorithms $(\mathsf{Share},\mathsf{Eval})$, where $\mathsf{Share}(1^\lambda ,(w_1,\ldots ,w_n))$ splits the input w into a pair of shares $(\mathsf{share}_0,\mathsf{share}_1)$, and $\mathsf{Eval}(b,\mathsf{share}, P, \delta , \beta )$ homomorphically evaluates P on $\mathsf{share}$, where the correct output is additively shared over $\mathbb {Z}_\beta$ except with error probability $\delta$. When $\beta$ is omitted it is understood to be $\beta =2$. We allow $\mathsf{Eval}$ to run in time polynomial in its input length and in $1/\delta$ and require that each $\mathsf{share}_b$ output by $\mathsf{Share}$ keeps w semantically secure.

Public-Key Variant. We further consider a stronger variant of the homomorphic secret sharing primitive that supports homomorphic computations on inputs contributed by different clients. In fact, what we achieve is stronger: there is a single public key that can be used to encrypt inputs as in a standard public-key encryption scheme. However, similar to the original notion of homomorphic secret sharing (and in contrast to standard homomorphic encryption schemes), homomorphic computations on encrypted inputs are done in a distributed way and require two separate (secret) evaluation keys. As before, we require the reconstruction of the output to be additive.

The corresponding security notion guarantees “semantic”-style secrecy of an encrypted value, given only the evaluation key of a single server. In a setting consisting of two servers and an arbitrary number of clients, the above security notion implies that inputs contributed by a set of uncorrupted clients remain secure even if one of the two servers colludes with all the remaining clients.

Definition 1

(Distributed-Evaluation Homomorphic Encryption). A (2-party) Distributed-Evaluation Homomorphic Encryption (DEHE) for a class of programs $\mathcal P$ consists of algorithms $(\mathsf{Gen},\mathsf{Enc},\mathsf{Eval})$ with the following syntax:

• $\mathsf{Gen}(1^\lambda )$: On input a security parameter $1^\lambda$, the key generation algorithm outputs a public key $\mathsf{pk}$ and a pair of evaluation keys $(\mathsf{ek}_0,\mathsf{ek}_1)$.

• $\mathsf{Enc}(\mathsf{pk},w)$: On a public key $\mathsf{pk}$ and a secret input value $w \in \{0,1\}$, the encryption algorithm outputs a ciphertext $\mathsf{ct}$.

• $\mathsf{Eval}(b,\mathsf{ek}, (\mathsf{ct}_1,\ldots ,\mathsf{ct}_n), P, \delta , \beta )$: On input party index $b \in \{0,1\}$, an evaluation key $\mathsf{ek}$, vector of n ciphertexts, a program $P \in \mathcal {P}$ with n input bits and m output bits, error bound $\delta >0$, and an integer $\beta \ge 2$, the homomorphic evaluation algorithm outputs $y_b \in \mathbb {Z}_\beta ^m$, constituting party b’s share of an output $y\in \{0,1\}^m$. When $\beta$ is omitted it is understood to be $\beta =2$.

The algorithms $\mathsf{Gen}$ and $\mathsf{Enc}$ are PPT algorithms, whereas $\mathsf{Eval}$ can run in time polynomial in its input length and in $1/\delta$.

The algorithms $(\mathsf{Gen},\mathsf{Enc},\mathsf{Eval})$ should satisfy the following correctness and security requirements:

• Correctness: There exists a negligible function $\nu$ such that for every positive integer $\lambda$, input $(w_1,\ldots ,w_n) \in \{0,1\}^n$, program $P \in \mathcal {P}$ with input length n, error bound $\delta >0$, and integer $\beta \ge 2$,

  

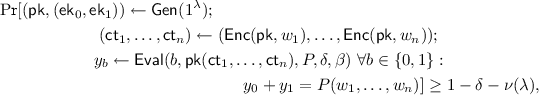
  where addition of $y_0$ and $y_1$ is carried out modulo $\beta$.

• Security: The two distribution ensembles $C_0(\lambda )$ and $C_1(\lambda )$ are computationally indistinguishable, where $C_w(\lambda )$ is obtained by letting $(\mathsf{pk}, (\mathsf{ek}_0,\mathsf{ek}_1)) \leftarrow \mathsf{Gen}(1^\lambda )$ and outputting $(\mathsf{pk},\mathsf{ek}_b,\mathsf{Enc}(\mathsf{pk},w))$.

2.1 DDH and Circular Security

Definition 2

(DDH). Let $\mathcal {G}=\{\mathbb {G}_\rho \}$ be a set of finite cyclic groups, where $|\mathbb {G}_\rho |=q$ and $\rho$ ranges over an infinite index set. We use multiplicative notation for the group operation and use $g \in \mathbb {G}_\rho$ to denote a generator of $\mathbb {G}_\rho$. Assume that there exists an algorithm running in polynomial time in $\log q$ that computes the group operation of $\mathbb {G}_\rho$. Assume further that there exists a PPT instance generator algorithm $\mathcal IG$ that on input $1^\lambda$ outputs an index $\rho$ which determines the group $\mathbb {G}_\rho$ and a generator $g \in \mathbb {G}_\rho$. We say that the Decisional Diffie-Hellman assumption (DDH) is satisfied on $\mathcal {G}$ if $\mathcal IG(1^\lambda )=(\rho ,g)$ and for every non-uniform PPT algorithm $\mathcal{A}$ and every three random $a, b, c \in \{0,\ldots ,q-1\}$ we have

$$|\text{ Pr }[\mathcal{A}(\rho ,g^a,g^b,g^{ab})=1]-\text{ Pr }[\mathcal{A}(\rho ,g^a,g^b,g^c)=1]| < \varepsilon (\lambda ),$$

for a negligible function $\varepsilon$. We will sometimes write $(\mathbb {G},g,q) \leftarrow \mathcal IG(1^\lambda )$.

A more efficient variant of our construction requires a circular security assumption on the underlying bit encryption scheme, in which an efficient adversary cannot distinguish encryptions of the bits of the secret key from encryptions of 0.

Definition 3

(Circular Security). We say that a public-key encryption scheme $(\mathsf{Gen},\mathsf{Enc},\mathsf{Dec})$ with key length $\ell (\lambda )$ and message space containing $\{0,1\}$ is circular secure if there exists a negligible function $\nu (\lambda )$ for which the following holds for every non-uniform PPT $\mathcal {A}$:

$$\begin{aligned} \Pr [ (\mathsf{pk},\mathsf{sk}) \leftarrow \mathsf{Gen}(1^\lambda ), b \leftarrow \{0,1\}, b' \leftarrow \mathcal {A}^{\mathcal {O}_b}(\mathsf{pk}) :~~ b' = b ] \le \frac{1}{2} + \nu (\lambda ), \end{aligned}$$

where the oracle $\mathcal {O}_b$ takes no input and outputs the following (where $\mathsf{sk}^{(i)}$ denotes the ith bit of $\mathsf{sk}$):

$$ (C_1,\ldots ,C_\ell ),~\text {where}~{\left\{ \begin{array}{ll} \forall i \in [\ell ], C_i \leftarrow \mathsf{Enc}(\mathsf{pk}, 0) &{}~~~\text {if}~b=0 \\ \forall i \in [\ell ], C_i \leftarrow \mathsf{Enc}(\mathsf{pk}, \mathsf{sk}^{(i)}) &{}~~~\text {if}~b=1 \end{array}\right. }. $$

3 Homomorphic Secret Sharing for Branching Programs

In this section, we present constructions of homomorphic secret sharing schemes that enable non-interactive evaluation of a certain class of programs, known as restricted-multiplication straight-line programs. In particular, this class will include deterministic branching programs.

Definition 4

(RMS programs). The class of Restricted Multiplication Straight-line (RMS) programs consists of an arbitrary sequence of the four following instructions, each with a unique identifier $\mathsf{id}$:

• Load an input into memory: $(\mathsf{id}, \hat{y}_j\leftarrow \hat{w}_i)$.

• Add values in memory: $(\mathsf{id}, \hat{y}_k \leftarrow \hat{y}_i + \hat{y}_j)$.

• Multiply value in memory by an input value: $(\mathsf{id}, \hat{y}_k \leftarrow \hat{w}_i \cdot \hat{y}_j)$.

• Output value from memory, as element of $\mathbb {Z}_\beta$: $(\mathsf{id},\beta , \hat{O}_j \leftarrow \hat{y}_i)$.

Our construction will support homomorphic evaluation of straight-line programs of this form over inputs $w_i \in \mathbb {Z}$, provided that all intermediate computation values in $\mathbb {Z}$ remain “small” (where the required runtime grows with this size bound). Our final result is a public-key variant—i.e., a homomorphic encryption scheme with distributed evaluation (as per Definition 1)—based on DDH, with ciphertext size $O(\ell )$ group elements per input (for $\ell$ the logarithm of the DDH group size), and where runtime for homomorphic evaluation of an RMS program of size S with intermediate computation values bounded by M is $\mathsf{poly}(\lambda ,S,M,1/\delta )$.

An important sub-procedure of our homomorphic share evaluation algorithms is a local share conversion algorithm $\mathsf{DistributedDLog}$, which intuitively converts a multiplicative secret sharing of $g^x$ to an additive secret sharing of the value x, with inverse polynomial probability of error.

In the following subsections, we present: (1) The share conversion procedure $\mathsf{DistributedDLog}$, (2) a simplified version of the homomorphic secret sharing scheme (in the secret-key setting), assuming circular security of ElGamal encryption, (3) the analogous public-key construction, and (4) the final public-key construction based on standard DDH.

3.1 Share Conversion Procedure

We now describe the local share conversion algorithm $\mathsf{DistributedDLog}$, which receives as input a group element $h \in \mathbb {G}$ and outputs an integer w. Loosely speaking, $\mathsf{DistributedDLog}$ outputs the distance on the cycle generated by $g \in \mathbb {G}$ between h and the first $z \in \mathbb {G}$ such that a pseudo-random function outputs 0 on z. $\mathsf{DistributedDLog}$ is a deterministic algorithm and consequently two invocations of the algorithm with the same element h result in the same output w. Two invocations of the algorithm on inputs h and $h \cdot g^\mu$ for a small $\mu$ result, with good probability, in outputs w and $w-\mu$. Therefore, the $\mathsf{DistributedDLog}$ algorithm converts a difference of small $\mu$ in the cycle generated by g in $\mathbb {G}$ to the same difference over $\mathbb {Z}$.

The detailed description of $\mathsf{DistributedDLog}_{\mathbb {G},g}$ follows. The algorithm is hard-wired with $\rho$ defining a group $\mathbb {G}=\mathbb {G}_\rho$ and a generator $g \in \mathbb {G}$. $\mathsf{DistributedDLog}_{\mathbb {G},g}$ receives as input $h\in \mathbb {G}$, an allowable error probability $\delta$, maximum difference $\mu \in \mathbb {N}$, and a pseudo-random function $\phi :\mathbb {G} \rightarrow \{0,1\}^{\log (4\mu /\delta )}$. The difference $\mu$ specifies the maximum distance from h, along the cycle that g generates, of an element that is the input to a parallel invocation of $\mathsf{DistributedDLog}_{\mathbb {G},g}$ within a given application.

Proposition 1

Let $\lambda$ be a security parameter, let $\mathcal{G}=\{\mathbb {G}_\rho \}$ be a set of finite cyclic groups and let the instance generator algorithm of the set running on input $1^\lambda$ return a group $\mathbb {G}=\mathbb {G}_\rho$ with generator g. Let $\delta >0$, let $\mu \in \mathbb {N}$, let $\mathcal {F}^r$ be a family of PRF defined over ${\mathcal G}$ and let $\phi :\mathbb {G} \rightarrow \{0,1\}^{\log (4/\delta )}$ be randomly chosen from all the members of $\mathcal {F}^r$ with domain $\mathbb {G}$. Then, for any $h \in \mathbb {G}$ and $\mu ' \le \mu$ we have that

$$\mathsf{DistributedDLog}_{\mathbb {G},g}(h,\delta ,\mu ,\phi )-\mathsf{DistributedDLog}_{\mathbb {G},g}(h \cdot g^{\mu '},\delta ,\mu ,\phi ) = \mu '$$

with probability greater than $1- \delta$.

Proof

The values of $\phi$ on the sequence of elements traversed by the variable z in an execution of $\mathsf{DistributedDLog}_{\mathbb {G},g}(h,\delta ,\mu ,\phi )$ can be divided into three cases. The first case is that $\phi (h\cdot g^c)=0^{\log (4\mu /\delta )}$ for some c in the range $0 \le c \le \mu -1$, the second case is that $\phi (h \cdot g^c) \ne 0^{\log (4\mu /\delta )}$ for $c=0,\ldots ,\mu -1$, but $\phi (h \cdot g^c)=0^{\log (4\mu /\delta )}$ for some c in the range $\mu \le c \le \frac{4\mu \ln (4/\delta )}{\delta }$ and the last case is that neither of the former occurs, i.e. $\phi (h \cdot g^c) \ne 0^{\log (4\mu /\delta )}$ for every $c=0,1,\ldots ,\frac{4\mu \ln (4/\delta )}{\delta }$.

In the second case, since $\phi (h \cdot g^c) \ne 0^{\log (4\mu /\delta )}$ for any $c=0,\ldots ,\mu -1$, the execution of $\mathsf{DistributedDLog}_{\mathbb {G},g}(h,\delta ,\mu ,\phi )$ returns the smallest $c, \mu \le c \le \frac{4\mu \ln (4/\delta )}{\delta }$ such that $\phi (h) = 0^{\log (4\mu /\delta )}$. In $\mathsf{DistributedDLog}_{\mathbb {G},g}(h \cdot g^\mu ,\delta ,\mu ,\phi )$ the variable z ranges over the elements $h \cdot g^\mu , \ldots , h \cdot g^{c+\mu }$ and the return value is $c-\mu$. Therefore, $\mathsf{DistributedDLog}_{\mathbb {G},g}(h,\delta ,\mu ,\phi )-\mathsf{DistributedDLog}_{\mathbb {G},g}(h \cdot g^\mu ,\delta ,\mu ,\phi ) = \mu$. By showing that the second case occurs with probability at least $1-\delta$ we complete the proof.

If R is a random function then the probability that $R(h \cdot g^c)=0^{\log (4\mu /\delta )}$ for some $c, 0 \le c \le \mu -1$ is exactly $1-(1-\delta /4\mu )^\mu$, which by induction is at most $1-(1-\mu \delta /4\mu )=\delta /4$. In addition,

$$\begin{aligned} \text{ Pr }[\forall c\in \{0,\ldots ,\frac{4\mu \ln \frac{4}{\delta }}{\delta }\} ~R(h g^c) \ne 0^{\log (4\mu /\delta )}]\le & {} (1-\frac{\delta }{4\mu })^{\frac{4\mu \ln (4/\delta )}{\delta }} \\< & {} e^{- \ln 4/\delta } = \frac{\delta }{4} \end{aligned}$$

Since $\phi$ is selected randomly from an appropriate family of pseudo-random functions any non-uniform PPT algorithm can distinguish between R and $\phi$ with negligible probability. Specifically, the probability of the first case is bound by $|\text{ Pr }[\exists c, 0 \le c \le \mu -1 ~ \phi (h \cdot g^c)=0^{\log (4/\delta )}]-\delta /4|<\varepsilon (\delta )$ (for a negligible function $\varepsilon (\delta )$), since otherwise an efficient non-uniform algorithm can distinguish between R and $\phi$ by testing their value on hard-coded element $(h,\delta ,\mu ,\phi )$ and returning 1 if the result is $0^{\log (4\mu /\delta )}$. Similarly, the probability of the third case is bound by $|\text{ Pr }[\forall c\in \{0,\ldots ,\frac{4\ln (4/\delta )}{\delta }\} ~ \phi (h g^c) \ne 0^{\log (4/\delta )}]-\delta /4|<\varepsilon (\delta )$.

The probability of the second case is therefore at least $1 - \frac{\delta }{2} -2\varepsilon (\delta )$.    $\square$

3.2 Homomorphic Secret Sharing

We now construct a simple version of the homomorphic secret sharing scheme, using the procedure $\mathsf{DistributedDLog}$ as a sub-routine. The resulting scheme will be a “secret-key” version. Further, the security of the scheme will rely on the assumption that ElGamal encryption is circular secure. These restrictions will be removed in the following subsections.

Consider a DDH group $\mathbb {G}$ of prime order q (with $\lambda$ bits of security) with generator g, and $\ell =\lceil \log _2 q \rceil$. We will use $c=c^{(1)},\ldots ,c^{(\ell )}$ to denote bits of an element $c \in \mathbb {Z}_q$ (i.e., $c = \sum _{i=0}^{\ell -1} 2^i c^{(i+1)}$).

Overview of construction. All values generated within the secret sharing and homomorphic evaluation sit within three “levels.” We will maintain notation as in the top portion of Fig. 1. Namely,

• Level 1: ElGamal Ciphertexts $[\![w ]\!]_c$.

  Initial input values w will be “uploaded” into the homomorphic evaluation system by generating an ElGamal encryption $[\![w ]\!]_c$ of the value w with respect to a common secret key c, as well as encryptions $[\![c^{(i)}w ]\!]_c$ of each of the products $c^{(i)}w$ for the bits $c^{(i)}$ of the corresponding key c.

• Level 2: Additive secret shares $\langle y \rangle$.

  Each value y in memory of the RMS program will be maintained via two sets of additive secret shares: $\langle y \rangle$ itself, and $\langle cy \rangle$ secret sharing the product of y with the ElGamal secret key c of the system. We start with secret shares of this form for each input value (e.g., in the secret-key setting, these will be generated as part of the $\mathsf{Share}$ procedure). Then, after each emulated RMS instruction, we will maintain the invariant that each newly computed memory value is stored as secret shares in this fashion.

• Level 3: Multiplicative secret shares $\langle \langle xy \rangle \rangle$.

  Multiplicative secret shares appear only as intermediate values during the execution of homomorphic evaluation (of multiplication), and are then converted back to additive shares via $\mathsf{DistributedDLog}$.

Fig. 1.

Notation for components of the homomorphic secret sharing scheme, and pairing operations for transforming between different components.

Remark 1

(Valid vs Random). We emphasize that a “valid” encoding (e.g., $[\![x ]\!]_c, \langle x \rangle$, or $\langle \langle x \rangle \rangle$) speaks only to the correctness of decoding, and does not imply that the encoding is a random such encoding (e.g., a randomly sampled ciphertext, or fresh secret shares).

The bottom portion of Fig. 1 describes two pairing operations that constitute cross-level computations. The first, $\mathsf{MultShares}$, “multiplies” a level-1 encoding by a level-2 encoding. Namely, it takes as input a level-1 (ElGamal ciphertext) encoding of x under key c, and level-2 (additive secret sharing) encodings of y, and of cy (the product of y with the ElGamal secret key), and outputs a level-3 (multiplicative secret sharing) encoding of the product xy. The second, $\mathsf{ConvertShares}$, converts from a level-3 (multiplicative) encoding back down to a level-2 (additive) encoding, with some probability of error, as dictated by given parameters.

Roughly, the intermediate values of homomorphic evaluation will be maintained in level-2 (additive) secret shared form. Any linear combination of such shares can be performed directly. Multiplication between a value in memory and an input value will be performed by performing the $\mathsf{MultShares}$ between the input value (encoded in level 1) and the relevant memory value (encoded in level 2). This will yield an encoding of the product, but in level 3 (i.e., as multiplicative shares). To return the computed product back to level 2, the parties will execute the pairing procedure $\mathsf{ConvertShares}$, which essentially runs the $\mathsf{DistributedDLog}$ procedure from the previous subsection.

Remark 2

(Variable Types). Note that the relevant values are nearly all elements of $\mathbb {G}$ (e.g., elements of ElGamal ciphertexts) or of $\mathbb {Z}_q$ (e.g., the values $cy_i$, as well as shares of $\mathsf{SubtShare}$). An important exception to this are the values $w_i, y_i$, which are interpreted as (small) integers. When necessary for computation, we will sometimes perform a type cast back and forth between $\mathbb {Z}$ and $\mathbb {Z}_q$, using the notation $(int)(x) \in \mathbb {Z}$ for $x \in \mathbb {Z}_q$, and $(x \mod q) \in \mathbb {Z}_q$ for $x \in \mathbb {Z}$.

A few calculations provides us with the following two claims on these pairing procedures (see full version of this work for details). A slight subtlety arises in the case of $\mathsf{ConvertShares}$, regarding the PRF. Namely, the share values on which we run $\mathsf{ConvertShares}$ are the results of partial computations and previous $\mathsf{ConvertShares}$ executions, meaning in particular that they depend on the choice of the sampled PRF $\phi$. However, this is not an issue due to two reasons: (1) this dependence is efficiently computable given oracle access to the PRF outputs, as specified in the algorithm $\mathsf{DistributedDLog}$, and (2) we will explicitly ensure the PRF is never used on the same input twice, by use of nonces $\mathsf{id}$. In such case, the PRF will still act as a random function in each $\mathsf{ConvertShares}$ invocation, and yield the required share conversion correctness guarantee.

Claim

(Pairing Operations).

• 1. $\mathsf{MultShares}$: For all values $x,y \in \mathbb {Z}_q$ and any key $c \in \mathbb {Z}_q$, then on input a valid level-1 encoding $[\![x ]\!]_c$ with respect to key c, and valid level-2 encodings $\langle y \rangle , \langle cy \rangle$, the output of $\mathsf{MultShares}([\![x ]\!]_c, \langle y \rangle , \langle cy \rangle )$ is a valid level-3 encoding $\langle \langle xy \rangle \rangle$ of the product $xy \in \mathbb {Z}_q$.

• 2. $\mathsf{ConvertShares}$: For every $\mathsf{id}\in \{0,1\}^\lambda , \delta > 0, M \in \mathbb {N}$, PPT $\mathcal {A}$, $\Pr [ \phi \leftarrow \mathsf{PRFGen}(1^\lambda ); (h,\mu ) \leftarrow \mathcal {A}^{\phi (\mathsf{id}',\cdot )}(1^\lambda ) : \mu < M ~ \wedge \mathsf{ConvertShares}(0, h, \mathsf{id}, \delta , M) + \mathsf{ConvertShares}(1, h^{-1} g^\mu , \mathsf{id}, \delta , M) \ne \mu ] \le M\delta ,$ where $\phi (\mathsf{id}',\cdot )$ is an oracle to the PRF $\phi$ on any input with prefix $\mathsf{id}' \ne \mathsf{id}$.

Fig. 2.

Share generation procedure $\mathsf{Share}_{\mathbb {G},g}$ for secret sharing an input w via the homomorphic secret sharing scheme.

Fig. 3.

Procedures for performing homomorphic operations on secret shares. Note that we distinguish variables of the straight-line program from the actual values by using $\hat{y}_i$ as opposed to $y_i$, etc. Here, notation $\langle y \rangle$ is used to represent this party’s share of the corresponding subtractive secret shared pair. Evaluation maintains the invariant that each of the additive secret shares $\langle y_i \rangle$ encode the correct current computation value of $\hat{y}_i$.

We present our secret sharing scheme $\mathsf{Share}$ in Fig. 2, and the corresponding homomorphic operations on shares $\mathsf{Eval}$ in Fig. 3.

We remark that our combined construction obtains a generalization of the notion of HSS from Sect. 2 both extending beyond the Boolean setting to support arithmetic computations over small integers, and allowing multiple outputs of the program from possibly different groups $\mathbb {Z}_\beta$ (as specified by the program description P). The restricted case of the definition coincides with our construction with size bound M set to 1 and all program outputs in a fixed group $\mathbb {Z}_\beta$.

Theorem 1

(Homomorphic Secret Sharing). Assume that ElGamal is circular secure (as per Definition 3). Then the scheme $(\mathsf{Share},\mathsf{Eval})$ as specified in Figs. 2, 3 is a secure homomorphic secret sharing scheme for the class of deterministic branching programs.

The theorem follows from the next two correctness and security lemmas. In particular, correctness is proved for the broader class of RMS programs with bounded-size intermediate computation values, which captures deterministic branching programs. We provide proof sketches and refer the reader to the full version for a complete analysis.

Lemma 1

(Correctness of $\mathsf{Eval}$ ). For every input $w_1,\ldots ,w_n \in \mathbb {Z}_q$ and every RMS program P (as in Definition 4) of size S for which all intermediate values $y_i \in \mathbb {Z}$ in the execution of P are bounded by $|y_i| \le M$,

Proof Sketch. We first address the probability of error due to execution of the Share Conversion Procedure $\mathsf{ConvertShares}$. Observe that the homomorphic evaluation of program P performs at most $S(\ell +1)$ executions of the Share Conversion Procedure (with error parameter $\delta ' = \delta /(\ell +1)MS$). By Claim 3.2, together with a union bound, this implies that no conversion errors will occur with probability $\delta '(\ell +1)MS=\delta$.

Assume, then, that every $\mathsf{ConvertShares}$ execution returns without error. We prove that following invariant is maintained at each step of homomorphic evaluation:

For every memory item $\hat{y}_i$, let $y_i \in \mathbb {Z}$ denote the correct value that should be presently stored in memory. Then the shares $\langle y_i \rangle = (y_i^A,y_i^B) \in \mathbb {Z}_q^2$ and $\langle cy_i \rangle = (v^A, v^B) \in \mathbb {Z}_q^2$ held by the parties satisfy:

• (a) $(int)(y_i^A + y_i^B) = y_i \in \mathbb {Z}$ (where addition is in $\mathbb {Z}_q$).

• (b) $v^A + v^B = cy_i \in \mathbb {Z}_q$.

Note that this invariant holds vacuously at the start of $\mathsf{Eval}$, as all memory locations are empty, and is preserved directly by our actions in each Load Input Into Memory and Add Values In Memory instructions, due to the structure of the additive secret sharing and since all intermediate values $y_i \in \mathbb {Z}$ in the execution are bounded by $M < q$ (so that relations over $\mathbb {Z}$ align with relations over the shares $\mathbb {Z}_q$).

For each instruction Multiply Input By Memory Value, consider the resulting shares $\langle y_k \rangle$ and $\langle cy_k \rangle$. By Claim 3.2, the shares $\langle \langle w_iy_j \rangle \rangle$ computed via $\mathsf{MultShares}$ constitute a valid level-3 sharing of the product $w_iy_j$ (as per Fig. 1). Since we are in the case where $\mathsf{ConvertShares}$ does not err, the resulting converted shares $\langle w_iy_j \rangle$ encode exactly the value $w_iy_j \in \mathbb {Z}_q$. Since $w_iy_j$ is an intermediate computation value $y_k$ in the evaluation of P, we have $0 \le w_iy_j \le M < q$. Thus, invariant (a) holds. Consider now $\langle c y_k \rangle$. From precisely the same argument (since we are in the case where $\mathsf{ConvertShares}$ does not err), we have for each $t \in [\ell ]$ that the computed intermediate value $\langle c^{(t)}y_k \rangle$ is a level-2 encoding of the corresponding value $v_t := c^{(t)}y_k \in \mathbb {Z}_q$ (where $y_k = w_iy_j$). Since $y_k$ is an intermediate computation value in P we have $0 \le y_k \le M < q$, and so for $c^{(t)}\in \{0,1\}$, then $0 \le c^{(t)}y_k \le M < q$. Thus, it holds $(int)(v_t^A - v_t^B) = c^{(t)}w_i y_j \in \mathbb {Z}$. Combining the respective values over $t \in [\ell ]$, it holds $\big (\sum _{t \in [\ell ]} 2^t v_t^A \big ) + \big ( \sum _{t \in [\ell ]} 2^t v_t^B \big ) = \sum _{t \in [\ell ]} 2^t (v_t^A + v_t^B) = \sum _{t \in [\ell ]} 2^t c^{(t)}w_i y_j = c w_i y_j \in \mathbb {Z}_q$. Therefore, invariant (b) holds.

Finally, for each Output Memory Value instruction, the shares of both parties are deliberately shifted by a (pseudo-)random value to avoid the bad “edge case” in which the shares $y^A,y^B$ of the desired output value y satisfy $(int)y^B \ge q-M$ and $(int)(y^A)-(int)(y^B) = y - q$ (where locally modding each share by $\beta$ may disrupt correctness), as opposed to the almost-everywhere case that $(int)(y^A)-(int)(y^B)=y$. The error probability is bounded by $M/q + \mathsf{negl}(\lambda )$, which is negligible.

Lemma 2

(Security of $\mathsf{Share}$ ). Based on the assumption that ElGamal is a weakly circular secure encryption scheme (as per Definition 3), then $\mathsf{Share}$ is a computationally secure secret sharing scheme.

Proof Sketch. We prove that the distribution of a single party’s share resulting from $\mathsf{Share}$ is computationally indistinguishable from a distribution that is independent of the shared values $w_1,\ldots ,w_n$, via three hybrids. In Hybrid 1, we replace all additive secret shares by random values. This yields an identical distribution, by the perfect security of the 2-out-of-2 additive secret sharing scheme. In Hybrid 2, we replace all ciphertexts of the form $\{[\![c^{(t)}w_i ]\!]_c \}$ with encryptions of 0, which we address below. In Hybrid 3, we rely on standard semantic security to further replace all ciphertexts of the form $[\![w_i ]\!]_c$ with encryptions of 0.

We now demonstrate that an efficient adversary $\mathcal {A}$ who distinguishes between Hybrids 2 and 3 for some choice of inputs $w_1,\ldots ,w_n$ can be used to break the circular security of ElGamal. In the circular security challenge, the adversary $\mathcal {B}$ receives an ElGamal public key $\mathsf{pk}$ and access to an oracle which provides either vectors of encryptions of the bits of the secret key, or vectors of encryptions of 0. To simulate the ciphertext vectors for $\mathcal {A}$ as either $\{[\![c^{(t)}w_i ]\!]_c \}$ (Hybrid 2) or $\{[\![0 ]\!]_c \}$ (Hybrid 3), $\mathcal {B}$ (with $w_1,\ldots ,w_n$ hardcoded) considers two cases. If $w_i=0$ then anyway $c^{(t)}w_i =0$, so he simply generates a vector of 0 ciphertexts. For each $w_i \ne 0$, he: queries his circular security oracle, receives a vector of ciphertexts $[\![x_{i,1}]\!]_c,\ldots ,[\![x_{i,\ell } ]\!]_c$, and then exponentiates each ciphertext (that is, each of the 2 group elements) by the corresponding input $w_i$. This operation maps ciphertexts of 0 to ciphertexts of 0, and ciphertexts of 1 to ciphertexts of $w_i$; further, since $w_i \ne 0$ and $\mathbb {Z}_q$ is a field, the resulting distribution of encryption randomness is also equally distributed (i.e., uniform). Therefore, either Hybrid 2 or 3 is exactly simulated, and so the adversary $\mathcal {A}$ enables $\mathcal {B}$ to distinguish, breaking circular security.

3.3 Public-Key HSS for Branching Programs

In the construction of the previous section, secret shares of an input w consisted of ElGamal encryptions $[\![w ]\!]_c, \{[\![c^{(t)}w ]\!]_c\}_{t \in [\ell ]}$ and additive secret shares $\langle w \rangle , \langle cw \rangle$, where c was a (freshly sampled) key for ElGamal. At face value, it would seem that one must know the value of the key c in order to generate these values—meaning, in turn, that homomorphic computation can only be performed on the data of a single user who generates the key c. In this section, we demonstrate that by leveraging the homomorphic properties of ElGamal encryption, we can in fact generate all required values for a secret sharing of w while maintaining security, given only “public key” information independent of the input w. That is, we obtain homomorphic encryption with distributed evaluation, as discussed in Sect. 2.

More formally, we now consider a separate procedure $\mathsf{Gen}$ for generating common setup information $\mathsf{pk}$ and secret evaluation keys $\mathsf{ek}_0,\mathsf{ek}_1$ (which we consider to be given to two servers). Given access to $\mathsf{pk}$, a user can “upload” his input w to the system via $\mathsf{Enc}$. Then, given their respective evaluation keys, two servers can perform non-interactive homomorphic computations on all users’ inputs via $\mathsf{Eval}$.

In our construction, the algorithm $\mathsf{Gen}$ samples an ElGamal key pair, and outputs $\mathsf{pk}$ consisting of encryptions $[\![1]\!]_c, \{[\![c^{(t)}]\!]_c\}_{t \in [\ell ]}$ and evaluation keys $\mathsf{ek}_b$ corresponding to additive secret shares of $\langle c \rangle$. In $\mathsf{Enc}$, a user computes the necessary ciphertexts $[\![w ]\!]_c$ and $\{[\![c^{(t)}w ]\!]_c\}_{t \in [\ell ]}$ for his input w by exponentiating the ciphertexts in $\mathsf{pk}$ component-wise by w, (i.e., using multiplicative homomorphism of ElGamal). The final required values $\langle w \rangle , \langle cw \rangle$ can be obtained directly by the servers within $\mathsf{Eval}$ by performing the procedure for a homomorphic multiplication between the “input value” w (i.e., given $[\![w ]\!]_c, \{[\![c^{(t)}]\!]_c\}_{t \in [\ell ]}$) together with “memory value” 1 (i.e., given a trivial sharing $\langle 1 \rangle$ together with $\langle c \rangle$ from $\mathsf{ek}$).

A formal description of the algorithms $\mathsf{Gen},\mathsf{Enc},\mathsf{Eval}$ is given in Fig. 4.

Fig. 4.

Construction of “public-key” variant of homomorphic secret sharing: i.e., homomorphic encryption with distributed evaluation.

Theorem 2

(DEHE). Assume that ElGamal is circular secure (as per Definition 3). Then the scheme $(\mathsf{Gen},\mathsf{Enc},\mathsf{Eval})$ as given in Fig. 4 is a secure Distributed-Evaluation Homomorphic Encryption scheme for the class of deterministic branching programs.

Proof

Correctness. To reduce to Theorem 1, it suffices to demonstrate: (1) the values $[\![w ]\!]_c, \{[\![c^{(t)}w ]\!]_c\}_{t \in [\ell ]}$ as generated in $\mathsf{Enc}$ are valid level-1 encodings of w and $\{c^{(t)}w\}_{t \in [\ell ]}$; and (2) the values $\langle w \rangle , \langle cw \rangle$ as generated in $\mathsf{Eval}$ are valid level-2 encodings of w and cw. Property (1): Recall $[\![w ]\!]_c$ was obtained as $(h_1^w,h_2^w)$ for $(h_1,h_2)$ a valid level-1 encoding of 1. This means $h_2 h_1^{-c} = g^1$, which implies $(h_2^w)(h_2^w)^{-c} = g^w$, as desired. Same for each $[\![c^{(t)}w ]\!]_c$. Property (2): Holds by the correctness of homomorphic RMS multiplication evaluation of $\mathsf{Eval}$ as per Theorem 1.

Security. Semantic security of the scheme follows as in Theorem 1, assuming circular security of ElGamal. Namely, the view of a server holding $\mathsf{ek}_b$ consists of information theoretically hiding secret shares, ciphertexts of values independent of the secret key, and vectors of ciphertexts encrypting the vector $(c^{(1)}w,\dots ,c^{(\ell )}w)$ for various inputs w. An adversary distinguishing between this view and one consisting of random share elements and ciphertexts of 0 can be used to break the circular security of ElGamal, precisely as in Theorem 1.

Comparing the complexity of the public-key scheme $(\mathsf{Gen},\mathsf{Enc},\mathsf{Eval})$ to that of the secret-key scheme $(\mathsf{Share},\mathsf{Eval})$ from the previous section, we see that the computation cost to the user for uploading inputs $w_1,\ldots ,w_n$ via $\mathsf{Enc}$ is essentially equivalent to the cost of sharing the inputs via $\mathsf{Share}$ (exponentiating given ciphertexts by the respective inputs in one case, versus encrypting the values directly in the other), but the cost of each “load input” instruction $(\mathsf{id}, \hat{y}_j \leftarrow \hat{w}_i)$ within the homomorphic evaluation now incurs the cost of a multiplication step to generate additive secret shares $\langle w_i \rangle , \langle c w_i \rangle$ given only $\langle c \rangle$ and the uploaded ElGamal ciphertexts associated with $w_i$, as opposed to being essentially for free for the client to generate $\langle w_i \rangle , \langle c w_i \rangle$ when he knew the values of $w_i, cw_i$.

3.4 Removing the Circular Security Assumption

We now show how to remove the ElGamal circular security assumption in the construction in the previous section, yielding a scheme that relies solely on DDH. As in the setting of FHE, this can be achieved directly in exchange for a multiplicative blowup of the computation depth in the share size, by considering a leveled version of the scheme (i.e., replacing the circular encryptions of bits of c under key c by bits of $c_i$ under key $c_{i+1}$ for a depth-length sequence of keys). However, we now demonstrate an alternative approach, which does not require increasing the share size with respect to the size of computation.

Our new construction replaces ElGamal encryption with the ElGamal-like cryptosystem of Boneh, Halevi, Hamburg, and Ostrovsky (BHHO) [5], which is provably circular secure based on DDH. At a high level, BHHO ciphertexts possess an analogous structure of “linear algebra in the exponent,” which allows us to mirror the procedure we used with ElGamal for multiplicatively pairing a ciphertext with an additively shared value.

It will be convenient to consider a slightly modified version of the BHHO scheme, given below, in which the message space is a subset of the exponent space $\mathbb {Z}_q$ instead of the group $\mathbb {G}$ itself (i.e., the multiplication by message m in standard encryption is replaced by $g^m$). Since decryption of such scheme requires taking discrete log, efficient decryption will hold for a polynomial-size message space.

Definition 5

(BHHO Encryption [5]). Let $\mathbb {G}$ be a group of prime order q and g a fixed generator of $\mathbb {G}$. The size of $\mathbb {G}$ is determined by a security parameter $\lambda$, in particular, 1 / q is negligible in $\lambda$. The BHHO public-key encryption scheme for polynomial-size message space $\mathsf{Msg}\subset \mathbb {Z}_q$ is as follows:

• Key Generation. Let $\ell := \lceil 3 \log _2 q \rceil$. Choose random $g_1,\ldots ,g_\ell \leftarrow \mathbb {G}$ and a random secret key vector $s = (s_1,\ldots ,s_\ell ) \leftarrow \{0,1\}^\ell$. Let $h = (g^{s_1}\cdots g_\ell ^{s_\ell })^{-1}$ and define the public and secret keys to be

  $$\begin{aligned} \mathsf{pk}_\mathsf{BHHO}:= (g_1,\ldots ,g_\ell ,h), ~~~ \mathsf{sk}_\mathsf{BHHO}= (g^{s_1},\ldots ,g^{s_\ell }). \end{aligned}$$

• Encryption. To encrypt $m \in \mathsf{Msg}$, choose a random $r \leftarrow \mathbb {Z}_q$ and output the ciphertext $(g_1^r,\ldots ,g_\ell ^r, h^r \cdot g^m).$

• Decryption. Let $(c_1,\ldots ,c_\ell , d)$ be a ciphertext and $\mathsf{sk}_\mathsf{BHHO}= (v_1,\ldots ,v_\ell )$ a secret key. Do:

  • Decode the secret key: For $i=1,\ldots ,\ell$, set $s_i \leftarrow 0$ if $v_i=1$ and $s_i \leftarrow 1$ otherwise.

  • Output $m \in \mathsf{Msg}$ for which $g^m = d \cdot (c_1^{s_1} \cdots c_\ell ^{s_\ell })$.

Theorem 3

(Circular Security of BHHO [5]). Assuming DDH, the BBHO encryption scheme satisfies circular security, as per Definition 3.

Fig. 5.

Modified DDH-based notation and pairing operations, making use of BHHO encryption [5].

Fig. 6.

DDH-based homomorphic encryption with distributed evaluation, making use of the BHHO cryptosystem.

In order to emulate the homomorphic evaluation procedure of the previous sections, there are two steps we must modify:

First, we must provide a means for pairing a BHHO ciphertext of an input w with additive secret sharings of a value x to obtain a multiplicative secret sharing of $g^{wx}$. For ElGamal this was done given $\langle x \rangle$ and $\langle cx \rangle$, and computing $h_2^{\langle x \rangle } h_1^{-\langle cx \rangle }$. Now, for BHHO, we can perform an analogous “partial decryption” procedure given shares $\langle x \rangle$ and $\{ \langle s_i x \rangle \}_{i \in [\ell ]}$, for the bits $s_i$ of the BHHO secret key. The corresponding pairing computation is given as $\mathsf{MultShares}$ in Fig. 5.

Once we obtain a multiplicative secret sharing of $g^{wx}$, we can perform the same share-conversion procedure $\mathsf{DistributedDLog}$ from the previous sections to return to an additive secret sharing of wx (with some error probability $\delta$). But, to be able to perform a future pairing as above, we additionally must generate additive secret sharings $\langle wx s_i \rangle$ for each of the bits $s_i$ of the secret key (analogous to generating $\langle cwx \rangle$ in the ElGamal case). Conveniently, this BHHO task is actually slightly simpler than that for ElGamal: whereas before we had to deal with the large size of the secret key $c \in \mathbb {Z}_q$ by operating on a bit decomposition of c and then reconstructing, here the secret key $(s_1,\ldots ,s_\ell )$ is already interpreted as a binary vector. This means we can perform the multiplication steps directly without requiring the decomposition/reconstruction steps.

We remark that BHHO ciphertexts are multiplicatively homomorphic in the same fashion as ElGamal, which allows us to obtain a public-key variant of the secret sharing scheme precisely as in the previous section. The required procedure of modifying a ciphertext of some message x to one encrypting xy given y is explicitly described as $([\![x]\!]_s)^y$ in Fig. 5.

Fig. 7.

Procedures for performing homomorphic operations on secret shares. Here, notation $\langle y \rangle$ is used to represent this party’s share of the corresponding subtractive secret shared pair. Evaluation maintains the invariant that each of the additive secret shares $\langle y_i \rangle$ encode the correct current computation value of $\hat{y}_i$.

In Fig. 5, we provide the modified notation and pairing procedures for this setting. The remaining notations $\langle x \rangle , \langle \langle x \rangle \rangle$ and pairing operation $\mathsf{ConvertShares}$ will remain as in the previous sections (Fig. 1). Given these sub-procedures, we present in Figs. 6 and 7 the corresponding algorithms $\mathsf{Gen},\mathsf{Enc},\mathsf{Eval}$. The resulting share size is roughly $\lambda$ times larger than in the previous section, as BHHO ciphertexts are $\lambda +1$ group elements in comparison to ElGamal which is 2. We refer the reader to the full version for a full proof of the following theorem.

Theorem 4

(DEHE from DDH). Assuming DDH, then the scheme $(\mathsf{Gen},\mathsf{Enc},\mathsf{Eval})$ as given in Figs. 6, 7 is a secure Distributed-Evaluation Homomorphic Encryption scheme for the class of deterministic branching programs.

4 Applications

In this section we describe applications of our homomorphic secret sharing scheme and its public-key variant in the context of secure computation. We restrict attention to security against semi-honest parties; to obtain similar asymptotic efficiency in the presence of malicious parties, one can apply general-purpose compilation techniques [23, 30]. For lack of space, formal protocol descriptions and security proofs are postponed to the full version.

4.1 Succinct Protocols for Branching Programs

Our protocols for branching programs can be based either on the weaker HSS primitive via the transformation from [6], or can be built more directly from the public-key variant. We present here the latter approach, which is more direct. For simplicity, we restrict attention to the case of evaluating a single branching program P on inputs $x_0,x_1$ held by Party 0 and Party 1 respectively. This can be extended in a straightforward way to functions with m bits of output that are computed either by m separate branching programs or by a single RMS program.

The simplest protocol proceeds as follows. The two parties run a general-purpose protocol (such as Yao’s protocol) to jointly evaluate the key generation $\mathsf{Gen}$. In the end of this sub-protocol, both parties hold a public key $\mathsf{pk}$ and each holds a secret evaluation key $\mathsf{ek}_b$. While this step may be expensive, its complexity depends (polynomially) only on the security parameter $\lambda$, and moreover the same key setup can be used for evaluating an arbitrary number of branching programs on an arbitrary number of inputs. In this basic version of the protocol, the key generation protocol is the only step that does not make a black-box use of the underlying DDH group.

Next, each party uses $\mathsf{Enc}(\mathsf{pk},\cdot )$ to encrypt every bit of its input, and sends the encryptions to the other party. Finally, the two parties locally run $\mathsf{Eval}$ to generate additive (mod-2) shares of the output $P(x_0,x_1)$. If $\mathsf{Eval}$ had negligible error, the parties could simply exchange their shares of the output, since the share sent to Party b is determined by the output and the share computed by Party b.

The fact that $\mathsf{Eval}$ has a non-negligible error $\delta$ is problematic for two reasons. First, it poses a correctness problem. This can be fixed by setting $\delta$ to be a constant (say, $\delta =1/4$), running $\sigma$ independent instances of $\mathsf{Eval}$, for a statistical security parameter $\sigma$,⁵ and outputting the majority value. However, this modification alone will not suffice, because the existence of errors within the homomorphic evaluation is dependent on the computation values, and as such the $\sigma$ output bits may leak information about the inputs. Instead, the parties apply the $\sigma$ instances of $\mathsf{Eval}$ locally (as before), and distribute the reconstruction function (computing majority of XORs) using general-purpose secure computation. This ensures that only the correct output is revealed (and no further information) with negligible correctness and secrecy error.

The communication complexity of the above protocol is $n\cdot \mathsf{poly}(\lambda )$, where $n=|x_0|+|x_1|$ is the combined length of the two parties’ inputs. This can be improved to $n+\mathsf{poly}(\lambda )$ by using the following hybrid encryption techniques [20]. Let $F_r$ be a pseudorandom function computable in NC$^1$, which can be based on DDH [31]. Following the key generation phase, each party encrypts a random key $r_b$ for F. Then, instead of separately encrypting each bit of $x_b$ using $\mathsf{Enc}$, Party b simply masks each bit i of its input using $F_{r_b}(i)$ and sends to the other party the encryption of $r_b$ and all of the masked bits. The value of program P on the inputs can now be expressed as the value of a (polynomially larger) publicly known branching program $P'$ on the inputs $r_0,r_1$, where $P'$ is determined by P and the masked inputs. The evaluation of $P'$ is repeated $\sigma$ times as before. This yields the following:

Theorem 5

Under the DDH assumption, there exists a constant-round secure 2-party protocol for evaluating branching programs of size S on inputs $(x_0,x_1)$ of total length n, using $n+\mathsf{poly}(\lambda )$ bits of communication.

4.2 Breaking the Circuit Size Barrier for “Well Structured” Circuits

We turn to the question of reducing the communication complexity of evaluating a deep boolean circuit C of size S and depth D. We assume for simplicity that the circuit is layered in the sense that its S gates can be partitioned into $D+1$ layers such that the gates from layer i (except input gates) receive their inputs from gates of layer $i-1$. This can be generalized to a broader class of “well-structured” circuits that captures most instances of circuits that arise naturally.

Given a layered circuit as above, we divide the layers into intervals of $\lceil \log S\rceil$ consecutive layers, and pick for every interval the layer that has the smallest number of gates (except for the input layer). Overall, we have at most $D/\log S$ “special” layers, whose total size is at most $S/\log S$. In addition, the output layer is considered the last special layer.

The crucial observation is that each output of a new special layer can be expressed as a circuit of depth $O(\log S)$ applied to values of the previous special layer. The protocol will compute the values of the special layers one at a time, by using the previous protocol for branching programs, except that the reconstruction protocol is only applied in the end. That is, given additive shares of special layer i, each party encrypts his shares and the parties apply $\mathsf{Eval}$ on a function (computable by polynomial-size branching programs) that first reconstructs the value and then computes the outputs of special layer $i+1$.

To avoid a multiplicative factor of $\sigma$ in communication, we need to apply a more efficient error correction procedure for intermediate layers. To this end, we apply an asymptotically good error-correcting code, with encoding and decoding in NC$^1$, for encoding the values of each special layer. (Many such codes are known to exist; see, e.g., [34]; moreover, by using a Las-Vegas type algorithm for the share conversion it suffices to correct erasures.) The computation performed by $\mathsf{Eval}$ will start by reconstructing the noisy encoding of layer i (using XOR), then apply a decoder to recover the actual values of layer i, then compute the outputs of layer $i+1$, and then encode these outputs. If the error probability $\delta$ of $\mathsf{Eval}$ is smaller than the relative error correction radius of the code, the error rate in the encoded output will be within the error-correction radius with overwhelming probability. Thus, we can use a general-purpose protocol for decoding the correct outputs from the shared noisy encoding. This approach yields the following theorem.

Theorem 6

Under the DDH assumption, there exists a secure 2-party protocol for evaluating any layered boolean circuit of size S, depth D, input length n, and output length m using $O(S/logS) + O(D \sigma /\log D) + n + m \cdot poly(\lambda )$ bits of communication (for $\sigma ,\lambda$ statistical and computational security parameters).

4.3 Function Secret Sharing and Generalized PIR

Function Secret Sharing. As discussed in the Introduction, homomorphic secret sharing can be viewed as a “dual” notion of function secret sharing, as defined in [6]. In a homomorphic secret sharing scheme for a class of programs $\mathcal {P}$, given a share of a secret input w and a public program $P \in \mathcal {P}$, one can locally compute a share of $\varPi (w)$. In a function secret sharing (FSS) scheme for function class $\mathcal {F}$, given a share of a secret function (represented by a “program”’) and a public input x, one can locally compute a share of f(x). In particular, given a homomorphic secret sharing scheme supporting a class of programs $\mathcal {P}$ containing a universal program U, one can directly obtain a FSS scheme for $\mathcal {P}$, by secret sharing a description of the secret program $P \in \mathcal {P}$, and then shares of the evaluation of P on an input x can be obtained by homomorphically evaluating the universal program $U_x(\cdot )$ on the given shares. If for each program $P \in \mathcal {P}$ the homomorphic secret sharing scheme produces output error on the evaluation of P with probability $\delta$ (over the randomness of the secret sharing), then for each input x in the domain of f, the resulting FSS scheme will also yield an output error with probability $\delta$.

Thus, as a corollary of our homomorphic secret sharing scheme, we obtain a DDH-based FSS scheme for branching program with an arbitrary inverse polynomial error. The resulting FSS key size corresponds to the size of a homomorphic secret share of a description of the secret function: namely, a fixed polynomial in the size of the branching program S and security parameter $\lambda$.

Private Information Retrieval. A motivating application regime of function secret sharing (and thus our homomorphic secret sharing scheme) is that of 2-server private information retrieval (PIR) for expressive query classes [6]. As we demonstrate, such applications can be achieved with negligible error even when starting with FSS with inverse-polynomial error $\delta$. Together with our construction of such $\delta$-FSS, this gives us DDH-based 2-server PIR for queries expressed by branching programs. Useful examples include counting or retrieving matches that are specified by conjunction queries or fuzzy match predicates (e.g., requiring that a document contains at least a given threshold of keywords from a given list).

A (standard) FSS scheme for a program class $\mathcal {P}$ can be used to obtain secure 2-server PIR schemes for classes of queries related to $\mathcal {P}$, via three basic steps. For simplicity, we focus our treatment to querying the count of database entries satisfying a (secret) predicate $f \in \mathcal {F}$.⁶ (1) The client generates FSS shares $P_0,P_1$ of the desired query P and sends one share to each server. (2) The servers locally compute, and reply with, the linear combination $\sum _{x \in DB} P_b(x)$ for database DB (where the output group of $P,P_0,P_1$ is $\mathbb {Z}_N$ for $N=|DB|$). (3) Then, leveraging the linearity of FSS reconstruction, the client can recover the desired output $\sum _{x \in DB} P(x) = \sum _{x \in DB} P_0(x) + \sum _{x \in DB} P_1(x)$. To extend this approach to $\delta$-FSS, we execute several independent parallel instances of the $\delta$-FSS scheme, and compute the majority of the resulting execution outputs. Note that here, unlike the secure computation application, there is no danger of releasing the (potentially noisy) outcomes of the parallel executions directly, as no hiding guarantees are required against the PIR client.

5 Examples and Optimizations

We now introduce several optimizations and trade-offs between computation and communication within our HSS construction, and describe their applications within two examples of using homomorphic secret sharing. We first consider a toy example of a client who computes the AND of n bits $x_1,\ldots ,x_n$ by homomorphic secret sharing. We then describe a partial match search in a PIR setting. All the examples and optimizations within this section assume the circular security of ElGamal.

The communication of our homomorphic secret sharing scheme is dominated by the $\ell +1$ ElGamal ciphertexts, or $2(\ell +1)$ group elements encoding each input bit (where $\ell = \log _2 |\mathbb {G}|$ for DDH group $\mathbb {G}$). The computation is dominated by running $\mathsf{MultShares}$ and $\mathsf{ConvertShares}$ $\ell +1$ times for each product of a memory variable and input variable.

$\mathsf{MultShares}$ consists of raising a group element to the power of a secret share, which given a sliding window implementation requires less than $3\ell /2$ group operations. The computation time of $\mathsf{ConvertShares}$ with target error $\delta '$ and maximum difference between two shares M is dominated by $\frac{4M\ln (4/\delta ')}{\delta '}$ group operations.

Consider the following optimizations and trade-offs.

• 1. Ciphertext description reduction. The first optimization is heuristically secure (or alternatively, secure in the random oracle model) and uses a PRG $G:\{0,1\}^\ell \rightarrow \mathbb {G}^{\ell +1}$ to reduce the communication by almost half. Let $G(\sigma )=(g^r,g^{r_1},\ldots ,g^{r_\ell })$ for a seed $\sigma \in \{0,1\}^\ell$. To encode an input bit, instead of sending $\ell +1$ complete ElGamal ciphertexts, a party will now send (a random) $\sigma$ and the $\ell +1$ group elements $(g^{rc+w_i}, g^{r_1c+w_ic_1},\ldots , g^{r_\ell c+w_ic_\ell })$, corresponding to the second terms of the prescribed ciphertexts, using the outputs of $G(\sigma )$ implicitly as the first terms. Given this information, each party can locally generate the full $\ell +1$ ciphertexts, and compute as before.

• 2. Modified key representation. A trade-off reducing communication and increasing computation is possible by changing the representation of the key c from $\sum _{j=0}^{\ell -1} c_j 2^j$ in base 2 to $\sum _{j=0}^{\ell '-1} c'_j B^j$ in base $B=2^b$ for some $b > 1$. Communication complexity and the number of $\mathsf{MultShares}$ and $\mathsf{ConvertShares}$ are reduced by a factor of b, as the $\ell$ encryptions of $\{ c_j w_i \}_{j \in [\ell ]}$ encoding input $w_i$ can be replaced by $\ell '$ encryptions of $\{ c_{j'} w_i \}_{j' \in [\ell ']}$. However, in $\mathsf{ConvertShares}$ the possible difference M between the shares held by the two parties (equivalently, the size of encoded values) increases from 1 to $B-1$, increasing the computation time by a factor of $B-1$.

• 3. Las-Vegas algorithm. A Las-Vegas type algorithm for share conversion can be used to relax the target error probability and reduce the computation time. $\mathsf{ConvertShares}$ potentially induces an error in one of two situations (these are the two error cases in the proof of Proposition 1) which can both be identified by the second party. In the proposed optimization, the second party outputs a flag indicating failure in each of these cases. The client is sure that the result is correct if the second player does not return a failure. Given target error probabilities $\delta$ for the whole protocol and, e.g., 1 / 4 for a single execution, we require that the number of independent executions of the algorithm $\gamma$ satisfies $(1/4)^{\gamma } < \delta$, or $\gamma > \frac{\ln 1/\delta }{\ln 4}$. Note that this optimization may reveal to the client information on intermediate computation values, since errors are input dependent. However, this type of leakage is harmless for applications like PIR.

• 4. Breaking computation into chunks. The final trade-off increases communication and decreases computation by breaking the computation into “chunks” and encrypting (and communicating) the input to each chunk separately. Loosely speaking, if the computation is split into $\zeta$ chunks, then the required communication increases by a factor of $\zeta$, and computation is reduced by a factor of $\zeta$ because the quadratic overhead in computing n gates is reduced to $\zeta$ times computing a quadratic overhead in $n/\zeta$ gates. In general this method requires up to $\zeta$ communication rounds, but in certain applications (like PIR) it does not require additional interaction.

Homomorphic n -bit AND. In the first (toy) example application, the communication complexity is dominated by $2(\ell +1)n$ group elements, to encode n bits. The operations are $n-1$ homomorphic evaluations of AND of bits, which amount to less than $n\ell$ applications of $\mathsf{MultShares}$ and $\mathsf{ConvertShares}$ or a total of less than $\frac{3 n\ell ^2}{2}+ \frac{4n^2 \ell \ln 4n/\delta }{\delta }$ group operations. In this example, communication is minimized by using the ciphertext reduction optimization and by representing c in base $B=2^b$. Communication complexity is about $\frac{(\ell +1)n}{b}$ group elements and computation is dominated by $\frac{3 n\ell ^2}{2b^2}+ \frac{4Bn^2\ell \ln 4n/\delta }{b\delta }$ group operations. Computation is minimized using ciphertext reduction, the Las-Vegas algorithm, and breaking into chunks. The communication complexity is increased by a factor of $\zeta$ for each of the $\lceil \frac{\ln 1/\delta }{\ln 4} \rceil$ invocations of the Las Vegas algorithm or $\lceil \frac{\ln 1/\delta }{\ln 4} \rceil \zeta n \ell$ group elements altogether. The computation requires at most

$$\left\lceil \frac{\ln 1/\delta }{\ln 4} \right\rceil \left( \frac{3 n\ell ^2}{2}+ \frac{16n^2 \ell \ln (16n/\zeta )}{\zeta ^2}\right) $$

group operations altogether.

2PC formula evaluation. The second example is a two-party computation of a formula $\psi$. This application requires the public-key variant of our protocol. The unoptimized version of this protocol is roughly similar in performance to the unoptimized version of homomorphic secret sharing. However, two of the optimizations, ciphertext reduction and the Las-Vegas algorithm do not apply in this case. Communication can be minimized by representing c in base B, reducing communication by $\log B$ and increasing computation by B compared to the unoptimized version. Computation can be minimized by breaking $\psi$ into $\zeta$ chunks increasing communication by $\zeta$ and reducing computation by $\zeta$ compared to the unoptimized version.