Humic substances are used in various sectors of the economy, mainly as plant growth stimulants, microfertilizers, and substances that neutralize ecotoxins. The presence of pronounced surface-active properties causes the use of these natural compounds in the composition of drilling fluids and for flushing aquifers contaminated with aromatic substances. Synthetic stimulants and surfactants are also used for these purposes, but, unlike them, humic preparations are completely safe for nature [1, 2]. All these factors put a problem for researchers to targeted humic substances, the solution of which is impossible without a fundamental understanding of their structure and properties.

Humic substances are poorly studied organic compounds, which consist of decomposition products of plant organisms and form a set of chaotic structures. A general scientific approach to the study of the structure and properties of humic substances has not yet been developed. According to a classification based on the different solubility of humic substances [3–5], they are subdivided into the following groups: humic acids, a fraction of humic substances soluble in alkalis and insoluble in acids (at pH < 2); fulvic acids, a fraction of humic substances soluble in water and alkaline and acidic solutions; and humin, a practically insoluble and nonextractable from natural bodies organic substance. Sometimes, hymatomelanic acids, which are a fraction of humic substances soluble in ethanol, are recognized.

The common feature for humic acids of various origins is the presence of an aromatic nucleus as the most mature and chemically stable part of the molecule substituted by alkyl radicals and the following functional groups: carboxyl (–COOH), hydroxyl (–OH), quinoid (>C=O), methoxy (–OCH3), and amino (–NH2) groups [2, 3, 7]. According to X-ray diffraction analysis, humic acid molecules are characterized by an ordered network structure, although they do not have a crystalline structure. Thus, humic substances are a mixture of chaotically folded natural organic compounds with a complex structure.

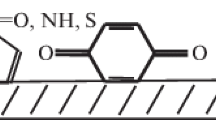
A generalized structural model is frequently used to systematize scientific concepts in the study of the structure and properties of complex natural compounds. Figure 1 shows a structural model of humic acids reported by Grinhut et al. [6] based on the data of elemental and quantitative functional analyzes obtained by modern physicochemical methods, such as gas chromatography–mass spectrometry, solid-phase NMR spectroscopy, and ionization mass spectroscopy. The proposed macromolecular structure of soil humic acid is based on the general characteristics given below. Elemental analysis (wt % on a daf basis): C, 53.6; N, 5.0; H, 5.8; O, 35.1; S, 0.5; and C/N, 10.7. Functional groups (cmol/g): carboxyl groups, 376; phenolic groups, 188; and total acidity, 564. According to NMR-spectroscopic analysis data, the distribution of carbon in the structural fragments of humic acids (% on a total carbon basis) is as follows: aliphatic, 18.1; aromatic, 20.9; carbohydrate, 23.7; methoxy group, 4.9; carboxyl, 8.4; ketone, 4.5; phenolic, 4.2; and other groups, 15.3 [4].

Fig. 1.
figure 1

Hypothetical structural fragment of soil humic acids [5].

Full size image

Currently, scientific research is underway to study the material and functional composition of humic substances for the purposeful change of their properties [2]. The structure and properties of humic substances can be judged only based on published average values [3, 5]. However, modern spectroscopic methods make it possible to establish with good accuracy the numbers of different functional groups per unit weight of humic substances [7]. The type and number of functional groups determine the solubility of humic substances. Therefore, chemical modification, which changes the number of functional groups of a given type, is a way to change the properties of humic substances.

The purpose of this work was to calculate the solvation energy of humic acids in various organic solvents and water with the use of modern quantum-chemical methods. The calculation was based on a model of the structure of humic acids. The results obtained make it possible to evaluate the efficiency of the use of various organic substances and water as solvents for these natural compounds.

Figure 2 shows the model structures of humic substances used for the calculation. The solvation of model structures in various solvents was calculated by the DFT b3lyp/sto-3g* quantum-chemical method using the software [9].

Fig. 2.
figure 2

Structural fragments of humic substances [8]: (a) molecular formula, С32NH15O14; functional groups, –СООН (2), –ОН (6), –О– (2), and >C=O (2); (b) molecular formula, С32NH15O14; functional groups, –OH (8), –О– (3), and >C=O (3). The numbers of functional groups of a certain type present in the considered structural model are given in parentheses.

Full size image

The solvation energy is the energy gain that results from transferring a mole of the test substances from a vacuum to a given solvent.

The polarizable continuum model (PCM) is a commonly used continuum solvation method. In the PCM, calculations were performed for both a vacuum and a solvent. In this model, the solvent is represented as a continuum with certain values of permittivity and polarizability. In the PCM model, the solvation energy is calculated as the sum of three contributions:

$${{E}_{{{\text{solv}}}}} = {{E}_{{{\text{cav}}}}} + {{E}_{{{\text{el}}}}} + {{E}_{{{\text{disp}}}}},$$

where Ecav is the cavitation energy, that is, the energy of formation of a cavity in the solvent, where the molecule of a solute is placed; Eel is the energy of electrostatic interaction between intrinsic and induced charges of the solute and solvent molecules; and Edisp is the dispersion component of the interaction energy, which takes into account the van der Waals interaction.

These components are the electrostatic (es) and dispersion-repulsive (dr) contributions to the free energy and cavitation energy (cav). All three terms are calculated using a cavity defined by interlocking van der Waals spheres centered at atomic sites. By definition, electrostatic energy is the work done when two charges approach each other from a greater distance to a given distance.

Organic solvents differ in dielectric constants. The dielectric constant ε shows how much the electric field strength E in a homogeneous dielectric is smaller than the strength in a vacuum.

The quantum-chemical calculations were carried out according to the DFT b3lyp/sto-3g* method taking into account the permittivity

$$\varepsilon = {{E}_{{\text{o}}}}{\text{/}}E.$$

The following energies were calculated:

$${{E}_{1}} = \langle \Psi (0){\text{|}}H{\text{|}}\Psi (0)\rangle ,$$
$${{E}_{2}} = \langle \Psi (0){\text{|}}H + V(0){\text{/}}2{\text{|}}\Psi (0)\rangle ,$$
$${{E}_{3}} = \langle \Psi (0){\text{|}}H + V(f){\text{/}}2{\text{|}}\Psi (0)\rangle ,$$
$${{E}_{4}} = \langle \Psi (f){\text{|}}H{\text{|}}\Psi (f)\rangle ,$$
$${{E}_{5}} = \langle \Psi (f){\text{|}}H + V(f){\text{/}}2{\text{|}}\Psi \rangle ,$$

where Ψ is the wave function of the system; H is the Hamiltonian of the system; V is the perturbation of the Hamiltonian; E1 is the energy of the unperturbed system, which is used as a reference energy for all subsequent stages of the calculation; E2 includes the interaction of a nonpolarized solute with a nonpolarized solvent; E3 is the interaction energy, which is the difference between the interaction in the solvent and in the gas phase, taken as a reference standard; E4 is the energy of interaction of a nonpolarized solute with a polarized solvent; and E5 is the polarization energy of the solvent upon interaction with a polarized solute.

The Gibbs energy of a solution (∆G (solution)) is the sum of the total electrostatic energy and the energy of nonelectrostatic origin.

Tables 1 and 2 summarize the results of calculations of the solvation of a humic substance with the empirical formula C32NH15O14 in various organic substances.

Table 1. Energy characteristics of the solvation of the model structure of humic substances with the empirical formula С32NH15O14 and the functional groups –СООН (2), –ОН (6), –О– (2), and >C=O (2) in various solvents
Full size table
Table 2. Energy characteristics of the solvation of the model structure of humic substances with the empirical formula С32NH18O14 and the functional groups –OH (8), –О– (2), and >C=O (2) in various solvents
Full size table

The results of the study of the solvation ability of water and organic compounds on the dissolution of a model structure of humic acids in terms of the Gibbs energy ∆G of solvation, calculated by the quantum-chemical DFT b3lyp/sto-3g* method, showed that the solvation of the model structure of humic substances with the empirical formula C32NH15O14 containing ‒COOH (2), –OH (6), –O– (2), and >C=O (2) functional groups occurs better in water and alcohols (∆Gwater = –22.67 kcal/mol, ∆Gmethanol = –25.72 kcal/mol, and ∆Gethanol = –28.50 kcal/mol). The following results were obtained for the solvation of the above model structure with different numbers of the functional groups –OH (8), –O– (3), and >C=O (3): (∆Gwater = –26.57 kcal/mol, ∆Gmethanol = –35.66 kcal/mol, and ∆Gethanol = –32.11 kcal/mol).

Thus, this study showed that the solvation of humic substances, even of the same elemental composition, depends on the quantitative content of functional groups. It was found that an increase in the number of phenolic and alcohol hydroxyls in the composition of humic substances increases their solubility in water and lower alcohols. This result in various modifications can be used in actual practice, in particular, for the fractionation of humic substances or in the selection of a solvent for the target-oriented chemical modification of these natural compounds.