INFLUENCE OF AMBIENT PRESSURE ON THE LOWEST OSCILLATION FREQUENCY OF A PLATE

Abstract

The lowest frequency of bending vibrations of a plate in contact with a liquid or gas is determined. The derivation of the expression for the distributed transverse load on the plate is given under the assumption of its cylindrical bending. The plate surfaces are in contact with a medium of different density and pressure. The medium can be compressible during surface deformation and incompressible. The influence on the bending of the interaction of the average pressure and changes in the curvature of the middle surface, as well as the added mass of the gaseous medium, is determined.

1 INTRODUCTION

Determination of the frequency spectrum of plates and shells in contact with liquid and gas is of great importance [1–3]. An extensive literature is devoted to this topic. It is also joined by a series of papers on vibrations of thin-walled bodies not in contact with the external environment.

The work [4] is devoted to an analytical solution for determining the natural frequencies and forms of bending vibrations of a square homogeneous plate clamped along the contour. The calculations were also compared with experimental data. The proposed research methodology and calculation algorithm can be used to study the bending vibrations of plates under other types of boundary conditions. In [5], the problem of calculating orthotropic polygonal plates subjected to acoustic action with a wide spectrum is considered.

Recently, the dynamic theory of plates has been widely used in the analysis of the behavior of elastic elements of micro- and nanosizes. Among the many applications of micro- and nanofilms, nanowires, and nanotubes, one can also mention their use as detectors and sensors in chemistry, biology, etc. [6–8]. Due to the unique application, the study of their operational properties is given much attention in the literature. For example, in [9, 10] a review of four hundred papers is given, mainly devoted to cantilever resonators made of nanofilms and nanowires. In [11], ultrasensitive nanomechanical resonators for structural studies of DNA-ligand complexes were reported. Electrostatically driven resonators have shown great potential in a wide range of applications such as sensors, communication devices, logic gates, and quantum measurements [12]. A mechanical nanosensor is used in [13] to detect and identify various bioparticles and estimate their sizes. The solution of the nonlinear equation is carried out using the Galerkin method. In [14], the dynamic instability of a cantilever nanobeam connected to a horizontal spring is analyzed.

However, in all these works, the interaction of the average pressure of the media and the difference between the areas of the convex and concave surfaces of the plate is not taken into account. This interaction is taken into account in papers [15, 16] in the case of light gases, when the added mass of media is small. Monographs [1–3] also do not take into account the above effect of average pressure. In [17], the frequency spectrum of a two-bearing resonator is determined taking into account the interaction of the average overpressure on the resonator surface and curvature, as well as the action of the axial load.

In this article, the lowest natural frequency of a plate is determined taking into account the interaction of the average overpressure on its surface and the curvature of the middle surface, as well as the effect of the added mass of the gaseous medium with distant boundaries. In contrast to the formulation of problems in [1–3], where the frequency is specified and the wave number is determined, here the half-wavelength is constructively specified and the frequency is determined. This setting is typical for resonators.

Of interest is the question of the mutual influence of the mean pressure effect and the effect of the added fluid mass known from the literature on the deformation of the plate. This is easier to find out in the case of an incompressible fluid. Further, taking into account the result obtained, we consider the case of a compressible fluid in a simpler setting (in particular, the contact conditions are not expanded in a Taylor series).

Assuming cylindrical bending of a thin plate, the following equation is considered

$$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} + {{\rho }}h\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = q,\quad D = \frac{{E{{h}^{3}}}}{{12(1 - {{{{\nu }}}^{2}})}},$$

(1.1)

where E, ν, ρ is the modulus of elasticity, Poisson’s ratio, material density, h is the plate thickness, w(x, t) is the deflection, х, t is the coordinate, time, q is the transverse distributed load.

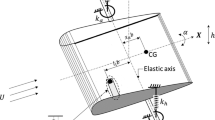
The pressures р₀ + р₁ and р₀ + р₂ of liquids with densities ρ₁ and ρ₂ act on the lower and upper surfaces of the plate (Fig. 1a). Here р₀ is the assembly pressure, in particular, atmospheric pressure acting on all surfaces, р₁, р₂ are excess pressures. When determining the load q we proceed from the assumption that ρ₁, ρ₂ and р₁, р₂ remain constant when the plate is bent.

Fig. 1.

(a) An example of plate mounting. (b) Element dx of the midsurface of the curved plate.

2 INCOMPRESSIBLE MEDIUM

We assume that the areas occupied by liquids extend indefinitely, the supports do not prevent the free flow of liquid along the plate in the direction of the x axis. The pressures arising from the movement of the plate will be denoted by ${{\bar {p}}_{1}}$ and ${{\bar {p}}_{2}}$. The equations for the dynamics of an incompressible fluid with respect to the velocity potential φ(x, z, t) have the form [1–3]

$$\frac{{{{\partial }^{2}}{{{{\varphi }}}_{{1,2}}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{{{\varphi }}}_{{1,2}}}}}{{\partial {{z}^{2}}}} = 0,\quad {{\bar {p}}_{{1,2}}} = - {{{{\rho }}}_{{1,2}}}\frac{{\partial {{{{\varphi }}}_{{1,2}}}}}{{\partial t}}.$$

(2.1)

Conditions on surfaces

$$\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} = \frac{{\partial w}}{{\partial t}}\left( {z = - \frac{h}{2} + w} \right),\quad \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} = \frac{{\partial w}}{{\partial t}}\left( {z = \frac{h}{2} + w} \right).$$

(2.2)

At a large distance from the surface, perturbations from the plate disappear

$$\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} = 0\left( {z = - \infty } \right),\quad \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} = 0\left( {z = \infty } \right).$$

(2.3)

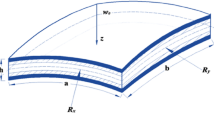
The elementary lengths dx₁, dx₂ of the lower and upper surfaces, expressed in terms of the length dx of the middle surface of the plate, are equal (Fig. 1b)

$$d{{x}_{1}} = \left( {1 + {{\varepsilon }_{x}}\left( { - \frac{h}{2}} \right)} \right)dx,\quad d{{x}_{2}} = \left( {1 + {{\varepsilon }_{x}}\left( {\frac{h}{2}} \right)} \right)dx,$$

(2.4)

where deformations in accordance with the Kirchhoff hypotheses [18]

$${{\varepsilon }_{x}}\left( { - \frac{h}{2}} \right) = \frac{h}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}},\quad {{\varepsilon }_{x}}\left( {\frac{h}{2}} \right) = - \frac{h}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}.$$

(2.5)

The distributed force q is determined by the formula [15, 16]

$$qdx = \left( {{{p}_{0}} + {{p}_{1}} + {{{\bar {p}}}_{1}}} \right)d{{x}_{1}} - \left( {{{p}_{0}} + {{p}_{2}} + {{{\bar {p}}}_{2}}} \right)d{{x}_{2}}.$$

(2.6)

We assume that a plate of unlimited length along the x axis rests on supports located at equal distances L and allowing free rotation. We take

$$w = W{{\sin\beta }}x{{\sin\omega }}t,\quad {{\beta }} = {{\pi /}}L,$$

(2.7)

which satisfies the conditions w = 0, ∂²w/∂x² = 0 for |x| = 0, L, 2L, …. Then in the functions

$${{{{\varphi }}}_{1}} = {{\Phi }_{1}}\left( z \right)\sin {{\beta }}x\cos {{\omega }}t,\quad {{{{\varphi }}}_{2}} = {{\Phi }_{2}}\left( z \right)\sin {{\beta }}x\cos {{\omega }}t$$

(2.8)

by (2.1) we have ${{\Phi }_{1}}\left( z \right) = {{A}_{1}}\exp \left( {{{\beta }}z} \right),{{\Phi }_{2}}\left( z \right) = {{A}_{2}}\exp \left( { - {{\beta }}z} \right)$. In this case, conditions (2.3) are satisfied.

Expanding the functions ∂φ₁/∂z, ∂φ₂/∂z into a Taylor series in the vicinity of z = 0, we reduce conditions (2.2) to the form

$$\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial z}} + \left( { - \frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial {{z}^{2}}}} = \frac{{\partial w}}{{\partial t}}\left( {z = 0} \right),\quad \frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial z}} + \left( {\frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial {{z}^{2}}}} = \frac{{\partial w}}{{\partial t}}\left( {z = 0} \right).$$

In a linear problem, the term with w under the given conditions must be omitted. Substituting expressions (2.7) and (2.8) here, taking into account Φ₁, Φ₂, we obtain

$${{A}_{1}} = W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}},\quad {{A}_{2}} = - W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}}.$$

Expressions (2.8) in terms of the deflection amplitude W take the form

$${{{{\varphi }}}_{1}} = W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}}\exp \left( {{{\beta }}z} \right)\sin {{\beta }}x\cos {{\omega }}t,$$

(2.9)

$${{{{\varphi }}}_{2}} = - W\frac{{{\omega }}}{{{\beta }}}{{\left( {1 - \frac{{{{\beta }}h}}{2}} \right)}^{{ - 1}}}\exp \left( { - {{\beta }}z} \right)\sin {{\beta }}x\cos {{\omega }}t.$$

When calculating the acoustic pressure on the plate surfaces z = – h/2 + w, z = h/2 + w, we also reduce expression (2.1) to the surface z = 0

$${{\bar {p}}_{1}} = - {{{{\rho }}}_{1}}\left[ {\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial t}} + \left( { - \frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{1}}}}{{\partial t\partial z}}} \right](z = 0),$$

$${{\bar {p}}_{2}} = - {{{{\rho }}}_{2}}\left[ {\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial t}} + \left( {\frac{h}{2} + w} \right)\frac{{{{\partial }^{2}}{{{{\varphi }}}_{2}}}}{{\partial t\partial z}}} \right](z = 0).$$

Let us substitute expressions (2.9) here, having previously omitted the non-linear terms with w. Then we get

$${{\bar {p}}_{1}} = W\frac{{{{{{\rho }}}_{1}}{{{{\omega }}}^{2}}}}{{{\beta }}}\sin {{\beta }}x\sin {{\omega }}t,\quad {{\bar {p}}_{2}} = - W\frac{{{{{{\rho }}}_{2}}{{{{\omega }}}^{2}}}}{{{\beta }}}\sin {{\beta }}x\sin {{\omega }}t.$$

Taking into account the ratio for the deflection, these expressions can be represented as

$${{\bar {p}}_{1}} = - \frac{{{{{{\rho }}}_{1}}}}{{{\beta }}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}},\quad {{\bar {p}}_{2}} = \frac{{{{{{\rho }}}_{2}}}}{{{\beta }}}\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}.$$

(2.10)

From (2.6), (2.4), (2.5) and (2.10) we find the distributed transverse load

$$q = {{p}_{1}} - {{p}_{2}} + \frac{{\left( {2{{p}_{0}} + {{p}_{1}} + {{p}_{2}}} \right)h}}{2} \cdot \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} - \frac{{{{{{\rho }}}_{1}} + {{{{\rho }}}_{2}}}}{{{\beta }}} \cdot \frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} + \left[ { - \frac{{{{{{\rho }}}_{1}} - {{{{\rho }}}_{2}}}}{{{\beta }}} \cdot \frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}}} \right]\frac{h}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}.$$

(2.11)

The last term in parentheses (2.11) must be omitted within the accepted approximation of the linear theory. It vanishes at ρ₁ = ρ₂.

Equation (1.1) in view of (2.11)

$$D\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} - \frac{{\left( {2{{p}_{0}} + {{p}_{1}} + {{p}_{2}}} \right)h}}{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \left( {{{\rho }}h + \frac{{{{{{\rho }}}_{1}} + {{{{\rho }}}_{2}}}}{{{\beta }}}} \right)\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} = {{p}_{1}} - {{p}_{2}}.$$

(2.12)

In the special case ρ₁ = ρ₂, p₁ = p₂ and the deflection function (2.7) from (2.12) we obtain for the lowest natural frequency ω

$${{{{\omega }}}^{2}} = {{\omega }}_{0}^{2}\frac{{1 + {{\alpha }}}}{{1 + {{\mu }}}},\quad {{\omega }}_{0}^{2} = \frac{{D{{{{\beta }}}^{4}}}}{{{{\rho }}h}},\quad {{\alpha }} = \frac{{\left( {{{p}_{0}} + {{p}_{1}}} \right)h}}{{D{{{{\beta }}}^{2}}}},\quad {{\mu }} = \frac{{2{{{{\rho }}}_{1}}}}{{{{\rho }}h{{\beta }}}}.$$

(2.13)

Here, ω₀ is the frequency of the plate not in contact with the liquid. Parameters α and μ determine the effect of pressure and density of the environment. Thus, the pressure increases, the density lowers the natural frequency of the plate. For α ≪ 1, μ ≪ 1 their influence disappears. Through the initial parameters α and μ we write

$${{\alpha }} \approx \frac{{{{p}_{0}} + {{p}_{1}}}}{E}{{\left( {\frac{L}{h}} \right)}^{2}},\quad {{\mu }} = \frac{{2{{{{\rho }}}_{1}}L}}{{{{\pi \rho }}h}}.$$

(2.14)

At E = 2 × 10⁵ MPa, ν = 0.3, ρ = 7.8 × 10³ kg/m³, ρ₁ = 10³ kg/m³, p₀ = 0, p₁ = 2 MPa, L/h = 10, α ≈ 10^–3, μ = 0.81. Therefore, there is no influence of pressure, there is a significant decrease in the natural frequency due to the added mass.

If p₁ = 20 MPa, L/h = 100, then $\alpha \approx {{10}^{{ - 4}}} \times {{10}^{4}} \approx 1$, μ = 8.1. According to the incompressible fluid model, in the case of water, there is only a decrease in natural frequency. This is a well-known result [1–3], however, taking into account the effect of pressure introduces some change in frequency.

The general assessment of the effects under consideration is that for α > μ, the frequency-increasing influence of the pressure of the medium predominates, and for α < μ, the decreasing effect of density (or the added mass) prevails. Through the input parameters, these inequalities have the form

$$\frac{{{{p}_{1}}\rho L}}{{E{{\rho }_{1}}h}} > 1,\quad \frac{{{{p}_{1}}\rho L}}{{E{{\rho }_{1}}h}} < 1.$$

The first case is realized for very thin plates made of a material with a low modulus of elasticity and at an extremely high pressure in the contacting medium. The second case is always realized at low pressures in a dense medium.

3 COMPRESSIBLE MEDIUM

According to the model of a compressible medium, instead of equations (2.1), we have [1–3]

$$\frac{{{{\partial }^{2}}{{\varphi }_{{1,2}}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{{\varphi }_{{1,2}}}}}{{\partial {{z}^{2}}}} - \frac{1}{{c_{{1,2}}^{2}}} \cdot \frac{{{{\partial }^{2}}{{\varphi }_{{1,2}}}}}{{\partial {{t}^{2}}}} = 0,\quad {{\bar {p}}_{{1,2}}} = - {{\rho }_{{1,2}}}\frac{{\partial {{\varphi }_{{1,2}}}}}{{\partial t}},\quad c_{{1,2}}^{2} = {{\kappa }_{{1,2}}}\frac{{{{p}_{{1,2}}}}}{{{{\rho }_{{1,2}}}}},$$

(3.1)

where c_{1, 2} is the speed of sound, ${{\kappa }_{{1,2}}}$ is the adiabatic coefficient. In contrast to the case of an incompressible fluid, here the pressure and density are not independent, but are related by an isothermal law.

Let us consider a particular case of identical media at identical pressures (ρ₁ = ρ₂, p₁ = p₂, c₁ = c₂). For functions (2.7) and (2.8)

$$w = W\sin \beta x\sin \omega t,\quad {{\varphi }_{{1,2}}} = {{\Phi }_{{1,2}}}\left( z \right)\sin \beta x\cos \omega t$$

(3.2)

from the wave equation (3.1) follows

$${{\Phi }_{{1,2}}} = {{A}_{{1,2}}}{{e}^{{kz}}} + {{B}_{{1,2}}}{{e}^{{ - kz}}},\quad {{k}^{2}} = {{\beta }^{2}} - \frac{{{{\omega }^{2}}}}{{c_{1}^{2}}}.$$

(3.3)

We will consider the case k² > 0. he substantiation of this condition is given below. Setting A₂ = 0, B₁ = 0 in accordance with conditions (2.3), we obtain a particular solution

$${{\varphi }_{1}} = {{A}_{1}}{{e}^{{kz}}}{\text{sin}}\beta x\cos \omega t,\,\,\,\,\,{{\varphi }_{2}} = {{B}_{2}}{{e}^{{ - kz}}}{\text{sin}}\beta x\cos \omega t.$$

(3.4)

As shown above, when determining the distributed load q, it is necessary to take into account the conditions at z = ±h/2, and when determining ${{\bar {p}}_{1}}$, ${{\bar {p}}_{2}}$, on the surfaces of the plate and satisfying conditions (3.2) in the linear problem, instead of z = ±h/2 + w, we can take z = 0. hen from conditions (3.4) A₁ = ωW/k, B₂ = – ωW/k and

$${{\bar {p}}_{1}} = - {{{{\rho }}}_{1}}\frac{{\partial {{{{\varphi }}}_{1}}}}{{\partial t}} = {{{{\rho }}}_{1}}\frac{{{{{{\omega }}}^{2}}}}{k}W\sin {{\beta }}x\sin \omega t,\quad {{\bar {p}}_{2}} = - {{{{\rho }}}_{2}}\frac{{\partial {{{{\varphi }}}_{2}}}}{{\partial t}} = - {{{{\rho }}}_{2}}\frac{{{{{{\omega }}}^{2}}}}{k}W\sin {{\beta }}x\sin \omega t.$$

The right side of equation (1.1) is equal to (ρ₁ = ρ₂, p₁ = p₂)

$$q = \left( {{{p}_{0}} + {{p}_{1}}} \right)h\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{\bar {p}}_{1}} - {{\bar {p}}_{2}} = {{p}_{1}}h\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{{2{{{{\rho }}}_{1}}{{{{\omega }}}^{2}}}}{k}W\sin \beta x\sin \omega t.$$

(3.5)

Substituting into (1.1) the expression for w and q from (3.2) and (3.5), we obtain for p₀ = 0

$$\begin{gathered} D{{\beta }^{4}} - \rho h{{{{\omega }}}^{2}} + {{p}_{1}}h{{{{\beta }}}^{2}} - \frac{{2{{{{\rho }}}_{1}}{{{{\omega }}}^{2}}}}{k} = 0, \\ {{\omega }}_{0}^{2} = \frac{{D{{\beta }^{4}}}}{{\rho h}},\quad {{k}^{2}} = {{\beta }^{2}} - \frac{{{{\omega }^{2}}}}{{c_{1}^{2}}},\quad {{\beta }} = \frac{\pi }{L}. \\ \end{gathered} $$

(3.6)

From (3.6) it follows

$${\text{1}} - Z + \alpha - \frac{{\mu Z}}{{\sqrt {1 - \eta {\text{Z}}} }} = 0,\quad \alpha = \frac{{{{p}_{1}}{{\beta }^{2}}}}{{\rho {{\omega }}_{0}^{2}}},\quad {{\mu }} = \frac{{2{{{{\rho }}}_{1}}}}{{{{\rho }}h{{\beta }}}},\quad \eta = \frac{{{{\omega }}_{0}^{2}}}{{c_{1}^{2}{{\beta }^{2}}}},\quad Z = \frac{{{{\omega }^{2}}}}{{\omega _{0}^{2}}}.$$

(3.7)

Consider the case $1 - \eta {\text{Z}} > 0$. We represent the frequency equation (3.7) in the form of a cubic

$$\begin{gathered} {{Z}^{3}} + {{b}_{1}}{{Z}^{2}} + {{b}_{2}}Z - {{b}_{3}} = 0, \\ {{b}_{1}} = - 2\delta - \frac{1}{\eta } + \frac{{{{\mu }^{2}}}}{\eta },\quad {{b}_{2}} = {{\delta }^{2}} + \frac{{2\delta }}{\eta },\quad {{b}_{3}} = - \frac{{{{\delta }^{2}}}}{\eta },\quad \delta = 1 + \alpha . \\ \end{gathered} $$

(3.8)

The lowest natural oscillation frequency is ${{f}_{1}} = {\omega \mathord{\left/ {\vphantom {\omega {2\pi ,\quad }}} \right. \kern-0em} {2\pi ,\quad }}\omega = {{\omega }_{0}}\sqrt Z .$

At E = 76 × 10³ MPa, ν = 037, ρ = 10 500 kg/m³, h = 20 nm, L = 2000 nm, ${{\kappa }_{{1,2}}}$ = 1.4, atmospheric pressure p_a = 0.1 MPa, air density ρ_1a = 1.2928 kg/m³, p₁ = 2 MPa, the numerical solution of Eq. (3.7) gives the root: Z = 1.10268. The corresponding frequency is f₁ = 6.894 MHz. The solution of the cubic equation (3.8) naturally gives the same root: Z = 1.10268.

To check the fulfillment of the condition k² > 0, we take into account the obtained expression $\omega = {{\omega }_{0}}\sqrt Z$, where ω₀ is given in (3.6). In the considered example, Z ≈ 1.1, that is, the influence of air pressure predominates over its density. Condition k² > 0 or

$${{\left( {\frac{c}{{{{c}_{1}}}}} \right)}^{2}}{{\left( {\frac{h}{L}} \right)}^{2}} < 10,\quad {{c}^{2}} = \frac{E}{{(1 - {{\nu }^{2}}){{\rho }}}}$$

at L/h > 10 is always satisfied in the case of a steel plate and water, and in the case of gases, at large values of L/h (for example, L/h > 15).

Let us present an approximate solution of Eq. (3.7). Let’s take Z = 1 – a, a³ ≪ 1. Substitute this expression in (3.7) and set it equal to zero, neglecting the term containing a³,

$$\begin{gathered} {{d}_{1}}{{a}^{2}} + {{d}_{2}}a + {{d}_{3}} = 0,\quad {{d}_{1}} = 2\delta \eta - 3\eta + 1 - {{\mu }^{2}}, \\ {{d}_{2}} = ({{\delta }^{2}} - 4\delta + 3)\eta + 2{{\mu }^{2}} + 2\delta - 2,\quad {{d}_{3}} = {{\left( {1 - \delta } \right)}^{2}}\left( {1 + \eta } \right) - {{\mu }^{2}}. \\ \end{gathered} $$

(3.9)

From (3.9) we find

$$a = \frac{{ - {{d}_{2}} + \sqrt {d_{2}^{2} - 4{{d}_{1}}{{d}_{3}}} }}{{2{{d}_{1}}}}.$$

If δ = 1, then d₁ = 1 – η – η², d₂ = 2µ², d₃ = – µ².

If we neglect the term containing a², then we get a = –d₃/d₂.

The results of calculating the lowest natural frequency of bending vibrations of the plate using approximate formulas (3.9) and a = –d₃/d₂ in accordance with the conditions for the value of a are summarized in Table 1. For air in the pressure range under consideration, the formula a = –d₃/d₂ gives an error of no more than 9%.

Table 1. First natural frequency of bending vibrations of the plate, p₁, MPa, f₁, MHz

We also present the solution of Eq. (3.7) in the form

$$Z = \frac{\delta }{{1 + {{\mu }}}}[{{C}_{1}} + {{C}_{2}}\eta \mu \delta + {{C}_{3}}{{\eta }^{2}}\mu {{\delta }^{2}}].$$

(3.10)

For η ≪ 1, we represent $\sqrt {1 - \eta {\text{Z}}}$ as

$$\sqrt {1 - \eta {\text{Z}}} \approx 1 - \frac{1}{2}\eta Z \approx \frac{1}{2}\frac{{\eta \delta \left( {{{C}_{1}} + {{C}_{1}}\mu + {{C}_{2}}\delta } \right)}}{{{{{\left( {1 + \mu } \right)}}^{2}}}}.$$

(3.11)

Substituting expressions (3.10) and (3.11) into Eq. (3.7), expanding the resulting relation in a series in powers of δ and equating the coefficients at δ, δ², δ³ to zero, we obtain a system of three linear equations, the solution of which is written

$${{C}_{1}} = 1,\quad {{C}_{2}} = - \frac{1}{{2{{{\left( {1 + {{\mu }}} \right)}}^{2}}}},\quad {{C}_{3}} = - \frac{{1 - \mu }}{{4{{{\left( {1 + {{\mu }}} \right)}}^{4}}}}.$$

It can be seen from the above calculations that the external pressure and the presence of gas have a significant effect on the oscillation frequencies of the plate. We also note the high accuracy of the approximate formula (3.9) and the solution in the form (3.10).

Figure 2, a shows the dependence of the first frequency of bending vibrations of the plate on pressure for different gases. From Fig. 2, a it can be seen that with increasing pressure, the natural frequency of oscillations increases. And with an increase in gas density, a decrease in the natural frequency of bending vibrations occurs. Figure 2b shows the pressure dependence of the first frequency of plate bending vibrations according to the formulas for incompressible and compressible liquids for carbon dioxide. It can be seen from Figure 2b that the frequencies according to the model for an incompressible fluid are higher than the frequencies according to the model for a compressible fluid due to an increase in density, and with increasing pressure, the difference in oscillation frequencies increases.

Fig. 2.

Dependence of the first bending vibration frequency of the plate f₁ (MHz) on the pressure p₁ (MPa): (а) for different gases: ρ₁ = 0.1785 (helium), 1.2928 (air), 1.9768 (carbon dioxide) kg/m³ (dotted, dashed, solid lines, respectively); (b) according to the formulas for incompressible (2.14) and compressible (3.7) liquids for carbon dioxide ρ₁ = 1.9768 kg/m³ (dotted and dashed lines, respectively).

4 CONCLUSIONS

It is well known from the literature (for example, [1–3]) that the eigenfrequencies of bending vibrations of a plate significantly decrease when it comes into contact with a liquid. This is due to the influence of the added mass of the liquid. It has been established [15, 16] that taking into account the difference in the areas of opposite surfaces of the plate, which is formed during its bending, can have an increasing effect on natural frequencies. Accounting for this effect leads to the appearance of a distributed transverse force equal to the product of the curvature of the middle surface and the average pressure on the plate surface.

The simultaneous influence of these factors on the lowest oscillation frequency in the case of an incompressible liquid depends on the ratio of the average pressure to the elastic modulus of the material, the densities of the material and liquid, and the ratio of the plate length to its thickness. For real parameters, the prevailing influence of the density of the medium over the pressure in it is typical. However, pressure can have a noticeable effect on the result.

For a compressible fluid, the influence is more complex, since the added mass depends on the speed of sound and on the frequency of oscillation itself. In addition, the pressure and density of the gaseous medium are not independent.

The influence of the contacting medium on the lowest oscillation frequency is significant for very thin plates and films with a low modulus of elasticity. It is necessary to take it into account, especially in the case of elements with micro- and nanoscale thicknesses.

As the pressure increases, the natural oscillation frequency increases. In the case of light gases (hydrogen, helium), the influence of pressure can prevail over their density. These results can be used in modeling the vibrations of plates in contact with liquid and gas, including those of micro- and nanosizes.