An anisotropic finite strain viscoelastic model considering different spin effects on the intermediate configuration

Abstract

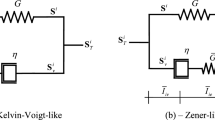
In this paper, a model of viscoelastic anisotropic deformation is proposed with the different inelastic spin effects considered. The model considering three different inelastic spin assumptions. Numerical simulations show that when the cyclic load is applied, the results corresponding to the model considering different inelastic spins are very different. Thus, when the viscoelastic model is used to simulate actual material, the inelastic spin assumption should be carefully selected.

THE FOURTH-ORDER TRANSFORMATION TENSOR

The Hill material strain is represented as follows:

$$\mathcal{E}\mathop {\text{ = }}\limits^{{\text{def}}} \sum\limits_{{\text{K}} = 1}^3 {f({{\lambda }_{{\text{K}}}}){{N}_{{\text{K}}}} \otimes {{N}_{{\text{K}}}}} .$$

(A-39)

The time derivative of the general material strain is [33]

$$\dot {\mathcal{E}} = \sum\limits_{I = 1}^3 {f{\kern 1pt} '\left( {{{\lambda }_{I}}} \right)\dot {\lambda }_{{\text{I}}}^{{}}{{N}_{I}} \otimes {{N}_{I}}} + \sum\limits_{I = 1}^3 {\sum\limits_{J \ne I}^3 {\left( {f\left( {{{\lambda }_{J}}} \right) - f\left( {{{\lambda }_{I}}} \right)} \right)\Omega _{{IJ}}^{\text{Lag}}} } {{N}_{I}} \otimes {{N}_{J}},$$

(A-40)

where $\boldsymbol\Omega _{{}}^{\text{Lag}}$ is Lagrangian spin. Considering $f\left( \lambda \right) = \ln \lambda$, then the time derivative of the logarithmic strain is

$$\dot{\boldsymbol{H}} = \sum\limits_{i = 1}^3 {\sum\limits_{j{\text{ = }}1}^3 {\frac{{2{{\lambda }_{i}}{{\lambda }_{j}}}}{{\lambda _{j}^{2} - \lambda _{i}^{2}}}\left( {\ln {{\lambda }_{j}} - \ln {{\lambda }_{i}}} \right){{N}_{i}} \otimes {{N}_{j}}\left( {{\boldsymbol{n}_{i}} \otimes {\boldsymbol{n}_{j}}:\boldsymbol{d}} \right)} } .$$

(A-41)

Notably, there is a limit

$$\mathop {\lim }\limits_{{{\lambda }_{j}} \to {{\lambda }_{i}}} \frac{{2{{\lambda }_{i}}{{\lambda }_{j}}}}{{\lambda _{j}^{2} - \lambda _{i}^{2}}}\left( {\ln {{\lambda }_{j}} - \ln {{\lambda }_{i}}} \right) = 1.$$

(A-42)

The time derivative of the logarithmic strain can also be expressed as follows:

$$\boldsymbol{R}\,\cdot \,\dot{\boldsymbol{H}}\,\cdot \,{\boldsymbol{R}^{\text{T}}} = \sum\limits_{{\text{i}} = 1}^3 {\sum\limits_{j{\text{ = }}1}^3 {\frac{{2{{\lambda }_{{\text{i}}}}{{\lambda }_{{\text{j}}}}}}{{\lambda _{{\text{j}}}^{2} - \lambda _{{\text{i}}}^{2}}}\left( {\ln {{\lambda }_{{\text{j}}}} - \ln {{\lambda }_{{\text{i}}}}} \right){\boldsymbol{a}_{i}} \boxtimes {\boldsymbol{a}_{j}}:\boldsymbol{d},} } $$

(A-43)

where ${\boldsymbol{a}_{i}} = {\boldsymbol{n}_{i}} \otimes {\boldsymbol{n}_{i}}$, the above-mentioned expression can be represented as follows:

$$\boldsymbol{R}\,\cdot \,\dot{\boldsymbol{H}}\,\cdot \,{\boldsymbol{R}^{\text{T}}} = \mathcal{T}:\boldsymbol{d},$$

(A-44)

where the transformation tensor is

$$\mathcal{T} = \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {\frac{{{{\lambda }_{i}}{{\lambda }_{j}}(\ln {{\lambda }_{j}} - \ln {{\lambda }_{i}})}}{{\lambda _{j}^{2} - \lambda _{i}^{2}}}({\boldsymbol{a}_{i}} \boxtimes {\boldsymbol{a}_{j}} + {\boldsymbol{a}_{i}}\,\overline \boxtimes \,{\boldsymbol{a}_{j}})} } .$$

(A-45)

Eq. (A-41) can also be expressed as follows:

$$\dot{\boldsymbol{H}} = \mathbb{T}:\hat{\boldsymbol{d}},$$

(A-46)

where

$$\mathbb{T} = {{\left( {\boldsymbol{R} \boxtimes \boldsymbol{R}} \right)}^{\text{T}}}:\mathcal{T}:\left( {\boldsymbol{R} \boxtimes \boldsymbol{R}} \right).$$

(A-47)

Thereby

$$\mathbb{T} = \sum\limits_{i = 1}^3 {\sum\limits_{j{\text{ = }}1}^3 {\frac{{{{\lambda }_{i}}{{\lambda }_{j}}(\ln {{\lambda }_{j}} - \ln {{\lambda }_{i}})}}{{\lambda _{j}^{2} - \lambda _{i}^{2}}}({\boldsymbol{A}_{i}} \boxtimes {\boldsymbol{A}_{i}} + {\boldsymbol{A}_{i}}\,\overline \boxtimes \,{\boldsymbol{A}_{i}})} } .$$

(A-48)