1 Introduction

Roll and pitch motions occur because of ocean environmental disturbances, such as waves, current, and wind. These motions result in limitations on conducting maritime operations or traveling by ship. Passenger discomfort with respect to the sea-keeping performance of a ship is related to pitch and roll motions. Seasickness mostly results from sensory conflict caused by vertical acceleration that accompanies heave, pitch, and roll motions. Thus, roll and pitch motions will adversely affect the efficiency of workers in commercial ships and combat vessels. Furthermore, maritime operations like ship-borne helicopter recovery, launch and recovery of submarines, and cargo transfer between a container ship and a mobile harbor (Hong and Ngo, 2012) are also severely restricted. The effects of ship motions on cargo transfer were investigated by Hong and Ngo (2012) by analyzing the dynamics of the container crane on a mobile harbor and adaptive control approaches were developed to ameliorate the ship motions (Ngo and Hong, 2012a; 2012b). There has been much research on reducing ship pitch and roll motions. The most commonly employed methods to reduce pitch and roll motions are the using of bilge keels, rudder, water tanks, gyro-actuators, and fins.

The first effort in ship motion reduction was using bilge keels in anti-roll control (Froude, 1865). Later, Watt (1883; 1885) permanently fixed Her Majesty’s Ship (HMS) Inflexible with water chambers to reduce roll motion. His research together with the work of Froude were probably the earliest attempts on anti-rolling passive water tanks. The work was followed by the development of the U-tank by Frahm (1911). This U-tank was found to be more effective than the free-surface tank previously used by Froude (1865) and Watt (1883; 1885). Schlick (1904) was the first to propose the use of gyroscopic effects of large rotating wheels as a roll control device.

However, when the forward speed is higher than 10–15 knots, active fins are the most effective stabilizer (Perez, 2005). A large proportion of modern ships is equipped with active fins for stabilization. Stabilizing fins have been widely studied since the 1950s, with most studies related to the reduction of roll motion. Stabilizing moments have been explored theoretically and experimentally (Allan, 1945), with the procedure for determining efficient types of fins and the design of the controller for active stabilizing fins addressed. Further discussion about ship motion and reduction was given by Bhattacharyya (1978). A state-feedback control algorithm was presented to control the active fins. The mechanism of lift loss resulting from the interaction among fins and bilge keels was studied in detail by Lloyd (1989). Here, the design methodology for stabilizing fins and controllers in time domain was also presented. To demonstrate the feasibility of using fins and rudders to oppose roll motion in the real ocean environment, a sea trial was conducted (Sharif et al., 1995; 1996). Experimental results suggested that stabilizing fins and rudders are effective. To overcome the nonlinearity in the active control problem, nonlinear approaches were used to design a controller for active fins. Liut (1999) and Liut et al. (2001) applied a neural network and fuzzy-logic controller for stabilizing fins, where ship motion was simulated in the time domain using a program based on the panel method. Perez and Goodwin (2008) proposed a model predictive controller to prevent the nonlinear effects of fins.

Compared with anti-rolling, anti-pitching has attracted relatively little interest. This is partly because the pitch moment of a ship is relatively large, and stabilizing fins with a large area would be necessary for stabilization. Therefore, it is well known that pitch stabilization is neither efficient nor applicable for practical purposes in ship design. However, pitch motion is one of the most damaging motions for a ship, and anti-pitching is the obvious choice after anti-rolling for improving the operability of ships. Early studies on pitch reduction focused on passive ways. Abkowitz (1959) and Stefun (1959) researched bow-fixed anti-pitching fins in both theoretical and experimental ways. It was shown that bow-fixed fins are effective in pitch reduction. However, bow-fixed fins always lead to vibration and speed loss, which was unexpected (Naito and Isshiki, 2005). In addition, the specification of the fin in the experiment was excessive, rendering it unrealistic in real-world application.

Active fins provide a relatively efficient way for anti-pitching. The efficiency of active stabilization mainly depends on controllers for active fins. Wu et al. (1999) employed a proportional integral derivative (PID) control scheme to actuate the stabilizing fins to reduce the pitch motion. Experiments in regular waves verify the designed controller. In Kim and Kim (2011), one or two pairs of stabilizing fins for roll and/or pitch motion of a cruise ship were studied. Control quality of controllers based on a PID and a linear quadratic Gaussian (LQG) algorithm were compared. Significant reduction of rolling was obtained using PID- or LQG-controlled stabilizing fins, particularly in moderate sea conditions. Roll and pitch motions were stabilized simultaneously using two pairs of stabilizing fins. However, determination of the gains in PID algorithm is non-adaptive. Satisfactory results can be obtained only when a proper set of gains is developed (Kim and Kim, 2011).

In this paper, a predictive controller for a ship equipped with two pairs of actives fins is proposed for joint pitch-roll stabilization. The controller is developed based on ship motion and hydrodynamic force predictions (SMHFP). The SMHFP controller is simple and data-driven. It consists of a short-term predictor, an external hydrodynamic force estimator, and a fin angle allocator. A short-term predictor based on an autoregressive (AR) approach serves to overcome control time delay by forecasting ship motions in the coming seconds. After that, predicted ship motions are applied in the external hydrodynamic force estimator to provide an accurate evaluation of the coming external forces acting on the ship. Finally, optimal attack angles for active fins are allocated based on the external hydrodynamic force forecasts. For validation purposes, a numerical simulation of the swaying motions of a ship equipped with two pairs of active fins in the time domain was carried out. The SMHFP controller was integrated into a sea-keeping assessing computer program which adopts a weakly nonlinear 2.5D method. Meanwhile, hydrodynamic coefficients involved in the external hydrodynamic force estimator were derived from the weakly nonlinear 2.5D approach and time-variation. Numerical simulations under various sea states were implemented to access the performance of the SMHFP controller.

2 Methodology

2.1 Theoretical formulations for the SMHFP controller

A virtual control system comprising the SMHFP controller and the ship motion simulator is shown in Fig. 1. The ship motion simulator was developed based on a weakly nonlinear 2.5D method which will be described in detail in Section 2.2. It was used to provide a simulation environment to validate the performance of the SMHFP controller.

Fig. 1
figure 1

Implementation procedure of the virtual control system

t suggests the present step; Fwave(t) indicates the wave excitation force; η(t), \(\dot \eta (t)\), and \(\ddot \eta (t)\) are vectors that represent the ship motion displacements, velocities, and accelerations, and their predictions in the next are presented by \(\hat {\eta} (t + 1)\), \(\hat \dot \eta (t + 1)\) and \(\hat \ddot \eta (t + 1)\), respectively; \({\hat F_4}(t + 1)\) and \({\hat F_5}(t + 1)\) are the predicted roll and pitch moments, respectively; α(t+1) is the attack angle vector for the active fins

Full size image

Fig. 1 shows that the SMHFP controller was designed by integrating a short-term predictor, a force estimator, and a fin angle allocator. Details about the short-term predictor, force estimator, and fin angle allocator are given in the following subsections. As suggested in Fig. 1, the ship motion displacements, velocities, and accelerations due to ocean waves are treated as inputs while allocated fin angles are regarded as outputs of the controller. The fin angles were allocated based on the estimated external hydrodynamic forces. Therefore, accurate evaluation of the external forces acting on the ship in the near future is critical in stabilizing control.

In this study, the proposed SMHFP controller adopts a short-term predictor and a force estimator to provide accurate prediction of the coming external ship hydrodynamic forces. A short-term predictor based on an AR approach serves to forecast ship motions based on input motion displacements, velocities, and accelerations. Afterwards, predicted ship motion displacements, velocities, and accelerations are applied in the external hydrodynamic force estimator to provide accurate evaluation of the coming external forces acting on the ship. Subsequently, the optimal attack angles for active fins can be allocated based on the estimated external hydrodynamic forces.

2.1.1 Short-term predictor

The AR model has been extensively used because of its advantages, such as convenience in model identification, data-driven, realization, and good frequency resolution (Zhang and Chu, 2005; Duan et al., 2015b; Huang et al., 2015). It is employed in short-term predictor for predicting accurate ship motions. The AR model considers that relations exist in the variables of time series. Therefore, the present variable is able to be represented by the previous in time. For a given time series {x(t), t=1, 2, …, n}, the AR model is formulated as

$$\begin{array}{*{20}c} {x(t) = {\varphi _{{1}}}x(t - {{1}}) + {\varphi _{{2}}}x(t - {{2}}) + \ldots + {\varphi _p}x(t - p) + a(t),}\\ {t = {{1}},{{2}}, \ldots, n,} \end{array}$$
(1)

where p is the model order, and {φ1, φ2, …, φp} are parameters of the AR model, which are unknown. {a(t), t=1, 2, …, n} is zero-mean white noise.

Identification of the AR model in Eq. (1) involves the determination of order p and corresponding parameters {φ1, φ2, …, φp}.

There are various approaches for estimating these parameters, of which the least mean square (LMS) method, recursive least square (RLS), and Levinson-Durbin (L-D) algorithms are the most widely studied. The RLS and L-D algorithms give faster convergence and remove the eigenvalue spread problem compared with the LMS algorithm (Myllylä, 2001). However, the RLS algorithm introduces problems: program code for the sliding-window RLS algorithm is complicated to implement, is memory intensive, and is potentially numerically-unstable (Douglas, 1996). Comparisons between the RLS and L-D algorithms were carried out by Duan et al. (2015a), where it was found that the L-D algorithm is superior. Consequently, the L-D algorithm is adopted in this study.

The basic ideas of the L-D recursion are first that it is easy to solve the system for p=1, and second that it is also very simple to solve a p+1 coefficients sized problem when a p coefficients sized problem has already been solved. For a given ship motion time sequence {x(t), t=1, 2, …, n} and model order p, a summary of the L-D algorithm is presented in Table 1 (Huang et al., 2015).

Table 1 Summary of Levinson-Durbin algorithm
Full size table

Another critical aspect in AR modeling is selecting an optimal order based on given samples. In the past decades, a variety of criteria have been proposed to determine the order for the AR model. Although it is a long time since it was proposed, the Aikaike information criterion (AIC) (Akaike, 1974) and Bayesian information criterion (BIC) (Akaike, 1979) are still the most popular approaches. However, even with infinite sample size, the model order determined by the AIC principle fails to converge to the true order (Akaike, 1979). Therefore, the BIC criterion is applied in order selection. The BIC value of the general AR(p) model is defined as

$${\rm{BIC}}(p) = {\rm{lg}}\sigma _p^2 + (p + 1)({\rm{lg}}N)/N,$$
(2)

where \({\sigma _p}^2\) is the covariance. The model order p0 that leads to the minimum BIC value is chosen as the optimal order.

A k-step-ahead adaptive predictor based on the model in Eq. (1) can be developed as

$$\hat x(t + k) = \left\{ {\begin{array}{*{20}c} {\sum\limits_{i = 1}^p {{\varphi _i}{{x}}(t + k - i),} \quad \quad \quad \quad \quad k = 1,\quad \quad }\\ {\sum\limits_{i = 1}^{k - 1} {{\varphi _i}\hat x{{(t + i)}_{N + i}}} + \sum\limits_{i = k}^p {{\varphi _i}x(t + k - i),\quad \quad \;} }\\ {k = 2, 3, \cdots, p,}\\ {\sum\limits_{i = 1}^p {{\varphi _i}\hat x(t + k - i)}, \quad \quad \quad \quad k > p,\quad } \end{array}} \right.$$
(3)

where \(\hat x(t + k)\) is the prediction value of k steps advancing.

2.1.2 Force estimator

Estimation of ship hydrodynamic forces is another part of the SMHFP controller. To describe the relation between ship motions and hydrodynamic forces, coordinate systems need to be established. All six possible degrees of freedom in ship motions are illustrated in Fig. 2. Whereas surge, sway, and heave are translational motions, roll, pitch, and yaw are rotational motions.

Fig. 2
figure 2

Ship motions and the coordinate systems

Full size image

Surge, sway, heave, roll, pitch, and yaw are represented as η1, η2, η3, η4, η5, and η6, respectively. As shown in Fig. 2, three coordinate systems are deployed to describe the mathematical model of ship motion. The inertial coordinate system O-X0Y0Z0 is fixed on the calm water surface and used to model the wave. The body-fixed coordinate system G-xyz with its origin at the ship’s center of gravity is moving with the ship motion.

Hydrodynamic forces and ship motion are described using the body-fixed coordinate. The horizontal body coordinate system o-x0y0z0 is also fixed on the calm water surface, but it translates with the ship along the forward direction. The hydrodynamic boundary value problem is solved under the horizontal body coordinate system.

The forces estimator calculates external hydrodynamic forces by applying the dynamic equilibrium between the external forces and ship motions. According to the motion equations as shown in Eqs. (4) and (5), the external hydrodynamic forces estimator that takes into account memory effects is formulated as follows:

$$\begin{array}{*{20}c} {\hat{{F}}_4(t - 1) = ({I_{xx}} + {\mu _{44}}){{\ddot \eta }_4} + \int\nolimits_0^{t + 1} {{K_{44}}(t - \tau){{\dot \eta }_4}{\rm{d}}\tau } }\\ { - F_4^{\rm{v}} + F_4^{\rm{s}} + F_4^{\rm{f}},\quad \quad \quad } \end{array}$$
(4)
$$\begin{array}{*{20}c} {{{\hat F}_5}(t + 1) = ({I_{yy}} + {\mu _{55}}){{\ddot \eta }_5} + \int\nolimits_0^{t + 1} {{K_{55}}(t - \tau){{\dot \eta }_5}{\rm{d}}\tau } }\\ { + {c_{55}}{\eta _5} + {\mu _{53}}{{\ddot \eta }_3} + {b_{53}}{{\dot \eta }_3}}\\ {\quad \quad \quad \quad + \int\nolimits_0^{t + 1} {{K_{53}}(t - \tau){{\dot \eta }_3}{\rm{d}}\tau } + F_5^{\rm{s}} + F_5^{\rm{f}},} \end{array}$$
(5)

where t indicates the present step while t+1 is the incoming step; \({\hat F_4}(t + 1)\) and \({\hat F_5}(t + 1)\) are the predicted roll and pitch moments that result from external wave excitations, respectively. Dots over the symbols represent differentiation with respect to time, and subscripts “jk” are related with forces, hydrodynamic coefficients in the kth direction due to an oscillatory motion in the jth mode. μjk represents the infinite frequency added mass coefficients, only depending on the ship geometry. bjk gives the radiated damping coefficients. cjk represents ship geometry and forward speed dependent constant that relates to the radiation restoring force. Kjk(t) represents the time-dependent memory function. Ixx and Iyy are the rolling and pitching moments of inertia; \({F_4}^{\rm{f}}\) and \({F_5}^{\rm{f}}\) are the roll and pitch stabilization moments; \({F_4}^{\rm{s}}\) and \({F_5}^{\rm{s}}\) are the hydrostatic restoring force due to rolling and pitching, respectively; \({F_4}^{\rm{v}}\) is the viscous roll damping.

With the above relations, the external hydrodynamic forces can be evaluated with the measured ship motions η(t). Conventionally, external hydrodynamic forces are estimated using the historical and present ship motions, resulting in a control delay. In this study, predicted motions produced by the AR predictor are employed in the force estimator to get the coming external hydrodynamic forces. The control time delay is thus overcome.

2.1.3 Fin angle allocator

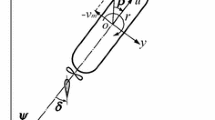
The fin angle allocator that computes attack angles for producing optimal stabilizing forces is the last part of the SMHFP controller. Active fin stabilizers consist of one or two pairs of hydrofoils mounted on rotatable stocks at the turn of the bilge. When a ship advances with forward speed, the hydrodynamic lift is generated if there is an angle between the flow and the fin. Stabilizing forces are results of the generated lifts and the locations of the fins on the hull. Assuming that the ship advances with forward speed U in the direction of x axis, the velocity vector of the incoming flow V and the effective attack angle αt(i) can be written as

$$\begin{array}{*{20}c} {V = ({V_x},{V_y}) = (U - {u_{\rm {w}}}(t),\quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{{\dot \eta }_3}(t) + {y_{\rm {f}}} + (i){{\dot \eta }_4}(t) - {x_{\rm {f}]}(i){{\dot \eta }_5}(t) - {v_{\rm {w}}}}(t)),} \end{array}$$
(6)
$${\alpha _{\rm{t}}}(i) = {\alpha _{\rm{f}}}(i) + {\eta _5} + \Delta \alpha (i),$$
(7)

where each component of αt(i) is illustrated in Fig. 3. αf(i) is the operational angle of the stabilizing fin. uw(t) and vw(t) are the horizontal and vertical velocity components of the fluid particle, respectively. Δα originates from the vertical velocity of ship and the velocity of the fluid particle, expressed as

$$\Delta \alpha (i) = \arctan {{{{\dot \eta }_3}(t) + {y_{\rm{f}}}(i){{\dot \eta }_4}(t) - {x_{\rm{f}}}(i){{\dot \eta }_5}(t) - {v_{\rm{w}}}(t)} \over {U - {u_{\rm{w}}}(t)}},$$
(8)

where xf(i), yf(i), and zf(i) are the x-, y-, and z-components of the distance between the quarter point of the ith fin and gravity center point of the ship, respectively.

Fig. 3
figure 3

Attack angle and forces of a stabilizing fin

Full size image

With the incoming flow, the lift force Lf(i) and the drag Df(i) of each fin attached to the ship are formulated as

$${L_{\rm{f}}}(i) = {1 \over 2}\rho {V^2}SC_{\rm{L}}^{{\alpha _{\rm{t}}}}{\alpha _{\rm{t}}}(i),\quad i = 1, 2, 3, 4,$$
(9)
$${D_{\rm{f}}}(i) = {1 \over 2}\rho {V^2}S{C_{\rm{D}}}, \quad \;i = 1,\;2,\;3,\;4,$$
(10)

where ρ represents the density of water; S gives the projected area of the fin; is derived from the time-varying lift coefficient CL with respect to effective attack angle αt(i), and CD is the drag coefficient.

In addition to the lift forces and drags, the vertical inertial forces of active fins due to ship motion also make a contribution to ship motion reduction. The vertical inertial force of a single fin can be determined from

$${K_{\rm{f}}}(i) = ({m_{\rm{f}}} + \Delta {m_{\rm{f}}})\left[ {{{\ddot \eta }_3}(t) - {y_{\rm{f}}}(i){{\ddot \eta }_4}(t) + {x_{\rm{f}}}(i){{\ddot \eta }_5}(t)} \right],$$
(11)

where mf is the inertial mass, and Δmf is the added mass of the stabilizing fin, which can be estimated approximately by

$$\Delta {m_{\rm{f}}} = {{\lambda _{\rm{f}}^2\pi \rho {S^2}} \over {4{{({S^2} + \lambda _{\rm{f}}^2)}^{1/2}}}},$$
(12)

where λf is the aspect ratio.

Stabilizing moments are consequences of the lift forces and drags. Time-varying moment arms should be also taken into consideration in the calculation. Stabilizing forces produced by two pairs of active fins are expressed as

$$\begin{array}{*{20}c} {F_4^{\rm{f}} = \sum\limits_{i = 1}^4 {{y_{\rm{f}}}(i)} \left[ {{1 \over 2}\rho {U^2}SC_{\rm{L}}^{{\alpha _{\rm{t}}}}{\alpha _{\rm{t}}}(i)\cos \Delta \alpha } \right.}\\ {\left. {\quad \quad \quad \quad \quad \quad \quad + {D_{\rm{f}}}(i)\sin \Delta \alpha + {K_{\rm{f}}}(i)} \right],} \end{array}$$
(13)
$$\begin{array}{*{20}c} {F_5^{\rm{f}} = \sum\limits_{i = 1}^4 { - {x_{\rm{f}}}(i)} \left[ {{1 \over 2}\rho {U^2}SC_{\rm{L}}^{{\alpha _{\rm{t}}}}{\alpha _{\rm{t}}}(i)\cos \Delta \alpha } \right.}\\ {\left. {\quad \quad \quad \quad \quad \quad + {D_{\rm{f}}}(i)\sin \Delta \alpha + {K_{\rm{f}}}(i)} \right].} \end{array}$$
(14)

The fin angle allocator decides optimal attack angles by applying the hydrodynamic forces forecasts to Eqs. (13) and (14). Wave excited forces (by external hydrodynamic forces) \({\hat F_4}\) and \({\hat F_5}\) are regarded as the required roll and pitch stabilization forces, respectively. Hence, expected attack angles αt(i) (i=1, 2, 3, 4) can be evaluated by solving the follow equation:

$$\left\{ {\begin{array}{*{20}c} {{{\hat F}_4} = F_4^{\rm{f}}\left[ {{\alpha _{\rm{t}}}(i)} \right],}\\ {{{\hat F}_5} = F_5^{\rm{f}}\left[ {{\alpha _{\rm{t}}}(i)} \right]{.}} \end{array}} \right.$$
(15)

2.2 Numerical method for ship motions in time domain

2.2.1 The 2.5D theory for ship hydrodynamics

Active fins perform effectively for ship motion reduction in a high-speed situation. The 2.5D theory is superior to other approaches in forecasting motions of high-speed vessels in that it produces better prediction accuracy with equivalent computation complexity compared with simple strip theory, and provides equivalent prediction accuracy with less computational complexity than the 3D panel method. Governing equations and boundary conditions for ship motion analysis based on 2.5D theory have been presented in many studies. Faltinsen and Zhao (1991) addressed a possible expression for 2.5D theory in simulating ship motions. The formulations are summarized as

$${{{\partial ^2}{\phi _j}} \over {\partial {y^2}}} + {{{\partial ^2}{\phi _j}} \over {\partial {z^2}}} = 0,\quad {\rm{in}}\;{\rm{fluid}}\;{\rm{domain}},$$
(16)
$${\rm{i}}\omega {\phi _j} - U{{\partial {\phi _j}} \over {\partial x}} + g{\zeta _j} = 0,\quad {\rm{on}}\;z = 0,$$
(17)
$${\rm{i}}\omega {\zeta _j} - U{{\partial {\zeta _j}} \over {\partial x}} - {{\partial {\phi _j}} \over {\partial z}} = 0,\quad {\rm{on}}\;z = 0,$$
(18)
$$\begin{array}{*{20}c} {{{\partial {\phi _j}} \over {\partial N}} = \left\{ {\begin{array}{*{20}c} {{\rm{i}}\omega {N_j} + U{m_j},\quad j = 2,3, \cdots, 6,}\\ { - {{\partial {\phi _0}} \over {\partial N}},\quad j = 7,\quad \quad \quad \quad \quad } \end{array}} \right.}\\ {\quad \quad \quad \quad \quad \quad {\rm{on}}\;{\rm{the}}\;{\rm{mean}}\;{\rm{wet}}\;{\rm{surface}},} \end{array}$$
(19)
$${\phi _j} = {{\partial {\phi _j}} \over {\partial x}} = 0,\quad x > {x_0},$$
(20)
$${\phi _j} \rightarrow 0,\quad z \rightarrow - \infty,$$
(21)

where ζj denotes the complex amplitude of free-surface elevation in the jth direction by the unit radiation and diffraction potential; x0 is the longitudinal position of the ship forward perpendicular; ω is the wave frequency; g is the acceleration of gravity; φj is the radiation potential due to unit motion in the jth direction (j=1, 2, …, 6); φ0 is the incident wave potential; Nj (j=2, 3) is the component of the inward unit normal vector of a point on the cross-sectional contour of the ship, i.e., (N2, N3)=(Ny, Nz). Nj (j=4, 5, 6) can be obtained through

$$({N_4},\;{N_5},\;{N_6}) = (y{N_z} - z{N_y},\; - x{N_z},\;z{N_y}){.}$$
(22)

mj is the second-order differential of the steady potential (−Ux+φs). If the effect of the steady perturbation φs is negligible, mj can be expressed as

$$\begin{array}{*{20}c} {{m_j} = 0\;{\rm{for}}\;j = 1,2,3,4,}\\ {{m_5} = {N_z},\quad {m_6} = - {N_y}{.}} \end{array}$$
(23)

In addition, an appropriate radiation condition should be imposed at the infinite boundary.

The boundary value problem has been further developed into time-dependent expressions by Ma et al. (2005). Here, time varying transfer functions t(x), ψj(t, y, z), and ζj(t, y, z) as shown in Eqs. (24)–(26) are substituted into Eqs. (16)–(21). Re-derived formulations for the time-dependent 2.5D approach are then given in Eqs. (27)–(32). A proper radiation condition at infinity is also required. Numerical details of implementing 2.5D can be found in Ma et al. (2005).

$$t(x) = (- x + {x_0})/U,$$
(24)
$${\psi _j}(t,y,z) = {\phi _j}(x,y,z){{\rm{e}}^{{\rm{i}}\omega t}},$$
(25)
$${\zeta _j}(t,y,z) = {\eta _j}(x,y,z){{\rm{e}}^{{\rm{i}}\omega t}},$$
(26)
$${{{\partial ^2}{\psi _j}} \over {\partial {y^2}}} + {{{\partial ^2}{\psi _j}} \over {\partial {z^2}}} = 0,\quad {\rm{in}}\;{\rm{fluid}}\;{\rm{domain}},$$
(27)
$${{\partial {\psi _j}} \over {\partial t}} + g{\zeta _j} = 0,\quad {\rm{on}}\;z = 0,$$
(28)
$${{\partial {\zeta _j}} \over {\partial t}} - {{\partial {\psi _j}} \over {\partial z}} = 0,\quad {\rm{on}}\;z = 0,$$
(29)
$$\begin{array}{*{20}c} {{{\partial {\psi _j}} \over {\partial N}} = \left\{ {\begin{array}{*{20}c} {(i\omega {N_j} + U{m_j}){{\rm{e}}^{{\rm{i}}\omega t}},\quad j = 2,3, \cdots, 6,}\\ { - {{\partial {\phi _0}} \over {\partial N}}{{\rm{e}}^{{\rm{i}}\omega t}},\quad j = 7,\quad \quad \quad \quad \quad \quad \quad } \end{array}} \right.}\\ {\quad \quad \quad \quad \quad {\rm{on}}\;{\rm{the}}\;{\rm{mean}}\;{\rm{wet}}\;{\rm{surface}},} \end{array}$$
(30)
$${\psi _j} = {{\partial {\psi _j}} \over {\partial t}} = 0,\quad t = 0,$$
(31)
$${\psi _j} \rightarrow 0,\quad z \rightarrow - \infty {.}$$
(32)

The potential in the control domain can be obtained by solving the initial boundary value problem based on 2.5D theory. Subsequently, the application of Bernoulli’s equation leads to the unsteady linearized hydrodynamic pressure:

$$p(x, y, z, t) = \rho [i{\omega _{\rm{e}}}\phi \prime + {W}\cdot\nabla \phi \prime ]{{\rm{e}}^{ - {\rm{i}}{\omega _{\rm {e}}}t}},$$
(33)

where ωe is the frequency of encounter; φ′ can be replaced by the incident wave potential φI, diffraction wave potential φD or -iωeξkφk; ξk is the amplitude of ship motion in the kth mode; W is the steady flow velocity around the ship, given by

$${{W}} = ({\omega _1}, {\omega _2}, {\omega _3}) = \nabla (- Ux + {\phi _{\rm{s}}}){.}$$
(34)

Hydrodynamic forces and moments acting on the ship can be obtained by integrating the fluid pressure p on the cross-sectional contour and then implementing integration along the longitudinal axis of the ship. They are respectively expressed as

$${{F}} = \int\limits_L {{\rm{d}}x} \int\limits_{{l_x}(t)} {p{{n}}{\rm{d}}l},$$
(35)
$${{M}} = \int\limits_L {{\rm{d}}x} \int\limits_{{l_x}(t)} {p{{r}} \times {{n}}{\rm{d}}l},$$
(36)

where L is the ship length, and lx(t) represents the instantaneous wetted cross-sectional contour in the location of x.

$$n = ({n_1},\;{n_2},\;{n_3}),\quad r \times n = ({n_4},\;{n_5},\;{n_6}),$$
(37)

where r is the position vector from the center of ship’s gravity to a point (x, y, z) on the hull surface.

Based on Eqs. (35) and (36), a generalized force consisting of three components of force, F1, F2, and F3, and three components of moment, F4, F5, and F6, along the x, y, and z axis, respectively, is defined as

$${F_j} = \iint \limits_{{s_0}} {p{n_j}{\rm{d}}s}, \quad j = {{1}},\;{{2}},\;\ldots,\;{{6}},$$
(38)

with the generalized normal nj defined in Eq. (37). s0 is the mean wetted ship hull surface.

Each part of the hydrodynamic force is briefly described as below.

  1. 1.

    Incident wave excitation force

    The instant wave elevation of the free surface is

    $$\begin{array}{*{20}c} {\zeta (t) = - {\rm{Re}}\left\{ {{1 \over g}{{\left. {{{D{\phi _{\rm{I}}}(t)} \over {Dt}}} \right\vert }_{z = 0}}} \right\}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ { = - {\rm{Re}}\left\{ {{1 \over g}{{\left. {\left[ {{\partial \over {\partial t}}{\phi _{\rm{I}}}(t) + {1 \over 2}\nabla {\phi _{\rm{I}}}(t)\cdot\nabla {\phi _{\rm{I}}}(t)} \right]} \right\vert }_{z = 0}}} \right\}.} \end{array}$$
    (39)

    Substituting the incident wave potential φI into Eq. (33), the incident wave pressure can be obtained from

    $${p^I}(x, y, z, t) = \rho [i{\omega _{\rm{e}}}{\phi _{\rm{I}}} + {{W}}\cdot\nabla {\phi _{\rm{I}}}]{{\rm{e}}^{ - {\rm{i}}{\omega _{\rm {e}}}t}},\quad z < \zeta (t){.}$$
    (40)

    Therefore, the incident wave exciting force FI(t) can be found by integrating incident wave pressure pI over the wetted hull surface:

    $$\begin{array}{*{20}c} {{{{F}}^{\rm{I}}}(t) = - \iint \limits_{{s_t}} {{p^{\rm I}}{{n}}{\rm{d}}s} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ { = - {\rm{Re}}\left\{ {{{\rm{e}}^{ - {\rm{i}}{\omega _e}t}}\iint \limits_{{s_t}} {\rho \left[ {{\rm{i}}{\omega _{\rm{e}}}{\phi _{\rm{I}}} + {{W}}\cdot\nabla {\phi _{\rm{I}}}} \right]{{n}}{\rm{d}}s} } \right\},} \end{array}$$
    (41)

    where st represents the instantaneous wetted ship hull surface.

  2. 2.

    Hydrostatic restoring force

    The hydrostatic pressure ps is proportional to the water depth z, formulated as

    $${p^{\rm{s}}} = - \rho g\left[ {\zeta (t) - z} \right],\quad z < \zeta (t).$$
    (42)

    As a result, the hydrostatic force Fs(t) is given by

    $${{{F}}^{\rm{s}}}(t) = \iint \limits_{{s_t}} {{p^{\rm{s}}}{{n}}{\rm{d}}s} = - \rho g\iint \limits_{{s_t}} {z{{n}}{\rm{d}}s} {.}$$
    (43)
  3. 3.

    Radiation force

    Using the radiated wave potential-iωeξkφk, we have the radiated wave pressure \({p_j}^{\rm{R}}\) from the jth mode ship motion:

    $$p_j^{\rm{R}} = \rho \left[ {\omega _{\rm{e}}^2{\xi _k}{\phi _k} - {\rm{i}}{\omega _{\rm{e}}}{\xi _k}{{W}}\cdot\nabla {\phi _k}} \right]{{\rm{e}}^{ - {\rm{i}}{\omega _{\rm {e}}}t}}{.}$$
    (44)

    The radiation forces \({F_j}^{\rm{R}}\) due to radiated waves can be obtained by integrating \({p_j}^{\rm{R}}\) over the wetted hull surface:

    $$\begin{array}{*{20}c} {F_j^{\rm{R}} = - \iint \limits_{{s_0}} {p_j^{\rm{R}}(x, y, z, t){n_j}{\rm{d}}s} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ { = - {\rm{Re}}\left\{ {\sum\limits_{k = 1}^6 {\left[ {(- \omega _{\rm{e}}^2){A_{jk}} + (- i{\omega _{\rm{e}}}){B_{jk}}} \right]{\xi _k}{{\rm{e}}^{ - {\rm{i}}{\omega _{\rm{e}}}t}}} } \right\},} \end{array}$$
    (45)

    where Ajk is the added mass and Bjk is the damping coefficient of a ship (Salvesen et al., 1970), and

    $${A_{jk}} = \rho \iint \limits_{{s_0}} {{\rm{Re}}({\phi _k}){n_j}{\rm{d}}s} - {\rho \over {{\omega _{\rm{e}}}}}\iint \limits_{{s_0}} {{\rm{Im}}({{W}}\cdot\nabla {\phi _k}){n_j}{\rm{d}}s},$$
    (46)
    $$\begin{array}{*{20}c} {{B_{jk}} = \rho {\omega _{\rm{e}}}\iint \limits_{{s_0}} {{\rm{Im}}({\phi _k}){n_j}{\rm{d}}s} + \rho \iint \limits_{{s_0}} {{\rm{Re}}({{W}}\cdot\nabla {\phi _k}){n_j}{\rm{d}}s},} \\ {\quad \quad \quad \quad \quad k = 2,3,\ldots,6;\;j = 2,3,\ldots,6{.}} \end{array}$$
    (47)

    However, solving Ajk and Bjk in the time domain suffers from a difficulty in numerical convergence. Time domain formulations representing the radiation forces have been re-derived by Cummins (1962) in terms of unknown velocity potentials, as follows:

    $$F_{jk}^{\rm{R}} = - {\mu _{jk}}{\ddot \eta _k} - {b_{jk}}{\dot \eta _k} - {c_{jk}}{\eta _k} - \int\nolimits_0^t {{K_{jk}}(t - \tau){{\dot \eta }_k}{\rm{d}}\tau } {.}$$
    (48)

    Radiation forces in Eq. (48) take memory effect into account (Cummins, 1962; Liapis, 1986). With the Kramers-Kronig relations (Cummins, 1962; Ogilvie, 1962) in the ship hydrodynamic,

    $${K_{jk}}(\tau) = {2 \over \pi }\int\nolimits_0^\infty {\left[ {{B_{jk}}({\omega _{\rm{e}}}) - {b_{jk}}} \right]\cos ({\omega _{\rm{e}}}\tau){\rm{d}}{\omega _{\rm{e}}}},$$
    (49)
    $${K_{jk}}(\tau) = {2 \over \pi }\int\nolimits_0^\infty {\left[ {{\omega _{\rm{e}}}{\mu _{jk}} - {\omega _{\rm{e}}}{A_{jk}}({\omega _{\rm{e}}}) - {c_{jk}}/{\omega _{\rm{e}}}} \right]\sin ({\omega _{\rm{e}}}\tau){\rm{d}}{\omega _{\rm{e}}}},$$
    (50)

    the radiation forces can be evaluated from Fourier transforms of the frequency domain hydrodynamic coefficients instead of solving the problem in the time domain. The computational efficiency is largely improved and the numerical deficiency is overcome.

  4. 4.

    Diffraction force

    Substituting the diffracted wave potential into Eq. (33), the diffracted wave pressure is expressed as

    $${p^{\rm{D}}}(x, y, z, t) = \rho \left({{\rm{i}}{\omega _{\rm{e}}}{\phi _{\rm{D}}} + {{W}}\cdot\nabla {\phi _{\rm{D}}}} \right){{\rm{e}}^{ - {\rm{i}}{\omega _{\rm{e}}}t}}{.}$$
    (51)

    Then, the diffraction force FD(t) can be obtained by integrating pD on the wetted hull surface:

    $$\begin{array}{*{20}c} {{{{F}}^{\rm{D}}}(t) = - \iint \limits_{{s_0}} {{p^{\rm{D}}}{{n}}{\rm{d}}s} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ { = - {\rm{Re}}\left[ {{{\rm{e}}^{ - {\rm{i}}{\omega _{\rm{e}}}t}}\iint \limits_{{s_0}} {\rho \left({{\rm{i}}{\omega _{\rm{e}}}{\phi _D} + {{W}}\cdot\nabla {\phi _{\rm{D}}}} \right){{n}}{\rm{d}}s} } \right]{.}} \end{array}$$
    (52)
  5. 5.

    Rolling damping force

    For the viscous rolling damping force \({F_4}^{\rm{v}}\), it can be simply obtained by

    $$F_4^{\rm{v}} = - {B_{44}}{\dot \eta _4} - B_{44}^2\dot \eta _4^2,$$
    (53)

    where B44 is the viscous rolling damping coefficient, which is obtained from either a free decay test or empirical formulations.

2.2.2 Motion equations of a ship in waves

Equations of ship motion begin with the application of Newton’s Law as a statement of dynamic equilibrium. The acceleration \(\ddot \eta \) of a ship balances the external forces including the hydrostatic force Fs, the incident wave force FI, the diffraction wave force FD, the radiation wave force FR, the viscous force Fv, and other external disturbance force Fother:

$$({{{M}}_{\rm{i}}} + {{{M}}_{\rm{a}}})\ddot \eta = {{{F}}^{\rm {s}}} + {{{F}}^{\rm {I}}} + {{{F}}^{\rm {D}}} + {{{F}}^{\rm {R}}} + {{{F}}^{\rm {v}}} + {{{F}}^{{\rm{other}}}},$$
(54)

where Mi and Ma are the inertial mass matrix and added mass matrix of the ship, respectively.

In this study, the roll and pitch motions of a ship and their reduction are main focuses. Thus, equations of three degrees of freedom ship motions with respect to heave, roll, and pitch are further derived based on Eq. (54), which are given as:

$$M{\ddot \eta _3} = F_3^{\rm{I}} + F_3^{\rm{S}} + F_{33}^{\rm{R}} + F_{35}^{\rm{R}} + F_3^{\rm{D}} - Mg + F_3^{{\rm{other}}},$$
(55)
$${I_{xx}}{\ddot \eta _4} = F_4^{\rm{I}} + F_4^{\rm{S}} + F_{44}^{\rm{R}} + F_4^{\rm{D}} + F_4^{\rm{v}} + F_4^{{\rm{other}}},$$
(56)
$${I_{yy}}{\ddot \eta _5} = F_5^{\rm{I}} + F_5^{\rm{S}} + F_{55}^{\rm{R}} + F_{53}^{\rm{R}} + F_5^{\rm{D}} + F_5^{{\rm{other}}},$$
(57)

where M is the mass of the ship.

Substituting radiation forces shown in Eq. (48) into Eqs. (55)–(57), the motion equations of a ship become

$$\left\{ {\begin{array}{*{20}c} {(M + {\mu _{33}}){{\ddot \eta }_3} + \int\nolimits_0^t {{K_{33}}(t - \tau){{\dot \eta }_3}{\rm{d}}\tau } + {\mu _{35}}{{\ddot \eta }_5} + {b_{35}}{{\dot \eta }_5}\quad \quad \quad }\\ { + \int\nolimits_0^t {{K_{35}}(t - \tau){{\dot \eta }_5}{\rm{d}}\tau } = F_3^{\rm{I}} + F_3^{\rm{S}} + F_3^{\rm{D}} - Mg + F_3^{\rm{f}},}\\ {({I_{xx}} + {\mu _{44}}){{\ddot \eta }_4} + \int\nolimits_0^t {{K_{44}}(t - \tau){{\dot \eta }_4}{\rm{d}}\tau } - F_4^{\rm{v}}\quad \quad \quad \quad \quad \quad \quad }\\ { = F_4^{\rm{I}} + F_4^{\rm{S}} + F_4^{\rm{D}} + F_4^{\rm{f}},\quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {({I_{yy}} + {\mu _{55}}){{\ddot \eta }_5} + \int\nolimits_0^t {{K_{55}}(t - \tau){{\dot \eta }_5}{\rm{d}}\tau } + {c_{55}}{\eta _5} + {\mu _{53}}{{\ddot \eta }_3} + {b_{53}}{{\dot \eta }_3}\quad }\\ { + \int\nolimits_0^t {{K_{53}}(t - \tau){{\dot \eta }_3}d\tau } = F_5^{\rm {I}} + F_5^{\rm {S}} + F_5^{\rm {D}} + F_5^{\rm {f}}{.}\quad \quad \quad } \end{array}} \right.$$
(58)

Thus, the mathematical model for ship motion is established in which external hydrodynamic forces acting on the ship are obtained simultaneously by solving the above described boundary value problems using a 2.5D approach in the time domain. The second-order ordinary differential Eq. (58) can be worked out by continuously implementing the fourth-order Rung-Kutta numerical schemes.

3 Numerical simulation models

3.1 Parameters of the ship and active fins

To validate the performance of the nonlinear 2.5D method in forecasting ship response in high-speed conditions, numerical simulations were implemented employing an 8000-TEU container ship and a warship model. The main features of the ship models are summarized in Table 2 and their body plans are plotted in Fig. 4. The model scale is 60. Numerical results of ship motions are compared with experimental results from model testing.

Fig. 4
figure 4

Body plans of the container ship (a) and warship model (b)

Full size image
Table 2 Main characteristics of container ship and warship model
Full size table

Another specification of the stabilizing fin is given to carry out numerical simulation of ship stabilization. The NACA0015 airfoil, as shown in Fig. 5, which has a symmetric section shape, is chosen as the section type of the lifting surface. The total area of the stabilizing fins is related to the water plane of the ship (Kim and Kim, 2011). The span and chord of each fin model are both 0.067 m, indicating that the aspect ratio is 1. Two pairs of fins are equipped to stabilize the coupled roll-pitch motion. Each pair of fins is located in the fore and aft of a ship, as shown in Fig. 6. Fig. 7 presents the installation position of the fins in the transverse section. These locations are determined by taking the general mechanical specifications of the stabilizing fins into consideration.

Fig. 5
figure 5

Cross section of NACA0015 airfoil

Full size image
Fig. 6
figure 6

Installation positions of the active fins in the longi-tudinal section

Full size image
Fig. 7
figure 7

Installation positions of the active fins in the trans-verse section

Full size image

In the present study, steady flow approximation is adopted in the calculation of lift forces and the ship motion is simulated every 0.1 s. The motion of the active fin, i.e., the rotating angle of the fin, is limited for mechanical reasons. Mechanical limitations, such as the maximum rotation angle and maximum angular speed, are required in the real operation of active fins. Thus, the movement of the fin is restricted. In particular, the maximum angle is assumed to be 25°.

3.2 Simulated sea conditions

To validate the weakly nonlinear 2.5D method, numerical simulation in various incident waves (Table 3) was carried out. Details of the sea conditions as shown in Table 3 are transferred according to the model scale, keeping consistency with the model testing. Incident waves with a fixed wave height of 60 mm offer a wave length to ship length ratio λ/Lpp of 1.00–2.00. Typically, the forward speed U of the ship model is assumed to be 1.75 m/s, corresponding to 24 knots for the full scale ship.

Table 3 Details of the calculation conditions in regular waves
Full size table

In this simulation, the warship model is used. To observe the feasibility and reduction efficiency of the SMHFP controller, the range of sea states 2–7 (Table 4) is considered. Waves in various sea states are simulated on the basis of International Towing Tank Conference (ITTC) wave spectra which were divided into 100 frequency components when implementing. The forward speed of the warship model U and the incident wave angle are assumed to be 1.75 m/s and 135°, respectively. Simulation details are presented in Table 4.

Table 4 Sea states for ship motion control simulations
Full size table

4 Numerical results and discussion

4.1 Validation of the ship motion simulator

Numerical results from the nonlinear 2.5D approach to the warship and container ship models without fins are compared with experimental results. The container ship is a kind of blunt hull shape ship while the warship is a kind of fine hull shape ship. Both blunt and fine hull shape ships were chosen in the hydrodynamic study to provide sufficient and general validation. Fig. 8 presents comparisons of the simulated heave and pitch response amplitude operators (RAOs) with the experimental results of the warship model. Comparisons for the container ship are then given in Fig. 9.

Fig. 8
figure 8

Heave (a) and pitch (b) RAOs of the warship model: Froude number F n =0.21, head sea with wave slope of 0.02

β is the angle between incident wave and ship heading (β=180° for head sea); STF method is the Salvesen Tuck Faltisen method

Full size image
Fig. 9
figure 9

Heave (a) and pitch (b) RAOs of the 8000-TEU container model: Froude number F n =0.21, head sea with wave slope of 0.02

Full size image

From Figs. 8 and 9, it is seen that the proposed nonlinear 2.5D method produces an ensemble higher accuracy in ship motions analysis than the conventional Salvesen Tuck Faltisen (STF) method (Salvesen et al., 1970). The improvements result from the modification by integrating on the instantaneous wet surface instead of the mean wet surface when calculating the incident wave force in Eq. (41) and the hydrostatic restoring force in Eq. (43).

4.2 Stabilization simulation results and analysis

To carry out the joint pitch-roll stabilization, pitch and roll stabilizing moments are needed simultaneously. Hence, installation of two pairs of stabilizing fins is reasonable. As the relative position of each pair of fins affects the performance of ship stabilization, the distance between these two pairs of fins should not be less than half the ship length (Kim and Kim, 2011). To produce pitch stabilizing moment, rotating directions of attack angles should be different between the fins fixed in the aft and fore parts of a ship, and the magnitudes of attack angles should be different between fins installed in the portside and starboard. Numerical results of the joint pitch-roll reduction using the SMHFP controller on a ship model in both regular and irregular waves are presented as follows. The incident angle of the waves is 135° and the forward speed of the ship model is 1.75 m/s. The effectiveness of the proposed SMHFP controller in stabilization is evaluated by comparing pitch and roll angle displacements and accelerations with and without fins.

4.2.1 Regular waves

Fig. 10 presents results of stabilization simulations in regular waves where the wavelength is equal to the ship length. Figs. 10a and 10c present comparisons of roll and pitch time series with and without fins, while acceleration comparisons are shown in Figs. 10b and 10d. Attack angles time series for stabilizers are given in Fig. 10e. Fig. 11 displays the roll and pitch time histories of ship motions under various regular wave conditions (λ/Lpp=1.0, 1.5, and 2.0). Table 5 summarizes the reduction ratios of motion root mean square (RMS) for joint pitch-roll under various wavelength regular wave conditions.

Fig. 10
figure 10

Numerical results of the joint pitch-roll stabilization in regular waves

(a) Roll angle; (b) Roll angular acceleration; (c) Pitch angle; (d) Pitch angular acceleration; (e) Attack angles time series for the fins. λ/Lpp=1.0, incident wave angle is 135°, wave height is 60 mm. U=1.75 m/s for (a)—(d), and U=2.33 m/s for (e)

Full size image
Fig. 11
figure 11

Roll (a) and pitch (b) time series of ship motions under the joint pitch-roll control in regular waves (incident wave angle is 135°, wave height is 60 mm, U=1.75 m/s, λ/L pp =1.0, 1.5, and 2.0)

Full size image
Table 5 Reduction ratios of motion RMS for joint pitch-roll control in regular waves
Full size table

Results reveal that the proposed SMHFP controller performs satisfactorily in the joint pitch-roll stabilization. It is clearly observable from Fig. 10 that pitch and roll motions in the regular wave with unit wavelength to ship length ratio are reduced instantaneously. The displacement and acceleration amplitudes of pitch and roll motions evidently decrease. This is confirmed by pitch and roll time series under the conditions of different wavelength to ship length ratios, as displayed in Fig. 11, where considerable reduction in amplitude of pitch and roll motions can be found. As a fixed sliding window with 20 s of ship motions was used to construct the AR model, the fin angle controller starts to work at 20 s.

The summary of the reduction ratios in Table 5 further demonstrates the effectiveness of the SMHFP controller in joint pitch-roll reduction. Motions controlled by the SMHFP controller slow down as not only the roll and pitch amplitudes but also their reduced accelerations. Periodical flat tops and bottoms in attack angle time series in Fig. 10e suggest that the fins have reached their maximum attack angles. Smooth variations of attack angles in time indicate that no vibrations will be induced by the proposed controller in operating the stabilizing fins.

In addition, comparison of stabilizing efficiencies between roll and pitch motions suggests that reduction of roll motion is better than that of pitch motion. As shown in Table 5, reduction ratios of roll motion are more than 50% while those of pitch motion are less than 50%. This is due to the fact that pitching moment is much larger than roll moment. Hence, pitch reduction requires a larger stabilizer or being allocated a larger valid attack angle.

4.2.2 Irregular waves

Fig. 12 exhibits simulated results of ship motion with and without fins in sea state 5. Figs. 12a–12d represent time series comparison of the roll, roll acceleration, pitch, and pitch acceleration, respectively. Attack angles time series produced by the SMHFP controller are plotted in Fig. 12e. Fig. 13 shows the RMSs of the roll and pitch motions at different sea states. Detailed reduction ratios with respect to the roll motion, roll acceleration, pitch motion, and pitch acceleration are summarized in Table 6 (p.413).

Fig. 12
figure 12

Numerical results of joint pitch-roll stabilization in sea state 5

(a) Roll angle; (b) Roll angular acceleration; (c) Pitch angle; (d) Pitch angular acceleration; (e) Attack angles time series. Incident wave angle is 135°, U=1.75 m/s

Full size image
Fig. 13
figure 13

Comparison of motion RMSs with and without active fins at various sea states: (a) roll angle; (b) roll angular acceleration; (c) pitch angle; (d) pitch angular acceleration

Full size image
Table 6 Reduction ratios of motion RMS for joint pitch-roll control in irregular waves
Full size table

Demonstration of the effectiveness of the proposed controller in joint pitch-roll stabilization is further confirmed by the numerical results presented in Fig. 12. Here considerable reductions are obtained for pitch and roll motions. Similar to Fig. 10e, attack angles in irregular wave simulation also change smoothly with time. This means that the SMHFP controller benefits the stabilizing related machines as no vibration is induced.

As Fig. 13 and Table 6 suggest, stabilizing fins applying the proposed controller show dramatic performance in the reduction of roll motion RMS especially for low sea conditions, such as sea states 2–4. The lowest reduction efficiency is more than 59%. However, the reduction efficiency diminishes sharply as the sea state becomes worse. In the results of rough seas, i.e., sea states 5–7, the performance of stabilization reduces by under half compared with the results of mild seas. The lowest reduction efficiency is only about 14%. Such a tendency originates from the limited capacity of the actuator rather than from the tuning of the controller.

Moreover, as discussed above, it is confirmed that the present roll stabilization is far more effective than pitch reduction, especially under severe sea conditions. For example, at sea state 6, reduction ratio of the roll motion is 61.48%, about 40% larger than the result for pitch. This is because pitch moment is larger than roll moment.

Relative poor stabilizing performance in severe conditions originates from the limitation of the control cost. Ship motions become larger under severe conditions so that more control cost is necessary to stabilize the motions effectively. The performance can be improved by increasing the speed of the ship or fitting a larger capacity actuator.

In addition, note that balance between the roll and pitch stabilizations needs to be regulated appropriately since the total capacity of the actuators is limited. Fig. 12e indicates that the portside fin and the starboard fin have almost the same phase in both the fore and aft parts of the ship. This implies that pitch stabilization dominates the control cost. Therefore, the performance of the roll stabilization may be inferior in the case of roll stabilization only. Balance between the roll and pitch stabilizations depends on the vertical acceleration due to the roll and pitch motions. The vertical acceleration of cruise ships affects passenger comfort in terms of seasickness.

5 Conclusions

In this study, an SMHFP controller for joint pitch-roll stabilization is proposed. The SMHFP controller consists of a short-term predictor, a force estimator, and a fin angle allocator. The short-term predictor is used to forecast the ship motion. The force estimator evaluates the incoming external hydrodynamic forces by applying the dynamic equilibrium between the external forces and the predicted ship motions. The fin angle allocator specifies attack angles for stabilizing fins according to the predicted hydrodynamic forces.

Numerical study of the proposed controller for joint pitch-roll stabilization on a ship model equipped with two pairs of active fins has been carried out. The SMHFP controller is applied to control four stabilizing fins simultaneously. The control system of the stabilizing fins and the SMHFP controller is integrated into the sea-keeping program based on a weakly nonlinear 2.5D method.

Validation of the weakly nonlinear 2.5D sea-keeping analysis approach is performed before the joint pitch-roll stabilization control was simulated. Results of both blunt and fine hull shape ships consistently show that the weakly nonlinear 2.5D approach consumes less computational time compared with 3D method with equivalent accuracy, and requires equivalent computational cost with obvious higher accuracy than the conventional 2D method.

Numerical simulations of joint pitch-roll stabilization in various regular wave conditions and sea states 2–7 are carried out. Pitch and roll motions are well controlled. Under the regular wave conditions, the average reduction ratios of roll motion are more than 70% while those of pitch motion are more than 30%. Under the typical condition of sea state 5, the average reduction ratio of roll motion is more than 69% while that of pitch motion is more than 31%. Simulation results under different sea conditions suggest the satisfactory performance of the proposed SMHFP controller. The low reduction ratios of pitch motion under severe sea conditions result from the limited capacity of the actuator.

The present numerical results should be a good example of a numerical study on joint pitch-roll reduction of a ship using the SMHFP controller. However, for practical engineering application, experimental study of the proposed SMHFP controller is needed.