1 Introduction

Regulatory civil aviation agencies are pushing aircraft manufacturers and operators to improve aircraft efficiency by reducing fuel consumption, cutting carbon dioxide \(CO_2\) and nitrogen oxide NOx emissions, and lowering the perceived external noise. One way to help achieve this goal is by using improved and innovative technologies targeting drag reduction, specifically, lift-induced drag reduction. The drag breakdown of a typical transport aircraft shows that the lift-induced drag can amount to as much as 40% of the total drag at cruise conditions and 80–90% of the total drag during take-off and climb conditions [1,2,3,4,5,6,7,8,9]. Reducing lift-induced drag is therefore of paramount importance to improve aircraft efficiency.

One way to reduce the lift-induced drag is by increasing the wingspan. However, increased wingspan requires strengthening the wing structure so that it can withstand the increased bending moments. Increasing the wingspan can also pose limitations in airport ground operations and gate clearance requirements. Another way of reducing lift-induced drag is by using wingtip devices, such as winglets (as illustrated in Fig. 1). Winglets do not all look the same; nevertheless, their ultimate goal is always lift-induced drag reduction by artificially increasing the span of the wings. But as for the case of wingspan increment, winglets increase bending moments; therefore, it might be necessary to reinforce the wings. From an aerodynamic point of view winglets are desirable; whereas, from a structural standpoint they are detrimental.

Fig. 1
figure 1

Different types of winglets and wingtip devices. a Whitcomb winglet. b Tip fence. c Canted winglet. d Vortex diffuser. e Raked winglet. f Blended winglet. g Blended split winglet. h Sharklet. i Spiroid winglet. j Downward canted winglet. k Active winglets. l Tip sails

Full size image

Many studies have found that winglets addition can achieve a fuel burn reduction of about 4–6%, reduce take-off distance and increase climb rate [1,2,3,4,5,6,7,8, 10,11,12,13]. Also, as less fuel is burned, emissions are reduced. Winglets can provide up to a 6% reduction in \(CO_2\) emissions and an 8% reduction in NOx emissions [14,15,16]. They also increase the aftermarket value of the aircraft and add more aesthetic to the airplane design. Winglets are among the most used fuel saving and performance improvement technologies in today’s aviation. The drag reduction gained by adding winglets can be seen as the equivalent decrease in aircraft weight required to carry a payload over a specific distance. A reduction of one drag count in cruise conditions on a subsonic civil transport airplane means about 200 lbs more in payload [17,18,19] (where one drag count is equal to the drag coefficient \(C_D\) multiplied by 10000 or \(\varDelta C_D = 10000 \times C_D\)). As fuel has a large direct operating cost impact in the air transport industry, fuel consumption reduction is translated in more savings, fewer emissions as less fuel is burn, extended operating range and increased payload.

The increment of wing root bending moment is among the few negative effects of winglets. They also increase parasite drag, which is the contribution of skin friction, interference drag, and pressure drag due to separation. Recall that the total drag of an aircraft or a wing is equal to the sum of parasite drag, lift-induced drag and wave drag. Winglets are aerodynamically viable only when the reduction of lift-induced drag is larger than the increment in parasite drag, and this situation is illustrated in Fig. 2, where we show the drag polars of two hypothetical wings, one wing with no winglets and one wing with winglets installed.

Fig. 2
figure 2

The drag polars of two hypothetical wings in an assumed flight condition. In this figure, we depict the comparison of the drag polar of a wing with no winglets and the drag polar of a wing with winglets installed. In the left image, the light grey area represents the climb range of the wings, and the dark grey area represents the cruise range of the wings. In the right image, we show the drag count difference, where negative \(\varDelta C_D\) means drag increment when using winglets, and positive \(\varDelta C_D\) means drag reduction when using winglets. The drag count difference is computed as the difference between the \(\varDelta C_D\) of the wing with no winglets and the \(\varDelta C_D\) of the wing with winglets

Full size image

In Fig. 2, we can evidence that when operating above the crossover line or the line that passes through the crossover point (which is the point where the two polars intersect), the total drag of the wing with winglets is lower than the total drag of the wing with no winglets. Conversely, when operating below the crossover line, the total drag of the wing with no winglets is lower than the total drag of the wing with winglets. Therefore, in order to justify the use of winglets in the hypothetical situation illustrated in this figure, we should look at the performance of the wing at a given flight condition. Thus, if the wing were to operate in cruise conditions most of the time (the dark grey region in Fig. 2), the use of winglets is not justified from a point of view of total drag reduction. On the other hand, if the wing were to operate in climb conditions (the light grey region in Fig. 2), the use of winglets is justified from an aerodynamic point of view, as the wing generates less drag for a given lift.

From the hypothetical scenario discussed previously, the justification of the use of winglets can be based on total drag reduction arguments. So for example and by looking at Fig. 2, if the crossover point for a given winglet design is located in the cruise region, the use of winglets is justified for that flight condition. The crossover point gives a simple way to measure the total drag reduction trade-off when using winglets. Although this criterion might be a little bit simplistic as a performance metric for a complex system such as a wing-winglet configuration, as a design metric, it can deliver clear trends. The reader should be aware that more sophisticated aerodynamic performance criteria exist for winglet design [20,21,22,23,24,25].

Winglets use can also be justified in the base of other factors, such as wing (or aircraft) performance at a different altitude. For example, if we climb to a higher altitude where the air is lighter, the wing in discussion would have to fly at a higher angle-of-attack (AOA) that might fall in the light grey region illustrated in Fig. 2; therefore, the use of winglets is justified based on total drag reduction arguments. As it can be guessed, there might exist different winglet configurations that might shift the crossover point below (or above) what is illustrated in Fig. 2.

During the 1970s oil crisis, commercial airlines and aircraft manufacturers explored many ways to reduce fuel consumption as a consequence of the high cost of jet fuel. It was not until the late 1970s that R.T. Whitcomb, an engineer at NASA Langley Research Center, pioneered the concept of the modern winglet we see in today’s aircraft, as a mean to reduce cruise drag and improve aircraft performance [11, 12]. Whitcomb’s work [12], marks the first time a winglet was seriously considered for large and heavy aircraft. Since Whitcomb breakthrough work on winglets, many variations have been designed (as depicted in Fig. 1), but all of them have been designed as passive or fixed devices attached at the wingtips. That is, the angle between the wing plane and the winglet plane (or cant angle) does not change; therefore, they are designed to deliver lift-induced drag reduction at a single design configuration, which might not be the best winglet configuration to generate the largest lift-induced drag reduction during different flight phases.

Hereafter, we propose the use of variable cant angle winglets that can be actuated by a mechanism (which is not described in this study). In the proposed arrangement, the winglet cant angle can be changed from a planar configuration up to a vertical layout (including intermediate cant angles) and vice-versa. Therefore, the winglet can be adjusted at different flight conditions to get the best lift-induced drag reduction for the given flight phase; or it can be kept in the vertical position while in ground so that it reduces wingspan while meeting gate and runaway clearance; or it can act as a load alleviation mechanism where in the case of gusts or strong sideslip velocities, the winglet can adjust itself, so it reduces the bending moment on the wing and the device itself. This study is an extension of a previous work conducted by the authors [26]; however, hereafter it is extended to cover Mach numbers values of 0.3 and 0.8395. In addition, a more detailed wave drag quantitative and qualitative analysis is presented, together with a discussion of the effect of compressibility on the aerodynamic performance. Also, based on the outcome of the numerical study it is proposed how the winglet cant angle could be set to obtain the best aerodynamic performance at a given flight phase.

It is worth mentioning that similar solutions have been already proposed, but most of them focused on the use of shape memory alloy materials [27,28,29,30,31,32], foldable wings during ground operations [33,34,35,36,37], load alleviation mechanisms [38,39,40,41,42], complaint surfaces [32, 43,44,45,46,47,48,49], and rotating systems for mitigating wingtip vortices [50,51,52,53,54]; but just a few of them have addressed variable cant angle winglets for drag reduction while flying [55,56,57,58,59].

The wing used in this study is the Onera M6 wing [60, 61] with a winglet installed. To study the effect of the variable cant angle winglet on the aerodynamic performance, different winglets with different cant angles were simulated. We conduct the study at two Mach numbers (\(Ma = 0.3\) and \(Ma = 0.8395\)) and different angle-of-attack values. Thus, we aim at covering take-off, climb, approach, descent, and cruise conditions. The concept presented hereafter represents an innovative approach that the authors’ hope holds potential to realize the goal of drag reduction to directly address the global challenge of improving aircraft fuel efficiency and reduce pollutant emissions, as highlighted in the reports ACARE—European aeronautics: A vision for 2020 [62] and ACARE—Flightpath 2050: Europe’s vision for aviation [63].

2 A brief review of lift-induced drag and its reduction using winglets

Before describing the numerical experiment and discussing the results, let us give a brief explanation of what is lift-induced drag and the role of winglets on lift-induced drag reduction. We would like to highlight that similar explanations can be found in references [2,3,4, 9, 13, 26, 64], among many.

Finite span wings generate lift due to the pressure imbalance between the bottom surface (high pressure) and the top surface (low pressure), as illustrated in Fig. 3. However, as a byproduct of this pressure differential, cross flow components of the velocity are generated (which are unavoidable but can be mitigated). The higher pressure air under the wing flows around the wingtips and tries to displace the lower pressure air on the top of the wing. This motion generates a trailing edge vortex, and at the wingtips, where the flow curls, large vortices are formed. This flow around the wingtips is sketched in Fig. 3. These structures are referred to as wingtip vortices, and high velocities and low pressure exist at their cores. These vortices (trailing edge vortices and wingtip vortices), produce a downward flow in the neighborhood of the wing, known as the downwash and is denoted with the letter w in Fig. 4. The downwash interacts with the free-stream velocity to induce a local relative wind deflected downward in the vicinity of each airfoil section of the wing, as sketched in Fig. 4. The presence of the downwash reduces the angle-of-attack that each section of the wing effectively sees, and it creates a component of drag, the lift-induced drag. This drag component is an unavoidable consequence of lift generation in finite span wings.

Fig. 3
figure 3

a Illustration of lift generation due to pressure imbalance and its associated trailing edge and wingtip vortices. b Illustration of wingtip vortices rotation and the associated downwash and upwash

Full size image
Fig. 4
figure 4

Illustration of lift-induced drag due to downwash. In the figure, the angle between the airfoil chord line and the direction of the undisturbed free-stream \(V_{\infty }\) is the angle-of-attack AOA. Notice that the local relative wind is inclined downward due to the downwash w, which gives rise to the induced angle-of-attack \(AOA_{ind}\). Therefore, the angle-of-attack actually seen by the local airfoil section is the angle between the chord line and the local relative wind, or the effective angle-of-attack \(AOA_{eff}\) (where \(AOA_{eff} = AOA - AOA_{ind}\)). This variation of the local AOA is more pronounced towards the wingtips, where the downwash is stronger

Full size image

One way of reducing lift-induced drag is by using wingtip devices, such as winglets. Well-designed winglets will reduce the trailing vortex strength (hence the wingtip vortex) and the average wing downwash by modifying the pressure distribution (which is related to the spanwise lift distribution), and shifting the shed vorticity away from the wing plane. They can also counteract the skin friction and interference drag of the winglets by generating a thrust force induced by the sidewash [2, 12, 64]. All this translate into less total drag due to the reduction of lift-induced drag and the parasite drag generated by the winglet.

3 Wing model, computational domain, boundary conditions, and initial conditions

The wing model used in this study is the Onera M6, as described in references [60, 61]. To model the variable cant angle winglet, an extension to the baseline Onera M6 wing was added (as shown in Fig. 5). Then, the cant angle is modeled by adding a small curvature radius at the wingtip join with the winglet, in such a way as to guarantee a smooth transition between the wing and the winglet (as illustrated in Fig. 6). The winglet span used in this study corresponds to a 20% of the wingspan of the baseline wing. This value was chosen on the basis of previous studies [1, 6, 12, 65,66,67,68], where the authors suggest the use of winglet span values between 10% to 20% of the wingspan. Additionally, we also studied the influence of the winglet sweep angle on the aerodynamic performance of the wing, where the sweep angle is defined as illustrated in Fig. 7. In Table 1, we report the cant angles, sweep angles, and angle-of-attack values used in this study. As a guideline, in Table 2 we report the wetted area of each wing used. Lastly, in Table 3, we report the values of the relative wingspan reduction in reference to the wing with winglet at cant angle \(0^{\circ }\).

Table 1 Design space explored in this study
Full size table
Fig. 5
figure 5

Wing and winglet extension. The winglet span used in this study corresponds to a 20% of the wing span of the original Onera M6 wing

Full size image
Fig. 6
figure 6

Winglet cant angle definition (left image). The winglet extension is bent upwards about the axis 1 (right image). This axis is located 40 mm away from the wingtip. For all cases studied, the curvature radius is no more than 30 mm

Full size image
Fig. 7
figure 7

Left image: winglet sweep angle definition. Right image: winglet geometry corresponding to a cant angle of \(80^{\circ }\) and a sweep angle of \(60^{\circ }\)

Full size image

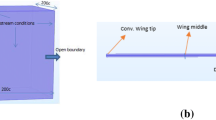
In Fig. 8, a sketch of the computational domain, dimensions, and the boundary conditions layout is depicted. The far-field boundary in this figure corresponds to a Dirichlet type boundary condition and the outflow to a Neumann type boundary condition. The boundaries were placed far enough of the wing surface so there are no significant gradients normal to the surface boundaries. The wing was modeled as a no-slip wall, where we used continuous wall function boundary conditions for the turbulence variables. In all cases, the average distance from the wing surface to the first cell center off the surface is approximately \(y^+ \approx 2.4\) viscous wall units, and the maximum value is approximately \(y^+ \approx 4\) viscous wall units.

Fig. 8
figure 8

Computational domain and boundary conditions (all dimensions are in meters). The illustration is not to scale

Full size image

A hybrid mesh was used for all the simulations, with prismatic cells close to the wing surface and tetrahedral cells for the rest of the domain. In the wing surface we placed enough prismatic layers so the boundary layer profile could be resolved (20 prismatic layers). Also, in the vicinity of the wing and wake region, we added a refinement region with uniform cell size (as illustrated in Fig. 9) so the integral length scales could be properly modeled. A typical mesh is made up of approximately 3.8 to 4.5 million cells, depending on the cant and sweep angle.

Fig. 9
figure 9

Domain mesh. The mesh is visualized in the symmetry plane and wing surface

Full size image

The lift force L and drag force D are calculated by integrating the pressure and wall-shear stresses over the wing surface; then, the lift coefficient \(C_L\) and drag coefficient \(C_D\) are computed as follows:

$$\begin{aligned} C_L = \frac{L}{0.5 \times \rho \times V_{\infty }^2 \times S_{ref}} \;\;\;\;\; \text {and} \;\;\;\;\; C_D = \frac{D}{0.5 \times \rho \times V_{\infty }^2 \times S_{ref}} \end{aligned}$$

where \(\rho\) is the air density, \(V_{\infty }\) the free-stream velocity, and \(S_{ref}\) is the wing reference area.

Table 2 Wetted area of each wing used in this study
Full size table
Table 3 Relative wingspan reduction in reference to the wing with winglet at cant angle \(0^{\circ }\)
Full size table

Finally, the AOA was changed by adjusting the incidence angle value of the inlet velocity, and all forces were computed in the reference system aligned with the inlet velocity. All the computations were initialized using free-stream values and the incoming flow is characterized by a turbulence intensity value equal to 5.0%. All the turbulence variables were initialized following the guidelines given in references [69,70,71].

4 Numerical method and validation

The compressible Reynolds-Averaged Navier–Stokes (RANS) equations are solved by using the finite volume solver Ansys Fluent [72]. The cell-centered values of the variables are interpolated at the face locations using a second-order centered difference scheme for the diffusive terms. The convective terms are discretized by means of the second-order upwind scheme [73]. For computing the gradients at cell-centers, the least squares cell-based reconstruction method is used. In order to prevent spurious oscillations, a multi-dimensional gradient limiter is used [74]. The pressure-velocity coupling is achieved by means of the SIMPLE algorithm [75, 76], where we used the default (or industry standard) under-relaxation factors. As the solution takes place in collocated meshes, the Rhie-Chow interpolation scheme is used to prevent the pressure checkerboard instability. For turbulence modeling, the \(k-\omega\) SST model is used [69,70,71]. The turbulence quantities, namely, turbulent kinetic energy k and specific dissipation rate \(\omega\), are discretized using the same scheme as for the convective terms.

Before proceeding with the parametric study, we assessed the accuracy of the numerical scheme and mesh resolution used. In this validation study, we compare the numerical solution outcome against the data of the physical experiments at the same operating conditions described by Schmitt and Charpin [60], that is, Reynolds number \(Re = 11.72 \times 10^6\), Mach number \(Ma = 0.8395\), and angle-of-attack equal to \(3.06^{\circ }\).

During this validation study, we used five different meshes, as listed in Table 4. As our main interest was the accurate prediction of the aerodynamic forces, we focused our attention on the mesh refinement of the surface mesh, prismatic layers, and the growth rate of the volume cells from the wing surface. For meshes 4 and 5, we used a non-uniform surface mesh in such a way to guarantee a proper resolution towards the leading edge and trailing edge sections. For meshes 1–3, we used uniform surface meshes, with aspect ratios smaller to those used in meshes 4 and 5. Also, in meshes 1–3, we used a smaller cell size in the wake region of the domain than that used on meshes 4–5 (refer to Fig. 9).

Table 4 Meshes used during the validation study
Full size table

In Fig. 10, we plot the mesh convergence of the lift and drag coefficients. In the same figure, the Richardson extrapolation values for both coefficients are also depicted. The Richardson extrapolation values were computed using the finer meshes (mesh 1 and mesh 2). To compute these values, we used Eq. 1, where we assumed an order of convergence p equal to 2, and a mesh refinement ratio r equal to 1.6 (in reference to the average \(y^+\) value). In Eq. 1, \(f_1\) represents the finer mesh (mesh 1 in our case). The value obtained using this equation represents the continuum value at zero grid spacing [79]. The results shown in this figure, appear to be approaching nearly the same results as the mesh is refined. Notice that the convergence of the lift coefficient shows an oscillatory behavior.

$$\begin{aligned} f_{h=0} \cong f = f_1 + \frac{f_1 - f_2}{r^p - 1} \end{aligned}$$
(1)

In Table 5, we show the values of the Richardson extrapolation and the outcome of the QoI of mesh 1. In Table 6, the percentage change between the meshes 1–5 and the Richardson extrapolation, and the percentage change between the meshes 2–5 and mesh 1, are listed. From these results, we can see how the error in reference to the Richardson extrapolation and the outcome of mesh 1 are reduced as the mesh is refined.

In base of the results presented in Fig. 10 and Table 6, we decided to use the reference values of mesh 3 (refer to Table 4) to conduct the parametrical study. It is worth mentioning that we also conducted a quantitative study related to the shock wave resolution, where the growth rate and surface refinement used in mesh 3 gave acceptable results compared to meshes 1 and 2. In conclusion, mesh 3 gave a good compromise between solution accuracy and computing speed.

Fig. 10
figure 10

Mesh convergence of the lift and drag coefficients. The dashed line represents the Richardson extrapolation of the lift coefficient, and the dashed-dotted line represents the Richardson extrapolation for the drag coefficient

Full size image
Table 5 Richardson extrapolation values (computed using mesh 1 and mesh 2), and the outcome of the QoI of mesh 1
Full size table
Table 6 Percentage change of the outcome between meshes
Full size table

In Fig. 11, we plot the pressure coefficient \(Cp = (p - p_{\infty }) / (0.5 \rho V_{\infty }^2)\) values obtained from the numerical simulations against the experimental values at different wingspan locations (using mesh 3). As it can be seen, the numerical solution shows a similar trend to the Cp distribution obtained in the wind tunnel experiments. Additionally, in Table 7 we compare the \(C_L\) and \(C_D\) values against the values obtained using different CFD solvers [61]. In this table, we can evidence a fairly good match among all solvers, even if the meshes and solution methods are different. In this validation study, the reference area used for \(C_L\) and \(C_D\) computations is equal to 0.7532 \(\mathrm{m}^2\), as described in reference [60].

As a side note, the turbulence model used in reference [61] was the Spalart–Allmaras whereas in this study we used the \(k-\omega\) SST. Additionally, we did not model the rounded wingtip as described in references [60, 61], so these two factors might represent a source of uncertainty, which however we deem to be negligible for the purposes of this study. Based on the results presented, we can state that the selected numerical scheme, turbulence model, and mesh resolution are adequate to resolve the physics involved.

Fig. 11
figure 11

Plot of the pressure coefficient Cp on the wing surface at different sections. Comparison of numerical and experimental results

Full size image
Table 7 Comparison of \(C_L\) and \(C_D\) obtained with different solvers (data taken from reference [61])
Full size table

Finally, during this study air was modeled using the equation of state for ideal gases, and the dynamic viscosity was computed using the Sutherland model. It is worth mentioning that the original Onera M6 wing report [60], does not give specific details about the working conditions; therefore, we assumed air at sea-level and at \(300^{\circ }\) K. The temperature was determined by using an iterative procedure so that Re and Ma conditions are matched, together with the equation of state \(p=\rho R T\), the speed of sound relationship \(a=\sqrt{\gamma R T}\), and the Sutherland dynamic viscosity equation \(\mu = (C_1 T^{3/2}) / (T + C_2)\) (where T is the temperature given in degrees Kelvin, and \(C_1\) and \(C_2\) are the coefficients of the Sutherland model). While it is difficult to determine if the operating conditions used in the simulations correspond to the same conditions of the wind tunnel experiments, the assumptions taken in this study appear to be justified given the good agreement between the physical experiments and the numerical simulations.

5 Numerical results and discussion

In this section, we discuss the results of the aerodynamic performance of the wing with variable cant angle winglet in reference to the baseline wing (original Onera M6 wing). An extensive campaign of simulations was carried out, as per the design space listed in Table 1. For all cases, the reference area used for \(C_L\) and \(C_D\) computations is equal to 1.0 \(\mathrm{m}^2\). The computations were carried out in parallel using 16 cores, and each simulation took approximately 4–6 h to convergence to a level where the forces showed either a non-oscillatory behavior or a periodic behavior. All the details regarding the computational domain, boundary conditions, initial conditions, and numerical method, are given in Sects. 3 and 4.

5.1 Aerodynamic performance at high Mach number: \(Ma=0.8395\)

Hereafter, we discuss the results at Mach number equal to 0.8395, which might corresponds to a typical velocity encountered at cruise conditions on subsonic civil transport aircraft. We explore AOA values up to \(10^{\circ }\), which correspond to the values of AOA that might be encountered during cruise and change of cruise level on medium and long-range subsonic transport aircraft.

We also present a quantitative and qualitative wave drag analysis. Recall that wave drag is related to compressibility effects and high speed flight, and is the drag component associated with the formation of shock waves. Wave drag manifests as a sudden increase in the total drag as the vehicle reaches the critical Mach number (which is the lowest Mach number at which the airflow over some point of the wing reaches the speed of sound). Therefore, it is important to study the influence of the winglet device on the wave drag.

Let us use the drag polars plotted in Figs. 12, 13 and 14 to study the influence of the winglet cant angle and sweep angle on the aerodynamic performance of the wing. By looking at these figures, we can notice a strong influence of the sweep angle on the drag polars, that is, as we increase the sweep angle, the drag polar curves are shifted upward, and this trend contributes to an improvement of the aerodynamic performance, i.e., for the same lift coefficient less drag is produced. For instance, in Fig. 12 (winglet sweep angle \(30^{\circ }\)) we can see that when the winglet cant angle is equal to \(80^{\circ }\) the overall performance of the wing is worse than that of the baseline wing, or in other words, for a given value of \(C_L\) the wing with winglet will produce more drag. However, as we increase the sweep angle, the drag polar is slightly shifted upwards, so eventually, the wing with winglet will produce less drag for a given \(C_L\) value when compared to the baseline wing. This situation is illustrated in Figs. 13 and 14, where for example, for a value of \(C_L = 0.3\) all the configurations studied will produce less drag than the baseline wing.

Fig. 12
figure 12

Drag polar at Mach number 0.8395, sweep angle \(30^{\circ }\) and different values of cant angle

Full size image
Fig. 13
figure 13

Drag polar at Mach number 0.8395, sweep angle \(45^{\circ }\) and different values of cant angle

Full size image
Fig. 14
figure 14

Drag polar at Mach number 0.8395, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image

The effect of the sweep angle on the aerodynamic performance can be explained by the fact that at higher sweep angles less skin friction drag and interference drag is produced. Another factor that contributes to the drag reduction at high Mach number is the impact of the winglet sweep angle on the wave drag. This particular wing is known to generate a shock wave system on the wing surface; this shock wave interacts with the winglet (as depicted in Figs. 15 and 16), therefore increasing the wave drag.

In Fig. 15, we illustrate the wing-winglet shock wave interaction (WWSWI) for two different winglet sweep angles and a cant angle of \(80^{\circ }\), where the shock wave region was computed using the criterion of Lovely and Haimes [77]. In this figure, we can observe that for larger sweep angles the shock wave intensity is reduced. Hence, as for wings designed for high-speed, the sweep-back angle have a positive effect in reducing the wave drag of the winglets. In Fig. 16, we show the WWSWI but this time for a sweep angle of \(60^{\circ }\) and three different cant angles. In this figure, we can observe that for large cant angle values the WWSWI region is larger; thus, qualitative speaking the wave drag is larger. It is worth mentioning that the WWSWI might also cause additional detrimental phenomena, such as boundary layer separation and buffeting.

Fig. 15
figure 15

Shock wave system for AOA \(2^{\circ }\), winglet cant angle \(80^{\circ }\) and two different values of winglet sweep angle. The left image corresponds to a winglet sweep angle of \(30^{\circ }\) and the right image to a sweep angle of \(60^{\circ }\). The shock wave region was computed using the criterion of Lovely and Haimes [77]

Full size image
Fig. 16
figure 16

Shock wave system for AOA \(2^{\circ }\), winglet sweep angle \(60^{\circ }\), and different values of winglet cant angle. The left image corresponds to a winglet cant angle of \(80^{\circ }\), the middle image to a cant angle of \(45^{\circ }\), and the right image to a cant angle of \(15^{\circ }\). The shock wave region was computed using the criterion of Lovely and Haimes [77]

Full size image

In Table 8, we quantify the wave drag ratio for five representative configurations at AOA \(2^{\circ }\). In this table, the wave drag ratio is calculated as the ratio of the wave drag of the given wing-winglet configuration and the wave drag of the configuration with a winglet sweep angle of \(30^{\circ }\) and a cant angle of \(80^{\circ }\) (the arrangement that generates the largest wave drag and parasite drag). In all cases, the wave drag was computed using the drag decomposition method described by Destarac and van der Vooren [78]. From these quantitative results, we can notice the influence of the cant angle on the wave drag, that is, as we decrease the cant angle from \(80^{\circ }\), the wave drag is reduced. The fact that the wave drag at \(80^{\circ }\) of cant angle is the largest value is due to strong interference effects, which suggest that the joint between the wing and the winglet should be carefully designed in order to mitigate this effect. We can also note that as we increase the winglet sweep angle, the wave drag is reduced. It is worth noting that the increment of the wave drag due to the winglet addition is almost proportional to the wingspan increment of the baseline wing (20%).

Table 8 Wing-winglet wave drag ratio at AOA \(2^{\circ }\)
Full size table

Let us now study the influence of the cant angle on the aerodynamic performance of the wing, and always in reference to Figs. 12, 13 and 14. In these figures and for the same winglet sweep angle values, we can evidence that low to moderate values of cant angle (\(0^{\circ }{-}45^{\circ }\)) have a minor effect on the drag polar curves at AOA values less than \(4^{\circ }\). On the other hand, for AOA values higher than \(4^{\circ }\) there is a tendency to shift the drag polar curves downwards, in particular for moderate to high values of cant angle (\(45^{\circ }{-}80^{\circ }\)). This decrease in the aerodynamic performance is related to two factors, the superior parasite drag generated by the winglet at high cant angles and the reduction of the pressure differential towards the wingtips.

To understand the reason of the pressure differential reduction, let us take a look at Fig. 17, where the pressure coefficient on the wing surface is displayed for a configuration with winglet sweep angle \(60^{\circ }\) and four cant angles. In this figure, we can observe that as we increase the cant angle, the winglet will work as a wall that will reduce the pressure differential between the bottom and top surfaces of the wing. This reduction of the pressure differential, which is stronger towards the wingtip, is responsible for the decrement of the maximum \(C_L\) and the slope of the lift curve. As we reduce the cant angle, the reduction in the pressure differential is lessened, therefore the maximum lift increases, as it can be confirmed in Fig. 18. The winglet effect of reduction of the pressure differential also affects drag, as it can be seen in Fig. 19. But in this case, the reduction of the pressure differential has a positive impact by reducing the drag and the intensity of the wingtip vortices.

Fig. 17
figure 17

Pressure coefficient on the wing surface at Mach number 0.8395. Winglet sweep angle equal to \(60^{\circ }\) and wing AOA equal to \(10^{\circ }\)

Full size image
Fig. 18
figure 18

Lift coefficient versus angle-of-attack at Mach number 0.8395, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image
Fig. 19
figure 19

Drag coefficient versus angle-of-attack at Mach number 0.8395, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image

Let us quantify the minimum drag coefficient \(C_{D_{min}}\) in the drag polar plots depicted in Figs. 12, 13 and 14. Hereafter, we compute the \(C_{D_{min}}\) percentage reduction (or increment) in reference to the baseline wing. For the wing with winglet sweep angle \(30^{\circ }\) (Fig. 12), the configuration with cant angle \(80^{\circ }\) increases \(C_{D_{min}}\) by approximately 30%, for cant angle \(45^{\circ }\) the \(C_{D_{min}}\) is increased by \(\approx 10\%\), for cant angle \(15^{\circ }\) the \(C_{D_{min}}\) is increased by \(\approx 7.0\%\), and for cant angle \(0^{\circ }\) the \(C_{D_{min}}\) is increased by \(\approx 4.0\%\). If we now take a look at Fig. 13 (wing with winglet sweep angle \(45^{\circ }\)), the situation is slightly different. In this figure, the configurations with cant angles \(0^{\circ }\) and \(15^{\circ }\) increase \(C_{D_{min}}\) by about 4.0%, for a cant angle of \(45^{\circ }\) the \(C_{D_{min}}\) is increased \(\approx 5.0\%\), and the \(C_{D_{min}}\) of the wing with winglet cant angle \(80^{\circ }\) is approximately 7.0% larger. Finally, in Fig. 14 (wing with winglet sweep angle \(60^{\circ }\)), the \(C_{D_{min}}\) of the wing with winglet cant angle \(80^{\circ }\) is approximately 2.5% larger, whereas the \(C_{D_{min}}\) for the other cant angles is increased by about 1.0%. These results clearly indicate that large cant angle values generate more parasite drag (possibly due to strong interference effects).

In the previous discussion, the reduction of \(C_{D_{min}}\) as the winglet sweep angle is increased, can be attributed to the fact that at higher sweep angles less skin friction drag and interference drag is produced. Also, the addition of the sweep angle to the winglet and the sidewash generated by the flow in the surroundings of the winglet, might modify the inboard lift force generated by the winglet which can contribute to reducing (or increasing) the \(C_{D_{min}}\) (as explained in references [1, 4, 64]). It is also important to note that in Fig. 14, none of the configurations with winglet installed have a strong detrimental crossover point. In all cases plotted in this figure and for AOA less than \(2^{\circ }\), the wings with winglet generate little less drag, or the difference is negligible respect to the baseline wing. For AOA larger than \(2^{\circ }\) the difference in \(C_D\) for the same \(C_L\) is more evident.

To make a comprehensive treatment of how the variable cant angle winglets could improve the wing aerodynamic performance, let us compute the \(C_D\) at three \(C_L\) targets, namely, 0.1, 0.2, and 0.35. In this hypothetical situation, the \(C_L\) targets could correspond to cruise conditions or \(0.1< C_L < 0.2\) (which corresponds to the maximum \(C_L/C_D\) ratio) and cruise climb conditions or \(C_L = 0.35\) (which approximately corresponds to the maximum \(C_L/C_D\) ratio and is on the limit of the linear regime of the lift curve). These results are summarized in Tables 9, 10 and 11 and as it can be seen, for cruise conditions (\(0.1< C_L < 0.2\)) the largest drag reduction is obtained at cant angles between \(0^{\circ }\) and \(45^{\circ }\), this suggest that the winglets could be adjusted in flight according to fuel consumption. For cruise climb (\(C_L = 0.35\)), the best results are obtained at a cant angle value of \(15^{\circ }\). However, values up to \(80^{\circ }\) are also acceptable as they produce less drag for the same \(C_L\).

These results show how winglets reduce the drag by artificially increasing the wingspan. The relative wingspan reduction is shown in Table 3, by cross-referencing these values with the results shown in Tables 9, 10 and 11, it can be seen that as we reduce the wingspan (by increasing the winglet cant angle), the aerodynamic performance is improved in reference to the baseline wing. In general, for cant angle \(80^{\circ }\) the gains in drag reduction are not the same to those achieved by merely extending the wingspan by an amount equal to the winglet span (equivalent to a winglet configuration with cant angle \(0^{\circ }\)), but approximately half that amount. For the other cant angle values (\(45^{\circ }\) and \(15^{\circ }\)) the drag reduction is about the same amount or even larger. In addition, increasing the winglet cant angle does not add the extra wing root bending moment that would be encountered if the wingspan were simply increased by the span of the winglet, and this is a desirable benefit from the structural point of view.

Table 9 \(C_D\) and drag reduction percentage for a target \(C_L\) equal to 0.1 at Mach number 0.8395
Full size table
Table 10 \(C_D\) and drag reduction percentage for a target \(C_L\) equal to 0.2 at Mach number 0.8395
Full size table
Table 11 \(C_D\) and drag reduction percentage for a target \(C_L\) equal to 0.35 at Mach number 0.8395
Full size table

For completeness, in Figs. 20, 21, 22 and 23 we plot the drag polars for fixed cant angles and different sweep angles. In these figures, we can better highlight the influence of the sweep angle on the aerodynamic performance. It is clear that as we increase the sweep angle the crossover point is shifted downwards, up to the point that the performance of the wing with winglets is better in the whole envelope of the drag polar. For the case with cant angle equal to \(45^{\circ }\) (Fig. 22), the crossover point is located approximately between \(2^{\circ }\) and \(3^{\circ }\) of AOA for all cases. For the cases with cant angle equal to \(80^{\circ }\) and sweep angles of \(45^{\circ }\) and \(60^{\circ }\) (Fig. 23), the crossover point is located approximately between \(2^{\circ }\) and \(3^{\circ }\) of AOA, and for a sweep angle of \(30^{\circ }\) (Fig. 23) the polars intersect at large \(C_L\) values (worst case scenario).

Fig. 20
figure 20

Drag polar at Mach number 0.8395. The figure corresponds to a fix cant angle of \(0^{\circ }\) and three different values of sweep angle

Full size image
Fig. 21
figure 21

Drag polar at Mach number 0.8395. The figure corresponds to a fix cant angle of \(15^{\circ }\) and three different values of sweep angle

Full size image
Fig. 22
figure 22

Drag polar at Mach number 0.8395. The figure corresponds to a fix cant angle of \(45^{\circ }\) and three different values of sweep angle

Full size image
Fig. 23
figure 23

Drag polar at Mach number 0.8395. The figure corresponds to a fix cant angle of \(80^{\circ }\) and three different values of sweep angle

Full size image

From the previous discussion, we found that the sweep angle has a strong influence on the aerodynamic performance and, the best performance is obtained for a winglet sweep angle equal to \(60^{\circ }\); therefore, for the remainder of this section we will focus our attention on the wing with a winglet sweep angle of \(60^{\circ }\).

In Fig. 18, the behavior of the lift coefficient is displayed as a function of the AOA. We can observe in this figure that up to an AOA of \(4^{\circ }\), the lift curves show a linear behavior. We can also note that the slope of the lift curve is almost the same for the cases with cant angles between \(0^{\circ }\) and \(45^{\circ }\) (\(\partial C_L/\partial AOA \approx 0.075\) per degree). For the case with cant angle equal to \(80^{\circ }\) the slope is lower (\(\partial C_L/\partial AOA \approx 0.068\) per degree), but still is higher than that of the baseline wing (\(\partial C_L/\partial AOA \approx 0.064\) per degree). In this figure, the maximum lift coefficient \(C_{L_{max}}\) is increased by as much as 10.5% for a cant angle of \(0^{\circ }\), approximately 9.1% for a cant angle of \(15^{\circ }\), about 4.2% for a cant angle of \(15^{\circ }\), and for a cant angle of \(80^{\circ }\) the value of \(C_{L_{max}}\) is reduced approximately \(1\%\). The reduction of \(C_{L_{max}}\) (as the cant angle is increased), is related to the reduction of the pressure differential towards the wingtip, as explained previously. Again, these results correlate well with the fact that winglets artificially increase the effective span of the wing; therefore, they have a direct impact on the lift behavior. Lastly, the use of the variable cant angle winglet does not appear to have any negative effect on the stall behavior.

It is important to mention that computing \(C_{L_{max}}\) and capturing the stall pattern in CFD is a difficult task, however, as we do not expect that the wing will operate at values close to \(C_{L_{max}}\) in cruise conditions, uncertainties in the computation of \(C_{L_{max}}\) can be tolerated.

It is also interesting to mention that even though the wing airfoil section is symmetric, the lift at zero AOA or \(C_{L_0}\) is not zero for large cant angles of the winglet device. For the winglet with a cant angle of \(45^{\circ }\) \(C_{L_0} \approx 0.0055\), and for a winglet cant angle of \(80^{\circ }\) \(C_{L_0} \approx 0.0065\). Although these values are low, they have the effect of introducing a small negative zero-lift angle or \(\alpha _{zl}\), which is in the order of \(-0.1^{\circ }\).

In Fig. 19, we plot the behavior of the drag coefficient as a function of the AOA. In this figure, we can observe that for AOA values ranging from \(0^{\circ }\) to \(2^{\circ }\) all the winglet configurations generate almost the same drag. Then, as we pass by AOA \(4^{\circ }\) higher cant angles (\(45^{\circ }\) and \(80^{\circ }\)) translate in less drag for the same AOA value. As the wing profile is symmetric, the minimum drag \(C_{D_{min}}\) is attained at AOA \(0^{\circ }\), and the use of the winglet does not appear to shift the horizontal location of \(C_{D_{min}}\).

The behavior of the lift-to-drag ratio (\(C_L/C_D\)) as a function of the AOA is plotted in Fig. 24. In this figure, it is found that \(C_L/C_D\) increases very rapidly up to about \(2^{\circ }\), at this point the maximum \(C_L/C_D\) value is reached, then, \(C_L/C_D\) gradually drops mainly because drag increases more rapidly than lift. For winglet cant angles of \(0^{\circ }\) and \(15^{\circ }\) the maximum \(C_L/C_D\) is increased by approximately 12.0% in reference to the baseline wing, for a cant angle of \(45^{\circ }\) the maximum \(C_L/C_D\) is increased \(\approx 8.8\%\), and for a cant angle of \(80^{\circ }\) the maximum \(C_L/C_D\) is increased \(\approx 4.8\%\). The main point of interest about the \(C_L/C_D\) curve is the fact that this ratio is maximum at an AOA of about \(2^{\circ }\) for all the configurations, that is, the use of the variable cant angle winglet does not change the AOA at which the maximum \(C_L/C_D\) occurs. It is at this AOA that the wings will generate as much \(C_L\) as possible with a small \(C_D\) production.

Fig. 24
figure 24

Lift-to-drag ratio versus angle-of-attack at Mach number 0.8395, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image

From the results presented, it is clear that there is not a single winglet configuration that can give the best all-around drag reduction at every AOA. It was also clear that the winglet configuration with a sweep angle equal to \(60^{\circ }\) gave the best results for different cant angle values. The results also show that \(C_{L_{max}}\) and the slope of the lift curves decreases as the winglet cant angle is increased, but the aerodynamic performance still is better or similar to that of the baseline wing. This suggests that the proposed variable cant angle winglet can also be used as a load alleviation mechanism. Thus, in the case of strong gusts or turbulence, the cant angle can be increased in order to reduce the lift force, hence decreasing the wing root bending moment.

5.2 Aerodynamic performance at low Mach number: \(Ma=0.3\)

Hereupon, we discuss the results at Mach number equal to 0.3, which might well correspond to the velocities encountered at take-off, climb, descent and approach flight conditions on subsonic civil transport aircraft. We explore AOA values up to \(20^{\circ }\), which correspond to the large values of AOA that could be encountered during take-off. It is also important to point out that the trends we will present in this section are very similar to those presented in Sect. 5.1, but as the Mach number is relative low, there are neither wave drag contributions nor compressibility effects.

In Figs. 25, 26 and 27, we plot the drag polars at a fixed sweep angle and different cant angles. As opposed to the cases at Mach number 0.8395, where it was clear that the sweep angle shifted upwards the drag polar, at this low Mach number we do not experience such large variations in the drag polars. For AOA values lower than \(6^{\circ }\) and for all cant angle configurations, the drag difference between the baseline wing and the wing with winglets is almost negligible or negative (meaning that it generates less drag). At AOA larger than \(6^{\circ }\), the effect on the improvement of the drag polars is clearer except for the case of cant angle equal to \(80^{\circ }\), where we can note a considerable reduction in \(C_L\).

Fig. 25
figure 25

Drag polar at Mach number 0.3, sweep angle \(30^{\circ }\) and different values of cant angle

Full size image
Fig. 26
figure 26

Drag polar at Mach number 0.3, sweep angle \(45^{\circ }\) and different values of cant angle

Full size image
Fig. 27
figure 27

Drag polar at Mach number 0.3, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image

The reduction of \(C_L\) seen in Figs. 25, 26 and 27 as the cant angle is increased, and that of \(C_{L_{max}}\) and the slope of the lift curve (Fig. 28), are due to the pressure differential reduction towards the wingtips, as already explained in Sect. 5.1. In Fig. 29, we plot the pressure coefficient on the wing surface for three configurations. In this figure, we can observe that for large winglet cant angles the pressure differential is reduced towards the wingtips, and this behavior is responsible for the decrement of the maximum \(C_L\) and the reduction of the slope of the lift curve seen in Fig. 28. As for the \(C_{D_{min}}\) concerns, for all cases shown in Figs. 25, 26 and 27, \(C_{D_{min}}\) is increased with respect to the baseline wing by approximately 4.0%.

In Tables 12, 13 and 14, we present the \(C_D\) for three \(C_L\) targets in the linear regime of the lift curves. The values studied correspond to \(C_L\) equal to 0.25 (approximately the \(C_L\) value corresponding to an AOA of \(4^{\circ }\) where the maximum \(C_L/C_D\) happens), and two high lift cases (\(C_L\) equal to 0.4 and 0.45). From the results summarized in these tables, we can deduce that as the cant angle is increased the gains in drag reduction are shortened, and the largest reductions of drag are obtained for cant angles between \(0^{\circ }\) and \(15^{\circ }\). In the results presented in Table 14, the gains in drag reduction are lessened because we are close to \(C_{L_{max}}\), and almost in the non-linear regime of the lift curves, hence, the slopes of the lift curves are lower.

Table 12 \(C_D\) and drag reduction percentage for a target \(C_L\) equal to 0.25 at Mach number 0.3
Full size table
Table 13 \(C_D\) and drag reduction percentage for a target \(C_L\) equal to 0.4 at Mach number 0.3
Full size table
Table 14 \(C_D\) and drag reduction percentage for a target \(C_L\) equal to 0.45 at Mach number 0.3
Full size table

In Fig. 28, we plot the lift coefficient as a function of the AOA for a sweep angle equal to \(60^{\circ }\). The curves depicted in this figure show a linear behavior up to approximately \(10^{\circ }\), then, \(C_{L_{max}}\) is reached, and the wings stall. It is noteworthy that the stall behavior of all the cases is similar. In this figure, \(C_{L_{max}}\) is increased in reference to the baseline wing for all winglet cant angle configurations. For a cant angle of \(0^{\circ }\) the maximum \(C_L\) is increased by as much as 13.0%, approximately 10.0% for a winglet cant angle of \(15^{\circ }\), for a cant angle of \(45^{\circ }\) by approximately 7.0%, and for a cant angle of \(80^{\circ }\), \(C_{L_{max}}\) is increased by approximately 1.0%. The slope of the lift curves is almost the same for the cases with cant angles between \(0^{\circ }\) and \(45^{\circ }\) (\(\partial C_L/\partial AOA \approx 0.053\) per degree). For the case with a cant angle equal to \(80^{\circ }\) the slope is \(\partial C_L/\partial AOA \approx 0.049\) per degree. Lastly, the slope of the baseline wing is \(\partial C_L/\partial AOA \approx 0.045\) per degree.

Fig. 28
figure 28

Lift coefficient versus angle-of-attack at Mach number 0.3, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image
Fig. 29
figure 29

Pressure coefficient on the wing surface at Mach number 0.3. Winglet sweep angle equal to \(60^{\circ }\) and wing AOA equal to \(14^{\circ }\)

Full size image

In Fig. 30, we plot the behavior of the drag coefficient as a function of the AOA. In this figure, we can observe that for AOA values ranging from \(0^{\circ }\) to \(6^{\circ }\) all the winglet configurations generate almost the same drag. Then, as we pass by AOA \(8^{\circ }\) higher cant angles (\(45^{\circ }\) and \(80^{\circ }\)) translate in less drag for the same AOA value. From the results presented, the largest drag reduction at high AOA is obtained with winglets at cant angle equal to \(80^{\circ }\); however, this winglet configuration greatly reduces the maximum \(C_L\) which is not desirable since at low Mach number large AOA are needed to reach the required lift, especially during take-off.

Fig. 30
figure 30

Drag coefficient versus angle-of-attack at Mach number 0.3, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image

The behavior of \(C_L/C_D\) as a function of the AOA is plotted in Fig. 31, where it can be seen that the maximum value of \(C_L/C_D\) occurs at \(4^{\circ }\) for all cases. For winglet cant angles of \(0^{\circ }\) and \(15^{\circ }\) the maximum \(C_L/C_D\) is increased by approximately 10.5% in reference to the baseline wing, for a cant angle of \(45^{\circ }\) the maximum \(C_L/C_D\) is increased \(\approx 5.0\%\), and for a cant angle of \(80^{\circ }\) the maximum \(C_L/C_D\) is increased \(\approx 3.0\%\).

Fig. 31
figure 31

Lift-to-drag ratio versus angle-of-attack at Mach number 0.3, sweep angle \(60^{\circ }\) and different values of cant angle

Full size image

Finally, as for the case at \(Ma = 0.8395\), the winglet configuration with a sweep angle equal to \(60^{\circ }\) gave the best results for different cant angle values.

5.3 Comparison of the aerodynamic performance at low and high Mach numbers

To better understand the impact of high Mach number and compressibility effects on the aerodynamic performance, in Figs. 32 and 33 we plot the results at \(Ma = 0.3\) and \(Ma = 0.8395\), together. In Fig. 32, we plot the drag polars for the two design Mach numbers, as it can be seen, compressibility plays an important role on the aerodynamic performance. At high Mach numbers, compressibility affects \(C_L\) and \(C_D\) detrimentally. First, it reduces \(C_{L_{max}}\), and secondly, it increases the drag for a given \(C_L\), especially for high AOA. This behavior stems from the alteration of the pressure distribution due to shock waves forming on the wing surface. It is interesting to highlight that at high Mach number and low AOA, the wing with winglets seem to work better than at low Mach number and low AOA, as \(C_{D_{min}}\) is slightly reduced in reference to the baseline wing.

The behavior of \(C_L\) as a function of AOA is plotted in Fig. 33, where we can identify two important aspects of the lift curves at high Mach number. First, the reduction of \(C_{L_{max}}\), and second, the increment of the lift curves slope, which in practice means that a smaller AOA is required to generate a given \(C_L\). However, more drag is produced due to compressibility effects (shock waves).

Fig. 32
figure 32

Drag polar for a winglet sweep angle of \(60^{\circ }\) and different cant angles. The results at \(Ma = 0.8395\) are plotted using continuous lines and those at \(Ma = 0.3\) are plotted with dashed lines

Full size image
Fig. 33
figure 33

Lift coefficient versus angle-of-attack for a winglet sweep angle of \(60^{\circ }\) and different cant angles. The results at \(Ma = 0.8395\) are plotted using continuous lines and those at \(Ma = 0.3\) are plotted with dashed lines

Full size image

5.4 Winglet settings during flight operations

From the previous discussion, it is clear that there is not a single winglet configuration that can give the best all-around drag reduction at every flight phase. It was also clear that the winglet configuration with a sweep angle equal to \(60^{\circ }\) gave the best results for different cant angle values. Hereafter, and based on the results presented in Sects. 5.1–5.3, we propose how the winglet cant angle could be set to obtain the best aerodynamic performance at a given flight phase. The suggested winglet settings for each flight phase are illustrated in Fig. 34. The recommended winglet configurations were chosen in base of the improvements in the aerodynamic performance with respect to the baseline wing. Hereafter, we summarized the best settings according to the given flight phase:

  • During ground operations, it is suggested to use a cant angle of \(80^{\circ }\) in order to reduce the wingspan and meet gate clearance requirements.

  • At take-off and initial climb (where compressibility effects are not strong), it is recommended to use a winglet cant angle of \(45^{\circ }\). This configuration has a higher lift-slope and generates less drag for a target lift. However, a winglet cant angle of \(15^{\circ }\) can also be used, this selection criterion can be based on weather conditions, take-off weight, or other operational requirements (such as climb rate).

  • At cruise (high Mach number), it is recommended to use a cant angle of \(15^{\circ }\). This setting will give the largest drag reduction for a given lift, with the exception for the case of cant angle equal to \(0^{\circ }\). This selection is justified mainly because it generates less wing root bending moments.

  • At cruise level change, it is recommended to use a cant angle of \(45^{\circ }\), but a value of \(15^{\circ }\) is also acceptable. These configurations have large lift-slope and generate less drag for a target lift.

  • During descent, it is recommended to use a cant angle of \(45^{\circ }\). In our analysis, we did not favor configurations with a cant angle value equal to \(80^{\circ }\) because they reduce the maximum lift coefficient and the slope of the lift curve.

  • After landing and when taxiing to the gate, it is suggested to use a cant angle of \(80^{\circ }\) in order to the reduce wingspan and meet gate clearance requirements.

The device studied can also be used as a load alleviation mechanism. So in case of strong gusts or turbulence, the cant angle can be increased to \(80^{\circ }\) reducing in this way the maximum lift and the slope of the lift curve, therefore reducing the wing root bending moments, and this might be particularly helpful during descent and landing with adverse weather conditions.

It is worth mentioning that the proposed winglet configurations show similar characteristics to those of fixed winglets already in use in civil transport aircraft. For example, the cant angle configuration of \(15^{\circ }\) is very similar to the raked winglet, and the cant angle configuration of \(45^{\circ }\) is close to the blended and canted winglets (refer to Fig. 1).

Fig. 34
figure 34

Winglet configuration during different flight phases

Full size image

6 Conclusions and perspectives

In this manuscript, we have studied the use of variable cant angle winglets which could potentially allow aircraft to get the best all-around performance in terms of drag reduction over different flight phases. While the wing studied does not correspond to an actual wing used in civil transport aircraft, the insight gathered can be used to set the guidelines for the design of variable cant angle winglets and the adjustment of their cant angle during flight.

During this work, we considered high and low Mach number values (0.8395 and 0.3, respectively) and different angle-of-attack values. Thus, we aimed at covering take-off, climb, descent, and cruise conditions. All the quantitative results suggest that by carefully controlling the winglet cant angle, noticeable drag reductions for the same lift value can be obtained at high and low Mach numbers. It was also observed that the variable cant angle winglets do not have adverse effects on the stall behavior and the AOA at which \(C_{L_{max}}\) and \(C_{D_{min}}\) occurs. It also worth noting that at high cant angle values (\(80^{\circ }\)), the maximum lift coefficient and the slope of the lift curve is reduced (but their values are still larger than the values of the baseline wing); therefore, the proposed winglet could potentially be used as a load alleviation system.

Furthermore, it was also found that large winglet sweep angle values have a positive impact on the aerodynamic performance improvements gained by using the proposed winglet. The improvement due to sweep angle is mainly due to a combination of reduced parasite drag, decreased wave drag at high Mach number, and the effect of the inboard lift force generated by the winglet.

In summary, the following benefits have been found:

  • Increased lift curve slope.

  • Increased maximum lift.

  • Increased lift-to-drag ratio.

  • No negative effects on stall behavior due to lift production enhancement.

  • For the same Mach number, the AOA for \(C_{L_{max}}\) and maximum \(C_L/C_D\) remains almost invariable.

  • Crossover point at AOA values below \(2^{\circ }{-}3^{\circ }\), and as low as \(0^{\circ }\). As a consequence, total drag reduction for the same lift above the crossover point.

  • The increase of the winglet cant angle does not add the extra wing root bending moment that would be encountered if the wingspan were simply increased by the span of the winglet.

On the other side, the following shortcomings have been found:

  • Increased parasite drag.

  • Increased wave drag at high Mach number and cant angle \(80^{\circ }\).

  • Noticeable reduction of \(C_{L_{max}}\) and lift curve slope for a winglet cant angle of \(80^{\circ }\).

  • Increased weight due to the device itself.

  • The addition of the winglet will require a structural study in order to support the local forces and bending moments at the winglet junction.

  • A new structural study of the wing to meet the new bending moments and flutter and fatigue requirements due to the addition of the winglet.

It is clear that to obtain the best trade-off between benefits and shortcomings, a multi-disciplinary design optimization study should be conducted, together with the use of more realistic wing geometries and additional winglet design variables, such as toe-angle, taper ratio, and span. Nevertheless, the concept studied in this manuscript represents an innovative approach that might help in addressing the challenge of improving aircraft fuel efficiency, reduce pollutant emissions, and lowering the perceived external noise.

We envisage conducting a flight performance study and estimating fuel savings for typical flight scenarios using more realistic wing-winglet configurations. Also, as the main focus of this work was the study of the aerodynamic performance of variable cant angle winglets, we did not give details about the mechanical design of the device and its performance (such as estimation of actuation power, weight, and so on); however, these topics are object of ongoing research.