Introduction of MMG standard method for ship maneuvering predictions

Abstract

A lot of simulation methods based on Maneuvering Modeling Group (MMG) model for ship maneuvering have been presented. Many simulation methods sometimes harm the adaptability of hydrodynamic force data for the maneuvering simulations since one method may be not applicable to other method in general. To avoid this, basic part of the method should be common. Under such a background, research committee on “standardization of mathematical model for ship maneuvering predictions” was organized by the Japan Society of Naval Architects and Ocean Engineers and proposed a prototype of maneuvering prediction method for ships, called “MMG standard method”. In this article, the MMG standard method is introduced. The MMG standard method is composed of 4 elements; maneuvering simulation model, procedure of the required captive model tests to capture the hydrodynamic force characteristics, analysis method for determining the hydrodynamic force coefficients for maneuvering simulations, and prediction method for maneuvering motions of a ship in fullscale. KVLCC2 tanker is selected as a sample ship and the captive mode test results are presented with a process of the data analysis. Using the hydrodynamic force coefficients presented, maneuvering simulations are carried out for KVLCC2 model and the fullscale ship for validation of the method. The present method can roughly capture the maneuvering motions and is useful for the maneuvering predictions in fullscale.

1 Introduction

MMG model is one of the solutions for ship maneuvering motion simulations developed in Japan. The model was proposed by a research group called Maneuvering Modeling Group (MMG) in Japanese Towing Tank Conference (JTTC), and the outline was reported in the Bulletin of Society of Naval Architects of Japan [1] in 1977. In the report, the concept for maneuvering simulations was mainly described, but concrete simulation model was not described in detail. According to MMG model concept, afterward, concrete methods including expression of hydrodynamic forces acting on ships were presented by Ogawa and Kasai [2], Matsumoto and Suemitsu [3], Inoue et al. [4] and so on. Nowadays, a lot of simulation methods based on MMG model are existing.

Many simulation methods sometimes harm the adaptability of hydrodynamic force data for the maneuvering simulations since one method may be not applicable to other method in general. To avoid this, basic part of the method should be common. The test procedure and the data analysis to determine the hydrodynamic force coefficients for the simulations should be also common since those often involve the quantitative value of the hydrodynamic coefficients.

Under such a background, the research committee on “standardization of mathematical model for ship maneuvering predictions” organized by the Japan Society of Naval Architects and Ocean Engineers has checked the details of existing MMG models such as the coordinate system, the motion equations, the hull and rudder hydrodynamic force models etc., in view of accuracy, simplicity, physical/theoretical background and adoptability to the captive model tests for capturing the hydrodynamic force characteristics. As the conclusion, a prototype of maneuvering simulation method for ships called “MMG standard method”, has been proposed [5].

This article introduces the MMG standard method which is composed of 4 elements:

• maneuvering simulation model,

• procedure of the required captive model tests to capture the hydrodynamic force characteristics,

• analysis method for determining the hydrodynamic force coefficients for maneuvering simulations, and

• prediction method for maneuvering motions of a ship in fullscale.

The basic simulation model described here is a combination of the existing models for expressing the hydrodynamic force characteristics with respect to ship hull, propeller, rudder, and their interaction components. The physical meaning of the models is described in detail for the better understanding. KVLCC2 tanker is selected as a sample ship and the captive mode test results [6, 7] are presented with a process of the data analysis. It may be a special feature of this article that the test procedure and the data analysis to determine the hydrodynamic force coefficients are presented in detail. Using the hydrodynamic force coefficients determined, maneuvering simulations are carried out for KVLCC2 model [8] and the fullscale ship for validation of the method.

2 Maneuvering simulation model

First, the motion equations to express the maneuvering motions for a ship with single propeller and single rudder, and the simulation model of hydrodynamic forces acting on the ship are described.

In this article, prime $'$ putting to the symbol means non-dimensionalized value. Force and moment are non-dimensionalized by $(1/2)\rho L_{pp} dU^2$ and $(1/2)\rho L_{pp}^2 dU^2$, respectively. In addition, mass and moment of inertia are non-dimensionalized by $(1/2)\rho L_{pp}^2 d$ and $(1/2)\rho L_{pp}^4 d$, respectively. Velocity component is non-dimensionalized by $U$ and length component is by $L_{pp}$.

2.1 Assumptions and coordinate systems

The following assumptions are employed:

• Ship is a rigid body.

• Hydrodynamic forces acting on the ship are treated quasi-steadily.

• Lateral velocity component is small compared with longitudinal velocity component.

• Ship speed is not fast that wave-making effect can be neglected.

• Metacentric height $\overline{GM}$ is sufficiently large, and the roll coupling effect on maneuvering is negligible.

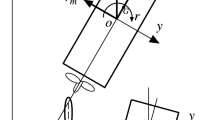
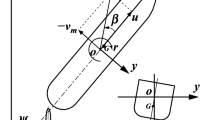
Figure 1 shows the coordinate systems used in the present article: the space-fixed coordinate system $o_0$–$x_0y_0z_0$, where $x_0$–$y_0$ plane coincides with the still water surface and $z_0$ axis points vertically downwards, and the moving ship-fixed coordinate system $o$–$xyz$, where $o$ is taken on the midship of the ship, and $x$, $y$ and $z$ axes point towards the ship’s bow, towards the starboard and vertically downwards, respectively. Heading angle $\psi$ is defined as the angle between $x_0$ and $x$ axes, $\delta$ the rudder angle and $r$ the yaw rate. $u$ and $v_m$ denote the velocity components in $x$ and $y$ directions, respectively; drift angle at midship position $\beta$ is defined by $\beta = \tan ^{-1}(-v_m/u)$, and the total velocity $U$, $U=\sqrt{u^2+v_m^2}$. Center of gravity of the ship $G$ is located at $(x_G, 0, 0)$ in $o$–$xyz$ system. Then, lateral velocity component at the center of gravity $v$ is expressed as

$$\begin{aligned} v&= v_m + x_Gr \end{aligned}$$

(1)

Fig. 1

Coordinate systems

One of the special feature of the present model is the use of the coordinate system fixed to the midship position. This may be convenient when considering the captive model tests with different load conditions like full and ballast loads. When employing the origin of the center of gravity, for instance, the coordinate of the rudder/propeller position changes in full and ballast load conditions since the longitudinal position of the center of gravity generally changes in different load conditions. Employing the midship-based coordinate system can avoid such the troublesome.

2.2 Motion equations

Maneuvering motions of a ship in still water are represented as surge, sway, and yaw. The motion equations are expressed as

$$\begin{aligned} \left. \begin{array}{l} m(\dot{u} - vr) = F_x \\ m(\dot{v} + ur) = F_y \\ I_{zG}\ \dot{r} = M_z \\ \end{array} \right\} \end{aligned}$$

(2)

In Eq. 2, unknown variables are $u$, $v$ and $r$. Here, $F_x$, $F_y$ and $M_z$ are expressed as follows:

$$\begin{aligned} \left. \begin{array}{l} F_x = -m_x \dot{u} + m_yv_mr + X \\ F_y = -m_y \dot{v}_m - m_xur + Y \\ M_z = -J_{z}\dot{r} + N_m - x_GF_y \end{array} \right\} \end{aligned}$$

(3)

Added mass coupling terms with respect to $v_m$ and $r$ are neglected in view of practical purposes.

Substituting Eqs. 1 and 3 into Eq. 2 for eliminating $v$, the following equations are obtained:

$$\begin{aligned}&\left. \begin{array}{l} (m+m_x)\dot{u} - (m+m_y)v_mr -x_Gmr^2 = X \\ (m+m_y)\dot{v}_m + (m+m_x)ur + x_Gm\dot{r} = Y \\ (I_{zG}+x_G^2m+J_{z})\dot{r} +x_Gm(\dot{v}_m + ur) = N_m \end{array} \right\} \end{aligned}$$

(4)

Eq. 4 is the motion equations to be solved.

The right-hand side of Eq. 4 $X$, $Y$ and $N_m$ is expressed as

$$\begin{aligned} \left. \begin{array}{l} X= X_{\rm H} + X_{\rm R} + X_{\rm P} \\ Y= Y_{\rm H} + Y_{\rm R} \\ N_m = N_{\rm H} + N_{\rm R} \end{array} \right\} \end{aligned}$$

(5)

Subscript H, R, and P means hull, rudder, and propeller, respectively.

2.3 Hydrodynamic forces acting on ship hull

$X_{\rm H}, Y_{\rm H}$ and $N_{\rm H}$ are expressed as follows:

$$\begin{aligned} \left. \begin{array}{l} X_{\rm H} = (1/2)\rho L_{pp}dU^2\, X_{\rm H}'(v_m',r') \\ Y_{\rm H} = (1/2)\rho L_{pp}dU^2\, Y_{\rm H}'(v_m',r') \\ N_{\rm H} = (1/2)\rho L_{pp}^2dU^2\, N_{\rm H}'(v_m',r'), \end{array} \right\} \end{aligned}$$

(6)

where $v_m'$ denotes non-dimensionalized lateral velocity defined by $v_m/U$, and $r'$ non-dimensionalized yaw rate by $rL_{pp}/U$. $X_{\rm H}'$ is expressed as the sum of resistance coefficient $R_0'$ and the 2nd and 4th order polynomial function of $v_m'$ and $r'$. $Y_{\rm H}'$ and $N_{\rm H}'$ are expressed as the 1st and 3rd order polynomial function of $v_m'$ and $r'$:

$$\begin{aligned} \left. \begin{array}{l} X_{\rm H}'(v_m',r')= -R_0' + X_{vv}'v_m'^2 + X_{vr}'v_m' r'+X_{rr}'r'^2 + X_{vvvv}'v_m'^4 \\ Y_{\rm H}'(v_m',r') = Y_v' v_m' + Y_{\rm R}'r' + Y_{vvv}'v_m'^3 + Y_{vvr}'v_m'^2 r' + Y_{vrr}'v_m' r'^2 + Y_{rrr}'r'^3 \\ N_{\rm H}'(v_m',r') = N_v' v_m' + N_{\rm R}'r' + N_{vvv}'v_m'^3 + N_{vvr}'v_m'^2 r' + N_{v rr}'v_m' r'^2 + N_{rrr}'r'^3, \end{array} \right\} \end{aligned}$$

(7)

where $X_{vv}'$, $X_{vr}'$, $X_{rr}'$, $X_{vvvv}'$, $Y_v'$, $Y_{\rm R}'$, $Y_{vvv}'$, $Y_{vvr}'$, $Y_{vrr}'$, $Y_{rrr}'$, $N_v'$, $N_{\rm R}'$, $N_{vvv}'$, $N_{vvr}'$, $N_{vrr}'$, and $N_{rrr}'$ are called the hydrodynamic derivatives on maneuvering. Note that the expression of the 1st and 3rd order polynomial function like Eq. 7 is superior to the other expression such as the 1st and 2nd order polynomial function in view of estimation accuracy for $Y_{\rm H}'$ and $N_{\rm H}'$ [3, 5].

2.4 Hydrodynamic force due to propeller

Surge force due to propeller $X_{\rm P}$ is expressed as

$$\begin{aligned} X_{\rm P} = (1-t_{\rm P})T \end{aligned}$$

(8)

Thrust deduction factor $t_{\rm P}$ is assumed to be constant at given propeller load for simplicity. Propeller thrust $T$ is written as

$$\begin{aligned} T&= \rho n_{\rm P}^2 D_{\rm P}^4 \, K_{T}(J_{\rm P}) \end{aligned}$$

(9)

$K_{T}$ is approximately expressed as 2nd polynomial function of propeller advanced ratio $J_{\rm P}$:

$$\begin{aligned} K_{T}(J_{\rm P})&= k_2J_{\rm P}^2 + k_1J_{\rm P} + k_0 \end{aligned}$$

(10)

$J_{\rm P}$ is written as

$$\begin{aligned} J_{\rm P}&= \frac{u(1-w_{\rm P})}{n_{\rm P} D_{\rm P}} \end{aligned}$$

(11)

The $w_{\rm P}$ changes with maneuvering motions in general and the several formulas have been presented, for instance,

$$\begin{aligned} w_{\rm P}/w_{\rm P0}&= \exp (-4\beta _{\rm P}^2) \end{aligned}$$

(12)

$$\begin{aligned} (1-w_{\rm P})/(1-w_{\rm P0})&= 1+C_1\left( \beta _{\rm P}+C_2\beta _{\rm P}|\beta _{\rm P}| \right) ^2 \end{aligned}$$

(13)

$$\begin{aligned} (1-w_{\rm P})/(1-w_{\rm P0})&= 1+( 1-\cos ^2\beta _{\rm P})(1-|\beta _{\rm P}|) , \end{aligned}$$

(14)

where $\beta _{\rm P}$ is the geometrical inflow angle to the propeller in maneuvering motions and defined as

$$\begin{aligned} \beta _{\rm P}&= \beta -x_{\rm P}'r' \end{aligned}$$

(15)

Eqs. 12–14 were presented in Refs. [4, 9, 10], respectively. However, the estimation accuracy of Eqs. 12 and 14 was not enough. Also, the physical meaning of $C_1$ and $C_2$ in Eq. 13 is not clear. In this article, a formula is introduced as

$$\begin{aligned} (1-w_{\rm P})/(1-w_{\rm P0})&= 1+\left\{ 1-\exp (-C_1|\beta _{\rm P}|) \right\} ( C_2-1 ) \end{aligned}$$

(16)

From Eq. 16, we see that

$$\begin{aligned} (1-w_{\rm P})/(1-w_{P0}) \rightarrow C_2 \quad \text{ at } |\beta _{\rm P}| \rightarrow \infty \end{aligned}$$

(17)

Therefore, $C_2$ means value of $(1-w_{\rm P})/(1-w_{\rm P0})$ at large $|\beta _{\rm P}|$. Then, $C_1$ represents the wake change characteristic versus $\beta _{\rm P}$. Thus, the physical meaning of $C_1$ and $C_2$ is clear for Eq. 16. The actual wake characteristic is asymmetry with respect to $\beta _{\rm P}$ due to the propeller rotational effect. Then, the different $C_2$ value should be taken for plus/minus $\beta _{\rm P}$ in Eq. 16. The fitting accuracy will be discussed in Sect. 4.3.

In the expression of $X_{\rm P}$, the steering effect on the propeller thrust $T$ is excluded. Instead of this, the effect is taken into account at the rudder force component $X_{\rm R}$ as shown in the next section.

2.5 Hydrodynamic forces by steering

Effective rudder forces $X_{\rm R}, Y_{\rm R}$ and $N_{\rm R}$ are expressed as

$$\begin{aligned} \left. \begin{array}{l} X_{\rm R} = - (1-t_{\rm R}) F_{N}\sin \delta \\ Y_{\rm R} = - (1+a_{\rm H}) F_{N}\cos \delta \\ N_{\rm R} = - (x_{\rm R}+a_{\rm H}x_{\rm H})F_{N}\cos \delta , \end{array} \right\} \end{aligned}$$

(18)

where $F_{N}$ is the rudder normal force. Note that the rudder tangential force is neglected in Eq. 18. The $t_{\rm R}, a_{\rm H}$ and $x_{\rm H}$ are the coefficients representing mainly hydrodynamic interaction between ship hull and rudder. The $t_{\rm R}$ is called the steering resistance deduction factor and defined the deduction factor of rudder resistance versus $F_{N}\sin \delta$ which means longitudinal component of $F_{N}$ [3]. Actually, $X_{\rm R}$ includes a component of the propeller thrust change due to steering as mentioned in Sect. 2.4. Therefore, $t_{\rm R}$ means a factor of both the rudder resistance deduction and the propeller thrust increase induced by steering. The propeller thrust increase occurs due to the increase of nominal wake at propeller position by steering. On the other hand, the mechanism of the rudder resistance deduction by steering is not clear at present, although the rudder tangential force component neglected in Eq. 19 may involve $t_{\rm R}$.

The $a_{\rm H}$ and $x_{\rm H}$ are called the rudder force increase factor and the position of an additional lateral force component, respectively. The $a_{\rm H}$ represents the factor of lateral force acting on ship hull by steering versus $F_{N}\cos \delta$ which means the lateral component of $F_{N}$. The magnitude of $a_{\rm H}$ was almost 0.3–0.4 in tank tests [9], and this means that the lateral force acting on the ship by steering increases about 30–40 % larger than the rudder normal force component. The $x_{\rm H}$ means the longitudinal acting point of the additional lateral force component. The measured value of $x_{\rm H}$ was almost $-0.45L_{pp}$ and the additional force acts on the stern part of the hull. This phenomena may be understandable when considering the hydrodynamic interaction of a wing with a flap. Then, ship hull and rudder are regarded as the main wing and the flap, respectively, as shown in Fig. 2. Lift force is induced on the rudder itself by steering, and at the same time, an additional force component, $\Delta Y$ in Fig. 2, is induced on the ship hull. The $\Delta Y$ comes from the hydrodynamic interaction between hull (main wing) and rudder (flap). Then, $a_{\rm H}$ is defined by $- \Delta Y/F_{N}\cos \delta$, and $x_{\rm H}$ can be regarded as the acting point of $\Delta Y$. This phenomena was pointed by Karasuno [11] and theoretically confirmed by Hess [12].

Fig. 2

Schematic figure of rudder force and the additional lateral force induced by steering

Rudder normal force $F_{N}$ is expressed as

$$\begin{aligned} F_{N}&= (1/2)\rho A_{\rm R}\,U_{\rm R}^2\,f_{\alpha }\,\sin \alpha _{\rm R} \end{aligned}$$

(19)

Here, the resultant rudder inflow velocity $U_{\rm R}$ and the angle $\alpha _{\rm R}$ are expressed as

$$\begin{aligned} U_{\rm R}&= \sqrt{u_{\rm R}^2 + v_{\rm R}^2} \end{aligned}$$

(20)

$$\begin{aligned} \alpha _{\rm R}&= \delta - \tan ^{-1}\left( \frac{v_{\text {R}}}{u_{\text {R}}}\right) \simeq \delta - \frac{v_{\text {R}}}{u_{\text {R}}} \end{aligned}$$

(21)

Assuming that the helm angle is zero when $\beta$ and $r'$ are zero, $v_{\rm R}$ can be expressed as follows:

$$\begin{aligned} v_{\rm R}&= U\,\gamma _{\rm R}\beta _{\rm R0} \end{aligned}$$

(22)

Here, $\gamma _{\rm R}$ is called the flow straightening coefficient and usually smaller than 1.0. This means that the actual inflow angle to rudder becomes smaller than the geometrical inflow angle $\beta _{\rm R0}$. The flow straightening phenomena comes from the presence of hull and propeller slip stream as shown in Fig. 3. The $\beta _{\rm R0}$ is expressed as the sum of hull drift angle $\beta$ and inflow velocity change due to yaw motion $-x_{\rm R}'r'$. Here, $x_{\rm R}'$ is non-dimensional longitudinal coordinate of rudder position and should be $-0.5$. However, obtaining the value of $x_{\rm R}'$ in the experiments actually, it was not $-0.5$ and close to $-1.0$ [9]. This means that the flow straightening phenomena in turning motion is not so simple. Here, the effective inflow angle to rudder $\beta _{\rm R}$ is newly defined using a new symbol $\ell _{\rm R}'$ instead of $x_{\rm R}'$. Then, $v_{\rm R}$ is expressed as

$$\begin{aligned} v_{\rm R}&= U\,\gamma _{\rm R}\beta _{\rm R} \end{aligned}$$

(23)

where

$$\begin{aligned} \beta _{\rm R}&= \beta - \ell _{\rm R}'r' \end{aligned}$$

(24)

Here, $\ell _{\rm R}'$ is treated as an experimental constant for expressing $v_{\rm R}$ accurately and can be obtained from the captive model test.

Fig. 3

Rudder inflow velocity and angle

The $\gamma _{\rm R}$ characteristic considerably affects the maneuvering simulation, so we have to capture it correctly. Value of $\gamma _{\rm R}$ generally takes different magnitude for port and starboard turning and this is one of the reasons for asymmetrical turning motions in port and starboard. The flow straightening effect was pointed out by Fujii and Tuda [13] first, and after that a form of Eq. 23 was proposed by Kose et al. [9].

A longitudinal inflow velocity component to rudder $u_{\rm R}$ is expressed referring to the derivation described in Appendix as follows:

$$\begin{aligned} u_{\rm R}&= \varepsilon \, u(1-w_{\rm P}) \sqrt{ \eta \left\{ 1+\kappa \left( \sqrt{1+\frac{8K_T}{\pi J_{\rm P}^2}}-1 \right) \right\} ^2 +(1-\eta ) }, \end{aligned}$$

(25)

where $\varepsilon$ means a ratio of wake fraction at rudder position to that at propeller position defined by $\varepsilon =(1-w_{\rm R})/(1-w_{\rm P})$. The $\kappa$ is an experimental constant.

3 Captive model test and the results

In this section, outline of captive model tests is described to capture the hydrodynamic force characteristics. As an example, the experimental data opened in SIMMAN2008 workshop [6] for KVLCC2 model is introduced.

3.1 A sample ship: KVLCC2

A VLCC tanker called KVLCC2 [7] was selected as a sample ship. Table 1 shows the principal particulars. In the table, the principal particulars of ship models with 2.909 m length (L3-model) and with 7.00 m length(L7-model) are shown together with those of fullscale ship. L3-model was used for the captive model tests conducted at National Maritime Research Institute, Japan, to capture the hydrodynamic force characteristics [6]. L7-model was used for the free-running model tests conducted in a square tank of MARIN[8]. The body plan is shown in Fig. 4. This ship has a mariner rudder. Note that $A_{\rm R}$ in Table 1 is a profile area of movable part of the rudder excluding the horn part.

Table 1 Principal particulars of a KVLCC2 tanker

Fig. 4

Body plan and profiles of KVLCC2 tanker

3.2 Outline of captive model tests

3.2.1 Kind of tests

The captive tests were carried out at propelled condition of a ship model with a rudder model. Ship speed $U_0$ was set at 0.76 m/s (equivalent to 15.5 kn in fullscale). As the propeller loading point the model point was selected in principle.

In advance of the captive model tests, resistance test, self-propulsion test, and propeller open water test were carried out. After that, the following tests were conducted:

• 1. Rudder force test in straight moving under various propeller loads.

• 2. Oblique towing test (OTT) and circular motion test (CMT).

• 3. Rudder force test in oblique towing and steady turning conditions (flow straightening coefficient test).

Rudder force test in straight moving is the test to measure the hydrodynamic forces acting on the ship model when the ship moves straight with keeping a certain rudder angle. From this test, the hull rudder interaction coefficients ($t_{\rm R}$, $a_{\rm H}$, $x_{\rm H}'$) and the parameters for representing the longitudinal inflow velocity component to rudder ($\kappa$, $\varepsilon$) can be obtained.

OTT and CMT are the test to measure the hydrodynamic forces acting on the ship model in oblique moving and/or steady turning. Then, the rudder angle should be zero. From the tests, the hydrodynamic forces acting on the ship and the wake fractions at propeller position in maneuvering motions can be obtained. Planar motion technique (PMM) test is widely used as a method to capture the hydrodynamic derivatives on turning. The hydrodynamic derivatives obtained by PMM test remarkably change due to influence of the motion frequency and the motion amplitude given in the test and it is difficult to select the proper values for the maneuvering simulations. To avoid the uncertainty, CMT was employed here instead of PMM test.

The flow straightening coefficient test is the test to capture the rudder angle where the normal force becomes zero ($\delta _{FN0}$) and the inclination of the normal force coefficient versus rudder angle at $\delta _{FN0}$ in oblique moving and/or steady turning ($dF_N'/d\delta$). The flow straightening coefficient ($\gamma _{\rm R}$) is determined from the results of $\delta _{FN0}$ and $dF_N'/d\delta$.

All the tests were carried out in the free condition for trim and sinkage of the model.

3.2.2 Measurement items

Measurement items in the tests are as follows:

• Surge force, lateral force and yaw moment around midship acting on the ship model ($X$, $Y$, $N_m$),

• rudder normal force ($F_{N}$),

• propeller thrust ($T$).

3.3 Test results

3.3.1 Rudder force test results in straight moving

Figure 5 shows the rudder force test results in straight moving under various propeller loads. In the test, the rudder angle was changed in the range of $-20^{\circ }$ to $20^{\circ }$ or $-35^{\circ }$ to $35^{\circ }$ with $5^{\circ }$ interval at several different propeller load conditions. Then, propeller revolution $n_{\rm P}$ was changed as 14.48, 17.95, and 24.87 rps with keeping $U_0$ constant so as to cover the range of both ship point and model point. Absolute values of the hydrodynamic force coefficients $Y'$, $N_m'$ and $F_{N}'$ increase with increase of the propeller revolution $n_{\rm P}$ and/or the rudder angle $\delta$.

Fig. 5

Rudder force test results in straight moving under various propeller loads for KVLCC2 model

3.3.2 OTT and CMT results

Hull drift angle $\beta$ was changed in the range of $-20^{\circ }$ to $20^{\circ }$ in OTT, and non-dimensional yaw rate $r'$ was changed in the range of $-0.8$–$0.8$ with 0.2 interval with a certain drift angle in CMT. The range of $\beta$ and $r'$ in the tests was determined so as to cover the actual maneuvering motions. Figure 6 shows OTT and CMT results: $X_{\rm mes}'$, $Y_{\rm mes}'$, $N_{\rm mes}'$, $F_N'$ and $T'$ versus $\beta$ and $r'$. Here, $X_{\rm mes}'$, $Y_{\rm mes}'$, and $N_{\rm mes}'$ are the actual measured forces in which the inertia forces such as the centrifugal force acting on the turning ship are included.

Fig. 6

OTT and CMT results for KVLCC2 model

3.3.3 Flow straightening coefficient test results

Direct measurements of $\delta _{FN0}$ and $dF_{N}'/d\delta$ are difficult in oblique moving and/or steady turning. These were captured by the following procedure:

• 1. Rudder normal forces are measured with changing 3 rudder angles. These 3 rudder angles have to be selected appropriately so as the rudder angle at zero normal force can be determined.

• 2. $\delta _{FN0}$ is determined by an interpolation based on 3 measured rudder normal force results versus $\delta$.

• 3. $dF_{N}'/d\delta$ is numerically calculated by taking an inclination of the rudder normal force coefficient versus $\delta$.

Figure 7 shows $\delta _{FN0}$ and $dF_N'/d\delta$ as functions of $\beta$ and $r'$. The $\delta _{FN0}$ increases with increasing $\beta$ or $r'$; however, $dF_{N}'/d\delta$ does not change very much with $\beta$ or $r'$.

Fig. 7

$\delta _{FN0}$ and $dF_{N}'/d\delta$ obtained in flow straightening coefficient test for KVLCC2 model

4 Determination of hydrodynamic force coefficients

Next, analysis methods are described to determine the hydrodynamic force coefficients defined in the simulation model referring to Ref. [5].

4.1 $t_{\rm R}$, $a_{\rm H}$ and $x_{\rm H}'$

The rudder force tests in straight moving are conducted in the condition of $\beta =r'=0$, so that $Y_{\rm H}$ and $N_{\rm H}$ should be zero in Eq. 5. Then, the non-dimensional forms of eq.(5) are written as follows:

$$\begin{aligned} \left. \begin{array}{l} X' = -R_0' + (1-t_{\rm P})T' - (1-t_{\rm R}) F_{N}'\sin \delta \\ Y' = - (1+a_{\rm H}) F_{N}'\cos \delta \\ N_m' = - (x_{\rm R}'+a_{\rm H}x_{\rm H}')F_{N}'\cos \delta \end{array} \right\} \end{aligned}$$

(26)

From Eq. 26, we know the following:

• ($1-t_{\rm R}$) is determined as an inclination of $X'$ versus $-F_{N}'\sin \delta$. Note that $R_0'$ and $(1-t_{\rm P})T'$ are not related to the rudder angle $\delta$ in the simulation model.

• ($1+a_{\rm H}$) is determined as an inclination of $Y'$ versus $-F_{N}'\cos \delta$.

• ($x_{\rm R}'+a_{\rm H}x_{\rm H}'$) is determined as an inclination of $N_m'$ versus $-F_{N}'\cos \delta$. Then, $x_{\rm H}'$ can be calculated since $x_{\rm R}'$ is $-0.5$ and $a_{\rm H}$ is known.

It is experimentally confirmed that the inclinations of $X'$, $Y'$ and $N_m'$ can be approximated as a linear function. Namely, $t_{\rm R}$, $a_{\rm H}$ and $x_{\rm H}'$ can be regarded as constant values at given propeller load. The hull rudder interaction coefficients are usually determined at a representative propeller load (in this case, $n_{\rm P}=17.95$ rps, model point), although there is a trend that $a_{\rm H}$ slightly decreases with increase of propeller load[14].

Figure 8 shows the figures used for determining the hull rudder interaction coefficients. From the figures, it was determined that $t_{\rm R}$, $a_{\rm H}$ and $x_{\rm H}'$ are 0.387, 0.312, and $-0.464$, respectively.

Fig. 8

Analysis results for hull and rudder interaction coefficients of KVLCC2 model

4.2 Hydrodynamic derivatives on maneuvering

The hydrodynamic derivatives on maneuvering are determined from OTT and CMT results. The inertia force components are included to the hydrodynamic forces measured in CMT. Then, the actual measured force coefficients ($X_{\rm mes}'$, $Y_{\rm mes}'$, $N_{\rm mes}'$) are theoretically expressed as follows:

$$\begin{aligned} \left. \begin{array}{l} X_{\rm mes}' = X_{\rm H}^{*'} + X_{\rm R}' + X_{\rm P}' \\ Y_{\rm mes}' = Y_{\rm H}^{*'} + Y_{\rm R}' \\ N_{\rm mes}' = N_{\rm H}^{*'} + N_{\rm R}' \end{array} \right\} \end{aligned}$$

(27)

where

$$\begin{aligned} \left. \begin{array}{l} X_{\rm H}^{*'} = X_{\rm H}' + (m' + m_y')v_m' r'+ x_G'm'r'^2 \\ Y_{\rm H}^{*'} = Y_{\rm H}' - (m' + m_x')r' \\ N_{\rm H}^{*'} = N_{\rm H}' - x_G'm'r' \end{array} \right\} \end{aligned}$$

(28)

Here, an approximation of $u'\simeq 1$ was employed. In Eq. 28, $(m' + m_y')v_m'r'$, $-(m' + m_x')r'$, etc. are inertia force terms including added mass components. Considering the situation in CMT, namely taking $\delta =0$ in Eq. 27, the following equations are obtained:

$$\begin{aligned} \left. \begin{array}{l} X_{\rm H}^{*'} = X_{\rm mes}' - (1-t_{\rm P})T' \\ Y_{\rm H}^{*'} = Y_{\rm mes}' + (1+a_{\rm H})F_{N}' \\ N_{\rm H}^{*'} = N_{\rm mes}' + (x_{\rm R}'+a_{\rm H}x_{\rm H}')F_{N}' \end{array} \right\} \end{aligned}$$

(29)

Using Eq. 29, $X_{\rm H}^{*'}$, $Y_{\rm H}^{*'}$ and $N_{\rm H}^{*'}$ can be calculated since $X_{\rm mes}'$, $Y_{\rm mes}'$, $N_{\rm mes}'$, $F_{N}'$, and $T'$ are measured, and $t_{\rm P}$, $t_{\rm R}$, $a_{\rm H}$, and $x_{\rm H}'$ are given. On the other hand, substituting Eq. 7 to Eq. 28, $X_{\rm H}^{*'}$, $Y_{\rm H}^{*'}$, and $N_{\rm H}^{*'}$ are written as a function of $v_m'$ and $r'$ as follows:

$$\begin{aligned} \left. \begin{array}{l} X_{\rm H}^{*'} = -R_0'+X_{vv}'v_m'^2 + (X_{vr}'+ m' + m_y')v_m'r'+( X_{rr}'+x_G'm')r'^2 + X_{vvvv}'v_m'^4 \\ Y_{\rm H}^{*'} = Y_v'v_m'+(Y_{\rm R}'-m'-m_x')r'+Y_{vvv}'v_m'^3+Y_{vvr}'v_m'^2r'+Y_{vrr}'v_m'r'^2+Y_{rrr}'r'^3 \\ N_{\rm H}^{*'} = N_v'v_m'+ (N_{\rm R}'-x_G'm')r'+N_{vvv}'v_m'^3+N_{vvr}'v_m'^2r'+N_{vrr}'v_m'r'^2+N_{rrr}'r'^3 \end{array} \right\} \end{aligned}$$

(30)

Each term in Eq. 30 such as $Y_v'$, $(Y_{\rm R}'-m'-m_x')$, $N_v'$, $(N_{\rm R}'-x_G'm')$, etc. is determined by a least square method (LSM) based on calculated $X_{\rm H}^{*'}$, $Y_{\rm H}^{*'}$ and $N_{\rm H}^{*'}$ using Eq. 29. In terms of $(X_{vr}'+ m' + m_y')$, $(X_{rr}'+x_G'm')$, $(Y_{\rm R}'- m' - m_x')$, and $(N_{\rm R}'-x_G'm')$, mass and added mass components are included. Then, $m'$ is given from the displacement volume of the ship, but $m_x'$ and $m_y'$ are unknown. The added mass components have to be estimated by other method.

Figure 9 shows obtained $X_{\rm H}^{*'}$, $Y_{\rm H}^{*'}$ and $N_{\rm H}^{*'}$. The hydrodynamic derivatives obtained by LSM are listed in Table 2. To confirm the accuracy of expression of Eq. 30, the fitting curves expressed as dotted line are also plotted in Fig. 9. The fitting accuracy is sufficient in view of practical purposes.

Fig. 9

Analysis results of hydrodynamic forces acting on KVLCC2 model @

Table 2 Resistance coefficient and hydrodynamic derivatives on maneuvering

4.3 $w_{\rm P}$

Wake coefficient in maneuvering motions $w_{\rm P}$ is obtained by the thrust identification method using the propeller open water characteristic based on the propeller thrust measured in OTT and CMT. Figure 10 shows the obtained wake fraction as the function of $\beta _{\rm P}$. As shown in Fig. 10, the wake characteristic is asymmetry with respect to the horizontal axis $\beta _{\rm P}$. The fitting line is also plotted using Eq. 16 with $C_{2}=1.6$ at $\beta _{\rm P}>0$ and $C_{2}=1.1$ at $\beta _{\rm P}<0$. Equation 16 has practically enough accuracy.

Fig. 10

Analysis results of wake fraction in maneuvering motions for KVLCC2 model

4.4 $\gamma _{\rm R}$ and $\ell _{\rm R}'$

The $\gamma _{\rm R}$ and $\ell _{\rm R}'$ are determined from the measured results of $\delta _{FN0}$ and $dF_N'/d\delta$. Basic formulas are derived for analysis of $\gamma _{\rm R}$ and $\ell _{\rm R}'$ here. Non-dimensionalizing Eq. by combining Eqs. 20 and 21, the following formula is obtained:

$$\begin{aligned} F_N' = \frac{A_{\rm R}}{L_{pp}d} (u'^2_{\rm R}+v'^2_{\rm R}) f_{\alpha }\,\sin \left( \delta -v'_{\rm R}/u'_{\rm R}\right) \end{aligned}$$

(31)

Differentiating Eq. 31 by $\delta$ is obtained as

$$\begin{aligned} \frac{dF_N'}{d\delta } = \frac{A_{\rm R}}{L_{pp}d} (u'^2_{\rm R}+v'^2_{\rm R}) f_{\alpha }\,\cos \left( \delta -v'_{\rm R}/u'_{\rm R}\right) \end{aligned}$$

(32)

Then, Eq. 32 is rewritten using a relation of $\delta _{FN0}=v_{\rm R}'/u_{\rm R}'$ as

$$\begin{aligned} \left. \frac{dF_N'}{d\delta }\right| _{\delta =\delta _{FN0}} = \frac{A_{\rm R}}{L_{pp}d} u_{\rm R}'^2 (1+\delta _{FN0}^2) f_{\alpha } \end{aligned}$$

(33)

From Eq. 33, the following formula is obtained:

$$\begin{aligned} u_{\rm R}' = \sqrt{\left. \frac{dF_N'}{d\delta }\right| _{\delta =\delta _{FN0}} \frac{L_{pp}d}{A_{\rm R}}\frac{1}{f_{\alpha } (1+\delta _{FN0}^2)}} \end{aligned}$$

(34)

The $u_{\rm R}'$ can be calculated by Eq. 34 since $\delta _{FN0}$ and $dF_N'/d\delta$ at $\delta =\delta _{FN0}$ are experimentally given.

The $v_{\rm R}'$ can be calculated using a relation of $v_{\rm R}'=u_{\rm R}'\delta _{FN0}$. On the other hand, $v_{\rm R}'$ is expressed from Eq. 23 as

$$\begin{aligned} v_{\rm R}' = \gamma _{\rm R} (\beta -\ell _{R}'r') \end{aligned}$$

(35)

The $\gamma _{\rm R}$ is determined based on the $v_{\rm R}'$ calculated in oblique towing condition as an inclination of the fitting line. After that, $\ell _{\rm R}'$ is determined in the same manner.

Figure 11 shows the analysis result of rudder inflow velocity $v_{\rm R}'$. The $v_{\rm R}'$ characteristic is obviously different in plus and minus of $\beta _{\rm R}$. From the figure, $\gamma _{\rm R}=0.395$ at $\beta _{\rm R}<0$ and $\gamma _{\rm R}=0.640$ at $\beta _{\rm R}>0$ were obtained.

Fig. 11

Analysis result of rudder inflow velocity $v_{\rm R}'$ for KVLCC2 model

4.5 $\kappa$ and $\varepsilon$

The $\varepsilon$ and $\kappa$ can be determined from the rudder force test results in straight moving under various propeller loads. Substituting $v_{\rm R}'=0$ into Eq. 32, the following formula is obtained:

$$\begin{aligned} \left. \frac{dF_N'}{d\delta }\right| _{\delta =0} = \frac{A_{\rm R}}{L_{pp}d} \ u'^2_{\rm R} \ f_{\alpha } \end{aligned}$$

(36)

The $u_{\rm R}'^2$ can be obtained from Eq. 36 since $dF_N'/d\delta |_{\delta =0}$ and $f_{\alpha }$ are known. On the other hand, $u_{\rm R}'^2$ is expressed from Eq. 25 as

$$\begin{aligned} u_{\rm R}'^2&= \varepsilon ^2 \,(1-w_{P})^2 \eta \left\{ 1+\kappa \left( \sqrt{1+\frac{8K_T}{\pi J_{\rm P}^2}}-1 \right) \right\} ^2 +(1-\eta ) \end{aligned}$$

(37)

The result of $u_{\rm R}'^2$ calculated using Eq. 37 has to coincide with the result of $u_{\rm R}'^2$ obtained using Eq. 36. The $\varepsilon$ and $\kappa$ are determined so as to minimize the difference between the two $u_{\rm R}'^2$. Then, the iterative procedure is needed to obtain $\varepsilon$ and $\kappa$.

Figure 12 shows $F_N'$ versus $\delta$ measured in the test and the fitting result using Eq. 37. As a result of the analysis, $\varepsilon =1.09$ and $\kappa =0.50$ were obtained. The fitting accuracy is sufficient in view of practical purposes, although some discrepancy between fitting line and experiments is observed due to existing of small helm angle in the experiments.

Fig. 12

Analysis results of rudder normal force in different propeller load conditions for KVLCC2 model

5 Maneuvering simulations

5.1 Details of simulations

Simulations are made for turning with $\delta =\pm 35^{\circ }$, and 10/10 and 20/20 zig-zag maneuvers. Table 3 shows the hydrodynamic force coefficients used in the simulations. Other parameters and treatments for the simulations are as follows:

• Hull resistance was calculated by a 3-dimensional extrapolation method based on Schoenherr’s frictional resistance coefficient formula.

• Parameters of propeller thrust open water characteristic were as follows: $(k_{0}, k_{1}, k_{2})=(0.2931, -0.2753, -0.1385)$.

• Effective wake in straight moving $w_{\rm P0}$ was assumed to be 0.40 for L7-model and 0.35 for fullscale.

• Added mass coefficients ($m_x'$, $m_y'$, $J_z'$) listed in Table 3 were estimated by Motora’s empirical charts [16–18].

• Rudder lift gradient coefficient $f_\alpha$ was estimated using Fujii’s formula expressed as [13]:

  $$\begin{aligned} f_{\alpha }&= \frac{6.13\Lambda }{\Lambda +2.25} \end{aligned}$$

  (38)

  This formula can be regarded as a modified version of Prandtl’s formula based on the lifting line theory. Here, $\Lambda$ is aspect ratio of a rudder including the horn part. Hirano et al. [15] proposed a practical treatment when applying Eq. 38 to Mariner rudder: a whole rudder with the horn part is used for determining $f_\alpha$ and a movable part area is used as a representative rudder area. Values of $f_\alpha$ and $A_{\rm R}$ were determined by this treatment.

• In the simulations, we set that an initial approach speed $U_0$ is 15.5 kn in fullscale, the rudder steering rate is $1.76\,^{\circ }/s$ in fullscale, and the radius of yaw gyration is 0.25$L_{pp}$. Propeller revolution is assumed to be kept the revolution at $U_0$ constant without torque rich.

Table 3 Hydrodynamic force coefficients used in the simulations

5.2 Comparison with free-running model test results

First, maneuvering simulations were made for L7-model of KVLCC2. Figure 13 shows comparison of calculation and experiment in turning trajectories with $\delta =\pm 35^{\circ }$. Table 4 shows comparison of turning indices such as $A_D'$ and $D_T'$. The turning simulation results roughly agree with the free-running model test results, although the turning indices calculated are about 5.8 % larger in maximum than the test results.

Fig. 13

Comparison of ship trajectories (L7-model, $\delta =\pm 35^{\circ }$)

Table 4 Comparison of turning indices

Figure 14 shows comparisons of calculation and experiment for time histories of rudder angle ($\delta$) and heading angle ($\psi$) in zig-zag maneuvers. The simulation results roughly agree with the free-running model test results, and the present method can capture the overall tendency of the zig-zag maneuvers. Table 5 shows comparison of overshoot angles (OSAs) in the zig-zag maneuvers. Maximum differences of OSA between calculation and experiment are about $3^{\circ }$ for 1st OSA and about $6^{\circ }$ for 2nd OSA of 10/10 zig-zag maneuver. It is difficult to predict OSA in the accuracy of a few degrees. All the OSAs calculated by the present method are smaller than the test results. There is a possibility that hull damping force used in the simulations is a bit too larger than actual one.

Fig. 14

Comparison of time histories of rudder angle and heading angle in zig-zag maneuvers (L7-model)

Table 5 Comparison of overshoot angles of zig-zag maneuvers (L7-model)

5.3 Simulation results in fullscale

Next, maneuvering simulations were made for fullscale ship of KVLCC2 tanker. In the simulations, the same hydrodynamic force coefficients used in the simulations of the ship model were used except the effective wake in straight moving $w_{\rm P0}$ and the frictional resistance coefficient calculated by Schoenherr’s formula. Figure 15 shows simulation results of turning trajectories with $\delta =\pm 35^{\circ }$ for L7-model and fullscale, and Table 6 the turning indices. Fullscale turning trajectories becomes look like expanding outside as shown in Fig. 15, and $A_D'$ and $D_T'$ in fullscale are about 10 % larger comparing with L7-model. This means that turning performance becomes worse in fullscale.

Fig. 15

Simulation results of turning trajectories for L7-model and fullscale ($\delta =\pm 35^{\circ }$)

Table 6 Simulation results of turning indices

Figure 16 shows time histories of $\delta$ and $\psi$ for L7-model and fullscale in zig-zag maneuvers. In Fig. 16, the horizontal axis means non-dimensionalized time defined as $t'\equiv tU_0/L_{pp}$. Table 7 shows overshoot angles for L7-model and fullscale. In fullscale, overshoot angle becomes large, timing of steering for zig-zag maneuver is slow, and yaw response against steering becomes worse. Thus, the course stability becomes worse in fullscale.

Fig. 16

Simulation results of time histories of rudder angle and heading angle in zig-zag maneuvers for L7-model and fullscale

Table 7 Simulation results of overshoot angles of zig-zag maneuvers

To know the reason for a change for the worse of not only turning performance but also course stability, time histories of the rudder normal force during turning with $\delta =35^{\circ }$ were compared in fullscale and model. Figure 17 shows the time histories of non-dimensionalized rudder normal force ($F_N'$) divided by $(1/2)\rho L_{pp} dU_0^2$. Peak value of $F_N'$ in fullscale is about 20% smaller than that of the ship model. This is a main cause for bad maneuverability in fullscale. At the steady turning stage, $F_N'$ in fullscale is about 40 % smaller than that of the model and the difference becomes large. Propeller load is relatively smaller in fullscale so that the rudder inflow velocity also becomes small. As a result, the rudder normal force becomes small in fullscale.

Fig. 17

Time histories of rudder normal force during turning for L7-model and fullscale ($\delta =35^{\circ }$)

6 Concluding remarks

In this article, a prototype of maneuvering prediction method for ships, called ”MMG standard method”, was introduced. The MMG standard method was composed of 4 elements: the maneuvering simulation model, the procedure of the required captive model tests to capture the hydrodynamic force characteristics, the analysis method for determining the hydrodynamic force coefficients for maneuvering simulations, and the prediction method for maneuvering motions in fullscale. KVLCC2 tanker was selected as a sample ship and the captive mode test results were presented with a process of the data analysis. Using the hydrodynamic force coefficients obtained, maneuvering simulations were carried out for KVLCC2 model [8] and the fullscale ship for validation of the method. It was confirmed that the present method can roughly capture the maneuvering motions and is useful for the maneuvering predictions in fullscale.

Collecting the hydrodynamic force coefficients determined by the MMG standard method in various ship kinds is the next work to make a useful data base of the force coefficients for ship maneuvering predictions.

Appendix A: Derivation of a formula representing inflow velocity component to rudder

Consider the longitudinal velocity component to rudder $u_{\rm R}$ according to Ref. [9]. The $u_{\rm R}$ is assumed to be expressed as

$$\begin{aligned} u_{\rm R}&= \sqrt{ \frac{A_{{\text {RP}}}}{A_{\rm R}}u_{\text {RP}}^2 +\frac{A_{\text {R0}}}{A_{\rm R}}u_{\text {R0}}^2 } \nonumber \\&= \sqrt{\eta u_{\text {RP}}^2 + (1-\eta )u_{\text {R0}}^2 }, \end{aligned}$$

(39)

where $A_{\rm RP}$ is the rudder area where propeller slip stream hits, $A_{\rm R0}$ the rudder area where it does not hit, and $A_{\rm R}$ the total rudder area (namely, $A_{\rm R}=A_{\rm R0}+A_{\rm RP}$). Equation 39 is obtained to take a weighted average of 2 velocity components, $u_{\rm RP}$ at $A_{\rm RP}$ and $u_{\rm R0}$ at $A_{\rm R0}$, as shown in Fig. 18. Here, $\eta$ is expressed as

$$\begin{aligned} \eta&= \frac{A_{\text {RP}}}{A_{\rm R}}\simeq \frac{D_{\rm P}}{H_{\rm R}} \end{aligned}$$

(40)

The $\eta$ can be calculated taking a ratio between propeller diameter $D_{\rm P}$ and rudder span length $H_{\rm R}$.

Fig. 18

A diagram of inflow velocity to rudder behind the propeller

The $u_{\rm R0}$ is expressed by introducing $w_{\rm R}$ which is wake coefficient at $A_{\rm R0}$ as

$$\begin{aligned} u_{\rm R0}&= (1-w_{\rm R})u \end{aligned}$$

(41)

Also, $u_{\rm RP}$ is assumed to be expressed as

$$\begin{aligned} u_{\rm RP}&= u_{\rm R0}+k_x \Delta u \end{aligned}$$

(42)

Here, $k_x \Delta u$ means the velocity increase due to influence of propeller slip stream, where $\Delta u$ is the theoretical velocity increase described later and $k_x$ the correction factor, and is expressed as $\Delta u=u_{\infty }-u_{\rm P}$ where $u_{\infty }$ is the velocity at infinite rear position, and $u_{\rm P}$ the propeller inflow velocity which is expressed as $u_{\rm P}=(1-w_{\rm P})u$. There exists a relation between $u_{\infty }$ and $u_{\rm P}$ from Bernoulli’s theorem as

$$\begin{aligned}&\Delta p+\frac{\rho }{2}u_{\rm P}^2=\frac{\rho }{2}u_{\infty }^2, \end{aligned}$$

(43)

where $\Delta p$ denotes a pressure difference between fore and aft at propeller disc. $T$ is expressed using $\Delta p$:

$$\begin{aligned} T&= \Delta p\, \pi \left( \frac{D_{\rm P}}{2}\right) ^2 \end{aligned}$$

(44)

In addition, taking expression of Eq. 9, $u_{\infty }$ is written as

$$\begin{aligned} u_{\infty }&= u_{\rm P}\sqrt{ 1+\frac{8K_T}{\pi J_{\rm P}^2}} \end{aligned}$$

(45)

Substituting Eqs. 41, 42, and 45 to Eq. 39 for eliminating $\Delta u$ and $u_{\infty }$, the following formula is obtained as

$$\begin{aligned} u_{\rm R}&= \varepsilon \, u_{\rm P} \sqrt{ \eta \left\{ 1+\kappa \left( \sqrt{1+\frac{8K_T}{\pi J_{\rm P}^2}}-1 \right) \right\} ^2 +(1-\eta ) }, \end{aligned}$$

(46)

where $\varepsilon$ is defined by $\varepsilon =(1-w_{\rm R})/(1-w_{\rm P})$, and $\kappa$ is a constant defined by $k_x/\varepsilon$.