1 Introduction

The carbonation of concrete is caused by the CO2 in atmosphere, around 380 ppm in concentration [1], its diffusion into pores and the subsequent reactions with the cement hydrates [2]. All structural concretes in atmosphere are exposed to CO2 actions, so the carbonation is the background for other durability processes [3]. The combined action of CO2 and chlorides is rather frequent as structural concretes are exposed to aerosol chlorides or de-icing salts. The aerosol chlorides, in form of chloride-contained liquid droplets, originate from sea water or in-land salt lakes, depositing on concrete surface while carbonation occurs simultaneously [4]. The action of de-icing salts refers to the intermittent, or seasonal, application of chloride-contained salts on concrete structures while the carbonation develops all along [5]. Recently, some laboratory studies highlighted the consequence of this action through accelerated tests using alternating schemes of carbonation-chloride ingress and found the chlorides transport further into concrete [6,7,8,9].

This combined action has been investigated extensively in the literature [9,10,11,12]. From the state-of-art knowledge, the carbonation impacts on chloride ingress through the change of concrete microstructure [13,14,15], pore chemistry [16], pore moisture state [17], and chloride sorption properties [17, 18]. For concrete microstructure, the precipitation of calcite (CaCO3) in pores from carbonation decreases the porosity [13, 14]. However, the change of related transport properties presents complex patterns: Page et al. [13] observed higher oxygen and chloride diffusivity for carbonated cement pastes; Jaafar [14] obtained decreased electrical conductivity but increased gas permeability, which is explained through the change of pore percolation by carbonation [15, 20]. For the chloride sorption, the carbonation is believed to destroy the chloride sorption capacity by consuming the adsorbent hydrates, calcium silicate hydrates (CSH) and Friedel’s salt (AFm) [18], releasing bound chlorides into pores to promote the chloride ingress [19]. Cement pastes incorporating different binders were observed to lose completely the chloride sorption capacity after total carbonation [18]. After carbonation, the pore saturation of concrete surface was observed to increase from 0.2 to 0.5 [21], and the ion strength was observed to decreased substantially, in addition to the drop of pH from 13.0 or higher to around 9.0 [22].

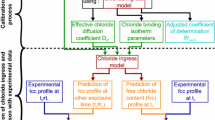
Despite the available knowledge, the quantification of the impact of carbonation on chloride diffusivity, key parameter for engineering use, is far from enough, and the different mechanisms of carbonation impact on chloride diffusivity have never been quantified systematically. Aiming at this lack, the study conceives a set of chloride ingress tests on carbonated and non-carbonated concrete specimens, and quantifies the chloride diffusivity in carbonated concretes from both experimental and theoretical aspects. Accordingly, this paper is organized as follows: the experiments are presented in Sect. 2 with analysis on the chloride ingress data; the main influential factors are investigated theoretically for the impact of carbonation on chloride diffusivity in Sect. 3; the results are applied to a design case of composite slab and the durability requirements are quantified considering the surface carbonation in Sect. 4; the concluding remarks are given in the end.

2 Experiments

2.1 Materials and experiments

Concrete specimens were prepared with two water-to-binder (w/b) ratios, 0.50 and 0.60, and two binders, OPC and OPC-FA-SG (noted as “SZC”), cf. Table 1. The OPC cement used is of Type PO42.5 according to Chinese classification, corresponding to CEM-II/A-M type [23]. Relatively large water to binder ratios, 0.50 and 0.60, were adopted to obtain measurable carbonation depth within reasonable experimental duration. The raw materials were mixed and cubic specimens of 100 mm were made. The specimens were cured to 28d/90d for the tests of compressive strength, gravimetry porosity, accelerated carbonation and chloride immersion. The concrete proportioning is given in Table 1.

Table 1 Proportioning and properties of concretes
Full size table

Twelve cube specimens were prepared for each concrete and moisture-cured (RH > 95%) at 20 °C, three specimens were taken out at 28d to measure the compressive strength, and the other specimens were moisture-cured to 90d. Six specimens of each concrete were subject to accelerated carbonation with RH = 65% and CO2 concentration of 20% during 90d [24]; the other three specimens were kept at RH = 65% without carbonation.

After accelerated carbonation, three carbonated specimens were split and the carbonation depth was determined by spraying with 2% phenolphthalein solution. Afterwards, one carbonated and one non-carbonated specimens were subject to porosity measurement through gravimetry method. Meanwhile, the remaining two carbonated and two non-carbonated specimens of each concrete were immersed into 165 g/L NaCl solution for 35d [25], then powder samples were ground from the specimen surface to different depths, the chloride content was measured for the acid-solvable and water-solvable chlorides following [26]. Also from the powder samples, the apparent pH values were measured through the immersion method [27]. Table 2 recapitulates the treatment procedure of concrete specimens for different tests.

Table 2 Treatment and test methods of concrete specimens for different tests
Full size table

2.2 Chloride ingress into carbonated concretes

Table 1 presents the compressive strength, the gravimetry porosity before/after carbonation, and the carbonation depth. The concretes achieve strength grade of C30-C35 and the porosity ranges between 11.2% and 13.3%. The carbonated depth was measured on the split surfaces of three cube specimens at 30 points of each surface, with average and standard deviation given in Table 1. The carbonation depths correlate strongly with w/b ratios. After carbonation, slices were taken within the carbonation depth, and the measured porosity decreases systematically by about 1%.

After the 35d immersion in NaCl solution, the ground concrete powder was collected for every 3 mm thickness from the surface to the depth of 30 mm. For each grinding depth, the obtained samples were divided into three portions, about 10 g each portion, and subject to acid-soluble chlorides (solid liquid ratio 1:10), water-soluble chlorides (solid liquid ratio 1:20) and apparent pH value measurements (solid liquid ratio 1:20). Note that such choice of solid to liquid ratio agrees with the international standards [28, 29] and practice [27]. For each material, two cubes were ground whilst the pH value was just measured on one cube. Conventionally, the acid-soluble chlorides are regarded as total chlorides in concrete and the water-soluble values as the free chlorides in pore solution. The difference between the acid/water soluble chlorides and total/free chlorides will be elaborated later while the two sets of chloride values are regarded as such in the following. Figure 1 illustrates the total chlorides, giving also the total chloride inflow during 35d immersion, Fig. 2 presents the free chlorides and the OH content, and the carbonation depth is also noted on both figures.

Fig. 1
figure 1

Total chloride content of concrete specimens from acid-soluble measurement

Full size image
Fig. 2
figure 2

Water-soluble chlorides and OH content of concrete specimens

Full size image

From Fig. 1, the impact of carbonation on the chloride ingress follows rather complex patterns: the total chlorides in carbonated zones seem to be higher than the non-carbonated case for the first measurement within 3 mm depth, then the two values are comparable in the remaining carbonation zone; beyond the carbonation zone, the profile is higher, expect for SZC-50 cases, for carbonated cases. However, the total chloride inflow quantity during 35d immersion is a more direct indicator: again except SZC-50, the chloride inflow is clearly higher in carbonated specimens than NC specimens. In other terms, except SZC-50, the carbonation, though to different depths, increases the chloride ingress globally. The underlying reason of SZC-50 will be discussed later.

From Fig. 2, the free chloride concentration is generally higher in carbonated zones than NC cases, due to the low chloride sorption capacity in the carbonation zone. For OPC-60 and SZC-60 specimens, the free chloride profiles are clearly higher than the NC specimens. On the same figure are noted the measured OH content. Due to the particular measurement procedure of OH, i.e. immersing the powder samples of 10 g into 200 ml de-ionized water to equilibrium and measuring the OH concentration from 20 ml extracted solution, the OH content, in mass to mass ratio, cannot be taken directly as the true value in pore solution because by such solid to liquid ratio more CH is to be dissolved into aqueous state compared to the intact pore solution [30]. Thus, the OH values bear only comparative sense. First observation is that the OH content decreases from the internal part to the surface for both NC/C cases. This is due to the OH transport towards the NaCl solution during the 35d immersion. Second, the OH content is at a very low level, if not zero, in carbonation zone, and gradually rises to normal level after the carbonation depth. The SZC-50 specimens show no systematic difference between NC/C cases in terms of OH content.

2.3 Chloride sorption analysis

From the total and free chlorides, one important quantity can be determined: the chloride sorptivity. Actually, the total chlorides, the free chlorides can be related through the mass density and the chloride sorptivity,

$$C_{\text{Cl}} = \frac{{M_{\text{Cl}} }}{{\rho_{\text{C}} }}\left( {s_{\text{l}} \phi_{\text{C}} c_{\text{Cl}} + s_{\text{Cl}} } \right)$$
(1)

Here the total chlorides content CCl takes the unit of mass ratio with respect to concrete (−), the term cCl refers to the chloride concentration in pore solution (mol/m3), ϕC is the concrete porosity (−), sl is the liquid (water) volumetric saturation in pores (−), sCl is the chloride sorptivity of concrete (mol/m3 concrete), MCl is the molar mass of chloride (0.0355 kg/mol) and ρC is the concrete mass density (kg/m3). In this study the concrete specimens are totally saturated, thus sl = 1.0. The chloride sorptivity sCl has been extensively studied in the literature, and its value has been found dependent on the aqueous chloride concentration in pore solution [31]. The most used sorption law is a linearized one,

$$s_{\text{Cl}} = \alpha_{\text{Cl}}^{\text{L}} c_{\text{Cl}} + s_{\text{Cl}}^{0}$$
(2)

with \(\alpha_{\text{Cl}}^{\text{L}}\) as the linearized sorption coefficient and \(s_{\text{Cl}}^{ 0}\) the initial sorption coefficient. The first term at the right side of Eq. (2) describes a linear physical sorption of chlorides by concrete matrix, and the second term refers to the chemical sorption of chloride, e.g. by formation of Friedel’s salts [32].

In the literature, the relation between the water soluble and free chlorides has been studied systematically, and such preparation details during the liquid extraction as the stirring time, temperature treatment and the solid to solution ratio are found to play an important role [33,34,35]. Due to lack of calibrated relationship for the concretes in this study, the water soluble chlorides are directly taken as the free chlorides in pore solution in this study. Certainly such treatment will introduce errors, and this inherent uncertainty is taken into account in the following analysis. Moreover, it can be seen from Fig. 2 that the non-carbonated specimens of OPC/SZC-60 show important leaching effect from the OH− ion profile. Since the pH value has influence on the chloride sorption [36], the points with very low OH content, e.g. the 1.5 mm/4.5 mm points, are left out in the sorption analysis. Using these assumptions, the linearized sorption law, in Eqs. (1) and (2), is regressed between the total and water soluble chlorides for NC/C concretes in Fig. 3, with the regressed parameters and sorption coefficients given in Table 3.

Fig. 3
figure 3

Linearized analysis of chloride sorption for non-carbonated and carbonated concretes: OPC (left) and SZC (right)

Full size image
Table 3 Regression of the chloride sorption parameters for OPC/SZC concretes
Full size table

For the non-carbonated specimens, the total and free chlorides observe quite well the linear relationship except for the small value range for free chlorides (< 0.05%). This range can involve the dissolution of the Friedel’s salts, different from the physical sorption of chlorides by solid matrix [37]. As for the linearized sorption coefficient \(\alpha_{\text{Cl}}^{\text{L}}\), no systematic difference is observed for OPC/SZC concretes, and the initial sorption capacity \(s_{\text{Cl}}^{ 0}\) is consistent with the literature values [5]. For the carbonated specimens, the intercept of linear regression is set to zero in Fig. 3, on the basis of assumption that the Friedel’s salts cannot form in the carbonation zone under low pH values. Comparing the sorption coefficient \(\alpha_{\text{Cl}}^{\text{L}}\) before and after carbonation, the OPC specimens lose 60% (OPC-50) to 75% (OPC-50) of sorption capacity by carbonation while the SZC-50/60 specimens lose about 50% of sorption capacity. Thus, a qualitative judgement is that considerable amount of chloride adsorbent, CSH, still remains in the specimens after accelerated carbonation.

3 Impact of carbonation on chloride ingress

3.1 Interpretation of chloride diffusivities

To address the impact of the carbonated depth on the chloride ingress, this paper uses the analytical solution to a diffusion problem in a composite semi-infinite domain: a semi-infinite domain plus a surface layer of thickness LC subject to a constant concentration cS on the surface (x = 0), cf. Figure 4. The chloride concentration c(x,t) refers to the concentration in pore solution, taking the unit mol/m3 or mol/L.

Fig. 4
figure 4

Illustration of composite semi-infinite diffusion problem

Full size image

The above diffusion problem has a surface layer with a constant diffusivity D1, different from the diffusivity D2 in the semi-infinite domain, and the mass conservation of chlorides writes,

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\partial c_{\text{Cl}} }}{\partial t} = D_{1} \frac{{\partial^{2} c_{\text{Cl}} }}{{\partial x^{2} }}} & {0 \le x \le L_{\text{C}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\frac{{\partial c_{\text{Cl}} }}{\partial t} = D_{2} \frac{{\partial^{2} c_{\text{Cl}} }}{{\partial x^{2} }}} & { \, x > L_{\text{C}} } \\ \end{array} } \\ \end{array}$$
(3)

with the initial and boundary conditions as

$$\begin{aligned} &c_{\text{Cl}} \left( {t = 0} \right) = c_{0} , \, c_{\text{Cl}} \left( {x = 0,t > 0} \right) = c_{\text{S}} > c_{0} \hfill \\ \hfill \\ &\left. {c_{\text{Cl}} } \right|_{{x = L_{\text{C}}^{ - } }} = \left. {c_{\text{Cl}} } \right|_{{x = L_{\text{C}}^{ + } }} , \, \left. {D_{1} \frac{{\partial c_{\text{Cl}} }}{\partial x}} \right|_{{x = L_{\text{C}}^{ - } }} = \left. {D_{2} \frac{{\partial c_{\text{Cl}} }}{\partial x}} \right|_{{x = L_{\text{C}}^{ + } }} \hfill \\ \end{aligned}$$
(4)

As the diffusivity D1,2 and the carbonation depth LC are constant, the solution is due to Crank [38] and the normalized chloride profile takes the following form,

$$\bar{c}\left( {x,t} \right) = \sum\limits_{n = 0}^{\infty } {\alpha^{n} \left\{ {{\text{erfc}}\left[ {\frac{{\left( {2n + 1} \right)L + x}}{{2\sqrt {D_{1} t} }}} \right] - \alpha {\text{erfc}}\left[ {\frac{{\left( {2n + 1} \right)L - x}}{{2\sqrt {D_{1} t} }}} \right]} \right\}} \,{\text{for}}\,0 \le x \le L_{\text{C}}$$
(5)
$$\bar{c}\left( {x,t} \right) = \frac{2k}{k + 1}\sum\limits_{n = 0}^{\infty } {\alpha^{n} {\text{erfc}}\left[ {\frac{{\left( {2n + 1} \right)L + kx}}{{2\sqrt {D_{1} t} }}} \right]} \,{\text{for}}\,x > L_{\text{C}}$$
(6)

with

$$\bar{c}\left( {x,t} \right) = \frac{{c_{\text{Cl}} \left( {x,t} \right) - c_{0} }}{{c_{S} - c_{0} }}, \, k = \sqrt {\frac{{D_{1} }}{{D_{2} }}} , \, \alpha { = }\frac{1 - k}{1 + k}$$
(7)

Here the term c0 refers to the initial chloride concentration in the pore solution. Using Eqs. (5–6), the values of chloride diffusivity can be regressed directly from the profiles of free (water soluble) chlorides in Fig. 2. Note that as D1 = D2 and k = 1, the carbonation is actually cancelled and the chloride profile is reduced to the classical solution of Fick’s second law with constant cS at the surface,

$$\bar{c}\left( {x,t} \right) = {\text{erfc}}\left( {\frac{x}{{2\sqrt {D_{2(1)} t} }}} \right)$$
(8)

The regression of chloride diffusivity values, in non-carbonated and carbonated concretes, is performed through two steps: first, the profiles of NC specimens are used to regress the apparent chloride diffusivity D2 using Eq. (8); second, for each carbonated concrete the diffusivity for carbonated concrete D1 is regressed using the obtained diffusivity for NC case as D2, and the measured carbonation depth as LC in Eqs. (3–4). This two-step regression is illustrated in Fig. 5. The obtained values of chloride diffusivity are given in Table 4. Considering the intrinsic dispersion of chloride concentration determined by the grinding method, the fit is regarded as satisfactory.

Fig. 5
figure 5

Regression of apparent chloride diffusivity: non-carbonated specimens (left) and carbonated specimens (right)

Full size image
Table 4 Regressed chloride diffusivity values for carbonated and non-carbonated concretes
Full size table

Note that the chloride diffusivity in Eq. (3) and regressed in Table 4 refers to the apparent chloride diffusivity DappCl, including both the chloride diffusivity in the aqueous pore solution, namely the effective chloride diffusivity DeffCl, and the chloride sorption sCl by the solid matrix of concrete [5],

$$D_{\text{Cl}}^{\text{app}} = \frac{{D_{\text{Cl}}^{\text{eff}} }}{{\phi s_{\text{l}} + \alpha_{\text{Cl}}^{L} }}$$
(9)

where ϕ, sl stand for the porosity and pore saturation, and \(\alpha_{\text{Cl}}^{\text{L}}\) for the linearized chloride soprtivity, cf. Section 2.3. From the regressed \(D_{\text{Cl}}^{\text{app}}\) values, the chloride diffusivity in the carbonated zone is larger than the NC value. Since the chloride ingress test was performed in immersion condition, the pore saturation sl = 1.0. Using this value, the porosity in Table 1 and \(\alpha_{\text{Cl}}^{\text{L}}\) in Table 3, the effective chloride diffusivity is also calculated in Table 4.

3.2 Theoretical model for impact of carbonation

The different values, \(D_{\text{Cl}}^{\text{app}}\) or \(D_{\text{Cl}}^{\text{eff}}\), of a same concrete before and after carbonation reflect the impact of carbonation on chloride diffusivity. The carbonation is believed to change the chloride diffusivity through the following mechanisms: (1) the precipitation of calcite, CaCO3, from the carbonation reactions, between dissolved CO2, and Portlandite (CH) and calcium silicate hydrates (CSH), can fill up the pore space, decrease the porosity and change the pore structure; (2) the change of pore chemistry is to change the ionic environment for chloride transport thus the aqueous diffusivity; (3) the consumption of CSH/AFm by carbonation releases the adsorbed chlorides back to the pore solution, thus changes the apparent chloride diffusivity. In this study, both the effective and apparent chloride diffusivities were regressed for immersion state, i.e. sl = 1.0, so the change of pore saturation from the free water release by carbonation is neglected. Conceptually, Eq. (9) can be rewritten to take into account of these three factors explicitly,

$$D_{\text{Cl,c}}^{\text{app}} = \frac{{D_{\text{Cl}}^{\text{eff}} \left( {\phi_{\text{c}} ,\varPhi } \right)}}{{\phi_{\text{c}} + \alpha_{\text{Cl,c}}^{L} }}{\text{ with }}s_{\text{l}} = 1.0$$
(10)

Here the terms with subscript “c” refer to the quantities after carbonation and Φ signifies the ionic environment after carbonation. We intend to quantify the impact of these three factors in the following. The impact of pore structure change can be expressed through the following form [39],

$$D_{\text{Cl}}^{\text{eff}} \left( {\phi_{\text{c}} ,\varPhi } \right) = \frac{{1 - \lambda_{\text{ca}} v_{\text{ca}} }}{{1 - \lambda_{\text{fa}} v_{\text{fa}} }}v_{\text{paste}} f_{\text{p,c}} \left( {\phi_{\text{c}} } \right)D_{\text{Cl}}^{\text{pore}} \left( \varPhi \right)$$
(11)

in which λca,fa are the coefficients for coarse and fine aggregates, vca,fa are the volumetric ratios of coarse and fine aggregates, fp,c is the pore percolation function after carbonation, ϕc is the concrete porosity after carbonation, and DporeCl the chloride diffusivity in pore solution.

Then, let us focus on the change of the ionic environment Φ and its impact on the chloride diffusivity. After carbonation, the OH− ions are greatly reduced by precipitation reactions and the alkaline ions, K+ and Na+, are also greatly decreased due to the ion sorption mechanisms by CSH with lowered Ca/Si ratio [40]. The chloride diffusion in multi-species ionic aqueous environment writes (Nernst-Planck equation),

$$J_{\text{Cl}} = D_{\text{Cl}}^{0} \left( {\nabla c_{\text{Cl}} + c_{\text{Cl}} \nabla \ln \gamma_{\text{Cl}} + \frac{F}{RT}z_{\text{Cl}} c_{\text{Cl}} \nabla \psi } \right)$$
(12)

where D0Cl refers to the chloride diffusivity in dilute solution, γCl stands for the activity of chloride ions in multi-species environments, ψ signifies the local electrical potential existing in the multi-species pore solution, and F,R,T for the Faraday’s constant (96 485.33 C/mol), ideal gas constant (8.314 J/K/mol) and absolute temperature (K) respectively. While this equation applies to a mass point of aqueous solution containing chlorides, here we apply this expression, at the macroscopic level, across the whole carbonation depth LC in Fig. 4: different ionic environments are given for concrete surface (x = 0) and the carbonation front (x = LC). To put into evidence the respective contribution of ion activity and local electrical potential, Eq. (12) is re-arranged as,

$$J_{\text{Cl}} = D_{\text{Cl}}^{0} \nabla c_{\text{Cl}} f_{\text{Cl}} \left( \varPhi \right){\text{ with }}f_{\text{Cl}} = 1 + \frac{{\Delta \ln \gamma_{\text{Cl}} }}{{\Delta \ln c_{\text{Cl}} }} + \frac{F}{RT}z_{\text{Cl}} \frac{\Delta \psi }{{\Delta \ln c_{\text{Cl}} }}$$
(13)

The literature data are used to represent the ion species and their concentrations for intact pore solution [41] with pH = 13.4. For the carbonated pore solution, the value pH = 9.0 is adopted, and the main ion species are evaluated from the dissolution constants for CO2 (K = 0.94), HCO3− (logK1 = − 7.66) and CO32− (logK2 = − 3.66). The ion concentrations are given in Table 5, together with the diffusivity values from literature [42].

Table 5 Composition of pore solutions and diffusivity of ions
Full size table

From the water soluble chlorides profiles in Fig. 2, the ion environment is set as carbonated pore solution with 3 M NaCl solution at the surface and NC pore solution with 1 M NaCl at the carbonation front. For comparison, the case of NC pore solution with 3 M NaCl at concrete surface and NC pore solution with 1 M NaCl at carbonation front is also analyzed, cf. Table 6. To quantify the contribution of activity of chloride ions, the experimental results of γCl for 1 M and 3 M NaCl solutions in [43] are adopted directly, considering that the ions Na+, Cl− dominate over other species in all cases. For the local electrical potential, the Henderson equation is employed for multi-species analysis [44],

$$\Delta \psi = - \frac{RT}{F}\frac{{\sum\nolimits_{i = 1}^{N} {} z_{i} D_{i} \left( {c_{i,2} - c_{i,1} } \right)}}{{\sum\nolimits_{i = 1}^{N} {z_{i}^{2} D_{i} \left( {c_{i,2} - c_{i,1} } \right)} }}\ln \frac{{\sum\nolimits_{i = 1}^{N} {z_{i}^{2} D_{i} c_{i,2} } }}{{\sum\nolimits_{i = 1}^{N} {z_{i}^{2} D_{i} c_{i,1} } }}$$
(14)
Table 6 Ion activity and local electrical potential analysis for chlorides
Full size table

Table 6 compares the respective contribution of the ion activity and the electrical potential to function fCl in Eq. (13). The lower concentration of Cl− on the carbonation front, 1 M versus 3 M, makes a negative contribution to the diffusivity due to the larger ion activity on the carbonation front against the diffusion. This effect is the same for NC/C cases. For the local electrical potential, both cases have negative potential against the chloride diffusion while the NC case has higher potential value, meaning the carbonation tends to relax this negative potential against the chloride. This potential effect contributes to the increase of effective chloride diffusivity by 11.1%.

The last point goes to the decrease of chloride sorption capacity of concrete solid matrix by carbonation. Conceptually, the carbonation decreases the chloride sorption through two mechanisms: consumption of CSH, the main adsorbent of chlorides, and the carbonation of the Friedel’s salt. Hence, both the physical-bound and chemical-bound chlorides can be released by carbonation. The free chloride and the total chloride in carbonated zone of concrete specimens have been illustrated in Fig. 3 with regressed sorption coefficients given in Table 3. After carbonation, the chloride sorption capacity of OPC is substantially decreased to below 30% of its original capacity while SZC concretes keep about 50% of chlorides sorption capacity, meaning that after accelerated carbonation there remains still a considerable quantity of CSH in both OPC/SZC specimens.

3.3 Summary on contribution from different factors

After this factor analysis of carbonation impact on the chloride diffusivity in saturated case, the experimental results in Table 4 and simulation results in Table 6 are used to quantify the respective contribution of each factor to the alteration of apparent chloride diffusivity by carbonation. On this basis, the relative change of DappCl in Eq. (10) by each factor is calculated and given in Table 7. Globally, the apparent chloride diffusivity increases by 7–83% by carbonation, the sorption change contributes to increase of 9–16%, the pore chemistry change contributes to 11%, and the contribution of pore structure change ranges from − 14 to 52%. Note that the impact of pore structure change is described by ϕc in Eq. (10) and fp,C in Eq. (11), and its impact is quantified from the total change and contributions of other factors.

Table 7 Analysis on the impact of carbonation on chloride diffusivity from different factors
Full size table

The results in Table 7 confirm the impact of pore structure alteration by carbonation on the diffusivity follows complex patterns: the carbonation promotes the pore percolation but decreases the global porosity, the percolation effect dominates over pore filling for OPC-50, OPC-60 and SZC-60 concretes, but the inverse is observed for SZC-50 concrete. However, the magnitude of the pore structure change should be taken with precaution because several strong assumptions were made during the regression and analysis, including the front-like carbonation boundary, the linearized chloride sorption law, and the approximate nature of the pore chemistry analysis as well. Nevertheless, the qualitative observation is clear: carbonation does promote chloride diffusion.

4 Application to design

The results obtained so far bear clear evidence that surface carbonation accelerates the external chloride ingress. This could constitute a real concern for durability of reinforced concrete (RC) as the structure is exposed simultaneously to carbonation and chloride ingress during a long service life. A real design case is retained here to illustrate this impact.

4.1 Design case: composite slabs for 150 years

The chosen case is the composite slabs of an ongoing sea-link project on the south-eastern coast of China. These composite slabs are exposed to marine atmospheric environments and have a design working life of more than 100 years. Figure 6 illustrates a typical cross section of composite slabs and the exposure conditions in different positions. The composite slabs are composed of RC top slabs and steel girders as supports. The RC top slabs and the steel girders are connected by extruding steel studs. Here the focus is on the RC top slabs exposed to the combined actions of surface carbonation by atmospheric CO2 and chloride ingress from the marine air-borne chlorides.

Fig. 6
figure 6

Cross section of composite slabs and different exposure conditions

Full size image

From Fig. 6, different exposure conditions can be identified: (1) the top side of RC slab (Zone 1) collects the air-borne chlorides, it is also exposed heavily to the atmospheric precipitation (1200 mm/year); thus the carbonation will be limited by the high water saturation, and qualitatively the impact of carbonation cannot be very important; (2) the flange of RC slab (Zone 2) is partially sheltered from natural precipitation and favours more the surface carbonation; as the chloride deposition can have the same order as Zone 1, the impact of carbonation can be more important than Zone 1; (3) the bottom side of concrete slab (Zone 3) is exposed to an enclosed space by the RC slab and steel girders, sheltered from precipitation; but this space is normally ventilated during service so the deposition of marine chlorides can still occur through ventilation; and the carbonation can develop faster than Zones 1,2.

4.2 Design for combined action of carbonation and chloride ingress

First the carbonation depth is estimated for the three zones for 150 years. To this purpose, the carbonation model from fib model code 2006 [45] is used to calculate the carbonation depth. The main parameters are retained as follows: design life tSL = 150 years, humidity factor ke = 0.618, curing factor for 24d curing kc = 0.675, carbonation resistance RACC,−10 = 3.1 10−11 (m2/s)/(kg/m3), CO2 concentration 0.00082 kg/m3, weather factor W(tSL) = 0.0738, 0.50, 1.0 for Zone 1, 2, 3 respectively. The carbonation depth is evaluated as 0.93, 6.28 and 12.56 mm for Zone 1, 2, 3 respectively. However, the surface carbonation and the chloride ingress occur simultaneously, different from the foregoing experimental study. To make use of the available results, a limit analysis is performed: the extended Fick’s model in Eqs. (5) and (6) is applied to the three zones with the final carbonation depth. In such a way, the impact of carbonation is certainly overestimated, but directs the design results to the safe (conservative) side. So this limit analysis still makes sense for durability design.

The design equation is described by the corrosion initiation of reinforcement steel by the external chloride ingress,

$$\left. {C_{\text{Cl}} \left( {x = d;t = t_{\text{SL}} } \right)} \right|_{{L_{\text{C}} = {\text{const}} .}} \le C_{\text{CR}}$$
(15)

Here the chloride content is noted in terms of mass ratio with respect to binder, CCl,CR denote the chloride content and the critical chloride concentration to initiate the steel corrosion (g/g), d is the thickness of concrete cover to steel reinforcement (mm). Using the experimental results in Table 3, the chloride diffusivity in carbonated concrete is conservatively retained as two times the value of its NC diffusivity. The concrete cover thickness and required chloride diffusivity for NC concrete are retained as design parameters, and the main parameters are given in Table 8. In order to obtained realistic design values, the time-dependence of chloride diffusivity is considered, the same way as for design for HZM project [46],

$$D_{\text{Cl,app}} \left( {t_{\text{SL}} } \right) = D_{\text{Cl}}^{{ 2 8 {\text{d}}}} \left( {\frac{{t_{0} }}{{t_{a} }}} \right)^{n}$$
(16)
Table 8 Parameters for durability design of composite slabs considering surface carbonation
Full size table

Using the parameters in Table 8, the required concrete cover thickness and the corresponding chloride diffusivity are solved via the extended model, and then the long-term diffusivity is converted to its 28d value via Eq. (16).

Figure 7 gives the needed chloride diffusivity and concrete cover thickness against the corrosion initiation of the reinforcement steel in composite slab for design life of 150 years in Zone 1–3. For comparison, the design values without considering the surface carbonation (NC) are also presented. The carbonation depth is very small in Zone 1 and nearly no difference is found for design with/without surface carbonation.

Fig. 7
figure 7

Concrete cover thickness (left) and additional cover thickness in terms of NC chloride diffusivity for Zone 1–3 (right)

Full size image

From the above results, some important conclusions can be obtained for this design case. The impact of carbonation on the chloride ingress depends strongly on the extent of surface carbonation. This impact can be negligible for concrete surface exposed to heavy natural precipitation because the carbonation is greatly limited in this case. However, the overall risk of steel corrosion is not low due to the high saturation of concrete, and thus the higher ingress rate of air-borne chlorides, which is the case of Zone 1 of the composite slabs. For the partially sheltered structural parts (Zone 2), the carbonation develops faster thus the chloride ingress can be accelerated to a notable extent, such that the durability requirements should be changed: for the same chloride diffusivity, the required concrete cover thickness increases by 3–4 mm for the flange of composite slabs. For the totally sheltered parts (Zone 3), surface carbonation shows the most important impact and the required concrete cover can increase by 6–8 mm, which should be taken into account in durability design.

5 Conclusions

  1. 1.

    From the immersion tests on the carbonated concrete specimens, the chloride profiles, total or water soluble, show different patterns in the carbonated and non-carbonated zones, and the integral chloride flow is a reliable quantity to represent the effect of carbonation. The sorption analysis shows that after carbonation OPC concretes lose 60–75% of the sorption capacity while the SZC concretes keep about 50% of their original sorption capacity. Except for the very small concentration range, the chloride sorption observes well the linear law.

  2. 2.

    An extended diffusion model is used to interpret the chloride diffusion during the immersion tests. The values of chloride diffusivity are regressed respectively for NC and carbonated specimens. The regressed diffusivity shows that carbonation accelerates the chloride diffusion and the apparent diffusivity in the carbonated zone is usually 60% higher. Then the respective contribution of the impact of carbonation is quantified for the sorption change, the pore chemistry change and the pore structure change. The pore structure change by carbonation seems to be the first influential factor for the chloride diffusivity change.

  3. 3.

    The extended model and results are applied to a design case of composite slab exposed to both marine air-borne chlorides and atmospheric CO2. For the design cases, limit analysis is performed for the combined action with the final carbonation depth as constant carbonation layer. The design results show that, for the exposed top side of RC slab the carbonation has little impact on the design results while for the completely sheltered parts the additional thickness of concrete cover due to the impact of carbonation can reach 8 mm.