Abstract
In this review we will focus on a topic of fundamental importance for both astrophysics and plasma physics, namely the occurrence of large-amplitude low-frequency fluctuations of the fields that describe the plasma state. This subject will be treated within the context of the expanding solar wind and the most meaningful advances in this research field will be reported emphasizing the results obtained in the past decade or so. As a matter of fact, Helios inner heliosphere and Ulysses’ high latitude observations, recent multi-spacecrafts measurements in the solar wind (Cluster four satellites) and new numerical approaches to the problem, based on the dynamics of complex systems, brought new important insights which helped to better understand how turbulent fluctuations behave in the solar wind. In particular, numerical simulations within the realm of magnetohydrodynamic (MHD) turbulence theory unraveled what kind of physical mechanisms are at the basis of turbulence generation and energy transfer across the spectral domain of the fluctuations. In other words, the advances reached in these past years in the investigation of solar wind turbulence now offer a rather complete picture of the phenomenological aspect of the problem to be tentatively presented in a rather organic way.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The whole heliosphere is permeated by the solar wind, a supersonic and super-Alfvén plasma flow of solar origin which continuously expands into the heliosphere. This medium offers the best opportunity to study directly collisionless plasma phenomena, mainly at low frequencies where high-amplitude fluctuations have been observed. During its expansion, the solar wind develops a strong turbulent character, which evolves towards a state that resembles the well known hydrodynamic turbulence described by Kolmogorov (1941, (1991). Because of the presence of a strong magnetic field carried by the wind, low-frequency fluctuations in the solar wind are usually described within a magnetohydrodynamic (MHD, hereafter) benchmark (Kraichnan, (1965; Biskamp, (1993; Tu and Marsch, (1995a; Biskamp, (2003; Petrosyan et al., (2010). However, due to some peculiar characteristics, the solar wind turbulence contains some features hardly classified within a general theoretical framework.
Turbulence in the solar heliosphere plays a relevant role in several aspects of plasma behavior in space, such as solar wind generation, high-energy particles acceleration, plasma heating, and cosmic rays propagation. In the 1970s and 80s, impressive advances have been made in the knowledge of turbulent phenomena in the solar wind. However, at that time, spacecraft observations were limited by a small latitudinal excursion around the solar equator and, in practice, only a thin slice above and below the equatorial plane was accessible, i.e., a sort of 2D heliosphere. A rather exhaustive survey of the most important results based on in-situ observations in the ecliptic plane has been provided in an excellent review by Tu and Marsch (1995a) and we invite the reader to refer to that paper. This one, to our knowledge, has been the last large review we find in literature related to turbulence observations in the ecliptic.
In the 1990s, with the launch of the Ulysses spacecraft, investigations have been extended to the high-latitude regions of the heliosphere, allowing us to characterize and study how turbulence evolves in the polar regions. An overview of Ulysses results about polar turbulence can also be found in Horbury and Tsurutani (2001). With this new laboratory, relevant advances have been made. One of the main goals of the present work will be that of reviewing observations and theoretical efforts made to understand the near-equatorial and polar turbulence in order to provide the reader with a rather complete view of the low-frequency turbulence phenomenon in the 3D heliosphere.
New interesting insights in the theory of turbulence derive from the point of view which considers a turbulent flow as a complex system, a sort of benchmark for the theory of dynamical systems. The theory of chaos received the fundamental impulse just through the theory of turbulence developed by Ruelle and Takens (1971) who, criticizing the old theory of Landau and Lifshitz (1971), were able to put the numerical investigation by Lorenz (1963) in a mathematical framework. Gollub and Swinney (1975) set up accurate experiments on rotating fluids confirming the point of view of Ruelle and Takens (1971) who showed that a strange attractor in the phase space of the system is the best model for the birth of turbulence This gave a strong impulse to the investigation of the phenomenology of turbulence from the point of view of dynamical systems (Bohr et al., (1998). For example, the criticism by Landau leading to the investigation of intermittency in fully developed turbulence was worked out through some phenomenological models for the energy cascade (cf. Frisch, (1995). Recently, turbulence in the solar wind has been used as a big wind tunnel to investigate scaling laws of turbulent fluctuations, multifractals models, etc. The review by Tu and Marsch (1995a) contains a brief introduction to this important argument, which was being developed at that time relatively to the solar wind (Burlaga, (1993; Carbone, (1993; Biskamp, (1993, (2003; Burlaga, (1995). The reader can convince himself that, because of the wide range of scales excited, space plasma can be seen as a very big laboratory where fully developed turbulence can be investigated not only per se, rather as far as basic theoretical aspects are concerned.
Turbulence is perhaps the most beautiful unsolved problem of classical physics, the approaches used so far in understanding, describing, and modeling turbulence are very interesting even from a historic point of view, as it clearly appears when reading, for example, the book by Frisch (1995). History of turbulence in interplanetary space is, perhaps, even more interesting since its knowledge proceeds together with the human conquest of space Thus, whenever appropriate, we will also introduce some historical references to show the way particular problems related to turbulence have been faced in time, both theoretically and technologically. Finally, since turbulence is a phenomenon visible everywhere in nature, it will be interesting to compare some experimental and theoretical aspects among different turbulent media in order to assess specific features which might be universal, not limited only to turbulence in space plasmas. In particular, we will compare results obtained in interplanetary space with results obtained from ordinary fluid flows on Earth, and from experiments on magnetic turbulence in laboratory plasmas designed for thermonuclear fusion.
1.1 What does turbulence stand for?
The word turbulent is used in the everyday experience to indicate something which is not regular. In Latin the word turba means something confusing or something which does not follow an ordered plan. A turbulent boy, in all Italian schools, is a young fellow who rebels against ordered schemes. Following the same line, the behavior of a flow which rebels against the deterministic rules of classical dynamics is called turbulent. Even the opposite, namely a laminar motion, derives from the Latin word lámina, which means stream or sheet, and gives the idea of a regular streaming motion. Anyhow, even without the aid of a laboratory experiment and a Latin dictionary, we experience turbulence every day. It is relatively easy to observe turbulence and, in some sense, we generally do not pay much attention to it (apart when, sitting in an airplane, a nice lady asks us to fasten our seat belts during the flight because we are approaching some turbulence!). Turbulence appears everywhere when the velocity of the flow is high enoughFootnote 1, for example, when a flow encounters an obstacle (cf., e.g., Figure 1) in the atmospheric flow, or during the circulation of blood, etc. Even charged fluids (plasma) can become turbulent. For example, laboratory plasmas are often in a turbulent state, as well as natural plasmas like the outer regions of stars. Living near a star, we have a big chance to directly investigate the turbulent motion inside the flow which originates from the Sun, namely the solar wind. This will be the main topic of the present review.
Turbulence that we observe in fluid flows appears as a very complicated state of motion, and at a first sight it looks (apparently!) strongly irregular and chaotic, both in space and time. The only dynamical rule seems to be the impossibility to predict any future state of the motion. However, it is interesting to recognize the fact that, when we take a picture of a turbulent flow at a given time, we see the presence of a lot of different turbulent structures of all sizes which are actively present during the motion. The presence of these structures was well recognized long time ago, as testified by the beautiful pictures of vortices observed and reproduced by the Italian genius Leonardo da Vinci, as reported in the textbook by Frisch (1995). Figure 2 shows, as an example, one picture from Leonardo which can be compared with Figure 3 taken from a typical experiment on a turbulent jet.
Three examples of vortices taken from the pictures by Leonardo da Vinci (cf. Frisch, (1995).
Turbulent features can be recognized even in natural turbulent systems like, for example, the atmosphere of Jupiter (see Figure 4). A different example of turbulence in plasmas is reported in Figure 5 where we show the result of a typical high resolution numerical simulations of 2D MHD turbulence In this case the turbulent field shown is the current density. These basic features of mixing between order and chaos make the investigation of properties of turbulence terribly complicated, although extraordinarily fascinating.
When we look at a flow at two different times, we can observe that the general aspect of the flow has not changed appreciably, say vortices are present all the time but the flow in each single point of the fluid looks different. We recognize that the gross features of the flow are reproducible but details are not predictable. We have to use a statistical approach to turbulence, just as it is done to describe stochastic processes, even if the problem is born within the strange dynamics of a deterministic system!
Turbulence increases the properties of transport in a flow. For example, the urban pollution, without atmospheric turbulence, would not be spread (or eliminated) in a relatively short time. Results from numerical simulations of the concentration of a passive scalar transported by a turbulent flow is shown in Figure 6. On the other hand, in laboratory plasmas inside devices designed to achieve thermo-nuclear controlled fusion, anomalous transport driven by turbulent fluctuations is the main cause for the destruction of magnetic confinement. Actually, we are far from the achievement of controlled thermo-nuclear fusion. Turbulence, then, acquires the strange feature of something to be avoided in some cases, or to be invoked in some other cases.
Turbulence became an experimental science since Osborne Reynolds who, at the end of 19th century, observed and investigated experimentally the transition from laminar to turbulent flow. He noticed that the flow inside a pipe becomes turbulent every time a single parameter, a combination of the viscosity coefficient η, a characteristic velocity U, and length L, would increase. This parameter Re = ULρ/η (ρ is the mass density of the fluid) is now called the Reynolds number. At lower Re, say Re ≤ 2300, the flow is regular (that is the motion is laminar), but when Re increases beyond a certain threshold of the order of Re ≃ 4000, the flow becomes turbulent. As Re increases, the transition from a laminar to a turbulent state occurs over a range of values of Re with different characteristics and depending on the details of the experiment. In the limit Re → ∞ the turbulence is said to be in a fully developed turbulent state. The original pictures by Reynolds are shown in Figure 7.
Concentration field c(x, y), at a given time, on the plane (x, y). The field has been obtained by a numerical simulation at resolution 2048 × 2048. The concentration is treated as a passive scalar, transported by a turbulent field. Low concentrations are reported in blue while high concentrations are reported in yellow (courtesy by A. Noullez).
The original pictures by Reynolds which show the transition to a turbulent state of a flow in a pipe, as the Reynolds number increases from top to bottom (see the website Reynolds, (1883).
1.2 Dynamics vs. statistics
In Figure 8 we report a typical sample of turbulence as observed in a fluid flow in the Earth’s atmosphere. Time evolution of both the longitudinal velocity component and the temperature is shown. Measurements in the solar wind show the same typical behavior. A typical sample of turbulence as measured by Helios 2 spacecraft is shown in Figure 9. A further sample of turbulence, namely the radial component of the magnetic field measured at the external wall of an experiment in a plasma device realized for thermonuclear fusion, is shown in Figure 10.
As it is well documented in these figures, the main feature of fully developed turbulence is the chaotic character of the time behavior. Said differently, this means that the behavior of the flow is unpredictable. While the details of fully developed turbulent motions are extremely sensitive to triggering disturbances, average properties are not. If this was not the case, there would be little significance in the averaging process. Predictability in turbulence can be recast at a statistical level. In other words, when we look at two different samples of turbulence, even collected within the same medium, we can see that details look very different. What is actually common is a generic stochastic behavior. This means that the global statistical behavior does not change going from one sample to the other. The idea that fully developed turbulent flows are extremely sensitive to small perturbations but have statistical properties that are insensitive to perturbations is of central importance throughout this review. Fluctuations of a certain stochastic variable ψ are defined here as the difference from the average value δψ = ψ−ψ, where brackets mean some averaging process. Actually, the method of taking averages in a turbulent flow requires some care. We would like to recall that there are, at least, three different kinds of averaging procedures that may be used to obtain statistically-averaged properties of turbulence The space averaging is limited to flows that are statistically homogeneous or, at least, approximately homogeneous over scales larger than those of fluctuations. The ensemble averages are the most versatile, where average is taken over an ensemble of turbulent flows prepared under nearly identical external conditions. Of course, these flows are not completely identical because of the large fluctuations present in turbulence Each member of the ensemble is called a realization. The third kind of averaging procedure is the time average, which is useful only if the turbulence is statistically stationary over time scales much larger than the time scale of fluctuations. In practice, because of the convenience offered by locating a probe at a fixed point in space and integrating in time, experimental results are usually obtained as time averages. The ergodic theorem (Halmos, (1956) assures that time averages coincide with ensemble averages under some standard conditions (see Appendix B).
Turbulence as measured in the atmospheric boundary layer. Time evolution of the longitudinal velocity and temperature are shown in the upper and lower panels, respectively. The turbulent samples have been collected above a grass-covered forest clearing at 5 m above the ground surface and at a sampling rate of 56 Hz (Katul et al., (1997).
A different property of turbulence is that all dynamically interesting scales are excited, that is, energy is spread over all scales. This can be seen in Figure 11 where we show the magnetic field intensity within a typical solar wind stream (see top panel). In the middle and bottom panels we show fluctuations at two different detailed scales. A kind of self-similarity (say a similarity at all scales) is observed.
Since fully developed turbulence involves a hierarchy of scales, a large number of interacting degrees of freedom are involved. Then, there should be an asymptotic statistical state of turbulence that is independent on the details of the flow. Hopefully, this asymptotic state depends, perhaps in a critical way, only on simple statistical properties like energy spectra, as much as in statistical mechanics equilibrium where the statistical state is determined by the energy spectrum (Huang, (1987). Of course, we cannot expect that the statistical state would determine the details of individual realizations, because realizations need not to be given the same weight in different ensembles with the same low-order statistical properties.
It should be emphasized that there are no firm mathematical arguments for the existence of an asymptotic statistical state. As we have just seen, reproducible statistical results are obtained from observations, that is, it is suggested experimentally and from physical plausibility. Apart from physical plausibility, it is embarrassing that such an important feature of fully developed turbulence, as the existence of a statistical stability, should remain unsolved. However, such is the complex nature of turbulence
2 Equations and Phenomenology
In this section, we present the basic equations that are used to describe charged fluid flows, and the basic phenomenology of low-frequency turbulence Readers interested in examining closely this subject can refer to the very wide literature on the subject of turbulence in fluid flows, as for example the recent books by, e.g., Pope (2000); McComb (1990); Frisch (1995) or many others, and the less known literature on MHD flows (Biskamp, (1993; Boyd and Sanderson, (2003; Biskamp, (2003). In order to describe a plasma as a continuous medium it will be assumed collisional and, as a consequence, all quantities will be functions of space r and time t. Apart for the required quasi-neutrality, the basic assumption of MHD is that fields fluctuate on the same time and length scale as the plasma variables, say ωτH ≃ 1 and kLH ≃ 1 (k and ω are, respectively, the wave number and the frequency of the fields, while τH and LH are the hydrodynamic time and length scale, respectively). Since the plasma is treated as a single fluid, we have to take the slow rates of ions. A simple analysis shows also that the electrostatic force and the displacement current can be neglected in the non-relativistic approximation. Then, MHD equations can be derived as shown in the following sections.
2.1 The Navier-Stokes equation and the Reynolds number
Equations which describe the dynamics of real incompressible fluid flows have been introduced by Claude-Louis Navier in 1823 and improved by George G. Stokes. They are nothing but the momentum equation based on Newton’s second law, which relates the acceleration of a fluid particleFootnote 2 to the resulting volume and body forces acting on it. These equations have been introduced by Leonhard Euler, however, the main contribution by Navier was to add a friction forcing term due to the interactions between fluid layers which move with different speed. This term results to be proportional to the viscosity coefficients η and ξ and to the variation of speed. By defining the velocity field u(r, t) the kinetic pressure p and the density ρ, the equations describing a fluid flow are the continuity equation to describe the conservation of mass
the equation for the conservation of momentum
and an equation for the conservation of energy
where s is the entropy per mass unit, T is the temperature, and χ is the coefficient of thermoconduction. An equation of state closes the system of fluid equations.
The above equations considerably simplify if we consider the incompressible fluid, where ρ = const. so that we obtain the Navier-Stokes (NS) equation
where the coefficient ν = η/ρ is the kinematic viscosity. The incompressibility of the flow translates in a condition on the velocity field, namely the field is divergence-free, i.e., ∇·u = 0. This condition eliminates all high-frequency sound waves and is called the incompressible limit. The non-linear term in equations represents the convective (or substantial) derivative. Of course, we can add on the right hand side of this equation all external forces, which eventually act on the fluid parcel.
We use the velocity scale U and the length scale L to define dimensionless independent variables, namely r = r’L (from which ∇ = ∇’/L) and t = t’(L/U), and dependent variables u = u’U andp = p’U2ρ. Then, using these variables in Equation (4), we obtain
The Reynolds number Re = UL/ν is evidently the only parameter of the fluid flow. This defines a Reynolds number similarity for fluid flows, namely fluids with the same value of the Reynolds number behaves in the same way. Looking at Equation (5) it can be realized that the Reynolds number represents a measure of the relative strength between the non-linear convective term and the viscous term in Equation (4). The higher Re, the more important the non-linear term is in the dynamics of the flow. Turbulence is a genuine result of the non-linear dynamics of fluid flows.
2.2 The coupling between a charged fluid and the magnetic field
Magnetic fields are ubiquitous in the Universe and are dynamically important. At high frequencies, kinetic effects are dominant, but at frequencies lower than the ion cyclotron frequency, the evolution of plasma can be modeled using the MHD approximation. Furthermore, dissipative phenomena can be neglected at large scales although their effects will be felt because of non-locality of non-linear interactions. In the presence of a magnetic field, the Lorentz force j × B, where j is the electric current density, must be added to the fluid equations, namely
and the Joule heat must be added to the equation for energy
where σ is the conductivity of the medium, and we introduced the viscous stress tensor
An equation for the magnetic field stems from the Maxwell equations in which the displacement current is neglected under the assumption that the velocity of the fluid under consideration is much smaller than the speed of light. Then, using
and the Ohm’s law for a conductor in motion with a speed u in a magnetic field
we obtain the induction equation which describes the time evolution of the magnetic field
together with the constraint ∇ · B = 0 (no magnetic monopoles in the classical case).
In the incompressible case, where ∇ · u = 0, MHD equations can be reduced to
and
Here Ptot is the total kinetic Pk = nkT plus magnetic pressure Pm = B2/8π, divided by the constant mass density ρ. Moreover, we introduced the velocity variables b = B/√πρ and the magnetic diffusivity η.
Similar to the usual Reynolds number, a magnetic Reynolds number Rm can be defined, namely
where cA = B0/√4πρ is the Alfvén speed related to the large-scale B0 magnetic field B0. This number in most circumstances in astrophysics is very large, but the ratio of the two Reynolds numbers or, in other words, the magnetic Prandtl number Pm = ν/η can differ widely. In absence of dissipative terms, for each volume V MHD equations conserve the total energy E(t)
the cross-helicity Hc(t), which represents a measure of the degree of correlations between velocity and magnetic fields
and the magnetic helicity H(t), which represents a measure of the degree of linkage among magnetic flux tubes
where b = ∇ × a.
The change of variable due to Elsäasser (1950), say z± = u ± b’, where we explicitly use the background uniform magnetic field b’ = b + cA (at variance with the bulk velocity, the largest scale magnetic field cannot be eliminated through a Galilean transformation), leads to the more symmetrical form of the MHD equations in the incompressible case
where 2ν± = ν±η are the dissipative coefficients, and F± are eventual external forcing terms. The relations ∇ · z± = 0 complete the set of equations. On linearizing Equation (15) and neglecting both the viscous and the external forcing terms, we have
which shows that z−(x − cAt) describes Alfvénic fluctuations propagating in the direction of B0, and z+(x + cAt) describes Alfvénic fluctuations propagating opposite to B0. Note that MHD Equations (15) have the same structure as the Navier-Stokes equation, the main difference stems from the fact that non-linear coupling happens only between fluctuations propagating in opposite directions. As we will see, this has a deep influence on turbulence described by MHD equations.
It is worthwhile to remark that in the classical hydrodynamics, dissipative processes are defined through three coefficients, namely two viscosities and one thermoconduction coefficient. In the hydromagnetic case the number of coefficients increases considerably. Apart from few additional electrical coefficients, we have a large-scale (background) magnetic field B0. This makes the MHD equations intrinsically anisotropic. Furthermore, the stress tensor (8) is deeply modified by the presence of a magnetic field B0, in that kinetic viscous coefficients must depend on the magnitude and direction of the magnetic field (Braginskii, (1965). This has a strong influence on the determination of the Reynolds number.
2.3 Scaling features of the equations
The scaled Euler equations are the same as Equations (4 and 5), but without the term proportional to R−1. The scaled variables obtained from the Euler equations are, then, the same. Thus, scaled variables exhibit scaling similarity, and the Euler equations are said to be invariant with respect to scale transformations. Said differently, this means that NS Equations (4) show scaling properties (Frisch, (1995), that is, there exists a class of solutions which are invariant under scaling transformations. Introducing a length scale ℓ, it is straightforward to verify that the scaling transformations ℓ ↑ λ ℓ’ and u → λhu’ (λ is a scaling factor and h is a scaling index) leave invariant the inviscid NS equation for any scaling exponent h, providing P → λ2hP’. When the dissipative term is taken into account, a characteristic length scale exists, say the dissipative scale ℓD. From a phenomenological point of view, this is the length scale where dissipative effects start to be experienced by the flow. Of course, since ℓD is in general very low, we expect that ℓD is very small. Actually, there exists a simple relationship for the scaling of .D with the Reynolds number, namely ℓD ~ LRe−3/4. The larger the Reynolds number, the smaller the dissipative length scale.
As it is easily verified, ideal MHD equations display similar scaling features. Say the following scaling transformations u → λhu’ and B → λβB’ (β here is a new scaling index different from h), leave the inviscid MHD equations unchanged, providing P → λ2βP’, T → λ2hT’, and ρ → λ2(β−h)ρ’. This means that velocity and magnetic variables have different scalings, say h ≠ β, only when the scaling for the density is taken into account. In the incompressible case, we cannot distinguish between scaling laws for velocity and magnetic variables.
2.4 The non-linear energy cascade
The basic properties of turbulence, as derived both from the Navier-Stokes equation and from phenomenological considerations, is the legacy of A. N. Kolmogorov (Frisch, (1995).Footnote 3 Phenomenology is based on the old picture by Richardson who realized that turbulence is made by a collection of eddies at all scales. Energy, injected at a length scale L, is transferred by non-linear interactions to small scales where it is dissipated at a characteristic scale ℓD, the length scale where dissipation takes place The main idea is that at very large Reynolds numbers, the injection scale L and the dissipative scale ℓD are completely separated. In a stationary situation, the energy injection rate must be balanced by the energy dissipation rate and must also be the same as the energy transfer rate ε measured at any scale ℓ within the inertial range ℓD ≪ ℓ ≪ L. From a phenomenological point of view, the energy injection rate at the scale L is given by ∈D ~ U2/τL, where τL is a characteristic time for the injection energy process, which results to be τL ~ L/U At the same scale L the energy dissipation rate is due to ∈D ~ U2/τD, where τD is the characteristic dissipation time which, from Equation (4), can be estimated to be of the order of τD ~ L2/ν. As a result, the ratio between the energy injection rate and dissipation rate is
that is, the energy injection rate at the largest scale L is Re-times the energy dissipation rate. In other words, in the case of large Reynolds numbers, the fluid system is unable to dissipate the whole energy injected at the scale L. The excess energy must be dissipated at small scales where the dissipation process is much more efficient. This is the physical reason for the energy cascade.
Fully developed turbulence involves a hierarchical process, in which many scales of motion are involved. To look at this phenomenon it is often useful to investigate the behavior of the Fourier coefficients of the fields. Assuming periodic boundary conditions the α-th component of velocity field can be Fourier decomposed as
where k = 2πn/L and n is a vector of integers. When used in the Navier-Stokes equation, it is a simple matter to show that the non-linear term becomes the convolution sum
where Mαβγ(k) = −ikβ(δαγ − kα − kβ/k2) (for the moment we disregard the linear dissipative term).
MHD equations can be written in the same way, say by introducing the Fourier decomposition for Elsäasser variables
and using this expression in the MHD equations we obtain an equation which describes the time evolution of each Fourier mode. However, the divergence-less condition means that not all Fourier modes are independent, rather k · z±(k, t) = 0 means that we can project the Fourier coefficients on two directions which are mutually orthogonal and orthogonal to the direction of k, that is,
with the constraint that k · e(a)(k) = 0. In presence of a background magnetic field we can use the well defined direction B0, so that
Note that in the linear approximation where the Elsäasser variables represent the usual MHD modes, z ±1 (k, t) represent the amplitude of the Alfvén mode while z ±2 (k, t) represent the amplitude of the incompressible limit of the magnetosonic mode. From MHD Equations (15) we obtain the following set of equations:
The coupling coefficients, which satisfy the symmetry condition Aabc (k, p, q) = −Abac(p, k, q), are defined as
and the sum in Equation (19) is defined as
where δk,p+q is the Kronecher’s symbol. Quadratic non-linearities of the original equations correspond to a convolution term involving wave vectors k, p and q related by the triangular relation p = k−q. Fourier coefficients locally couple to generate an energy transfer from any pair of modes p and q to a mode k = p + q.
The pseudo-energies E±(t) are defined as
and, after some algebra, it can be shown that the non-linear term of Equation (19) conserves separately E±(t). This means that both the total energy E(t) = E+ + E− and the cross-helicity Ec(t) = E+−E−, say the correlation between velocity and magnetic field, are conserved in absence of dissipation and external forcing terms.
In the idealized homogeneous and isotropic situation we can define the pseudo-energy tensor, which using the incompressibility condition can be written as
brackets being ensemble averages, where q±(k) is an arbitrary odd function of the wave vector k and represents the pseudo-energies spectral density. When integrated over all wave vectors under the assumption of isotropy
where we introduce the spectral pseudo-energy E±(k, t) = 4πk2q±(k, t). This last quantity can be measured, and it is shown that it satisfies the equations
We use ν = η in order not to worry about coupling between + and − modes in the dissipative range. Since the non-linear term conserves total pseudo-energies we have
so that, when integrated over all wave vectors, we obtain the energy balance equation for the total pseudo-energies
This last equation simply means that the time variations of pseudo-energies are due to the difference between the injected power and the dissipated power, so that in a stationary state
Looking at Equation (20), we see that the role played by the non-linear term is that of a redistribution of energy among the various wave vectors. This is the physical meaning of the non-linear energy cascade of turbulence
2.5 The inhomogeneous case
Equations (20) refer to the standard homogeneous and incompressible MHD. Of course, the solar wind is inhomogeneous and compressible and the energy transfer equations can be as complicated as we want by modeling all possible physical effects like, for example, the wind expansion or the inhomogeneous large-scale magnetic field. Of course, simulations of all turbulent scales requires a computational effort which is beyond the actual possibilities. A way to overcome this limitation is to introduce some turbulence modeling of the various physical effects. For example, a set of equations for the cross-correlation functions of both Elsäasser fluctuations have been developed independently by Marsch and Tu (1989), Zhou and Matthaeus (1990), Oughton and Matthaeus (1992), and Tu and Marsch (1990a), following Marsch and Mangeney (1987) (see review by Tu and Marsch, (1996), and are based on some rather strong assumptions: i) a two-scale separation, and ii) small-scale fluctuations are represented as a kind of stochastic process (Tu and Marsch, (1996). These equations look quite complicated, and just a comparison based on order-of-magnitude estimates can be made between them and solar wind observations (Tu and Marsch, (1996).
A different approach, introduced by Grappin et al. (1993), is based on the so-called “expandingbox model” (Grappin and Velli, (1996; Liewer et al., (2001; Hellinger et al., (2005). The model uses transformation of variables to the moving solar wind frame that expands together with the size of the parcel of plasma as it propagates outward from the Sun. Despite the model requires several simplifying assumptions, like for example lateral expansion only for the wave-packets and constant solar wind speed, as well as a second-order approximation for coordinate transformation Liewer et al. (2001) to remain tractable, it provides qualitatively good description of the solar wind expansions, thus connecting the disparate scales of the plasma in the various parts of the heliosphere.
2.6 Dynamical system approach to turbulence
In the limit of fully developed turbulence, when dissipation goes to zero, an infinite range of scales are excited, that is, energy lies over all available wave vectors. Dissipation takes place at a typical dissipation length scale which depends on the Reynolds number Re through ℓD ~ LRe−3/4 (for a Kolmogorov spectrum E(k) ~ k−5/3). In 3D numerical simulations the minimum number of grid points necessary to obtain information on the fields at these scales is given by N ~ (L/ℓD)3 ~ Re9/4. This rough estimate shows that a considerable amount of memory is required when we want to perform numerical simulations with high Re. At present, typical values of Reynolds numbers reached in 2D and 3D numerical simulations are of the order of 104 and 103, respectively. At these values the inertial range spans approximately one decade or a little more.
Given the situation described above, the question of the best description of dynamics which results from original equations, using only a small amount of degree of freedom, becomes a very important issu. This can be achieved by introducing turbulence models which are investigated using tools of dynamical system theory (Bohr et al., (1998). Dynamical systems, then, are solutions of minimal sets of ordinary differential equations that can mimic the gross features of energy cascade turbulence These studies are motivated by the famous Lorenz’s model (Lorenz, (1963) which, containing only three degrees of freedom, simulates the complex chaotic behavior of turbulent atmospheric flows, becoming a paradigm for the study of chaotic systems.
The Lorenz’s model has been used as a paradigm as far as the transition to turbulence is concerned. Actually, since the solar wind is in a state of fully developed turbulence, the topic of the transition to turbulence is not so close to the main goal of this review. However, since their importance in the theory of dynamical systems, we spend few sentences abut this central topic. Up to the Lorenz’s chaotic model, studies on the birth of turbulence dealt with linear and, very rarely, with weak non-linear evolution of external disturbances. The first physical model of laminar-turbulent transition is due to Landau and it is reported in the fourth volume of the course on Theoretical Physics (Landau and Lifshitz, (1971). According to this model, as the Reynolds number is increased, the transition is due to a infinite series of Hopf bifurcations at fixed values of the Reynolds number. Each subsequent bifurcation adds a new incommensurate frequency to the flow whose dynamics become rapidly quasi-periodic. Due to the infinite number of degree of freedom involved, the quasi-periodic dynamics resembles that of a turbulent flow.
The Landau transition scenario is, however, untenable because incommensurate frequencies cannot exist without coupling between them. Ruelle and Takens (1971) proposed a new mathematical model, according to which after few, usually three, Hopf bifurcations the flow becomes suddenly chaotic. In the phase space this state is characterized by a very intricate attracting subset, a strange attractor. The flow corresponding to this state is highly irregular and strongly dependent on initial conditions. This characteristic feature is now known as the butterfly effect and represents the true definition of deterministic chaos. These authors indicated as an example for the occurrence of a strange attractor the old strange time behavior of the Lorenz’s model. The model is a paradigm for the occurrence of turbulence in a deterministic system, it reads
where x(t), y(t), and z(t) represent the first three modes of a Fourier expansion of fluid convective equations in the Boussinesq approximation, Pr is the Prandtl number, b is a geometrical parameter, and R is the ratio between the Rayleigh number and the critical Rayleigh number for convective motion. The time evolution of the variables x(t), y(t), and z(t) is reported in Figure 12. A reproduction of the Lorenz butterfly attractor, namely the projection of the variables on the plane (x, z) is shown in Figure 13. A few years later, Gollub and Swinney (1975) performed very sophisticated experiments,Footnote 4 concluding that the transition to turbulence in a flow between co-rotating cylinders is described by the Ruelle and Takens (1971) model rather than by the Landau scenario.
After this discovery, the strange attractor model gained a lot of popularity, thus stimulating a large number of further studies on the time evolution of non-linear dynamical systems. An enormous number of papers on chaos rapidly appeared in literature, quite in all fields of physics, and transition to chaos became a new topic. Of course, further studies on chaos rapidly lost touch with turbulence studies and turbulence, as reported by Feynman et al. (1977), still remains ... the last great unsolved problem of the classical physics. Furthermore, we like to cite recent theoretical efforts made by Chian and coworkers (Chian et al., (1998, (2003) related to the onset of Alfvénic turbulence These authors, numerically solved the derivative non-linear Schrödinger equation (Mjølhus, (1976; Ghosh and Papadopoulos, (1987) which governs the spatio-temporal dynamics of non-linear Alfvén waves, and found that Alfvénic intermittent turbulence is characterized by strange attractors. Note that, the physics involved in the derivative non-linear Schrödinger equation, and in particular the spatio-temporal dynamics of non-linear Alfvén waves, cannot be described by the usual incompressible MHD equations. Rather dispersive effects are required. At variance with the usual MHD, this can be satisfied by requiring that the effect of ion inertia be taken into account. This results in a generalized Ohm’s law by including a (j̲ × B̲)-term, which represents the compressible Hall correction to MHD, say the so-called compressible Hall-MHD model.
Time evolution of the variables x(t), y(t), and z(t) in the Lorenz’s model (see Equation (22)). This figure has been obtained by using the parameters Pr = 10, b = 8/3, and R = 28.
The Lorenz butterfly attractor, namely the time behavior of the variables z(t) vs. x(t) as obtained from the Lorenz’s model (see Equation (22)). This figure has been obtained by using the parameters Pr = 10, b = 8/3, and R = 28.
In this context turbulence can evolve via two distinct routes: Pomeau.Manneville intermittency (Pomeau and Manneville, (1980) and crisis-induced intermittency (Ott and Sommerer, (1994). Both types of chaotic transitions follow episodic switching between different temporal behaviors. In one case (Pomeau.Manneville) the behavior of the magnetic fluctuations evolve from nearly periodic to chaotic while, in the other case the behavior intermittently assumes weakly chaotic or strongly chaotic features.
2.7 Shell models for turbulence cascade
Since numerical simulations, in some cases, cannot be used, simple dynamical systems can be introduced to investigate, for example, statistical properties of turbulent flows which can be compared with observations. These models, which try to mimic the gross features of the time evolution of spectral Navier-Stokes or MHD equations, are often called “shell models” or “discrete cascade models”. Starting from the old papers by Siggia (1977) different shell models have been introduced in literature for 3D fluid turbulence (Biferale, (2003). MHD shell models have been introduced to describe the MHD turbulent cascade (Plunian et al., (2012), starting from the paper by Gloaguen et al. (1985).
The most used shell model is usually quoted in literature as the GOY model, and has been introduced some time ago by Gledzer (1973) and by Ohkitani and Yamada (1989). Apart from the first MHD shell model (Gloaguen et al., (1985), further models, like those by Frick and Sokoloff (1998) and Giuliani and Carbone (1998) have been introduced and investigated in detail. In particular, the latter ones represent the counterpart of the hydrodynamic GOY model, that is they coincide with the usual GOY model when the magnetic variables are set to zero.
In the following, we will refer to the MHD shell model as the FSGC model. The shell model can be built up through four different steps:
-
a)
Introduce discrete wave vectors:
As a first step we divide the wave vector space in a discrete number of shells whose radii grow according to a power kn = k0λn, where λ > 1 is the inter-shell ratio, k0 is the fundamental wave vector related to the largest available length scale L, and n = 1, 2, ..., N.
-
b)
Assign to each shell discrete scalar variables:
Each shell is assigned two or more complex scalar variables un(t) and bn(t), or Elsäasser variables Z ±n (t) = un ± bn(t). These variables describe the chaotic dynamics of modes in the shell of wave vectors between kn and kn+1. It is worth noting that the discrete variable, mimicking the average behavior of Fourier modes within each shell, represents characteristic fluctuations across eddies at the scale ℓn ~ k −1n . That is, the fields have the same scalings as field differences, for example Z ±n ~ |Z±(x + ℓn) − Z±(x)| ~ ℓ hn in fully developed turbulence In this way, the possibility to describe spatial behavior within the model is ruled out. We can only get, from a dynamical shell model, time series for shell variables at a given kn, and we loose the fact that turbulence is a typical temporal and spatial complex phenomenon.
-
c)
Introduce a dynamical model which describes non-linear evolution:
Looking at Equation (19) a model must have quadratic non-linearities among opposite variables Z ±n (t) and Z ∓n (t), and must couple different shells with free coupling coefficients.
-
d)
Fix as much as possible the coupling coefficients:
This last step is not standard. A numerical investigation of the model might require the scanning of the properties of the system when all coefficients are varied. Coupling coefficients can be fixed by imposing the conservation laws of the original equations, namely the total pseudo-energies
$$E^ \pm (t) = \frac{1} {2}\sum\limits_n {\left| {Z_n^ \pm } \right|^2 },$$((22a))that means the conservation of both the total energy and the cross-helicity:
$$\begin{array}{*{20}c} {E(t) = \frac{1} {2}\sum\limits_n {\left| {u_n } \right|^2 + \left| {b_n } \right|^2 ;} } & {H_c (t) = \sum\limits_n {2\Re e(u_n b_n^* )} } \\ \end{array},$$((22b))where Re indicates the real part of the product unbn*. As we said before, shell models cannot describe spatial geometry of non-linear interactions in turbulence, so that we loose the possibility of distinguishing between two-dimensional and three-dimensional turbulent behavior. The distinction is, however, of primary importance, for example as far as the dynamo effect is concerned in MHD. However, there is a third invariant which we can impose, namely
$$H(t) = \sum\limits_n {\left| { - 1} \right|^n \frac{{\left| {b_n } \right|^2 }} {{k_n^\alpha }}},$$((23))which can be dimensionally identified as the magnetic helicity when α = 1, so that the shell model so obtained is able to mimic a kind of 3D MHD turbulence (Giuliani and Carbone (1998).
After some algebra, taking into account both the dissipative and forcing terms, FSGC model can be written as
where
whereFootnote 5 λ = 2, a = 1/2, and c = 1/3. In the following, we will consider only the case where the dissipative coefficients are the same, i.e., ν = μ.
2.8 The phenomenology of fully developed turbulence: Fluid-like case
Here we present the phenomenology of fully developed turbulence, as far as the scaling properties are concerned. In this way we are able to recover a universal form for the spectral pseudo-energy in the stationary case. In real space a common tool to investigate statistical properties of turbulence is represented by field increments Δz ±ℓ (r) = [z±(r + ℓ) − z±(r)] · e, being e the longitudinal direction. These stochastic quantities represent fluctuationsFootnote 6 across eddies at the scale ℓ. The scaling invariance of MHD equations (cf. Section 2.3), from a phenomenological point of view, implies that we expect solutions where Δz ±ℓ ~ ℓh. All the statistical properties of the field depend only on the scale ℓ, on the mean pseudo-energy dissipation rates ε±, and on the viscosity ν. Also, ε± is supposed to be the common value of the injection, transfer and dissipation rates. Moreover, the dependence on the viscosity only arises at small scales, near the bottom of the inertial range. Under these assumptions the typical pseudo-energy dissipation rate per unit mass scales as ε± ~ (Δz ±ℓ ±)2/t ±ℓ . The time t ±ℓ associated with the scale . is the typical time needed for the energy to be transferred on a smaller scale, say the eddy turnover time t ±ℓ ~ ℓ/Δz ∓ℓ , so that
When we conjecture that both Δz± fluctuations have the same scaling laws, namely Δz± ~ ℓh we recover the Kolmogorov scaling for the field increments
Usually, we refer to this scaling as the K41 model (Kolmogorov, (1941, (1991; Frisch, (1995). Note that, since from dimensional considerations the scaling of the energy transfer rate should be ε± ~ ℓ1−3h, h = 1/3 is the choice to guarantee the absence of scaling for ε±.
In the real space turbulence properties can be described using either the probability distribution functions (PDFs hereafter) of increments, or the longitudinal structure functions, which represents nothing but the higher order moments of the field. Disregarding the magnetic field, in a purely fully developed fluid turbulence, this is defined as S (p)ℓ = 〈Δu pℓ 〉. These quantities, in the inertial range, behave as a power law S (p)ℓ ~ ℓξp, so that it is interesting to compute the set of scaling exponent ξp. Using, from a phenomenological point of view, the scaling for field increments (see Equation (26)), it is straightforward to compute the scaling laws S (p)ℓ ~ ℓp/3. Then ξp = p/3 results to be a linear function of the order p.
When we assume the scaling law Δz ±ℓ ~ ℓh, we can compute the high-order moments of the structure functions for increments of the Elsäasser variables, namely 〈(Δz ±ℓ )p〉 ~ ℓξp, thus obtaining a linear scaling ξp = p/3, similar to usual fluid flows. For Gaussianly distributed fields, a particular role is played by the second-order moment, because all moments can be computed from S (2)ℓ . It is straightforward to translate the dimensional analysis results to Fourier spectra. The spectral property of the field can be recovered from S (2)ℓ , say in the homogeneous and isotropic case
where k ~ 1/ℓ is the wave vector, so that in the inertial range where Equation (42) is verified
The Kolmogorov spectrum (see Equation (27)) is largely observed in all experimental investigations of turbulence, and is considered as the main result of the K41 phenomenology of turbulence (Frisch, (1995). However, spectral analysis does not provide a complete description of the statistical properties of the field, unless this has Gaussian properties. The same considerations can be made f.o[.r the spectral pseudo-energies E±(k), which are related to the 2nd order structure functions 〈[±z ±ℓ ]2〉.
2.9 The phenomenology of fully developed turbulence: Magnetically-dominated case
The phenomenology of the magnetically-dominated case has been investigated by Iroshnikov (1963) and Kraichnan (1965), then developed by Dobrowolny et al. (1980b) to tentatively explain the occurrence of the observed Alfvénic turbulence, and finally by Carbone (1993) and Biskamp (1993) to get scaling laws for structure functions. It is based on the Alfvén effect, that is, the decorrelation of interacting eddies, which can be explained phenomenologically as follows. Since non-linear interactions happen only between opposite propagating fluctuations, they are slowed down (with respect to the fluid-like case) by the sweeping of the fluctuations across each other. This means that ε± ~ (Δz ±ℓ )2/T ±ℓ but the characteristic time T ±ℓ required to efficiently transfer energy from an eddy to another eddy at smaller scales cannot be the eddy-turnover time, rather it is increased by a factor t ±ℓ /tA (tA ~ ℓ/cA < t ±ℓ is the Alfvén time), so that T ±ℓ ~ (t ±ℓ )2/tA. Then, immediately
This means that both ± modes are transferred at the same rate to small scales, namely ∈+ ~ ∈− ~ ∈, and this is the conclusion drawn by Dobrowolny et al. (1980b). In reality, this is not fully correct, namely the Alfvén effect yields to the fact that energy transfer rates have the same scaling laws for ± modes but, we cannot say anything about the amplitudes of ε+ and ε− (Carbone, (1993). Using the usual scaling law for fluctuations, it can be shown that the scaling behavior holds ∈ → λ1−4hε’. Then, when the energy transfer rate is constant, we found a scaling law different from that of Kolmogorov and, in particular,
Using this phenomenology the high-order moments of fluctuations are given by S (p)∓ ~ ℓp/4. Even in this case, ξp = p/4 results to be a linear function of the order p. The pseudo-energy spectrum can be easily found to be
This is the Iroshnikov-Kraichnan spectrum. However, in a situation in which there is a balance between the linear Alfvén time scale or wave period, and the non-linear time scale needed to transfer energy to smaller scales, the energy cascade is indicated as critically balanced (Goldreich and Sridhar, (1995). In these conditions, it can be shown that the power spectrum P(k) would scale as f−5/3 when the angle θB between the mean field direction and the flow direction is 90° while, the same scaling would follow f−2 in case θB = 0° and the spectrum would also have a smaller energy content than in the other case.
2.10 Some exact relationships
So far, we have been discussing about the inertial range of turbulence What this means from a heuristic point of view is somewhat clear, but when we try to identify the inertial range from the spectral properties of turbulence, in general the best we can do is to identify the inertial range with the intermediate range of scales where a Kolmogorov’s spectrum is observed. The often used identity inertial range ≃ intermediate range, is somewhat arbitrary. In this regard, a very important result on turbulence, due to Kolmogorov (1941, (1991), is the so-called “4/5-law” which, being obtained from the Navier-Stokes equation, is “... one of the most important results in fully developed turbulence because it is both exact and nontrivial” (cf. Frisch, (1995). As a matter of fact, Kolmogorov analytically derived the following exact relation for the third order structure function of velocity fluctuations:
where r is the sampling direction, ℓ is the corresponding scale, and ∈ is the mean energy dissipation per unit mass, assumed to be finite and nonvanishing.
This important relation can be obtained in a more general framework from MHD equations. A Yaglom’s relation for MHD can be obtained using the analogy of MHD equations with a transport equation, so that we can obtain a relation similar to the Yaglom’s equation for the transport of a passive quantity (Monin and Yaglom, (1975). Using the above analogy, the Yaglom’s relation has been extended some time ago to MHD turbulence by Chandrasekhar (1967), and recently it has been revised by Politano et al. (1998) and Politano and Pouquet (1998) in the framework of solar wind turbulence In the following section we report an alternative and more general derivation of the Yaglom’s law using structure functions (Sorriso-Valvo et al., (2007; Carbone et al., (2009c).
2.11 Yaglom’s law for MHD turbulence
To obtain a general law we start from the incompressible MHD equations. If we write twice the MHD equations for two different and independent points xi and xi’ = xi + ℓi, by substraction we obtain an equation for the vector differences Δz ±i = (z ±i )’ − z ±i . Using the hypothesis of independence of points xi’ and xi with respect to derivatives, namely ∂i(z ±i )’ = ∂i’z ±j = 0 (where ∂i’ represents derivative with respect to xi’), we get
(ΔP = Ptot’ − Ptot). We look for an equation for the second-order correlation tensor 〈Δz ±i Δz ±j 〉 related to pseudo-energies. Actually the more general thing should be to look for a mixed tensor, namely 〈Δz ±i Δz ∓j 〉, taking into account not only both pseudo-energies but also the time evolution of the mixed correlations 〈z +i z −j 〉 and 〈z −i z +j 〉. However, using the DIA closure by Kraichnan, it is possible to show that these elements are in general poorly correlated (Veltri, (1980). Since we are interested in the energy cascade, we limit ourselves to the most interesting equation that describes correlations about Alfvénic fluctuations of the same sign. To obtain the equations for pseudo-energies we multiply Equations (31) by Δz ±j , then by averaging we get
where we used the hypothesis of local homogeneity and incompressibility. In Equation (32) we defined the average dissipation tensor
The first and second term on the r.h.s. of the Equation (32) represent respectively a tensor related to large-scales inhomogeneities
and the tensor related to the pressure term
Furthermore, In order not to worry about couplings between Elsäasser variables in the dissipative terms, we make the usual simplifying assumption that kinematic viscosity is equal to magnetic diffusivity, that is ν± = ν∓ = ν. Equation (32) is an exact equation for anisotropic MHD equations that links the second-order complete tensor to the third-order mixed tensor via the average dissipation rate tensor. Using the hypothesis of global homogeneity the term Λij = 0, while assuming local isotropy Πij = 0. The equation for the trace of the tensor can be written as
where the various quantities depends on the vector ℓα. Moreover, by considering only the trace we ruled out the possibility to investigate anisotropies related to different orientations of vectors within the second-order moment. It is worthwhile to remark here that only the diagonal elements of the dissipation rate tensor, namely ∈ ±ii are positive defined while, in general, the off-diagonal elements ∈ ±ij are not positive. For a stationary state the Equation (36) can be written as the divergenceless condition of a quantity involving the third-order correlations and the dissipation rates
from which we can obtain the Yaglom’s relation by projecting Equation (37) along the longitudinal ℓα = ℓer direction. This operation involves the assumption that the flow is locally isotropic, that is fields depends locally only on the separation ℓ, so that
The only solution that is compatible with the absence of singularity in the limit ℓ → 0 is
which reduces to the Yaglom’s law for MHD turbulence as obtained by Politano and Pouquet (1998) in the inertial range when ν → 0
Finally, in the fluid-like case where z +i = z −i = ui we obtain the usual Yaglom’s law for fluid flows
which in the isotropic case, where 〈Δu 3ℓ 〉 = 3〈ΔuℓΔu 2y 〉 = 3〈ΔuℓΔu 2z 〉 (Monin and Yaglom, (1975), immediately reduces to the Kolmogorov’s law
(the separation ℓ has been taken along the streamwise x-direction).
The relations we obtained can be used, or better, in a certain sense they might be used, as a formal definition of inertial range. Since they are exact relationships derived from Navier-Stokes and MHD equations under usual hypotheses, they represent a kind of “zeroth-order” conditions on experimental and theoretical analysis of the inertial range properties of turbulence It is worthwhile to remark the two main properties of the Yaglom’s laws. The first one is the fact that, as it clearly appears from the Kolmogorov’s relation (Kolmogorov, (1941), the third-order moment of the velocity fluctuations is different from zero. This means that some non-Gaussian features must be at work, or, which is the same, some hidden phase correlations. Turbulence is something more complicated than random fluctuations with a certain slope for the spectral density. The second feature is the minus sign which appears in the various relations. This is essential when the sign of the energy cascade must be inferred from the Yaglom relations, the negative asymmetry being a signature of a direct cascade towards smaller scales. Note that, Equation (40) has been obtained in the limit of zero viscosity assuming that the pseudo-energy dissipation rates ∈ ±ii remain finite in this limit. In usual fluid flows the analogous hypothesis, namely ν remains finite in the limit ν → 0, is an experimental evidence, confirmed by experiments in different conditions (Frisch, (1995). In MHD turbulent flows this remains a conjecture, confirmed only by high resolution numerical simulations (Mininni and Pouquet, (2009).
From Equation (37), by defining ΔZ ±i = Δui ± Δbi we immediately obtain the two equations
where we defined the energy fluctuations ΔE = |Δui|2 + |Δbi|2 and the correlation fluctuations ΔC = ΔuiΔbi. In the same way the quantities ∈E = (∈ +ii + ∈ −ii )/2 and ∈C = (∈ +ii − ∈ −ii /2 represent the energy and correlation dissipation rate, respectively. By projecting once more on the longitudinal direction, and assuming vanishing viscosity, we obtain the Yaglom’s law written in terms of velocity and magnetic fluctuations
2.12 Density-mediated Elsäasser variables and Yaglom’s law
Relation (40), which is of general validity within MHD turbulence, requires local characteristics of the turbulent fluid flow which can be not always satisfied in the solar wind flow, namely, largescale homogeneity, isotropy, and incompressibility. Density fluctuations in solar wind have a low amplitude, so that nearly incompressible MHD framework is usually considered (Montgomery et al., (1987; Matthaeus and Brown, (1988; Zank and Matthaeus, (1993; Matthaeus et al., (1991; Bavassano and Bruno, (1995). However, compressible fluctuations are observed, typically convected structures characterized by anticorrelation between kinetic pressure and magnetic pressure (Tu and Marsch, (1994). Properties and interaction of the basic MHD modes in the compressive case have also been considered (Goldreich and Sridhar, (1995; Cho and Lazarian, (2002).
A first attempt to include density fluctuations in the framework of fluid turbulence was due to Lighthill (1955). He pointed out that, in a compressible energy cascade, the mean energy transfer rate per unit volume ∈V ~ ρu3/ℓ should be constant in a statistical sense (u being the characteristic velocity fluctuations at the scale ℓ), thus obtaining the scaling relation u ~ (ℓ/ρ)1/3. Fluctuations of a density-weighted velocity field u ≡ ρ1/3v should thus follow the usual Kolmogorov scaling u3 ~ ℓ. The same phenomenological arguments can be introduced in MHD turbulence Carbone et al. (2009a) by considering the pseudoenergy dissipation rates per unit volume ∈ ±V = ρ∈ ±ii and introducing density-weighted Elsäasser fields, defined as w± ≡ ρ1/3z±. A relation equivalent to the Yaglom-type relation (40)
(C is some constant assumed to be of the order of unit) should then hold for the density-weighted increments Δw±. Relation W ±ℓ reduces to Y ±ℓ in the case of constant density, allowing for comparison between the Yaglom’s law for incompressible MHD flows and their compressible counterpart. Despite its simple phenomenological derivation, the introduction of the density fluctuations in the Yaglom-type scaling (47) should describe the turbulent cascade for compressible fluid (or magnetofluid) turbulence Even if the modified Yaglom’s law (47) is not an exact relation as (40), being obtained from phenomenological considerations, the law for the velocity field in a compressible fluid flow has been observed in numerical simulations, the value of the constant C results negative and of the order of unity (Padoan et al., (2007; Kowal and Lazarian, (2007).
2.13 Yaglom’s law in the shell model for MHD turbulence
As far as the shell model is concerned, the existence of a cascade towards small scales is expressed by an exact relation, which is equivalent to Equation (41). Using Equations (24), the scale-by-scale pseudo-energy budget is given by
The second and third terms on the right hand side represent, respectively, the rate of pseudoenergy dissipation and the rate of pseudo-energy injection. The first term represents the flux of pseudo-energy along the wave vectors, responsible for the redistribution of pseudo-energies on the wave vectors, and is given by
Using the same assumptions as before, namely: i) the forcing terms act only on the largest scales, ii) the system can reach a statistically stationary state, and iii) in the limit of fully developed turbulence, ν → 0, the mean pseudo-energy dissipation rates tend to finite positive limits ∈±, it can be found that
This is an exact relation which is valid in the inertial range of turbulence Even in this case it can be used as an operative definition of the inertial range in the shell model, that is, the inertial range of the energy cascade in the shell model is defined as the range of scales kn, where the law from Equation (49) is verified.
3 Early Observations of MHD Turbulence in the Ecliptic
Here we briefly present the history, since the first Mariner missions during the 1960s, of the main steps towards the completion of an observational picture of turbulence in interplanetary space This retrospective look at all the advances made in this field shows that space flights allowed us to discover a very large laboratory in space As a matter of fact, in a wind tunnel we deal with characteristic dimensions of the order of L ≤ 10 m and probes of the size of about d ≃ 1 cm. In space, L ≃ 108 m, while “probes” (say spacecrafts) are about d ≃ 5 m. Thus, space provides a much larger laboratory. Most measurements are single point measurements, the ESA-Cluster project providing for multiple measurements only recently.
3.1 Turbulence in the ecliptic
When dealing with laboratory turbulence it is important to know all the aspects of the experimental device where turbulent processes take place in order to estimate related possible effects driven or influenced by the environment. In the solar wind, the situation is, in some aspects, similar although the plasma does not experience any confinement due to the “experimental device”, which would be represented by free interplanetary space However, it is a matter of fact that the turbulent state of the wind fluctuations and the subsequent radial evolution during the wind expansion greatly differ from fast to slow wind, and it is now well accepted that the macrostructure convected by the wind itself plays some role (see reviews by Tu and Marsch, (1995a; Goldstein et al., (1995b).
Fast solar wind originates from the polar regions of the Sun, within the open magnetic field line regions identified by coronal holes. Beautiful observations by SOHO spacecraft (see animation of Figure 14) have localized the birthplace of the solar wind within the intergranular lane, generally where three or more granules get together. Clear outflow velocities of up to 10 km s−1 have been recorded by SOHO/SUMER instrument (Hassler et al., (1999).
mpg-Movie (2362.87792969 KB) Still from a movie showing An animation built on SOHO/EIT and SOHO/SUMER observations of the solar-wind source regions and magnetic structure of the chromospheric network. Outflow velocities, at the network cell boundaries and lane junctions below the polar coronal hole, reach up to 10 km s−1 are represented by the blue colored areas (original figures from Hassler et al., (1999). (For video see appendix)
Slow wind, on the contrary, originates from the equatorial zone of the Sun. The slow wind plasma leaks from coronal features called “helmets”, which can be easily seen protruding into the Sun’s atmosphere during a solar eclipse (see Figure 15). Moreover, plasma emissions due to violent and abrupt phenomena also contribute to the solar wind in these regions of the Sun. An alternative view is that both high- and low-speed winds come from coronal holes (defined as open field regions) and that the wind speed at 1 AU is determined by the rate of flux-tube expansion near the Sun as firstly suggested by Levine et al. (1977) (Wang and Sheeley Jr, (1990; Bravo and Stewart, (1997; Arge and Pizzo, (2000; Poduval and Zhao, (2004; Whang et al., (2005, see also:) and/or by the location and strength of the coronal heating (Leer and Holzer, (1980; Hammer, (1982; Hollweg, (1986; Withbroe, (1988; Wang, (1993, (1994; Sandbaek et al., (1994; Hansteen and Leer, (1995; Cranmer et al., (2007).
However, this situation greatly changes during different phases of the solar activity cycle. Polar coronal holes, which during the maximum of activity are limited to small and not well defined regions around the poles, considerably widen up during solar minimum, reaching the equatorial regions (Forsyth et al., (1997; Forsyth and Breen, (2002; Balogh et al., (1999). This new configuration produces an alternation of fast and slow wind streams in the ecliptic plane, the plane where most of the spacecraft operate and record data. During the expansion, a dynamical interaction between fast and slow wind develops, generating the so called “stream interface”, a thin region ahead of the fast stream characterized by strong compressive phenomena.
Figure 16 shows a typical situation in the ecliptic where fast streams and slow wind were observed by Helios 2 s/c during its primary mission to the Sun. At that time, the spacecraft moved from 1 AU (around day 17) to its closest approach to the Sun at 0.29 AU (around day 108). During this radial excursion, Helios 2 had a chance to observe the same co-rotating stream, that is plasma coming from the same solar source, at different heliocentric distances. This fortuitous circumstance, gave us the unique opportunity to study the radial evolution of turbulence under the reasonable hypothesis of time-stationarity of the source regions. Obviously, similar hypotheses decay during higher activity phase of the solar cycle since, as shown in Figure 17, the nice and regular alternation of fast co-rotating streams and slow wind is replaced by a much more irregular and spiky profile also characterized by a lower average speed.
Figure 18 focuses on a region centered on day 75, recognizable in Figure 16, when the s/c was at approximately 0.7 AU from the Sun. Slow wind on the left-hand side of the plot, fast wind on the right hand side, and the stream interface in between, can be clearly seen. This is a sort of canonical situation often encountered in the ecliptic, within the inner heliosphere, during solar activity minimum. Typical solar wind parameters, like proton number density ρp proton temperature Tp, magnetic field intensity |B|, azimuthal angle Φ, and elevation angle Θ are shown in the panels below the wind speed profile. A quick look at the data reveals that fast wind is less dense but hotter than slow wind. Moreover, both proton number density and magnetic field intensity are more steady and, in addition, the bottom two panels show that magnetic field vector fluctuates in direction much more than in slow wind. This last aspect unravels the presence of strong Alfvénic fluctuations which act mainly on magnetic field and velocity vector direction, and are typically found within fast wind (Belcher and Davis Jr, (1971; Belcher and Solodyna, (1975). The region just ahead of the fast wind, namely the stream interface, where dynamical interaction between fast and slow wind develops, is characterized by compressive effects which enhance proton density, temperature and field intensity. Within slow wind, a further compressive region precedes the stream interface but it is not due to dynamical effects but identifies the heliospheric current sheet, the surface dividing the two opposite polarities of the interplanetary magnetic field. As a matter of fact, the change of polarity can be noted within the first half of day 73 when the azimuthal angle Φ rotates by about 180°. Detailed studies (Bavassano et al., (1997) based on interplanetary scintillations (IPS) and in-situ measurements have been able to find a clear correspondence between the profile of path-integrated density obtained from IPS measurements and in-situ measurements by Helios 2 when the s/c was around 0.3 AU from the Sun.
High velocity streams and slow wind as seen in the ecliptic during solar minimum as function of time [yyddd]. Streams identified by labels are the same co-rotating stream observed by Helios 2, during its primary mission to the Sun in 1976, at different heliocentric distances. These streams, named “The Bavassano.Villante streams” after Tu and Marsch (1995a), have been of fundamental importance in understanding the radial evolution of MHD turbulence in the solar wind.
Figure 19 shows measurements of several plasma and magnetic field parameters. The third panel from the top is the proton number density and it shows an enhancement within the slow wind just preceding the fast stream, as can be seen at the top panel. In this case the increase in density is not due to the dynamical interaction between slow and fast wind but it represents the profile of the heliospheric current sheet as sketched on the left panel of Figure 19. As a matter of fact, at these short distances from the Sun, dynamical interactions are still rather weak and this kind of compressive effects can be neglected with respect to the larger density values proper of the current sheet.
3.1.1 Spectral properties
First evidences of the presence of turbulent fluctuations were showed by Coleman (1968), who, using Mariner 2 magnetic and plasma observations, investigated the statistics of interplanetary fluctuations during the period August 27 - October 31, 1962, when the spacecraft orbited from 1.0 to 0.87 AU. At variance with Coleman (1968), Barnes and Hollweg (1974) analyzed the properties of the observed low-frequency fluctuations in terms of simple waves, disregarding the presence of an energy spectrum. Here we review the gross features of turbulence as observed in space by Mariner and Helios spacecraft. By analyzing spectral densities, Coleman (1968) concluded that the solar wind flow is often turbulent, energy being distributed over an extraordinarily wide frequency range, from one cycle per solar rotation to 0.1 Hz. The frequency spectrum, in a range of intermediate frequencies [2 × 10−5 −2.3 × 10−3], was found to behave roughly as f−1.2, the difference with the expected Kraichnan f−1.5 spectral slope was tentatively attributed to the presence of high-frequency transverse fluctuations resulting from plasma garden-hose instability (Scarf et al., (1967). Waves generated by this instability contribute to the spectrum only in the range of frequencies near the proton cyclotron frequency and would weaken the frequency dependence relatively to the Kraichnan scaling. The magnetic spectrum obtained by Coleman (1968) is shown in Figure 20.
Left panel: a simple sketch showing the configuration of a helmet streamer and the density profile across this structure. Right panel: Helios 2 observations of magnetic field and plasma parameters across the heliospheric current sheet. From top to bottom: wind speed, magnetic field azimuthal angle, proton number density, density fluctuations and normalized density fluctuations, proton temperature, magnetic field magnitude, total pressure, and plasma beta, respectively. Image reproduced by permission from Bavassano et al. (1997), copyright by AGU.
The magnetic energy spectrum as obtained by Coleman (1968).
Spectral properties of the interplanetary medium have been summarized by Russell (1972), who published a composite spectrum of the radial component of magnetic fluctuations as observed by Mariner 2, Mariner 4, and OGO 5 (see Figure 21). The frequency spectrum so obtained was divided into three main ranges: i) up to about 10−4 Hz the spectral slope is about 1/f; ii) at intermediate frequencies 10−4 ≤ f ≤ 10−1 Hz a spectrum which roughly behaves as f3/2 has been found; iii) the high-frequency part of the spectrum, up to 1 Hz, behaves as 1/f2. The intermediate rangeFootnote 7 of frequencies shows the same spectral properties as that introduced by Kraichnan (1965) in the framework of MHD turbulence It is worth reporting that scatter plots of the values of the spectral index of the intermediate region do not allow us to distinguish between a Kolmogorov spectrum f−5/3 and a Kraichnan spectrum f−3/2 (Veltri, (1980).
A composite figure of the magnetic spectrum obtained by Russell (1972).
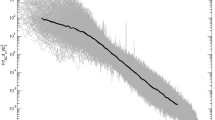
Only lately, Podesta et al. (2007) addressed again the problem of the spectral exponents of kinetic and magnetic energy spectra in the solar wind. Their results, instead of clarifying once forever the ambiguity between f−5/3 and f−3/2 scaling, placed new questions about this unsolved problem.
As a matter of fact, Podesta et al. (2007) chose different time intervals between 1995 and 2003 lasting 2 or 3 solar rotations during which WIND spacecraft recorded solar wind velocity and magnetic field conditions. Figure 22 shows the results obtained for the time interval that lasted about 3 solar rotations between November 2000 and February 2001, and is representative also of the other analyzed time intervals. Quite unexpectedly, these authors found that the power law exponents of velocity and magnetic field fluctuations often have values near 3/2 and 5/3, respectively. In addition, the kinetic energy spectrum is characterized by a power law exponent slightly greater than or equal to 3/2 due to the effects of density fluctuations.
It is worth mentioning that this difference was first observed by Salem (2000) years before, but, at that time, the accuracy of the data was questioned Salem et al. (2009). Thus, to corroborate previous results, Salem et al. (2009) investigated anomalous scaling and intermittency effects of both magnetic field and solar wind velocity fluctuations in the inertial range using WIND data. These authors used a wavelet technique for a systematic elimination of intermittency effects on spectra and structure functions in order to recover the actual scaling properties in the inertial range. They found that magnetic field and velocity fluctuations exhibit a well-defined, although different, monofractal behavior, following a Kolmogorov −5/3 scaling and a Iroshnikov-Kraichnan −3/2 scaling, respectively. These results are clearly opposite to the expected scaling for kinetic and magnetic fluctuations which should follow Kolmogorov and Kraichnan scaling, respectively (see Section 2.8). However, as remarked by Roberts (2007), Voyager observations of the velocity spectrum have demonstrated a likely asymptotic state in which the spectrum steepens towards a spectral index of −5/3, finally matching the magnetic spectrum and the theoretical expectation of Kolmogorov turbulence Moreover, the same authors examined Ulysses spectra to determine if the Voyager result, based on a very few sufficiently complete intervals, were correct. Preliminary results confirmed the −5/3 slope for velocity fluctuations at ~5 AU from the Sun in the ecliptic.
A composite figure of the magnetic spectrum obtained by Russell (1972).
Figure 23, taken from Roberts (2007), shows the evolution of the spectral index during the radial excursion of Ulysses. These authors examined many intervals in order to develop a more general picture of the spectral evolution in various conditions, and how magnetic and velocity spectra differ in these cases. The general trend shown in Figure 23 is towards −5/3 as the distance increases. Lower values are due to the highly Alfvénic fast polar wind while higher values, around 2, are mainly due to the jumps at the stream fronts as previously shown by Roberts (2007). Thus, the discrepancy between magnetic and velocity spectral slope is only temporary and belongs to the evolutionary phase of the spectra towards a well developed Kolmogorov like turbulence spectrum.
A composite figure of the magnetic spectrum obtained by Russell (1972).
Horbury et al. (2008) performed a study on the anisotropy of the energy spectrum of magnetohydrodynamic (MHD) turbulence with respect to the magnetic field orientation to test the validity of the critical balance theory (Goldreich and Sridhar, (1995) in space plasma environment. This theory predicts that the power spectrum P(k) would scale as f−5/3 when the angle θB between the mean field direction and the flow direction is 90°. On the other hand, in case θB = 0° the scaling would follow θ−2. Moreover, the latter spectrum would also have a smaller energy content.
Horbury et al. (2008) used 30 days of Ulysses magnetic field observations (1995, days 100 – 130) with a resolution of 1 second. At that time, Ulysses was immersed in the steady high speed solar wind coming from the Sun’s Northern polar coronal hole at 1.4 AU from the Sun. These authors studied the anisotropies of the turbulence by measuring how the spacecraft frame spectrum of magnetic fluctuations varies with θB. They adopted a method based on wavelet analysis which was sensitive to the frequent changes of the local magnetic field direction.
The lower panel of Figure 24 clearly shows that for angles larger than about 45. the spectral index smoothly fluctuates around −5/3 while, for smaller angles, it tends to a value of −2, as predicted by the critical balance type of cascade. However, although the same authors recognize that a spectral index of .2 has not been routinely observed in the fast solar wind and that the range of θB over which the spectral index deviates from −5/3 is wider than expected, they consider these findings to be a robust evidence of the validity of critical balance theory in space plasma environment.
3.1.2 Experimental evaluation of Reynolds number in the solar wind
Properties of solar wind fluctuations have been widely studied in the past, relying on the “frozen-in approximation” (Taylor, (1938). The hypothesis at the basis of Taylor’s approximation is that, since large integral scales in turbulence contain most of the energy, the advection due to the smallest turbulent scales fluctuations can be disregarded and, consequently, the advection of a turbulent field past an observer in a fixed location is considered solely due to the larger scales. In experimental physics, this hypothesis allows time series measured at a single point in space to be interpreted as spatial variations in the mean flow being swept past the observer. However, the canonical way to establish the presence of spatial structures relies in the computation of two-point single time measurements. Only recently, the simultaneous presence of several spacecraft sampling solar wind parameters allowed to correlate simultaneous in-situ observations in two different observing locations in space Matthaeus et al. (2005) and Weygand et al. (2007) firstly evaluated the twopoint correlation function using simultaneous measurements of interplanetary magnetic field from the Wind, ACE, and Cluster spacecraft. Their technique allowed to compute for the first time fundamental turbulence parameters previously determined from single spacecraft measurements. In particular, these authors evaluated the correlation scale λC and the Taylor microscale λT which allow to determine empirically the effective magnetic Reynolds number.
Top panel: Trace of power in the magnetic field as a function of the angle between the local magnetic field and the sampling direction at a spacecraft frequency of 61 mHz. The larger scatter for θB > 90 is the result of fewer data points at these angles. Bottom panel: spectral index of the trace, fitted over spacecraft frequencies from 15.98 mHz. Image reproduced by permission from Horbury et al. (2008), copyright by APS.
As a matter of fact, there are three standard turbulence length scales which can be identified in a typical turbulence power spectrum as shown in Figure 25: the correlation length λC, the Taylor scale λT and the Kolmogorov scale λK. The Correlation or integral length scale represents the largest separation distance over which eddies are still correlated, i.e., the largest turbulent eddy size. The Taylor scale is the scale size at which viscous dissipation begins to affect the eddies, it is several times larger than Kolmogorov scale and marks the transition from the inertial range to the dissipation range. The Kolmogorov scale is the one that characterizes the smallest dissipation-scale eddies.
The Taylor scale λT and the correlation length λC, as indicated in Figure 26, can be obtained from the two-point correlation function being the former the radius of curvature of the Correlation function at the origin and the latter the scale at which turbulent fluctuation are no longer correlated. Thus, λT can be obtained from from Taylor expansion of the two point correlation function for r → 0 (Tennekes and Lumely, (1972):
where r is the spacecraft separation and R(r) = 〈b(x) · b(x + r). is the auto-correlation function computed along the x direction for the fluctuating field b(x). On the other hand, the correlation length λC can be obtained integrating the normalized correlation function along a chosen direction of integration ξ:
Typical interplanetary magnetic field power spectrum at 1 AU. The low frequency range refers to Helios 2 observations (adapted from Bruno et al., (2009) while the high frequency refers to WIND observations (adapted from Leamon et al., (1998). Vertical dashed lines indicate the correlative, Taylor and Kolmogorov length scales.
At this point, following Batchelor (1970) it is possible to obtain the effective magnetic Reynolds number:
Figure 27 shows estimates of the correlation function from ACE-Wind for separation distances 20 − 350 RE and two sets of Cluster data for separations 0.02 − 0.04 RE and 0.4 − 1.2 RE, respectively.
Estimates of the correlation function from ACE-Wind for separation distances 20 . 350 RE and two sets of Cluster data for separations 0.02 − 0.04 RE and 0.4 − 1.2 RE, respectively. Image adapted from Matthaeus et al. (2005).
Following the definitions of λC and λT given above, Matthaeus et al. (2005) were able to fit the first data set of Cluster, i.e., the one with shorter separations, with a parabolic fit while they used an exponential fit for ACE-Wind and the second Cluster data set. These fits provided estimates for λC and λT from which these authors obtained the first empirical determination of R effm which resulted to be of the order of 2.3 × 105, as illustrated in Figure 28.
3.1.3 Evidence for non-linear interactions
As we said previously, Helios 2 s/c gave us the unique opportunity to study the radial evolution of turbulent fluctuations in the solar wind within the inner heliosphere. Most of the theoretical studies which aim to understand the physical mechanism at the base of this evolution originate from these observations (Bavassano et al., (1982b; Denskat and Neubauer, (1983).
In Figure 29 we consider again similar observations taken by Helios 2 during its primary mission to the Sun together with observations taken by Ulysses in the ecliptic at 1.4 and 4.8 AU in order to extend the total radial excursion.
Helios 2 power density spectra were obtained from the trace of the spectral matrix of magnetic field fluctuations, and belong to the same co-rotating stream observed on day 49, at a heliocentric distance of 0.9 AU, on day 75 at 0.7 AU and, finally, on day 104 at 0.3 AU. Ulysses spectra, constructed in the same way as those of Helios 2, were taken at 1.4 and 4.8 AU during the ecliptic phase of the orbit. Observations at 4.8 AU refer to the end of 1991 (fast wind period started on day 320, slow wind period started on day 338) while observations taken at 1.4 AU refer to fast wind observed at the end of August of 2007, starting on day 241:12.
Left panel: parabolic fit at small scales in order to estimate λT Right panel: exponential fit at intermediate and large scales in order to estimate λC. The square of the ratio of these two length scales gives an estimate of the effective magnetic Reynolds number. Image adapted from Matthaeus et al. (2005).
While the spectral index of slow wind does not show any radial dependence, being characterized by a single Kolmogorov type spectral index, fast wind is characterized by two distinct spectral slopes: about −1 within low frequencies and about a Kolmogorov like spectrum at higher frequencies. These two regimes are clearly separated by a knee in the spectrum often referred to as “frequency break”. As the wind expands, the frequency break moves to lower and lower frequencies so that larger and larger scales become part of the Kolmogorov-like turbulence spectrum, i.e., of what we will indicate as “inertial range” (see discussion at the end of the previous section). Thus, the power spectrum of solar wind fluctuations is not solely function of frequency f, i.e., P(f), but it also depends on heliocentric distance r, i.e., P(f) → P(f, r).
Figure 30 shows the frequency location of the spectral breaks observed in the left-hand-side panel of Figure 29 as a function of heliocentric distance The radial distribution of these 5 points suggests that the frequency break moves at lower and lower frequencies during the wind expansion following a power-law of the order of R−1.5. Previous results, obtained for long data sets spanning hundreds of days and inevitably mixing fast and slow wind, were obtained by Matthaeus and Goldstein (1986) who found the breakpoint around 10 h at 1 AU, and Klein et al. (1992) who found that the breakpoint was near 16 h at 4 AU. Obviously, the frequency location of the breakpoint provided by these early determinations is strongly affected by the fact that mixing fast and slow wind would shift the frequency break to lower frequencies with respect to solely fast wind. In any case, this frequency break is strictly related to the correlation length (Klein, (1987) and the shift to lower frequency, during the wind expansion, is consistent with the growth of the correlation length observed in the inner (Bruno and Dobrowolny, (1986) and outer heliosphere (Matthaeus and Goldstein, (1982a). Analogous behavior for the low frequency shift of the spectral break, similar to the one observed in the ecliptic, has been reported by Horbury et al. (1996a) studying the rate of turbulent evolution over the Sun’s poles. These authors used Ulysses magnetic field observations between 1.5 and 4.5 AU selecting mostly undisturbed, high speed polar flows. They found a radial gradient of the order of R−1.1, clearly slower than the one reported in Figure 30 or that can be inferred from results by Bavassano et al. (1982b) confirming that the turbulence evolution in the polar wind is slower than the one in the ecliptic, as qualitatively predicted by Bruno (1992), because of the lack of large scale stream shears. However, these results will be discussed more extensively in in Section 4.1.
Left panel: power density spectra of magnetic field fluctuations observed by Helios 2 between 0.3 and 1 AU within the trailing edge of the same corotating stream shown in Figure 16, during the first mission to the Sun in 1976 and by Ulysses between 1.4 and 4.8 AU during the ecliptic phase. Ulysses observations at 4.8 AU refer to the end of 1991 while observations taken at 1.4 AU refer to the end of August of 2007. While the spectral index of slow wind does not show any radial dependence, the spectral break, clearly present in fast wind and marked by a blue dot, moves to lower and lower frequency as the heliocentric distance increases. Image adapted from Bruno et al. (2009).
However, the phenomenology described above only apparently resembles hydrodynamic turbulence where the large eddies, below the frequency break, govern the whole process of energy cascade along the spectrum (Tu and Marsch, (1995b). As a matter of fact, when the relaxation time increases, the largest eddies provide the energy to be transferred along the spectrum and dissipated, with a decay rate approximately equal to the transfer rate and, finally, to the dissipation rate at the smallest wavelengths where viscosity dominates. Thus, we expect that the energy containing scales would loose energy during this process but would not become part of the turbulent cascade, say of the inertial range. Scales on both sides of the frequency break would remain separated. Accurate analysis performed in the solar wind (Bavassano et al., (1982b; Marsch and Tu, (1990b; Roberts, (1992) have shown that the low frequency range of the solar wind magnetic field spectrum radially evolves following the WKB model, or geometrical optics, which predicts a radial evolution of the power associated with the fluctuations ~ r−3. Moreover, a steepening of the spectrum towards a Kolmogorov like spectral index can be observed. On the contrary, the same in-situ observations established that the radial decay for the higher frequencies was faster than ~r−3 and the overall spectral slope remained unchanged. This means that the energy contained in the largest eddies does not decay as it would happen in hydrodynamic turbulence and, as a consequence, the largest eddies cannot be considered equivalent to the energy containing eddies identified in hydrodynamic turbulence So, this low frequency range is not separated from the inertial range but becomes part of it as the turbulence ages. These observations cast some doubts on the applicability of hydrodynamic turbulence paradigm to interplanetary MHD turbulence A theoretical help came from adopting a local energy transfer function (Tu et al., (1984; Tu, (1987a,b, (1988), which would take into account the non-linear effects between eddies of slightly differing wave numbers, together with a WKB description which would mainly work for the large scale fluctuations. This model was able to reproduce the displacement of the frequency break with distance by combining the linear WKB law and a model of nonlinear coupling besides most of the features observed in the magnetic power spectra P(f, r) observed by Bavassano et al. (1982b). In particular, the concept of the “frequency break”, just mentioned, was pointed out for the first time by Tu et al. (1984) who, developing the analytic solution for the radially evolving power spectrum P(f, r) of fluctuations, obtained a critical frequency “fc” such that for frequencies f ≪ fc, P(f, r) ∝ f−1 and for f≫ fc, P(f, r) ∝ f−1.5.
Radial dependence of the frequency break observed in the ecliptic within fast wind as shown in the previous Figure 29. The radial dependence seems to be governed by a power-law of the order of R−1.5.
3.1.4 Fluctuations anisotropy
Interplanetary magnetic field (IMF) and velocity fluctuations are rather anisotropic as for the first time observed by Belcher and Davis Jr (1971); Belcher and Solodyna (1975); Chang and Nishida (1973); Burlaga and Turner (1976); Solodyna and Belcher (1976); Parker (1980); Bavassano et al. (1982a); Tu et al. (1989a); and Marsch and Tu (1990a). This feature can be better observed if fluctuations are rotated into the minimum variance reference system (see Appendix D).
Sonnerup and Cahill (1967) introduced the minimum variance analysis which consists in determining the eigenvectors of the matrix
where i and j denote the components of magnetic field along the axes of a given reference system. The statistical properties of eigenvalues approximately satisfy the following statements:
-
One of the eigenvalues of the variance matrix is always much smaller than the others, say λ1 ≪ (λ2, λ3), and the corresponding eigenvector Ṽ1 is the minimum-variance direction (see Appendix D.1 for more details). This indicates that, at least locally, the magnetic fluctuations are confined in a plane perpendicular to the minimum-variance direction.
-
In the plane perpendicular to Ṽ1, fluctuations appear to be anisotropically distributed, say λ3 > λ2. Typical values for eigenvalues are λ3 : λ2 : λ1 = 10 : 3.5 : 1.2 (Chang and Nishida, (1973; Bavassano et al., (1982a).
-
The direction Ṽ1 is nearly parallel to the average magnetic field B0, that is, the distribution of the angles between Ṽ1 and B0 is narrow with width of about 10° and centered around zero.
As shown in Figure 31, in this new reference system it is readily seen that the maximum and intermediate components have much more power compared with the minimum variance component. Generally, this kind of anisotropy characterizes Alfvénic intervals and, as such, it is more commonly found within high velocity streams (Marsch and Tu, (1990a).
A systematic analysis for both magnetic and velocity fluctuations was performed by Klein et al. (1991, (1993) between 0.3 and 10 AU. These studies showed that magnetic field and velocity minimum variance directions are close to each other within fast wind and mainly clustered around the local magnetic field direction. The effects of expansion are such as to separate field and velocity minimum variance directions. While magnetic field fluctuations keep their minimum variance direction loosely aligned with the mean field direction, velocity fluctuations tend to have their minimum variance direction oriented along the radial direction. The depleted alignment to the background magnetic field would suggest a smaller anisotropy of the fluctuations. As a matter of fact, Klein et al. (1991) found that the degree of anisotropy, which can be defined as the ratio between the power perpendicular to and that along the minimum variance direction, decreases with heliocentric distance in the outer heliosphere.
At odds with these conclusions were the results by Bavassano et al. (1982a) who showed that the ratio λ1/λ3, calculated in the inner heliosphere within a co-rotating high velocity stream, clearly decreased with distance, indicating that the degree of magnetic anisotropy increased with distance Moreover, this radial evolution was more remarkable for fluctuations of the order of a few hours than for those around a few minutes. Results by Klein et al. (1991) in the outer heliosphere and by Bavassano et al. (1982a) in the inner heliosphere remained rather controversial until recent studies (see Section 10.2), performed by Bruno et al. (1999b), found a reason for this discrepancy.
A different approach to anisotropic fluctuations in solar wind turbulence have been made by Bigazzi et al. (2006) and Sorriso-Valvo et al. (2006, (2010b). In these studies the full tensor of the mixed second-order structure functions has been used to quantitatively measure the degree of anisotropy and its effect on small-scale turbulence through a fit of the various elements of the tensor on a typical function (Sorriso-Valvo et al., (2006). Moreover three different regions of the near-Earth space have been studied, namely the solar wind, the Earth’s foreshock and magnetosheath showing that, while in the undisturbed solar wind the observed strong anisotropy is mainly due to the largescale magnetic field, near the magnetosphere other sources of anisotropy influence the magnetic field fluctuations (Sorriso-Valvo et al., (2010b).
Power density spectra of the three components of IMF after rotation into the minimum variance reference system. The black curve corresponds to the minimum variance component, the blue curve to the maximum variance, and the red one to the intermediate component. This case refers to fast wind observed at 0.3 AU and the minimum variance direction forms an angle of ~ 8° with respect to the ambient magnetic field direction. Thus, most of the power is associated with the two components quasi-transverse to the ambient field.
3.1.5 Simulations of anisotropic MHD
In the presence of a DC background magnetic field B0 which, differently from the bulk velocity field, cannot be eliminated by a Galilean transformation, MHD incompressible turbulence becomes anisotropic (Shebalin et al., (1983; Montgomery, (1982; Zank and Matthaeus, (1992; Carbone and Veltri, (1990; Oughton, (1993). The main effect produced by the presence of the background field is to generate an anisotropic distribution of wave vectors as a consequence of the dependence of the characteristic time for the non-linear coupling on the angle between the wave vector and the background field. This effect can be easily understood if one considers the MHD equation. Due to the presence of a term (B0 · ∇)z±, which describes the convection of perturbations in theaverage magnetic field, the non-linear interactions between Alfvénic fluctuations are weakened, since convection decorrelates the interacting eddies on a time of the order (k · B0)−1. Clearly fluctuations with wave vectors almost perpendicular to B0 are interested by such an effect much less than fluctuations with k ∥ B0. As a consequence, the former are transferred along the spectrum much faster than the latter (Shebalin et al., (1983; Grappin, (1986; Carbone and Veltri, (1990).
To quantify anisotropy in the distribution of wave vectors k for a given dynamical variable Q(k, t) (namely the energy, cross-helicity, etc.), it is useful to introduce the parameter
(Shebalin et al., (1983; Carbone and Veltri, (1990), where the average of a given quantity g(k) is defined as
For a spectrum with wave vectors perpendicular to B0 we have a spectral anisotropy Ω = 90°, while for an isotropic spectrum Ω = 45°. Numerical simulations in 2D configuration by Shebalin et al. (1983) confirmed the occurrence of anisotropy, and found that anisotropy increases with the Reynolds number. Unfortunately, in these old simulations, the Reynolds numbers used are too small to achieve a well defined spectral anisotropy. Carbone and Veltri (1990) started from the spectral equations obtained through the Direct Interaction Approximation closure by Veltri et al. (1982), and derived a shell model analogous for the anisotropic MHD turbulence Of course the anisotropy is over-simplified in the model, in particular the Alfvén time is assumed isotropic. However, the model was useful to investigate spectral anisotropy at very high Reynolds numbers. The phenomenological anisotropic spectrum obtained from the model, for both pseudo-energies obtained through polarizations a = 1, 2 defined through Equation (18), can be written as
The spectral anisotropy is different within the injection, inertial, and dissipative ranges of turbulence (Carbone and Veltri, (1990). Wave vectors perpendicular to B0 are present in the spectrum, but when the process of energy transfer generates a strong anisotropy (at small times), a competing process takes place which redistributes the energy over all wave vectors. The dynamical balance between these tendencies fixes the value of the spectral anisotropy Ω ≃ 55° in the inertial range. On the contrary, since the redistribution of energy cannot take place, in the dissipation domain the spectrum remains strongly anisotropic, with Ω ≃ 80°. When the Reynolds number increases, the contribution of the inertial range extends, and the increases of the total anisotropy tends to saturate at about Ω ≃ 60° at Reynolds number of 105. This value corresponds to a rather low value for the ratio between parallel and perpendicular correlation lengths ℓ∥/ℓ⊥ ≥ 2, too small with respect to the observed value ℓ∥/ℓ⊥ ≥ 10. This suggests that the non-linear dynamical evolution of an initially isotropic spectrum of turbulence is perhaps not sufficient to explain the observed anisotropy. These results have been confirmed numerically (Oughton et al., (1994).
3.1.6 Spectral anisotropy in the solar wind
The correlation time, as defined in Appendix A, estimates how much an element of our time series x(t) at time t1 depends on the value assumed by x(t) at time t0, being t1 = t0 + δt. This concept can be transferred from the time domain to the space domain if we adopt the Taylor hypothesis and, consequently, we can talk about spatial scales.
Correlation lengths in the solar wind generally increase with heliocentric distance (Matthaeus and Goldstein, (1982b; Bruno and Dobrowolny, (1986), suggesting that large scale correlations are built up during the wind expansion. This kind of evolution is common to both fast and slow wind as shown in Figure 32, where we can observe the behavior of the Bz correlation function for fast and slow wind at 0.3 and 0.9 AU.
Moreover, the fast wind correlation functions decrease much faster than those related to slow wind. This behavior reflects also the fact that the stochastic character of Alfvénic fluctuations in the fast wind is very efficient in decorrelating the fluctuations of each of the magnetic field components.
More detailed studies performed by Matthaeus et al. (1990) provided for the first time the twodimensional correlation function of solar wind fluctuations at 1 AU. The original dataset comprised approximately 16 months of almost continuous magnetic field 5-min averages. These results, based on ISEE 3 magnetic field data, are shown in Figure 33, also called the “The Maltese Cross”.
This figure has been obtained under the hypothesis of cylindrical symmetry. Real determination of the correlation function could be obtained only in the positive quadrant, and the whole plot was then made by mirroring these results on the remaining three quadrants. The iso-contour lines show contours mainly elongated along the ambient field direction or perpendicular to it. Alfvénic fluctuations with k ⊥ B0 contribute to contours elongated parallel to r⊥. Fluctuations in the two-dimensional turbulence limit (Montgomery, (1982) contribute to contours elongated parallel to r⊥. This two-dimensional turbulence is characterized for having both the wave vector k and the perturbing field δb perpendicular to the ambient field B0. Given the fact that the analysis did not select fast and slow wind, separately, it is likely that most of the slab correlations came from the fast wind while the 2D correlations came from the slow wind. As a matter of fact, Dasso et al. (2005), using 5 years of spacecraft observations at roughly 1 AU, showed that fast streams are dominated by fluctuations with wavevectors quasi-parallel to the local magnetic field, while slow streams are dominated by quasi-perpendicular fluctuation wavevectors. Anisotropic turbulence has been observed in laboratory plasmas and reverse pinch devices (Zweben et al., (1979).
Bieber et al. (1996) formulated an observational test to distinguish the slab (Alfvénic) from the 2D component within interplanetary turbulence These authors assumed a mixture of transverse fluctuations, some of which have wave vectors perpendicular k ⊥ B0 and polarization of fluctuations δB(k⊥) perpendicular to both vectors (2D geometry with k ∥ ≃ 0), and some parallel to the mean magnetic field k ∥ B0, the polarization of fluctuations δB(k∥) being perpendicular to the direction of B0 (slab geometry with k⊥ ≃ 0). The magnetic field is then rotated into the same mean field coordinate system used by Belcher and Davis Jr (1971) and Belcher and Solodyna (1975), where the y-coordinate is perpendicular to both B0 and the radial direction, while the x-coordinate is perpendicular to B0 but with a component also in the radial direction. Using that geometry, and defining the power spectrum matrix as
it can be found that, assuming axisymmetry, a two-component model can be written in the frequency domain
where the anisotropic energy spectrum is the sum of both components:
Here f is the frequency, Cs is a constant defining the overall spectrum amplitude in wave vector space, Uw is the bulk solar wind speed and ψ is the angle between B0 and the wind direction. Finally, r is the fraction of slab components and (1 − r) is the fraction of 2D components.
Contour plot of the 2D correlation function of interplanetary magnetic field fluctuations as a function of parallel and perpendicular distance with respect to the mean magnetic field. The separation in r∥ and r⊥ is in units of 1010 cm. Image reproduced by permission from Matthaeus et al. (1990), copyright by AGU.
The ratio test adopted by these authors was based on the ratio between the reduced perpendicular spectrum (fluctuations ⊥ to the mean field and solar wind flow direction) and the reduced quasi-parallel spectrum (fluctuations ⊥ to the mean field and in the plane defined by the mean field and the flow direction). This ratio, expected to be 1 for slab turbulence, resulted to be ~ 1.4 for fluctuations within the inertial range, consistent with 74% of 2D turbulence and 26% of slab. A further test, the anisotropy test, evaluated how the spectrum should vary with the angle between the mean magnetic field and the flow direction of the wind. The measured slab spectrum should decrease with the field angle while the 2D spectrum should increase, depending on how these spectra project on the flow direction. The results from this test were consistent with with 95% of 2D turbulence and 5% of slab. In other words, the slab turbulence due to Alfvénic fluctuations would be a minor component of interplanetary MHD turbulence A third test derived from Mach number scaling associated with the nearly incompressible theory (Zank and Matthaeus, (1992), assigned the same fraction ~ 80% to the 2D component. However, the data base for this analysis was derived from Helios magnetic measurements, and all data were recorded near times of solar energetic particle events. Moreover, the quasi totality of the data belonged to slow solar wind (Wanner and Wibberenz, (1993) and, as such, this analysis cannot be representative of the whole phenomenon of turbulence in solar wind. As a matter of fact, using Ulysses observations, Smith (2003) found that in the polar wind the percentage of slab and 2D components is about the same, say the high latitude slab component results unusually higher as compared with ecliptic observations.
Successive theoretical works by Ghosh et al. (1998a,b) in which they used compressible models in large variety of cases were able to obtain, in some cases, parallel and perpendicular correlations similar to those obtained in the solar wind. However, they concluded that the “Maltese” cross does not come naturally from the turbulent evolution of the fluctuations but it strongly depends on the initial conditions adopted when the simulation starts. It seems that the existence of these correlations in the initial data represents an unavoidable constraint. Moreover, they also stressed the importance of time-averaging since the interaction between slab waves and transverse pressurebalanced magnetic structures causes the slab turbulence to evolve towards a state in which a two-component correlation function emerges during the process of time averaging.
The presence of two populations, i.e., a slab-like and a quasi-2D like, was also inferred by Dasso et al. (2003). These authors computed the reduced spectra of the normalized cross-helicity and the Alfvén ratio from ACE dataset. These parameters, calculated for different intervals of the angle θ between the flow direction and the orientation of the mean field B0, showed a remarkable dependence on θ.
The geometry used in these analyses assumes that the energy spectrum in the rest frame of the plasma is axisymmetric and invariant for rotations about the direction of B0. Even if these assumption are good when we want to translate results coming from 2D numerical simulations to 3D geometry, these assumptions are quite in contrast with the observational fact that the eigenvalues of the variance matrix are different, namely λ3 ≠ λ2.
Going back from the correlation tensor to the power spectrum is a complicated technical problem. However, Carbone et al. (1995a) derived a description of the observed anisotropy in terms of a model for the three-dimensional energy spectra of magnetic fluctuations. The divergence-less of the magnetic field allows to decompose the Fourier amplitudes of magnetic fluctuations in two independent polarizations: The first one I[1](k) corresponds, in the weak turbulence theory, to the Alfvénic mode, while the second polarization I[2](k) corresponds to the magnetosonic mode. By using only the hypothesis that the medium is statistically homogeneous and some algebra, authors found that the energy spectra of both polarizations can be related to the two-points correlation tensor and to the variance matrix. Through numerical simulations of the shell model (see later in the review) it has been shown that the anisotropic energy spectrum can be described in the inertial range by a phenomenological expression
where ki are the Cartesian components of the wave vector k, and Cs, ℓ [s]i , and μs (s = 1, 2 indicates both polarizations; i = x, y, z) are free parameters. In particular, Cs gives information on the energy content of both polarizations, ℓ [s]i represent the spectral extensions along the direction of a given system of coordinates, and μs are two spectral indices.
A fit to the eigenvalues of the variance matrix allowed Carbone et al. (1995a) to fix the free parameters of the spectrum for both polarizations. They used data from Bavassano et al. (1982a) who reported the values of λi at five wave vectors calculated at three heliocentric distances, selecting periods of high correlation (Alfvénic periods) using magnetic field measured by the Helios 2 spacecraft. They found that the spectral indices of both polarizations, in the range 1.1 ≤ μ1 ≤ 1.3 and 1.46 ≤ μ2 ≤ 1.8 increase systematically with increasing distance from the Sun, the polarization [2] spectra are always steeper than the corresponding polarization [1] spectra, while polarization [1] is always more energetic than polarization [2]. As far as the characteristic lengths are concerned, it can be found that ℓ [1]x > ℓ [1]y ≫ ℓz[1], indicating that wave vectors k ∥ B0 largely dominate. Concerning polarization [2], it can be found that ℓx[2] ≫ ℓ [2]y ≃ ∓ [2]z , indicating that the spectrum I[2](k) is strongly flat on the plane defined by the directions of B0 and the radial direction. Within this plane, the energy distribution does not present any relevant anisotropy.
Let us compare these results with those by Matthaeus et al. (1990), the comparison being significant as far as the plane yz is taken into account. The decomposition of Carbone et al. (1995a) in two independent polarizations is similar to that of Matthaeus et al. (1990), a contour plot of the trace of the correlation tensor Fourier transform T(k) = I[1](k) + I[2](k) on the plane (ky; kz) shows two populations of fluctuations, with wave vectors nearly parallel and nearly perpendicular to B0, respectively. The first population is formed by all the polarization [1] fluctuations and by the fluctuations with k ∥ B0 belonging to polarization [2]. The latter fluctuations are physically indistinguishable from the former, in that when k is nearly parallel to B0, both polarization vectors are quasi-perpendicular to B0. On the contrary, the second population is almost entirely formed by fluctuations belonging to polarization [2]. While it is clear that fluctuations with k nearly parallel to B0 are mainly polarized in the plane perpendicular to B0 (a consequence of ∇ · B = 0), fluctuations with k nearly perpendicular to B0 are polarized nearly parallel to B0.
Although both models yield to the occurrence of two populations, Matthaeus et al. (1990) give an interpretation of their results which is in contrast with that of Carbone et al. (1995a). Namely Matthaeus et al. (1990) suggest that a nearly 2D incompressible turbulence characterized by wave vectors and magnetic fluctuations, both perpendicular to B0, is present in the solar wind. However, this interpretation does not arise from data analysis, rather from the 2D numerical simulations by Shebalin et al. (1983) and from analytical studies (Montgomery, (1982). Let us note, however, that in the former approach, which is strictly 2D, when k ⊥ B0 magnetic fluctuations are necessarily parallel to B0. In the latter one, along with incompressibility, it is assumed that the energy in the fluctuations is much less than in the DC magnetic field; both hypotheses do not apply to the solar wind case. On the contrary, results by Carbone et al. (1995a) can be directly related to the observational data. In any case, it is worth reporting that a model like that discussed here, that is a superposition of fluctuations with both slab and 2D components, has been used to describe turbulence also in the Jovian magnetosphere (Saur et al., (2002, (2003). In addition, several theoretical and observational works indicate that there is a competition between the radial axis and the mean field axis in shaping the polarization and spectral anisotropies in the solar wind.
In this respect, Grappin and Velli (1996) used numerical simulations of MHD equations which included expansion effects (Expanding Box Model) to study the formation of anisotropy in the wind and the interaction of Alfvén waves within a transverse magnetic structures. These authors found that a large-scale isotropic Alfvénic eddy stretched by expansion naturally mixes with smaller scale transverse Alfvén waves with a different anisotropy.
Saur and Bieber (1999), on the other hand, employed three different tests on about three decades of solar wind observations at 1 AU in order to better understand the anisotropic nature of solar wind fluctuations. Their data analysis strongly supported the composite model of a turbulence made of slab and 2-D fluctuations.
Narita et al. (2011b), using the four Cluster spacecraft, determined the three-dimensional wavevector spectra of fluctuating magnetic fields in the solar wind within the inertial range. These authors found that the spectra are anisotropic throughout the analyzed frequency range and the power is extended primarily in the directions perpendicular to the mean magnetic field, as might be expected of 2-D turbulence, however, the analyzed fluctuations cannot be considered axisymmetric.
Finally, Turner et al. (2011) suggested that the non-axisymmetry anisotropy of the frequency spectrum observed using in-situ observations may simply arise from a sampling effect related to the fact that the s/c samples three dimensional fluctuations as a one-dimensional series and that the energy density is not equally distributed among the different scales (i.e., spectral index > 1).
3.1.7 Magnetic helicity
Magnetic helicity Hm, as defined in Appendix B.1, measures the “knottedness” of magnetic field lines (Moffatt, (1978). Moreover, Hm is a pseudo scalar and changes sign for coordinate inversion. The plus or minus sign, for circularly polarized magnetic fluctuations in a slab geometry, indicates right or left-hand polarization. Statistical information about the magnetic helicity is derived from the Fourier transform of the magnetic field auto-correlation matrix Rij(r) = 〈Bi(x) · Bj(x+r)〉 as shown by Matthaeus and Goldstein (1982b). While the trace of the symmetric part of the spectral matrix accounts for the magnetic energy, the imaginary part of the spectral matrix accounts for the magnetic helicity (Batchelor, (1970; Montgomery, (1982; Matthaeus and Goldstein, (1982b). However, what is really available from in-situ measurements in space experiments are data from a single spacecraft, and we can obtain values of R only for collinear sequences of r along the x direction which corresponds to the radial direction from the Sun. In these conditions the Fourier transform of R allows us to obtain only a reduced spectral tensor along the radial direction so that Hm(k) will depend only on the wave-number k in this direction. Although the reduced spectral tensor does not carry the complete spectral information of the fluctuations, for slab and isotropic symmetries it contains all the information of the full tensor. The expression used by Matthaeus and Goldstein (1982b) to compute the reduced Hm is given in Appendix B.2. In the following, we will drop the suffix r for sake of simplicity.
The general features of the reduced magnetic helicity spectrum in the solar wind were described for the first time by Matthaeus and Goldstein (1982b) in the outer heliosphere, and by Bruno and Dobrowolny (1986) in the inner heliosphere. A useful dimensionless way to represent both the degree of and the sense of polarization is the normalized magnetic helicity σm (see Appendix B.2). This quantity can randomly vary between +1 and −1, as shown in Figure 34 from the work by Matthaeus and Goldstein (1982b) and relative to Voyager’s data taken at 1 AU. However, net values of ±1 are reached only for pure circularly polarized waves.
Based on these results, Goldstein et al. (1991) were able to reproduce the distribution of the percentage of occurrence of values of σm(f) adopting a model where the magnitude of the magnetic field was allowed to vary in a random way and the tip of the vector moved near a sphere. By this way they showed that the interplanetary magnetic field helicity measurements were inconsistent with the previous idea that fluctuations were randomly circularly polarized at all scales and were also magnitude preserving.
σm vs. frequency and wave number relative to an interplanetary data sample recorded by Voyager 1 at approximately 1 AU. Image reproduced by permission from Matthaeus and Goldstein (1982b), copyright by AGU.
However, evidence for circular polarized MHD waves in the high frequency range was provided by Polygiannakis et al. (1994), who studied interplanetary magnetic field fluctuations from various datasets at various distances ranging from 1 to 20 AU. They also concluded that the difference between left- and right-hand polarizations is significant and continuously varying.
As already noticed by Smith et al. (1983, (1984), knowing the sign of σm and the sign of the normalized cross-helicity σc it is possible to infer the sense of polarization of the fluctuations. As a matter of fact, a positive cross-helicity indicates an Alfvén mode propagating outward, while a negative cross-helicity indicates a mode propagating inward. On the other hand, we know that a positive magnetic-helicity indicates a right-hand polarized mode, while a negative magnetichelicity indicates a left-hand polarized mode. Thus, since the sense of polarization depends on the propagating direction with respect to the observer, σm(f)σc(f) < 0 will indicate right circular polarization while σm(f)σc(f) > 0 will indicate left circular polarization. Thus, each time magnetic helicity and cross-helicity are available from measurements in a super-Alfvénic flow, it is possible to infer the rest frame polarization of the fluctuations from a single point measurements, assuming the validity of the slab geometry.
The high variability of σm, observable in Voyager’s data (see Figure 34), was equally observed in Helios 2 data in the inner heliosphere (Bruno and Dobrowolny, (1986). The authors of this last work computed the difference (MH > 0) − |MH < 0| of magnetic helicity for different frequency bands and noticed that most of the resulting magnetic helicity was contained in the lowest frequency band. This result supported the theoretical prediction of an inverse cascade of magnetic helicity from the smallest to the largest scales during turbulence development (Pouquet et al., (1976).
Numerical simulations of the incompressible MHD equations by Mininni et al. (2003a), discussed in Section 3.1.9, clearly confirm the tendency of magnetic helicity to follow an inverse cascade. The generation of magnetic field in turbulent plasmas and the successive inverse cascade has strong implications in the emergence of large scale magnetic fields in stars, interplanetary medium and planets (Brandenburg, (2001).
This phenomenon was firstly demonstrated in numerical simulations based on the eddy damped quasi normal Markovian (EDQNM) closure model of three-dimensional MHD turbulence by Pouquet et al. (1976). Successively, other investigators confirmed such a tendency for the magnetic helicity to develop an inverse cascade (Meneguzzi et al., (1981; Cattaneo and Hughes, (1996; Brandenburg, (2001).
Mininni et al. (2003a) performed the first direct numerical simulations of turbulent Hall dynamo. They showed that the Hall current can have strong effects on turbulent dynamo action, enhancing or even suppressing the generation of the large-scale magnetic energy. These authors injected a weak magnetic field at small scales in a system kept in a stationary regime of hydrodynamic turbulence and followed the exponential growth of magnetic energy due to the dynamo action. This evolution can be seen in Figure 35 in the same format described for Figure 40, shown in Section 3.1.9. Now, the forcing is applied at wave number kforce = 10 in order to give enough room for the inverse cascade to develop. The fluid is initially in a strongly turbulent regime as a result of the action of the external force at wave number kforce = 10. An initial magnetic fluctuation is introduced at t = 0 at kseed = 35. The magnetic energy starts growing exponentially fast and, when the saturation is reached, the magnetic energy is larger than the kinetic energy. Notably, it is much larger at the largest scales of the system (i.e., k = 1). At these large scales, the system is very close to a magnetostatic equilibrium characterized by a force-free configuration.
mpg-Movie (1752.1640625 KB) Still from a movie showing A numerical simulation of the incompressible MHD equations in three dimensions, assuming periodic boundary conditions (see details in Mininni et al., (2003a). The left panel shows the power spectra for kinetic energy (green), magnetic energy (red), and total energy (blue) vs. time. The right panel shows the spatially integrated kinetic, magnetic, and total energies vs. time. The vertical (orange) line indicates the current time. These results correspond to a 1283 simulation with an external force applied at wave number kforce = 10 (movie kindly provided by D. Gómez). (For video see appendix)
3.1.8 Alfvén correlations as incompressive turbulence
In a famous paper, Belcher and Davis Jr (1971) showed that a strong correlation exists between velocity and magnetic field fluctuations, in the form
where the sign of the correlation is given by the sign[−k · B0], being k the wave vector and B0 the background magnetic field vector. These authors showed that in about 25 d of data from Mariner 5, out of the 160 d of the whole mission, fluctuations were described by Equation (59), and the sign of the correlation was such to indicate always an outward sense of propagation with respect to the Sun. Authors also noted that these periods mainly occur within the trailing edges of high-speed streams. Moreover, in the regions where Equation (59) is verified to a high degree, the magnetic field magnitude is almost constant (B2 ~ const.).
Today we know that Alfvén correlations are ubiquitous in the solar wind and that these correlations are much stronger and are found at lower and lower frequencies, as we look at shorter and shorter heliocentric distances. In the right panel of Figure 36 we show results from Belcher and Solodyna (1975) obtained on the basis of 5 min averages of velocity and magnetic field recorded by Mariner 5 in 1967, during its mission to Venus. On the left panel of Figure 36 we show results from a similar analysis performed by Bruno et al. (1985) obtained on the basis of 1 h averages of velocity and magnetic field recorded by Helios 2 in 1976, when the s/c was at 0.29 AU from the Sun. These last authors found that, in their case, Alfvén correlations extended to time periods as low as 15 h in the s/c frame at 0.29 AU, and to periods a factor of two smaller near the Earth’s orbit. Now, if we think that this long period of the fluctuations at 0.29 AU was larger than the transit time from the Sun to the s/c, this results might be the first evidence for a possible solar origin for these fluctuations, probably caused by the shuffling of the foot-points of the solar surface magnetic field.
Alfvénic modes are not the only low frequency plasma fluctuations allowed by the MHD equations but they certainly are the most frequent fluctuations observed in the solar wind. The reason why other possible propagating modes like the slow sonic mode and the fast magnetosonic mode cannot easily be found, besides the fact that the eigenvectors associated with these modes are not directly identifiable because they necessitate prior identification of wavevectors, contrary to the simple Alfvénic eigenvectors, depends also on the fact that these compressive modes are strongly damped in the solar wind shortly after they are generated (see Section 6). On the contrary, Alfvén fluctuations, which are difficult to be damped because of their incompressive nature, survive much longer and dominate solar wind turbulence Nevertheless, there are regions where Alfvén correlations are much stronger like the trailing edge of fast streams, and regions where these correlations are weak like intervals of slow wind (Belcher and Davis Jr, (1971; Belcher and Solodyna, (1975). However, the degree of Alfvén correlations unavoidably fades away with increasing heliocentric distance, although it must be reported that there are cases when the absence of strong velocity shears and compressive phenomena favor a high Alfvén correlation up to very large distances from the Sun (Roberts et al., (1987a; see Section 5.1).
Just to give a qualitative quick example about Alfvénic correlations in fast and slow wind, we show in Figure 37 the speed profile for about 100 d of 1976 as observed by Helios 2, and the traces of velocity and magnetic field Z components (see Appendix D for the orientation of the reference system) VZ and BZ (this last one expressed in Alfvén units, see Appendix B.1) for two different time intervals, which have been enlarged in the two inserted small panels. The high velocity interval shows a remarkable anti-correlation which, since the mean magnetic field B0 is oriented away from the Sun, suggests a clear presence of outward oriented Alfvénic fluctuations given that the sign of the correlation is the sign[−k · B0]. At odds with the previous interval, the slow wind shows that the two traces are rather uncorrelated. For sake of brevity, we omit to show the very similar behavior for the other two components, within both fast and slow wind.
The discovery of Alfvén correlations in the solar wind stimulated fundamental remarks by Kraichnan (1974) who, following previous theoretical works by Kraichnan (1965) and Iroshnikov (1963), showed that the presence of a strong correlation between velocity and magnetic fluctuations renders non-linear transfer to small scales less efficient than for the Navier-Stokes equations, leading to a turbulent behavior which is different from that described by Kolmogorov (1941). In particular, when Equation (59) is exactly satisfied, non-linear interactions in MHD turbulent flows cannot exist. This fact introduces a problem in understanding the evolution of MHD turbulence as observed in the interplanetary space Both a strong correlation between velocity and magnetic fluctuations and a well defined turbulence spectrum (Figures 29, 37) are observed, and the existence of the correlations is in contrast with the existence of a spectrum which in turbulence is due to a non-linear energy cascade. Dobrowolny et al. (1980b) started to solve the puzzle on the existence of Alfvén turbulence, say the presence of predominately outward propagation and the fact that MHD turbulence with the presence of both Alfvén modes present will evolve towards a state where one of the mode disappears. However, a lengthy debate based on whether the highly Alfvén nature of fluctuations is what remains of the turbulence produced at the base of the corona or the solar wind itself is an evolving turbulent magnetofluid, has been stimulating the scientific community for quite a long time.
3.1.9 Radial evolution of Alfvénic turbulence
The degree of correlation not only depends on the type of wind we look at, i.e., fast or slow, but also on the radial distance from the Sun and on the time scale of the fluctuations.
Figure 38 shows the radial evolution of σc (see Appendix B.1) as observed by Helios and Voyager s/c (Roberts et al., (1987b). It is clear enough that σc not only tends to values around 0 as the heliocentric distance increases, but larger and larger time scales are less and less Alfvénic. Values of σc ~ 0 suggest a comparable amount of “outward” and “inward” correlations.
The radial evolution affects also the Alfvén ratio rA (see Appendix B.3.1) as it was found by Bruno et al. (1985). However, early analyses (Belcher and Davis Jr, (1971; Solodyna and Belcher, (1976; Matthaeus and Goldstein, (1982b) had already shown that this parameter is usually less than unit. Spectral studies by Marsch and Tu (1990a), reported in Figure 39, showed that within slow wind it is the lowest frequency range the one that experiences the strongest decrease with distance, while the highest frequency range remains almost unaffected. Moreover, the same study showed that, within fast wind, the whole frequency range experiences a general depletion. The evolution is such that close to 1 AU the value of rA in fast wind approaches that in slow wind.
Moreover, comparing these results with those by Matthaeus and Goldstein (1982b) obtained from Voyager at 2.8 AU, it seems that the evolution recorded within fast wind tends to a sort of limit value around 0.4 ∓ 0.5.
Also Roberts et al. (1990), analyzing fluctuations between 9 h and 3 d found a similar radial trend. These authors showed that rA dramatically decreases from values around unit at the Earth’s orbit towards 0.4 . 0.5 at approximately 8 AU. For larger heliocentric distances, rA seems to stabilize around this last value.
The reason why rA tends to a value less than unit is still an open question although MHD computer simulations (Matthaeus, (1986) showed that magnetic reconnection and high plasma viscosity can produce values of rA < 1 within the inertial range. Moreover, the magnetic energy excess can be explained as a competing action between the equipartition trend due to linear propagation (or Alfvén effect, Kraichnan (1965)), and a local dynamo effect due to non-linear terms (Grappin et al., (1991), see closure calculations by Grappin et al. (1983); DNS by Müller and Grappin (2005).
However, this argument forecasts an Alfvén ratio rA ≠ 1 but, it does not say whether it would be larger or smaller than “1”, i.e., we could also have a final excess of kinetic energy.
Histograms of normalized cross-helicity σc showing its evolution between 0.3 (circles), 2 (triangles), and 20 (squares) AU for different time scales: 3 h (top panel), 9 h (middle panel), and 81 h (bottom panel). Image Image reproduced by permission Roberts et al. (1987b, copyright by AGU.
Values of the Alfvén ratio rA as a function of frequency and heliocentric distance, within slow (left column) and fast (right column) wind. Image reproduced by permission from Marsch and Tu (1990a), copyright by AGU.
Similar unbalance between magnetic and kinetic energy has recently been found in numerical simulations by Mininni et al. (2003a), already cited in Section 3.1.7. These authors studied the effect of a weak magnetic field at small scales in a system kept in a stationary regime of hydrodynamic turbulence In these conditions, the dynamo action causes the initial magnetic energy to grow exponentially towards a state of quasi equipartition between kinetic and magnetic energy. This simulation was aiming to provide more insights on a microscopic theory of the alpha-effect, which is responsible to convert part of the toroidal magnetic field on the Sun back to poloidal to sustain the cycle. However, when the simulation saturates, the unbalance between kinetic and magnetic energy reminds the conditions in which the Alfvén ratio is found in interplanetary space Results from the above study can be viewed in the animation of Figure 40. At very early time the fluid is in a strongly turbulent regime as a result of the action of the external force at wave number kforce = 3. An initial magnetic fluctuation is introduced at t = 0 at kseed = 35. The magnetic energy starts growing exponentially fast and, when the simulation reaches the saturation stage, the magnetic power spectrum exceeds the kinetic power spectrum at large wave numbers (i.e., k > kforce), as also observed in Alfvénic fluctuations of the solar wind (Bruno et al., (1985; Tu and Marsch, (1990a) as an asymptotic state (Roberts et al., (1987a,b; Bavassano et al., (2000b) of turbulence
However, when the two-fluid effect, such as the Hall current and the electron pressure (Mininni et al., (2003b), is included in the simulation, the dynamo can work more efficiently and the final stage of the simulation is towards equipartition between kinetic and magnetic energy.
On the other hand, Marsch and Tu (1993a) analyzed several intervals of interplanetary observations to look for a linear relationship between the mean electromotive force ε = δVδB, generated by the turbulent motions, and the mean magnetic field B0, as predicted by simple dynamo theory (Krause and Rädler, (1980). Although sizable electromotive force was found in interplanetary fluctuations, these authors could not establish any simple linear relationship between B0 and ε.
Lately, Bavassano and Bruno (2000) performed a three-fluid analysis of solar wind Alfvénic fluctuations in the inner heliosphere, in order to evaluate the effect of disregarding the multifluid nature of the wind on the factor relating velocity and magnetic field fluctuations. It is well known that converting magnetic field fluctuations into Alfvén units we divide by the factor Fp = (4πMpNp)1/2. However, fluctuations in velocity tend to be smaller than fluctuations in Alfvén units. In Figure 41 we show scatter plots between the z-component of the Alfvén velocity and the proton velocity fluctuations. The z-direction has been chosen as the same of Vp×B, where Vp is the proton bulk flow velocity and B is the mean field direction. The reason for such a choice is due to the fact that this direction is the least affected by compressive phenomena deriving from the wind dynamics. These results show that although the correlation coefficient in both cases is around −0.95, the slope of the best fit straight line passes from 1 at 0.29 AU to a slope considerably different from 1 at 0.88 AU.
Scatter plot between the z-component of the Alfvén velocity and the proton velocity fluctuations at about 2 mHz. Data refer to Helios 2 observations at 0.29 AU (left panel) and 0.88 AU (right panel). Image adapted from Bavassano and Bruno (2000).
Belcher and Davis Jr (1971) suggested that this phenomenon had to be ascribed to the presence of α particles and to an anisotropy in the thermal pressure. Moreover, taking into account the multi-fluid nature of the solar wind, the dividing factor should become F = FpFiFa, where Fi would take into account the presence of other species besides protons, and Fa would take into account the presence of pressure anisotropy P∥ ≠ P⊥, where ∥ and ⊥ refer to the background field direction. In particular, following Bavassano and Bruno (2000), the complete expressions for Fi and Fi are
and
where the letter “s” stands for the s-th species, being Us = Vs − V its velocity in the center of mass frame of reference Vs is the velocity of the species “s” in the s/c frame and V = (ΣsMsNsVs)/(ΣsMsNs) is the velocity of the center of mass.
Bavassano and Bruno (2000) analyzed several time intervals within the same co-rotating high velocity stream observed at 0.3 and 0.9 AU and performed the analysis using the new factor “F” to express magnetic field fluctuations in Alfvén units, taking into account the presence of α particles and electrons, besides the protons. However, the correction resulted to be insufficient to bring back to “1” the slope of the δVPz ∓ δVAz relationship shown in the right panel of Figure 41. In conclusion, the radial variation of the Alfvén ratio rA towards values less than 1 is not completely due to a missed inclusion of multi-fluid effects in the conversion from magnetic field to Alfvén units. Thus, we are left with the possibility that the observed depletion of rA is due to a natural evolution of turbulence towards a state in which magnetic energy becomes dominant (Grappin et al., (1991; Roberts et al., (1992; Roberts, (1992), as observed in the animation of Figure 40 taken from numerical simulations by Mininni et al. (2003a) or, it is due to the increased presence of magnetic structures like MFDT (Tu and Marsch, (1993).
3.2 Turbulence studied via Elsässer variables
The Alfvénic character of solar wind fluctuations,especially within co-rotating high velocity streams, suggests to use the Elsässer variables (Appendix B.3) to separate the “outward” from the “inward” contribution to turbulence These variables, used in theoretical studies by Dobrowolny et al. (1980a,b); Veltri et al. (1982); Marsch and Mangeney (1987); and Zhou and Matthaeus (1989), were for the first time used in interplanetary data analysis by Grappin et al. (1990) and Tu et al. (1989b). In the following, we will describe and discuss several differences between “outward” and “inward” modes, but the most important one is about their origin. As a matter of fact, the existence of the Alfvénic critical point implies that only “outward” propagating waves of solar origin will be able to escape from the Sun. “Inward” waves, being faster than the wind bulk speed, will precipitate back to the Sun if they are generated before this point. The most important implication due to this scenario is that “inward” modes observed beyond the Alfvénic point cannot have a solar origin but they must have been created locally by some physical process. Obviously, for the other Alfvénic component, both solar and local origins are still possible.
3.2.1 Ecliptic scenario
Early studies by Belcher and Davis Jr (1971), performed on magnetic field and velocity fluctuations recorded by Mariner 5 during its trip to Venus in 1967, already suggested that the majority of the Alfvénic fluctuations are characterized by an “outward” sense of propagation, and that the best regions where to observe these fluctuations are the trailing edge of high velocity streams. Moreover, Helios spacecraft, repeatedly orbiting around the Sun between 0.3 to 1 AU, gave the first and unique opportunity to study the radial evolution of turbulence (Bavassano et al., (1982b; Denskat and Neubauer, (1983). Successively, when Elsässer variables were introduced in the analysis (Grappin et al., (1989), it was finally possible not only to evaluate the “inward” and “outward” Alfvénic contribution to turbulence but also to study the behavior of these modes as a function of the wind speed and radial distance from the Sun.
Figure 42 (Tu et al., (1990) clearly shows the behavior of e± (see Appendix B.3) across a high speed stream observed at 0.3 AU. Within fast wind e+ is much higher than e− and its spectral slope shows a break. Lower frequencies have a flatter slope while the slope of higher frequencies is closer to a Kolmogorov-like. e− has a similar break but the slope of lower frequencies follows the Kolmogorov slope, while higher frequencies form a sort of plateau.
This configuration vanishes when we pass to the slow wind where both spectra have almost equivalent power density and follow the Kolmogorov slope. This behavior, for the first time reported by Grappin et al. (1990), is commonly found within co-rotating high velocity streams, although much more clearly expressed at shorter heliocentric distances, as shown below.
Spectral power associated with outward (right panel) and inward (left panel) Alfvénic fluctuations, based on Helios 2 observations in the inner heliosphere, are concisely reported in Figure 43. The e− spectrum, if we exclude the high frequency range of the spectrum relative to fast wind at 0.4 AU, shows an average power law profile with a slope of −1.64, consistent with Kolmogorov’s scaling. The lack of radial evolution of e− spectrum brought Tu and Marsch (1990a) to name it “the background spectrum” of solar wind turbulence
Power density spectra e± computed from δz± fluctuations for different time intervals indicated by the arrows. Image reproduced by permission from Tu et al. (1990), copyright by AGU.
Power density spectra e− and e+ computed from δz− and δz+ fluctuations. Spectra have been computed within fast (H) and slow (L) streams around 0.4 and 0.9 AU as indicated by different line styles. The thick line represents the average power spectrum obtained from all the about 50 e− spectra, regardless of distances and wind speed. The shaded area is the 1σ width related to the average. Image reproduced by permission from Tu and Marsch (1990b), copyright by AGU.
Quite different is the behavior of e+ spectrum. Close to the Sun and within fast wind, this spectrum appears to be flatter at low frequency and steeper at high frequency. The overall evolution is towards the “background spectrum” by the time the wind reaches 0.8 AU.
In particular, Figure 43 tells us that the radial evolution of the normalized cross-helicity has to be ascribed mainly to the radial evolution of e+ rather than to both Alfvénic fluctuations (Tu and Marsch, (1990a). In addition, Figure 44, relative to the Elsässer ratio rE, shows that the hourly frequency range, up to ~ 2 × 10−3 Hz, is the most affected by this radial evolution.
Ratio of e− over e+ within fast wind at 0.3 and 0.9 AU in the left and right panels, respectively. Image reproduced by permission from Marsch and Tu (1990a), copyright by AGU.
As a matter of fact, this radial evolution can be inferred from Figure 45 where values of e− and e+ together with solar wind speed, magnetic field intensity, and magnetic field and particle density compression are shown between 0.3 and 1 AU during the primary mission of Helios 2. It clearly appears that enhancements of e− and depletion of e+ are connected to compressive events, particularly within slow wind. Within fast wind the average level of e− is rather constant during the radial excursion while the level of e+ dramatically decreases with a consequent increase of the Elsässer ratio (see Appendix B.3.1).
Further ecliptic observations (see Figure 46) do not indicate any clear radial trend for the Elsässer ratio between 1 and 5 AU, and its value seems to fluctuate between 0.2 and 0.4.
However, low values of the normalized cross-helicity can also be associated with a particular type of incompressive events, which Tu and Marsch (1991) called Magnetic Field Directional Turnings or MFDT. These events, found within slow wind, were characterized by very low values of δc close to zero and low values of the Alfvén ratio, around 0.2. Moreover, the spectral slope of e+, e− and the power associated with the magnetic field fluctuations was close to the Kolmogorov slope. These intervals were only scarcely compressive, and short period fluctuations, from a few minutes to about 40 min, were nearly pressure balanced. Thus, differently from what had previously been observed by Bruno et al. (1989), who found low values of cross-helicity often accompanied by compressive events, these MFDTs were mainly incompressive. In these structures most of the fluctuating energy resides in the magnetic field rather than velocity as shown in Figure 47 taken from Tu and Marsch (1991). It follows that the amplitudes of the fluctuating Alfvénic fields δz± result to be comparable and, consequently, the derived parameter σc → 0. Moreover, the presence of these structures would also be able to explain the fact that rA < 1. Tu and Marsch (1991) suggested that these fluctuations might derive from a special kind of magnetic structures, which obey the MHD equations, for which (B · ∇)B = 0, field magnitude, proton density, and temperature are all constant. The same authors suggested the possibility of an interplanetary turbulence mainly made of outwardly propagating Alfvén waves and convected structures represented by MFDTs. In other words, this model assumed that the spectrum of e− would be caused by MFDTs. The different radial evolution of the power associated with these two kind of components would determine the radial evolution observed in both σc and rA. Although the results were not quantitatively satisfactory, they did show a qualitative agreement with the observations.
Upper panel: solar wind speed and solar wind speed multiplied by σc. In the lower panels the authors reported: σc, rE, e−, e+, magnetic compression, and number density compression, respectively. Image reproduced by permission from Bruno and Bavassano (1991), copyright by AGU.
Ratio of e− over e+ within fast wind between 1 and 5 AU as observed by Ulysses in the ecliptic. Image reproduced by permission from Bavassano et al. (2001), copyright by AGU.
Left column: e+ and e− spectra (top) and σc (bottom) during a slow wind interval at 0.9 AU. Right column: kinetic eu and magnetic eB energy spectra (top) computed from the trace of the relative spectral tensor, and spectrum of the Alfvén ratio rA (bottom) Image reproduced by permission from Tu and Marsch (1991).
These convected structures are an important ingredient of the turbulent evolution of the fluctuations and can be identified as the 2D incompressible turbulence suggested by Matthaeus et al. (1990) and Tu and Marsch (1991).
As a matter of fact, a statistical analysis by Bruno et al. (2007) showed that magnetically dominated structures represent an important component of the interplanetary fluctuations within the MHD range of scales. As a matter of fact, these magnetic structures and Alfvénic fluctuations dominate at scales typical of MHD turbulence For instance, this analysis suggested that more than 20% of all analyzed intervals of 1 hr scale are magnetically dominated and only weakly Alfvénic. Observations in the ecliptic performed by Helios and WIND s/c and out of the ecliptic, performed by Ulysses, showed that these advected, mostly incompressive structures are ubiquitous in the heliosphere and can be found in both fast and slow wind.
It proves interesting enough to look at the radial evolution of interplanetary fluctuations in terms of normalized cross-helicity σc and normalized residual energy σr (see Appendix B.3).
These results, shown in the left panels of Figure 48, highlight the presence of a radial evolution of the fluctuations towards a double-peaked distribution during the expansion of the solar wind. The relative analysis has been performed on a co-rotating fast stream observed by Helios 2 at three different heliocentric distances over consecutive solar rotations (see Figure 16 and related text). Closer to the Sun, at 0.3 AU, the distribution is well centered around σr = 0 and σc = 1, suggesting that Alfvénic fluctuations, outwardly propagating, dominate the scenario. By the time the wind reaches 0.7 AU, the appearance of a tail towards negative values of σr and lower values of σc indicates a partial loss of the Alfvénic character in favor of fluctuations characterized by a stronger magnetic energy content. This clear tendency ends up with the appearance of a secondary peak by the time the wind reaches 0.88 AU. This new family of fluctuations forms around σr = −1 and σc = 0. The values of σr and σc which characterize this new population are typical of MFDT structures described by Tu and Marsch (1991). Together with the appearance of these fluctuations, the main peak characterized by Alfvén like fluctuations looses much of its original character shown at 0.3 AU. The yellow straight line that can be seen in the left panels of Figure 48 would be the linear relation between σr and σc in case fluctuations were made solely by Alfvén waves outwardly propagating and advected MFDTs (Tu and Marsch, (1991) and it would replace the canonical, quadratic relation σ 2r + σ 2c ≤ 1 represented by the yellow circle drawn in each panel. However, the yellow dashed line shown in the left panels of Figure 48 does not seem to fit satisfactorily the observed distributions.
Left, from top to bottom: frequency histograms of σr vs. σc (here σC and σR) for fast wind observed by Helios 2 at 0.29, 0.65 and 0.88 AU, respectively. The color code, for each panel, is normalized to the maximum of the distribution. The yellow circle represents the limiting value given by σ 2c σ 22 = 1 while, the yellow dashed line represents the relation σr = σr − 1, see text for details. Right, from top to bottom: frequency histograms of σr vs. σc (here σC and σR) for slow wind observed by Helios 2 at 0.32, 0.69 and 0.90 AU, respectively. The color code, for each panel, is normalized to the maximum of the distribution. Image reproduced by permission from Bruno et al. (2007), copyright EGU.
Quite different is the situation within slow wind, as shown in the right panels of Figure 48. As a matter of fact, these histograms do not show any striking radial evolution like in the case of fast wind. High values of σc are statistically much less relevant than in fast wind and a well defined population characterized by σc = −1 and σc = 0, already present at 0.3 AU, becomes one of the dominant peaks of the histogram as the wind expands. This last feature is really at odds with what happens in fast wind and highlights the different nature of the fluctuations which, in this case, are magnetically dominated. The same authors obtained very similar results for fast and slow wind also from the same type of analysis performed on WIND and Ulysses data which, in addition, confirmed the incompressive character of the Alfvénic fluctuations and highlighted a low compressive character also for the populations characterized by σr ~ −1 and σc ~ 0.
About the origin of these structures, these authors suggest that they might be not only created locally during the non linear evolution of the fluctuations but they might also have a solar origin. The reason why they are not seen close to the Sun, within fast wind, might be due to the fact that these fluctuations, mainly non-compressive, change the direction of the magnetic field similarly to Alfvénic fluctuations but produce a much smaller effect since the associated δb is smaller than the one corresponding to Alfvénic fluctuations. As the wind expands, the Alfvénic component undergoes non-linear interactions which produce a transfer of energy to smaller and smaller scales while, these structures, being advected, have a much longer lifetime. As the expansion goes on, the relative weight of these fluctuations grows and they start to be detected.
3.2.2 On the nature of Alfvénic fluctuations
The Alfvénic nature of outward modes has been widely recognized through several frequency decades up to periods of the order of several hours in the s/c rest frame (Bruno et al., (1985). Conversely, the nature of those fluctuations identified by δd−, called “inward Alfvén modes”, is still not completely clear. There are many clues which would suggest that these fluctuations, especially in the hourly frequencies range, have a non-Alfvénic nature. Several studies on this topic in the low frequency range have suggested that structures convected by the wind could well mimic non-existent inward propagating modes (see the review by Tu and Marsch, (1995a). However, other studies (Tu et al., (1989b) have also found, in the high frequency range and within fast streams, a certain anisotropy in the components which resembles the same anisotropy found for outward modes. So, these observations would suggest a close link between inward modes at high frequency and outward modes, possibly the same nature.
Power density spectra for e+ and e− during a high velocity stream observed at 0.3 AU. Best fit lines for different frequency intervals and related spectral indices are also shown. Vertical lines fix the limits of five different frequency intervals analyzed by Bruno et al. (1996). Image reproduced by permission, copyright by AIP.
Figure 49 shows power density spectra for e+ and e− during a high velocity stream observed at 0.3 AU (similar spectra can be also found in the paper by Grappin et al., (1990 and Tu et al., (1989b). The observed spectral indices, reported on the plot, are typically found within high velocity streams encountered at short heliocentric distances. Bruno et al. (1996) analyzed the power relative to e+ and e− modes, within five frequency bands, ranging from roughly 12 h to 3 min, delimited by the vertical solid lines equally spaced in log-scale. The integrated power associated with e+ and e− within the selected frequency bands is shown in Figure 50. Passing from slow to fast wind e+ grows much more within the highest frequency bands. Moreover, there is a good correlation between the profiles of e− and e+ within the first two highest frequency bands, as already noticed by Grappin et al. (1990) who looked at the correlation between daily averages of e− and e+ in several frequency bands, even widely separated in frequency. The above results stimulated these authors to conclude that it was reminiscent of the non-local coupling in k-space between opposite modes found by Grappin et al. (1982) in homogeneous MHD. Expansion effects were also taken into account by Velli et al. (1990) who modeled inward modes as that fraction of outward modes back-scattered by the inhomogeneities of the medium due to expansion effects (Velli et al., (1989). However, following this model we would often expect the two populations to be somehow related to each other but, in situ observations do not favor this kind of forecast (Bavassano and Bruno, (1992).
An alternative generation mechanism was proposed by Tu et al. (1989b) based on the parametric decay of e+ in high frequency range (Galeev and Oraevskii, (1963). This mechanism is such that large amplitude Alfvénic waves, unstable to perturbations of random field intensity and density fluctuations, would decay into two secondary Alfvénic modes propagating in opposite directions and a sound-like wave propagating in the same direction of the pump wave. Most of the energy of the mother wave would go into the sound-like fluctuation and the backward propagating Alfvénic mode. On the other hand, the production of e− modes by parametric instability is not particularly fast if the plasma β ~ 1, like in the case of solar wind (Goldstein, (1978; Derby, (1978), since this condition slows down the growth rate of the instability. It is also true that numerical simulations by Malara et al. (2000, (2001a, (2002), and Primavera et al. (2003) have shown that parametric decay can still be thought as a possible mechanism of local production of turbulence within the polar wind (see Section 4). However, the strong correlation between e+ and e− profiles found only within the highest frequency bands would support this mechanism and would suggest that e− modes within these frequency bands would have an Alfvénic nature. Another feature shown in Figure 50 that favors these conclusions is the fact that both δz+ and δz− keep the direction of their minimum variance axis aligned with the background magnetic field only within the fast wind, and exclusively within the highest frequency bands. This would not contradict the view suggested by Barnes (1981). Following this model, the majority of Alfvénic fluctuations propagating in one direction have the tip of the magnetic field vector randomly wandering on the surface of half a sphere of constant radius, and centered along the ambient field B∘. In this situation the minimum variance would be oriented along B∘, although this would not represent the propagation direction of each wave vector which could propagate even at large angles from this direction. This situation can be seen in the right hand panel of Figure 98 of Section 10, which refers to a typical Alfvénic interval within fast wind. Moreover, δz+ fluctuations show a persistent anisotropy throughout the fast stream since the minimum variance axis remains quite aligned to the background field direction. This situation downgrades only at the very low frequencies where θ+, the angle between the minimum variance direction of δz+ and the direction of the ambient magnetic field, starts wandering between 0° and 90°. On the contrary, in slow wind, since Alfvénic modes have a smaller amplitude, compressive structures due to the dynamic interaction between slow and fast wind or, of solar origin, push the minimum variance direction to larger angles with respect to B。, not depending on the frequency range.
Left panel: wind speed profile is shown in the top panel. Power density associated with e+ (thick line) and e− (thin line), within the five frequency bands chosen, is shown in the lower panels. Right panel: wind speed profile is shown in the top panel. Values of the angle θ± between the minimum variance direction of δz+ (thick line) and δz− (thin line) and the direction of the ambient magnetic field are shown in the lower panels, relatively to each frequency band. Image reproduced by permission from Bruno et al. (1996), copyright by AIP.
In a way, we can say that within the stream, both θ+ and θ−, the angle between the minimum variance direction of δz− and the direction of the ambient magnetic field, show a similar behavior as we look at lower and lower frequencies. The only difference is that θ− reaches higher values at higher frequencies than θ+. This was interpreted (Bruno et al., (1996) as due to the fact that transverse fluctuations of δz− carry much less power than those of δz+ and, consequently, they are more easily influenced by perturbations represented by the background, convected structure of the wind (e.g., TD’s and PBS’s). As a consequence, at low frequency δz− fluctuations may represent a signature of the compressive component of the turbulence while, at high frequency, they might reflect the presence of inward propagating Alfvén modes. Thus, while for periods of several hours δz+ fluctuations can still be considered as the product of Alfvén modes propagating outward (Bruno et al., (1985), δz− fluctuations are rather due to the underlying convected structure of the wind. In other words, high frequency turbulence can be looked at mainly as a mixture of inward and outward Alfvénic fluctuations plus, presumably, sound-like perturbations (Marsch and Tu, (1993a). On the other hand, low frequency turbulence would be made of outward Alfvénic fluctuations and static convected structures representing the inhomogeneities of the background medium.
4 Observations of MHD Turbulence in the Polar Wind
In 1994 – 1995, Ulysses gave us the opportunity to look at the solar wind out-of-the-ecliptic, providing us with new exciting observations. For the first time heliospheric instruments were sampling pure, fast solar wind, free of any dynamical interaction with slow wind. There is one figure that within our scientific community has become as popular as “La Gioconda” by Leonardo da Vinci within the world of art. This figure produced at LANL (McComas et al., (1998) is shown in the upper left panel of Figure 51, which has been taken from a successive paper by (McComas et al., (2003), and summarizes the most important aspects of the large scale structure of the polar solar wind during the minimum of the solar activity phase, as indicated by the low value of the Wolf’s number reported in the lower panel. It shows speed profile, proton number density profile and magnetic field polarity vs. heliographic latitude during the first complete Ulysses’ polar orbit. Fast wind fills up north and south hemispheres of the Sun almost completely, except a narrow latitudinal belt around the equator, where the slow wind dominates. Flow velocity, which rapidly increases from the equator towards higher latitudes, quickly reaches a plateau and the wind escapes the polar regions with a rather uniform speed. Moreover, polar wind is characterized by a lower number density and shows rather uniform magnetic polarity of opposite sign, depending on the hemisphere. Thus, the main difference between ecliptic and polar wind is that this last one completely lacks of dynamical interactions with slower plasma and freely flows into the interplanetary space The presence or not of this phenomenon, as we will see in the following pages, plays a major role in the development of MHD turbulence during the wind expansion.
During solar maximum (look at the upper right panel of Figure 51) the situation dramatically changes and the equatorial wind extends to higher latitudes, to the extent that there is no longer difference between polar and equatorial wind.
Large scale solar wind profile as a function of latitude during minimum (left panel) and maximum (right panel) solar cycle phases. The sunspot number is also shown at the bottom panels. Image reproduced by permission from McComas et al. (2003), copyright by AGU.
4.1 Evolving turbulence in the polar wind
Ulysses observations gave us the possibility to test whether or not we could forecast the turbulent evolution in the polar regions on the basis of what we had learned in the ecliptic. We knew that, in the ecliptic, velocity shear, parametric decay, and interaction of Alfvénic modes with convected structures (see Sections 3.2.1, 5.1) all play some role in the turbulent evolution and, before Ulysses reached the polar regions of the Sun, three possibilities were given:
-
i.
Alfvénic turbulence would have not relaxed towards standard turbulence because the large scale velocity shears would have been much less relevant (Grappin et al., (1991);
-
ii.
since the magnetic field would be smaller far from the ecliptic, at large heliocentric distances, even small shears would lead to an isotropization of the fluctuations and produce a turbulent cascade faster than the one observed at low latitudes, and the subsequent evolution would take less time (Roberts et al., (1990);
-
iii.
there would still be evolution due to interaction with convected plasma and field structures but it would be slower than in the ecliptic since the power associated with Alfvénic fluctuations would largely dominate over the inhomogeneities of the medium. Thus, Alfvénic correlations should last longer than in the ecliptic plane, with a consequent slower evolution of the normalized cross-helicity (Bruno, (1992).
A fourth possibility was added by Tu and Marsch (1995a), based on their model (Tu and Marsch, (1993). Following this model they assumed that polar fluctuations were composed by outward Alfvénic fluctuations and MFDT. The spectra of these components would decrease with radial distance because of a WKB evolution and convective effects of the diverging flow. As the distance increases, the field becomes more transverse with respect to the radial direction, the s/c would sample more convective structures and, as a consequence, would observe a decrease of both σc and rA.
Today we know that polar Alfvénic turbulence evolves in the same way it does in the ecliptic plane, but much more slowly. Moreover, the absence of strong velocity shears and enhanced compressive phenomena suggests that also some other mechanism based on parametric decay instability might play some role in the local production of turbulence (Bavassano et al., (2000a; Malara et al., (2001a, (2002; Primavera et al., (2003).
The first results of Ulysses magnetic field and plasma measurements in the polar regions, i.e., above ±30. latitude (left panel of Figure 51), revealed the presence of Alfvénic correlations in a frequency range from less than 1 to more than 10 h (Balogh et al., (1995; Smith et al., (1995; Goldstein et al., (1995a) in very good agreement with ecliptic observations (Bruno et al., (1985). However, it is worth noticing that Helios observations referred to very short heliocentric distances around 0.3 AU while the above Ulysses observations were taken up to 4 AU. As a matter of fact, these long period Alfvén waves observed in the ecliptic, in the inner solar wind, become less prominent as the wind expands due to stream-stream dynamical interaction effects (Bruno et al., (1985) and strong velocity shears (Roberts et al., (1987a). At high latitude, the relative absence of enhanced dynamical interaction between flows at different speed and, as a consequence, the absence of strong velocity shears favors the survival of these extremely low frequency Alfvénic fluctuations for larger heliocentric excursions.
Figure 52 shows the hourly correlation coefficient for the transverse components of magnetic and velocity fields as Ulysses climbs to the south pole and during the fast latitude scanning that brought the s/c from the south to the north pole of the Sun in just half a year. While the equatorial phase of Ulysses journey is characterized by low values of the correlation coefficients, a gradual increase can be noticed starting at half of year 1993 when the s/c starts to increase its heliographic latitude from the ecliptic plane up to 80.2° south, at the end of 1994. Not only the degree of δb − δv correlation resembled Helios observations but also the spectra of these fluctuations showed characteristics which were very similar to those observed in the ecliptic within fast wind like the spectral index of the components, that was found to be flat at low frequency and more Kolmogorov-like at higher frequencies (Smith et al., (1995). Balogh et al. (1995) and Forsyth et al. (1996) discussed magnetic fluctuations in terms of latitudinal and radial dependence of their variances. Similarly to what had been found within fast wind in the ecliptic (Mariani et al., (1978; Bavassano et al., (1982b; Tu et al., (1989b; Roberts et al., (1992), variance of magnetic magnitude was much less than the variance associated with the components. Moreover, transverse variances had consistently higher values than the one along the radial direction and were also much more sensitive to latitude excursion, as shown in Figure 53. In addition, the level of the normalized hourly variances of the transverse components observed during the ecliptic phase, right after the compressive region ahead of co-rotating interacting regions, was maintained at the same level once the s/c entered the pure polar wind. Again, these observations showed that the fast wind observed in the ecliptic was coming from the equatorward extension of polar coronal holes.
Magnetic field and velocity hourly correlation vs. heliographic latitude. Image reproduced by permission from Smith et al. (1995), copyright by AGU.
Horbury et al. (1995c) and Forsyth et al. (1996) showed that the interplanetary magnetic field fluctuations observed by Ulysses continuously evolve within the fast polar wind, at least out to 4 AU. Since this evolution was observed within the polar wind, rather free of co-rotating and transient events like those characterizing low latitudes, they concluded that some other mechanism was at work and this evolution was an intrinsic property of turbulence.
Results in Figure 54 show the evolution of the spectral slope computed across three different time scale intervals. The smallest time scales show a clear evolution that keeps on going past the highest latitude on day 256, strongly suggesting that this evolution is radial rather than latitudinal effect. Horbury et al. (1996a) worked on determining the rate of turbulent evolution for the polar wind.
They calculated the spectral index at different frequencies from the scaling of the second order structure function (see Section 7 and papers by Burlaga, (1992a,b; Marsch and Tu, (1993a; Ruzmaikin et al., (1995; and Horbury et al., (1996b) since the spectral scaling α is related to the scaling of the structure function s by the following relation: α = s+1 (Monin and Yaglom, (1975). Horbury et al. (1996a), studying variations of the spectral index with frequency for polar turbulence, found that there are two frequency ranges where the spectral index is rather steady. The first range is around 10−2 Hz with a spectral index around ∡5/3, while the second range is at very low frequencies with a spectral index around −1. This last range is the one where Goldstein et al. (1995a) found the best example of Alfvénic fluctuations. Similarly, ecliptic studies found that the best Alfvénic correlations belonged to the hourly, low frequency regime (Bruno et al., (1985).
Normalized magnetic field components and magnitude hourly variances plotted vs. heliographic latitude during a complete latitude survey by Ulysses. Image reproduced by permission from Forsyth et al. (1996), copyright by AGU.
Spectral indexes of magnetic fluctuations within three different time scale intervals as indicated in the plot. The bottom panel shows heliographic latitude and heliocentric distance of Ulysses. Image reproduced by permission from Horbury et al. (1995c), copyright by AGU.
Horbury et al. (1995a) presented an analysis of the high latitude magnetic field using a fractal method. Within the solar wind context, this method has been described for the first time by Burlaga and Klein (1986) and Ruzmaikin et al. (1993), and is based on the estimate of the scaling of the length function L(τ) with the scale τ. This function is closely related to the first order structure function and, if statistical self-similar, has scaling properties L(τ) ~ τℓ, where ℓ is the scaling exponent. It follows that L(τ) is an estimate of the amplitude of the fluctuations at scale τ, and the relation that binds L(τ) to the variance of the fluctuations (δB)2 ~ τs(2) is:
where N(τ) represents the number of points at scale τ and scales like τ−1. Since the power density spectrum fW(f) is related to (δB)2 through the relation fW(f) ~ (δB)2, if W(f) ~ f−α, then s(2) = α − 1, and, as a consequence α = 2ℓ + 3 (Marsch and Tu, (1996). Thus, it results very easy to estimate the spectral index at a given scale or frequency, without using spectral methods but simply computing the length function.
Spectral exponents for the Bz component estimated from the length function computed from Ulysses magnetic field data, when the s/c was at about 4 AU and ~ −50° latitude. Different symbols refer to different time intervals as reported in the graph. Image reproduced by permission from (from Horbury et al., 1995a).
Results in Figure 55 show the existence of two different regimes, one with a spectral index around the Kolmogorov scaling extending from 101.5 to 103 s and, separated by a clear breakpoint at scales of 103 s, a flatter and flatter spectral exponent for larger and larger scales. These observations were quite similar to what had been observed by Helios 2 in the ecliptic, although the turbulence state recorded by Ulysses resulted to be more evolved than the situation seen at 0.3 AU and, perhaps, more similar to the turbulence state observed around 1 AU, as shown by Marsch and Tu (1996). These authors compared the spectral exponents, estimated using the same method of Horbury et al. (1995a), from Helios 2 magnetic field observations at two different heliocentric distances: 0.3 and 1.0 AU. The comparison with Ulysses results is shown in Figure 56 where it appears rather clear that the slope of the Bz spectrum experiences a remarkable evolution during the wind expansion between 0.3 and 4 AU. Obviously, this comparison is meaningful in the reasonable hypothesis that fluctuations observed by Helios 2 at 0.3 AU are representative of out-of- the-ecliptic solar wind (Marsch and Tu, 1996). This figure also shows that the degree of spectral evolution experienced by the fluctuations when observed at 4 AU at high latitude, is comparable to Helios observations at 1 AU in the ecliptic. Thus, the spectral evolution at high latitude is present although quite slower with respect to the ecliptic.
Spectral exponents for the Bz component estimated from the length function computed from Helios and Ulysses magnetic field data. Ulysses length function (dotted line) is the same shown in the paper by Horbury et al. (1995a) when the s/c was at about 4 AU and ~ −50° latitude. Image reproduced by permission from Marsch and Tu (1996), copyright by AGU.
Forsyth et al. (1996) studied the radial dependence of the normalized hourly variances of the components BR, BT and BN and the magnitude |B| of the magnetic field (see Appendix D to learn about the |B| reference system). The variance along the radial direction was computed as σR2 = 〈BR2 > − < BR2 and successively normalized to |B|2 to remove the field strength dependence Moreover, variances along the other two directions T and N were similarly defined. Fitting the radial dependence with a power law of the form r−α, but limiting the fit to the radial excursion between 1.5 and 3 AU, these authors obtained α = 3.39 ± 0.07 for σ 2r , α = 3.45 ± 0.09 for σ 2T , α = 3.37 ± 0.09 for σ 2N , and α = 2.48 ± 0.14 for σ 2B . Thus, for hourly variances, the power associated with the components showed a radial dependence stronger than the one predicted by the WKB approximation, which would provide α = 3. These authors also showed that including data between 3 and 4 AU, corresponding to intervals characterized by compressional features mainly due to high latitude CMEs, they would obtain less steep radial gradients, much closer to a WKB type. These results suggested that compressive effects can feed energy at the smallest scales, counteracting dissipative phenomena and mimicking a WKB-like behavior of the fluctuations. However, they concluded that for lower frequencies, below the frequency break point, fluctuations do follow the WKB radial evolution.
Horbury and Balogh (2001) presented a detailed comparison between Ulysses and Helios observations about the evolution of magnetic field fluctuations in high-speed solar wind. Ulysses results, between 1.4 and 4.1 AU, were presented as wave number dependence of radial and latitudinal power scaling. The first results of this analysis showed (Figure 3 of their work) a general decrease of the power levels with solar distance, in both magnetic field components and magnitude fluctuations. In addition, the power associated with the radial component was always less than that of the transverse components, as already found by Forsyth et al. (1996). However, Horbury and Balogh (2001), supposing a possible latitude dependence, performed a multiple linear regression of the type:
where w is the power density integrated in a given spectral band, r is the radial distance and θ is the heliolatitude (0° at the equator). Moreover, the same procedure was applied to spectral index estimates α of the form α = Aα + Bα log10 r + Cα sin θ. Results obtained for Bp, Cp, Bα, Cα are shown in Figure 58.
Hourly variances of the components and the magnitude of the magnetic field vs. radial distance from the Sun. The meaning of the different symbols is also indicated in the upper right corner. Image reproduced by permission from Forsyth et al. (1996), copyright by AGU.
On the basis of variations of spectral index and radial and latitudinal dependencies, these authors were able to identify four wave number ranges as indicated by the circled numbers in the top panel of Figure 58. Range 1 was characterized by a radial power decrease weaker than WKB (−3), positive latitudinal trend for components (more power at higher latitude) and negative for magnitude (less compressive events at higher latitudes). Range 2 showed a more rapid radial decrease of power for both magnitude and components and a negative latitudinal power trend, which implies less power at higher latitudes. Moreover, the spectral index of the components (bottom panel) is around 0.5 and tends to 0 at larger scales. Within range 3 the power of the components follows a WKB radial trend and the spectral index is around −1 for both magnitude and components. This hourly range has been identified as the most Alfvénic at low latitudes and its radial evolution has been recognized to be consistent with WKB radial index (Roberts, (1989; Marsch and Tu, (1990a). Even within this range, and also within the next one, the latitude power trend is slightly negative for both components and magnitude. Finally, range 4 is clearly indicative of turbulent cascade with a radial power trend of the components much faster than WKB expectation and becoming even stronger at higher wave numbers. Moreover, the radial spectral index reveals that steepening is at work only for the previous wave number ranges as expected since the breakpoint moves to smaller wave number during spectrum evolution. The spectral index of the components tends to −5/3 with increasing wave number while that of the magnitude is constantly flatter. The same authors gave an estimate of the radial scale-shift of the breakpoint during the wind expansion around k ∝ r1.1, in agreement with earlier estimates (Horbury et al., 1996a).
Although most of these results support previous conclusions obtained for the ecliptic turbulence, the negative value of the latitudinal power trend that starts within the second range, is unexpected. As a matter of fact, moving towards more Alfvén regions like the polar regions, one would perhaps expect a positive latitudinal trend similarly to what happens in the ecliptic when moving from slow to fast wind.
(a) Scale dependence of radial power, (b) latitudinal power, (c) radial spectral index, (d) latitudinal spectral index, and (e) spectral index computed at 2.5 AU. Solid circles refer to the trace of the spectral matrix of the components, open squares refer to field magnitude. Correspondence between wave number scale and time scale is based on a wind velocity of 750 km s−1. Image reproduced by permission from Horbury and Balogh (2001), copyright by AGU.
Horbury and Balogh (2001) and Horbury and Tsurutani (2001) estimated that the power observed at 80° is about 30% less than that observed at 30°. These authors proposed a possible effect due to the over-expansion of the polar coronal hole at higher latitudes. In addition, within the fourth range, field magnitude fluctuations radially decrease less rapidly than the fluctuations of the components, but do not show significant latitudinal variations. Finally, the smaller spectral index reveals that the high frequency range of the field magnitude spectrum shows a flattening.
The same authors investigated the anisotropy of these fluctuations as a function of radial and latitudinal excursion. Their results, reported in Figure 59, show that, at 2.5 AU, the lowest compressibility is recorded within the hourly frequency band (third and part of the fourth band), which has been recognized as the most Alfvénic frequency range. The anisotropy of the components confirms that the power associated with the transverse components is larger than that associated with the radial one, and this difference slightly tends to decrease at higher wave numbers.
(a) Scale dependence of power anisotropy at 2.5 AU plotted as the log10 of the ratio of BR (solid circles), BT (triangles), BN (diamonds), and |B| (squares) to the trace of the spectral matrix; (b) the radial, and (c) latitudinal behavior of the same values, respectively. Image reproduced by permission from Horbury and Balogh (2001), copyright by AGU.
As already shown by Horbury et al. (1995b), around the 5 min range, magnetic field fluctuations are transverse to the mean field direction the majority of the time. The minimum variance direction lies mainly within an angle of about 26° from the average background field direction and fluctuations are highly anisotropic, such that the ratio between perpendicular to parallel power is about 30. Since during the observations reported in Horbury and Balogh (2001) and Horbury and Tsurutani (2001) the mean field resulted to be radially oriented most of the time, the radial minimum variance direction at short time scales is an effect induced by larger scales behavior.
Anyhow, radial and latitudinal anisotropy trends tend to disappear for higher frequencies. In the mean time, interesting enough, there is a strong radial increase of magnetic field compression (top panel of Figure 59), defined as the ratio between the power density associated with magnetic field intensity fluctuations and that associated with the fluctuations of the three components (Bavassano et al., (1982a; Bruno and Bavassano, (1991). The attempt to attribute this phenomenon to parametric decay of large amplitude Alfvén waves or dynamical interactions between adjacent flux tubes or interstellar pick-up ions was not satisfactory in all cases.
Comparing high latitude with low latitude results for high speed streams, Horbury and Balogh (2001) found remarkable good agreement between observations by Ulysses at 2.5 AU and by Helios at 0.7 AU. In particular, Figure 60 shows Ulysses and Helios 1 spectra projected to 1 AU for comparison.
It is interesting to notice that the spectral slope of the spectrum of the components for Helios 1 is slightly higher than that of Ulysses, suggesting a slower radial evolution of turbulence in the polar wind (Bruno, (1992; Bruno and Bavassano, (1992). However, the faster spectral evolution at low latitudes does not lead to strong differences between the spectra.
Power spectra of magnetic field components (solid circles) and magnitude (open squares) from Ulysses (solid line) and Helios 1 (dashed line). Spectra have been extrapolated to 1 AU using radial trends in power scalings estimated from Ulysses between 1.4 and 4.1 AU and Helios between 0.3 and 1 AU. Image reproduced by permission from Horbury and Balogh (2001), copyright by AGU.
4.2 Polar turbulence studied via Elsässer variables
Goldstein et al. (1995a) for the first time showed a spectral analysis of Ulysses observations based on Elsässer variables during two different time intervals, at 4 AU and close to −40°, and at 2 AU and around the maximum southern pass, as shown in Figure 61. Comparing the two Ulysses observations it clearly appears that the spectrum closer to the Sun is less evolved than the spectrum measured farther out, as will be confirmed by the next Figure 62, where these authors reported the normalized cross-helicity and the Alfvén ratio for the two intervals. Moreover, following these authors, the comparison between Helios spectra at 0.3 AU and Ulysses at 2 and 4 AU suggests that the radial scaling of e+ at the low frequency end of the spectrum follows the WKB prediction of 1/r decrease (Heinemann and Olbert, 1980). However, the selected time interval for Helios s/c was characterized by rather slow wind taken during the rising phase the solar cycle, two conditions which greatly differ from those referring to Ulysses data. As a consequence, comparing Helios results with Ulysses results obtained within the fast polar wind might be misleading. It would be better to choose Helios observations within high speed co-rotating streams which resemble much better solar wind conditions at high latitude.
Anyhow, results relative to the normalized cross-helicity σc (see Figure 62) clearly show high values of σc, around 0.8, which normally we observe in the ecliptic at much shorter heliocentric distances (Tu and Marsch, (1995a). A possible radial effect would be responsible for the depleted level of σc at 4 AU. Moreover, a strong anisotropy can also be seen for frequencies between 10−6 − 10−5 Hz with the transverse σc much larger than the radial one. This anisotropy is somewhat lost during the expansion to 4 AU.
The Alfvén ratio (bottom panels of Figure 62) has values around 0.5 for frequencies higher than roughly 10.5 Hz, with no much evolution between 2 and 4 AU. A result similar to what was originally obtained in the ecliptic at about 1 AU (Martin et al., (1973; Belcher and Solodyna, (1975; Solodyna et al., (1977; Neugebauer et al., (1984; Bruno et al., (1985; Marsch and Tu, (1990a; Roberts et al., (1990). The low frequency extension of rA⊥ together with σc⊥, where the subscript ⊥ indicates that these quantities are calculated from the transverse components only, was interpreted by the authors as due to the sampling of Alfvénic features in longitude rather than to a real presence of Alfvénic fluctuations. However, by the time Ulysses reaches to 4 AU, σc⊥ has strongly decreased as expected while rA⊥ gets closer to 1, making the situation less clear. Anyhow, these results suggest that the situation at 2 AU and, even more at 4 AU, can be considered as an evolution of what Helios 2 recorded in the ecliptic at shorter heliocentric distance Ulysses observations at 2 AU resemble more the turbulence conditions observed by Helios at 0.9 AU rather than at 0.3 AU.
Trace of e+ (solid line) and e− (dash-dotted line) power spectra. The central and right panels refer to Ulysses observations at 2 and 4 AU, respectively, when Ulysses was embedded in the fast southern polar wind during 1993 – 1994. The leftmost panel refers to Helios observations during 1978 at 0.3 AU. Image reproduced by permission from Goldstein et al. (1995a), copyright by AGU.
Normalized cross-helicity and Alfvén ratio at 2 and 4 AU, as observed by Ulysses at −80° and −40° latitude, respectively. Image reproduced by permission from Goldstein et al. (1995a), copyright by AGU.
Bavassano et al. (2000a) studied in detail the evolution of the power e+ and e− associated with outward δz+ and inward δz− Alfvénic fluctuations, respectively. The study referred to the polar regions, during the wind expansion between 1.4 and 4.3 AU. These authors analyzed 1 h variances of δz± and found two different regimes, as shown in Figure 63. Inside 2.5 AU outward modes e+ decrease faster than inward modes e−, in agreement with previous ecliptic observations performed within the trailing edge of co-rotating fast streams (Bruno and Bavassano, (1991; Tu and Marsch, (1990b; Grappin et al., (1989). Beyond this distance, the radial gradient of e− becomes steeper and steeper while that of e+ remains approximately unchanged. This change in e− is rather fast and both species keep declining with the same rate beyond 2.5 AU. The radial dependence of e+ between r−1.39 and r−1.48, reported by Bavassano et al. (2000a), indicate a radial decay faster than r−1 predicted by WKB approximation. This is in agreement with the analysis performed by Forsyth et al. (1996) using magnetic field observations only.
Left panel: values of hourly variance of δz− (i.e., e±) vs. heliocentric distance, as observed by Ulysses. Helios observations are shown for comparison and appear to be in good agreement. Right panel: Elsässer ratio (top) and Alfvén ratio (bottom) are plotted vs. radial distance while Ulysses is embedded in the polar wind. Image reproduced by permission from Bavassano et al. (2000a), copyright by AGU.
This different radial behavior is readily seen in the radial plot of the Elsässer ratio rE shown in the top panel of the right column of Figure 63. Before 2.5 AU this ratio continuously grows to about 0.5 near 2.5 AU. Beyond this region, since the radial gradient of the inward and outward components is approximately the same, rE stabilizes around 0.5.
On the other hand, also the Alfvén ratio rA shows a clear radial dependence that stops at about the same limit distance of 2.5 AU. In this case, rA constantly decreases from ~ 0.4 at 1.4 AU to ~ 0.25 at 2.5 AU, slightly fluctuating around this value for larger distances. A different interpretation of these results was offered by Grappin (2002). For this author, since Ulysses has not explored the whole three-dimensional heliosphere, solar wind parameters experience different dependencies on latitude and distance which would result in the same radial distance variation along Ulysses trajectory as claimed in Bavassano’s works. Another interesting feature observed in polar turbulence is unraveled by Figure 64 from Bavassano et al. (1998, 2000b). The plot shows 2D histograms of normalized cross-helicity and normalized residual energy (see Appendix B.3.1 for definition) for different heliospheric regions (ecliptic wind, mid-latitude wind with strong velocity gradients, polar wind). A predominance of outward fluctuations (positive values of σc) and of magnetic fluctuations (negative values of σr) seems to be a general feature. It results that the most Alfvénic region is the one at high latitude and at shorter heliocentric distances. However, in all the panels there is always a relative peak at σc ≃ 0 and σr ≃ −1, which might well be due to magnetic structures like the MFDT found by Tu and Marsch (1991) in the ecliptic.
Left panel: values of hourly variance of δz− (i.e., e±) vs. heliocentric distance, as observed by Ulysses. Helios observations are shown for comparison and appear to be in good agreement. Right panel: Elsässer ratio (top) and Alfvén ratio (bottom) are plotted vs. radial distance while Ulysses is embedded in the polar wind. Image reproduced by permission from Bavassano et al. (2000a), copyright by AGU.
In a successive paper, Bavassano et al. (2002a) tested whether or not the radial dependence observed in e± was to be completely ascribed to the radial expansion of the wind or possible latitudinal dependencies also contributed to the turbulence evolution in the polar wind.
As already discussed in the previous section, Horbury and Balogh (2001), using Ulysses data from the northern polar pass, evaluated the dependence of magnetic field power levels on solar distance and latitude using a multiple regression analysis based on Equation (60). In the Alfvénic range, the latitudinal coefficient “C” for power in field components was appreciably different from 0 (around 0.3). However, this analysis was limited to magnetic field fluctuations alone and cannot be transferred sic et simpliciter to Alfvénic turbulence In their analysis, Bavassano et al. (2002b) used the first southern and northern polar passes and removed from their dataset all intervals with large gradients in plasma velocity, and/or plasma density, and/or magnetic field magnitude, as already done in Bavassano et al. (2000a). As a matter of fact, the use of Elsässer variables (see Appendix B.3.1) instead of magnetic field, and of selected data samples, leads to very small values of the latitudinal coefficient as shown in Figure 65, where different contributions are plotted with different colors and where the top panel refers to the same dataset used by Horbury and Balogh (2001), while the bottom panel refers to a dataset omni-comprehensive of south and north passages free of strong compressive events (Bavassano et al., (2000a). Moreover, the latitudinal effect appears to be very weak also for the data sample used by Horbury and Balogh (2001), although this is the sample with the largest value of the “C” coefficient.
Results from the multiple regression analysis showing radial and latitudinal dependence of the power e+ associated with outward modes (see Appendix B.3.1). The top panel refers to the same dataset used by Horbury and Balogh (2001). The bottom panel refers to a dataset omni-comprehensive of south and north passages free of strong compressive events (Bavassano et al., (2000a). Values of e+ have been normalized to the value e+° assumed by this parameter at 1.4 AU, closest approach to the Sun. The black line is the total regression, the blue line is the latitudinal contribution and the red line is the radial contribution. Image reproduced by permission from Bavassano et al. (2002a), copyright by AGU.
A further argument in favor of radial vs. latitudinal dependence is represented by the comparison of the radial gradient of e+ in different regions, in the ecliptic and in the polar wind. These results, shown in Figure 66, provide the radial slopes for e+ (red squares) and e+ (blue diamonds) in different regions. The first three columns (labeled EQ) summarize ecliptic results obtained with different values of an upper limit (TBN) for relative fluctuations of density and magnetic intensity. The last two columns (labeled POL) refer to the results for polar turbulence (north and south passes) outside and inside 2.6 AU, respectively. A general agreement exists between slopes in ecliptic and in polar wind with no significant role left for latitude, the only exception being e+ in the region inside 2.6 AU. The behavior of the inward component cannot be explained by a simple power law over the range of distances explored by Ulysses. Moreover, a possible latitudinal effect has been clearly rejected by the results from a multiple regression analysis performed by Bavassano et al. (2002a) similar to that reported above for e+.
e+ (red) and e− (blue) radial gradient for different latitudinal regions of the solar wind. The first three columns, labeled EQ, refer to ecliptic observations obtained with different values of the upper limit of TBN defined as the relative fluctuations of density and magnetic intensity. The last two columns, labeled POL, refer to observations of polar turbulence outside and inside 2.6 AU, respectively. Image reproduced by permission from Bavassano et al. (2001), copyright by AGU.
5 Numerical Simulations
Numerical simulations currently represent one of the main source of information about non-linear evolution of fluid flows. The actual super-computers are now powerful enough to simulate equations (NS or MHD) that describe turbulent flows with Reynolds numbers of the order of 104 in twodimensional configurations, or 103 in three-dimensional one. Of course, we are far from achieving realistic values, but now we are able to investigate turbulence with an inertial range extended for more than one decade. Rather the main source of difficulties to get results from numerical simulations is the fact that they are made under some obvious constraints (say boundary conditions, equations to be simulated, etc.), mainly dictated by the limited physical description that we are able to use when numerical simulations are made, compared with the extreme richness of the phenomena involved: numerical simulations, even in standard conditions, are used tout court as models for the solar wind behavior. Perhaps the only exception, to our knowledge, is the attempt to describe the effects of the solar wind expansion on turbulence evolution like, for example, in the papers by Velli et al. (1989, (1990); Hellinger and Trávníček (2008). Even with this far too pessimistic point of view, used here solely as a few words of caution, simulations in some cases were able to reproduce some phenomena observed in the solar wind.
Nevertheless, numerical simulations have been playing a key role, and will continue to do so in our seeking an understanding of turbulent flows. Numerical simulations allows us to get information that cannot be obtained in laboratory. For example, high resolution numerical simulations provide information at every point on a grid and, for some times, about basic vector quantities and their derivatives. The number of degree of freedom required to resolve the smaller scales is proportional to a power of the Reynolds number, say to Re9/4, although the dynamically relevant number of modes may be much less. Then one of the main challenge remaining is how to handle and analyze the huge data files produced by large simulations (of the order of Terabytes). Actually a lot of papers appeared in literature on computer simulations related to MHD turbulence The interested reader can look at the book by Biskamp (1993) and the reviews by Pouquet (1993, (1996).
5.1 Local production of Alfvénic turbulence in the ecliptic
The discovery of the strong correlation between velocity and magnetic field fluctuations has represented the motivation for some MHD numerical simulations, aimed to confirm the conjecture by Dobrowolny et al. (1980b). The high level of correlation seems to be due to a kind of selforganization (dynamical alignment) of MHD turbulence, generated by the natural evolution of MHD towards the strongest attractive fixed point of equations (Ting et al., (1986; Carbone and Veltri, (1987, (1992). Numerical simulations (Carbone and Veltri, (1992; Ting et al., (1986) confirmed this conjecture, say MHD turbulence spontaneously can tends towards a state were correlation increases, that is, the quantity σc = 2Hc/E, where Hc is the cross-helicity and E the total energy of the flow (see Appendix B.1), tends to be maximal.
The picture of the evolution of incompressible MHD turbulence, which comes out is rather nice but solar wind turbulence displays a more complicated behavior. In particular, as we have reported above, observations seems to point out that solar wind evolves in the opposite way. The correlation is high near the Sun, at larger radial distances, from 1 to 10 AU the correlation is progressively lower, while the level in fluctuations of mass density and magnetic field intensity increases. What is more difficult to understand is why correlation is progressively destroyed in the solar wind, while the natural evolution of MHD is towards a state of maximal normalized cross-helicity. A possible solution can be found in the fact that solar wind is neither incompressible nor statistically homogeneous, and some efforts to tentatively take into account more sophisticated effects have been made.
A mechanism, responsible for the radial evolution of turbulence, was suggested by Roberts and Goldstein (1988); Goldstein et al. (1989); and Roberts et al. (1991, (1992) and was based on velocity shear generation. The suggestion to adopt such a mechanism came from a detailed analysis made by Roberts et al. (1987a,b) of Helios and Voyager interplanetary observations of the radial evolution of the normalized cross-helicity σc at different time scales. Moreover, Voyager’s observations showed that plasma regions, which had not experienced dynamical interactions with neighboring plasma, kept the Alfvénic character of the fluctuations at distances as far as 8 AU (Roberts et al., (1987b). In particular, the vicinity of Helios trajectory to the interplanetary current sheet, characterized by low velocity flow, suggested Roberts et al. (1991) to include in his simulations a narrow low speed flow surrounded by two high speed flows. The idea was to mimic the slow, equatorial solar wind between north and south fast polar wind. Magnetic field profile and velocity shear were reconstructed using the six lowest Z± Fourier modes as shown in Figure 67. An initial population of purely outward propagating Alfvénic fluctuations (z+) was added at large k and was characterized by a spectral slope of k−1. No inward modes were present in the same range. Results of Figure 67 show that the time evolution of z+ spectrum is quite rapid at the beginning, towards a steeper spectrum, and slows down successively. At the same time, z− modes are created by the generation mechanism at higher and higher k but, along a Kolmogorov-type slope k−5/3.
These results, although obtained from simulations performed using 2D incompressible spectral and pseudo-spectral codes, with fairly small Reynolds number of Re ≃ 200, were similar to the spectral evolution observed in the solar wind (Marsch and Tu, (1990a). Moreover, spatial averages across the simulation box revealed a strong cross-helicity depletion right across the slow wind, representing the heliospheric current sheet. However, magnetic field inversions and even relatively small velocity shears would largely affect an initially high Alfvénic flow (Roberts et al., (1992). However, Bavassano and Bruno (1992) studied an interaction region, repeatedly observed between 0.3 and 0.9 AU, characterized by a large velocity shear and previously thought to be a good candidate for shear generation (Bavassano and Bruno, (1989). They concluded that, even in the hypothesis of a very fast growth of the instability, inward modes would not have had enough time to fill up the whole region as observed by Helios 2.
The above simulations by Roberts et al. (1991) were successively implemented with a com- pressive pseudo-spectral code (Ghosh and Matthaeus, (1990) which provided evidence that, during this turbulence evolution, clear correlations between magnetic field magnitude and density fluctuations, and between z− and density fluctuations should arise. However, such a clear correlation, by-product of the non-linear evolution, was not found in solar wind data (Marsch and Tu, (1993b; Bruno et al., (1996). Moreover, their results did not show the flattening of e− spectrum at higher frequency, as observed by Helios (Tu et al., (1989b). As a consequence, velocity shear alone cannot explain the whole phenomenon, other mechanisms must also play a relevant role in the evolution of interplanetary turbulence
Time evolution of the power density spectra of z+ and z− showing the turbulent evolution of the spectra due to velocity shear generation (from Roberts et al., (1991).
Compressible numerical simulations have been performed by Veltri et al. (1992) and Malara et al. (1996, (2000) which invoked the interactions between small scale waves and large scale magnetic field gradients and the parametric instability, as characteristic effects to reduce correlations. In a compressible, statistically inhomogeneous medium such as the heliosphere, there are many processes which tend to destroy the natural evolution toward a maximal correlation, typical of standard MHD. In such a medium an Alfvén wave is subject to parametric decay instability (Viñas and Goldstein, 1991; Del Zanna et al., 2001; Del Zanna, 2001), which means that the mother wave decays in two modes: i) a compressive mode that dissipates energy because of the steepening effect, and ii) a backscattered Alfvénic mode with lower amplitude and frequency. Malara et al. (1996) showed that in a compressible medium, the correlation between the velocity and the magnetic field fluctuations is reduced because of the generation of the backward propagating Alfvénic fluctuations, and of a compressive component of turbulence, characterized by density fluctuations δρ ≠ 0 and magnetic intensity fluctuations δ|B| ≠ 0.
From a technical point of view it is worthwhile to remark that, when a large scale field which varies on a narrow region is introduced (typically a tanh-like field), periodic boundaries conditions should be used with some care. Roberts et al. (1991, 1992) used a double shear layer, while Malara et al. (1992) introduced an interesting numerical technique based on both the glue between two simulation boxes and a Chebyshev expansion, to maintain a single shear layer, say non periodic boundary conditions, and an increased resolution where the shear layer exists.
Grappin et al. (1992) observed that the solar wind expansion increases the lengths normal to the radial direction, thus producing an effect similar to a kind of inverse energy cascade. This effect perhaps should be able to compete with the turbulent cascade which transfers energy to small scales, thus stopping the non-linear interactions. In absence of non-linear interactions, the natural tendency towards an increase of σc is stopped. These inferences have been corroborated by further studies like those by Grappin and Velli (1996) and Goldstein and Roberts (1999). A numerical model treating the evolution of e+ and e−, including parametric decay of e+, was presented by Marsch and Tu (1993a). The parametric decay source term was added in order to reproduce the decreasing cross-helicity observed during the wind expansion. As a matter of fact, the cascade process, when spectral equations for both e+ and e− are included and solved self-consistently, can only steepen the spectra at high frequency. Results from this model, shown in Figure 68, partially reproduce the observed evolution of the normalized cross-helicity. While the radial evolution of e+ is correctly reproduced, the behavior of e− shows an over-production of inward modes between 0.6 and 0.8 AU probably due to an overestimation of the strength of the pump-wave. However, the model is applied to the situation observed by Helios at 0.3 AU where a rather flat e− spectrum already exists.
Radial evolution of e+ and e− spectra obtained from the Marsch and Tu (1993a) model, in which a parametric decay source term was added to the Tu’s model (Tu et al., (1984) that was, in turn, extended by including both spectrum equations for e+ and e− and solved them self-consistently. Image reproduced by permission from Marsch and Tu (1993a), copyright by AGU.
5.2 Local production of Alfvénic turbulence at high latitude
An interesting solution to the radial behavior of the minority modes might be represented by local generation mechanisms, like parametric decay (Malara et al., (2001a; Del Zanna et al., 2001), which might saturate and be inhibited beyond 2.5 AU.
Parametric instability has been studied in a variety of situations depending on the value of the plasma β (among others Sagdeev and Galeev, (1969; Goldstein, (1978; Hoshino and Goldstein, (1989; Malara and Velli, (1996). Malara et al. (2000) and Del Zanna et al. (2001) recently studied the non-linear growth of parametric decay of a broadband Alfvén wave, and showed that the final state strongly depends on the value of the plasma β (thermal to magnetic pressure ratio). For β < 1 the instability completely destroys the initial Alfvénic correlation. For β ~ 1 (a value close to solar wind conditions) the instability is not able to go beyond some limit in the disruption of the initial correlation between velocity and magnetic field fluctuations, and the final state is σc ~ 0.5 as observed in the solar wind (see Section 4.2).
These authors solved numerically the fully compressible, non-linear MHD equations in a onedimensional configuration using a pseudo-spectral numerical code. The simulation starts with a non-monochromatic, large amplitude Alfvén wave polarized on the yz plane, propagating in a uniform background magnetic field. Successively, the instability was triggered by adding some noise of the order 10−6 to the initial density level.
During the first part of the evolution of the instability the amplitude of unstable modes is small and, consequently, non-linear couplings are negligible. A subsequent exponential growth, predicted by the linear theory, increases the level of both e− and density compressive fluctuations. During the second part of the development of the instability, non-linear couplings are not longer disregardable and their effect is firstly to slow down the exponential growth of unstable modes and then to saturate the instability to a level that depends on the value of the plasma β.
Spectra of e± are shown in Figure 69 for different times during the development of the instability. At the beginning the spectrum of the mother-wave is peaked at k = 10, and before the instability saturation (t ≤ 35) the back-scattered e− and the density fluctuations eρ are peaked at k = 1 and k = 11, respectively. After saturation, as the run goes on, the spectrum of e− approaches that of e+ towards a common final state characterized by a Kolmogorov-like spectrum and e+ slightly larger than e−.
The behavior of outward and inward modes, density and magnetic magnitude variances and the normalized cross-helicity σc is summarized in the left column of Figure 70. The evolution of σc, when the instability reaches saturation, can be qualitatively compared with Ulysses observations (courtesy of B. Bavassano) in the right panel of the same figure, which shows a similar trend.
Obviously, making this comparison, one has to take into account that this model has strong limitations like the presence of a peak in e+ not observed in real polar turbulence Another limitation, partly due to dissipation that has to be included in the model, is that the spectra obtained at the end of the instability growth are steeper than those observed in the solar wind. Finally, a further limitation is represented by the fact that this code is 1D. However, although for an incompressible 1-D simulation we do not expect to have turbulence development, in this case, since parametric decay is based on compressive phenomena, an energy transfer along the spectrum might be at work.
In addition, Umeki and Terasawa (1992) studying the non-linear evolution of a large-amplitude incoherent Alfvén wave via 1D magnetohydrodynamic simulations, reported that while in a low beta plasma (B ≈ 0.2) the growth of backscattered Alfvén waves, which are opposite in helicity and propagation direction from the original Alfvén waves, could be clearly detected, in a high beta plasma (B ≈ 2) there was no production of backscattered Alfvén waves. Consequently, although numerical results obtained by Malara et al. (2001b) are very encouraging, the high beta plasma (B ≈ 2), characteristic of fast polar wind at solar minimum, plays against a relevant role of parametric instability in developing solar wind turbulence as observed by Ulysses. However, these simulations do remain an important step forward towards the understanding of turbulent evolution in the polar wind until other mechanisms will be found to be active enough to justify the observations shown in Figure 63.
Top left panel: time evolution of e+ (solid line) and e− (dashed line). Middle left panel: density (solid line) and magnetic magnitude (dashed line) variances. Bottom left panel: normalized cross helicity σc. Right panel: Ulysses observations of σc radial evolution within the polar wind (left column is from Malara et al., 2001b, right panel is a courtesy of B. Bavassano).
6 Compressive Turbulence
Interplanetary medium is slightly compressive, magnetic field intensity and proton number density experience fluctuations over all scales and the compression depends on both the scale and the nature of the wind. As a matter of fact, slow wind is generally more compressive than fast wind, as shown in Figure 71 where, following Bavassano et al. (1982a) and Bruno and Bavassano (1991), we report the ratio between the power density associated with magnetic field intensity fluctuations and that associated with the fluctuations of the three components. In addition, as already shown by Bavassano et al. (1982a), this parameter increases with heliocentric distance for both fast and slow wind as shown in the bottom panel, where the ratio between the compression at 0.9 AU and that at 0.3 AU is generally greater than 1. It is also interesting to notice that within the Alfvénic fast wind, the lowest compression is observed in the middle frequency range, roughly between 10−4 − 10−3 Hz. On the other hand, this frequency range has already been recognized as the most Alfvénic one, within the inner heliosphere (Bruno et al., (1996).
As a matter of fact, it seems that high Alfvénicity is correlated with low compressibility of the medium (Bruno and Bavassano, (1991; Klein et al., (1993; Bruno and Bavassano, (1993) although compressibility is not the only cause for a low Alfvénicity (Roberts et al., (1991, (1992; Roberts, (1992).
The radial dependence of the normalized number density fluctuations δn/n for the inner and outer heliosphere were studied by Grappin et al. (1990) and Roberts et al. (1987b for the hourly frequency range, but no clear radial trend emerged from these studies. However, interesting enough, Grappin et al. (1990) found that values of e− were closely associated with enhancements of δn/n on scales longer than 1 h.
On the other hand, a spectral analysis of proton number density, magnetic field intensity, and proton temperature performed by Marsch and Tu (1990b) and Tu et al. (1991) in the inner heliosphere, separately for fast and slow wind (see Figure 72), showed that normalized spectra of the above parameters within slow wind were only marginally dependent on the radial distance On the contrary, within fast wind, magnetic field and proton density normalized spectra showed not only a clear radial dependence but also similar level of power for k < 4×10−4 km s−1. For larger k these spectra show a flattening that becomes steeper for increasing distance, as was already found by Bavassano et al. (1982b) for magnetic field intensity. Normalized temperature spectra does not suffer any radial dependence neither in slow wind nor in fast wind.
Spectral index is around .5/3 for all the spectra in slow wind while, fast wind spectral index is around −5/3 for k < 4 × 10−4 km.1 and slightly less steep for larger wave numbers.
6.1 On the nature of compressive turbulence
Considerable efforts, both theoretical and observational, have been made in order to disclose the nature of compressive fluctuations. It has been proposed (Montgomery et al., (1987; Matthaeus and Brown, (1988; Zank et al., (1990; Zank and Matthaeus, (1990; Matthaeus et al., (1991; Zank and Matthaeus, (1992) that most of compressive fluctuations observed in the solar wind could be accounted for by the Nearly Incompressible (NI) model. Within the framework of this model, (Montgomery et al., (1987) showed that a spectrum of small scale density fluctuations follows a k−5/3 when the spectrum of magnetic field fluctuations follows the same scaling. Moreover, it was showed (Matthaeus and Brown, (1988; Zank and Matthaeus, (1992) that if compressible MHD equations are expanded in terms of small turbulent sonic Mach numbers, pressure balanced structures, Alfvénic and magnetosonic fluctuations naturally arise as solutions and, in particular, the RMS of small density fluctuations would scale like M2, being M = δu/Cs the turbulent sonic Mach number, δu the RMS of velocity fluctuations and Cs the sound speed. In addition, if heat conduction is allowed in the approximation, temperature fluctuations dominate over magnetic and density fluctuations, temperature and density are anticorrelated and would scale like M. However, in spite of some examples supporting this theory (Matthaeus et al., (1991 reported 13% of cases satisfied the requirements of NI-theory), wider statistical studies, conducted by Tu and Marsch (1994), Bavassano et al. (1995) and Bavassano and Bruno (1995), showed that NI theory is not applicable sic et simpliciter to the solar wind. The reason might be in the fact that interplanetary medium is highly inhomogeneous because of the presence of an underlying structure convected by the wind. As a matter of fact, Thieme et al. (1989) showed evidence for the presence of time intervals characterized by clear anti-correlation between kinetic pressure and magnetic pressure while the total pressure remained fairly constant. These pressure balance structures were for the first time observed by Burlaga and Ogilvie (1970) for a time scale of roughly one to two hours. Later on, Vellante and Lazarus (1987) reported strong evidence for anti-correlation between field intensity and proton density, and between plasma and field pressure on time scales up to 10 h. The anti-correlation between kinetic and magnetic pressure is usually interpreted as indicative of the presence of a pressure balance structure since slow magnetosonic modes are readily damped (Barnes, (1979).
The first two rows show magnetic field compression (see text for definition) for fast (left column) and slow (right column) wind at 0.3 AU (upper row) and 0.9 AU (middle row). The bottom panels show the ratio between compression at 0.9 AU and compression at 0.3 AU. This ratio is generally greater than 1 for both fast and slow wind.
These features, observed also in their dataset, were taken by Thieme et al. (1989) as evidence of stationary spatial structures which were supposed to be remnants of coronal structures convected by the wind. Different values assumed by plasma and field parameters within each structure were interpreted as a signature characterizing that particular structure and not destroyed during the expansion. These intervals, identifiable in Figure 73 by vertical dashed lines, were characterized by pressure balance and a clear anti-correlation between magnetic field intensity and temperature.
These structures were finally related to the fine ray-like structures or plumes associated with the underlying chromospheric network and interpreted as the signature of interplanetary flowtubes. The estimated dimension of these structures, back projected onto the Sun, suggested that they over-expand in the solar wind. In addition, Grappin et al. (2000) simulated the evolution of Alfvén waves propagating within such pressure equilibrium ray structures in the framework of global Eulerian solar wind approach and found that the compressive modes in these simulations are very much reduced within the ray structures, which indeed correspond to the observational findings (Buttighoffer et al., (1995, (1999).
From top to bottom: field intensity |B|; proton and alpha particle velocity up and uα; corrected proton velocity upc = up − δuA, where uA is the Alfvén speed; proton and alpha number density np and nα; proton and alpha temperature Tp and Tα; kinetic and magnetic pressure Pk and Pm, which the authors call Pgas and Pmag; total pressure Ptot and β = Pgas/Pmag (from Tu and Marsch, (1995a).
The idea of filamentary structures in the solar wind dates back to Parker (1964), followed by other authors like McCracken and Ness (1966), Siscoe et al. (1968), and more recently has been considered again in the literature with new results (see Section 10). These interplanetary flow tubes would be of different sizes, ranging from minutes to several hours and would be separated from each other by tangential discontinuities and characterized by different values of plasma parameters and a different magnetic field orientation and intensity. This kind of scenario, because of some similarity to a bunch of tangled, smoking “spaghetti” lifted by a fork, was then named “spaghetti-model”.
A spectral analysis performed by Marsch and Tu (1993a) in the frequency range 6×10−3 – 6×10−6 showed that the nature and intensity of compressive fluctuations systematically vary with the stream structure. They concluded that compressive fluctuations are a complex superposition of magnetoacoustic fluctuations and pressure balance structures whose origin might be local, due to stream dynamical interaction, or of coronal origin related to the flow tube structure. These results are shown in Figure 74 where the correlation coefficient between number density n and total pressure Ptot (indicated with the symbols pT in the figure), and between kinetic pressure Pk and magnetic pressure Pm (indicated with the symbols pk and pb, respectively) is plotted for both Helios s/c relatively to fast wind. Positive values of correlation coefficients C(n, pT) and C(pk, pb) identify magnetosonic waves, while positive values of C(n, pT) and negative values of C(pk, pb) identify pressure balance structures. The purest examples of each category are located at the upper left and right corners.
Correlation coefficient between number density pT and total pressure pT plotted vs. the correlation coefficient between kinetic pressure and magnetic pressure for both Helios relatively to fast wind. Image reproduced by permission from Marsch and Tu (1993b).
Following these observations, Tu and Marsch (1994) proposed a model in which fluctuations in temperature, density, and field directly derive from an ensemble of small amplitude pressure balanced structures and small amplitude fast perpendicular magnetosonic waves. These last ones should be generated by the dynamical interaction between adjacent flow tubes due to the expansion and, eventually, they would experience also a non-linear cascade process to smaller scales. This model was able to reproduce most of the correlations described by Marsch and Tu (1993a) for fast wind.
Later on, Bavassano et al. (1996a) tried to characterize compressive fluctuations in terms of their polytropic index, which resulted to be a useful tool to study small scale variations in the solar wind. These authors followed the definition of polytropic fluid given by Chandrasekhar (1967): “a polytropic change is a quasi-static change of state carried out in such a way that the specific heat remains constant (at some prescribed value) during the entire process”. For such a variation of state the adiabatic laws are still valid provided that the adiabatic index γ is replaced by a new adiabatic index γ’ = (cp − c)/(cv − c) where c is the specific heat of the polytropic variation, and cp and cv are the specific heat at constant pressure and constant volume, respectively. This similarity is lost if we adopt the definition given by Courant and Friedrichs (1976), for whom a fluid is polytropic if its internal energy is proportional to the temperature. Since no restriction applies to the specific heats, relations between temperature, density, and pressure do not have a simple form as in Chandrasekhar approach (Zank and Matthaeus, (1991). Bavassano et al. (1996a) recovered the polytropic index from the relation between density n and temperature T changes for the selected scale Tn1−γ’ = const. and used it to determine whether changes in density and temperature were isobaric (γ’ = 0), isothermal (γ’ = 1), adiabatic (γ’ = γ), or isochoric (γ’ = ∞). Although the role of the magnetic field was neglected, reliable conclusions could be obtained whenever the above relations between temperature and density were strikingly clear. These authors found intervals characterized by variations at constant thermal pressure P. They interpreted these intervals as a subset of total-pressure balanced structures where the equilibrium was assured by the thermal component only, perhaps tiny flow tubes like those described by Thieme et al. (1989) and Tu and Marsch (1994). Adiabatic changes were probably related to magnetosonic waves excited by contiguous flow tubes (Tu and Marsch, (1994). Proton temperature changes at almost constant density were preferentially found in fast wind, close to the Sun. These regions were characterized by values of B and N remarkable stable and by strong Alfvénic fluctuations (Bruno et al., (1985). Thus, they suggested that these temperature changes could be remnants of thermal features already established at the base of the corona.
Thus, the polytropic index offers a very simple way to identify basic properties of solar wind fluctuations, provided that the magnetic field does not play a major role.
6.2 Compressive turbulence in the polar wind
Compressive fluctuations in high latitude solar wind have been extensively studied by Bavassano et al. (2004) looking at the relationship between different parameters of the solar wind and comparing these results with predictions by existing models.
These authors indicated with N, Pm, Pk, and Pt the proton number density n, magnetic pressure, kinetic pressure and total pressure (Ptot = Pm + Pk), respectively, and computed correlation coefficients ρ between these parameters. Figure 75 clearly shows that a pronounced positive correlation for N − Pt and a negative pronounced correlation for Pm − Pk is a constant feature of the observed compressive fluctuations. In particular, the correlation for N − Pt is especially strong within polar regions at small heliocentric distance In mid-latitude regions the correlation weakens, while almost disappears at low latitudes. In the case of Pm − Pk, the anticorrelation remains strong throughout the whole latitudinal excursion. For polar wind the anticorrelation appears to be less strong at small distances, just where the N − Pt correlation is highest.
The role played by density and temperature in the anticorrelation between magnetic and thermal pressures is investigated in Figure 76, where the magnetic field magnitude is directly compared with proton density and temperature. As regards the polar regions, a strong B-T anticorrelation is clearly apparent at all distances (right panel). For B-N an anticorrelation tends to emerge when solar distance increases. This means that the magnetic-thermal pressure anticorrelation is mostly due to an anticorrelation of the magnetic field fluctuations with respect to temperature fluctuations, rather than density (see, e.g., Bavassano et al., (1996a,b). Outside polar regions the situation appears in part reversed, with a stronger role for the B-N anticorrelation.
In Figure 77 scatter plots of total pressure vs. density fluctuations are used to test a model by Tu and Marsch (1994), based on the hypothesis that the compressive fluctuations observed in solar wind are mainly due to a mixture of pressure-balanced structures (PBS) and fast magnetosonic waves (W).Waves can only contribute to total pressure fluctuations while both waves and pressurebalanced structures may contribute to density fluctuations. A tunable parameter in the model is the relative PBS/W contribution to density fluctuations α. Straight lines in Figure 77 indicate the model predictions for different values of α. It is easily seen that for all polar wind samples the great majority of experimental data fall in the α > 1 region. Thus, pressure-balanced structures appear to play a major role with respect to magnetosonic waves. This is a feature already observed by Helios in the ecliptic wind (Tu and Marsch, (1994), although in a less pronounced way. Different panels of Figure 77 refer to different heliocentric distances within the polar wind. Namely, going from P1 to P4 is equivalent to move from 1.4 to 4 AU. A comparison between these panels indicates that the observed distribution tends to shift towards higher values of α (i.e., pressure-balanced structures become increasingly important), which probably is a radial distance effect.
Histograms of ρ(N − Pt) and ρ(Pm − Pk) per solar rotation. The color bar on the left side indicates polar (red), mid-latitude (blue), and low latitude (green) phases. Moreover, universal time UT, heliocentric distance, and heliographic latitude are also indicated on the left side of the plot. Occurrence frequency is indicated by the color bar shown on the right hand side of the figure. Image reproduced by permission from Bavassano et al. (2004), copyright EGU.
Finally, the relative density fluctuations dependence on the turbulent Mach number M (the ratio between velocity fluctuation amplitude and sound speed) is shown in Figure 78. The aim is to look for the presence, in the observed fluctuations, of nearly incompressible MHD behaviors. In the framework of the NI theory (Zank and Matthaeus, (1991, (1993) two different scalings for the relative density fluctuations are possible, as M or as M2, depending on the role that thermal conduction effects may play in the plasma under study (namely a heat-fluctuation-dominated or a heat-fluctuation-modified behavior, respectively). These scalings are shown in Figure 78 as solid (for M) and dashed (for M2) lines.
It is clearly seen that for all the polar wind samples no clear trend emerges in the data. Thus, NI-MHD effects do not seem to play a relevant role in driving the polar wind fluctuations. This confirms previous results in the ecliptic by Helios in the inner heliosphere (Bavassano et al., (1995; Bavassano and Bruno, (1995) and by Voyagers in the outer heliosphere (Matthaeus et al., (1991). It is worthy of note that, apart from the lack of NI trends, the experimental data from Ulysses, Voyagers, and Helios missions in all cases exhibit quite similar distributions. In other words, for different heliospheric regions, solar wind regimes, and solar activity conditions, the behavior of the compressive fluctuations in terms of relative density fluctuations and turbulent Mach numbers seems almost to be an invariant feature.
Scatter plots of the relative amplitudes of total pressure vs. density fluctuations for polar wind samples P1 to P4. Straight lines indicate the Tu and Marsch (1994) model predictions for different values of α, the relative PBS/W contribution to density fluctuations. Image reproduced by permission from Bavassano et al. (2004), copyright EGU.
Relative amplitude of density fluctuations vs. turbulent Mach number for polar wind. Solid and dashed lines indicate the M and M2 scalings, respectively. Image reproduced by permission from Bavassano et al. (2004), copyright EGU.
The above observations fully support the view that compressive fluctuations in high latitude solar wind are a mixture of MHD modes and pressure balanced structures. It has to be reminded that previous studies (McComas et al., (1995, (1996; Reisenfeld et al., (1999) indicated a relevant presence of pressure balanced structures at hourly scales. Moreover, nearly-incompressible (see Section 6.1) effects do not seem to play any relevant role. Thus, polar observations do not show major differences when compared with ecliptic observations in fast wind, the only possible difference being a major role of pressure balanced structures.
6.3 The effect of compressive phenomena on Alfvénic correlations
A lack of δV − δB correlation does not strictly indicate a lack of Alfvénic fluctuations since a superposition of both outward and inward oriented fluctuations of the same amplitude would produce a very low correlation as well. In addition, the rather complicated scenario at the base of the corona, where both kinetic and magnetic phenomena contribute to the birth of the wind, suggest that the imprints of such a structured corona is carried away by the wind during its expansion. At this point, we would expect that solar wind fluctuations would not solely be due to the ubiquitous Alfvénic and other MHD propagating modes but also to an underlying structure convected by the wind, not necessarily characterized by Alfvén-like correlations. Moreover, dynamical interactions between fast and slow wind, built up during the expansion, contribute to increase the compressibility of the medium.
It has been suggested that disturbances of the mean magnetic field intensity and plasma density act destructively on δV − δB correlation. Bruno and Bavassano (1993) analyzed the loss of the Alfvénic character of interplanetary fluctuations in the inner heliosphere within the low frequency part of the Alfvénic range, i.e., between 2 and 10 h. Figure 79, from their work, shows the wind speed profile, σc, the correlation coefficients, phase and coherence for the three components (see Appendix B.2.1), the angle between magnetic field and velocity minimum variance directions, and the heliocentric distance Magnetic field sectors were rectified (see Appendix B.3) and magnetic field and velocity components were rotated into the magnetic field minimum variance reference system (see Appendix D). Although the three components behave in a similar way, the most Alfvénic ones are the two components Y and Z transverse to the minimum variance component X. As a matter of fact, for an Alfvén mode we would expect a high δV − δB correlation, a phase close to zero for outward waves and a high coherence Moreover, it is rather clear that the most Alfvénic intervals are located within the trailing edges of high velocity streams. However, as the radial distance increases, the Alfvénic character of the fluctuations decreases and the angle Θbu increases. The same authors found that high values of Θbu are associated with low values of σc and correspond to the most compressive intervals. They concluded that the depletion of the Alfvénic character of the fluctuations, within the hourly frequency range, might be driven by the interaction with static structures or magnetosonic perturbations able to modify the homogeneity of the background medium on spatial scales comparable to the wavelength of the Alfvénic fluctuations. A subsequent paper by Klein et al. (1993) showed that the δV − δB decoupling increases with the plasma β, suggesting that in regions where the local magnetic field is less relevant, compressive events play a major role in this phenomenon.
Wind speed profile V and |σc|V are shown in the top panel. The lower three panels refer to correlation coefficient, phase angle and coherence for the three components of δV and δB fluctuations, respectively. The successive panel indicates the value of the angle between magnetic field and velocity fluctuations minimum variance directions. The bottom panel refers to the heliocentric distance (from Bruno and Bavassano, (1993).
7 A Natural Wind Tunnel
The solar wind has been used as a wind tunnel by Burlaga who, at the beginning of the 1990s, started to investigate anomalous fluctuations (Burlaga, (1991a,b,c, (1995) as observed by measurements in the outer heliosphere by the Voyager spacecraft. In 1991, Marsch, in a review on solar wind turbulence given at the Solar Wind Seven conference, underlined the importance of investigating scaling laws in the solar wind and we like to report his sentence: “The recent work by Burlaga (1991a,b) opens in my mind a very promising avenue to analyze and understand solar wind turbulence from a new theoretical vantage point. ...This approach may also be useful for MHD turbulence Possible connections between intermittent turbulence and deterministic chaos have recently been investigated ...We are still waiting for applications of these modern concepts of chaos theory to solar wind MHD fluctuations.” (cf. Marsch, (1992, p. 503). A few years later Carbone (1993) and, independently, Biskamp (1993) faced the question of anomalous scaling from a theoretical point of view. More than ten years later the investigation of statistical mechanics of MHD turbulence from one side, and of low-frequency solar wind turbulence on the other side, has produced a lot of papers, and is now mature enough to be tentatively presented in a more organic way.
7.1 Scaling exponents of structure functions
The phenomenology of turbulence developed by Kolmogorov (1941) deals with some statistical hypotheses for fluctuations. The famous footnote remark by Landau (Landau and Lifshitz, (1971) pointed out a defect in the Kolmogorov theory, namely the fact that the theory does not take proper account of spatial fluctuations of local dissipation rate (Frisch, (1995). This led different authors to investigate the features related to scaling laws of fluctuations and, in particular, to investigate the departure from the Kolmogorov’s linear scaling of the structure functions (cf. Section 2.8). An up-to-date comprehensive review of these theoretical efforts can be found in the book by Frisch (1995).
Here we are interested in understanding what we can learn from solar wind turbulence about the basic features of scaling laws for fluctuations. We use velocity and magnetic fields time series, and we investigate the scaling behavior of the high-order moments of stochastic variables defined as variations of fields separated by a timeFootnote 8 interval τ. First of all, it is worthwhile to remark that scaling laws and, in particular, the exact relation (41) which defines the inertial range in fluid flows, is valid for longitudinal (streamwise) fluctuations. In common fluid flows the Kolmogorov linear scaling law is compared with the moments of longitudinal velocity differences. In the same way for the solar wind turbulence we investigate the scaling behavior of Δuτ = u(t+τ)−u(t), where u(t) represents the component of the velocity field along the radial direction. As far as the magnetic differences are concerned Δbτ = B(t+τ) − B(t), we are free for different choices and, in some sense, this is more interesting from an experimental point of view. We can use the reference system where B(t) represents the magnetic field projected along the radial direction, or the system where B(t) represents the magnetic field along the local background magnetic field, or B(t) represents the field along the minimum variance direction. As a different case we can simply investigate the scaling behavior of the fluctuations of the magnetic field intensity.
Let us consider the p-th moment of both absolute valuesFootnote 9 of velocity fluctuations Rp(τ) = 〈|Δuτ|p〉 and magnetic fluctuations Sp(τ) = 〈|Δbτ|p〉, also called p-th order structure function in literature (brackets being time average). Here we use magnetic fluctuations across structures at intervals τ calculated by using the magnetic field intensity. Typical structure functions of magnetic field fluctuations, for two different values of p, for both a slow wind and a fast wind at 0.9 AU, are shown in Figures 80. The magnetic field we used is that measured by Helios 2 spacecraft. Structure functions calculated for the velocity fields have roughly the same shape. Looking at these Figures the typical scaling features of turbulence can be observed. Starting from low values at small scales, the structure functions increase towards a region where Sp → const. at the largest scales. This means that at these scales the field fluctuations are uncorrelated. A kind of “inertial range”, that is a region of intermediate scales τ where a power law can be recognized for both
is more or less visible only for the slow wind. In this range correlations exists, and we can obtain the scaling exponents ζp and ξp through a simple linear fit.
Since as we have seen, Yaglom’s law is observed only in some few samples, the inertial range in the whole solar wind is not well defined. A look at Figure 80 clearly shows that we are in a situation similar to a low-Reynolds number fluid flow. In order to compare scaling exponents of the solar wind turbulent fluctuations with other experiments, it is perhaps better to try to recover exponents using the Extended Self-Similarity (ESS), introduced some time ago by Benzi et al. (1993), and used here as a tool to determine relative scaling exponents. In the fluid-like case, the third-order structure function can be regarded as a generalized scaling using the inverse of Equation (42) or of Equation (41) (Politano et al., (1998). Then, we can plot the p-th order structure function vs. the third-order one to recover at least relative scaling exponents ζp/ζ3 and ζp/ξ3 (61). Quite surprisingly (see Figure 81), we find that the range where a power law can be recovered extends well beyond the inertial range, covering almost all the experimental range. In the fluid case the scaling exponents which can be obtained through ESS at low or moderate Reynolds numbers, coincide with the scaling exponents obtained for high Reynolds, where the inertial range is very well defined Benzi et al. (1993). This is due to the fact that, since by definition ζ3 = 1 in the inertial range (Frisch, (1995), whatever its extension might be. In our case scaling exponents obtained through ESS can be used as a surrogate, since we cannot be sure that an inertial range exists.
It is worthwhile to remark (as shown in Figure 81) that we can introduce a general scaling relation between the q-th order velocity structure function and the q-th order structure function, with a relative scaling exponent αp(q). It has been found that this relation becomes an exact relation
when the velocity structure functions are normalized to the average velocity within each period used to calculate the structure function (Carbone et al., (1996a). This is very interesting because it implies (Carbone et al., (1996a) that the above relationship is satisfied by the following probability distribution function, if we assume that odd moments are much smaller than the even ones:
That is, for each scale τ the knowledge of the relative scaling exponents αp(q) completely determines the probability distribution of velocity differences as a function of a single parameter Sp(τ).
Relative scaling exponents, calculated by using data coming from Helios 2 at 0.9 AU, are reported in Table 1. As it can be seen, two main features can be noted:
-
i.
There is a significant departure from the Kolmogorov linear scaling, that is, real scaling exponents are anomalous and seem to be non-linear functions of p, say ζp/ζ3 > p/3 for p < 3, while ζp/ζ3 < p/3 for p > 3. The same behavior can be observed for ξp/ξ3. In Table 1 we report also the scaling exponents obtained in usual fluid flows for velocity and temperature, the latter being a passive scalar. Scaling exponents for velocity field are similar to scaling exponents obtained in turbulent flows on Earth, showing a kind of universality in the anomaly. This effect is commonly attributed to the phenomenon of intermittency in fully developed turbulence (Frisch, (1995). Turbulence in the solar wind is intermittent, just like its fluid counterpart on Earth.
-
ii.
The degree of intermittency is measured through the distance between the curve ζp/ζ3 and the linear scaling p/3. It can be seen that the magnetic field is more intermittent than the velocity field. The same difference is observed between the velocity field and a passive scalar (in our case the temperature) in ordinary fluid flows (Ruíz-Chavarría et al., (1995). That is the magnetic field, as long as intermittency properties are concerned, has the same scaling laws of a passive field. Of course this does not mean that the magnetic field plays the same role as a passive field. Statistical properties are in general different from dynamical properties.
In Table 1 we show scaling exponents up to the sixth order. Actually, a question concerns the validation of high-order moments estimates, say the maximum value of the order p which can be determined with a finite number of points of our dataset. As the value of p increases, we need an increasing number of points for an optimal determination of the structure function (RuíTennekes). Anomalous scaling laws are generated by rare and intense events due to singularities in the gradients: the higher their intensity the more rare these events are. Of course, when the data set has a finite extent, the probability to get singularities stronger than a certain value approaches zero. In that case, scaling exponents ζp of order higher than a certain value become linear functions of p. Actually, the structure function Sp(τ) depends on the probability distribution function PDF(Δuτ) through
and, the function Sp is determined only when the integral converges. As p increases, the function Fp(δuτ) = Δu pτ PDF(Δuτ) becomes more and more disturbed, with some spikes, so that the integral becomes more and more undefined, as can be seen for example in Figure 1 of the paper by Dudok de Wit (2004). A simple calculation (Dudok de Wit, (2004) for the maximum value of the order pm which can reliably be estimated with a given number N of points in the dataset, gives
the empirical criterion pm ≃ log N. Structure functions of order p > pm cannot be determined accurately.
Only few large structures are enough to generate the anomalous scaling laws. In fact, as shown by Salem et al. (2009), by suppressing through wavelets analysis just a few percentage of large structures on all scales, the scaling exponents become linear functions of p, respectively p/4 and p/3 for the kinetic and magnetic fields.
As far as a comparison between different plasmas is concerned, the scaling exponents of magnetic structure functions, obtained from laboratory plasma experiments of a Reversed-Field Pinch at different distances from the external wall (Carbone et al., (2000) are shown in Table 2. In laboratory plasmas it is difficult to measure all the components of the vector field at the same time, thus, here we show only the scaling exponents obtained using magnetic field differences Br(t+τ)−Br(t) calculated from the radial component in a toroidal device where the z-axis is directed along the axis of the torus. As it can be seen, intermittency in magnetic turbulence is not so strong as it appears to be in the solar wind, actually the degree of intermittency increases when going toward the external wall. This last feature appears to be similar to what is currently observed in channel flows, where intermittency also increases when going towards the external wall (Pope, (2000).
Scaling exponents of structure functions for Alfvén variables, velocity, and magnetic variables have been calculated also for high resolution 2D incompressible MHD numerical simulations (Politano et al., (1998). In this case, we are freed from the constraint of the Taylor hypothesis when calculating the fluctuations at a given scale. From 2D simulations we recover the fields u(r, t) and b(r, t) at some fixed times. We calculate the longitudinal fluctuations directly in space at a fixed time, namely Δu∓ = [u(r+ℓ, t)− u(r, t)] · ℓ/ℓ (the same are made for different fields, namely the magnetic field or the Elsässer fields). Finally, averaging both in space and time, we calculate the scaling exponents through the structure functions. These scaling exponents are reported in Table 3. Note that, even in numerical simulations, intermittency for magnetic variables is stronger than for the velocity field.
7.2 Probability distribution functions and self-similarity of fluctuations
The presence of scaling laws for fluctuations is a signature of the presence of self-similarity in the phenomenon. A given observable u(ℓ), which depends on a scaling variable ℓ, is invariant with respect to the scaling relation ℓ → λℓ, when there exists a parameter μ(λ) such that u(ℓ) = μ(λ)u(λℓ). The solution of this last relation is a power law u(ℓ) = Cℓh, where the scaling exponent is h = −logλμ.
Since, as we have just seen, turbulence is characterized by scaling laws, this must be a signature of self-similarity for fluctuations. Let us see what this means. Let us consider fluctuations at two different scales, namely Δz ±ℓ and Δz ±λℓ . Their ratio Δz ±λℓ /Δz ±ℓ depends only on the value of h, and this should imply that fluctuations are self-similar. This means that PDFs are related through
Let us consider the normalized variables
When h is unique or in a pure self-similar situation, PDFs are related through P(y ±ℓ ) = PDF(y ±λℓ ), say by changing scale PDFs coincide.
The PDFs relative to the normalized magnetic fluctuations δbτ = Δbτ/〈Δb 2τ 〉1/2, at three different scales τ, are shown in Figure 82. It appears evident that the global self-similarity in real turbulence is broken. PDFs do not coincide at different scales, rather their shape seems to depend on the scale τ. In particular, at large scales PDFs seem to be almost Gaussian, but they become more and more stretched as τ decreases. At the smallest scale PDFs are stretched exponentials. This scaling dependence of PDFs is a different way to say that scaling exponents of fluctuations are anomalous, or can be taken as a different definition of intermittency. Note that the wings of PDFs are higher than those of a Gaussian function. This implies that intense fluctuations have a probability of occurrence higher than that they should have if they were Gaussianly distributed. Said differently, intense stochastic fluctuations are less rare than we should expect from the point of view of a Gaussian approach to the statistics. These fluctuations play a key role in the statistics of turbulence The same statistical behavior can be found in different experiments related to the study of the atmosphere (see Figure 83) and the laboratory plasma (see Figure 84).
Left panel: normalized PDFs for the magnetic fluctuations observed in the solar wind turbulence by using Helios data. Right panel: distribution function of waiting times Δt between structures at the smallest scale. The parameter β is the scaling exponent of the scaling relation PDF(Δt) ~ Δt−β for the distribution function of waiting times.
Left panel: normalized PDFs of velocity fluctuations in atmospheric turbulence. Right panel: distribution function of waiting times Δt between structures at the smallest scale. The parameter β is the scaling exponent of the scaling relation PDF(Δt) ~ Δt−β for the distribution function of waiting times. The turbulent samples have been collected above a grass-covered forest clearing at 5 m above the ground surface and at a sampling rate of 56 Hz (Katul et al., (1997).
Left panel: normalized PDFs of the radial magnetic field collected in RFX magnetic turbulence (Carbone et al., (2000). Right panel: distribution function of waiting times Δt between structures at the smallest scale. The parameter β is the scaling exponent of the scaling relation PDF(Δt) ~ Δt−β for the distribution function of waiting times.
7.3 What is intermittent in the solar wind turbulence? The multifractal approach
Time dependence of Δuτ and Δbτ for three different scales τ is shown in Figures 85 and 86, respectively. These plots show that, as τ becomes small, intense fluctuations become more and more important, and they dominate the statistics. Fluctuations at large scales appear to be smooth while, as the scale becomes smaller, intense fluctuations becomes visible. These dominating fluctuations represent relatively rare events. Actually, at the smallest scales, the time behavior of both Δuτ and Δbτ is dominated by regions where fluctuations are low, in between regions where fluctuations are intense and turbulent activity is very high. Of course, this behavior cannot be described by a global self-similar behavior. Allowing the scaling laws to vary with the region of turbulence we are investigating would be more convincing.
The behavior we have just described is at the heart of the multifractal approach to turbulence (Frisch, (1995). In that description of turbulence, even if the small scales of fluid flow cannot be globally self-similar, self-similarity can be reintroduced as a local property. In the multifractal description it is conjectured that turbulent flows can be made by an infinite set of points Sh(r), each set being characterized by a scaling law ΔZ ±ℓ ~ ℓh(r), that is, the scaling exponent can depend on the position r. The usual dimension of that set is then not constant, but depends on the local value of h, and is quoted as D(h) in literature. Then, the probability of occurrence of a given fluctuation can be calculated through the weight the fluctuation assumes within the whole flow, i.e.,
and the p-th order structure function is immediately written through the integral over all (continuous) values of . weighted by a smooth function μ(h) ~ 0(1), i.e.,
A moment of reflection allows us to realize that in the limit ℓ → 0 the integral is dominated by the minimum value (over .) of the exponent and, as shown by Frisch (1995), the integral can be formally solved using the usual saddle-point method. The scaling exponents of the structure function can then be written as
In this way, the departure of ζp from the linear Kolmogorov scaling and thus intermittency, can be characterized by the continuous changing of D(h) as h varies. That is, as p varies we are probing regions of fluid where even more rare and intense events exist. These regions are characterized by small values of h, that is, by stronger singularities of the gradient of the field.
Owing to the famous Landau footnote on the fact that fluctuations of the energy transfer rate must be taken into account in determining the statistics of turbulence, people tried to interpret the non-linear energy cascade typical of turbulence theory, within a geometrical framework. The old Richardson’s picture of the turbulent behavior as the result of a hierarchy of eddies at different scales has been modified and, as realized by Kraichnan (1974), once we leave the idea of a constant energy cascade rate we open a “Pandora’s box” of possibilities for modeling the energy cascade. By looking at scaling laws for Δz ±ℓ and introducing the scaling exponents for the energy transfer rate 〈∈ pℓ ~ rτp, it can be found that ζp = p/m + τp/m (being m = 3 when the Kolmogorov-like phenomenology is taken into account, or m = 4 when the Iroshnikov-Kraichnan phenomenology holds). In this way the intermittency correction are determined by a cascade model for the energy transfer rate. When τp is a non-linear function of p, the energy transfer rate can be described within the multifractal geometry (see, e.g., Meneveau, (1991, and references therein) characterized by the generalized dimensions Dp = 1 − τp/(p − 1) (Hentschel and Procaccia, (1983). The scaling exponents of the structure functions are then related to Dp by
The correction to the linear scaling p/m is positive for p < m, negative for p > m, and zero for p = m. A fractal behavior where Dp = const. < 1 gives a linear correction with a slope different from 1/m.
7.4 Fragmentation models for the energy transfer rate
Cascade models view turbulence as a collection of fragments at a given scale ℓ, which results from the fragmentation of structures at the scale ℓ’ > ℓ, down to the dissipative scale (Novikov, (1969). Sophisticated statistics are applied to obtain scaling exponents ζp for the p-th order structure function.
The starting point of fragmentation models is the old β-model, a “pedagogical” fractal model introduced by Frisch et al. (1978) to account for the modification of the cascade in a simple way. In this model, the cascade is realized through the conjecture that active eddies and non-active eddies are present at each scale, the space-filling factor for the fragments being fixed for each scale. Since it is a fractal model, the β-model gives a linear modification to ζp. This can account for a fit on the data, as far as small values of p are concerned. However, the whole curve ζp is clearly nonlinear, and a multifractal approach is needed.
The random-β model (Benzi et al., (1984), a multifractal modification of the β-model, can be derived by invoking that the space-filling factor for the fragments at a given scale in the energy cascade is not fixed, but is given by a random variable β. The probability of occurrence of a given β is assumed to be a bimodal distribution where the eddies fragmentation process generates either space-filling eddies with probability ξ or planar sheets with probability (1 − ξ) (for conservation 0 ≤ ξ ≤ 1). It can be found that
where the free parameter ξ can be fixed through a fit on the data.
The p-model (Meneveau, (1991; Carbone, (1993) consists in an eddies fragmentation process described by a two-scale Cantor set with equal partition intervals. An eddy at the scale ℓ, with an energy derived from the transfer rate ∈r, breaks down into two eddies at the scale ℓ/2, with energies μ∈r and (1 − μ)∈r. The parameter 0.5 ≤ μ ≤ 1 is not defined by the model, but is fixed from the experimental data. The model gives
In the model by She and Leveque (see, e.g., She and Leveque, (1994; Politano and Pouquet, (1998) one assumes an infinite hierarchy for the moments of the energy transfer rates, leading to ∈ (p+1)r ~ [∈ (p)r ]β[∈ (∞)r ]1−β, and a divergent scaling law for the infinite-order moment ∈ (∞)r ~ r−x, which describes the most singular structures within the flow. The model reads
The parameter C = x/(1 − β) is identified as the codimension of the most singular structures. In the standard MHD case (Politano and Pouquet, (1995) x = β = 1/2, so that C = 1, that is, the most singular dissipative structures are planar sheets. On the contrary, in fluid flows C = 2 and the most dissipative structures are filaments. The large p behavior of the p-model is given by ζp ~ (p/m) log2(1/μ) + 1, so that Equations (64, 65) give the same results providing μ ≃ 2−x. As shown by Carbone et al. (1996b) all models are able to capture intermittency of fluctuations in the solar wind. The agreement between the curves ζp and normalized scaling exponents is excellent, and this means that we realistically cannot discriminate between the models we reported above. The main problem is that all models are based on a conjecture which gives a curve ζp as a function of a single free parameter, and that curve is able to fit the smooth observed behavior of ζp. Statistics cannot prove, just disprove. We can distinguish between the fractal model and multifractal models, but we cannot realistically distinguish among the various multifractal models.
7.5 A model for the departure from self-similarity
Besides the idea of self-similarity underlying the process of energy cascade in turbulence, a different point of view can be introduced. The idea is to characterize the behavior of the PDFs through the scaling laws of the parameters, which describe how the shape of the PDFs changes when going towards small scales. The model, originally introduced by Castaing et al. (2001), is based on a multiplicative process describing the cascade. In its simplest form the model can be introduced by saying that PDFs of increments δZ ±ℓ , at a given scale, are made as a sum of Gaussian distributions with different widths σ = 〈(δZ ±ℓ )2〉1/2. The distribution of widths is given by Gλ(σ), namely
In a purely self-similar situation, where the energy cascade generates only a trivial variation of σ with scales, the width of the distribution Gλ(σ) is zero and, invariably, we recover a Gaussian distribution for P(δZ ±ℓ ). On the contrary, when the cascade is not strictly self-similar, the width of Gλ(σ) is different from zero and the scaling behavior of the width λ2 of Gλ(σ) can be used to characterize intermittency.
7.6 Intermittency properties recovered via a shell model
Shell models have remarkable properties which closely resemble those typical of MHD phenomena (Gloaguen et al., (1985; Biskamp, (1994; Giuliani and Carbone (1998; Plunian et al., (2012). However, the presence of a constant forcing term always induces a dynamical alignment, unless the model is forced appropriately, which invariably brings the system towards a state in which velocity and magnetic fields are strongly correlated, that is, where Z ±n ≠ = 0 and Z ∓n ≠ = 0. When we want to compare statistical properties of turbulence described by MHD shell models with solar wind observations, this term should be avoided. It is possible to replace the constant forcing term by an exponentially time-correlated Gaussian random forcing which is able to destabilize the Alfvénic fixed point of the model (Giuliani and Carbone (1998), thus assuring the energy cascade. The forcing is obtained by solving the following Langevin equation:
where μ(t) is a Gaussian stochastic process δ-correlated in time 〈μ(t)μ(t’) = 2Dδ(t’ − t). This kind of forcing will be used to investigate statistical properties.
A statistically stationary state is reached by the system Gloaguen et al. (1985); Biskamp (1994); Giuliani and Carbone (1998); Plunian et al. (2012), with a well defined inertial range, say a region where Equation (49) is verified. Spectra for both the velocity |un(t)|2 and magnetic |bn(t)|2 variables, as a function of kn, obtained in the stationary state using the GOY MHD shell model, are shown in Figures 87 and 88. Fluctuations are averaged over time. The Kolmogorov spectrum is also reported as a solid line. It is worthwhile to remark that, by adding a random term like iknB0(t)Z ±n to a little modified version of the MHD shell models (B0 is a random function with some statistical characteristics), a Kraichnan spectrum, say E(kn) ~ k −3/2n , where E(kn) is the total energy, can be recovered (Biskamp, (1994; Hattori and Ishizawa, (2001). The term added to the model could represent the effect of the occurrence of a large-scale magnetic field.
Intermittency in the shell model is due to the time behavior of shell variables. It has been shown (Okkels, (1997) that the evolution of GOY model consists of short bursts traveling through the shells and long period of oscillations before the next burst arises. In Figures 89 and 90 we report the time evolution of the real part of both velocity variables un(t) and magnetic variables bn(t) at three different shells. It can be seen that, while at smaller kn variables seems to be Gaussian, at larger kn variables present very sharp fluctuations in between very low fluctuations.
The time behavior of variables at different shells changes the statistics of fluctuations. In Figure 91 we report the probability distribution functions P(δun) and P(δBn), for different shells n, of normalized variables
where Re indicates that we take the real part of un and bn. Typically we see that PDFs look differently at different shells: At small kn fluctuations are quite Gaussian distributed, while at large kn they tend to become increasingly non-Gaussian, by developing fat tails. Rare fluctuations have a probability of occurrence larger than a Gaussian distribution. This is the typical behavior of intermittency as observed in usual fluid flows and described in previous sections.
The same phenomenon gives rise to the departure of scaling laws of structure functions from a Kolmogorov scaling. Within the framework of the shell model the analogous of structure functions are defined as
For MHD turbulence it is also useful to report mixed correlators of the flux variables, i.e.,
Scaling exponents have been determined from a least square fit in the inertial range 3 ≤ n ≤ 12. The values of these exponents are reported in Table 4. It is interesting to notice that, while scaling exponents for velocity are the same as those found in the solar wind, scaling exponents for the magnetic field found in the solar wind reveal a more intermittent character. Moreover, we notice that velocity, magnetic and Elsässer variables are more intermittent than the mixed correlators and we think that this could be due to the cancelation effects among the different terms defining the mixed correlators.
Time intermittency in the shell model generates rare and intense events. These events are the result of the chaotic dynamics in the phase-space typical of the shell model (Okkels, (1997). That dynamics is characterized by a certain amount of memory, as can be seen through the statistics of waiting times between these events. The distributions P(δt) of waiting times is reported in the bottom panels of Figures 91, at a given shell n = 12. The same statistical law is observed for the bursts of total dissipation (Boffetta et al., (1999).
In the first three panels we report PDFs of both velocity (left column) and magnetic (right column) shell variables, at three different shells ℓn. The bottom panels refer to probability distribution functions of waiting times between intermittent structures at the shell n = 12 for the corresponding velocity and magnetic variables.
8 Observations of Yaglom’s Law in Solar Wind Turbulence
To avoid the risk of misunderstanding, let us start by recalling that Yaglom’s law (40) has been derived from a set of equations (MHD) and under assumptions which are far from representing an exact mathematical model for the solar wind plasma. Yaglom’s law is valid in MHD under the hypotheses of incompressibility, stationarity, homogeneity, and isotropy. Also, the form used for the dissipative terms of MHD equations is only valid for collisional plasmas, characterized by quasi-Maxwellian distribution functions, and in case of equal kinematic viscosity and magnetic diffusivity coefficients (Biskamp, (2003). In solar wind plasmas the above hypotheses are only rough approximations, and MHD dissipative coefficients are not even defined (Tu and Marsch, (1995a). At frequencies higher than the ion cyclotron frequency, kinetic processes are indeed present, and a number of possible dissipation mechanisms can be discussed. When looking for the Yaglom’s law in the SW, the strong conjecture that the law remains valid for any form of the dissipative term is needed.
Despite the above considerations, Yaglom’s law results surprisingly verified in some solar wind samples. Results of the occurrence of Yaglom’s law in the ecliptic plane, has been reported by MacBride et al. (2008, (2010) and Smith et al. (2009) and, independently, in the polar wind by Sorriso-Valvo et al. (2007). It is worthwhile to note that, the occurrence of Yaglom’s law in polar wind, where fluctuations are Alfvénic, represents a double surprising feature because, according to the usual phenomenology of MHD turbulence, a nonlinear energy cascade should be absent for Alfénic turbulence.
In a first attempt to evaluate phenomenologically the value of the energy dissipation rate, MacBride et al. (2008) analyzed the data from ACE to evaluate the occurrence of both the Kolmogorov’s 4/5-law and their MHD analog (40). Although some words of caution related to spikes in wind speed, magnetic field strength caused by shocks and other imposed heliospheric structures that constitute inhomogeneities in the data, authors found that both relations are more or less verified in solar wind turbulence They found a distribution for the energy dissipation rate, defined in the above paper as ∈ = (∈ +ii + ∈ −ii )/2, with an average of about ∈ ≃ 1.22 × 104 J/Kg s.
In order to avoid variations of the solar activity and ecliptic disturbances (like slow wind sources, coronal mass ejections, ecliptic current sheet, and so on), and mainly mixing between fast and slow wind, Sorriso-Valvo et al. (2007) used high speed polar wind data measured by the Ulysses spacecraft. In particular, authors analyze the first seven months of 1996, when the heliocentric distance slowly increased from 3 AU to 4 AU, while the heliolatitude decreased from about 55° to 30°. The third-order mixed structure functions have been obtained using 10-days moving averages, during which the fields can be considered as stationary. A linear scaling law, like the one shown in Figure 92, has been observed in a significant fraction of samples in the examined period, with a linear range spanning more than two decades. The linear law generally extends from few minutes up to 1 day or more, and is present in about 20 periods of a few days in the 7 months considered. This probably reflects different regimes of driving of the turbulence by the Sun itself, and it is certainly an indication of the nonstationarity of the energy injection process. According to the formal definition of inertial range in the usual fluid flows, authors attribute to the range where Yaglom’s law appear the role of inertial range in the solar wind turbulence (Sorriso-Valvo et al., (2007). This range extends on scales larger than the usual range of scales where a Kolmogorov relation has been observed, say up to about few hours (cf. Figure 25).
An example of the linear scaling for the third-order mixed structure functions Y±, obtained in the polar wind using Ulysses measurements. A linear scaling law represents a range of scales where Yaglom’s law is satisfied. Image reproduced by permission from Sorriso-Valvo et al. (2007), copyright by APS.
Several other periods are found where the linear scaling range is reduced and, in particular, the sign of Y ±ℓ is observed to be either positive or negative. In some other periods the linear scaling law is observed either for Y +ℓ or Y −ℓ rather than for both quantities. It is worth noting that in a large fraction of cases the sign switches from negative to positive (or viceversa) at scales of about 1 day, roughly indicating the scale where the small scale Alfvénic correlations between velocity and magnetic fields are lost. This should indicate that the nature of fluctuations changes across the break. The values of the pseudo-energies dissipation rates ∈± has been found to be of the order of magnitude about few hundreds of J/Kg s, higher than that found in usual fluid flows which result of the order of 1 ÷ 50 J/Kg s.
The occurrence of Yaglom’s law in solar wind turbulence has been evidenced by a systematic study by MacBride et al. (2010), which, using ACE data, found a reasonable linear scaling for the mixed third-order structure functions, from about 64 s. to several hours at 1 AU in the ecliptic plane. Assuming that the third-order mixed structure function is perpendicular to the mean field, or assuming that this function varies only with the component of the scale ℓα that is perpendicular to the mean field, and is cylindrically symmetric, the Yaglom’s law would reduce to a 2D state. On the other hand, if the third-order function is parallel to the mean field or varies only with the component of the scale that is parallel to the mean field, the Yaglom’slaw would reduce to a 1D-like case. In both cases the result will depend on the angle between the average magnetic field and the flow direction. In both cases the energy cascade rate varies in the range 103 ÷ 104 J/Kg s (see MacBride et al., (2010, for further details).
Quite interestingly, Smith et al. (2009) found that the pseudo-energy cascade rates derived from Yaglom’s scaling law reveal a strong dependence on the amount of cross-helicity. In particular, they showed that when the correlation between velocity and magnetic fluctuations are higher than about 0.75, the third-order moment of the outward-propagating component, as well as of the total energy and cross-helicity are negative. As already made by Sorriso-Valvo et al. (2007), they attribute this phenomenon to a kind of inverse cascade, namely a back-transfer of energy from small to large scales within the inertial range of the dominant component. We should point out that experimental values of energy transfer rate in the incompressive case, estimated with different techniques from different data sets (Vasquez et al., (2007; MacBride et al., (2010), are only partially in agreement with that obtained by Sorriso-Valvo et al. (2007). However, the different nature of wind (ecliptic vs. polar, fast vs. slow, at different radial distances from the Sun) makes such a comparison only indicative.
As far as the scaling law (47) is concerned, Carbone et al. (2009a) found that a linear scaling for W ±ℓ as defined in (47), appears almost in all Ulysses dataset. In particular, the linear scaling for W ±ℓ is verified even when there is no scaling at all for Y ±ℓ (40). In particular, it has been observed (Carbone et al., (2009a) that a linear scaling for W +ℓ . appears in about half the whole signal, while W −ℓ displays scaling on about a quarter of the sample. The linear scaling law generally extends on about two decades, from a few minutes up to one day or more, as shown in Figure 93. At variance to the incompressible case, the two fluxes W ±ℓ coexist in a large number of cases. The pseudoenergies dissipation rates so obtained are considerably larger than the relative values obtained in the incompressible case. In fact it has been found that on average ∈+ ≃ 3 × 103 J/Kg s. This result shows that the nonlinear energy cascade in solar wind turbulence is considerably enhanced by density fluctuations, despite their small amplitude within the Alfvénic polar turbulence Note that the new variables Δw ±i are built by coupling the Elsässer fields with the density, before computing the scale-dependent increments. Moreover, the third-order moments are very sensitive to intense field fluctuations, that could arise when density fluctuations are correlated with velocity and magnetic field. Similar results, but with a considerably smaller effect, were found in numerical simulations of compressive MHD (Mac Low and Klessen, (2004).
The linear scaling relation is reported for both the usual third-order structure function Y +ℓ and the same quantity build up with the density-mediated variables W +ℓ . A linear relation full line is clearly observed. Data refer to the Ulysses spacecraft. Image reproduced by permission from Carbone et al. (2009a), copyright by APS.
Finally, it is worth reporting that the presence of Yaglom’s law in solar wind turbulence is an interesting theoretical topic, because this is the first real experimental evidence that the solar wind turbulence, at least at large-scales, can be described within the magnetohydrodynamic model. In fact, Yaglom’s law is an exact law derived from MHD equations and, let us say once more, their occurrence in a medium like the solar wind is a welcomed surprise. By the way, the presence of the law in the polar wind solves the paradox of the presence of Alfvénic turbulence as first pointed out by Dobrowolny et al. (1980a). Of course, the presence of Yaglom’s law generates some controversial questions about data selection, reliability and a brief discussion on the extension of the inertial range. The interested reader can find some questions and relative answers in Physical Review Letters (Forman et al., (2010; Sorriso-Valvo et al., (2010a).
9 Intermittency Properties in the 3D Heliosphere: Taking a Look at the Data
In this section, we present a reasoned look at the main aspect of what has been reported in literature about the problem of intermittency in the solar wind turbulence In particular, we present results from data analysis.
9.1 Structure functions
Apart from the earliest investigations on the fractal structure of magnetic field as observed in interplanetary space (Burlaga and Klein, (1986), the starting point for the investigation of intermittency in the solar wind dates back to 1991, when Burlaga (1991a) started to look at the scaling of the bulk velocity fluctuations at 8.5 AU using Voyager 2 data. This author found that anomalous scaling laws for structure functions could be recovered in the range 0.85 ≤ r ≤ 13.6 h. This range of scales has been arbitrarily identified as a kind of “inertial range”, say a region were a linear scaling exists between log S (p)r and log r, and the scaling exponents have been calculated as the slope of these curves. However, structure functions of order p ≤ 20 were determined on the basis of only about 4500 data points. Nevertheless the scaling was found to be quite in agreement with that found in ordinary fluid flows. Although the data might be in agreement with the random-β model, from a theoretical point of view Carbone (1993, (1994b) showed that normalized scaling exponents ζp/ζ4 calculated by Burlaga (1991a) would be better fitted by using a p-model derived from the Kraichnan phenomenology (Kraichnan, (1965; Carbone, (1993), and considering the parameter μ ≃ 0.77. The same author (Burlaga, 1991b) investigated the multifractal structure of the interplanetary magnetic field near 25 AU and analyzed positive defined fields as magnetic field strength, temperature, and density using the multifractal machinery of dissipation fields (Paladin and Vulpiani, 1987; Meneveau, (1991). Burlaga (1991c) showed that intermittent events observed in co-rotating streams at 1 AU should be described by a multifractal geometry. Even in this case the number of points used was very low to assure the reliability of high-order moments.
Marsch and Liu (1993) investigated the structure of intermittency of the turbulence observed in the inner heliosphere by using Helios 2 data. They analyzed both bulk velocity and Alfvén speed to calculate structure functions in the whole range 40.5 s (the instrument resolution) up to 24 h to estimate the p-th order scaling exponents. Note that also in this analysis the number of data points used was too small to assure a reliability for order p = 20 structure functions as reported by Marsch and Liu (1993). From the analysis analogous to Burlaga (1991a), authors found that anomalous scaling laws are present. A comparison between fast and slow streams at two heliocentric distances, namely 0.3 AU and 1 AU, allows authors to conjecture a scenario for high speed streams were Alfvénic turbulence, originally self-similar (or poorly intermittent) near the Sun, “... loses its self-similarity and becomes more multifractal in nature” (Marsch and Liu, (1993), which means that intermittent corrections increase from 0.3 AU to 1 AU. No such behavior seems to occur in the slow solar wind. From a phenomenological point of view, Marsch and Liu (1993) found that data can be fitted with a piecewise linear function for the scaling exponents ζp, namely a β-model ζpp = 3 − D +p(D−2)/3, where D ≃ 3 for p ≤ 6 and D ≃ 2.6 for p > 6. Authors say that “We believe that we see similar indications in the data by Burlaga, who still prefers to fit his whole ζp dataset with a single fit according to the non-linear random β-model”. We like to comment that the impression by Marsch and Liu (1993) is due to the fact that the number of data points used was very small. As a matter of fact, only structure functions of order p ≤ 4 are reliably described by the number of points used by Burlaga (1991a).
However, the data analyses quoted above, which in some sense present some contradictory results, are based on high order statistics which is not supported by an adequate number of data points and the range of scales, where scaling laws have been recovered, is not easily identifiable. To overcome these difficulties Carbone et al. (1996a) investigated the behavior of the normalized ratios ζp/ζ3 through the ESS procedure described above, using data coming from low-speed streams measurements of Helios 2 spacecraft. Using ESS the whole range covered by measurements is linear, and scaling exponent ratios can be reliably calculated. Moreover, to have a dataset with a high number of points, authors mixed in the same statistics data coming from different heliocentric distances (from 0.3 AU up to 1 AU). This is not correct as far as fast wind fluctuations are taken into account, because, as found by Marsch and Liu (1993) and Bruno et al. (2003b), there is a radial evolution of intermittency. Results showed that intermittency is a real characteristic of turbulence in the solar wind, and that the curve ζp/ζ3 is a non-linear function of p as soon as values of p ≤ 6 are considered.
Marsch et al. (1996) for the first time investigated the geometrical and scaling properties of the energy flux along the turbulent cascade and dissipation rate of kinetic energy. They showed the multifractal nature of the dissipation field and estimated, for the first time in solar wind MHD turbulence, the associated singularity spectrum which resulted to be very similar to those obtained for ordinary fluid turbulence (Meneveau and Sreenivasan, (1987). They also estimated the energy dissipation rate for time scales of 102 s to be around 5.4 × 10−16 erg cm−3 s−1. This value was similar to the theoretical heating rate required in the model by Tu (1988) with Alfvén waves to explain the radial temperature dependence observed in fast solar wind. Looking at the literature, it can be realized that often scaling exponents ζp, as observed mainly in the high-speed streams of the inner solar wind, cannot be explained properly by any cascade model for turbulence This feature has been attributed to the fact that this kind of turbulence is not in a fully-developed state with a well defined spectral index. Models developed by Tu et al. (1984) and Tu (1988) were successful in describing the evolution of the observed power spectra. Using the same idea Tu et al. (1996) and Marsch and Tu (1997). investigated the behavior of an extended cascade model developed on the base of the p-model (Meneveau and Sreenivasan, (1987; Carbone, (1993). Authors conjectured that: i) the scaling laws for fluctuations are still valid in the form δZ ±ℓ ~ ℓh, even when turbulence is not fully developed; ii) the energy cascade rate is not constant, its moments rather depend not only on the generalized dimensions Dp but also on the spectral index α of the power spectrum, say 〈∈ pr 〉 ~ ∈p (ℓ, α)ℓ(p−1)Dp, where the averaged energy transfer rate is assumed to be
being Pℓ ~ ℓα the usual energy spectrum (ℓ ~ 1/k). The model gives
where the generalized dimensions are recovered from the usual p-model
In the limit of “fully developed turbulence”, say when the spectral slope is α = 2/m + 1 the usual Equation (64) is recovered. The Helios 2 data are consistent with this model as far as the parameters are μ ≃ 0.77 and α ≃ 1.45, and the fit is relatively good (Tu et al., (1996). Recently, Horbury et al. (1997) and Horbury and Balogh (1997) studied the magnetic field fluctuations of the polar high-speed turbulence from Ulysses measurements at 3.1 AU and at 63. heliolatitude. These authors showed that the observed magnetic field fluctuations were in agreement with the intermittent turbulence p-model of Meneveau and Sreenivasan (1987). They also showed that the scaling exponents of structure functions of order p ≤ 6, in the scaling range 20 ≤ r ≤ 300 s followed the Kolmogorov scaling instead of Kraichnan scaling as expected. In addition, the same authors (Horbury et al., 1997) estimated the applicability of the model by Tu et al. (1996) and Marsch and Tu (1997). to the spectral transition range where the spectral index changes during the spectral evolution and concluded that this model was able to fit the observations much better than the p-model when values of the parameters p change continuously with the scale.
Analysis of scaling exponents of p-th order structure functions has been performed using different spacecraft datasets of Ulysses spacecraft. Horbury et al. (1995a) and Horbury et al. (1995c) investigated the structure functions of magnetic field as obtained from observations recorded between 1.7 and 4 AU, and covering a heliographic latitude between 40° and 80° south. By investigating the spectral index of the second order structure function, they found a decrease with heliocentric distance attributed to the radial evolution of fluctuations. Further investigations (see, e.g., Ruzmaikin et al., (1995) were obtained using structure functions to study the Ulysses magnetic field data in the range of scales 1 ≤ r ≤ 32 min. Ruzmaikin et al. (1995). showed that intermittency is at work and developed a bi-fractal model to describe Alfvénic turbulence They found that intermittency may change the spectral index of the second order structure function and this modifies the calculation of the spectral index (Carbone, (1994a.). Ruzmaikin et al. (1995). found that polar Alfvénic turbulence should be described by a Kraichnan phenomenology (Kraichnan, (1965). However, the same data can be fitted also with a fluid-like scaling law (Tu et al., (1996) and, due to the relatively small amount of data, it is difficult to decide, on the basis of the second order structure function, which scaling relation describes appropriately intermittency in the solar wind.
In a further paper Carbone et al. (1995b) provided evidence for differences in the ESS scaling laws between ordinary fluid flows and solar wind turbulence Through the analysis of different datasets collected in the solar wind and in ordinary fluid flows, it was shown that normalized scaling exponents ζp/ζ3 are the same as far as p ≤ 8 are considered. This indicates a kind of universality in the scaling exponents for the velocity structure functions. Differences between scaling exponents calculated in ordinary fluid flows and solar wind turbulence are confined to highorder moments. Nevertheless, the differences found in the datasets were related to different kind of singular structures in the model described by Equation (65). Solar wind data can be fitted by that model as soon as the most intermittent structures are assumed to be planar sheets C = 1 and m = 4, that is a Kraichnan scaling is used. On the contrary, ordinary fluid flows can be fitted only when C = 2 and m = 3, that is, structures are filaments and the Kolmogorov scaling have been used. However it is worthwhile to remark that differences have been found for high-order structure functions, just where measurements are unreliable.
9.2 Probability distribution functions
As said in Section 7.2 the statistics of turbulent flows can be characterized by the PDF of field differences over varying scales. At large scales PDFs are Gaussian, while tails become higher than Gaussian (actually, PDFs decay as exp[−δZ ±ℓ ]) at smaller scales.
Marsch and Tu (1994) started to investigate the behavior of PDFs of fluctuations against scales and they found that PDFs are rather spiky at small scales and quite Gaussian at large scales. The same behavior have been obtained by Sorriso-Valvo et al. (1999, (2001) who investigated Helios 2 data for both velocity and magnetic field.
In order to make a quantitative analysis of the energy cascade leading to the scaling dependence of PDFs just described, the distributions obtained in the solar wind have been fitted (Sorriso-Valvo et al., (1999) by using the log-normal ansatz
The width of the log-normal distribution of σ is given by λ2(ℓ) = √〈(δσ)2〉, while σ0 is the most probable value of σ.
The Equation (66) has been fitted to the experimental PDFs of both velocity and magnetic intensity, and the corresponding values of the parameter λ have been recovered. In Figure 94 the solid lines show the curves relative to the fit. It can be seen that the scaling behavior of PDFs, in all cases, is very well described by Equation (66). At every scale r, we get a single value for the width λ2(r), which can be approximated by a power law λ2(r) = μr−γ for r < 1 h, as it can be seen in Figure 95. The values of parameters μ and γ obtained in the fit, along with the values of σ0, are reported in Table 5. The fits have been obtained in the range of scales τ ≤ 0.72 h for the magnetic field, and τ ≤ 1.44 h for the velocity field. The analysis of PDFs shows once more that magnetic field is more intermittent than the velocity field.
Left: normalized PDFs of fluctuations of the longitudinal velocity field at four different scales τ. Right: normalized PDFs of fluctuations of the magnetic field magnitude at four different scales τ. Solid lines represent the fit made by using the log-normal model. Image reproduced by permission from Sorriso-Valvo et al. (1999), copyright by AGU.
The same analysis has been repeated by Forman and Burlaga (2003). These authors used 64 s averages of radial solar wind speed reported by the SWEPAM instrument on the ACE spacecraft, increments have been calculated over a range of lag times from 64 s to several days. From the PDF obtained through the Equation (69) authors calculated the structure functions and compared the free parameters of the model with the scaling exponents of the structure functions. Then a fit on the scaling exponents allows to calculate the values of λ2 and σ0. Once these parameters have been calculated, the whole PDF is evaluated. The same authors found that the PDFs do not precisely fit the data, at least for large values of the moment order. Interesting enough, Forman and Burlaga (2003) investigated the behavior of PDFs when different kernels Gλ(σ), derived from different cascade models, are taken into account in Equation (66). They discussed the physical content of each model, concluding that a cascade model derived from lognormal or log-Lévy theories,Footnote 10 modified by self-organized criticality proposed by Schertzer et al. (1997), seems to avoid all problems present in other cascade models.
10 Turbulent Structures
The non-linear energy cascade towards smaller scales accumulates fluctuations only in relatively small regions of space, where gradients become singular. As a rather different point of view (see Farge, (1992) these regions can be viewed as localized zones of fluid where phase correlation exists, in some sense coherent structures. These structures, which dominate the statistics of small scales, occur as isolated events with a typical lifetime greater than that of stochastic fluctuations surrounding them. The idea of a turbulence in the solar wind made by a mixture of structures convected by the wind and stochastic fluctuations is not particularly new (see, e.g., Tu and Marsch, (1995a). However, these large-scale structures cannot be considered as intermittent structures at all scales. Structures continuously appear and disappear apparently in a random fashion, at some random location of fluid, and carry a great quantity of energy of the flow. In this framework intermittency can be considered as the result of the occurrence of coherent (non-Gaussian) structures at all scales, within the sea of stochastic Gaussian fluctuations.
This point of view is the result of data analysis of scaling laws of turbulent fluctuations made by using wavelets filters (see Appendix C) instead of the usual Fourier transform. Unlike the Fourier basis, wavelets allow a decomposition both in time and frequency (or space and scale). In analyzing intermittent structures it is useful to introduce a measure of local intermittency, as for example the Local Intermittency Measure (LIM) introduced by Farge (1992) (see Appendix C).
The spatial structures generating intermittency have been investigated by Veltri and Mangeney (1999), using the Haar basis applied to time series of thirteen months of velocity and magnetic data from ISEE s/c. Analyzing intermittent events, they found that intermittent events occur on time scale of the order of few minutes and that they are one-dimensional structures (in agreement with Carbone et al., 1995b). In particular, they found different types of structures which can represent two different categories:
-
i.
i. Some of the structures are the well known one-dimensional current sheets, characterized by pressure balance and almost constant density and temperature. When a minimum variance analysis is made on the magnetic field near the structure, it can be seen that the most variable component of the magnetic field changes sign. This component is perpendicular to the average magnetic field, the third component being zero. An interesting property of these structures is that the correlation between velocity and magnetic field within them is opposite with respect to the rest of fluctuations. That is, when they occur during Alfvénic periods velocity and magnetic field correlation is low; on the contrary, during non-Alfvénic periods the correlation of structure increases.
-
ii.
ii. A different kind of structures looks like a shock wave. They can be parallel shocks or slowmode shocks. In the first case they are observed on the radial component of the velocity field, but are also seen on the magnetic field intensity, proton temperature, and density. In the second case they are characterized by a very low value of the plasma β parameter, constant pressure, anti-correlation between density and proton temperature, no magnetic fluctuations, and velocity fluctuations directed along the average magnetic field.
However, Salem et al. (2009), as already anticipated in Section 3.1.1, demonstrated that a monofractal can be recovered and intermittency eliminated simply by subtracting a small subset of the events at small scales.
Given a turbulent time series, as derived in the solar wind, a very interesting statistics can be made on the time separation between the occurrence of two consecutive structures. Let us consider a signal, for example u(t) or b(t) derived from solar wind, and let us define the wavelets set ws(r, t) as the set which captures, at time t, the occurrence of structures at the scale r. Then define the waiting times δt, as that time between two consecutive structures at the scale r, that is, between ws(r, t) and ws(r, t + δt). The PDFs of waiting times P(δt) are reported in Figure 82. As it can be seen, waiting times are distributed according to a power law P(δt) ~ δt−β extended over at least two decades. This property is very interesting, because this means that the underlying process for the energy cascade is non-Poissonian. Waiting times occurring between isolated Poissonian events, must be distributed according to an exponential function. The power law for P(δt) represents the asymptotic behavior of a LLevy function with characteristic exponent α = β − 1. This describes self-affine processes and are obtained from the central limit theorem by relaxing the hypothesis that the variance of variables is finite. The power law for waiting times we found is a clear evidence that long-range correlation (or in some sense “memory”) exists in the underlying cascade process.
On the other hand, Bruno et al. (2001), analyzing the statistics of the occurrence of waiting times of magnetic field intensity and wind speed intermittent events for a short time interval within the trailing edge of a high velocity stream, found a possible Poissonian-like behavior with a characteristic time around 30 min for both magnetic field and wind speed. These results are to be compared with previous estimates of the occurrence of interplanetary discontinuities performed by Tsurutani and Smith (1979), who found a waiting time around 14 min. In addition, Bruno et al. (2001), taking into account the wind speed and the orientation of the magnetic field vector at the site of the observation, in the hypothesis of spherical expansion, estimated the corresponding size at the Sun surface that resulted to be of the order of the photospheric structures estimated also by Thieme et al. (1989). Obviously, the Poissonian statistics found by these authors does not agree with the clear power law shown in Figure 82. However, Bruno et al. (2001) included intermittent events found at all scales while results shown in Figure 82 refer to waiting times between intermittent events extracted at the smallest scale, which results to be about an order of magnitude smaller than the time resolution used by Bruno et al. (2001). A detailed study on this topic would certainly clarify possible influences on the waiting time statistics due to the selection of intermittent events according to the corresponding scale.
In the same study by Bruno et al. (2001), these authors analyzed in detail an event characterized by a strong intermittent signature in the magnetic field intensity. A comparative study was performed choosing a close-by time interval which, although intermittent in velocity, was not characterized by strong magnetic intermittency. This time interval was located a few hours apart from the previous one. These two intervals are indicated in Figure 96 by the two vertical boxes labeled 1 and 2, respectively. Wind speed profile and magnetic field magnitude are shown in the first two panels. In the third panel, the blue line refers to the logarithmic value of the magnetic pressure Pm, here indicated by PB; the red line refers to the logarithmic value of the thermal pressure Pk, here indicated by PK and the black line refers to the logarithmic value of the total pressure Ptot, here indicated by PT = PB + PK, including an average estimate of the electrons and αs contributions. Magnetic field intensity residuals, obtained from the LIM technique, are shown in the bottom panel. The first interval is characterized by strong magnetic field intermittency while the second one is not. In particular, the first event corresponds to a relatively strong field discontinuity which separates two regions characterized by a different bulk velocity and different level of total pressure. While kinetic pressure (red trace) does not show any major jump across the discontinuity but only a light trend, magnetic pressure (blue trace) clearly shows two distinct levels.
A minimum variance analysis further reveals the intrinsic different nature of these two intervals as shown in Figure 97 where original data have been rotated into the field minimum variance reference system (see Appendix D.1) where maximum, intermediate and minimum variance components are identified by λ3, λ2, and λ1, respectively. Moreover, at the bottom of the column we show the hodogram on the maximum variance plane λ3 − λ2, as a function of time on the vertical axis.
The good correlation existing between magnetic and velocity variations for both time intervals highlights the presence of Alfvénic fluctuations. However, only within the first interval the magnetic field vector describes an arc-like structure larger than 90° on the maximum variance plane (see rotation from A to B on the 3D graph at the bottom of the left column in Figure 97) in correspondence with the time interval identified, in the profile of the magnetic field components, by the green color. At this location, the magnetic field intensity shows a clear discontinuity, B[λ3] changes sign, B[λ2] shows a hump whose maximum is located where the previous component changes sign and, finally, B[λ1] keeps its value close to zero across the discontinuity. Velocity fluctuations are well correlated with magnetic field fluctuations and, in particular, the minimum variance component V[λ2] has the same value on both sides of the discontinuity, approximately 350 km s−1, indicating that there is no mass flux through the discontinuity. During this interval, which lasts about 26 min, the minimum variance direction lies close to the background magnetic field direction at 11.9° so that the arc is essentially described on a plane perpendicular to the average background magnetic field vector. However, additional although smaller and less regular arc-like structures can be recognized on the maximum variance plane λ2 −λ3, and they tend to cover the whole 2τ interval.
From top to bottom: 81 s averages of velocity wind profile in km s−1, magnetic field intensity in nT, the logarithmic value of magnetic (blue line), thermal (red line), and total pressure (black line) in dyne/cm2 and field intensity residuals in nT. The two vertical boxes delimit the two time intervals #1 and #2 which were chosen for comparison. While the first interval shows strong magnetic intermittency, the second one does not. Image reproduced by permission from Bruno et al. (2001), copyright by Elsevier.
Within the second interval, magnetic field intensity is rather constant and the three components do not show any particular fluctuation, which could resemble any sort of rotation. In other words, the projection on the maximum variance plane does not show any coherent path. Even in this case, these fluctuations happen to be in a plane almost perpendicular to the average field direction since the angle between this direction and the minimum variance direction is about 9.3°.
Further insights about differences between these two intervals can be obtained when we plot the trajectory followed by the tip of the magnetic field vector in the minimum variance reference system, as shown in Figure 98. The main difference between these two plots is that the one relative to the first interval shows a rather patchy trajectory with respect to the second interval. As a matter of fact, if we follow the displacements of the tip of the vector as the time goes by, we observe that the two intervals have a completely different behavior.
Left column, from top to bottom: we show magnetic field intensity, maximum λ3, intermediate λ2 and minimum λ1 variance components for magnetic field (blue color) and wind velocity relative to the time interval #1 shown in Figure 96. Right below, we show the hodogram on the maximum variance plane λ3 − λ2, as a function of time (blue color line). The red lines are the projection of the blue line. The large arc, from A to B, corresponds to the green segment in the profile of the magnetic field components shown in the upper panel. The same parameters are shown for interval #2 (Figure 96), in the same format, on the right hand side of the figure. The time resolution of the data is 81 s. Image reproduced by permission from Bruno et al. (2001), copyright by Elsevier.
Within the first time interval, the magnetic field vector experiences for some time small displacements around a given direction in space and then it suddenly performs a much larger displacement towards another direction in space, about which it starts to wander again. This process keeps on going several times within this time interval. In particular, the thick green line extending from label A to label B refers to the arc-like discontinuity shown in Figure 97, which is also the largest directional variation within this time interval. Within the second interval, the vector randomly fluctuates in all direction and, as a consequence, both the 3D trajectory and its projection on the maximum variance plane do not show any large empty spot. In practice, the second time interval, although longer, is similar to any sub-interval corresponding to one of the trajectory patches recognizable in the left hand side panel. As a matter of fact, selecting a single patch from the first interval and performing a minimum variance analysis, the maximum variance plane would result to be perpendicular to the local average magnetic field direction and the tip of the vector would randomly fluctuate in all directions. The first interval can be seen as a collection of several sub-intervals similar to interval #2 characterized by different field orientations and, possibly, intensities. Thus, magnetic field intermittent events mark the border between adjacent intervals populated by stochastic Alfvénic fluctuations.
Trajectory followed by the tip of the magnetic field vector (blue color line) in the minimum variance reference system for interval #1 (left) and #2 (right). Projections on the three planes (red color lines) formed by the three eigenvectors λ1, λ2, λ3, and the average magnetic field vector, with its projections on the same planes, are also shown. The green line extending from label A to label B refers to the arc-like discontinuity shown in Figure 97. The time resolution of the magnetic field averages is 6 s. Image reproduced by permission from Bruno et al. (2001), copyright by Elsevier. (To see animations relative to similar time intervals click on Figures 99 for a timeseries affected by the intermittency phenomenon or at 100 for non-intermittent and intermittent samples.
These differences in the dynamics of the orientation of the field vector can be appreciated running the two animations behind Figures 99 and 100. Although the data used for these movies do not exactly correspond to the same time intervals analyzed in Figure 96, they show the same dynamics that the field vector has within intervals #1 and #2. In particular, the animation corresponding to Figure 99 represents interval #2 while, Figure 100 represents interval #1.
The observations reported above suggested these authors to draw the sketch shown in Figure 101 that shows a simple visualization of hypothetical flux tubes, convected by the wind, which tangle up in space Each flux tube is characterized by a local field direction and intensity, and within each flux tube the presence of Alfvénic fluctuations makes the magnetic field vector randomly wander bout this direction. Moreover, the large scale is characterized by an average background field direction aligned with the local interplanetary magnetic field. This view, based on the idea that solar wind fluctuations are a superposition of propagating Alfvén waves and convected structures (Bavassano and Bruno, (1989), strongly recalls the work by Tu and Marsch (1990a, (1993) who suggested the solar wind fluctuations being a uperposition of pressure balance structure (PBS) type flux tubes and Alfvén waves. In the inner heliosphere these PBS-type flux tubes are embedded in the large structure of fast solar wind streams and would form a kind of spaghetti-like sub-structure, which probably has its origin t the base of the solar atmosphere.
mpg-Movie (4926.71972656 KB) Still from a movie showing Trajectory followed by the tip of the magnetic field vector in the minimum variance reference system during a time interval not characterized by intermittency. The duration of the interval is 2000 × 6 s but the magnetic field vector moves only for 100 × 6 s in order to make a smaller file (movie kindly provided by A. Vecchio). (For video see appendix)
mpg-Movie (3897.08105469 KB) Still from a movie showing Trajectory followed by the tip of the magnetic field vector in the minimum variance reference system during a time interval characterized by intermittent events. The duration of the interval is 2000 × 6 s but the magnetic field vector moves only for 100 × 6 s in order to make a smaller file (movie kindly provided by A. Vecchio). (For video see appendix)
The border between these flux tubes can be a tangential discontinuity where the total pressure on both sides of the discontinuity is in equilibrium or, as in the case of interval #1, the discontinuity is located between two regions not in pressure equilibrium. If the observer moves across these tubes he will record the patchy configuration shown in Figure 100 relative to interval #1. Within each flux tube he will observe a local average field direction and the magnetic field vector would mainly fluctuate on a plane perpendicular to this direction. Moving to the next tube, the average field direction would rapidly change and magnetic vector fluctuations would cluster around this new direction. Moreover, if we imagine a situation with many flux tubes, each one characterized by a different magnetic field intensity, moving across them would possibly increase the intermittent level of the fluctuations. On the contrary, moving along a single flux tube, the same observer would constantly be in the situation typical of interval #2, which is mostly characterized by a rather constant magnetic field intensity and directional stochastic fluctuations mainly on a plane quasi perpendicular to the average magnetic field direction. In such a situation, magnetic field intensity fluctuations would not increase their intermittency.
Simple visualization of hypothetical flux tubes which tangle up in space. Each flux tube is characterized by a local field direction, and within each flux tube the presence of Alfvénic fluctuations makes the magnetic field vector randomly wander about this direction. Moreover, the large scale is characterized by an average background field direction aligned with the local interplanetary magnetic field. Moving across different flux-tubes, characterized by a different values of |B|, enhances the intermittency level of the magnetic field intensity time series (cf. Bruno et al., (2001).
A recent theoretical effort by Chang et al. (2004), Chang (2003), and Chang and Wu (2002) models MHD turbulence in a way that recalls the interpretation of the interplanetary observations given by Bruno et al. (2001) and, at the same time, reminds also the point of view expressed by Farge (1992) in this section. These authors stress the fact that propagating modes and coherent, convected structures share a common origin within the general view described by the physics of complexity. Propagating modes experience resonances which generate coherent structures, possibly flux tubes, which, in turn, will migrate, interact, and, eventually, generate new modes. This process, schematically represented in Figure 102, which favors the local generation of coherent structures in the solar wind, fully complement the possible solar origin of the convected component of interplanetary MHD turbulence.
Composite figure made adapting original figures from the paper by Chang et al. (2004). The first element on the upper left corner represents field-aligned spatio-temporal coherent structures. A cross-section of two of these structures of the same polarity is shown in the upper right corner. Magnetic flux iso-contours and field polarity are also shown. The darkened area represents intense current sheet during strong magnetic shear. The bottom element of the figure is the result of 2D MHD simulations of interacting coherent structures, and shows intermittent spatial distribution of intense current sheets. In this scenario, new fluctuations are produced which can provide new resonance sites, possibly nucleating new coherent structures.
10.1 On the statistics of magnetic field directional fluctuations
Interesting enough is to look at the statistics of the angular jumps relative to the orientation of the magnetic field vector. Studies of this kind can help to infer the relevance of modes and advected structures within MHD turbulent fluctuations. Bruno et al. (2004) found that PDFs of interplanetary magnetic field vector angular displacements within high velocity streams can be reasonably fitted by a double log-normal distribution, reminiscent of multiplicative processes following turbulence evolution. As a matter of fact, the multiplicative cascade notion was introduced by Kolmogorov into his statistical theory (Kolmogorov, (1941, (1991, (1962) of turbulence as a phenomenological framework to accommodate extreme behavior observed in real turbulent fluids.
The same authors, studying the radial behavior of the two lognormal components of this distribution concluded that they could be associated with Alfvénic fluctuations and advected structures, respectively. In particular, it was also suggested that the nature of these advected structures could be intimately connected to tangential discontinuities separating two contiguous flux tubes (Bruno et al., (2001). Whether or not these fluctuations should be identified with the 2D turbulence was uncertain since their relative PDF, differently from the one associated with Alfvénic fluctuations, did not show a clear radial evolution. As a matter of fact, since 2D turbulence is characterized by having its k vectors perpendicular to the local field it should experience a remarkable evolution given that the turbulent cascade acts preferably on wave numbers perpendicular to the ambient magnetic field direction, as suggested by the three-wave resonant interaction (Shebalin et al., (1983). Obviously, an alternative solution would be the solar origin of these fluctuations. However, it is still unclear whether these structures come directly from the Sun or are locally generated by some mechanism. Some theoretical results (Primavera et al., (2003) would indicate that coherent structures causing intermittency in the solar wind (Bruno et al., (2003a), might be locally created by parametric decay of Alfvén waves. As a matter of fact, coherent structures like current sheets are continuously created when the instability is active (Primavera et al., (2003).
Probability distributions of the angular displacements experienced by magnetic vector on a time scale of 6 s at 0.3 and 0.9 AU, for a fast wind, respectively. Solid curves refer to lognormals contributing to form the thick solid curve which best fits the distribution. Image reproduced by permission from Bruno et al. (2004), copyright EGU.)
A more recent analysis (Borovsky, (2008) on changes in the field direction experienced by the solar wind magnetic field vector reproposed the picture that the inner heliosphere is filled with a network of entangled magnetic flux tubes (Bruno et al., (2001) and interpreted these flux tubes like fossil structures that originate at the solar surface These tubes are characterized by strong changes in the magnetic field direction as shown by the distribution illustrated in Figure 104 that refers to the occurrence of changes in the magnetic field direction observed by ACE for about 7 years for a time scale of roughly 2 minutes. Two exponential curves have been used to fit the distribution, one for the small angular change population and one for the large angular change population. The small angular-change population is associated with fluctuations active within the flux tube while, the second population would be due to large directional jumps identifying the crossing of the border between adjacent flux tubes. The same authors performed similar analyses on several plasma and magnetic field parameters like velocity fluctuations, alpha to proton ratio, proton and electron entropies, and found that also for these parameters small/large changes of these parameters are associated with small/large angular changes confirming the different nature of these two populations. Larger flux tubes, originating at the Sun, thanks to wind expansion which would inhibit reconnection, would eventually reach 1 AU.
Measurements of angular differences of magnetic field direction on time scale of 128 s. Data set is from ACE measurements for the years 1998 – 2004. Exponential fits to two portions of the distribution are shown as dashed curves. Images reproduced by permission from Borovsky (2008), copyright by AGU.
In another recent paper, Li (2008) developed a genuine data analysis method to localize individual current sheets from a turbulent solar wind magnetic field sample. He noticed that, in the presence of a current sheet, a scaling law appears for the cumulative distribution function of the angle between two magnetic field vectors separated by some time lags. In other words, if we define the function F(θ, ζ) to represent the frequency of having the measured angle between magnetic vectors separated by a time lag θ larger than θ we expect to have the following scaling relation:
As a matter of fact, if the distribution function F(θ, ζ) above a certain critical angle θ0 is dominated by current-sheet crossing separating two adjacent flux tubes, we expect to find the scaling represented by relation 70. On the contrary, if we are observing these fluctuations within the same side of the current sheet F(θ, ζ) is dominated by small angular fluctuations and we do not expect to find any scaling.
Using the same methodology, Li et al. (2008) also studied fluctuations in the Earth’s magnetotail to highlight the absence of similar structures and to conclude that most of those advected structures observed in the solar wind must be of solar origin.
10.2 Radial evolution of intermittency in the ecliptic
Marsch and Liu (1993) investigated for the first time solar wind scaling properties in the inner heliosphere. These authors provided some insights on the different intermittent character of slow and fast wind, on the radial evolution of intermittency, and on the different scaling characterizing the three components of velocity. In particular, they found that fast streams were less intermittent than slow streams and the observed intermittency showed a weak tendency to increase with heliocentric distance They also concluded that the Alfvénic turbulence observed in fast streams starts from the Sun as self-similar but then, during the expansion, decorrelates becoming more multifractal. This evolution was not seen in the slow wind, supporting the idea that turbulence in fast wind is mainly made of Alfvén waves and convected structures (Tu and Marsch, (1993), as already inferred by looking at the radial evolution of the level of cross-helicity in the solar wind (Bruno and Bavassano, (1991).
Distribution function for two time periods. The left panels show the dependence of F(θ, ζ) on θ, and the right panels show the dependence of F(θ, ζ) on ζ. The presence of a current sheet makes ζ) on θ to increases linearly with ζ (dashed lines in the right panels). Image reproduced by permission from Li (2008), copyright by AAS.
Bruno et al. (2003a) investigated the radial evolution of intermittency in the inner heliosphere, using the behavior of the flatness of the PDF of magnetic field and velocity fluctuations as a function of scale. As a matter of fact, probability distribution functions of fluctuating fields affected by intermittency become more and more peaked at smaller and smaller scales. Since the peakedness of a distribution is measured by its flatness factor, they studied the behavior of this parameter at different scales to estimate the degree of intermittency of their time series, as suggested by Frisch (1995).
In order to study intermittency they computed the following estimator of the flatness factor F:
where τ is the scale of interest and S pτ = 〈|V(t+τ)−V(t)|p〉 is the structure function of order p of the generic function V(t). They considered a given function to be intermittent if the factor F increased when considering smaller and smaller scales or, equivalently, higher and higher frequencies.
In particular, vector field, like velocity and magnetic field, encompasses two distinct contributions, a compressive one due to intensity fluctuations that can be expressed as δ|B(t, τ)| = |B(t + τ)| − |B(t)|, and directional one due to changes in the vector orientation δB(t, τ) = √Σi=x,y,z,(Bi(t + τ) − Bi(t))2. Obviously, relation δB(t, τ) takes into account also compressive contributions, and the expression δB(t, τ) ≥ |δ|B(t, τ)|| is always true.
Flatness F vs. time scale τ relative to magnetic field fluctuations. The left column (panels A and C) refers to slow wind and the right column (panels B and D) refers to fast wind. The upper panels refer to compressive fluctuations and the lower panels refer to directional fluctuations. Vertical bars represent errors associated with each value of F. The three different symbols in each panel refer to different heliocentric distances as reported in the legend. Image reproduced by permission from Bruno et al. (2003b), copyright by AGU.
Flatness F vs. time scale τ relative to wind velocity fluctuations. In the same format of Figure 106 panels A and C refer to slow wind and panels B and D refer to fast wind. The upper panels refer to compressive fluctuations and the lower panels refer to directional fluctuations. Vertical bars represent errors associated with each value of F. Image reproduced by permission from Bruno et al. (2003b), copyright by AGU.
Looking at Figures 106 and 107, taken from the work of Bruno et al. (2003a), the following conclusions can be drawn:
-
Magnetic field fluctuations are more intermittent than velocity fluctuations.
-
Compressive fluctuations are more intermittent than directional fluctuations.
-
Slow wind intermittency does not show appreciable radial dependence
-
Fast wind intermittency, for both magnetic field and velocity, clearly increases with distance
-
Magnetic and velocity fluctuations have a rather Gaussian behavior at large scales, as expected, regardless of type of wind or heliocentric distance.
Moreover, they also found that the intermittency of the components rotated into the mean field reference system (see Appendix D.1) showed that the most intermittent component of the magnetic field is the one along the mean field, while the other two show a similar level of intermittency within the associated uncertainties. Finally, with increasing the radial distance, the component along the mean field becomes more and more intermittent with respect to the transverse components. These results agree with conclusions drawn by Marsch and Tu (1994) who, analyzing fast and slow wind at 0.3 AU in Solar Ecliptic (SE hereafter) coordinate system, found that the PDFs of the fluctuations of transverse components of both velocity and magnetic fields, constructed for different time scales, were appreciably more Gaussian-like than fluctuations observed for the radial component, which resulted to be more and more spiky for smaller and smaller scales.
However, at odds with results by Bruno et al. (2003a), Tu et al. (1996) could not establish any radial dependence due to the fact that their analysis was performed in the SE reference system instead of the mean field reference system as in the analysis of Bruno et al. (2003a). As a matter of fact, the mean field reference system is a more natural reference system where to study magnetic field fluctuations.
The reason is that components normal to the mean field direction are more influenced by Alfvénic fluctuations and, as a consequence, their fluctuations are more stochastic and less intermittent. This effect largely reduces during the radial excursion mainly because in the SE reference system cross-talking between different components is artificially introduced. As a matter of fact, the presence of the large scale spiral magnetic field breaks the spatial symmetry introducing a preferential direction parallel to the mean field. The same Bruno et al. (2003b) showed that it was not possible to find a clear radial trend unless magnetic field data were rotated into this more natural reference system.
On the other hand, it looks more difficult to reconcile the radial evolution of intermittency found by Bruno et al. (2003b) and Marsch and Liu (1993) in fast wind with conclusions drawn by Tu et al. (1996), who stated that “Neither a clear radial evolution nor a clear anisotropy can be established. The value of P1 in high-speed and low-speed wind are not prominent different.”. However, it is very likely that the conclusions given above are related with how to deal with the flat slope of the spectrum in fast wind near 0.3 AU. Tu et al. (1996) concluded, indeed: “It should be pointed out that the extended model cannot be used to analyze the intermittency of such fluctuations which have a flat spectrum. If the index of the power spectrum is near or less than unity ... P1 would be 0.5. However, this does not mean there is no intermittency. The model simply cannot be used in this case, because the structure function(1) does not represent the effects of intermittency adequately for those fluctuations which have a flat spectrum and reveal no clear scaling behavior”.
Bruno et al. (2003a) suggested that, depending on the type of solar wind sample and on the heliocentric distance, the observed scaling properties would change accordingly. In particular, as the radial distance increases, convected, coherent structures of the wind assume a more relevant role since the Alfvénic component of the fluctuations is depleted. This would be reflected in the increased intermittent character of the fluctuations. The coherent nature of the convected structures would contribute to increase intermittency while the stochastic character of the Alfvénic fluctuations would contribute to decrease it. This interpretation would also justify why compressive fluctuations are always more intermittent than directional fluctuations. As a matter of fact, coherent structures would contribute to the intermittency of compressive fluctuations and, at the same time, would also produce intermittency in directional fluctuations. However, since directional fluctuations are greatly influenced by Alfvénic stochastic fluctuations, their intermittency will be more or less reduced depending on the amplitude of the Alfvén waves with respect to the amplitude of compressive fluctuations.
The radial dependence of the intermittency behavior of solar wind fluctuations stimulated Bruno et al. (1999b) to reconsider previous investigations on fluctuations anisotropy reported in Section 3.1.4. These authors studied magnetic field and velocity fluctuations anisotropy for the same co-rotating, high velocity stream observed by Bavassano et al. (1982a) within the framework of the dynamics of non-linear systems. Using the Local Intermittency Measure (Farge et al., (1990; Farge, (1992; Bruno et al., (1999b) were able to justify the controversy between results by Klein et al. (1991) in the outer heliosphere and Bavassano et al. (1982a) in the inner heliosphere. Exploiting the possibility offered by this technique to locate in space and time those events which produce intermittency, these authors were able to remove intermittent events and perform again the anisotropy analysis. They found that intermittency strongly affected the radial dependence of magnetic fluctuations while it was less effective on velocity fluctuations. In particular, after intermittency removal, the average level of anisotropy decreased for both magnetic and velocity field at all distances. Although magnetic fluctuations remained more anisotropic than their kinetic counterpart, the radial dependence was eliminated. On the other hand, the velocity field anisotropy showed that intermittency, although altering the anisotropic level of the fluctuations, does not markedly change its radial trend.
10.3 Radial evolution of intermittency at high latitude
Recently, Pagel and Balogh (2003), studied intermittency in the outer heliosphere using Ulysses observations at high heliographic latitude, well within high speed solar wind. In particular, these authors used Castaing distribution Castaing et al. (2001) to study the Probability Distribution Functions (PDF) of the fluctuations of magnetic field components (see Section 9.2 for description of Castaing distribution and related governing parameters definition λ and σ). They found that intermittency of small scales fluctuations, within the inertial range, increased with increasing the radial distance from the Sun as a consequence of the growth to larger scales of the inertial range.
As a matter of fact, using the scaling found by Horbury et al. (1996a) between the transition scale (the inverse of the frequency corresponding to the break-point in the magnetic field spectrum) RB ~ r1.1±0.1, Pagel and Balogh (2003), quantitatively evaluated how the top of the inertial range in their data should shift to larger time scales with increasing heliocentric distance Moreover, taking into account that inside the inertial range λ2 ~ τ−β ⟹ λ2 = aτ−β and that the proposed scaling from Castaing et al. (2001) would be λ2 ~ const.(τ/T)−β, we should expect that for τ = T the parameter λ2 = const.. Thus, these authors calculated σ2 and λσ2 at different heliocentric distances and made the hypothesis of a similar scaling for λ2 and σ2, although this is not assured by the model. Figure 108 reports values of λ2 and σ2 vs. distance calculated for the top of the inertial range at that distance using the above procedure. The radial behavior shown in this figure suggests that there is no radial dependence for these parameters for all the three components (indicated by different symbols), as expected if the observed radial increase of intermittency in the inertial range is due to a broadening of the inertial range itself.
They also found that, in the RTN reference system, transverse magnetic field components exhibit less Gaussian behavior with respect to the radial component. This result should be compared with results from similar studies by Marsch and Tu (1994) and Bruno et al. (2003b) who, studying the radial evolution of intermittency in the ecliptic, found that the components transverse to the local magnetic field direction, are the most Gaussian ones. Probably, the above discrepancy depends totally on the reference system adopted in these different studies and it would be desirable to perform a new comparison between high and low latitude intermittency in the mean-field reference system.
Values of λ2 (upper panel) and σ2 (lower panel) vs. heliocentric distance (see Section 9.2 for description of Castaing distribution and definition of λ and σ). These values have been calculated for the projected low frequency beginning of the inertial range relative to each distance (see text for details). R, T, and N components are indicated by asterisks, crosses and circles, respectively. Image reproduced by permission from Pagel and Balogh (2003), copyright by AGU.
Pagel and Balogh (2002) focused also on the different intermittent level of magnetic field fluctuations during two fast latitudinal scans which happened to be during solar minimum the first one, and during solar maximum the second one. Their results showed a strong latitudinal dependence but were probably not, or just slightly, affected by radial dependence given the short heliocentric radial variations during these time intervals. They analyzed the anomalous scaling of the third order magnetic field structure functions looking at the value of the parameter μparticular, this last model was an obtained from the best fit performed using the p-model (see Section 7.4). In a previous analysis of the same kind, but focalized on the first latitudinal scan, the same authors tested three intermittency models, namely: “lognormal”, “p” and “G-infinity” models. In particular, this last model was an empirical model introduced by Pierrehumbert (1999), and Cho et al. (2000), and was not intended for turbulent systems. Anyhow, the best fits were obtained with the lognormal and Kolmogorov-p model. These authors concluded that magnetic field components display a very high level of intermittency throughout minimum and maximum phases of solar cycle, and slow wind shows a lower level of intermittency compared with the Alfvénic polar flows. These results do not seem to agree with ecliptic observations (Marsch and Liu, (1993,; Bruno et al., (2003a) which showed that fast wind is generally less intermittent than slow wind not only for wind speed and magnetic field magnitude, but also for the components. At this point, since it has been widely recognized that low latitude fast wind collected within co-rotating streams and fast polar wind share many common turbulence features, they should be expected to have many similarities also as regards intermittency. Thus, it is possible that also in this case the reference system in which the analysis is performed plays some role in determining some of the results regarding the behavior of the components. In any case, further analyses should clarify the reasons for this discrepancy.
11 Solar Wind Heating by the Turbulent Energy Cascade
The Parker theory of solar wind (Parker, (1964) predicts an adiabatic expansion from the hot corona without further heating. For such a model, the proton temperature T(r) should decrease with the heliocentric distance r as T(r) ~ r−4/3. The radial profile of proton temperature have been obtained from measurements by the Helios spacecraft at 0.3 AU (Marsch et al., (1982,; Marsch, (1983,; Schwenn, (1983,; Freeman, (1988,; Goldstein, (1996), up to 100 AU or more by Voyager and Pioneer spacecrafts (Gazis, (1984,; Gazis et al., (1994,; Richardson et al., (1995). These measurements show that the temperature decay is in fact considerably slower than expected. Fits of the radial temperature profile gave an effective decrease T ~ T0(r0/r)ξ in the ecliptic plane, with the exponent ξ ∈ [0.7; 1], much smaller than the adiabatic case. Actually ξ ≃ 1 within 1 AU, while ξ flattens to ξ ≃ 0.7 beyond 30 AU, where pickup ions probably contribute significantly (Richardson et al., (1995,; Zank et al., (1996,; Smith et al., (2001b). These observations imply that some heating mechanism must be at work within the wind plasma to supply the energy required to slow down the decay. The nature of the heating process of solar wind is an open problem.
The primary process governing the solar wind heating is probably active locally in the wind. However, since collisions are very rare in the solar wind plasma, the usual viscous coefficients have no meaning, say energy must be transferred to very small scales before it can be efficiently dissipated, perhaps by kinetic processes. As a consequence, the presence of a turbulent energy flux is the crucial first step towards the understanding of solar wind heating (Coleman, (1968,; Tu and Marsch, (1995a) because, as said in Section 2.4, the turbulent energy cascade represents nothing but the way for energy to be efficiently dissipated in a high-Reynolds number flow.Footnote 11 In other words, before to face the problem of what actually be the physical mechanisms responsible for energy dissipation, if we conjecture that these processes happens at small scales, the turbulent energy flux towards small scales must be of the same order of the heating rate.
Using the hypothesis that the energy dissipation rate is equal to the heat addition, one can use the omnidirectional power law spectrum derived by Kolmogorov
(CK is the Kolmogorov constant that can be obtained from measurements) to infer the energy dissipation rate (Leamon et al., (1999)
where k = 2πf/V (f is the frequency in the spacecraft frame and V is the solar wind speed). The same conjecture can be made by using Elsässer variables, thus obtaining a generalized Kolmogorov phenomenology for the power spectra P±(k) of the Elsässer variables (Zhou and Matthaeus, (1989, (1990; Marsch, (1991)
Even if the above expressions are affected by the presence of intermittency, namely extreme fluctuations of the energy transfer rate, and an estimated value for the Kolmogorov constant is required, the estimated energy dissipation rates roughly agree with the heating rates derived from gradients of the thermal proton distribution (MacBride et al., (2010).
A different estimate for the energy dissipation rate in spherical symmetry can be derived from an expression that uses the adiabatic cooling in combination with local heating rate ∈. In a steady state situation the equation for the radial profile of ions temperature can be written as (Verma et al., (1995)
where mp is the proton mass and VSW(r) is the radial profile of the bulk wind speed in km s−1. (kB is the Boltzmann constant). Equation (74) can be solved using the actual radial profile of temperature thus obtaining an expression for the radial profile of the heating rate needed to heat the wind at the actual value (Vasquez et al., (2007)
This relation is obtained by considering a polytropic index γ = 5/3 for the adiabatic expansion of the solar wind plasma, the protons being the only particles heated in the process. Such assumptions are only partially correct, since the electrons could play a relevant role in the heat exchange. Heating rates obtained using Equation (75) should thus be only seen as a first approximation that could be improved with better models of the heating processes. Using the expected solar wind parameters at 1 AU, the expected heating rate ranges from 102 J/Kg s for cold wind to 104 J/Kg s in hot wind. Cascade rates estimated from the energy-containing scale of turbulence at 1 AU obtained by evaluating triple correlations of fluctuations and the correlation length scale of turbulence give values in this range (Smith et al., (2001a, (2006; Isenberg, (2005,; Vasquez et al., (2007)
Rather than estimating the heating rate by typical solar wind fluctuations and the Kolmogorov constant, it is perhaps much more convenient to get a direct estimate of the energy dissipation rate by measurements of the turbulent energy cascade using the Yaglom’s law, say from measurements of the third-order mixed moments of fluctuations. In fact, the roughly constant values of Y ±ℓ /ℓ, or alternatively their compressible counterpart W ±ℓ /. will result in an estimate for the pseudo-energy dissipation rates ∈± (at least within a constant of order unity), over a range of scales ℓ, which by definition is unaffected by intermittency. This has been done both in the ecliptic plane (MacBride et al., (2008, (2010) and in polar wind (Marino et al., (2009,; Carbone et al., (2009b). Even preliminary attempts (MacBride et al., (2008) result in an estimate for the energy dissipation rate ∈E which is close to the value required for the heating of solar wind. However, refined analysis (MacBride et al., (2010) give results which indicate that at 1 AU in the ecliptic plane the solar wind can be heated by a turbulent energy cascade. As a different approach, Marino et al. (2009), using the data from the Ulysses spacecraft in the polar wind, calculate the values of the pseudo-energies from the relation Y ±ℓ /ℓ, and compare these values with the radial profile of the heating rate (75) required to maintain the observed temperature against the adiabatic cooling. The Ulysses database provides two different estimates for the temperature, T1, indicated as Tlarge in literature, and T2, known as Tsmall. In general, T1 and T2 are known to sometimes give an overestimate and an underestimate of the true temperature, respectively, so that analysis are performed using both temperatures (Marino et al., (2009). The heating rate are estimated at the same positions for which the energy cascade was observed. As shown in Figure 109 results indicate that turbulent transfer rate represents a significant amount of the expected heating, say the MHD turbulent cascade contributes to the in situ heating of the wind from 8% to 50% (for T1 and T2 respectively), up to 100% in some cases. The authors concluded that, although the turbulent cascade in the polar wind must be considered an important ingredient of the heating, the turbulent cascade alone seems unable to provide all the heating needed to explain the observed slowdown of the temperature decrease, in the framework of the model profile given in Equation (75). The situation is completely different as far as compressibility is taken into account. In fact, when the pseudo-energy transfer rates have been calculated through W ±ℓ /ℓ, the radial profile of energy dissipation rate is well described thus indicating that the turbulent energy cascade provides the amount of energy required to locally heat the solar wind to the observed values.
11.1 Dissipative/dispersive range in the solar wind turbulence
As we saw in Section 8, the energy cascade in turbulence can be recognized by looking at Yaglom’s law. The presence of this law in the solar wind turbulence showed that an energy cascade is at work, thus transferring energy to small scales where it is dissipated by some mechanism. While, as we showed before, the inertial range of turbulence in solar wind can be described more or less in a fluid framework, the small scales dissipative region can be much more (perhaps completely) different. The main motivation for this is the fact that the collision length in the solar wind, as a rough estimate the thermal velocity divided by the collision frequency, results to be of the order of 1 AU. Then the solar wind behaves formally as a collisionless plasma, that is the usual viscous dissipation is negligible. At the same time, in a magnetized plasma there are a number of characteristic scales, then understanding the physics of the generation of the small-scale region of turbulence in solar wind is a challenging topic from the point of view of basic plasma physics. With small-scales we mean scales ranging between the ion-cyclotron frequency fci = eB/mi (which in the solar wind at 1 AU is about fci ≃ 0.1 Hz), or the ion inertial length λi = c/ωpi, and the electron-cyclotron frequency. At these scales the usual MHD approximation could breaks down in favour of a more complex description of plasma where kinetic processes must take place.
Some times ago Leamon et al. (1998), analyzed small-scales magnetic field measurements at 1 AU, by using 33 one-hour intervals of the MFI instrument on board Wind spacecraft. Figure 110 shows the trace of the power spectral density matrix for hour 1300 on day 30 of 1995, which is the typical interplanetary power spectrum measured by Leamon et al. (1998),. It is evident that a spectral break exists at about fbr ≃ 0.44 Hz, close to the ion-cyclotron frequency. Below the ioncyclotron frequency, the spectrum follows the usual power law f−α, where the spectral index is close to the Kolmogorov value α ≃ 5/3. At small-scales, namely at frequencies above fbr, the spectrum steepens significantly, but is still described by a power law with a slope in the range α ∈ [2 − 4] (Leamon et al., (1998; Smith et al., (2006), typically α ≃ 7/3. As a direct analogy to hydrodynamic where the steepening of the inertial range spectrum corresponds to the onset of dissipation, the authors attribute the steepening of the spectrum to the occurrence of a “dissipative” range (Leamon et al., (1998). Statistical analysis by Smith et al. (2006), showed that the distribution of spectral slopes (cf. Figure 2 of Smith et al., (2006), is broader for the high-frequency region, while it is more peaked around the Kolmogorov’s value in the low-frequency region. Moreover, as a matter of fact, the high-frequency region of the spectrum seems to be related to the low-frequency region (Smith et al., (2006). In particular, the steepening of the high-frequency range spectrum is clearly dependent on the rate of the energy cascade ∈ obtained as a rough estimate (cf. Figure 4 of Smith et al., (2006).
a) Typical interplanetary magnetic field power spectrum obtained from the trace of the spectral matrix. A spectral break at about ~ 0.4 Hz is clearly visible. b) Corresponding magnetic helicity spectrum. Image reproduced by permission from Leamon et al. (1998), copyright by AGU.
Further properties of turbulence in the high-frequency region have been evidenced by looking at solar wind observations by the FGM instrument onboard Cluster satellites (Alexandrova et al., (2008) spanning a 0.02 ÷ 0.5 Hz frequency range. The authors found that the same spectral break by Leamon et al. (1998), exists when different datasets (Helios for large scales and Cluster for small scales) are used. The break (cf. Figure 1 of Alexandrova et al., (2008) has been found at about fbr ≃ 0.3 Hz, near the ion cyclotron frequency fci ≃ 0.1 Hz, which roughly corresponds to spatial scales of about 1900 km ≃ 15λi (being λi ≃ 130 km the ion-skin-depth). However, as evidenced in Figure 1 of Alexandrova et al. (2008), the compressible magnetic fluctuations, measured by magnetic field parallel spectrum S∥, are enhanced at small scales. This means that, after the break compressible fluctuations become much more important than in the low-frequency part. The parameter 〈S∥〉/〈S〉/ ≃ 0.03 in the low-frequency range (S is the total power spectrum density and brackets means averages value over the whole range) while compressible fluctuations are increased to about 〈S∥〉/〈S〉/ ≃ 0.26 in the high-frequency part. The increase of the above ratio were already noted in the paper by Leamon et al. (1998),. Moreover, Alexandrova et al. (2008), found that, as results in the low-frequency region (cf. Section 7.2), intermittency is a basic property of the high-frequency range. In fact, the authors found that PDFs of normalized magnetic field increments strongly depend on the scale (Alexandrova et al., (2008), a typical signature of intermittency in fully developed turbulence (cf. Section 7.2). More quantitatively, the behavior of the fourth-order moment of magnetic fluctuations at different frequencies K(f) is shown in Figure 111
The fourth-order moment K(f) of magnetic fluctuations as a function of frequency f is shown. Dashed line refers to data from Helios spacecraft while full line refers to data from Cluster spacecrafts at 1 AU. The inset refers to the number of intermittent structures revealed as da function of frequency. Image reproduced by permission from Alexandrova et al. (2008), copyright by AAS.
It is evident that this quantity increases as the frequency becomes smaller, thus indicating the presence of intermittency. However the rate at which K(f) increases is pronounced above the ion cyclotron frequency, meaning that intermittency in the high-frequency range is much more effective than in the low-frequency region. Recently, by analyzing a different dataset from Cluster spacecraft, Kiyani et al. (2009), using high-order statistics of magnetic differences, showed that the scaling exponents of structure functions, evaluated at small scales, are no more anomalous as the low-frequency range, even if the situation is not so clear (Yordanova et al., (2008, (2009). This is a good example of absence of universality in turbulence, a topic which received renewed attention in the last years (Chapman et al., (2009; Lee et al., (2010; Matthaeus, (2009).
12 The Origin of the High-Frequency Region
How is the high-frequency region of the spectrum generated? This has become the urgent topic which must be addressed. Ghosh et al. (1996) appeals to change of invariants in controlling the flow of spectral energy transfer in the cascade process, and in this picture no dissipation is required to explain the steepening of the magnetic power spectrum. Furthermore it is believed that the high-frequency region is highly anisotropic, with a significant fraction of turbulent energy cascades mostly in the quasi 2D structures, perpendicular to the background magnetic field. How magnetic energy dissipated in the anisotropic energy cascade still remains an open question.
12.1 A dissipation range
As we have already said, in their analysis of Wind data Leamon et al. (1998), attribute the presence of the region at frequencies higher than the ion-cyclotron frequency to a kind of dissipative range. Apart for the power spectrum, the authors examined the normalized reduced magnetic helicity σ(f), and they found an excess of negative values at high frequencies. Since this quantity is a measure of the spatial handedness of the magnetic field (Moffatt, (1978) and can be related to the polarization in the plasma frame once the direction propagation direction is known (Smith et al., (1983), the above observations should be consistent with the ion-cyclotron damping of Alfvén waves. Using a reference system relative to the mean magnetic field direction eB and radial direction eR as (eB × eR, eB × (eB × eR), eB), they conclude that transverse fluctuations are less dominant than in the inertial range and the high frequency range is best described by a mixture of 46% slab waves and of 54% 2D geometry. Since in the low-frequency range they found 11% and 89% respectively, the increased slab fraction my be explained by the preferential dissipation of oblique structures. Thermal particles interactions with the 2D slab component may be responsible for the formation of dissipative range, even if the situation seems to be more complicated. In fact they found that kinetic Alfvén waves propagating at large angles to the background magnetic field might be also consistent with the observations and may form some portion of the 2D component.
Recently the question of the increased anisotropy of the high-frequency region has been addressed by Perri et al. (2009) who investigated the scaling behavior of the eigenvalues of the variance matrix of magnetic fluctuations, which give information on the anisotropy due to different polarizations of fluctuations. The authors investigated data coming from Cluster spacecrafts when satellites orbited in front of the Earth’s parallel Bow Shock (Perri et al., (2009). Results indicates that magnetic turbulence in the high-frequency region is strongly anisotropic, the minimum variance direction being almost parallel to the background magnetic field at scales larger than the ion cyclotron scale. A very interesting result is the fact that the eigenvalues of the variance matrix have a strong intermittent behavior, with very high localized fluctuations below the ion cyclotron scale. This behavior, never investigated before, generates a cross-scale effect in magnetic turbulence Indeed, PDFs of eigenvalues evolve with the scale, namely they are almost Gaussian above the ion cyclotron scale and become power laws at scales smaller than the ion cyclotron scale. As a consequence it is not possible to define a characteristic value (as the average value) for the eigenvalues of the variance matrix at small scales. Since the wave-vector spectrum of magnetic turbulence is related to the characteristic eigenvalues of the variance matrix (Carbone et al., (1995a), the absence of a characteristic value means that a typical power spectrum at small scales cannot be properly defined. This is a feature which received little attention, and represents a further indication for the absence of universal characteristics of turbulence at small scales.
12.2 A dispersive range
The presence of a magnetic power spectrum with a slope close to 7/3 (Leamon et al., (1998; Smith et al., (2006), suggests the fact that the high-frequency region above the ion-cyclotron frequency might be interpreted as a kind of different energy cascade due to dispersive effects. Then turbulence in this region can be described through the Hall-MHD models, which is the most simple model to investigate dispersive effects in a fluid-like framework. In fact, at variance with the usual MHD, when the effect of ion inertia is taken into account the generalized Ohm’s law reads
where the second term on the r.h.s. of this equation represents the Hall term (mi being the ion mass). This means that MHD equations are enriched by a new term in the equation describing the magnetic field and derived from the induction equation
which is quadratic in the magnetic field. The above equation contains three different physical processes characterized by three different times. By introducing a length scale ℓ and characteristic fluctuations ρℓ, Bℓ, and uℓ, we can define an eddy-turnover time TNL ~ ℓ/uℓ, related to the convective process, an Hall time TH ~ ρℓℓ2/Bℓ which characterizes typical processes related to the presence of the Hall term, and a dissipative time TD ~ ℓ2/η. At large scales the first term on the r.h.s. of Equation (76) describes the Alfvénic turbulent cascade, realized in a time TNL. At very small scales, the dissipative time becomes the smallest timescale, and dissipation takes place.Footnote 12 However, one can conjecture that at intermediate scales a cascade is realized in a time which is no more TNL and not yet TD, rather the cascade is realized in a time TH. This happens when TH ~ TNL. Since at these scales density fluctuations becomes important, the mean volume rate of energy transfer can be defined as ∈V ~ B 2ℓ /TH ~ B 3ℓ /ℓ2ρℓ, where TH is used as a characteristic time for the cascade. Using the usual Richardson’s cartoon for the energy cascade which is viewed as a hierarchy of eddies at different scales, and following (von Weizsäcker, (1951), the ratio of the mass density ρℓ at two successive levels ℓv > ℓv+1 of the hierarchy is related to the corresponding scale size by
where 0 ≤ |r| ≤ 1 is a measure of the degree of compression at each level ℓv. Using a scaling law for compressive effects ρℓ ~ ℓ−3r and assuming a constant spectrum energy transfer rate, we have Bℓ ~ ℓ(2/3−2r), from which the spectral energy density
The observed range of scaling exponents observed in solar wind α ∈ [2, 4] (Leamon et al., (1998; Smith et al., (2006), can then be reproduced by different degree of compression of the solar wind plasma −5/6 ≤ r ≤ 1/6.
13 Two Further Questions About Small-Scale Turbulence
The most “conservative” way to describe the presence of a dissipative/dispersive region in the solar wind turbulence, as we reported before, is for example through the Hall-MHD model. While when dealing with large scale we can successfully approach the problem of turbulence by saying that some form of dissipation must exist at small scales, the dissipationless character of solar wind cannot be avoided when we deal with small scales. The full understanding of the physical mechanisms that allow the dissipation of energy in the absence of collisional viscosity would be a step of crucial importance in the problem of high frequency turbulence in space plasmas. Another fundamental question concerns the dispersive properties of small-scale turbulence beyond the spectral break. This last question has been reformulated by saying: what are the principal constituent modes of small-scale turbulence? This approach explicitly assumes that small-scale fluctuations in solar wind can be described through a weak turbulence framework. In other words, a dispersion relation, namely a precise relationship between the frequency ω and the wave-vector k, is assumed.
As it is well known from basic plasma physics, linear theory for homogeneous, collisionless plasma yields three kind of modes at and below the proton cyclotron frequency Ωp. At wavevectors transverse to the background magnetic field and Ωp > ωr (being ωr the real part of the frequency of fluctuation), two modes are present, namely a left-hand polarized Alfvén cyclotron mode and a right-hand polarized magnetosonic mode. A third ion-acoustic (slow) mode exists but is damped, except when Te ≫ Tp, which is not common in solar wind turbulence At quasiperpendicular propagation the Alfvénic branch evolves into Kinetic Alfvén Waves (KAW), while magnetosonic modes may propagate at Ωp ≪ ωr as whistler modes. As the wave-vector becomes oblique to the background magnetic field both modes develop a nonzero magnetic compressibility where parallel fluctuations becomes important. There are two distinct scenarios for the subsequent energy cascade of KAW and whistlers (Gary and Smith, (2009).
13.1 Whistler modes scenario
This scenario involves a two-mode cascade process, both Alfvénic and magnetosonic modes which are only weakly damped as the plasma β ≤ 1, transfer energy to quasi-perpendicular propagating wave-vectors. The KAW are damped by Landau damping which is proportional to k 2⊥ , so that they cannot contribute to the formation of dispersive region (unless for fluctuations propagating along the perpendicular direction). Even left-hand polarized Alfvén modes at quasi-parallel propagation suffer for proton cyclotron damping at scales k∥ ~ ωp/c and do not contribute. Quasi-parallel magnetosonic modes are not damped at the above scale, so that a weak cascade of right-hand polarized fluctuations can generate a dispersive region of whistler modes (Stawicki et al., (2001; Gary and Borovsky, (2004, (2008; Goldstein et al., (1994). The cascade of weakly damped whistler modes has been reproduced through electron MHD numerical simulations (Biskamp et al., (1996, (1999; Wareing and Hollerbach, (2009; Cho and Lazarian, (2004) and Particle-in-Cell (PIC) codes (Gary et al., (2008; Saito et al., (2008).
13.2 Kinetic Alfvén waves scenario
In this scenario (Howes, (2008; Schekochihin et al., (2009) long-wavelength Alfvénic turbulence transfer energy to quasi-perpendicular propagation for the primary turbulent cascade up to the thermal proton gyroradius where fluctuations are subject to the proton Landau damping. The remaining fluctuation energy continues the cascade to small scales as KAW at quasi-perpendicular propagation and at frequencies ωr < Ωp Bale et al. (2005); Sahraoui et al. (2009)). Fluctuations are completely damped via electron Landau resonance at wavelength of the order of the electron gyroradius. This scenario has been observed through gyrokinetic numerical simulations Howes et al. (2008b)), where the spectral breakpoint k⊥ ~ Ωp/uth (being uth the proton thermal speed) has been observed.
13.3 Where does the fluid-like behavior break down in solar wind turbulence?
Up to now spacecraft observations do not allow us to unambiguously distinguish between both previous scenarios. As stated by Gary and Smith (2009) at our present level of understanding of linear theory, the best we can say is that quasi-parallel whistlers, quasi-perpendicular whistlers, and KAW all probably could contribute to dispersion range turbulence in solar wind. Thus, the critical question is not which mode is present (if any exists in a nonlinear, collisionless medium as solar wind), but rather, what are the conditions which favor one mode over the others. On the other hand, starting from observations, we cannot rule out the possibility that strong turbulence rather than “modes” are at work to account for the high-frequency part of the magnetic energy spectrum. One of the most striking observations of small-scale turbulence is the fact that the electric field is strongly enhanced after the spectral break (Bale et al., (2005)). This means that turbulence at small scales is essentially electrostatic in nature, even if weak magnetic fluctuations are present. The enhancement of the electrostatic part has been viewed as a strong indication for the presence of KAW, because gyrokinetic simulations show the same phenomenon Howes et al. (2008b)). However, as pointed out by Matthaeus et al. (2008)) (see also the Reply by Howes et al., (2008a) to the comment by Matthaeus et al., (2008)), the enhancement of electrostatic fluctuations can be well reproduced by Hall-MHD turbulence, without the presence of KAW modes. Actually, the enhancement of the electric field turns out to be a statistical property of the inviscid Hall MHD (Servidio et al., 2008), that is in the absence of viscous and dissipative terms the statistical equilibrium ensemble of Hall- MHD equations in the wave-vectors space is build up with an enhancement of the electric field at large wave-vectors. This represents a thermodynamic equilibrium property of equations, and has little to do with a non-equilibrium turbulent cascadeFootnote 13. This would means that the enhancement of the electrostatic part of fluctuations cannot be seen as a proof firmly establishing that KAW are at work in the dispersive region.
One of the most peculiar possibility from the Cluster spacecraft was the possibility to separate the time domain from the space domain, using the tetrahedral formation of the four spacecrafts which form the Cluster mission (Escoubet et al., (2001)). This allows us to obtain a 3D wavevector spectrum and the possibility to identify the actual dispersion relation of solar wind turbulence, if any exists, at small scales. This can be made by using the k-filtering technique which is based on the strong assumption of plane-wave propagation (Glassmeier et al., (2001)). Of course, due to the relatively small distances between spacecrafts, this cannot be applied to large-scale turbulence.
Apart for the spectral break identified by Leamon et al. (1998), a new break has been identified in the solar wind turbulence using high-frequency Cluster data, at about few tens of Hz. In fact, Cluster data at the burst mode can reach the characteristic electron inertial scale λe and the electron Larmor radius ρe. Using FluxGate Magnetometer and Spatiotemporal Analysis of Field Fluctuations experiment/search coil, Sahraoui et al. (2009)) showed that the turbulent spectrum changes shape at wavevectors of about kρe ~ kλe ≃ 1. This result, which perhaps identify the occurrence of a dissipative range in solar wind turbulence, has been obtained in the upstream solar wind magnetically connected to the bow shock. However, in these studies the plasma β was of the order of β ≃ 1, thus not allowing the separation between both scales. Alexandrova et al. (2009)), using three instruments onboard Cluster spacecrafts operating in different frequency ranges, resolved the spectrum up to 300 Hz. They confirmed the presence of the high-frequency spectral break at about kρe ~ [0.1, 1] and, what is mainly interesting, they fitted this part of the spectrum through an exponential decay ~ exp[− √kρe], thus indicating the onset of dissipation.
The 3D spectral shape reveals poor surprise, that is the energy distribution exhibits anisotropic features characterized by a prominently extended structure perpendicular to the mean magnetic field preferring the ecliptic north direction and also by a moderately extended structure parallel to the mean field (Narita et al., (2010)). Results of the 3D energy distribution suggest the dominance of quasi 2D turbulence toward smaller spatial scales, overall symmetry to changing the sign of the wave vector (reflectional symmetry) and absence of spherical and axial symmetry. This last was one of the main hypothesis for the Maltese Cross (Matthaeus et al., (1990)), even if bias due to satellite fly through can generate artificial deviations from axisymmetry (Turner et al., (2011)).
More interestingly, (Sahraoui et al., (2010b) investigate the occurrence of a dispersion relation. They claim that the energy cascade should be carried by highly oblique KAW with doppler-shifted plasma frequency ωplas ≤ 0.1ωci down to k⊥ρi ~ 2. Each wavevector spectrum in the direction perpendicular to an “average” magnetic field B0 shows two scaling ranges separated by a breakpoint in the interval [0.1, 1]k⊥ρi, say a Kolmogorov scaling followed by a steeper scaling. The authors conjecture that the turbulence undergoes a transition-range, where part of energy is dissipated into proton heating via Landau damping, and the remaining energy cascades down to electron scales where Electron Landau damping may dominate. The dispersion relation, compared with linear solutions of the Maxwell.Vlasov equations (Sahraoui et al., (2010b), cf. Figure 5 of), seems to identify KAW as responsible for the cascade at small scales. The conjecture by Sahraoui et al. (2010b)) does not take into account the fact that Landau damping is rapidly saturating under solar wind conditions (Marsch, (2006); Valentini et al., (2008)).
TObserved dispersion relations (dots), with estimated error bars, compared to linear solutions of the Maxwell.Vlasov equations for three observed angles between the k vector and the local magnetic field direction (damping rates are represented by the dashed lines). Proton and electron Landau resonances are represented by the black curves Lp,e. Proton cyclotron resonance are shown by the curves Cp (the electron cyclotron resonance lies out of the plotted frequency range). Image reproduced by permission from Sahraoui et al. (2010a)), copyright by APS.
The question of the existence of a dispersion relation was investigated by Narita et al. (2011a)), which investigated three selected time intervals of magnetic field data of CLUSTER FGM in the solar wind. They used a refined version of the k-filtering technique, called MSR technique, to obtain high-resolution energy spectra in the wavevector domain. Like the wave telescope, the MSR technique performs fitting of the measured data with a propagating plane wave as a function of frequency and wave vector. The main result is the strong spread in the frequency-wavevector domain, namely none of the three intervals exhibits a clear organization of dispersion relation (see Figure 113). Frequencies and wave vectors appear to be strongly scattered, thus not allowing for the identification of wave-like behavior.
Top: Angles between the wave vectors and the mean magnetic field as a function of the wave number. Bottom: Frequency-wave number diagram of the identified waves in the plasma rest frame. Magnetosonic (MS), whistler (WHL), and kinetic Alfvén waves (KAW)dispersion relations are represented by dashed, straight, and dotted lines, respectively. Image reproduced by permission from Narita et al. (2011a)), copyright by AGU.
The above discussed papers shed some “darkness” on the scenario of small scales solar wind turbulence as made by “modes”, or at least they indicate that solar wind turbulence, at least at small scales, is far from universality. As a further stroke of the grey brush, Perri et al. (2011)) simply calculated the frequency of the spectral break as a function of radial distances from the Sun. In fact, since plasma parameters, and in particular the magnetic field intensity, changes when going towards large radial distances, the frequency break should change accordingly. They used Messenger data, as far as the inner heliosphere is concerned, and Ulysses data for outer heliosphere. Data from 0.5 AU, up to 5 AU, are summarized in Figure 2 of Perri et al. (2011)). While the characteristic frequencies of plasma lower going to higher radial distances, the position of the spectral break remains constant over all the interval of distances investigated. That is the observed high-frequency spectral break seems to be independent of the distance from the Sun, and then of both the ion-cyclotron frequency and the proton gyroradius. So, where does the fluid-like behavior break down in solar wind turbulence?
13.4 What physical processes replace “dissipation” in a collisionless plasma?
As we said before, the understanding of the small-scale termination of the turbulent energy cascade in collisionless plasmas is nowadays one of the outstanding unsolved problem in space plasma physics. In the absence of collisional viscosity and resistivity the dynamics of small scales is kinetic in nature and must be described by the kinetic theory of plasma. The identification of the physical mechanism that “replaces” dissipation in the collisionless solar wind plasma and establishes a link between the macroscopic and the microscopic scales would open new scenarios in the study of the turbulent heating in space plasmas. This problem is yet in its infancy. Kinetic theory is known since long time from plasma physics, the interested reader can read the excellent review by Marsch (2006)). However, it is restricted mainly to linear theoretical arguments. The fast technological development of supercomputers gives nowadays the possibility of using kinetic Eulerian Vlasov codes that solve the Vlasov.Maxwell equations in multi-dimensional phase space The only limitation to the “dream” of solving 3D-3V problems (3D in real space and 3D in velocity space) resides in the technological development of fast enough solvers. The use of almost noiseless codes is crucial and allows for the first time the possibility of analyzing kinetic nonlinear effects as the nonlinear evolution of particles distribution function, nonlinear saturation of Landau damping, etc. Of course, faster numerical way to solve the dissipation issue in collisionless plasmas might consist in using intermediate gyrokinetic descriptions (Brizard and Hahm, (2007)) based on a gyrotropy and strong anisotropy assumptions k∥ ≪ k⊥.
As we said before, observations of small-scale turbulence showed the presence of a significant level of electrostatic fluctuations (Gurnett and Anderson, (1977); Gurnett and Frank, (1978); Gurnett et al., (1979); Bale et al., (2005)). Old observations of plasma wave measurements on the Helios 1 and 2 spacecrafts (Gurnett and Anderson, (1977); Gurnett and Frank, (1978); Gurnett et al., (1979)) have revealed the occurrence of electric field wave-like turbulence in the solar wind at frequencies between the electron and ion plasma frequencies. Wavelength measurements using the IMP 6 spacecraft provided strong evidence for the presence of electric fluctuations which were identified as ion acoustic waves which are Doppler-shifted upward in frequency by the motion of the solar wind (Gurnett and Frank, (1978)). Comparison of the Helios results showed that the ion acoustic wave-like turbulence detected in interplanetary space has characteristics essentially identical to those of bursts of electrostatic turbulence generated by protons streaming into the solar wind from the earth’s bow shock (Gurnett and Frank, (1978); Gurnett et al., (1979)). Gurnett and Frank (1978)) observed that in a few cases of Helios data, ion acoustic wave intensities are enhanced in direct association with abrupt increases in the anisotropy of the solar wind electron distribution. This relationship strongly suggests that the ion acoustic wave-like structures detected by Helios far from the earth are produced by an electron heat flux instability or by protons streaming into the solar wind from the earth’s bow shock. Further evidences (Marsch, (2006)) revealed the strong association between the electrostatic peak and nonthermal features of the velocity distribution function of particles like temperature anisotropy and generation of accelerated beams.
Araneda et al. (2008) using Vlasov kinetic theory and one-dimensional Particle-in-Cell hybrid simulations provided a novel explanation of the bursts of ion-acoustic activity occurring in the solar wind. These authors studied the effect on the proton velocity distributions in a low-β plasma of compressible fluctuations driven by the parametric instability of Alfvén-cyclotron waves. Simulations showed that field-aligned proton beams are generated during the saturation phase of the wave-particle interaction, with a drift speed which is slightly greater than the Alfvén speed. As a consequence, the main part of the distribution function becomes anisotropic due to phase mixing. This observation is relevant, because the same anisotropy is typically observed in the velocity distributions measured in the fast solar wind (Marsch, (2006).
In recent papers, Valentini et al. (2008) and Valentini and Veltri (2009) used hybrid Vlasov. Maxwell model where ions are considered as kinetic particles, while electrons are treated as a fluid. Numerical simulations have been obtained in 1D-3V phase space (1D in the physical space and 3D in the velocity space) where a turbulent cascade is triggered by the nonlinear coupling of circularly left-hand polarized Alfvén waves, in the perpendicular plane and in parallel propagation, at plasma-β of the order of unity. Numerical results show that energy is transferred to short scales in longitudinal electrostatic fluctuations of the acoustic form. The numerical dispersion relation in the k − ω plane displays the presence of two branches of electrostatic waves. The upper branch, at higher frequencies, consists of ion-acoustic waves while the new lower frequency branch consists of waves propagating with a phase speed of the order of the ion thermal speed. This new branch is characterized by the presence of a plateau around the thermal speed in the ion distribution function, which is a typical signature of the nonlinear saturation of wave-particle interaction process.
Numerical simulations show that energy should be “dissipated” at small scales through the generation of an ion-beam in the velocity distribution function as a consequence of the trapping process and the nonlinear saturation of Landau damping, which results in bursts of electrostatic activity. Whether or not this picture, which seems to be confirmed by recent numerical simulations (Araneda et al., (2008; Valentini et al., (2008; Valentini and Veltri, (2009), represents the final fate of the real turbulent energy cascade observed at macroscopic scales, requires further investigations. Available measurements in the interplanetary space, even using Cluster spacecrafts, do not allow analysis at typical kinetic scales.
14 Conclusions and Remarks
Now that the reader finally reached the conclusions, hoping that he was so patient to read the whole paper, we suggest him to go back for a moment to the List of Contents, not to start all over again, but just to take a look at the various problems that have been briefly touched by this review. He will certainly realize how complex is the phenomenon of turbulence in general and, in particular, in the solar wind. Almost four decades of observations and theoretical efforts have not yet been sufficient to fully understand how this natural and fascinating phenomenon really works in the solar wind. We certainly are convinced that we cannot think of a single mechanism able to reproduce all the details we have directly observed since physical boundary conditions favor or inhibit different generation mechanisms, like for instance, velocity-shear or parametric decay, depending on where we are in the heliosphere.
On the other hand, there are some aspects which we believe are at the basis of turbulence generation and evolution like: a) we do need non-linear interactions to develop the observed Kolmogorov-like spectrum; b) in order to have non-linear interactions we need to have inward modes and/or convected structures which the majority of the modes can interact with; c) outward and inward modes can be generated by different mechanisms like velocity shear or parametric decay; d) convected structures actively contribute to turbulent development of fluctuations and can be of solar origin or locally generated.
In particular, ecliptic observations have shown that what we call Alfvénic turbulence, mainly observed within high velocity streams, tends to evolve towards the more “standard” turbulence that we mainly observe within slow wind regions, i.e., a turbulence characterized by e+ ~ e−, an excess of magnetic energy, and a Kolmogorov-like spectral slope. Moreover, the presence of a well established “background” spectrum already at short heliocentric distances and the low Alfvénicity of the fluctuations suggest that within slow wind turbulence is mainly due to convected structures frozen in the wind which may well be the remnants of turbulent processes already acting within the first layers of the solar corona. In addition, velocity shear, whenever present, seems to have a relevant role in driving turbulence evolution in low-latitude solar wind.
Polar observations performed by Ulysses, combined with previous results in the ecliptic, finally allowed to get a comprehensive view of the Alfvénic turbulence evolution in the 3D heliosphere, inside 5 AU. However, polar observations, when compared with results obtained in the ecliptic, do not appear as a dramatic break. In other words, the polar evolution is similar to that in the ecliptic, although slower. This is a middle course between the two opposite views (a non-relaxing turbulence, due to the lack of velocity shear, or a quick evolving turbulence, due to the large relative amplitude of fluctuations) which were popular before the Ulysses mission. The process driving the evolution of polar turbulence still is an open question although parametric decay might play some role. As a matter of fact, simulations of non-linear development of the parametric instability for large-amplitude, broadband Alfvénic fluctuations have shown that the final state resembles values of σc not far from solar wind observations, in a state in which the initial Alfvénic correlation is partially preserved. As already observed in the ecliptic, polar Alfvénic turbulence appears characterized by a predominance of outward fluctuations and magnetic fluctuations. As regards the outward fluctuations, their dominant character extends to large distances from the Sun. At low solar activity, with the polar wind filling a large fraction of the heliosphere, the outward fluctuations should play a relevant role in the heliospheric physics. Relatively to the imbalance in favor of the magnetic energy, it does not appear to go beyond an asymptotic value. Several ways to alter the balance between kinetic and magnetic energy have been proposed (e.g., 2D processes, propagation in a non-uniform medium, and effect of magnetic structures, among others). However, convincing arguments to account for the existence of such a limit have not yet been given, although promising results from numerical simulations seem to be able to qualitatively reproduce the final imbalance in favor of the magnetic energy.
Definitely, the relatively recent adoption of numerical methods able to highlight scaling laws features hidden to the usual spectral methods, allowed to disclose a new and promising way to analyze turbulent interplanetary fluctuations. Interplanetary space is now looked at as a natural wind tunnel where scaling properties of the solar wind can be studied on scales of the order of (or larger than) 109 times than laboratory scales. Within this framework, intermittency represents an important topic in both theoretical and observational studies. Intermittency properties have been recovered via very promising models like the MHD shell models, and the nature of intermittent events has finally been disclosed thanks to new numerical techniques based on wavelet transforms. Moreover, similar techniques have allowed to tackle the problem of identify the spectral anisotropic scaling although no conclusive and final analyses have been reported so far. In addition, recent studies on intermittency of magnetic field and velocity vector fluctuations, together with analogous analyses on magnitude fluctuations, contributed to sketch a scenario in which propagating stochastic Alfvénic fluctuations and advected structures, possibly flux tubes embedded in the wind, represent the main ingredients of interplanetary turbulence The varying predominance of one of the two species, waves or structures would make the observed turbulence more or less intermittent. However, the fact that we can make measurements just at one point of this natural wind tunnel represented by the solar wind does not allow us to discriminate temporal from spatial phenomena. As a consequence, we do not know whether these advected structures are somehow connected to the complicated topology observed at the Sun surface or can be considered as by-product of chaotic developing phenomena. Comparative studies based on the intermittency phenomenon within fast and slow wind during the wind expansion would suggest a solar origin for these structures which would form a sort of turbulent background frozen in the wind. As a matter of fact, intermittency in the solar wind is not limited to the dissipation range of the spectrum but abundantly extends orders of magnitude away from dissipative scales, possibly into the inertial range which can be identified taking into account all the possible caveats related to this problem and briefly reported in this review. This fact introduces serious differences between hydrodynamic turbulence and solar wind MHD turbulence, and the same “intermittency” assumes a different intrinsic meaning when observed in interplanetary turbulence In practice, coherent structures observed in the wind are at odds with filaments or vortices observed in ordinary fluid turbulence since these last ones are dissipative structures continuously created and destroyed by turbulent motion.
Small-scale turbulence, namely observations of turbulent fluctuations at frequencies greater than say 0.1 Hz. revealed a rich and yet poorly understood physics, mainly related to the big problem of dissipation in a dissipationless plasma. Data analysis received a strong impulse from the Cluster spacecrafts, thus revealing a few number of well established and not contradictory observations, as the presence of a double spectral breaks. However, the interpretation of the presence of a power spectrum at small scales is far from being clear and a number of contradictory interpretations can be found in literature. Numerical simulations, based on Vlasov-Maxwell, gyrokinetic and PIC codes, have been made possible due to the increasingly power of computers. They indicated some possible interpretation of the high-frequency part of the turbulent spectrum, but unfortunately the interpretation is not unequivocal. The study of high-frequency part of the turbulent spectrum is a rapidly growing field of research, here we reported the up to date state of the art, while a more complete, systematic and thought-out analysis of the wide literature will be done in a future version of the paper.
As a final remark, we would like to point out that we tried to start writing a particular point of view on the turbulence in the solar wind. We apologize for the lack of some aspects of the phenomenon at hand which can be found in the existing literature. There are still several topics which we did not discuss in this revised version of our review.
In particular, we leave for a future version:
-
recent (non-shell) turbulent modeling;
-
simulation of turbulence in the expanding solar wind;
-
numerical simulations of anisotropic turbulence;
-
a deeper view on Vlasov-Maxwell and gyrokinetic approaches.
Fortunately, we are writing a Living Review paper and mistakes and/or omissions will be adequately fixed in the next version also with the help of all our colleagues, whom we strongly encourage to send us comments and/or different points of view on particularly interesting topics which we have not yet taken into account or discussed properly.
Notes
This concept will be explained better in the next sections.
A fluid particle is defined as an infinitesimal portion of fluid which moves with the local velocity. As usual in fluid dynamics, infinitesimal means small with respect to large scale, but large enough with respect to molecular scales.
These authors were the first ones to use physical technologies and methodologies to investigate turbulent flows from an experimental point of view. Before them, experimental studies on turbulence were motivated mainly by engineering aspects.
We can use a different definition for the third invariant H(t), for example a quantity positive defined, without the term (−1)n and with α = 2. This can be identified as the surrogate of the square of the vector potential, thus investigating a kind of 2D MHD. In this case, we obtain a shell model with λ = 2, a = 5/4, and c = .1/3. However, this model does not reproduce the inverse cascade of the square of magnetic potential observed in the true 2D MHD equations.
We have already defined fluctuations of a field as the difference between the field itself and its average value. This quantity has been defined as ..... Here, the differences Δψℓ of the field separated by a distance ℓ represents characteristic fluctuations at the scale ℓ, say characteristic fluctuations of the field across specific structures (eddies) that are present at that scale. The reader can realize the difference between both definitions.
To be precise, it is worth remarking again that there are no convincing arguments to identify as inertial range the intermediate range of frequencies where the observed spectral properties are typical of fully developed turbulence. From a theoretical point of view here the association “intermediate range” ≃ “inertial range” is somewhat arbitrary. Really an operative definition of inertial range of turbulence is the range of scales ℓ where relation (42) (for fluid flows) or (41) (for MHD flows) is verified.
Since the solar wind moves at supersonic speed Vsw, the usual Taylor’s hypothesis is verified, and we can get information on spatial scaling laws ℓ by using time differences τ = ℓ/Vsw.
Note that, according to the occurrence of the Yaglom’s law, that is a third-order moment is different from zero, the fluctuations at a given scale in the inertial range must present some non-Gaussian features. From this point of view the calculation of structure functions with the absolute value is unappropriate because in this way we risk to cancel out non-Gaussian features. Namely we symmetrize the probability density functions of fluctuations. However, in general, the number of points at disposal is much lower than required for a robust estimate of odd structure functions, even in usual fluid flows. Then, as usually, we will obtain structure functions by taking the absolute value, even if some care must be taken in certain conclusions which can be found in literature.
The lognormal model is derived by using a multiplicative process, where random variable generates the cascade. Then, according to the Central Limit Theorem, the process converges to a lognormal distribution of finite variance. The log-Lévy model is a modification of the lognormal model. In such case, the Central Limit Theorem is used to derive the limit distribution of an infinite sum of random variables by relaxing the hypothesis of finite variance usually used. The resulting limit function is a Lévy function.
For a discussion on non-turbulent mechanism of solar wind heating cf. Tu and Marsch (1995a).
Of course, this is based on classical turbulence. As said before, in the solar wind the dissipative term is unknown, even if it might happens at very small kinetic scales.
It is worthwhile to remark that a turbulent fluid flows is out of equilibrium, say the cascade requires the injection of energy (input) and a dissipation mechanism (output), usually lying on well separated scales, along with a transfer of energy. Without input and output, the nonlinear term of equations works like an energy redistribution mechanism towards an equilibrium in the wave vectors space. This generates an equilibrium energy spectrum which should in general be the same as that obtained when the cascade is at work (cf., e.g., Frisch et al., (1975). However, even if the turbulent spectra could be anticipated by looking at the equilibrium spectra, the physical mechanisms are different. Of course, this should also be the case for the Hall MHD.
References
Alexandrova, O., Carbone, V., Veltri, P. and Sorriso-Valvo, L., 2008, “Small-Scale Energy Cascade of the Solar Wind Turbulence”, Astrophys. J., 674, 1153–1157. [DOI], [ADS], [arXiv:0710.0763] (Cited on pages 146 and 147.)
Alexandrova, O., Saur, J., Lacombe, C., Mangeney, A., Mitchell, J., Schwartz, S.J. and Robert, P., 2009, “Universality of Solar-Wind Turbulent Spectrum from MHD to Electron Scales”, Phys. Rev. Lett., 103(16), 165003. [DOI], [ADS], [arXiv:0906.3236 [physics.plasm-ph]] (Cited on page 152.)
Araneda, J.A., Marsch, E. and F.-Viñas, A., 2008, “Proton Core Heating and Beam Formation via Parametrically Unstable Alfvén-Cyclotron Waves”, Phys. Rev. Lett., 100, 125003. [DOI], [ADS] (Cited on pages 154 and 155.)
Arge, C.N. and Pizzo, V.J., 2000, “Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates”, J. Geophys. Res., 105, 10,465–10,479. [DOI], [ADS] (Cited on page 34.)
Bale, S.D., Kellogg, P.J., Mozer, F.S., Horbury, T.S. and Reme, H., 2005, “Measurement of the Electric Fluctuation Spectrum of Magnetohydrodynamic Turbulence”, Phys. Rev. Lett., 94, 215002. [DOI], [ADS], [arXiv:physics/0503103] (Cited on pages 150, 151, and 154.)
Balogh, A., Horbury, T.S., Forsyth, R.J. and Smith, E.J., 1995, “Variances of the components and magnitude of the polar heliospheric magnetic field”, in Solar Wind Eight, Proceedings of the Eighth International Solar Wind Conference, Dana Point, CA 1995, (Eds.) Winterhalter, D., Gosling, J.T., Habbal, S.R., Kurth, W.S., Neugebauer, M., AIP Conference Proceedings, 382, pp. 38–43, American Institute of Physics, Woodbury, NY. [ADS] (Cited on page 75.)
Balogh, A., Forsyth, R.J., Lucek, E.A., Horbury, T.S. and Smith, E.J., 1999, “Heliospheric magnetic field polarity inversions at high heliographic latitudes”, Geophys. Res. Lett., 26, 631–634. [DOI], [ADS] (Cited on page 34.)
Barnes, A., 1979, “Hydromagnetic waves and turbulence in the solar wind”, in Solar System Plasma Physics, (Eds.) Parker, E.N., Kennel, C.F., Lanzerotti, L.J., 1, pp. 249–319, North-Holland, Amsterdam; New York (Cited on page 96.)
Barnes, A., 1981, “Interplanetary Alfvénic fluctuations: a stochastic model”, J. Geophys. Res., 86, 7498–7506. [DOI], [ADS] (Cited on page 72.)
Barnes, A. and Hollweg, J.V., 1974, “Large-amplitude hydromagnetic waves”, J. Geophys. Res., 79, 2302–2318. [DOI], [ADS] (Cited on page 36.)
Batchelor, G.K., 1970, Theory of Homogeneous Turbulence, Cambridge University Press, Cambridge; New York. [Google Books]. Originally published 1953 (Cited on pages 44, 55, 162, 164, and 165.)
Bavassano, B. and Bruno, R., 1989, “Evidence of local generation of Alfvénic turbulence in the solar wind”, J. Geophys. Res., 94(13), 11,977–11,982. [DOI], [ADS] (Cited on pages 89 and 133.)
Bavassano, B. and Bruno, R., 1992, “On the role of interplanetary sources in the evolution of low-frequency Alfvénic turbulence in the solar wind”, J. Geophys. Res., 97(16), 19,129–19,137. [DOI], [ADS] (Cited on pages 71 and 89.)
Bavassano, B. and Bruno, R., 1995, “Density fluctuations and turbulent Mach number in the inner solar wind”, J. Geophys. Res., 100, 9475–9480. [ADS] (Cited on pages 31, 96, and 100.)
Bavassano, B. and Bruno, R., 2000, “Velocity and magnetic field fluctuations in Alfvénic regions of the inner solar wind: Three-fluid observations”, J. Geophys. Res., 105(14), 5113–5118. [DOI], [ADS] (Cited on pages 62 and 63.)
Bavassano, B., Dobrowolny, M., Fanfoni, G., Mariani, F. and Ness, N.F., 1982a, “Statistical properties of MHD fluctuations associated with high-speed streams from Helios 2 observations”, Solar Phys., 78, 373–384. [DOI], [ADS] (Cited on pages 48, 54, 82, 94, and 141.)
Bavassano, B., Dobrowolny, M., Mariani, F. and Ness, N.F., 1982b, “Radial evolution of power spectra of interplanetary Alfvénic turbulence”, J. Geophys. Res., 87, 3617–3622. [DOI], [ADS] (Cited on pages 44, 46, 47, 64, 76, and 94.)
Bavassano, B., Bruno, R. and Klein, L., 1995, “Density-Temperature correlation in solar wind MHD fluctuations: a test for nearly incompressible models”, J. Geophys. Res., 100, 5871–5875. [DOI], [ADS] (Cited on pages 96 and 100.)
Bavassano, B., Bruno, R. and Rosenbauer, H., 1996a, “Compressive fluctuations in the solar wind and their polytropic index”, Ann. Geophys., 14(5), 510–517. [DOI], [ADS] (Cited on pages 98 and 99.)
Bavassano, B., Bruno, R. and Rosenbauer, H., 1996b, “MHD compressive turbulence in the solar wind and the nearly incompressible approach”, Astrophys. Space Sci., 243, 159–169. [DOI] (Cited on page 99.)
Bavassano, B., Woo, R. and Bruno, R., 1997, “Heliospheric plasma sheet and coronal streamers”, Geophys. Res. Lett., 24, 1655–1658. [DOI], [ADS] (Cited on pages 36 and 37.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 1998, “Cross-helicity and residual energy in solar wind turbulence. Radial evolution and latitudinal dependence in the region from 1 to 5 AU”, J. Geophys. Res., 103(12), 6521–6530. [DOI], [ADS] (Cited on page 86.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 2000a, “On the evolution of outward and inward Alfvénic fluctuations in the polar wind”, J. Geophys. Res., 105(14), 15,959–15,964. [DOI], [ADS] (Cited on pages 75, 85, and 87.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 2000b, “Alfvénic turbulence in the polar wind: A statistical study on cross helicity and residual energy variations”, J. Geophys. Res., 105(14), 12,697–12,704. [DOI], [ADS] (Cited on pages 62 and 86.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 2001, “Radial evolution of outward and inward Alfvénic fluctuations in the solar wind: A comparison between equatorial and polar observations by Ulysses”, J. Geophys. Res., 106(15), 10,659–10,668. [DOI], [ADS] (Cited on pages 67 and 88.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 2002a, “Alfvénic turbulence in high-latitude solar wind: Radial versus latitudinal variations”, J. Geophys. Res., 107(A12), 1452. [DOI], [ADS] (Cited on pages 86 and 87.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 2002b, “On parametric instability and MHD turbulence evolution in high-latitude heliosphere”, in Solspa 2001, Proceedings of the Second Solar Cycle and Space Weather Euroconference, 24–29 September 2001, Vico Equense, Italy, (Ed.) Sawaya-Lacoste, H., ESA Conference Proceedings, SP-477, pp. 313–316, ESA Publications Division, Noordwijk. [ADS] (Cited on page 86.)
Bavassano, B., Pietropaolo, E. and Bruno, R., 2004, “Compressive fluctuations in high-latitude solar wind”, Ann. Geophys., 22(2), 689–696. [DOI], [ADS] (Cited on pages 99, 100, 101, and 102.)
Belcher, J.W. and Davis Jr, L., 1971, “Large-Amplitude Alfvén Waves in the Interplanetary Medium, 2”, J. Geophys. Res., 76(16), 3534–3563. [DOI] (Cited on pages 34, 48, 52, 58, 59, 60, 63, and 64.)
Belcher, J.W. and Solodyna, C.V., 1975, “Alfvén waves and directional discontinuities in the interplanetary medium”, J. Geophys. Res., 80(9), 181–186. [DOI], [ADS] (Cited on pages 34, 48, 52, 58, 59, and 83.)
Bendat, J.S. and Piersol, A.G., 1971, Random Data: Analysis and Measurement Procedures, Wiley-Interscience, New York. [Google Books] (Cited on page 165.)
Benzi, R., Paladin, G., Vulpiani, A. and Parisi, G., 1984, “On the multifractal nature of fully developed turbulence and chaotic systems”, J. Phys. A: Math. Gen., 17, 3521–3531. [DOI], [ADS] (Cited on page 113.)
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. and Succi, S., 1993, “Extended self-similarity in turbulent flows”, Phys. Rev. E, 48, 29–35. [DOI] (Cited on pages 105 and 106.)
Bianchini, L., Pietropaolo, E. and Bruno, R., 1999, “An improved method for local intermittency recognition”, in Magnetic Fields and Solar Processes, Proceedings of the 9th European Meeting on Solar Physics, 12–18 September 1999, Florence, Italy, (Ed.) Wilson, A., ESA Conference Proceedings, SP-448, pp. 1141–1146, ESA Publications Division, Noordwijk. [ADS] (Cited on page 169.)
Bieber, J.W., Wanner, W. and Matthaeus, W.H., 1996, “Dominant two-dimensional solar wind turbulence with implications for cosmic ray transport”, J. Geophys. Res., 101(A2), 2511–2522. [DOI], [ADS] (Cited on page 51.)
Biferale, L., 2003, “Shell Models of Energy Cascade in Turbulence”, Annu. Rev. Fluid Mech., 35, 441–468. [DOI], [ADS] (Cited on page 25.)
Bigazzi, A., Biferale, L., Gama, S.M.A. and Velli, M., 2006, “Small-Scale Anisotropy and Intermittence in High- and Low-Latitude Solar Wind”, Astrophys. J., 638, 499–507. [DOI], [ADS], [arXiv:astroph/0412320] (Cited on page 48.)
Biskamp, D., 1993, Nonlinear Magnetohydrodynamics, Cambridge Monographs on Plasma Physics, 1, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on pages 7, 16, 28, 88, and 104.)
Biskamp, D., 1994, “Cascade models for magnetohydrodynamic turbulence”, Phys. Rev. E, 50, 2702–2711. [DOI], [ADS] (Cited on page 115.)
Biskamp, D., 2003, Magnetohydrodynamic Turbulence, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on pages 7, 16, and 119.)
Biskamp, D., Schwarz, E. and Drake, J.F., 1996, “Two-Dimensional Electron Magnetohydrodynamic Turbulence”, Phys. Rev. Lett., 76, 1264–1267. [DOI], [ADS] (Cited on page 150.)
Biskamp, D., Schwarz, E., Zeiler, A., Celani, A. and Drake, J.F., 1999, “Electron magnetohydrodynamic turbulence”, Phys. Plasmas, 6, 751–758. [DOI], [ADS] (Cited on page 150.)
Boffetta, G., Carbone, V., Giuliani, P., Veltri, P. and Vulpiani, A., 1999, “Power Laws in Solar Flares: Self-Organized Criticality or Turbulence?”, Phys. Rev. Lett., 83, 4662–4665. [DOI], [ADS] (Cited on page 119.)
Bohr, T., Jensen, M.H., Paladin, G. and Vulpiani, A., 1998, Dynamical Systems Approach to Turbulence, Cambridge Nonlinear Science Series, 8, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on pages 7 and 22.)
Borovsky, J.E., 2008, “Flux tube texture of the solar wind: Strands of the magnetic carpet at 1 AU?”, J. Geophys. Res., 113, A08110. [DOI], [ADS] (Cited on pages 135 and 136.)
Boyd, T.J.M. and Sanderson, J.J., 2003, The Physics of Plasmas, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on page 16.)
Braginskii, S.I., 1965, “Transport processes in plasma”, in Review of Plasma Physics, (Ed.) Leontovich, M.A., Review of Plasma Physics, 1, pp. 201–311, Consultants Bureau, New York (Cited on page 19.)
Brandenburg, A., 2001, “The Inverse Cascade and Nonlinear Alpha-Effect in Simulations of Isotropic Helical Hydromagnetic Turbulence”, Astrophys. J., 550, 824–840. [DOI], [ADS], [arXiv:astro-ph/0006186] (Cited on page 57.)
Bravo, S. and Stewart, G.A., 1997, “Flux tube expansion factors and solar wind velocity: Results from a self-consistent MHD model”, Adv. Space Res., 20, 35. [DOI], [ADS] (Cited on page 34.)
Brizard, A.J. and Hahm, T.S., 2007, “Foundations of nonlinear gyrokinetic theory”, Rev. Mod. Phys., 79, 421–468. [DOI], [ADS] (Cited on page 154.)
Bruno, R., 1992, “Inner heliosphere observations of MHD turbulence in the solar wind — Challenges to theory”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 423–428, Pergamon Press, Oxford; New York (Cited on pages 46, 75, and 82.)
Bruno, R. and Bavassano, B., 1991, “Origin of low cross-helicity regions in the solar wind”, J. Geophys. Res., 96, 7841–7851. [DOI], [ADS] (Cited on pages 67, 82, 85, 94, and 137.)
Bruno, R. and Bavassano, B., 1992, “Evolution of the Alfvénic correlation in the solar wind”, Nuovo Cimento C, 15, 599–605. [DOI], [ADS] (Cited on page 82.)
Bruno, R. and Bavassano, B., 1993, “Cross-helicity depletions in the inner heliosphere, and magnetic field and velocity fluctuation decoupling”, Planet. Space Sci., 41, 677–685. [DOI], [ADS] (Cited on pages 94, 102, and 103.)
Bruno, R. and Dobrowolny, M., 1986, “Spectral measurements of magnetic energy and magnetic helicity between 0.29 and 0.97 AU”, Ann. Geophys., 4, 17–22. [ADS] (Cited on pages 46, 50, 55, and 56.)
Bruno, R., Bavassano, B. and Villante, U., 1985, “Evidence for Long Period Alfvén Waves in the Inner Solar System”, J. Geophys. Res., 90(9), 4373–4377. [DOI], [ADS] (Cited on pages 58, 60, 62, 70, 73, 75, 78, 83, and 99.)
Bruno, R., Bavassano, B., Rosenbauer, H. and Mariani, F., 1989, “On the local generation of interplanetary Alfvénic fluctuations”, Adv. Space Res., 9, 131–133. [DOI], [ADS] (Cited on page 66.)
Bruno, R., Bavassano, B. and Pietropaolo, E., 1996, “On the nature of Alfvénic ‚inward’ modes in the solar wind”, in Solar Wind Eight, Proceedings of the Eighth International Solar Wind Conference, Dana Point, CA 1995, (Eds.) Winterhalter, D., Gosling, J.T., Habbal, S.R., Kurth, W.S., Neugebauer, M., AIP Conference Proceedings, 382, pp. 229–232, American Institute of Physics, Woodbury, NY. [DOI], [ADS] (Cited on pages 71, 72, 73, 90, and 94.)
Bruno, R., Bavassano, B., Bianchini, L., Pietropaolo, E., Villante, U., Carbone, V. and Veltri, P., 1999a, “Solar wind intermittency studied via Local Intermittency Measure”, in Magnetic Fields and Solar Processes, The 9th European Meeting on Solar Physics, held 12–18 September, 1999, in Florence, Italy, (Ed.) Wilson, A., ESA Conference Proceedings, SP-448, pp. 1147–1152, ESA, Noordwijk. [ADS] (Cited on page 169.)
Bruno, R., Bavassano, B., Pietropaolo, E., Carbone, V. and Veltri, P., 1999b, “Effects of intermittency on interplanetary velocity and magnetic field fluctuations anisotropy”, Geophys. Res. Lett., 26, 3185–3188. [DOI], [ADS] (Cited on pages 48 and 141.)
Bruno, R., Carbone, V., Veltri, P., Pietropaolo, E. and Bavassano, B., 2001, “Identifying intermittent events in the solar wind”, Planet. Space Sci., 49, 1201–1210. [DOI], [ADS] (Cited on pages 128, 129, 130, 131, 133, 134, and 135.)
Bruno, R., Carbone, V., Sorriso-Valvo, L. and Bavassano, B., 2003a, “On the role of coherent and stochastic fluctuations in the evolving solar wind MHD turbulence: Intermittency”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 453–456, American Institute of Physics, Melville, NY (Cited on pages 135, 137, 140, and 142.)
Bruno, R., Carbone, V., Sorriso-Valvo, L. and Bavassano, B., 2003b, “Radial evolution of solar wind intermittency in the inner heliosphere”, J. Geophys. Res., 108(3), 8–24. [DOI], [ADS] (Cited on pages 123, 138, 139, 140, and 142.)
Bruno, R., Carbone, V., Primavera, L., Malara, F., Sorriso-Valvo, L., Bavassano, B. and Veltri, P., 2004, “On the probability distribution function of small-scale interplanetary magnetic field fluctuations”, Ann. Geophys., 22, 3751–3769. [DOI], [ADS], [arXiv:physics/0409056] (Cited on pages 134 and 135.)
Bruno, R., D'Amicis, R., Bavassano, B., Carbone, V. and Sorriso-Valvo, L., 2007, “Magnetically dominated structures as an important component of the solar wind turbulence”, Ann. Geophys., 25, 1913–1927. [DOI], [ADS] (Cited on pages 68 and 69.)
Bruno, R., Carbone, V., Vörös, Z. et al., 2009, “Coordinated Study on Solar Wind Turbulence During the Venus-Express, ACE and Ulysses Alignment of August 2007”, Earth Moon Planets, 104, 101–104. [DOI], [ADS] (Cited on pages 43 and 46.)
Burlaga, L.F., 1991a, “Intermittent turbulence in the solar wind”, J. Geophys. Res., 96(15), 5847–5851. [DOI], [ADS] (Cited on pages 104 and 122.)
Burlaga, L.F., 1991b, “Multifractal Structure of the Interplanetary Magnetic Field: Voyager 2 Observations near 25 AU, 1987 - 1988”, Geophys. Res. Lett., 18, 69–72. [DOI], [ADS] (Cited on pages 104 and 122.)
Burlaga, L.F., 1991c, “Multifractal structure of speed fluctuations in recurrent streams at 1 AU and near 6 AU”, Geophys. Res. Lett., 18, 1651–1654. [DOI], [ADS] (Cited on pages 104 and 122.)
Burlaga, L.F., 1992a, “Multifractal structure of the magnetic field and plasma in recurrent streams at 1 AU”, J. Geophys. Res., 97(16), 4283–4293. [DOI], [ADS] (Cited on page 76.)
Burlaga, L.F., 1992b, “Multifractals in the solar wind”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 429–432, Pergamon Press, Oxford; New York (Cited on page 76.)
Burlaga, L.F., 1993, “Intermittent turbulence in large-scale velocity fluctuations at 1 AU near solar maximum”, J. Geophys. Res., 98(17), 17,467–17,474. [DOI], [ADS] (Cited on page 7.)
Burlaga, L.F., 1995, Interplanetary Magnetohydrodynamics, International Series on Astronomy and Astrophysics, 3, Oxford University Press, New York. [Google Books] (Cited on pages 7 and 104.)
Burlaga, L.F. and Klein, L.W., 1986, “Fractal structure of the interplanetary magnetic field”, J. Geophys. Res., 91(10), 347–350. [DOI] (Cited on pages 78 and 122.)
Burlaga, L.F. and Ogilvie, K.W., 1970, “Magnetic and Thermal Pressures in the Solar Wind”, Solar Phys., 15, 61–99. [DOI], [ADS] (Cited on page 96.)
Burlaga, L.F. and Turner, J.M., 1976, “Microscale’ Alfvén waves’ in the solar wind at 1 AU”, J. Geophys. Res., 81(10), 73–77. [DOI], [ADS] (Cited on page 48.)
Buttighoffer, A., Pick, M., Roelof, E.C., Hoang, S., Mangeney, A., Lanzerotti, L.J., Forsyth, R.J. and Phillips, J.L., 1995, “Coronal electron stream and Langmuir wave detection inside a propagation channel at 4.3 AU”, J. Geophys. Res., 100, 3369–3381. [DOI], [ADS] (Cited on page 97.)
Buttighoffer, A., Lanzerotti, L.J., Thomson, D.J., Maclennan, C.G. and Forsyth, R.J., 1999, “Spectral analysis of the magnetic field inside particle propagation channels detected by ULYSSES”, Astron. Astrophys., 351, 385–392. [ADS] (Cited on page 97.)
Carbone, V., 1993, “Cascade model for intermittency in fully developed magnetohydrodynamic turbulence”, Phys. Rev. Lett., 71, 1546–1548. [DOI], [ADS] (Cited on pages 7, 28, 104, 114, 122, and 123.)
Carbone, V., 1994a, “Scale similarity of the velocity structure functions in fully developed magnetohydrodynamic turbulence”, Phys. Rev. E, 50, 671–674. [DOI], [ADS] (Cited on page 124.)
Carbone, V., 1994b, “Scaling exponents of the velocity structure functions in the interplanetary medium”, Ann. Geophys., 12(7), 585–590. [DOI], [ADS] (Cited on page 122.)
Carbone, V. and Veltri, P., 1987, “A simplified cascade model for MHD turbulence”, Astron. Astrophys., 188, 239–250 (Cited on page 89.)
Carbone, V. and Veltri, P., 1990, “A shell model for anisotropic magnetohydrodynamic turbulence”, Geophys. Astrophys. Fluid Dyn., 52, 153–181. [DOI] (Cited on pages 49 and 50.)
Carbone, V. and Veltri, P., 1992, “Relaxation processes in magnetohydrodynamics: a triad-interaction model”, Astron. Astrophys., 259, 359–372. [ADS] (Cited on page 89.)
Carbone, V., Malara, F. and Veltri, P., 1995a, “A model for the three-dimensional magnetic field correlation spectra of low-frequency solar wind fluctuations during Alfvénic periods”, J. Geophys. Res., 100(9), 1763–1778. [DOI], [ADS] (Cited on pages 53, 54, and 148.)
Carbone, V., Veltri, P. and Bruno, R., 1995b, “Experimental Evidence for Differences in the Extended Self-Similarity Scaling Laws between Fluid and Magnetohydrodynamic Turbulent Flows”, Phys. Rev. Lett., 75, 3110–3113. [DOI], [ADS] (Cited on pages 124 and 127.)
Carbone, V., Bruno, R. and Veltri, P., 1996a, “Evidences for extended self-similarity in hydromagnetic turbulence”, Geophys. Res. Lett., 23, 121–124. [DOI], [ADS] (Cited on pages 106 and 123.)
Carbone, V., Veltri, P. and Bruno, R., 1996b, “Solar wind low-frequency magnetohydrodynamic turbulence: extended self-similarity and scaling laws”, Nonlinear Proc. Geophys., 3, 247–261. [DOI], [ADS] (Cited on page 114.)
Carbone, V., Sorriso-Valvo, L., Martines, E., Antoni, V. and Veltri, P., 2000, “Intermittency and turbulence in a magnetically confined fusion plasma”, Phys. Rev. E, 62, 49–56. [DOI], [ADS] (Cited on pages 108 and 111.)
Carbone, V., Marino, R., Sorriso-Valvo, L., Noullez, A. and Bruno, R., 2009a, “Scaling Laws of Turbulence and Heating of Fast Solar Wind: The Role of Density Fluctuations”, Phys. Rev. Lett., 103(6), 061102. [DOI], [ADS], [arXiv:1003.0533 [physics.space-ph]] (Cited on pages 31 and 121.)
Carbone, V., Marino, R., Sorriso-Valvo, L., Noullez, A. and Bruno, R., 2009b, “Scaling Laws of Turbulence and Heating of Fast Solar Wind: The Role of Density Fluctuations”, Phys. Rev. Lett., 103(6), 061102. [DOI], [ADS], [arXiv:1003.0533 [physics.space-ph]] (Cited on page 144.)
Carbone, V., Sorriso-Valvo, L. and Marino, R., 2009c, “On the turbulent energy cascade in anisotropic magnetohydrodynamic turbulence”, Europhys. Lett., 88, 25 001. [DOI], [ADS] (Cited on page 29.)
Carlson, C.W., Curtis, D.W., Paschmann, G. and Michael, W., 1982, “An instrument for rapidly measuring plasma distribution functions with high resolution”, Adv. Space Res., 2, 67.70. [DOI], [ADS] (Cited on page 174.)
Castaing, B., Gagne, Y. and Hopfinger, V., 2001, “Velocity probability density functions of high Reynolds number turbulence”, Physica D, 46, 177–200 (Cited on pages 114 and 141.)
Cattaneo, F. and Hughes, D.W., 1996, “Nonlinear saturation of the turbulent α effect”, Phys. Rev. E, 54, R4532–R4535. [DOI], [ADS] (Cited on page 57.)
Chandrasekhar, S., 1967, An Introduction to the Study of Stellar Structure, Dover, Mineola, NY. [ADS], [Google Books] (Cited on pages 29 and 98.)
Chang, S.C. and Nishida, A., 1973, “Spatial Structure of Transverse Oscillations in the Interplanetary Magnetic Field”, Astrophys. Space Sci., 23, 301–301. [DOI] (Cited on page 48.)
Chang, T., 2003, “Complexity Induced Plasma Turbulence in Coronal Holes and the Solar Wind”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 481–484, American Institute of Physics, Melville, NY (Cited on page 133.)
Chang, T. and Wu, C., 2002, “Complexity and anomalous transport in space plasmas”, Phys. Plasmas, 9, 3679–3684. [DOI], [ADS] (Cited on page 133.)
Chang, T., Tam, S.W.Y. and Wu, C., 2004, “Complexity induced anisotropic bimodal intermittent turbulence in space plasmas”, Phys. Plasmas, 11, 1287–1299. [DOI], [ADS] (Cited on pages 133 and 134.)
Chapman, S.C., Nicol, R.M., Leonardis, E., Kiyani, K. and Carbone, V., 2009, “Observation of Universality in the Generalized Similarity of Evolving Solar Wind Turbulence as Seen by Ulysses”, Astrophys. J. Lett., 695, L185–L188. [DOI], [ADS] (Cited on page 147.)
Chian, A.C.L., Borotto, F.A. and Gonzalez, W.D., 1998, “Alfvén Intermittent Turbulence Driven by Temporal Chaos”, Astrophys. J., 505, 993–998. [DOI], [ADS] (Cited on page 23.)
Chian, A.C.L., Rempel, E.L., Macau, E.E.N., Rosa, R.R. and Christiansen, F., 2003, “Alfvén Turbulence Driven by High-Dimensional Interior Crisis in the Solar Wind”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 558–561, American Institute of Physics, Melville, NY (Cited on page 23.)
Cho, J. and Lazarian, A., 2002, “Numerical Simulations of Compressible MHD turbulence”, Bull. Am. Astron. Soc., 34, 1124. [ADS] (Cited on page 31.)
Cho, J. and Lazarian, A., 2004, “The Anisotropy of Electron Magnetohydrodynamic Turbulence”, Astrophys. J. Lett., 615, L41–L44. [DOI], [ADS], [arXiv:astro-ph/0406595] (Cited on page 150.)
Cho, J.Y.N., Newell, R.E. and Sachse, G.W., 2000, “Anomalous scaling of mesoscale tropospheric humidity fluctuations”, Geophys. Res. Lett., 27, 377–380. [DOI], [ADS] (Cited on page 142.)
Coleman, P.J., 1968, “Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma”, Astrophys. J., 153, 371–388. [DOI], [ADS] (Cited on pages 36, 38, and 143.)
Courant, R. and Friedrichs, K.O., 1976, Supersonic Flow and Shock Waves, Applied Mathematical Sciences, 21, Springer, Berlin; New York. [Google Books] (Cited on page 99.)
Cranmer, S.R., van Ballegooijen, A.A. and Edgar, R.J., 2007, “Self-consistent Coronal Heating and Solar Wind Acceleration from Anisotropic Magnetohydrodynamic Turbulence”, Astrophys. J. Suppl. Ser., 171, 520–551. [DOI], [ADS], [arXiv:astro-ph/0703333] (Cited on page 34.)
Dasso, S., Milano, L.J., Matthaeus, W.H. and Smith, C.W., 2003, “Cross-helicity correlations in the solar wind”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 546–549, American Institute of Physics, Melville, NY (Cited on page 53.)
Dasso, S., Milano, L.J., Matthaeus, W.H. and Smith, C.W., 2005, “Anisotropy in Fast and Slow Solar Wind Fluctuations”, Astrophys. J. Lett., 635, L181–L184. [DOI], [ADS] (Cited on page 51.)
Del Zanna, L., 2001, “Parametric decay of oblique arc-polarized Alfvén waves”, Geophys. Res. Lett., 28, 2585–2588. [DOI], [ADS] (Cited on page 90.)
Del Zanna, L., Velli, M. and Londrillo, P., 2001, “Parametric decay of circularly polarized Alfvén waves: Multidimensional simulations in periodic and open domains”, Astron. Astrophys., 367, 705–718. [DOI], [ADS] (Cited on pages 90 and 92.)
Denskat, K.U. and Neubauer, F.M., 1983, “Observations of hydromagnetic turbulence in the solar wind”, in Solar Wind Five, Proceedings of a conference held in Woodstock, Vermont, November 1–5 1982, (Ed.) Neugebauer, M., NASA Conference Publication, 2280, pp. 81–91, NASA, Washington, DC (Cited on pages 44 and 64.)
Derby, N.F., 1978, “Modulational instability of finite-amplitude, circularly polarized Alfvén waves”, Astrophys. J., 224, 1013–1016. [DOI], [ADS] (Cited on page 72.)
Dobrowolny, M., Mangeney, A. and Veltri, P., 1980a, “Fully developed anisotropic hydromagnetic turbulence in interplanetary space”, Phys. Rev. Lett., 45, 144–147. [DOI], [ADS] (Cited on pages 64 and 121.)
Dobrowolny, M., Mangeney, A. and Veltri, P., 1980b, “Properties of magnetohydrodynamic turbulence in the solar wind”, Astron. Astrophys., 83, 26–32. [ADS] (Cited on pages 28, 60, 64, 89, and 166.)
Doob, J.L., 1953, Stochastic Processes, Wiley, New York (Cited on page 162.)
Dudok de Wit, T., 2004, “Can high-order moments be meaningfully estimated from experimental turbulence measurements?”, Phys. Rev. E, 70, 055302(R). [DOI] (Cited on page 107.)
Elsässer, W.M., 1950, “The hydromagnetic equations”, Phys. Rev., 79, 183. [DOI] (Cited on pages 18 and 166.)
Escoubet, C.P., Fehringer, M. and Goldstein, M., 2001, “Introduction: The Cluster mission”, Ann. Geophys., 19, 1197–1200. [DOI], [ADS] (Cited on page 151.)
Farge, M., 1992, “Wavelet transforms and their applications to turbulence”, Annu. Rev. Fluid Mech., 24, 395–457. [DOI], [ADS] (Cited on pages 127, 133, 141, and 168.)
Farge, M., Holschneider, M. and Colonna, J.F., 1990, “Wavelet analysis of coherent structures in two-dimensional turbulent flows”, in Topological Fluid Mechanics, Proceedings of the IUTAM Symposium, Cambridge, UK, 13–18 August 1989, (Ed.) Moffat, H.K., pp. 765–766, Cambridge University Press, Cambridge; New York (Cited on pages 141 and 168.)
Feynman, R.P., Leighton, R.B. and Sands, M., 1977, The Feynman Lectures on Physics, Vol. II: The Electromagnetic Field, Addison-Wesley, Reading, MA, 6th edn. (Cited on page 23.)
Forman, M.A. and Burlaga, L.F., 2003, “Exploring the Castaing Distribution Function to Study Intermittence in the Solar Wind at L1 in June 2000”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 554–557, American Institute of Physics, Melville, NY (Cited on page 125.)
Forman, M.A., Smith, C.W. and Vasquez, B.J., 2010, “Comment on 'scaling Laws of Turbulence and Heating of Fast Solar Wind: The Role of Density Fluctuations”', Phys. Rev. Lett., 104(18), 189001. [DOI], [ADS] (Cited on page 121.)
Forsyth, R.J. and Breen, A., 2002, “Meeting report: The 3-D Sun and heliosphere at solar maximum”, Astron. Geophys., 43, 3–32. [DOI], [ADS] (Cited on page 34.)
Forsyth, R.J., Horbury, T.S., Balogh, A. and Smith, E.J., 1996, “Hourly variances of fluctuations in the heliospheric magnetic field out of the ecliptic plane”, Geophys. Res. Lett., 23, 595–598. [DOI], [ADS] (Cited on pages 75, 76, 77, 79, 80, and 85.)
Forsyth, R.J., Balogh, A., Horbury, T.S. and Smith, E.J., 1997, “The heliospheric magnetic field at solar minimum as observed by ULYSSES”, Adv. Space Res., 19, 839–842. [DOI], [ADS] (Cited on page 34.)
Freeman, J.W., 1988, “Estimates of solar wind heating inside 0.3 AU”, Geophys. Res. Lett., 15, 88–91. [DOI], [ADS] (Cited on page 143.)
Frick, P. and Sokoloff, D.D., 1998, “Cascade and dynamo action in a shell model of magnetohydrodynamic turbulence”, Phys. Rev. E, 57, 4155–4164. [DOI], [ADS] (Cited on page 25.)
Frisch, U., 1995, Turbulence: The Legacy of A.N. Kolmogorov, Cambridge University Press, Cambridge; New York. [ADS], [Google Books] (Cited on pages 7, 8, 9, 16, 19, 27, 28, 31, 104, 106, 107, 111, 113, and 137.)
Frisch, U., Pouquet, A., Leorat, J. and Mazure, A., 1975, “Possibility of an inverse cascade of magnetic helicity in magnetohydrodynamic turbulence”, J. Fluid Mech., 68, 769–778. [DOI], [ADS] (Cited on pages 151 and 162.)
Frisch, U., Sulem, P.-L. and Nelkin, M., 1978, “A simple dynamical model of intermittent fully developed turbulence”, J. Fluid Mech., 87, 719–736. [DOI], [ADS] (Cited on page 113.)
Galeev, A.A. and Oraevskii, V.N., 1963, “The stability of Alfvén waves”, Sov. Phys. Dokl., 7, 988–1003 (Cited on page 71.)
Gary, S.P. and Borovsky, J.E., 2004, “Alfvén-cyclotron fluctuations: Linear Vlasov theory”, J. Geophys. Res., 109, A06105. [DOI], [ADS] (Cited on page 150.)
Gary, S.P. and Borovsky, J.E., 2008, “Damping of long-wavelength kinetic Alfvén fluctuations: Linear theory”, J. Geophys. Res., 113, A12104. [DOI], [ADS] (Cited on page 150.)
Gary, S.P. and Smith, C.W., 2009, “Short-wavelength turbulence in the solar wind: Linear theory of whistler and kinetic Alfvén fluctuations”, J. Geophys. Res., 114, A12105. [DOI], [ADS] (Cited on pages 150 and 151.)
Gary, S.P., Saito, S. and Li, H., 2008, “Cascade of whistler turbulence: Particle-in-cell simulations”, Geophys. Res. Lett., 35, L02104. [DOI], [ADS] (Cited on page 150.)
Gazis, P.R., 1984, “Observations of plasma bulk parameters and the energy balance of the solar wind between 1 and 10 AU”, J. Geophys. Res., 89, 775–785. [DOI], [ADS] (Cited on page 143.)
Gazis, P.R., Barnes, A., Mihalov, J.D. and Lazarus, A.J., 1994, “Solar wind velocity and temperature in the outer heliosphere”, J. Geophys. Res., 99, 6561–6573. [DOI], [ADS] (Cited on page 143.)
Ghosh, S. and Matthaeus, W.H., 1990, “Relaxation processes in a turbulent compressible magnetofluid”, Phys. Fluids B, 2, 1520–1534. [DOI], [ADS] (Cited on page 90.)
Ghosh, S. and Papadopoulos, K., 1987, “The onset of Alfvénic turbulence”, Phys. Fluids, 30, 1371–1387. [DOI], [ADS] (Cited on page 23.)
Ghosh, S., Siregar, E., Roberts, D.A. and Goldstein, M.L., 1996, “Simulation of high-frequency solar wind power spectra using Hall magnetohydrodynamics”, J. Geophys. Res., 101, 2493–2504. [DOI], [ADS] (Cited on page 148.)
Ghosh, S., Matthaeus, W.H., Roberts, D.A. and Goldstein, M.L., 1998a, “Waves, structures, and the appearance of two-component turbulence in the solar wind”, J. Geophys. Res., 103(A10), 23,705–23,716. [DOI], [ADS] (Cited on page 53.)
Ghosh, S., Matthaeus, W.H., Roberts, D.A. and Goldstein, M.L., 1998b, “The evolution of slab fluctuations in the presence of pressure-balanced magnetic structures and velocity shears”, J. Geophys. Res., 103(A10), 23,691–23,704. [DOI], [ADS] (Cited on page 53.)
Giuliani, P. and Carbone, V., 1998, “A note on shell models for MHD turbulence”, Europhys. Lett., 43, 527–532. [DOI], [ADS] (Cited on pages 25, 26, and 115.)
Glassmeier, K.-H., Motschmann, U., Dunlop, M. et al., 2001, “Cluster as a wave telescope - first results from the fluxgate magnetometer”, Ann. Geophys., 19, 1439–1447. [DOI], [ADS] (Cited on page 151.)
Gledzer, E.B., 1973, “System of hydrodynamic type admitting two quadratic integrals of motion”, Sov. Phys. Dokl., 18, 216 (Cited on page 25.)
Gloaguen, C., Léorat, J., Pouquet, A. and Grappin, R., 1985, “A scalar model for MHD turbulence”, Physica D, 17, 154–182. [DOI], [ADS] (Cited on pages 25 and 115.)
Goldreich, P. and Sridhar, S., 1995, “Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence”, Astrophys. J., 438, 763–775. [DOI], [ADS] (Cited on pages 28, 31, and 41.)
Goldstein, B.E., Smith, E.J., Balogh, A., Horbury, T.S., Goldstein, M.L. and Roberts, D.A., 1995a, “Properties of magnetohydrodynamic turbulence in the solar wind as observed by Ulysses at high heliographic latitudes”, Geophys. Res. Lett., 22, 3393–3396. [DOI], [ADS] (Cited on pages 75, 76, 83, and 84.)
Goldstein, M.L., 1978, “An instability of finite amplitude circularly polarized Alfvén waves”, Astrophys. J., 219, 700–704. [DOI], [ADS] (Cited on pages 72 and 92.)
Goldstein, M.L., 1996, “Turbulence in the solar wind: Kinetic effects”, in Solar Wind Eight, Proceedings of the Eighth International Solar Wind Conference, Dana Point, CA 1995, (Eds.) Winterhalter, D., Gosling, J.T., Habbal, S.R., Kurth, W.S., Neugebauer, M., AIP Conference Proceedings, 382, pp. 239–244, American Institute of Physics, Woodbury, NY. [DOI], [ADS] (Cited on page 143.)
Goldstein, M.L. and Roberts, D.A., 1999, “Magnetohydrodynamic turbulence in the solar wind”, Phys. Plasmas, 6, 4154–4160. [DOI], [ADS] (Cited on page 91.)
Goldstein, M.L., Roberts, D.A. and Matthaeus, W.H., 1986, “Systematic errors in determining the propagation direction of interplanetary Alfvénic fluctuations”, J. Geophys. Res., 91(10), 13,357–13,365. [DOI], [ADS] (Cited on page 166.)
Goldstein, M.L., Roberts, D.A. and Matthaeus, W.H., 1989, “Numerical Simulation of Interplanetary and Magnetospheric Phenomena: The Kelvin-Helmholtz Instability”, in Solar System Plasma Physics, Papers presented at the Yosemite Conference on Outstanding Problems in Solar System Plasma Physics: Theory and Instrumentation, Yosemite National Park, Calif., February 2–5, 1988, (Eds.) Waite Jr, J.H., Burch, J.L., Moore, R.L., Geophysical Monograph, 54, p. 113, American Institute of Physics, Washington, DC (Cited on page 89.)
Goldstein, M.L., Roberts, D.A. and Fitch, C.A., 1991, “The structure of helical interplanetary magnetic fields”, Geophys. Res. Lett., 18, 1505–1508. [DOI], [ADS] (Cited on page 55.)
Goldstein, M.L., Roberts, D.A. and Fitch, C.A., 1994, “Properties of the fluctuating magnetic helicity in the inertial and dissipation ranges of solar wind turbulence”, J. Geophys. Res., 99, 11 519–11 538. [DOI], [ADS] (Cited on page 150.)
Goldstein, M.L., Roberts, D.A. and Matthaeus, W.H., 1995b, “Magnetohydrodynamic Turbulence in the Solar Wind”, Annu. Rev. Astron. Astrophys., 33, 283–326. [DOI], [ADS] (Cited on page 33.)
Gollub, J.P. and Swinney, H.L., 1975, “Onset of turbulence in a Rotating Fluid”, Phys. Rev. Lett., 35, 927–930. [DOI] (Cited on pages 7 and 23.)
Grappin, R., 1986, “Onset and decay of two-dimensional magnetohydrodynamic turbulence with velocity magnetic field correlation”, Phys. Fluids, 29, 2433–2443. [DOI], [ADS] (Cited on page 50.)
Grappin, R., 2002, “Comment on ‘Alfvénic turbulence in the polar wind: A statistical study on cross helicity and residual energy variations’ by B. Bavassano et al.”, J. Geophys. Res., 107, 1247. [DOI], [ADS] (Cited on page 86.)
Grappin, R. and Velli, M., 1996, “Waves and streams in the expanding solar wind”, J. Geophys. Res., 101, 425–444. [DOI], [ADS] (Cited on pages 22, 55, and 91.)
Grappin, R., Frisch, U., Pouquet, A. and Leorat, J., 1982, “Alfvénic fluctuations as asymptotic states of MHD turbulence”, Astron. Astrophys., 105, 6–14. [ADS] (Cited on page 71.)
Grappin, R., Leorat, J. and Pouquet, A., 1983, “Dependence of MHD turbulence spectra on the velocity field-magnetic field correlation”, Astron. Astrophys., 126, 51–58. [ADS] (Cited on page 60.)
Grappin, R., Mangeney, A. and Marsch, E., 1989, “On the origin of solar wind turbulence: Helios data revisited”, in Turbulence and Nonlinear Dynamics in MHD Flows, Proceedings of the Workshop, Cargèse, France, July 4. 8, 1988, (Eds.) Meneguzzi, M., Pouquet, A., Sulem, P.L., pp. 81–86, North-Holland, Amsterdam; New York. [ADS] (Cited on pages 64, 85, and 166.)
Grappin, R., Mangeney, A. and Marsch, E., 1990, “On the origin of solar wind MHD turbulence. HELIOS data revisited”, J. Geophys. Res., 95(14), 8197–8209. [DOI], [ADS] (Cited on pages 64, 71, and 94.)
Grappin, R., Velli, M. and Mangeney, A., 1991, “Alfvénic versus standard turbulence in the solar wind”, Ann. Geophys., 9, 416–426. [ADS] (Cited on pages 60, 64, and 75.)
Grappin, R., Mangeney, A. and Velli, M., 1992, “MHD turbulence: theory/simulations”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 451–456, Pergamon Press, Oxford; New York (Cited on page 91.)
Grappin, R., Velli, M. and Mangeney, A., 1993, “Nonlinear wave evolution in the expanding solar wind”, Phys. Rev. Lett., 70, 2190–2193. [DOI], [ADS] (Cited on page 22.)
Grappin, R., L'eorat, J. and Buttighoffer, A., 2000, “Alfvén wave propagation in the high solar corona”, Astron. Astrophys., 362, 342–358. [ADS] (Cited on page 97.)
Gurnett, D.A. and Anderson, R.R., 1977, “Plasma Wave Electric Fields in the Solar Wind: Initial Results From Helios 1”, J. Geophys. Res., 82, 632–650. [DOI], [ADS] (Cited on page 154.)
Gurnett, D.A. and Frank, L.A., 1978, “Ion acoustic waves in the solar wind”, J. Geophys. Res., 83, 58–74. [DOI], [ADS] (Cited on page 154.)
Gurnett, D.A., Marsch, E., Pilipp, W., Schwenn, R. and Rosenbauer, H., 1979, “Ion acoustic waves and related plasma observations in the solar wind”, J. Geophys. Res., 84, 2029–2038. [DOI], [ADS] (Cited on page 154.)
Halmos, P.R., 1956, Lectures on Ergodic Theory, Chelsea, New York. [Google Books] (Cited on page 12.)
Hammer, R., 1982, “Energy balance and stability”, Adv. Space Res., 2, 261–269. [DOI], [ADS] (Cited on page 34.)
Hansteen, V.H. and Leer, E., 1995, “Coronal heating, densities, and temperatures and solar wind acceleration”, J. Geophys. Res., 100, 21,577–21,594. [DOI], [ADS] (Cited on page 34.)
Hassler, D.M., Dammasch, I.E., Lemaire, P., Brekke, P., Curdt, W., Mason, H.E., Vial, J.-C. and Wilhelm, K., 1999, “Solar Wind Outflow and the Chromospheric Magnetic Network”, Science, 283(5403), 810–813. [DOI], [ADS] (Cited on page 33.)
Hattori, Y. and Ishizawa, A., 2001, “Characteristic time scales and energy transfer in MHD turbulence”, in IUTAM Symposium on Geometry and Statistics of Turbulence, Held in Hayama, Japan, November 1–5, 1999, (Eds.) Kambe, T., Nakano, T., Miyauchi, T., Fluid Mechanics and its Applications, 59, pp. 89–94, Kluwer, Dordrecht; Boston (Cited on page 115.)
Heinemann, M. and Olbert, S., 1980, “Non-WKB Alfvén waves in the Solar Wind”, J. Geophys. Res., 85(A3), 1311–1327. [DOI], [ADS] (Cited on page 83.)
Hellinger, P. and Trávníček, P.M., 2008, “Oblique proton fire hose instability in the expanding solar wind: Hybrid simulations”, J. Geophys. Res., 113(12), A10109. [DOI], [ADS] (Cited on page 88.)
Hellinger, P., Velli, M., Trávníček, P., Gary, S.P., Goldstein, B.E. and Liewer, P.C., 2005, “Alfvén wave heating of heavy ions in the expanding solar wind: Hybrid simulations”, J. Geophys. Res., 110(9), A12109. [DOI], [ADS] (Cited on page 22.)
Hentschel, H.G.E.F. and Procaccia, I., 1983, “The infinite number of generalized dimensions of fractals and strange attractor”, Physica D, 8, 435–444. [DOI], [ADS] (Cited on page 113.)
Hollweg, J.V., 1986, “Transition region, corona, and solar wind in coronal holes”, J. Geophys. Res., 91, 4111–4125. [DOI], [ADS] (Cited on page 34.)
Horbury T.S. and Balogh, A., 1997, “Structure function measurements of the intermittent MHD turbulent cascade”, Nonlinear Proc. Geophys., 4, 185–199. [DOI], [ADS] (Cited on page 123.)
Horbury, T.S. and Balogh, A., 2001, “Evolution of magnetic field fluctuations in high-speed solar wind streams: Ulysses and Helios observations”, J. Geophys. Res., 106(A8), 15,929–15,940. [DOI], [ADS] (Cited on pages 79, 81, 82, 83, 86, and 87.)
Horbury, T.S. and Tsurutani, B., 2001, “Ulysses measurements of waves, turbulence and discontinuities”, in The Heliosphere Near Solar Minimum: The Ulysses perspective, (Eds.) Balogh, A., Marsden, R.G., Smith, E.J., Springer-Praxis Books in Astronomy and Space Sciences, pp. 167–227, Springer; Praxis, Berlin; New York; Chichester. [ADS], [Google Books] (Cited on pages 7, 81, and 82.)
Horbury, T.S., Balogh, A., Forsyth, R.J. and Smith, E.J., 1995a, “ULYSSES magnetic field observations of fluctuations within polar coronal flows”, Ann. Geophys., 13, 105–107. [ADS] (Cited on pages 78, 79, and 124.)
Horbury, T.S., Balogh, A., Forsyth, R.J. and Smith, E.J., 1995b, “Anisotropy of inertial range turbulence in the polar heliosphere”, Geophys. Res. Lett., 22, 3405–3408. [DOI], [ADS] (Cited on page 82.)
Horbury, T.S., Balogh, A., Forsyth, R.J. and Smith, E.J., 1995c, “Observations of evolving turbulence in the polar solar wind”, Geophys. Res. Lett., 22, 3401–3404. [DOI], [ADS] (Cited on pages 76, 77, and 124.)
Horbury, T.S., Balogh, A., Forsyth, R.J. and Smith, E.J., 1996a, “The rate of turbulent evolution over the Sun's poles”, Astron. Astrophys., 316, 333–341. [ADS] (Cited on pages 46, 76, 80, and 141.)
Horbury, T.S., Balogh, A., Forsyth, R.J. and Smith, E.J., 1996b, “Magnetic field signatures of unevolved turbulence in solar polar flows”, J. Geophys. Res., 101(10), 405–414. [DOI], [ADS] (Cited on page 76.)
Horbury, T.S., Balogh, A., Forsyth, R.J. and Smith, E.J., 1997, “ULYSSES observations of intermittent heliospheric turbulence”, Adv. Space Res., 19, 847–850. [DOI], [ADS] (Cited on page 123.)
Horbury, T.S., Forman, M.A. and Oughton, S., 2008, “Anisotropic scaling of magnetohydrodynamic turbulence”, Phys. Rev. Lett., 807(17), 175005. [DOI], [ADS], [arXiv:0807.3713] (Cited on pages 41 and 42.)
Hoshino, M. and Goldstein, M.L., 1989, “Time evolution from linear to nonlinear stages in magnetohydrodynamic parametric instabilities”, Phys. Fluids B, 1, 1405–1415. [DOI] (Cited on page 92.)
Howes, G.G., 2008, “Inertial range turbulence in kinetic plasmas”, Phys. Plasmas, 15(5), 055904. [DOI], [ADS], [arXiv:0711.4358] (Cited on page 150.)
Howes, G.G., Cowley, S.C., Dorland, W., Hammett, G.W., Quataert, E., Schekochihin, A.A. and Tatsuno, T., 2008a, “Howes et al. Reply:”, Phys. Rev. Lett., 101(14), 149502. [DOI], [ADS] (Cited on page 151.)
Howes, G.G., Dorland, W., Cowley, S.C., Hammett, G.W., Quataert, E., Schekochihin, A.A. and Tatsuno, T., 2008b, “Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas”, Phys. Rev. Lett., 100, 065004. [DOI], [ADS], [arXiv:0711.4355] (Cited on pages 150 and 151.)
Huang, K., 1987, Statistical Mechanics, Wiley, New York, 2nd edn. (Cited on page 15.)
Hunt, J.C.R., Phillips, O.M. and Williams, D. (Eds.), 1991, Turbulence and Stochastic Processes: Kolmogorov's Ideas 50 Years On, Proc. R. Soc. London, Ser. A, 434, The Royal Society, London (Cited on page 19.)
Iroshnikov, P.S., 1963, “Turbulence of a Conducting Fluid in a Strong Magnetic Field”, Sov. Astron. 7, 566 (Cited on pages 28 and 60.)
Isenberg, P.A., 2005, “Turbulence-driven Solar Wind Heating and Energization of Pickup Protons in the Outer Heliosphere”, Astrophys. J., 623, 502–510. [DOI], [ADS] (Cited on page 144.)
Katul, G.G., Hsieh, C.I. and Sigmon, J., 1997, “Energy-inertial scale interaction for temperature and velocity in the unstable surface layer”, Boundary-Layer Meteorol., 82, 49–80. [DOI], [ADS] (Cited on pages 12 and 110.)
Kiyani, K.H., Chapman, S.C., Khotyaintsev, Y.V., Dunlop, M.W. and Sahraoui, F., 2009, “Global Scale-Invariant Dissipation in Collisionless Plasma Turbulence”, Phys. Rev. Lett., 103(7), 075006. [DOI], [ADS], [arXiv:0906.2830 [physics.plasm-ph]] (Cited on page 147.)
Klein, L., Bruno, R., Bavassano, B. and Rosenbauer, H., 1993, “Anisotropy and minimum variance of magnetohydrodynamic fluctuations in the inner heliosphere”, J. Geophys. Res., 98(17), 17,461–17,466. [DOI], [ADS] (Cited on pages 48, 94, and 103.)
Klein, L.W., 1987, Observations of Turbulence and Fluctuations in the Solar Wind, Ph.D. thesis, Catholic University of America, Washington, DC (Cited on page 46.)
Klein, L.W., Roberts, D.A. and Goldstein, M.L., 1991, “Anisotropy and minimum variance directions of solar wind fluctuations in the outer heliosphere”, J. Geophys. Res., 96(15), 3779–3788. [DOI], [ADS] (Cited on pages 48 and 141.)
Klein, L.W., Matthaeus, W.H., Roberts, D.A. and Goldstein, M.L., 1992, “Evolution of spatial and temporal correlations in the solar wind — Observations and interpretation”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 197–200, Pergamon Press6, Oxford; New York. [ADS] (Cited on page 45.)
Kolmogorov, A.N., 1941, “The local structure turbulence in incompressible viscous fluids for very large Reynolds numbers”, Dokl. Akad. Nauk. SSSR, 30, 301–305. [ADS]. Reprinted in Proc. R. Soc. London, Ser. A 434 (1991) 9–13 (Cited on pages 7, 19, 27, 28, 30, 60, 104, and 134.)
Kolmogorov, A.N., 1962, “A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number”, J. Fluid Mech., 13, 82–85. [DOI] (Cited on page 134.)
Kolmogorov, A.N., 1991, “The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers”, Proc. R. Soc. London, Ser. A, 434, 9–13. [ADS] (Cited on pages 7, 19, 27, 28, and 134.)
Kowal, G. and Lazarian, A., 2007, “Scaling Relations of Compressible MHD Turbulence”, Astrophys. J. Lett., 666, L69–L72. [DOI], [ADS], [arXiv:0705.2464] (Cited on page 32.)
Kraichnan, R.H., 1965, “Inertial Range Spectrum of Hydromagnetic Turbulence”, Phys. Fluids, 8, 1385–1387 (Cited on pages 7, 28, 38, 60, 122, and 124.)
Kraichnan, R.H., 1974, “On Kolmogorov's Inertial-Range Theories”, J. Fluid Mech., 62, 305–330. [DOI], [ADS] (Cited on pages 60 and 113.)
Krause, F. and Rädler, K.H., 1980, Mean field magnetohydrodynamics and dynamo theory, Akademie-Verlag, Berlin (Cited on page 62.
Landau, L.D. and Lifshitz, E.M., 1971, Physique théorique, Vol. 6: Mécanique des fluides, Editions MIR, Moscow (Cited on pages 7, 23, and 104.)
Leamon, R.J., Smith, C.W., Ness, N.F., Matthaeus, W.H. and Wong, H.K., 1998, “Observational constraints on the dynamics of the interplanetary magnetic field dissipation range”, J. Geophys. Res., 103, 4775.4787.[DOI], [ADS] (Cited on pages 43, 145, 146, 147, 148, 149, and 151.)
Leamon, R.J., Smith, C.W., Ness, N.F. and Wong, H.K., 1999, “Dissipation range dynamics: Kinetic Alfvén waves and the importance of βe”, J. Geophys. Res., 104, 22 331.22 344. [DOI], [ADS] (Cited on page 143.)
Lee, E., Brachet, M.E., Pouquet, A., Mininni, P.D. and Rosenberg, D., 2010, “Lack of universality in decaying magnetohydrodynamic turbulence”, Phys. Rev. E, 81(1), 016318. [DOI], [ADS], [arXiv:0906.2506 [physics.flu-dyn]] (Cited on page 147.)
Leer, E. and Holzer, T.E., 1980, “Energy addition in the solar wind”, J. Geophys. Res., 85, 4681–4688. [DOI], [ADS] (Cited on page 34.)
Levine, R.H., Altschuler, M.D. and Harvey, J.W., 1977, “Solar sources of the interplanetary magnetic field and solar wind”, J. Geophys. Res., 82, 1061–1065. [DOI], [ADS] (Cited on page 34.)
Li, G., 2008, “Identifying Current-Sheet-like Structures in the Solar Wind”, Astrophys. J., 672, L65–L68. [DOI], [ADS] (Cited on pages 136 and 137.)
Li, G., Lee, E. and Parks, G., 2008, “Are there current-sheet-like structures in the Earth's magnetotail as in the solar wind — results and implications from high time resolution magnetic field measurements by Cluster”, Ann. Geophys., 26, 1889–1895. [DOI], [ADS] (Cited on page 136.)
Liewer, P.C., Velli, M. and Goldstein, B.E., 2001, “Alfvén wave propagation and ion cyclotron interactions in the expanding solar wind: One-dimensional hybrid simulations”, J. Geophys. Res., 106(A12), 29,261–29,282. [DOI], [ADS] (Cited on page 22.)
Lighthill, M.J., 1955, “The Effect of Compressibility on Turbulence”, in Gas Dynamics of Cosmic Clouds, A Symposium held at Cambridge, England, July 6–11, 1953, IAU Symposium, 2, pp. 121–130, North-Holland, Amsterdam. [ADS] (Cited on page 31.)
Lorenz, E.N., 1963, “Deterministic Nonperiodic Flow”, J. Atmos. Sci., 20, 130. [DOI] (Cited on pages 7 and 23.)
Mac Low, M.-M. and Klessen, R.S., 2004, “Control of star formation by supersonic turbulence”, Rev. Mod. Phys., 76, 125–194. [DOI], [ADS], [arXiv:astro-ph/0301093] (Cited on page 121.)
MacBride, B.T., Smith, C.W. and Forman, M.A., 2008, “The Turbulent Cascade at 1 AU: Energy Transfer and the Third-Order Scaling for MHD”, Astrophys. J., 679, 1644–1660. [DOI], [ADS] (Cited on pages 119 and 144.)
MacBride, B.T., Smith, C.W. and Vasquez, B.J., 2010, “Inertial-range anisotropies in the solar wind from 0.3 to 1 AU: Helios 1 observations”, J. Geophys. Res., 115(A14), 7105. [DOI], [ADS] (Cited on pages 119, 120, and 144.)
Malara, F. and Velli, M., 1996, “Parametric instability of a large-amplitude nonmonochromatic Alfvén wave”, Phys. Plasmas, 3, 4427–4433. [DOI], [ADS] (Cited on page 92.)
Malara, F., Veltri, P. and Carbone, V., 1992, “Competition among nonlinear effects in tearing instability saturation”, Phys. Fluids B, 4, 3070. [DOI], [ADS] (Cited on page 90.)
Malara, F., Primavera, L. and Veltri, P., 1996, “Compressive fluctuations generated by time evolution of Alfvénic perturbations in the solar wind current sheet”, J. Geophys. Res., 101(A10), 21,597.21,617. [DOI], [ADS] (Cited on page 90.)
Malara, F., Primavera, L. and Veltri, P., 2000, “Nonlinear evolution of parametric instability of a large-amplitude nonmonochromatic Alfvén wave”, Phys. Plasmas, 7, 2866–2877. [DOI], [ADS] (Cited on pages 72, 90, and 92.)
Malara, F., Primavera, L. and Veltri, P., 2001a, “Parametric Instability of a Broad-band Alfvén Wave: Nonlinear Evolution and Saturation”, in Recent insights into the physics of the sun and heliosphere: Highlights from SOHO and other space missions, Proceedings of the 24th General Assembly of the IAU held at Manchester, United Kingdom, 7–11 August 2000, (Eds.) Brekke, P., Fleck, B., Gurman, J.B., IAU Symposia, 203, pp. 511–513, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on pages 72, 75, and 92.)
Malara, F., Primavera, L. and Veltri, P., 2001b, “Nonlinear evolution of the parametric instability: numerical predictions versus observations in the heliosphere”, Nonlinear Proc. Geophys., 8, 159–166. [DOI], [ADS] (Cited on pages 92 and 93.)
Malara, F., Primavera, L. and Veltri, P., 2002, “Parametric instability of Alfvénic fluctuations in high-latitude solar wind”, in Solspa 2001, Proceedings of the Second Solar Cycle and Space Weather Euroconference, 24–29 September 2001, Vico Equense, Italy, (Ed.) Sawaya-Lacoste, H., ESA Conference Proceedings, SP-477, pp. 309–312, ESA Publications Division, Noordwijk. [ADS] (Cited on pages 72 and 75.)
Mariani, F., Ness, N.F., Burlaga, L.F., Bavassano, B. and Villante, U., 1978, “The large-scale structure of the interplanetary magnetic field between 1 and 0.3 AU during the primary mission of HELIOS 1”, J. Geophys. Res., 83(12), 5161–5166. [DOI], [ADS] (Cited on page 76.)
Marino, R., Sorriso-Valvo, L., Carbone, V., Noullez, A., Bruno, R. and Bavassano, B., 2009, “The Energy Cascade in Solar Wind MHD Turbulence”, Earth Moon Planets, 104, 115–119. [DOI], [ADS] (Cited on page 144.)
Marsch, E., 1983, “Radial evolution of ion distribution functions”, in Solar Wind Five, Proceedings of a conference held inWoodstock, Vermont, November 1–5, 1982, (Ed.) Neugebauer, M., NASA Conference Publication, 2280, pp. 355–367, NASA, Washington, DC. [ADS] (Cited on page 143.)
Marsch, E., 1991, “Turbulence in the Solar Wind”, in Reviews in Modern Astronomy, (Ed.) Klare, G., Reviews in Modern Astronomy, 4, pp. 145–156, Springer, Berlin; New York. [ADS] (Cited on page 143.)
Marsch, E., 1992, “Introduction to kinetic physics, waves and turbulence in the solar wind”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 499–504, Pergamon Press, Oxford; New York (Cited on page 104.)
Marsch, E., 2006, “Kinetic Physics of the Solar Corona and Solar Wind”, Living Rev. Solar Phys., 3, lrsp–2006–1. [DOI], [ADS]. URL (accessed 16 June 2011): http://www.livingreviews.org/lrsp-2006-1 (Cited on pages 152 and 154.)
Marsch, E. and Liu, S., 1993, “Structure functions and intermittency of velocity fluctuations in the inner solar wind”, Ann. Geophys., 11, 227–238. [ADS] (Cited on pages 122, 123, 136, 140, and 142.)
Marsch, E. and Mangeney, A., 1987, “Ideal MHD equations in terms of compressive Elsässer variables”, J. Geophys. Res., 92(11), 7363–7367. [DOI], [ADS] (Cited on pages 22 and 64.)
Marsch, E. and Tu, C.-Y., 1989, “Dynamics of correlation functions with Elsässer variables for inhomogeneous MHD turbulence”, J. Plasma Phys., 41, 479–491. [DOI], [ADS] (Cited on pages 22 and 166.)
Marsch, E. and Tu, C.-Y., 1990a, “On the radial evolution of MHD turbulence in the inner heliosphere”, J. Geophys. Res., 95(14), 8211–8229. [DOI], [ADS] (Cited on pages 48, 60, 61, 66, 80, 83, and 89.)
Marsch, E. and Tu, C.-Y., 1990b, “Spectral and spatial evolution of compressible turbulence in the inner solar wind”, J. Geophys. Res., 95(14), 11,945–11,956. [DOI], [ADS] (Cited on pages 47, 94, and 96.)
Marsch, E. and Tu, C.-Y., 1993a, “Modeling results on spatial transport and spectral transfer of solar wind Alfvénic turbulence”, J. Geophys. Res., 98(17), 21 045–21 059. [DOI], [ADS] (Cited on pages 62, 73, 76, 91, 97, and 98.)
Marsch, E. and Tu, C.-Y., 1993b, “Correlations between the fluctuations of pressure, density, temperature and magnetic field in the solar wind”, Ann. Geophys., 11, 659–677. [ADS] (Cited on pages 90 and 98.)
Marsch, E. and Tu, C.-Y., 1994, “Non-Gaussian probability distributions of solar wind fluctuations”, Ann. Geophys., 12(12), 1127–1138. [DOI], [ADS] (Cited on pages 124, 140, and 142.)
Marsch, E. and Tu, C.-Y., 1996, “Spatial evolution of the magnetic field spectral exponent in the solar wind: Helios and Ulysses comparison”, J. Geophys. Res., 101(10), 11,149–11,152. [DOI], [ADS] (Cited on pages 78 and 79.)
Marsch, E. and Tu, C.-Y., 1997, “Intermittency, non-Gaussian statistics and fractal scaling of MHD fluctuations in the solar wind”, Nonlinear Proc. Geophys., 4, 101–124. [DOI], [ADS] (Cited on page 123.)
Marsch, E., Schwenn, R., Rosenbauer, H., Mühlhäuser, K.-H., Pilipp, W. and Neubauer, F.M., 1982, “Solar wind protons: Three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 AU”, J. Geophys. Res., 87, 52–72. [DOI], [ADS] (Cited on page 143.)
Marsch, E., Tu, C.-Y. and Rosenbauer, H., 1996, “Multifractal scaling of the kinetic energy flux in solar wind turbulence”, Ann. Geophys., 14(3), 259–269. [DOI], [ADS] (Cited on page 123.)
Martin, R.N., Belcher, J.W. and Lazarus, A.J., 1973, “Observation and analysis of abrupt changes in the interplanetary plasma velocity and magnetic field”, J. Geophys. Res., 78, 3653. [DOI], [ADS] (Cited on page 83.)
Matthaeus, W.H., 1986, “The Alfvén effect reconsidered”, Sherwood Controlled Fusion Theory Conference, Courant Institute of Mathematical Sciences, New York, conference paper (Cited on page 60.)
Matthaeus, W.H., 2009, “Prospects for universality in MHD turbulence with cross helicity, anisotropy and shear (Invited)”, Eos Trans. AGU, 90(52), NG21A–05. [ADS] (Cited on page 147.)
Matthaeus, W.H. and Brown, M.R., 1988, “Nearly incompressible magnetohydrodynamics at low Mach number”, Phys. Fluids, 31, 3634–3644. [DOI], [ADS] (Cited on pages 31 and 94.)
Matthaeus, W.H. and Goldstein, M.L., 1982a, “Stationarity of magnetohydrodynamic fluctuations in the solar wind”, J. Geophys. Res., 87(16), 10 347–10 354. [DOI], [ADS] (Cited on pages 46 and 162.)
Matthaeus, W.H. and Goldstein, M.L., 1982b, “Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind”, J. Geophys. Res., 87(16), 6011–6028. [DOI], [ADS] (Cited on pages 50, 55, 56, 60, 163, and 165.)
Matthaeus, W.H. and Goldstein, M.L., 1986, “Low-frequency 1/f noise in the interplanetary magnetic field”, Phys. Rev. Lett., 57, 495–498. [DOI], [ADS] (Cited on page 45.)
Matthaeus, W.H., Goldstein, M.L. and Roberts, D.A., 1990, “Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind”, J. Geophys. Res., 95, 20 673–20 683. [DOI], [ADS] (Cited on pages 51, 52, 54, 68, and 152.)
Matthaeus, W.H., Klein, L.W., Ghosh, S. and Brown, M.R., 1991, “Nearly incompressible magnetohydrodynamics, pseudosound, and solar wind fluctuations”, J. Geophys. Res., 96(15), 5421–5435. [DOI], [ADS] (Cited on pages 31, 94, 96, and 100.)
Matthaeus, W.H., Dasso, S., Weygand, J.M., Milano, L.J., Smith, C.W. and Kivelson, M.G., 2005, “Spatial Correlation of Solar-Wind Turbulence from Two-Point Measurements”, Phys. Rev. Lett., 95(23), 231101. [DOI], [ADS] (Cited on pages 42, 44, and 45.)
Matthaeus, W.H., Servidio, S. and Dmitruk, P., 2008, “Comment on ‘Kinetic Simulations of Magnetized Turbulence in Astrophysical Plasmas”', Phys. Rev. Lett., 101(14), 149501. [DOI], [ADS], [arXiv:0812.2493] (Cited on page 151.)
McComas, D.J., Barraclough, B.L., Gosling, J.T., Hammond, C.M., Phillips, J.L., Neugebauer, M., Balogh, A. and Forsyth, R.J., 1995, “Structures in the polar solar wind: Plasma and field observations from Ulysses”, J. Geophys. Res., 100(9), 19 893–19 902. [DOI], [ADS] (Cited on page 102.)
McComas, D.J., Hoogeveen, G.W., Gosling, J.T., Phillips, J.L., Neugebauer, M., Balogh, A. and Forsyth, R.J., 1996, “Ulysses observations of pressure-balance structures in the polar solar wind”, Astron. Astrophys., 316, 368–373. [ADS] (Cited on page 102.)
McComas, D.J., Bame, S.J., Barraclough, B.L. et al., 1998, “Ulysses’ return to the slow solar wind”, Geophys. Res. Lett., 25, 1–4. [DOI], [ADS] (Cited on page 74.)
McComas, D.J., Elliott, H.A., Schwadron, N.A., Gosling, J.T., Skoug, R.M. and Goldstein, B.E., 2003, “The three-dimensional solar wind around solar maximum”, Geophys. Res. Lett., 30(10), 1517. [DOI], [ADS] (Cited on page 74.)
McComb, W.D., 1990, The Physics of Fluid Turbulence, Oxford Engineering Science Series, 25, Oxford University Press, Oxford; New York. [Google Books] (Cited on page 16.)
McCracken, K.G. and Ness, N.F., 1966, “The collimation of cosmic rays by the interplanetary magnetic field”, J. Geophys. Res., 71, 3315–3325 (Cited on page 97.)
Meneguzzi, M., Frisch, U. and Pouquet, A., 1981, “Helical and nonhelical turbulent dynamos”, Phys. Rev. Lett., 47, 1060–1064. [DOI], [ADS] (Cited on page 57.)
Meneveau, C., 1991, “Analysis of turbulence in the orthonormal wavelet rapresentation”, J. Fluid Mech., 232, 469–520. [DOI], [ADS] (Cited on pages 113, 114, and 122.)
Meneveau, C. and Sreenivasan, K.R., 1987, “Simple multifractal cascade model for fully developed turbulence”, Phys. Rev. Lett., 59, 1424–1427. [DOI], [ADS] (Cited on page 123.)
Mininni, P.D. and Pouquet, A., 2009, “Finite dissipation and intermittency in magnetohydrodynamics”, Phys. Rev. E, 80(2), 025401. [DOI], [ADS], [arXiv:0903.3265 [astro-ph.SR]] (Cited on page 31.)
Mininni, P.D., Gómez, D.O. and Mahajan, S.M., 2003a, “Dynamo Action in Magnetohydrodynamics and Hall-Magnetohydrodynamics”, Astrophys. J., 587, 472–481. [DOI], [ADS] (Cited on pages 56, 57, 62, and 64.)
Mininni, P.D., Gómez, D.O. and Mahajan, S.M., 2003b, “Role of the Hall Current in Magnetohydrodynamic Dynamos”, Astrophys. J., 584, 1120–1126. [DOI], [ADS] (Cited on page 62.)
Mjølhus, E., 1976, “On the modulational instability of hydromagnetic waves parallel to the magnetic field”, J. Plasma Phys., 16, 321–334. [DOI], [ADS] (Cited on page 23.)
Moffatt, H.K., 1978, Magnetic Field Generation in Electrically Conducting Fluids, Cambridge Monographs on Mechanics and Applied Mathematics, Cambridge University Press, Cambridge; New York (Cited on pages 55 and 148.)
Monin, A.S. and Yaglom, A.M., 1975, Statistical fluid mechanics — Mechanics of turbulence, Vol. 2, MIT Press, Cambridge (Cited on pages 29, 30, and 76.)
Montgomery, D., 1982, “Major disruptions, inverse cascades, and the Strauss equations”, Phys. Scripta, 2, 83–88. [DOI], [ADS] (Cited on pages 49, 51, 54, and 55.)
Montgomery, D., 1983, “Theory of hydromagnetic turbulence”, in Solar Wind Five, Proceedings of a conference held in Woodstock, Vermont, November 1–5 1982, (Ed.) Neugebauer, M., NASA Conference Publication, 2280, pp. 107–130, NASA, Washington, DC (Cited on page 165.)
Montgomery, D., Brown, M.R. and Matthaeus, W.H., 1987, “Density fluctuation spectra in magnetohydrodynamic turbulence”, J. Geophys. Res., 92(11), 282–284. [DOI], [ADS] (Cited on pages 31 and 94.)
MSFC, “Solar Physics: Coronal Features”, project homepage, NASA/Marshall Space Flight Center. URL (accessed 11 November 2013): http://solarscience.msfc.nasa.gov/ (Cited on page 34.)
Müller, W.-C. and Grappin, R., 2005, “Spectral Energy Dynamics in Magnetohydrodynamic Turbulence”, Phys. Rev. Lett., 95, 114502. [DOI], [ADS], [arXiv:physics/0509019] (Cited on page 60.)
Narita, Y., Glassmeier, K.-H., Sahraoui, F. and Goldstein, M.L., 2010, “Wave-Vector Dependence of Magnetic-Turbulence Spectra in the Solar Wind”, Phys. Rev. Lett., 104(17), 171101. [DOI], [ADS] (Cited on page 152.)
Narita, Y., Gary, S.P., Saito, S., Glassmeier, K.-H. and Motschmann, U., 2011a, “Dispersion relation analysis of solar wind turbulence”, Geophys. Res. Lett., 38, L05101. [DOI], [ADS] (Cited on pages 152 and 153.)
Narita, Y., Glassmeier, K.-H., Goldstein, M.L., Motschmann, U. and Sahraoui, F., 2011b, “Three-dimensional spatial structures of solar wind turbulence from 10 000-km to 100-km scales”, Ann. Geophys., 29, 1731.1738. [DOI], [ADS] (Cited on page 55.)
Neugebauer, M., Clay, D.R., Goldstein, B.E., Tsurutani, B.T. and Zwickl, R.D., 1984, “A reexamination of rotational and tangential discontinuities in the solar wind”, J. Geophys. Res., 89, 5395.5408. [DOI], [ADS] (Cited on page 83.)
Novikov, E.A., 1969, “Scale similarity for random fields”, Sov. Phys. Dokl., 14, 104–107 (Cited on page 113.)
Ohkitani, K. and Yamada, M., 1989, “Temporal intermittency in the energy cascade process and local Lyapunov analysis in fully-developed model turbulence”, Prog. Theor. Phys., 89, 329.341. [DOI], [ADS] (Cited on page 25.)
Okkels, F., 1997, The Intermittent Dynamics in Turbulent Shell Models, Master's thesis, University of Copenhagen, Copenhagen. Online version (accessed 7 September 2005): http://www.nbi.dk/CATS/theses.html (Cited on pages 115 and 116.)
Onorato, M., Camussi, R. and Iuso, G., 2000, “Anomalous scaling and bursting process in an experimental turbulent channel flow”, Phys. Rev. E, 61, 1447–1460. [DOI] (Cited on page 169.)
Ott, E. and Sommerer, J.C., 1994, “Blowout bifurcations: the occurrence of riddled basins and on-off intermittency”, Phys. Lett. A, 188, 39–47. [DOI], [ADS] (Cited on page 25.)
Oughton, S., 1993, Transport of solar wind fluctuations: A turbulence approach, Ph.D. thesis, Delaware University, Wilmington. [ADS] (Cited on page 49.)
Oughton, S. and Matthaeus, W.H., 1992, “Evolution of solar wind fluctuations and the influence of turbulent ‘mixing'”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 523–526, Pergamon Press, Oxford; New York (Cited on page 22.)
Oughton, S., Priest, E.R. and Matthaeus, W.H., 1994, “The influence of a mean magnetic field on three-dimensional MHD turbulence”, J. Fluid Mech., 280, 95.117. [DOI], [ADS] (Cited on page 50.)
Padoan, P., Nordlund, Å, Kritsuk, A.G., Norman, M.L. and Li, P.S., 2007, “Two Regimes of Turbulent Fragmentation and the Stellar Initial Mass Function from Primordial to Present-Day Star Formation”, Astrophys. J., 661, 972–981. [DOI], [ADS], [arXiv:astro-ph/0701795] (Cited on page 32.)
Pagel, C. and Balogh, A., 2002, “Intermittency in the solar wind: A comparison between solar minimum and maximum using Ulysses data”, J. Geophys. Res., 107(A8), 1178. [DOI], [ADS] (Cited on page 142.)
Pagel, C. and Balogh, A., 2003, “Radial dependence of intermittency in the fast polar solar wind magnetic field using Ulysses”, J. Geophys. Res., 108(A1), 1012. [DOI], [ADS] (Cited on pages 141 and 142.)
Paladin, G. and Vulpiani, A., 1987, “Anomalous scaling laws in multifractal objects”, Phys. Rep., 156, 147–225. [DOI], [ADS] (Cited on page 122.)
Parker, E.N., 1964, “Theory of Solar Wind”, in Proceedings of the International Conference on Cosmic Rays, Vol. 1: Solar Particles and Sun-Earth Relations, Jaipur, India, December 2–14 1963, p. 175, Tata Institute of Fundamental Research, Bombay, India (Cited on pages 97 and 143.)
Parker, E.N., 1980, “Book note: Cosmical magnetic fields: Their origin and their activity”, Astron. Quart., 3, 201–201 (Cited on page 48.)
Paschmann, G., Fazakerley, A.N. and Schwartz, S., 1998, “Moments of Plasma Velocity Distributions”, in Analysis Methods for Multi-Spacecraft Data, (Eds.) Paschmann, G., Daly, P.W., ISSI Scientific Report, SR-001, pp. 125–158, ESA Publication Divisions for ISSI, Noordwijk. Online version (accessed 7 September 2005): http://www.issi.unibe.ch/publi_scirep.html (Cited on page 176.)
Perri, S. and Balogh, A., 2010, “Stationarity in Solar Wind Flows”, Astrophys. J., 714, 937–943. [DOI], [ADS] (Cited on page 162.)
Perri, S., Yordanova, E., Carbone, V., Veltri, P., Sorriso-Valvo, L., Bruno, R. and André, M., 2009, “Magnetic turbulence in space plasmas: Scale-dependent effects of anisotropy”, J. Geophys. Res., 114(A13), 2102. [DOI], [ADS] (Cited on page 148.)
Perri, S., Carbone, V., Yordanova, E., Bruno, R. and Balogh, A., 2011, “Scaling law of the reduced magnetic helicity in fast streams”, Planet. Space Sci., 59, 575–579. [DOI], [ADS] (Cited on page 153.)
Petrosyan, A., Balogh, A., Goldstein, M.L. et al., 2010, “Turbulence in the Solar Atmosphere and Solar Wind”, Space Sci. Rev., 156, 135.238. [DOI], [ADS] (Cited on page 7.)
Pfaff, R.F., Borovsky, J.E. and Young, D.T. (Eds.), 1998a, Measurement Techniques in Space Plasmas, Vol. 1: Particles, Geophysical Monograph, 102, American Geophysical Union, Washington, DC (Cited on page 174.)
Pfaff, R.F., Borovsky, J.E. and Young, D.T. (Eds.), 1998b, Measurement Techniques in Space Plasmas, Vol. 2: Fields, Geophysical Monograph, 102, American Geophysical Union, Washington, DC (Cited on pages 174 and 177.)
Pierrehumbert, R.T., 1999, “Huascaran δ18O as an indicator of tropical climate during the Last Glacial Maximum”, Geophys. Res. Lett., 26, 1345.1348. [DOI], [ADS] (Cited on page 142.)
Plunian, F., Stepanov, R. and Frick, P., 2012, “Shell models of magnetohydrodynamic turbulence”, Phys. Rep., 523, 1.60. [DOI], [ADS], [arXiv:1209.3844] (Cited on pages 25 and 115.)
Podesta, J.J., Roberts, D.A. and Goldstein, M.L., 2007, “Spectral Exponents of Kinetic and Magnetic Energy Spectra in Solar Wind Turbulence”, Astrophys. J., 664, 543.548. [DOI], [ADS] (Cited on pages 39 and 40.)
Poduval, B. and Zhao, X.P., 2004, “Discrepancies in the prediction of solar wind using potential field source surface model: An investigation of possible sources”, J. Geophys. Res., 109(A18), A08102. [DOI], [ADS] (Cited on page 34.)
Politano, H. and Pouquet, A., 1995, “Model of intermittency in magnetohydrodynamic turbulence”, Phys. Rev. E, 52, 636–641. [DOI], [ADS] (Cited on page 114.)
Politano, H. and Pouquet, A., 1998, “von Kármán-Howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions”, Phys. Rev. E, 57, R21–R25. [DOI], [ADS] (Cited on pages 29, 30, and 114.)
Politano, H., Pouquet, A. and Carbone, V., 1998, “Determination of anomalous exponents of structure functions in two-dimensional magnetohydrodynamic turbulence”, Europhys. Lett., 43, 516–521. [DOI], [ADS] (Cited on pages 29, 105, 108, and 109.)
Polygiannakis, J.M., Moussas, X., Quenby, J.J. and Smith, E.J., 1994, “Spectral polarization analysis of the interplanetary magnetic field fluctuations”, Solar Phys., 149, 381–389. [DOI], [ADS] (Cited on page 56.)
Pomeau, Y. and Manneville, P., 1980, “Intermittent transition to turbulence in dissipative dynamical systems”, Commun. Math. Phys., 74, 189–197. [DOI], [ADS] (Cited on page 25.)
Pope, S.B., 2000, Turbulent flows, Cambridge University Press, Cambridge; New York. [Google Books] (Cited on pages 16 and 108.)
Pouquet, A., 1993, “Magnetohydrodynamic Turbulence”, in Les Houches Summer School on Astrophysical Fluid Dynamics, Proceedings of the Les Houches Summer School, Course XLVII, 29 June–31 July, 1987, (Eds.) Zahn, J.-P., Zinn-Justin, J., p. 139, Elsevier, Amsterdam (Cited on page 88.)
Pouquet, A., 1996, “Turbulence, Statistics and Structures: an Introduction”, in Plasma Astrophysics, Lectures held at the Astrophysics School VII in San Miniato, Italy, 3–14 October 1994, (Eds.) Chiuderi, C., Einaudi, G., Lecture Notes in Physics, 468, pp. 163–212, Springer, Berlin; New York. [DOI] (Cited on page 88.)
Pouquet, A., Frish, U. and Leorat, J., 1976, “Strong MHD helical turbulence and the nonlinear dynamo effect”, J. Fluid Mech., 77, 321–354. [DOI], [ADS] (Cited on pages 56 and 57.)
Primavera, L., Malara, F. and Veltri, P., 2003, “Parametric instability in the solar wind: numerical study of the nonlinear evolution”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 505–508, American Institute of Physics, Melville, NY (Cited on pages 72, 75, and 135.)
Reisenfeld, D.B., McComas, D.J. and Steinberg, J.T., 1999, “Evidence of a solar origin for pressure balance structures in the high-latitude solar wind”, Geophys. Res. Lett., 26, 1805–1808. [DOI], [ADS] (Cited on page 102.)
Reynolds, O., 1883, “An Experimental Investigation of the Circumstances which determine whether the Motion of Water shall be Direct or Sinuous, and the Law of Resistance in Parallel Channels”, Philos. Trans. R. Soc. London, 174, 935–982. [DOI] (Cited on page 11.)
Richardson, J.D., Paularena, K.I., Lazarus, A.J. and Belcher, J.W., 1995, “Radial evolution of the solar wind from IMP 8 to Voyager 2”, Geophys. Res. Lett., 22, 325–328. [DOI], [ADS] (Cited on page 143.)
Roberts, D.A., 1989, “Interplanetary observational constraints on Alfvén wave acceleration of the solar wind”, J. Geophys. Res., 94(13), 6899–6905. [DOI], [ADS] (Cited on page 80.)
Roberts, D.A., 1992, “Observation and simulation of the radial evolution and stream structure of solar wind turbulence”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 533–538, Pergamon Press, Oxford; New York (Cited on pages 47, 64, and 94.)
Roberts, D.A., 2007, “The Evolution of the Spectrum of Velocity Fluctuations in the Solar Wind”, Eos Trans. AGU, 88(52), SH31B–06. [ADS] (Cited on pages 40 and 41.)
Roberts, D.A. and Goldstein, M.L., 1988, “Simulation of Interplanetary Dynamical Processes”, in Proceedings of the Third International Conference on Supercomputing, (Eds.) Kartashev, L.P., Kartashev, S.I., p. 370, International Supercomputing Institute, St. Petersburg (Cited on page 89.)
Roberts, D.A., Goldstein, M.L., Klein, L.W. and Matthaeus, W.H., 1987a, “The nature and evolution of magnetohydrodynamic fluctuations in the solar wind: Voyager observations”, J. Geophys. Res., 92(11), 11 021–11 040. [ADS] (Cited on pages 59, 62, 75, 89, and 166.)
Roberts, D.A., Goldstein, M.L., Klein, L.W. and Matthaeus, W.H., 1987b, “Origin and evolution of fluctuations in the solar wind: HELIOS observations and Helios.Voyager comparisons”, J. Geophys. Res., 92(11), 12 023–12 035. [DOI], [ADS] (Cited on pages 60, 61, 62, 89, 94, and 166.)
Roberts, D.A., Goldstein, M.L. and Klein, L.W., 1990, “The amplitudes of interplanetary fluctuations — Stream structure, heliocentric distance, and frequency dependence”, J. Geophys. Res., 95(14), 4203–4216. [DOI], [ADS] (Cited on pages 60, 75, and 83.)
Roberts, D.A., Ghosh, S., Goldstein, M.L. and Matthaeus, W.H., 1991, “Magnetohydrodynamic simulation of the radial evolution and stream structure of solar-wind turbulence”, Phys. Rev. Lett., 67, 3741–3744. [DOI], [ADS] (Cited on pages 89, 90, and 94.)
Roberts, D.A., Goldstein, M.L., Matthaeus, W.H. and Ghosh, S., 1992, “Velocity shear generation of solar wind turbulence”, J. Geophys. Res., 97(16), 17,115. [DOI], [ADS] (Cited on pages 64, 76, 89, 90, and 94.)
Ruelle, D. and Takens, F., 1971, “On the nature of turbulence”, Commun. Math. Phys., 20, 167 (Cited on pages 7 and 23.)
Ruíz-Chavarría, G., Baudet, C. and Ciliberto, S., 1995, “Extended Self Similarity of passive scalars in fully developed turbulence”, Europhys. Lett., 32, 319 (Cited on page 107.)
Russell, C.T., 1972, “Comments on the Measurement of Power Spectra of the Interplanetary Magnetic Field”, in Solar Wind, Proceedings of a conference held March 21–26, 1971, at the Asilomar Conference Grounds, Pacific Grove, Calif., (Eds.) Sonett, C.P., Coleman, P.J., Wilcox, J.M., pp. 365–374, NASA, Washington, DC (Cited on pages 38 and 39.)
Ruzmaikin, A., Lyannaya, I.P., Styashkin, V.A. and Eroshenko, E.A., 1993, “The spectrum of the interplanetary magnetic field near 1.3 AU”, J. Geophys. Res., 98(17), 13 303–13 306. [DOI], [ADS] (Cited on page 78.)
Ruzmaikin, A.A., Feynman, J., Goldstein, B.E., Smith, E.J. and Balogh, A., 1995, “Intermittent turbulence in solar wind from the south polar hole”, J. Geophys. Res., 100(9), 3395–3403. [DOI], [ADS] (Cited on pages 76 and 124.)
Sagdeev, R.Z. and Galeev, A.A., 1969, Nonlinear Plasma Theory, Benjamin, New York (Cited on page 92.)
Sahraoui, F., Goldstein, M.L., Robert, P. and Khotyaintsev, Y.V., 2009, “Evidence of a Cascade and Dissipation of Solar-Wind Turbulence at the Electron Gyroscale”, Phys. Rev. Lett., 102(23), 231102. [DOI], [ADS] (Cited on pages 150 and 151.)
Sahraoui, F., Goldstein, M.L., Belmont, G., Canu, P. and Rezeau, L., 2010a, “Three Dimensional Anisotropic k Spectra of Turbulence at Subproton Scales in the Solar Wind”, Phys. Rev. Lett., 105(13), 131101. [DOI], [ADS] (Cited on page 152.)
Sahraoui, F., Goldstein, M.L., Belmont, G., Canu, P. and Rezeau, L., 2010b, “Three Dimensional Anisotropic k Spectra of Turbulence at Subproton Scales in the Solar Wind”, Phys. Rev. Lett., 105(13), 131101. [DOI], [ADS] (Cited on page 152.)
Saito, S., Gary, S.P., Li, H. and Narita, Y., 2008, “Whistler turbulence: Particle-in-cell simulations”, Phys. Plasmas, 15(10), 102305. [DOI], [ADS] (Cited on page 150.)
Salem, C., Mangeney, A., Bale, S.D. and Veltri, P., 2009, “Solar Wind Magnetohydrodynamics Turbulence: Anomalous Scaling and Role of Intermittency”, Astrophys. J., 702, 537–553. [DOI], [ADS] (Cited on pages 39, 108, and 127.)
Salem, C.J., 2000, Ondes, turbulence et phénomènes dissipatifs dans le vent solaire à partir des observations de la sonde WIND, Ph.D. thesis, Université Paris VII, Observatoire de Paris, Paris (Cited on page 39.)
Sandbaek, O., Leer, E. and Hansteen, V.H., 1994, “On the relation between coronal heating, flux tube divergence, and the solar wind proton flux and flow speed”, Astrophys. J., 436, 390–399. [DOI], [ADS] (Cited on page 34.)
Saur, J. and Bieber, J.W., 1999, “Geometry of low-frequency solar wind magnetic turbulence: Evidence for radially aligned Alfénic fluctuations”, J. Geophys. Res., 104, 9975–9988. [DOI], [ADS] (Cited on page 55.)
Saur, J., Politano, H., Pouquet, A. and Matthaeus, W.H., 2002, “Evidence for weak MHD turbulence in the middle magnetosphere of Jupiter”, Astron. Astrophys., 386, 699–708. [DOI], [ADS] (Cited on page 54.)
Saur, J., Pouquet, A. and Matthaeus, W.H., 2003, “Correction to ‘An acceleration mechanism for the generation of the main auroral oval on Jupiter”', Geophys. Res. Lett., 30, 19–22. [ADS] (Cited on page 54.)
Scarf, F.L., Wolfe, J.H. and Silva, R.W., 1967, “A Plasma Instability Associated with Thermal Anisotropies in the Solar Wind”, J. Geophys. Res., 72(11), 993–999. [DOI], [ADS] (Cited on page 38.)
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Quataert, E. and Tatsuno, T., 2009, “Astrophysical Gyrokinetics: Kinetic and Fluid Turbulent Cascades in Magnetized Weakly Collisional Plasmas”, Astrophys. J. Suppl. Ser., 182, 310–377. [DOI], [ADS], [arXiv:0704.0044] (Cited on page 150.)
Schertzer, D., Lovejoy, S., Schmitt, F., Chigirinskaya, Y. and Marsan, D., 1997, “Multifractal Cascade Dynamics and Turbulent Intermittency”, Fractals, 5, 427–471. [DOI] (Cited on page 126.)
Schwenn, R., 1983, “The ‘average’ solar wind in the inner heliosphere: Structures and slow variations”, in Solar Wind Five, Proceedings of a conference held in Woodstock, Vermont, November 1–5, 1982, (Ed.) Neugebauer, M., NASA Conference Publication, 2280, pp. 489–507, NASA, Washington, DC. [ADS] (Cited on page 143.)
Servidio, S., Matthaeus, W.H. and Carbone, V., 2008, “Statistical properties of ideal three-dimensional Hall magnetohydrodynamics: The spectral structure of the equilibrium ensemble”, Phys. Plasmas, 15(4), 042314. [DOI], [ADS] (Cited on page 151.)
She, Z.-S. and Leveque, E., 1994, “Universal scaling laws in fully developed turbulence”, Phys. Rev. Lett., 72, 336–339. [DOI], [ADS] (Cited on page 114.)
Shebalin, J.V., Matthaeus, W.H. and Montgomery, D., 1983, “Anisotropy in MHD turbulence due to a mean magnetic field”, J. Plasma Phys., 29, 525–547. [DOI], [ADS] (Cited on pages 49, 50, 54, and 134.)
Siggia, E.D., 1977, “Origin of intermittency in fully developed turbulence”, Phys. Rev. A, 15, 1730–1750. [DOI], [ADS] (Cited on page 25.)
Siscoe, G.L., Davis, L., Coleman, P.J., Smith, E.J. and Jones, D.E., 1968, “Power Spectra and Discontinuities of the Interplanetary Magnetic Field: Mariner 4”, J. Geophys. Res., 73(12), 61–99. [DOI], [ADS] (Cited on page 97.)
Smith, C.W., 2003, “The Geometry of Turbulent Magnetic Fluctuations at High Heliographic Latitudes”, in Solar Wind Ten, Proceedings of the Tenth International Solar Wind Conference, Pisa, Italy, 17–21 June 2002, (Eds.) Velli, M., Bruno, R., Malara, F., AIP Conference Proceedings, 679, pp. 413–416, American Institute of Physics, Melville, NY (Cited on page 53.)
Smith, C.W., Goldstein, M.L. and Matthaeus, W.H., 1983, “Turbulence Analysis of the Jovian Upstream ‘Wave’ Phenomenon”, J. Geophys. Res., 88(17), 5581–5593. [DOI], [ADS] (Cited on pages 56 and 148.)
Smith, C.W., Goldstein, M.L., Matthaeus, W.H. and Viñas, A.F., 1984, “Erratum: Correction to ‘Turbulence analysis of the Jovian upstream ‘wave’ phenomenon”', J. Geophys. Res., 89(18), 9159–9160. [DOI] (Cited on page 56.)
Smith, C.W., Matthaeus, W.H., Zank, G.P., Ness, N.F., Oughton, S. and Richardson, J.D., 2001a, “Heating of the low-latitude solar wind by dissipation of turbulent magnetic fluctuations”, J. Geophys. Res., 106, 8253–8272. [DOI], [ADS] (Cited on page 144.)
Smith, C.W., Mullan, D.J., Ness, N.F., Skoug, R.M. and Steinberg, J., 2001b, “Day the solar wind almost disappeared: Magnetic field fluctuations, wave refraction and dissipation”, J. Geophys. Res., 106, 18,625–18,634. [DOI], [ADS] (Cited on page 143.)
Smith, C.W., Hamilton, K., Vasquez, B.J. and Leamon, R.J., 2006, “Dependence of the Dissipation Range Spectrum of Interplanetary Magnetic Fluctuationson the Rate of Energy Cascade”, Astrophys. J. Lett., 645, L85–L88. [DOI], [ADS] (Cited on pages 144, 146, and 149.)
Smith, C.W., Stawarz, J.E., Vasquez, B.J., Forman, M.A. and MacBride, B.T., 2009, “Turbulent Cascade at 1 AU in High Cross-Helicity Flows”, Phys. Rev. Lett., 103(20), 201101. [DOI], [ADS] (Cited on pages 119 and 120.)
Smith, E.J., Balogh, A., Neugebauer, M. and McComas, D.J., 1995, “Ulysses observations of Alfvén waves in the southern and northern solar hemispheres”, Geophys. Res. Lett., 22, 3381–3384. [DOI] (Cited on pages 75 and 76.)
Solodyna, C.V. and Belcher, J.W., 1976, “On the minimum variance direction of magnetic field fluctuations in the azimuthal velocity structure of the solar wind”, Geophys. Res. Lett., 3, 565–568. [DOI], [ADS] (Cited on pages 48 and 60.)
Solodyna, C.V., Belcher, J.W. and Sari, J.W., 1977, “Plasma field characteristics of directional discontinuities in the interplanetary medium”, J. Geophys. Res., 82, 10–14. [DOI], [ADS] (Cited on page 83.)
Sonnerup, B.U.O. and Cahill, L.J., 1967, “Magnetopause Structure and Attitude from Explorer 12 Observations”, J. Geophys. Res., 72(11), 171. [DOI] (Cited on pages 48 and 170.)
Sorriso-Valvo, L., Carbone, V., Veltri, P., Consolini, G. and Bruno, R., 1999, “Intermittency in the solar wind turbulence through probability distribution functions of fluctuations”, Geophys. Res. Lett., 26, 1801–1804. [DOI], [ADS] (Cited on pages 124, 125, and 126.)
Sorriso-Valvo, L., Carbone, V., Giuliani, P., Veltri, P., Bruno, R., Antoni, V. and Martines, E., 2001, “Intermittency in plasma turbulence”, Planet. Space Sci., 49, 1193–1200. [DOI], [ADS] (Cited on page 124.)
Sorriso-Valvo, L., Carbone, V., Bruno, R. and Veltri, P., 2006, “Persistence of small-scale anisotropy of magnetic turbulence as observed in the solar wind”, Europhys. Lett., 75, 832–838. [DOI], [ADS], [arXiv:physics/0607128] (Cited on pages 48 and 49.)
Sorriso-Valvo, L., Marino, R., Carbone, V. et al., 2007, “Observation of Inertial Energy Cascade in Interplanetary Space Plasma”, Phys. Rev. Lett., 99(11), 115001. [DOI], [ADS], [arXiv:astro-ph/0702264] (Cited on pages 29, 119, and 120.)
Sorriso-Valvo, L., Carbone, V., Marino, R., Noullez, A., Bruno, R. and Veltri, P., 2010a, “Sorriso-Valvo et al. Reply:”, Phys. Rev. Lett., 104(18), 189002. [DOI], [ADS] (Cited on page 121.)
Sorriso-Valvo, L., Yordanova, E. and Carbone, V., 2010b, “On the scaling properties of anisotropy of interplanetary magnetic turbulent fluctuations”, Europhys. Lett., 90, 59001. [DOI], [ADS] (Cited on pages 48 and 49.)
Stawicki, O., Gary, S.P. and Li, H., 2001, “Solar wind magnetic fluctuation spectra: Dispersion versus damping”, J. Geophys. Res., 106(A5), 8273–8282. [DOI], [ADS] (Cited on page 150.)
Taylor, G.I., 1938, “The Spectrum of Turbulence”, Proc. R. Soc. London, Ser. A, 164, 476–490 (Cited on page 41.)
Tennekes, H. and Lumely, J.L., 1972, A First Course In Turbulence, MCFL-49, MIT Press, Cambridge, MA. [Google Books] (Cited on page 42.)
Tennekes, H. and Wyngaard, J., 1972, “The intermittent small-scale structure of turbulence: Data-processing hazards”, J. Fluid Mech., 55, 93. [DOI], [ADS] (Cited on page 107.)
Thieme, K.M., Schwenn, R. and Marsch, E., 1989, “Are structures in high-speed streams signatures of coronal fine structures?”, Adv. Space Res., 9, 127–130. [DOI], [ADS] (Cited on pages 96, 99, and 128.)
Ting, A.C., Matthaeus, W.H. and Montgomery, D., 1986, “Turbulent relaxation processes in magnetohydrodynamics”, Phys. Fluids, 29, 3261–3274. [DOI], [ADS] (Cited on page 89.)
Tsurutani, B.T. and Smith, E.J., 1979, “Interplanetary discontinuities — Temporal variations and the radial gradient from 1 to 8-5 AU”, J. Geophys. Res., 84(13), 2773–2787. [DOI], [ADS] (Cited on page 128.)
Tu, C.-Y., 1987a, “A Self-Consistent Two-Time Scale Solar Wind Model”, in Solar Wind Six, Proceedings of the Sixth International Solar Wind Conference held 23–28 August, 1987 at YMCA of the Rockies, Estes Park, Colorado, (Eds.) Pizzo, V.J., Holzer, T., Sime, D.G., NCAR Technical Notes, 306, p. 112, Natl. Cent. for Atmos. Res., Boulder, CO (Cited on page 47.)
Tu, C.-Y., 1987b, “A solar wind model with the power spectrum of Alfvénic fluctuations”, Solar Phys., 109, 149–186. [DOI], [ADS] (Cited on page 47.)
Tu, C.-Y., 1988, “The damping of interplanetary Alfvénic fluctuations and the heating of the solar wind”, J. Geophys. Res., 93, 7–20. [DOI], [ADS] (Cited on pages 47 and 123.)
Tu, C.-Y. and Marsch, E., 1990a, “Transfer equations for spectral densities of inhomogeneous MHD turbulence”, J. Plasma Phys., 44, 103–122. [DOI], [ADS] (Cited on pages 22, 62, 66, 133, and 166.)
Tu, C.-Y. and Marsch, E., 1990b, “Evidence for a ‘background’ spectrum of solar wind turbulence in the inner heliosphere”, J. Geophys. Res., 95(14), 4337–4341. [DOI], [ADS] (Cited on pages 65 and 85.)
Tu, C.-Y. and Marsch, E., 1991, “A case study of very low cross-helicity fluctuations in the solar wind”, Ann. Geophys., 9, 319–332. [ADS] (Cited on pages 66, 68, 70, and 86.)
Tu, C.-Y. and Marsch, E., 1993, “A model of solar wind fluctuations with two components:Alfvén waves and convective structures”, J. Geophys. Res., 98(17), 1257–1276. [DOI], [ADS] (Cited on pages 64, 75, 133, and 136.)
Tu, C.-Y. and Marsch, E., 1994, “On the nature of compressive fluctuations in the solar wind”, J. Geophys. Res., 99(18), 21,481–21,509. [ADS] (Cited on pages 31, 96, 98, 99, 100, and 101.)
Tu, C.-Y. and Marsch, E., 1995a, “MHD structures, waves and turbulence in the solar wind: Observations and theories”, Space Sci. Rev., 73(1/2), 1–210. [DOI], [ADS] (Cited on pages 7, 33, 35, 70, 75, 83, 97, 119, 127, 143, and 167.)
Tu, C.-Y. and Marsch, E., 1995b, “Comment on ‘Evolution of energy-containing turbulent eddies in the solar wind' by W.H. Matthaeus, S. Oughton, D.H. Pontius, Jr., and Y. Zhou”, J. Geophys. Res., 100(9), 12,323–12,328. [DOI], [ADS] (Cited on page 47.)
Tu, C.-Y. and Marsch, E., 1996, “Energy spectrum transfer equations of solar wind turbulence”, in Solar Wind Eight, Proceedings of the Eighth International Solar Wind Conference, Dana Point, CA 1995, (Eds.) Winterhalter, D., Gosling, J.T., Habbal, S.R., Kurth, W.S., Neugebauer, M., AIP Conference Proceedings, 382, pp. 233–238, American Institute of Physics, Woodbury, NY (Cited on page 22.)
Tu, C.-Y., Pu, Z.-Y. and Wei, F.-S., 1984, “The power spectrum of interplanetary Alfvénic fluctuations Derivation of the governing equation and its solution”, J. Geophys. Res., 89(18), 9695–9702. [DOI], [ADS] (Cited on pages 47, 91, and 123.)
Tu, C.-Y., Freeman, J.W. and Lopez, R.E., 1989a, “The proton temperature and the total hourly variance of the magnetic field components in different solar wind speed regions”, Solar Phys., 119, 197–206. [DOI], [ADS] (Cited on page 48.)
Tu, C.-Y., Marsch, E. and Thieme, K.M., 1989b, “Basic properties of solar wind MHD turbulence near 0.3 AU analyzed by means of Elsaesser variables”, J. Geophys. Res., 94(13), 11,739–11,759. [DOI], [ADS] (Cited on pages 64, 70, 71, 76, and 90.)
Tu, C.-Y., Roberts, D.A. and Goldstein, M.L., 1989c, “Spectral evolution and cascade constant of solar wind Alfvénic turbulence”, J. Geophys. Res., 94(13), 13 575–13 578. [DOI], [ADS] (Cited on page 166.)
Tu, C.-Y., Marsch, E. and Rosenbauer, H., 1990, “The dependence of MHD turbulence spectra on the inner solar wind stream structure near solar minimum”, Geophys. Res. Lett., 17, 283–286. [DOI], [ADS] (Cited on pages 64 and 65.)
Tu, C.-Y., Marsch, E. and Rosenbauer, H., 1991, “Temperature fluctuation spectra in the inner solar wind”, Ann. Geophys., 9, 748–753. [ADS] (Cited on pages 94 and 96.)
Tu, C.-Y., Marsch, E. and Rosenbauer, H., 1996, “An extended structure-function model and its application to the analysis of solar wind intermittency properties”, Ann. Geophys., 14(3), 270–285. [DOI], [ADS] (Cited on pages 123, 124, and 140.)
Turner, A.J., Gogoberidze, G., Chapman, S.C., Hnat, B. and Müller, W.-C., 2011, “Nonaxisymmetric Anisotropy of Solar Wind Turbulence”, Phys. Rev. Lett., 107, 095002. [DOI], [ADS] (Cited on pages 55 and 152.)
Umeki, H. and Terasawa, T., 1992, “Decay instability of incoherent Alfvén waves in the solar wind”, J. Geophys. Res., 97(16), 3113–3119. [DOI], [ADS] (Cited on page 92.)
Valentini, F. and Veltri, P., 2009, “Electrostatic Short-Scale Termination of Solar-Wind Turbulence”, Phys. Rev. Lett., 102(22), 225001. [DOI], [ADS] (Cited on pages 154 and 155.)
Valentini, F., Veltri, P., Califano, F. and Mangeney, A., 2008, “Cross-Scale Effects in Solar-Wind Turbulence”, Phys. Rev. Lett., 101(2), 025006. [DOI], [ADS] (Cited on pages 152, 154, and 155.)
Van Dyke, M., 1982, An Album of Fluid Motion, The Parabolic Press, Stanford, CA (Cited on page 9.)
Vasquez, B.J., Smith, C.W., Hamilton, K., MacBride, B.T. and Leamon, R.J., 2007, “Evaluation of the turbulent energy cascade rates from the upper inertial range in the solar wind at 1 AU”, J. Geophys. Res., 112(A11), 7101. [DOI], [ADS] (Cited on pages 120 and 144.)
Vellante, M. and Lazarus, A.J., 1987, “An analysis of solar wind fluctuations between 1 and 10 AU”, J. Geophys. Res., 92(17), 9893–9900. [DOI], [ADS] (Cited on page 96.)
Velli, M., Grappin, R. and Mangeney, A., 1989, “Turbulent cascade of incompressible unidirectional Alfvén waves in the interplanetary medium”, Phys. Rev. Lett., 63, 1807–1810. [DOI], [ADS] (Cited on pages 71 and 88.)
Velli, M., Grappin, R. and Mangeney, A., 1990, “Solar wind expansion effects on the evolution of hydromagnetic turbulence in the interplanetary medium”, Comput. Phys. Commun., 59, 153–162. [DOI], [ADS] (Cited on pages 71 and 88.)
Veltri, P., 1980, “An observational picture of solar-wind MHD turbulence”, Nuovo Cimento C, 3, 45–55. [DOI] (Cited on pages 29 and 39.)
Veltri, P. and Mangeney, A., 1999, “Scaling laws and intermittent structures in solar wind MHD turbulence”, in Solar Wind Nine, Proceedings of the Ninth International Solar Wind Conference, Nantucket, MA, 5–9 October 1998, (Eds.) Habbal, S.R., Hollweg, J.V., Isenberg, P.A., AIP Conference Proceedings, 471, pp. 543–546, American Institute of Physics, Woodbury, NY. [DOI] (Cited on pages 127 and 169.)
Veltri, P., Mangeney, A. and Dobrowolny, M., 1982, “Cross-helicity effects in anisotropic MHD turbulence”, Nuovo Cimento B, 68, 235–251. [DOI], [ADS] (Cited on pages 50 and 64.)
Veltri, P., Malara, F. and Primavera, L., 1992, “Correlation, anisotropy and compressibility of low frequency fluctuations in solar wind”, in Solar Wind Seven, Proceedings of the 3rd COSPAR Colloquium held in Goslar, Germany, 16–20 September 1991, (Eds.) Marsch, E., Schwenn, R., COSPAR Colloquia Series, 3, pp. 423–428, Pergamon Press, Oxford; New York (Cited on page 90.)
Verma, M.K., Roberts, D.A. and Goldstein, M.L., 1995, “Turbulent heating and temperature evolution in the solar wind plasma”, J. Geophys. Res., 100, 19 839–19 850. [DOI], [ADS] (Cited on page 144.)
Viñas, A.F. and Goldstein, M.L., 1991, “Parametric instabilities of circularly polarized large-amplitude dispersive Alfvén waves: excitation of obliquely-propagating daughter and side-band waves”, J. Plasma Phys., 46, 129–152. [DOI] (Cited on page 90.)
von Weizsäcker, C.F., 1951, “The Evolution of Galaxies and Stars”, Astrophys. J., 114, 165. [DOI], [ADS] (Cited on page 149.)
Wang, Y.-M., 1993, “Flux-tube divergence, coronal heating, and the solar wind”, Astrophys. J. Lett., 410, L123–L126. [DOI], [ADS] (Cited on page 34.)
Wang, Y.-M., 1994, “Two types of slow solar wind”, Astrophys. J. Lett., 437, L67–L70. [DOI], [ADS] (Cited on page 34.)
Wang, Y.-M. and Sheeley Jr, N.R., 1990, “Solar wind speed and coronal flux-tube expansion”, Astrophys. J., 355, 726–732. [DOI], [ADS] (Cited on page 34.)
Wanner, W. and Wibberenz, G., 1993, “A study of the propagation of solar energetic protons in the inner heliosphere”, J. Geophys. Res., 98(17), 3513–3528. [DOI], [ADS] (Cited on page 53.)
Wareing, C.J. and Hollerbach, R., 2009, “Forward and inverse cascades in decaying two-dimensional electron magnetohydrodynamic turbulence”, Phys. Plasmas, 16(4), 042307. [DOI], [ADS], [arXiv:0904.4825 [physics.plasm-ph]] (Cited on page 150.)
Weygand, J.M., Matthaeus, W.H., Dasso, S., Kivelson, M.G. and Walker, R.J., 2007, “Taylor scale and effective magnetic Reynolds number determination from plasma sheet and solar wind magnetic field fluctuations”, J. Geophys. Res., 112, A10201. [DOI], [ADS] (Cited on page 42.)
Whang, Y.C., Wang, Y.-M., Sheeley Jr, N.R. and Burlaga, L.F., 2005, “Global structure of the out-of-ecliptic solar wind”, J. Geophys. Res., 110(A9), A03103. [DOI], [ADS] (Cited on page 34.)
Withbroe, G.L., 1988, “The temperature structure, mass, and energy flow in the corona and inner solar wind”, Astrophys. J., 325, 442–467. [DOI], [ADS] (Cited on page 34.)
Yordanova, E., Vaivads, A., André, M., Buchert, S.C. and Vörös, Z., 2008, “Magnetosheath Plasma Turbulence and Its Spatiotemporal Evolution as Observed by the Cluster Spacecraft”, Phys. Rev. Lett., 100(20), 205003. [DOI], [ADS] (Cited on page 147.)
Yordanova, E., Balogh, A., Noullez, A. and von Steiger, R., 2009, “Turbulence and intermittency in the heliospheric magnetic field in fast and slow solar wind”, J. Geophys. Res., 114, A08101. [DOI], [ADS] (Cited on page 147.)
Zank, G.P. and Matthaeus, W.H., 1990, “Nearly incompressible hydrodynamics and heat conduction”, Phys. Rev. Lett., 64, 1243–1246. [DOI], [ADS] (Cited on page 94.)
Zank, G.P. and Matthaeus, W.H., 1991, “The equations of nearly incompressible fluids. I. Hydrodynamics, turbulence, and waves”, Phys. Fluids A, 3, 69–82. [DOI], [ADS] (Cited on pages 99 and 100.)
Zank, G.P. and Matthaeus, W.H., 1992, “Waves and turbulence in the solar wind”, J. Geophys. Res., 97(16), 17 189–17 194. [DOI], [ADS] (Cited on pages 49, 53, and 94.)
Zank, G.P. and Matthaeus, W.H., 1993, “Nearly incompressible fluids. II - Magnetohydrodynamics, turbulence, and waves”, Phys. Fluids, 5, 257–273. [ADS] (Cited on pages 31 and 100.)
Zank, G.P., Matthaeus, W.H. and Klein, L.W., 1990, “Temperature and density anti-correlations in solar wind fluctuations”, Geophys. Res. Lett., 17, 1239–1242. [DOI], [ADS] (Cited on page 94.)
Zank, G.P., Matthaeus, W.H. and Smith, C.W., 1996, “Evolution of turbulent magnetic fluctuation power with heliospheric distance”, J. Geophys. Res., 101, 17,093–17,108. [DOI], [ADS] (Cited on page 143.)
Zhou, Y. and Matthaeus, W.H., 1989, “Non-WKB evolution of solar wind fluctuations: A turbulence modeling approach”, Geophys. Res. Lett., 16, 755–758. [DOI], [ADS] (Cited on pages 64 and 143.)
Zhou, Y. and Matthaeus, W.H., 1990, “Transport and turbulence modeling of solar wind fluctuations”, J. Geophys. Res., 95(14), 10,291–10,311. [DOI], [ADS] (Cited on pages 22 and 143.)
Zweben, S.J., Menyuk, C.R. and Taylor, R.J., 1979, “Small-Scale Magnetic Fluctuations Inside the Macrotor Tokamak”, Phys. Rev. Lett., 42, 1720. [ADS] (Cited on page 51.)
Acknowledgments
Writing a large review paper is not an easy task and it would not have been possible to accomplish this goal without having a good interaction with our colleagues, whom we have been working with in our Institutions. To this regard, we like to acknowledge the many discussions (more or less “heated”) we had with and the many advices and comments we had from all of them, particularly from B. Bavassano and P. Veltri. We also like to acknowledge the use of plasma and magnetic field data from Helios spacecraft to freshly produce some of the figures shown in the present review. In particular, we like to thank H. Rosenbauer and R. Schwenn, PIs of the plasma experiment, and F. Mariani and N.F. Ness, PIs of the second magnetic experiment on board Helios. We thank A. Pouquet, H. Politano, and V. Antoni for the possibility we had to compare solar wind data with both high-resolution numerical simulations and laboratory plasmas. Finally, we owe special thanks to E. Marsch and S.K. Solanki for giving us the opportunity to write this review.
Finally, we greatly appreciate the great effort made by an anonymous referee to review such a long paper. We like to thank her/him for her/his meticulous, efficient, and competent analysis of this first updated version of our review which helped us to make a better and more readable document.
Author information
Authors and Affiliations
Corresponding author
A Some Characteristic Solar Wind Parameters
Although solar wind is a highly variable medium, it is possible to identify some characteristic values for its most common parameters. Since the wind is an expanding medium, we ought to choose one heliocentric distance to refer to and, usually, this distance is 1 AU. In the following, we will provide different tables referring to several solar wind parameters, velocities, characteristic times, and lengths.
As it can be seen, the solar wind is a super-Alfvénic, collisionless plasma, and MHD turbulence can be investigated for frequencies smaller than ~ 10−1 Hz.
B Tools to Analyze MHD Turbulence in Space Plasmas
No matter where we are in the solar wind, short scale data always look rather random as shown in Figure 114.
Figure 114:
BY component of the IMF recorded within a high velocity stream.
This aspect introduces the problem of determining the time stationarity of the dataset. The concept of stationarity is related to ensembled averaged properties of a random process. The random process is the collection of the N samples x(t), it is called ensemble and indicated as {x(t)}.
Properties of a random process {x(t)} can be described by averaging over the collection of all the N possible sample functions x(t) generated by the process. So, chosen a begin time t1, we can define the mean value μx and the autocorrelation function Rx, i.e., the first and the joint moment:
In case μx(t1) and Rx(t1, t1 + τ) do not vary as time t1 varies, the sample function x(t) is said to be weakly stationary, i.e.,
Strong stationarity would require all the moments and joint moments to be time independent. However, if x(t) is normally distributed, the concept of weak stationarity naturally extends to strong stationarity.
Generally, it is possible to describe the properties of {x(t)} simply computing time-averages over just one x(t). If the random process is stationary and μx(t) and Rx(τ, k) do not vary when computed over different sample functions, the process is said ergodic. This is a great advantage for data analysts, especially for those who deals with data from s/c, since it means that properties of stationary random phenomena can be properly measured from a single time history. In other words, we can write:
Thus, the concept of stationarity, which is related to ensembled averaged properties, can now be transferred to single time history records whenever properties computed over a short time interval do not vary from one interval to the next more than the variation expected for normal dispersion.
Fortunately, Matthaeus and Goldstein (1982a) established that interplanetary magnetic field often behaves as a stationary and ergodic function of time, if coherent and organized structures are not included in the dataset. Actually, they proved the weak stationarity of the data, i.e., the stationarity of the average and two-point correlation function. In particular, they found that the average and the autocorrelation function computed within a subinterval would converge to the values estimated from the whole interval after a few correlation times tc. More recent analysis (Perri and Balogh, (2010) extended the above studies to different parameter ranges by using Ulysses data, showing that the stationarity assumption in the inertial range of turbulence on timescales of 10 min to 1 day is reasonably satisfied in fast and uniform solar wind flows, but that in mixed, interacting fast, and slow solar wind streams the assumption is frequently only marginally valid. if our time series approximates a Markov process (a process whose relation to the past does not extend beyond the immediately preceding observation), its autocorrelation function can be shown (Doob, (1953) to approximate a simple exponential:
Just to have an idea of the correlation time of magnetic field fluctuations, we show in Figure 115 magnetic field correlation time computed at 1 AU using Voyager 2’s data. In this case, using the above definition, tc ≃ 3.2 × 103 s.
B.1 Statistical description of MHD turbulence
When an MHD fluid is turbulent, it is impossible to know the detailed behavior of velocity field u(x, t) and magnetic field b(x, t), and the only description available is the statistical one. Very useful is the knowledge of the invariants of the ideal equations of motion for which the dissipative terms μ∇2b and v∇2v are equal to zero because the magnetic resistivity μ and the viscosity v are both equal to zero. Following Frisch et al. (1975) there are three quadratic invariants of the ideal system which can be used to describe MHD turbulence: total energy E, cross-helicity Hc, and magnetic helicity Hm. The above quantities are defined as follows:
Figure 115:
Magnetic field auto-correlation function at 1 AU. Image reproduced by permission from Matthaeus and Goldstein (1982b), copyright by AGU.
In particular, in order to describe the degree of correlation between u and b, it is convenient to use the normalized cross-helicity σc:
B.2 Spectra of the invariants in homogeneous turbulence
Statistical information about the state of a turbulent fluid is contained in the n-point correlation function of the fluctuating fields. In homogeneous turbulence these correlations are invariant under arbitrary translation or rotation of the experimental apparatus. We can define the magnetic field auto-correlation matrix
However, in space experiments, especially in the solar wind, data from only a single spacecraft are available. This provides values of R bij , R uij , and R ubij , for separations along a single direction r. In this situation, only reduced (i.e., one-dimensional) spectra can be measured. If r1 is the direction of co-linear separations, we may only determine Rij(r1, 0, 0) and, as a consequence, the Fourier transform on Rij yields the reduced spectral matrix
Then, we define H rm , H rc , and Er = E rb + E ru as the reduced spectra of the invariants, depending only on the wave number k1. Complete information about Sij might be lost when computing its reduced version since we integrate over the two transverse k. However, for isotropic symmetry no information is lost performing the transverse wave number integrals (Batchelor, (1970). That is, the same spectral information is obtained along any given direction.
Coming back to the ideal invariants, now we have to deal with the problem of how to extract information about Hm from Rij(r). We know that the Fourier transform of a real, homogeneous matrix Rij(r) is an Hermitian form Sij, i.e., {ie164}, and that any square matrix A can be decomposed into a symmetric and an antisymmetric part, As and Aa:
It has been shown (Batchelor, (1970; Matthaeus and Goldstein, (1982b; Montgomery, (1983) that, while the trace of the symmetric part of the spectral matrix accounts for the magnetic energy, the imaginary part of the spectral matrix accounts for the magnetic helicity. In particular, Matthaeus and Goldstein (1982b) showed that
Hm can be interpreted as a measure of the correlation between the two transverse components, being one of them shifted by 90° in phase at frequency f. This parameter gives also an estimate of how magnetic field lines are knotted with each other. Hm can assume positive and negative values depending on the sense of rotation of the correlation between the two transverse components.
However, another parameter, which is a combination of Hm and Eb, is usually used in place of Hm alone. This parameter is the normalized magnetic helicity
Since the cross-correlation function is not necessarily an even function, the cross-spectral density function is generally a complex number:
In polar notation
B.3 Introducing the ElsNasser variables
The Alfvénic character of turbulence suggests to use the ElsNasser variables to better describe the inward and outward contributions to turbulence. Following Elsässer (1950); Dobrowolny et al. (1980b); Goldstein et al. (1986); Grappin et al. (1989); Marsch and Tu (1989); Tu and Marsch (1990a); and Tu et al. (1989c), ElsNasser variables are defined as
If we express b in Alfvén units, that is we normalize it by √4πρ we can use the following handy formulas relative to definitions of fields and second order moments. Fields:
We expect an Alfvèn wave to satisfy the following relations:
A spectral analysis of interplanetary data can be performed using z+ and z− fields. Following Tu and Marsch (1995a) the energy spectrum associated with these two variables can be defined in the following way:
Obviously, using Equations (125 and 126), we can redefine in the frequency domain all the parameters introduced in the previous section.
C Wavelets as a Tool to Study Intermittency
Following Farge et al. (1990) and Farge (1992), intermittent events can be viewed as localized zones of fluid where phase correlation exists, in some sense coherent structures. These structures, which dominate the statistics of small scales, occur as isolated events with a typical lifetime which is greater than that of stochastic fluctuations surrounding them. Structures continuously appear and disappear, apparently in a random fashion, at some random location of fluid, and they carry most of the flow energy. In this framework, intermittency can be considered as the result of the occurrence of coherent (non-Gaussian) structures at all scales, within the sea of stochastic Gaussian fluctuations.
It follows that, since these structures are well localized in spatial scale and time, it would be advisable to analyze them using wavelets filter instead of the usual Fourier transform. Unlike the Fourier basis, wavelets allow a decomposition both in time and frequency (or space and scale). The wavelet transform W{f(t)} of a function f(t) consists of the projection of f(t) on a wavelet basis to obtain wavelet coefficients w(τ, t). These coefficients are obtained through a convolution between the analyzed function and a shifted and scaled version of an optional wavelet base
Since the Parceval’s theorem exists, the square modulus |ω(τ, t)|2 represents the energy content of fluctuations f(t + τ) − f(t) at the scale τ at position t.
In analyzing intermittent structures it is useful to introduce a measure of local intermittency, as for example the Local Intermittency Measure (LIM) introduced by Farge (see, e.g., Farge et al., (1990; Farge, (1992)
Figure 116:
Some examples of Mexican Hat wavelet, for different values of the parameters τ and t’.
In our analyses we adopted a recursive method (Bianchini et al., (1999; Bruno et al., (1999a) similar to the one introduced by Onorato et al. (2000) to study experimental turbulent jet flows. The method consists in eliminating, for each scale, those events which cause LIM to exceed a given threshold. Subsequently, the flatness value for each scale is checked and, in case this value exceeds the value of 3 (characteristic of a Gaussian distribution), the threshold is lowered, new events are eliminated and a new flatness is computed. The process is iterated until the flatness is equal to 3, or reaches some constant value, for each scale of the wavelet decomposition. This process is usually accomplished eliminating only a few percent of the wavelet coefficients for each scale, and this percentage reduces moving from small to large scales.
The black curve in Figure 117 shows the original profile of the magnetic field intensity observed by Helios 2 between day 50 and 52 within a highly velocity stream at 0.9 AU. The overlapped red profile refers to the same time series after intermittent events have been removed using the LIM method. Most of the peaks, present in the original time series, are not longer present in the LIMed curve. The intermittent component that has been removed can be observed as the blue curve centered around zero.
Figure 117:
The black curve indicates the original time series, the red one refers to the LIMed data, and the blue one shows the difference between these two curves.
D Reference Systems
Interplanetary magnetic field and plasma data are provided, usually, in two main reference systems: RTN and SE.
The RTN system (see top part of Figure 118) has the R axis along the radial direction, positive from the Sun to the s/c, the T component perpendicular to the plane formed by the rotation axis of the Sun Ω and the radial direction, i.e., T = Ω × R, and the N component resulting from the vector product N = R × T.
The Solar Ecliptic reference system SE, is shown (see bottom part of Figure 118) in the configuration used for Helios magnetic field data, i.e., s/c centered, with the X-axis positive towards the Sun, and the Y-axis lying in the ecliptic plane and oriented opposite to the orbital motion. The third component Z is defined as Z = X × Y. However, solar wind velocity is given in the Sun-centered SE system, which is obtained from the previous one after a rotation of 180. around the Z-axis.
Sometimes, studies are more meaningful if they are performed in particular reference systems which result to be rotated with respect to the usual systems, in which the data are provided in the data centers, for example RTN or SE. Here we will recall just two reference systems commonly used in data analysis.
D.1 Minimum variance reference system
The minimum variance reference system, i.e., a reference system with one of its axes aligned with a direction along whit the field has the smallest fluctuations (Sonnerup and Cahill, (1967). This method provides information on the spatial distribution of the fluctuations of a given vector.
Given a generic field B(x, y, z), the variance of its components is
Figure 118:
The top reference system is the RTN while the one at the bottom is the Solar Ecliptic reference system. This last one is shown in the configuration used for Helios magnetic field data, with the X-axis positive towards the Sun.
Let us assume, for sake of simplicity, that all the three components of B fluctuate around zero, then
Then, the variance VS can be written as
At this point, M is a symmetric matrix and is the matrix of the quadratic form VS which, in turn, is defined positive since it represents a variance. It is possible to determine a new reference system [x, y, z] such that the quadratic form VS does not contain mix terms, i.e.,
Thus, the problem reduces to compute the eigenvalues λi and eigenvectors Ṽi of the matrix M. The eigenvectors represent the axes of the new reference system, the eigenvalues indicate the variance along these axes as shown in Figure 119.
Figure 119:
Original reference system [x, y, z] and minimum variance reference system whose axes are V1, V2, and V3 and represent the eigenvectors of M. Moreover, λ1, λ2, and λ3 are the eigenvalues of M.
At this point, since we know the components of unit vectors of the new reference system referred to the old reference system, we can easily rotate any vector, defined in the old reference system, into the new one.
D.2 The mean field reference system
The mean field reference system (see Figure 120) reduces the problem of cross-talking between the components, due to the fact that the interplanetary magnetic field is not oriented like the axes of the reference system in which we perform the measurement. As a consequence, any component will experience a contribution from the other ones.
Let us suppose to have magnetic field data sampled in the RTN reference system. If the largescale mean magnetic field is oriented in the [x, y, z] direction, we will look for a new reference system within the RTN reference system with the x-axis oriented along the mean field and the other two axes lying on a plane perpendicular to this direction.
Thus, we firstly determine the direction of the unit vector parallel to the mean field, normalizing its components
At this point, we can rotate our data into the new reference system. Data indicated as B(x, y, z) in the old reference system, will become B’(x’, y’, z’) in the new reference system. The transformation is obtained applying the rotation matrix A
Figure 120:
Mean field reference system.
E On-board Plasma and Magnetic Field Instrumentation
In this section, we briefly describe the working principle of two popular instruments commonly used on board spacecraft to measure magnetic field and plasma parameters. For sake of brevity, we will only concentrate on one kind of plasma and field instruments, i.e., the top-hat ion analyzer and the flux-gate magnetometer. Ample review on space instrumentation of this kind can be found, for example, in Pfaff et al. (1998a,b).
E.1 Plasma instrument: The top-hat
The top-hat electrostatic analyzer is a well known type of ion deflector and has been introduced by Carlson et al. (1982). It can be schematically represented by two concentric hemispheres, set to opposite voltages, with the outer one having a circular aperture centered around the symmetry axis (see Figure 121). This entrance allows charged particles to penetrate the analyzer for being detected at the base of the electrostatic plates by the anodes, which are connected to an electronic chain. To amplify the signal, between the base of the plates and the anodes are located the Micro- Channel Plates (not shown in this picture). The MCP is made of a huge amount of tiny tubes, one close to the next one, able to amplify by a factor up to 106 the electric charge of the incoming particle. The electron avalanche that follows hits the underlying anode connected to the electronic chain. The anode is divided in a certain number of angular sectors depending on the desired angular resolution.
Figure 121:
Outline of a top-hat plasma analyzer.
The electric field E(r) generated between the two plates when an electric potential difference δV is applied to them, is simply obtained applying the Gauss theorem and integrating between the internal (R1) and external (R2) radii of the analyzer
In order to have the particle q to complete the whole trajectory between the two plates and hit the detector located at the bottom of the analyzer, its centripetal force must be equal to the electric force acting on the charge. From this simple consideration we easily obtain the following relation between the kinetic energy of the particle Ek and the electric field E(r):
Replacing E(r) with its expression from Equation (129) and differentiating, we get the energy resolution of the analyzer
Such an energy filter would be able to discriminate particles within a narrow energy interval (Ek, Ek + δEk) and coming from a small element dΩ of the solid angle. Given a certain energy resolution, the 3D particle velocity distribution function would be built sampling the whole solid angle 4π, within the energy interval to be studied.
E.2 Measuring the velocity distribution function
In this section, we will show how to reconstruct the average density of the distribution function starting from the particles detected by the analyzer. Let us consider the flux through a unitary surface of particles coming from a given direction. If f(ux, uy, uz) is the particle distribution function in phase space, f(ux, uy, uz) duxduyduz is the number of particles per unit volume (pp/cm3) with velocity between ux and ux + dux, uy and duy, uz and uz + duz, the consequent incident flux Φi through the unit surface is
The transmitted flux Ct will be less than the incident flux Φi because not all the incident particles will be transmitted and Φi will be multiplied by the effective surface S(< 1), i.e.,
Figure 122:
Unit volume in phase space.
E.3 Computing the moments of the velocity distribution function
Once we are able to measure the density particle distribution function fφ,θ,u, we can compute the most used moments of the distribution in order to obtain the particle number density, velocity, pressure, temperature, and heat-flux (Paschmann et al., (1998).
If we simply indicate with f(u) the density particle distribution function, we define as moment of order n of the distribution the quantity Mn, i.e.,
It follows that the first 4 moments of the distribution are the following:
-
the number density
$$n = \int {(v)d^3 \omega },$$((137))the number flux density vector
$$nV = \int {f(v)vd^3 \omega },$$((138)) -
the momentum flux density tensor
$$\Pi = m\int {f(v)vvd^3 \omega },$$((139)) -
the energy flux density vector
$$Q = \frac{m} {2}\int {f(v)v^2 vd^3 \omega }.$$((140))
Once we have computed the zero-order moment, we can obtain the velocity vector from Equation (138). Moreover, we can compute Π and Q in terms of velocity differences with respect to the bulk velocity, and Equations (139) and (140) become
The new Equations (141) and (142) represent the pressure tensor and the heat flux vector, respectively. Moreover, using the relation P = nKT we extract the temperature tensor from Equations (141) and (137). Finally, the scalar pressure P and temperature T can be obtained from the trace of the relative tensors
E.4 Field instrument: The flux-gate magnetometer
There are two classes of instruments to measure the ambient magnetic field: scalar and vector magnetometers. While nuclear precession and optical pumping magnetometers are the most common scalar magnetometers used on board s/c (see Pfaff et al., (1998b, for related material), the flux-gate magnetometer is, with no doubt, the mostly used one to perform vector measurements of the ambient magnetic field. In this section, we will briefly describe only this last instrument just for those who are not familiar at all with this kind of measurements in space.
The working principle of this magnetometer is based on the phenomenon of magnetic hysteresis. The primary element (see Figure 123) is made of two bars of high magnetic permeability material. A magnetizing coil is spooled around the two bars in an opposite sense so that the magnetic field created along the two bars will have opposite polarities but the same intensity. A secondary coil wound around both bars will detect an induced electric potential only in the presence of an external magnetic field.
Figure 123:
Outline of a flux-gate magnetometer. The driving oscillator makes an electric current, at frequency f, circulate along the coil. This coil is such to induce along the two bars a magnetic field with the same intensity but opposite direction so that the resulting magnetic field is zero. The presence of an external magnetic field breaks this symmetry and the resulting field ≠ 0 will induce an electric potential in the secondary coil, proportional to the intensity of the component of the ambient field along the two bars.
The field amplitude BB produced by the magnetizing field H is such that the material periodically saturates during its hysteresis cycle as shown in Figure 124.
In absence of an external magnetic field, the magnetic field B1 and B2 produced in the two bars will be exactly the same but out of phase by 180° since the two coils are spooled in an opposite sense. As a consequence, the resulting total magnetic field would be 0 as shown in Figure 124. In these conditions no electric potential would be induced on the secondary coil because the magnetic flux Φ through the secondary is zero.
Figure 124:
Left panel: This figure refers to any of the two sensitive elements of the magnetometer. The thick black line indicates the magnetic hysteresis curve, the dotted green line indicates the magnetizing field H, and the thin blue line represents the magnetic field B produced by H in each bar. The thin blue line periodically reaches saturation producing a saturated magnetic field B. The trace of B results to be symmetric around the zero line. Right panel: magnetic fields B1 and B2 produced in the two bars, as a function of time. Since B1 and B2 have the same amplitude but out of phase by 180°, they cancel each other.
On the contrary, in case of an ambient field HA ≠ 0, its component parallel to the axis of the bar is such to break the symmetry of the resulting B (see Figure 125). HA represents an offset that would add up to the magnetizing field H, so that the resulting field B would not saturate in a symmetric way with respect to the zero line. Obviously, the other sensitive element would experience a specular effect and the resulting field B = B1 + B2 would not be zero, as shown in Figure 125.
In these conditions the resulting field B, fluctuating at frequency f, would induce an electric potential V = dΦ/dt, where Φ is the magnetic flux of B through the secondary coil.
At this point, the detector would measure this voltage which would result proportional to the component of the ambient field HA along the axis of the two bars. To have a complete measurement of the vector magnetic field B it will be sufficient to mount three elements on board the spacecraft, like the one shown in Figure 123, mutually orthogonal, in order to measure all the three Cartesian components.
Figure 125:
Left panel: the net effect of an ambient field HA is that of introducing an offset which will break the symmetry of B with respect to the zero line. This figure has to be compared with Figure 124 when no ambient field is present. The upper side of the B curve saturates more than the lower side. An opposite situation would be shown by the second element. Right panel: trace of the resulting magnetic field B = B1 + B2. The asymmetry introduced by HA is such that the resulting field B is different from zero.
Figure 126:
Time derivative of the curve B = B1 + B2 shown in Figure 125 assuming the magnetic flux is referred to a unitary surface.
F Spacecraft and Datasets
Measurements performed by spacecrafts represent a unique chance to investigate a wide range of scales of low-frequency turbulence in a magnetized medium. The interested readers are strongly encouraged to visit the web pages of each specific space mission or, more simply, the Heliophysics Data Portal (formerly VSPO) (http://heliophysicsdata.gsfc.nasa.gov) as a wide source of information. This portal represents an easy way to access all the available datasets, related to magnetospheric and heliospheric missions, allowing the user to quickly find data files and interfaces to data from a large number of space missions and ground-based observations.
Two of the s/c which have contributed most to the study of MHD turbulence are the old Helios and Voyager spacecraft, which explored the inner and outer heliosphere, respectively, providing us with an almost complete map of the gross features of low-frequency plasma turbulence. The Helios project was a German-American mission consisting in two interplanetary probes: Helios 1, which was launched in December 1974, and Helios 2, launched one year later. These s/c had a highly elliptic orbit, lying in the ecliptic, which brought the s/c from 1 AU to 0.3 AU in only 6 months. Helios dataset is, with no doubt, the most important and unique one to study MHD turbulence in the inner heliosphere. Most of the knowledge we have today about this topic is based on Helios data mainly because this s/c is the only one that has gone so close to the Sun. As a matter of fact, the orbit of this s/c allowed to observe the radial evolution of turbulence within regions of space (< 0.7 AU) where dynamical processes between fast and slow streams have not yet reprocessed the plasma.
The two Voyagers were launched in 1977. One of them, Voyager 1 will soon reach the termination shock and enter the interstellar medium. As a consequence, for the first time, we will be able to measure interstellar particles and fields not affected by the solar wind. Within the study of MHD turbulence, the importance of the two Voyagers in the outer heliosphere is equivalent to that of the two Helios in the inner regions of the heliosphere. However, all these s/c have been limited to orbit in the, or close to the ecliptic plane.
Finally, in October 1990, Ulysses was launched and, after a fly-by with Jupiter it reached its final orbit tilted at 80.2° with respect to the solar equator. For the first time, we were able to sample the solar wind coming from polar coronal holes, the pure fast wind not “polluted” by the dynamical interaction with slow equatorial wind. As a matter of fact, the Ulysses scientific mission has been dedicated to investigate the heliospheric environment out of the ecliptic plane. This mission is still providing exciting results.
Another spacecraft called WIND was launched in November 1994 and is part of the ISTP Project. WIND, was initially located at the Earth-Sun Lagrangian point L1 to sample continuously the solar wind. Afterwards, it was moved to a much more complicated orbit which allows the spacecraft to repeatedly visit different regions of space around Earth, while continuing to sample the solar wind. The high resolution of magnetic field and plasma measurements of WIND makes this spacecraft very useful to investigate small scales phenomena, where kinetic effects start to play a key role.
The Advanced Composition Explorer (ACE) represents another solar wind monitor located at L1. This spacecraft was launched by NASA in 1997 and its solar wind instruments are characterized by a high rate sampling. Finally, we like to call the attention of the reader on the possibility to easily view and retrieve from the web real time solar wind data from both WIND and ACE.
A few years ago, Voyager 1 and Voyager 2 reached the termination shock, extending our exploration to almost the whole heliosphere. However, the exploration will not be complete until we will reach the base of the solar corona. All the fundamental physical processes concurring during the birth of the solar wind take place in this part of the heliosphere. Moreover, this is a key region also for the study of turbulence, since here non-linear interactions between inward and outward modes start to be active and produce the turbulence spectrum that we observe in the heliosphere.
This region is so important for our understanding of the solar wind that both ESA and NASA are planning space mission dedicated to explore it. In particular, the European Space Agency is planning to launch the Solar Orbiter mission in January 2017 (http://sci.esa.int/ solarorbiter).
Solar Orbiter is proposed as a space mission dedicated to study the solar surface, the corona, and the solar wind by means of remote sensing and in-situ measurements, respectively. Consequently, the s/c will carry a heliospheric package primarily designed to measure ions and electrons of the solar wind, energetic particles, radio waves, and magnetic fields and a remote sensing package for for EUV/X-ray spectroscopy and imaging of the disk and the extended corona. In particular, the high resolution imaging of the Sun will give close-up observations of the solar atmosphere, with the capability of resolving fine structures (of the order of 100 km) in the transition region and corona. This will certainly represent a major step forward in investigating the occurrence of intermittent structures of turbulence at very small scales.
The observations provided by Helios 25 years ago and, more recently, by Ulysses suggest that the local production of Alfvén waves is much stronger in the region just inside 0.3 AU, and Solar Orbiter, repeatedly reaching 0.28 AU, will provide excellent observations to study problems related to local generation and non-linear coupling between outward and inward waves. Moreover, the high data sampling will provide extremely useful and totally new insight about wave dissipation via wave-particle coupling mechanism and the role that the damping of slow, fast, and Alfvén waves can have in the heating of the solar wind ions. Finally, the opportunity given by Solar Orbiter to correlate in-situ plasma measures with the simultaneous imaging of the same flow element of the solar wind during the co-rotation phase, will provide the possibility to separate temporal effects from spatial effects for the first time in the solar wind. This will be of primary importance for finally understand the physical mechanisms at the basis of the solar wind generation.
A similar mission, Solar Probe Plus (http://solarprobe.jhuapl.edu/), is under development by NASA, on a schedule to launch no later than 2018. Solar Probe Plus will orbit the Sun 24 times, gradually approaching the Sun with each pass. On the final three orbits, Solar Probe Plus will fly to within 8.5 solar radii of the Sun’s surface. This mission, although very risky, will allow us to tremendously advance our knowledge about the physical processes that heat and accelerate the solar wind.
Thus, future key missions for investigating turbulence properties in the solar wind plasma are not just behind the corner and, for the time being, we have to use observations from already flown or still flying spacecraft. This does not mean that exciting results are over, while we wait for these new missions. The main difference with the past is that now we are in a different phase of our research. This phase aims to refine many of the concepts we learned in the past, especially those concerning the radial evolution and the local production of turbulence. As a consequence more refined data analysis and computer simulations are now discovering new and very interesting aspects of MHD turbulence which, we hope, we contributed to illustrate in this review.
Electronic supplementary material
41116_2015_9159_MOESM1_ESM.mpg
mpg-Movie (2362.87792969 KB) Still from a movie showing An animation built on SOHO/EIT and SOHO/SUMER observations of the solar-wind source regions and magnetic structure of the chromospheric network. Outflow velocities, at the network cell boundaries and lane junctions below the polar coronal hole, reach up to 10 km s−1 are represented by the blue colored areas (original figures from Hassler et al., (1999).
Electronic supplementary material
41116_2015_9159_MOESM2_ESM.avi
mpg-Movie (1752.1640625 KB) Still from a movie showing A numerical simulation of the incompressible MHD equations in three dimensions, assuming periodic boundary conditions (see details in Mininni et al., (2003a). The left panel shows the power spectra for kinetic energy (green), magnetic energy (red), and total energy (blue) vs. time. The right panel shows the spatially integrated kinetic, magnetic, and total energies vs. time. The vertical (orange) line indicates the current time. These results correspond to a 1283 simulation with an external force applied at wave number kforce = 10 (movie kindly provided by D. Gómez).
Electronic supplementary material
41116_2015_9159_MOESM3_ESM.avi
mpg-Movie (1780.71484375 KB) Still from a movie showing A 1283 numerical simulation, as in Figure 35, but with an external force applied at wave number kforce = 3 (movie kindly provided by D. Gómez).
Electronic supplementary material
Fig127
mpg-Movie (4926.71972656 KB) Still from a movie showing Trajectory followed by the tip of the magnetic field vector in the minimum variance reference system during a time interval not characterized by intermittency. The duration of the interval is 2000 × 6 s but the magnetic field vector moves only for 100 × 6 s in order to make a smaller file (movie kindly provided by A. Vecchio).
Electronic supplementary material
Fig128
mpg-Movie (4926.71972656 KB) Still from a movie showing Trajectory followed by the tip of the magnetic field vector in the minimum variance reference system during a time interval not characterized by intermittency. The duration of the interval is 2000 × 6 s but the magnetic field vector moves only for 100 × 6 s in order to make a smaller file (movie kindly provided by A. Vecchio).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bruno, R., Carbone, V. The Solar Wind as a Turbulence Laboratory. Living Rev. Sol. Phys. 10, 2 (2013). https://doi.org/10.12942/lrsp-2013-2
Published:
DOI: https://doi.org/10.12942/lrsp-2013-2
Keywords
Article history
Latest
The Solar Wind as a Turbulence Laboratory- Published:
- 29 May 2013
DOI: https://doi.org/10.12942/lrsp-2013-2
Original
The Solar Wind as a Turbulence Laboratory- Published:
- 20 September 2005
- Accepted:
- 09 September 2005
DOI: https://doi.org/10.12942/lrsp-2005-4